Effect of Cover Plate on the Ballistic Performance of Ceramic Armor
Abstract
:1. Introduction
2. Numerical Simulations
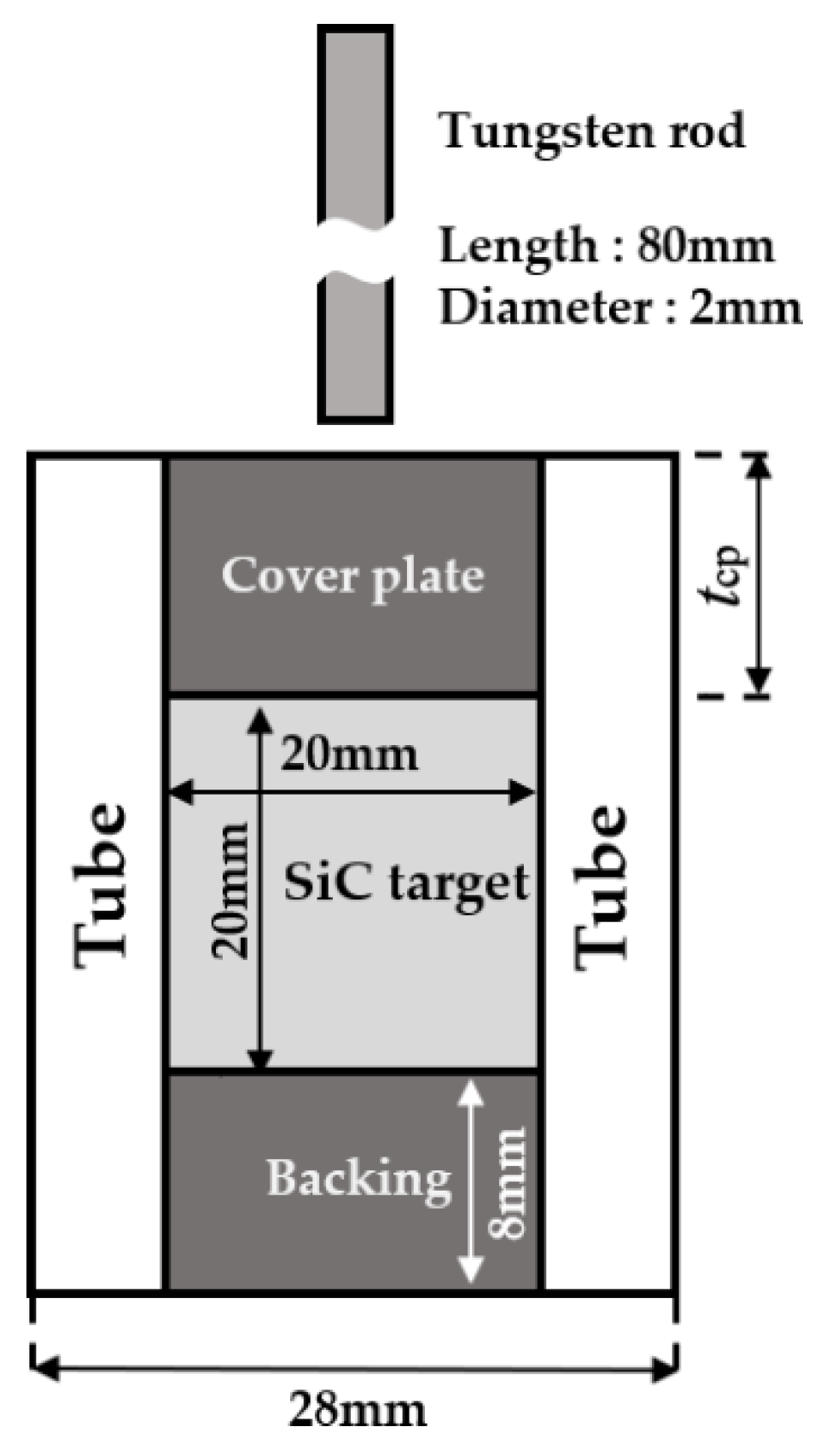
2.1. Numerical Model
2.2. Material Models and Constants
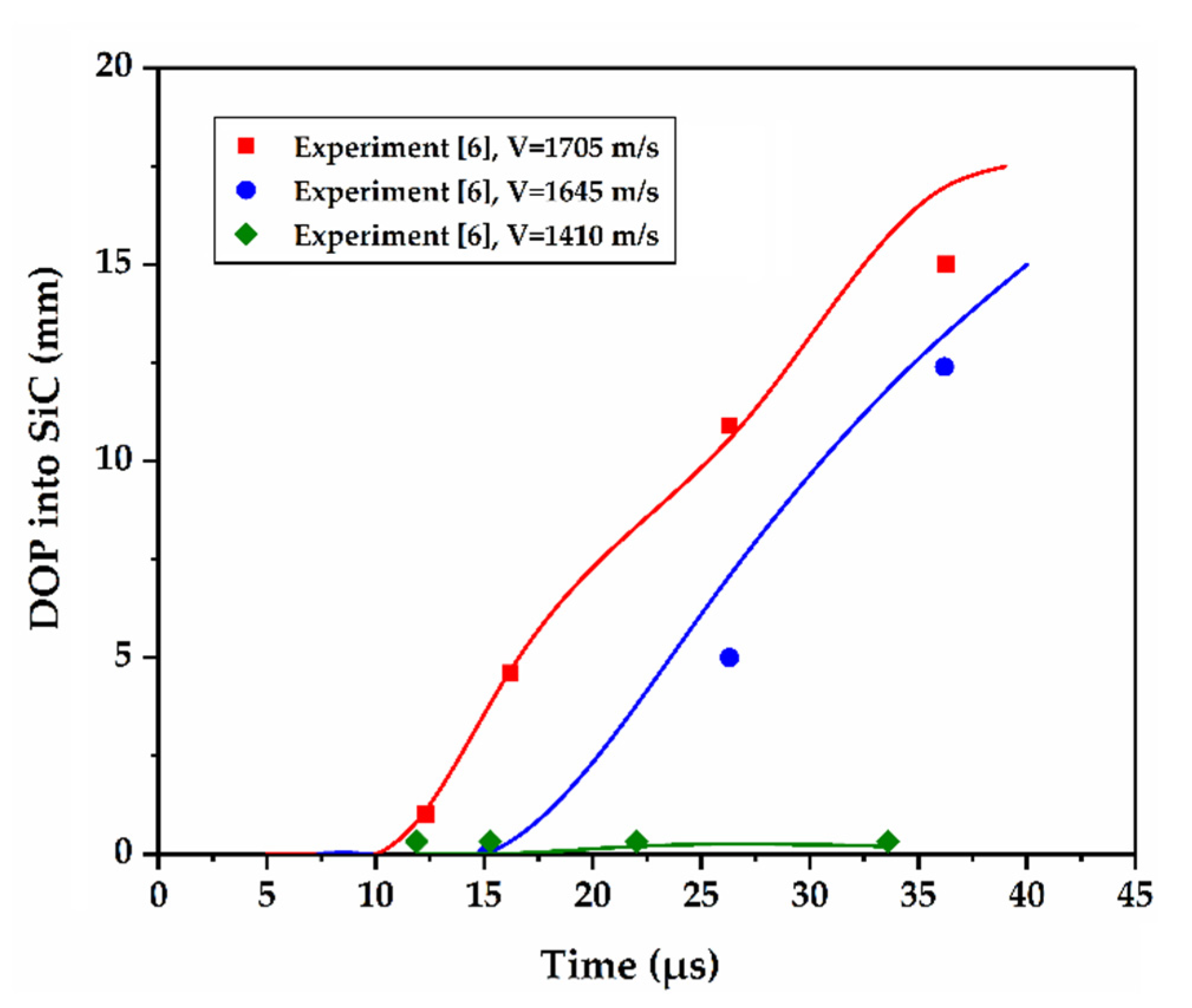
2.3. Validation of the Numerical Model
3. Results and Discussion
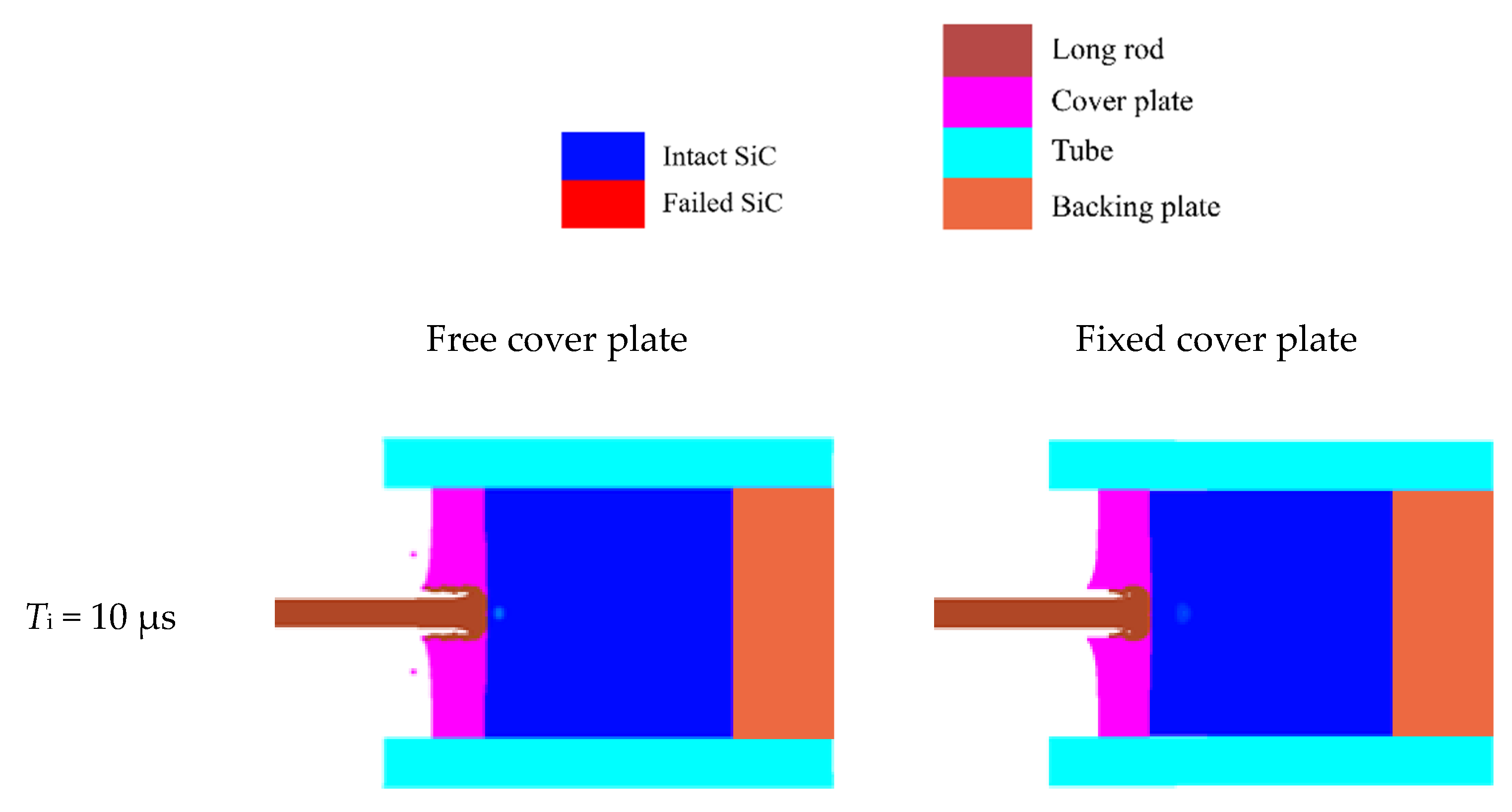
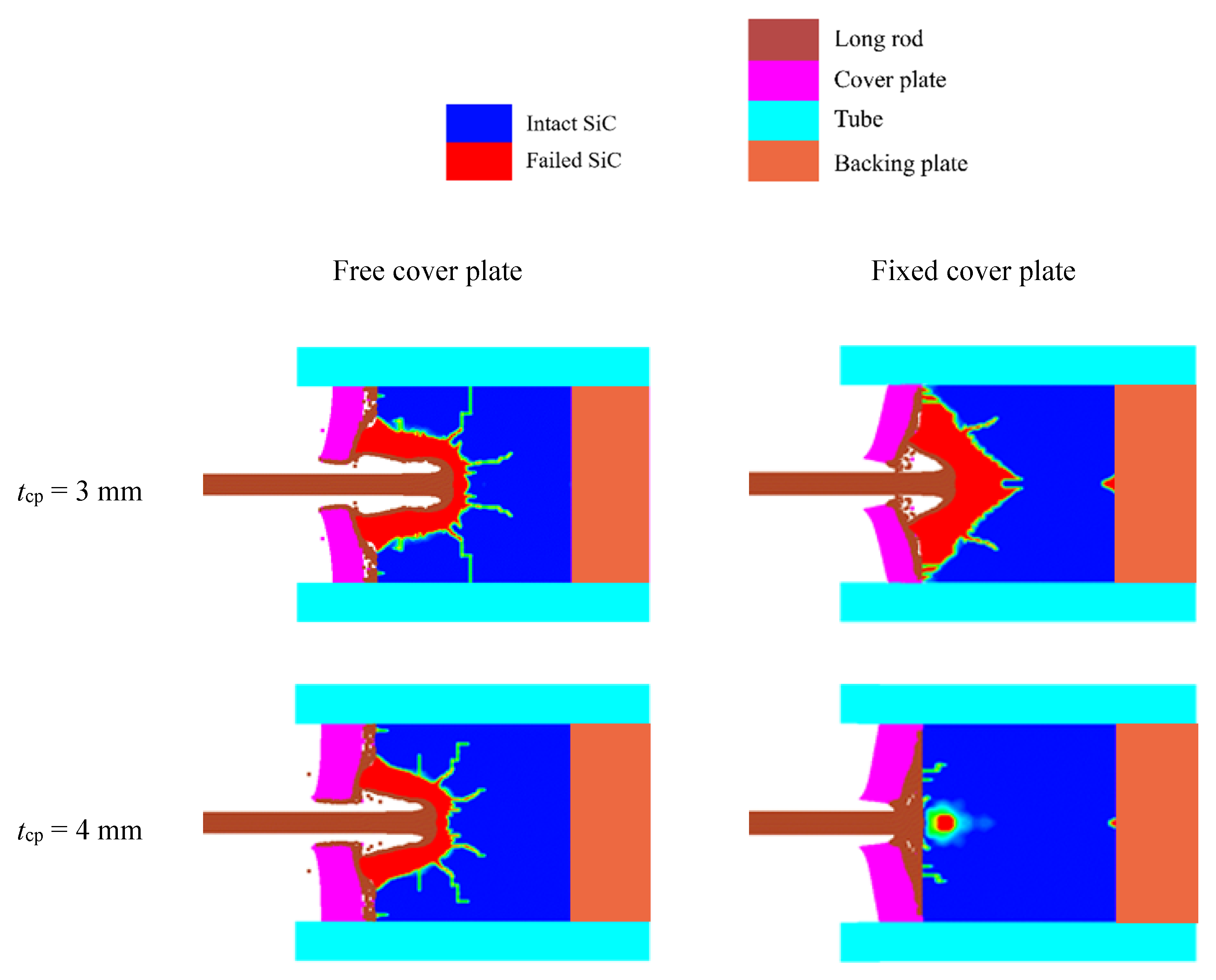
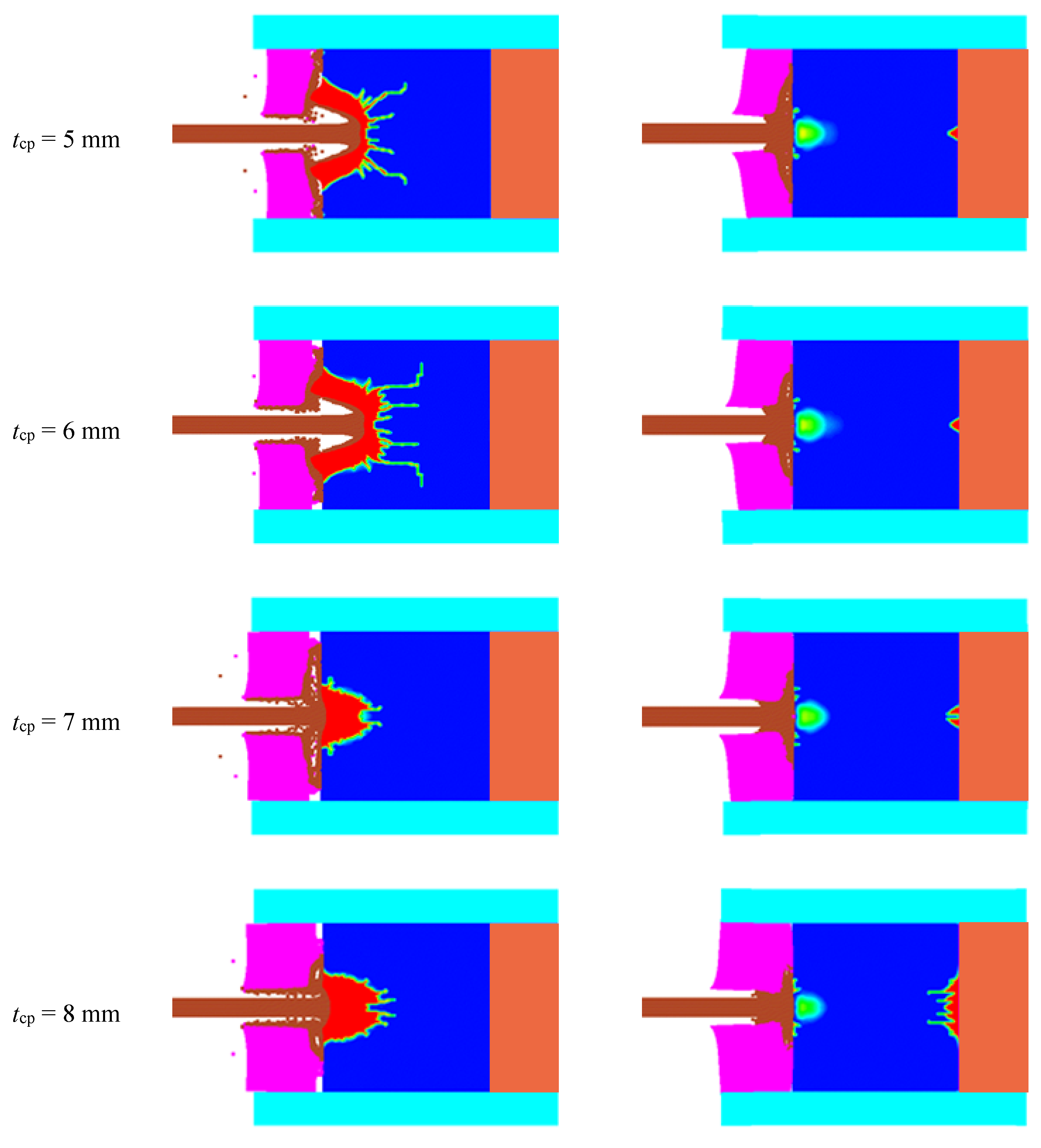
3.1. Damage Mechanism of SiC Target with Different Connection Modes
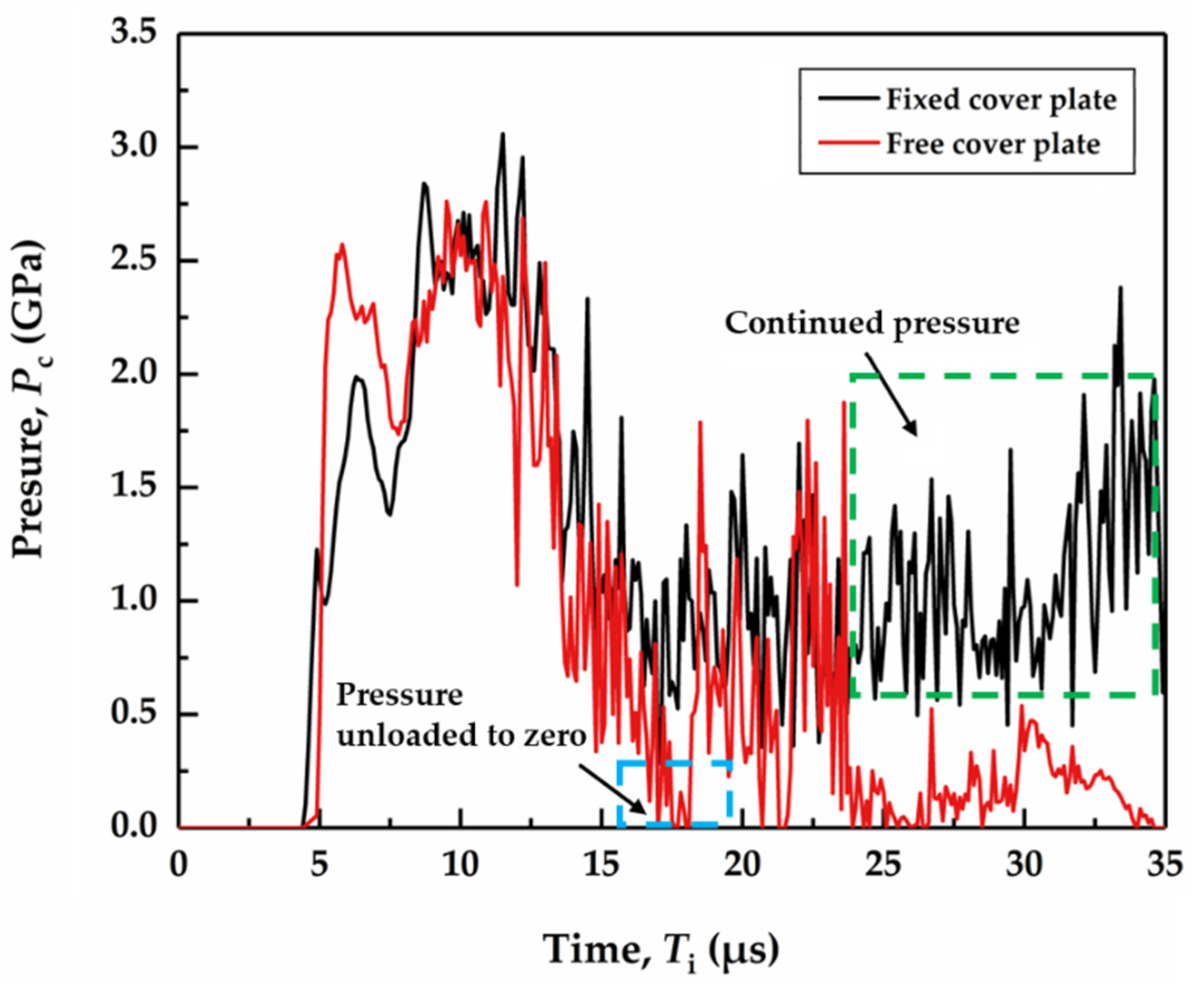
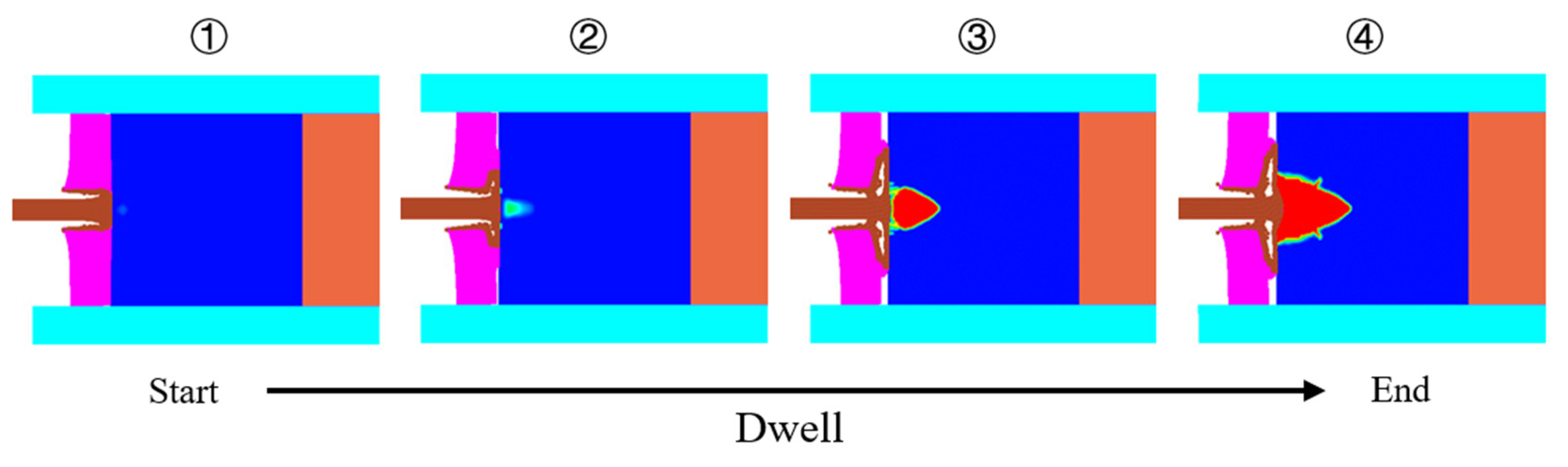
3.2. Dwell Duration
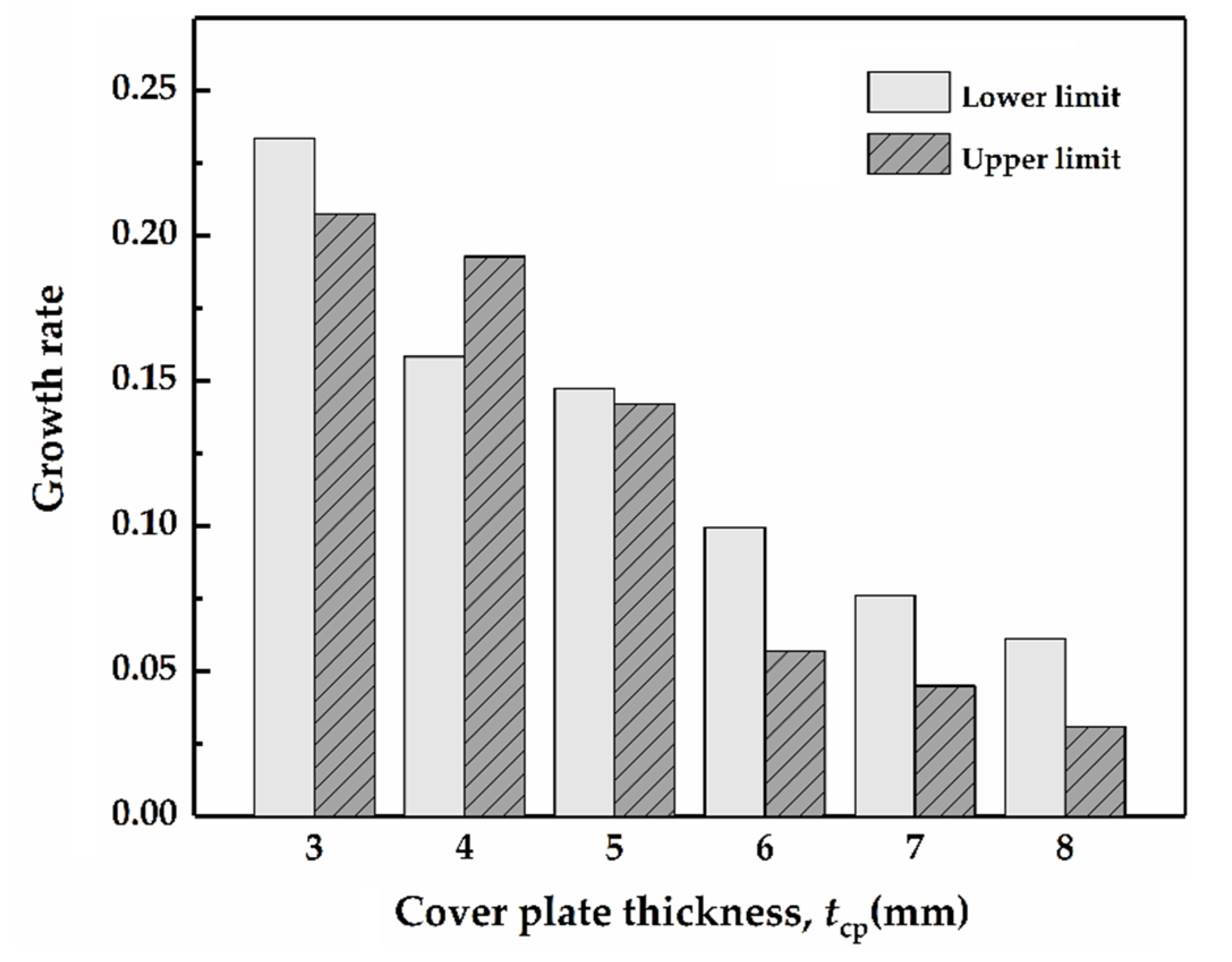
3.3. Transition Impact Velocity
4. Conclusions
- (1)
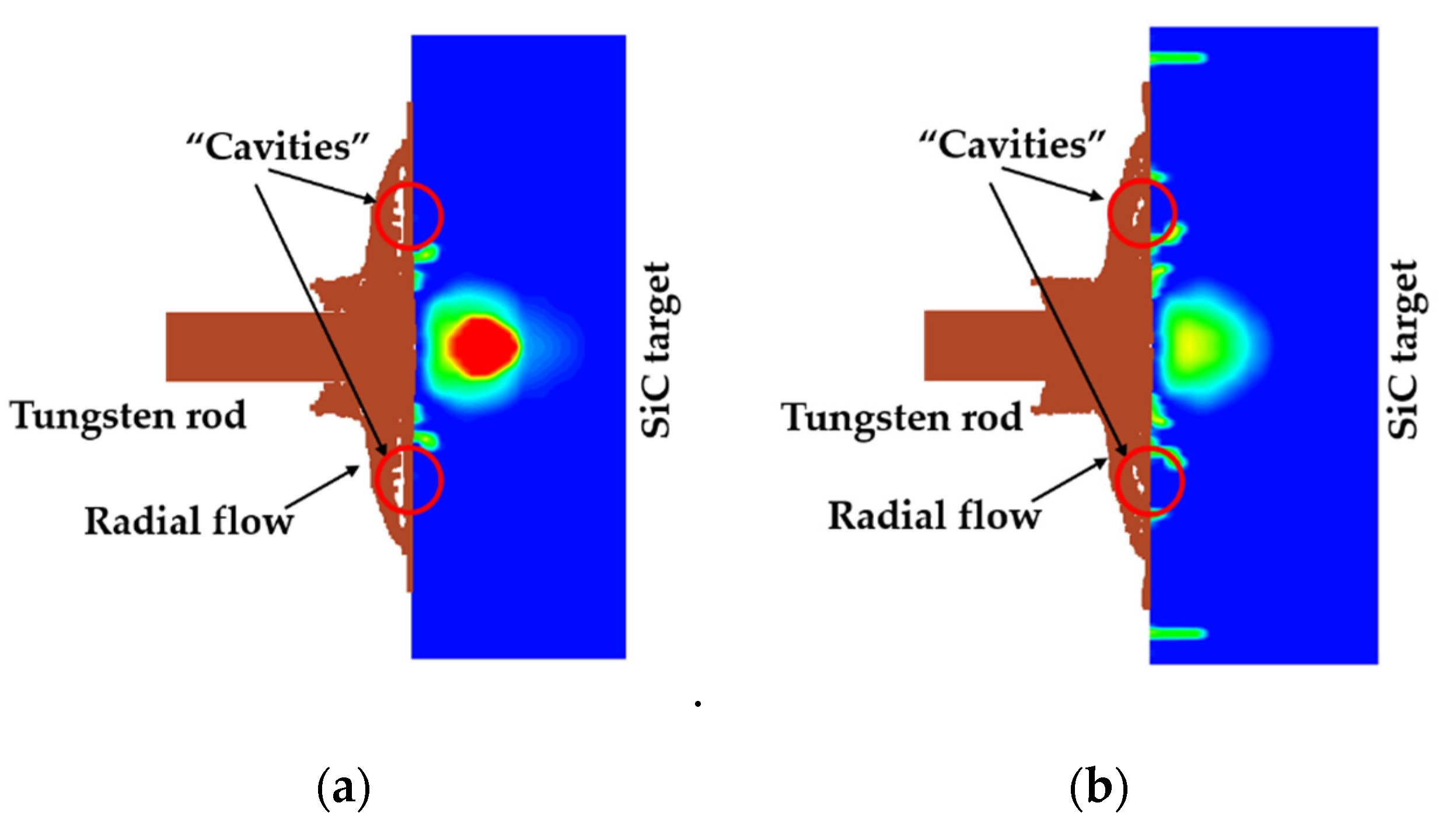
- The fixed cover plates change the damage process of the SiC target compared to the free cover plate. The radial flow generated during dwell introduces a higher pressure in the SiC target through wedging into the gap between the fixed cover plate and the SiC target surface, thereby delaying the SiC damage evolution. The ballistic performance of the SiC target represented by dwell duration and the upper and lower limits of transition impact velocity is better for the fixed-mode than that for the free-mode.
- (2)
- The dwell duration and the upper and lower limits of transition impact velocity increase with increasing cover plate thickness generally. Considering ballistic performance and economy, the cover plate with the thickness ranging from 3 mm to 5 mm, i.e., 1.5~2.5 times the tungsten rod diameter, is ideal for the structural dimensions in this paper.
- (3)
- The effects of cover plate thickness and its connection mode become more insignificant when the impact velocity exceeds a certain value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rosenberg, Z.; Dekel, E. Terminal Ballistics; Springer: Berlin, Germany, 2012. [Google Scholar]
- Zhang, R.; Han, B.; Lu, T.J. Confinement effects on compressive and ballistic performance of ceramics: A review. Int. Mater. Rev. 2020, 65, 1–26. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. Modeling prestressed ceramic and its effect on ballistic performance. Int. J. Impact Eng. 2005, 31, 113–127. [Google Scholar] [CrossRef]
- Holmquist, T.; Johnson, G. Modeling projectile impact onto prestressed ceramic targets. In Proceedings of Journal de Physique IV; EDP Sciences: Les Ulis, France, 2003; Volume 110, pp. 597–602. [Google Scholar]
- Lundberg, P.; Renström, R.; Andersson, O. Influence of confining prestress on the transition from interface defeat to penetration in ceramic targets. Def. Technol. 2016, 12, 263–271. [Google Scholar] [CrossRef] [Green Version]
- Lundberg, P.; Renström, R.; Lundberg, B. Impact of metallic projectiles on ceramic targets: Transition between interface defeat and penetration. Int. J. Impact Eng. 2000, 24, 259–275. [Google Scholar] [CrossRef]
- Lynch, N.; Bless, S.; Cullis, I.; Berry, D. The influence of confinement on the penetration of ceramic targets by KE projectiles at 1.8 and 2.6 km/s. Int. J. Impact Eng. 2006, 33, 390–401. [Google Scholar] [CrossRef]
- Savio, S.; Ramanjaneyulu, K.; Madhu, V.; Bhat, T.B. An experimental study on ballistic performance of boron carbide tiles. Int. J. Impact Eng. 2011, 38, 535–541. [Google Scholar] [CrossRef]
- Doyoyo, M. Experiments on the penetration of thin long-rod projectiles into thick long-cylindrical borosilicate targets under pressure-free polycarbonate, aluminum and steel confinements. Int. J. Solids Struct. 2003, 40, 5455–5475. [Google Scholar] [CrossRef]
- Hauver, G.; Netherwood, P.; Benck, R.; Gooch, W.; Perciballi, W.; Burkins, M. Variation of target resistance during long rod penetration into ceramics. In Proceedings of the 13th International Symposium on Ballistics, Stockholm, Sweden, 1–3 June 1992; pp. 1–3. [Google Scholar]
- Ning, J.; Ren, H.; Guo, T.; Li, P. Dynamic response of alumina ceramics impacted by long tungsten projectile. Int. J. Impact Eng. 2013, 62, 60–74. [Google Scholar] [CrossRef]
- Tan, M.; Zhang, X.; Goh, W.L.; Luo, B.; Bao, K. Study on transition from dwell/interface defeat to penetration of long-rod projectile impacting silicon carbide. Int. J. Fract. 2019, 219, 65–87. [Google Scholar] [CrossRef]
- Sarva, S.; Nemat-Nasser, S.; McGee, J.; Isaacs, J. The effect of thin membrane restraint on the ballistic performance of armor grade ceramic tiles. Int. J. Impact Eng. 2007, 34, 277–302. [Google Scholar] [CrossRef]
- Lundberg, P. Interface Defeat and Penetration: Two Modes of Interaction between Metallic Projectiles and Ceramic Targets. Ph.D. Thesis, Acta Universitatis Upsaliensis, Uppsala, Sweden, 2004. [Google Scholar]
- Uth, T.; Deshpande, V.S. Unsteady penetration of a target by a liquid jet. Proc. Natl. Acad. Sci. USA 2013, 110, 20028–20033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renström, R.; Lundberg, P.; Lundberg, B. Stationary contact between a cylindrical metallic projectile and a flat target surface under conditions of dwell. Int. J. Impact Eng. 2004, 30, 1265–1282. [Google Scholar] [CrossRef]
- Zhai, Y.; Wu, H.; Fang, Q. Interface defeat studies of long-rod projectile impacting on ceramic targets. Def. Technol. 2020, 16, 50–68. [Google Scholar] [CrossRef]
- Holmquist, T.; Anderson, C.; Behner, T.; Orphal, D. Mechanics of dwell and post-dwell penetration. Adv. Appl. Ceram. 2010, 109, 467–479. [Google Scholar] [CrossRef]
- Espinosa, H.; Brar, N.; Yuan, G.; Xu, Y.; Arrieta, V. Enhanced ballistic performance of confined multi-layered ceramic targets against long rod penetrators through interface defeat. Int. J. Solids Struct. 2000, 37, 4893–4913. [Google Scholar] [CrossRef]
- Tabiei, A.; Nilakantan, G. Ballistic impact of dry woven fabric composites: A review. Appl. Mech. Rev. 2008, 61. [Google Scholar] [CrossRef]
- Rahbek, D.B.; Simons, J.W.; Johnsen, B.B.; Kobayashi, T.; Shockey, D.A. Effect of composite covering on ballistic fracture damage development in ceramic plates. Int. J. Impact Eng. 2017, 99, 58–68. [Google Scholar] [CrossRef] [Green Version]
- Rahbek, D.B.; Johnsen, B.B. Fragmentation of an armour piercing projectile after impact on composite covered alumina tiles. Int. J. Impact Eng. 2019, 133, 103332. [Google Scholar] [CrossRef]
- Crouch, I.G.; Appleby-Thomas, G.; Hazell, P.J. A study of the penetration behaviour of mild-steel-cored ammunition against boron carbide ceramic armours. Int. J. Impact Eng. 2015, 80, 203–211. [Google Scholar] [CrossRef] [Green Version]
- Luo, D.; Wang, Y.; Wang, F.; Cheng, H.; Zhang, B.; Zhu, Y. The influence of metal cover plates on ballistic performance of silicon carbide subjected to large-scale tungsten projectile. Mater. Des. 2020, 191, 108659. [Google Scholar] [CrossRef]
- Quan, X.; Clegg, R.; Cowler, M.; Birnbaum, N.; Hayhurst, C. Numerical simulation of long rods impacting silicon carbide targets using JH-1 model. Int. J. Impact Eng. 2006, 33, 634–644. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R. Response of silicon carbide to high velocity impact. J. Appl. Phys. 2002, 91, 5858–5866. [Google Scholar] [CrossRef]
- Luo, D.; Wang, Y.; Wang, F.; Cheng, H.; Zhu, Y. Ballistic behavior of oblique ceramic composite structure against long-rod tungsten projectiles. Materials 2019, 12, 2946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chi, R.; Serjouei, A.; Sridhar, I.; Geoffrey, T.E. Pre-stress effect on confined ceramic armor ballistic performance. Int. J. Impact Eng. 2015, 84, 159–170. [Google Scholar] [CrossRef]
- Lee, J.K. Analysis of Multi-Layered Materials under High Velocity Impact Using CTH. Ph.D. Thesis, Department of Aeronautics and Astronautics Engineering, Air University, Lima, OH, USA, 2008. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Holmquist, T.; Johnson, G. A detailed computational analysis of interface defeat, dwell and penetration for a variety of ceramic targets. In Proceedings of the 20th International Symposium on Ballistics, Orlando, FL, USA, 23–27 September 2002; pp. 746–753. [Google Scholar]
- Behner, T.; Heine, A.; Wickert, M. Dwell and penetration of tungsten heavy alloy long-rod penetrators impacting unconfined finite-thickness silicon carbide ceramic targets. Int. J. Impact Eng. 2016, 95, 54–60. [Google Scholar] [CrossRef]






| Parameters | SiC |
|---|---|
| Density, ρ0 (kg/m3) | 3215 |
| Bulk modulus, K1 (GPa) | 220 |
| Pressure constant, K2 (GPa) | 361 |
| Pressure constant, K3 (GPa) | 0 |
| Bulking factor, β | 1.0 |
| Shear modulus, G (GPa) | 193 |
| Hugoniot elastic limit, HEL (GPa) | 11.7 |
| Intact Strength Constant, S1 (GPa) | 7.1 |
| Intact Strength Constant, P1 (GPa) | 2.5 |
| Intact Strength Constant, S2 (GPa) | 12.2 |
| Intact Strength Constant, P2 (GPa) | 10.0 |
| Strain rate constant, C | 0.009 |
| Maximum fracture strength, (GPa) | 1.3 |
| Failed strength constant, α | 0.4 |
| Hydrostatic tensile limit, T* (GPa) | −0.75 |
| Principal tensile failure stress, Tf (GPa) | 1.3 |
| Damage constant, | 0.5 |
| Damage Constant, P3 (GPa) | 99.75 |
| Fracture energy, Gf (J/m2) | 37.3 |
| Parameters | Tungsten Alloy | Steel 4340 |
|---|---|---|
| Shear modulus, G (GPa) | 160 | 77 |
| Static yield stress, A’ (GPa) | 1.506 | 0.75 |
| Strain hardening constant, B’(GPa) | 0.177 | 0.51 |
| Strain hardening exponent, n | 0.12 | 0.26 |
| Strain rate constant, C’ | 0.016 | 0.014 |
| Reference strain rate, | 1 | 1 |
| Thermal softening exponent, m | 1 | 1.03 |
| Melting temperature, tm (K) | 1723 | 1793 |
| Parameters | Tungsten Alloy | Steel 4340 |
|---|---|---|
| Damage Constant, D1 | 0 | 0.05 |
| Damage Constant, D2 | 0.33 | 3.44 |
| Damage Constant, D3 | −1.5 | −2.12 |
| Damage Constant, D4 | 0 | 0.003 |
| Damage Constant, D5 | 0 | 0.61 |
| Parameters. | Tungsten Alloy | Steel 4340 | Steel Mar 350 |
|---|---|---|---|
| EOS | Shock | Linear | Linear |
| Density, ρ0 (kg/m3) | 17,600 | 7830 | 8080 |
| Bulk Modulus, K1 (GPa) | 285 | 159 | 140 |
| Gruneisen constant | 1.54 | − | − |
| Parameter C1 (m/s) | 4029 | − | − |
| Parameter S | 1.237 | − | − |
| Reference temperature, t0 (K) | 300 | 300 | 293 |
| Specific heat, Ct (H/kg K) | 134 | 477 | − |
| Velocity (m/s) | Tdu (μs) | |||||
|---|---|---|---|---|---|---|
| tcp = 3 mm | tcp = 4 mm | tcp = 5 mm | tcp = 6 mm | tcp = 7 mm | tcp = 8 mm | |
| 1200 | − | − | − | − | − | − |
| 1400 | 18 | 19 | 20 | 19 | 25 | 34 |
| 1600 | 2 | 8 | 8 | 9 | 11 | 11 |
| Velocity (m/s) | Tdu (μs) | |||||
|---|---|---|---|---|---|---|
| tcp = 3 mm | tcp = 4 mm | tcp = 5 mm | tcp = 6 mm | tcp = 7 mm | tcp = 8 mm | |
| 1200 | 14 | 15 | 21 | − | − | − |
| 1400 | 8 | 9 | 11 | 10 | 18 | 18 |
| 1600 | × | × | 4 | 5 | 5 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Cao, W.; Hu, D.; Zhang, N.; Chi, R. Effect of Cover Plate on the Ballistic Performance of Ceramic Armor. Materials 2021, 14, 1. https://doi.org/10.3390/ma14010001
Sun M, Cao W, Hu D, Zhang N, Chi R. Effect of Cover Plate on the Ballistic Performance of Ceramic Armor. Materials. 2021; 14(1):1. https://doi.org/10.3390/ma14010001
Chicago/Turabian StyleSun, Miao, Wuxiong Cao, Diqi Hu, Nana Zhang, and Runqiang Chi. 2021. "Effect of Cover Plate on the Ballistic Performance of Ceramic Armor" Materials 14, no. 1: 1. https://doi.org/10.3390/ma14010001
APA StyleSun, M., Cao, W., Hu, D., Zhang, N., & Chi, R. (2021). Effect of Cover Plate on the Ballistic Performance of Ceramic Armor. Materials, 14(1), 1. https://doi.org/10.3390/ma14010001





