Determination of Phase Transition and Critical Behavior of the As-Cast GdGeSi-(X) Type Alloys (Where X = Ni, Nd and Pr)
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pecharsky, V.K.; Gscheidner, K.A., Jr. Tunable magnetic regenerator alloys with a giant magnetocaloric effect for magnetic refrigeration from ~20 to 290 K. Appl. Phys. Lett. 1997, 70, 3299–3301. [Google Scholar] [CrossRef]
- Liu, X.B.; Altounian, Z. Effect of Co content on magnetic entropy change and structure of La(Fe1−xCox)11.4Si1.6. J. Magn. Magn. Mater. 2003, 264, 209–213. [Google Scholar] [CrossRef]
- Gębara, P.; Pawlik, P. Broadening of temperature working range in magnetocaloric La(Fe,Co,Si)13- based multicomposite. J. Magn. Magn. Mater. 2017, 442, 145–151. [Google Scholar] [CrossRef]
- Moran, O.; Gomez, A.; Supelano, I.; Parra, C.A.; Izquierdo, J.L. Assessment of the critical behavior near the FM to PM phase transition in nano-crystalline La0.7Ca0.3Mn1−xNixO3 (x=0, 0.02, 0.07, 0.1) samples synthesized by auto-combustion. J. Magn. Magn. Mater. 2019, 477, 22–26. [Google Scholar] [CrossRef]
- Samantaray, B.; Ravi, S.; Perumal, A. Critical behavior studies in ferromagnetic (Nd, K)–Mn–O compounds. J. Magn. Magn. Mater. 2010, 322, 3391–3395. [Google Scholar] [CrossRef]
- Leitao, V.B.; van der Haar, M.; Lefering, A.; Brück, E. Magnetic and Magnetocaloric Exploration of Fe rich (Mn,Fe)2(P,Ge). J. Magn. Magn. Mater. 2013, 344, 49–54. [Google Scholar] [CrossRef] [Green Version]
- Gębara, P.; Śniadecki, Z. Structure, magnetocaloric properties and thermodynamic modeling of enthalpies of formation of (Mn,X)-Co-Ge (X = Zr, Pd) alloys. J. All. Compd. 2019, 796, 153–159. [Google Scholar]
- Gębara, P.; Kutynia, K. Magnetocaloric Effect in Annealed (Mn,W)-Co-Ge Alloy. Acta Phys. Pol. A 2019, 135, 298–300. [Google Scholar]
- Law, J.Y.; Franco, V.; Moreno-Ramirez, L.M.; Conde, A.; Karpenkov, D.Y.; Radulov, I.; Skokov, K.P.; Gutfleisch, O. A quantitative criterion for determining the order of magnetic phase transitions using the magnetocaloric effect. Nat. Commun. 2018, 9, 2680. [Google Scholar] [CrossRef]
- Hasiak, M. Microstructure and magnetocaloric effect in as-quenched GdGeSi alloys with addition of Ni and Ce. Phys. Stat. Sol. A. 2016, 213, 1130–1137. [Google Scholar] [CrossRef]
- Gębara, P.; Hasiak, M. Investigation of Critical Behavior in Gd75Ge15Si5Ce5 Alloy. Acta Phys. Pol. A 2017, 131, 1232–1235. [Google Scholar] [CrossRef]
- Kouvel, J.S.; Fisher, M.E. Detailed Magnetic Behavior of Nickel Near its Curie Point. Phys. Rev. 1964, 136, A1626. [Google Scholar] [CrossRef]
- Hasiak, M. Microstructure and Thermomagnetic Properties of As-Quenched Gd75Ge15Si5Pr5 Alloy. Acta Phys. Pol. A 2018, 133, 684–687. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Wood, M.E.; Potter, W.H. General analysis of magnetic refrigeration and its optimization using a new concept: Maximization of refrigerant capacity. Cryogenics 1985, 25, 667–683. [Google Scholar] [CrossRef]
- Franco, V.; Blazquez, J.S.; Conde, A. The influence of Co addition on the magnetocaloric effect of Nanoperm-type amorphous alloys. J. Appl. Phys. 2006, 100, 064307. [Google Scholar] [CrossRef]
- Franco, V.; Conde, C.F.; Conde, A.; Kiss, L.F. A constant magnetocaloric response in FeMoCuB amorphous alloys with different Fe/B ratios. J. Appl. Phys. 2007, 101, 093903. [Google Scholar] [CrossRef]
- Świerczek, J. Superparamagnetic behavior and magnetic entropy change in partially crystallized Fe–Mo–Cu–B alloy. Phys. Status Solidi A 2014, 211, 1567–1576. [Google Scholar] [CrossRef]
- Banerjee, S.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16. [Google Scholar] [CrossRef]
- Brück, E. Developments in magnetocaloric refrigeration. J. Phys. D: Appl. Phys. 2005, 38, R381–R391. [Google Scholar]
- Fisher, M.E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967, 30, 615. [Google Scholar] [CrossRef]
- Deschizeax, M.N.; Delevey, G. Équation magnétique d’état du gadolinium au voisinage du point de Curie. J. Phys. France 1971, 32, 319. [Google Scholar] [CrossRef]
- Franco, V.; Conde, A.; Provenzano, V.; Shull, R.D. Scaling analysis of the magnetocaloric effect in Gd5Si2Ge1.9X0.1 (X=Al, Cu, Ga, Mn, Fe, Co). J. Magn. Magn. Mater. 2010, 322, 218. [Google Scholar] [CrossRef]
- Widom, B. Equation of State in the Neighborhood of the Critical Point. J. Chem. Phys. 1965, 43, 3898. [Google Scholar] [CrossRef]
- Arrott, A.; Noakes, J.E. Approximate Equation of State for Nickel Near Its Critical Temperature. Phys. Rev. Lett. 1967, 19, 786. [Google Scholar] [CrossRef]
- Kim, D.; Revaz, B.; Zink, B.L.; Hellman, F.; Rhyme, J.J.; Mitchell, J.F. Tricritical point and the doping dependence of the order of the ferromagnetic phase transition of La1−xCaxMnO3. Phys. Rev. Lett. 2002, 89, 227202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
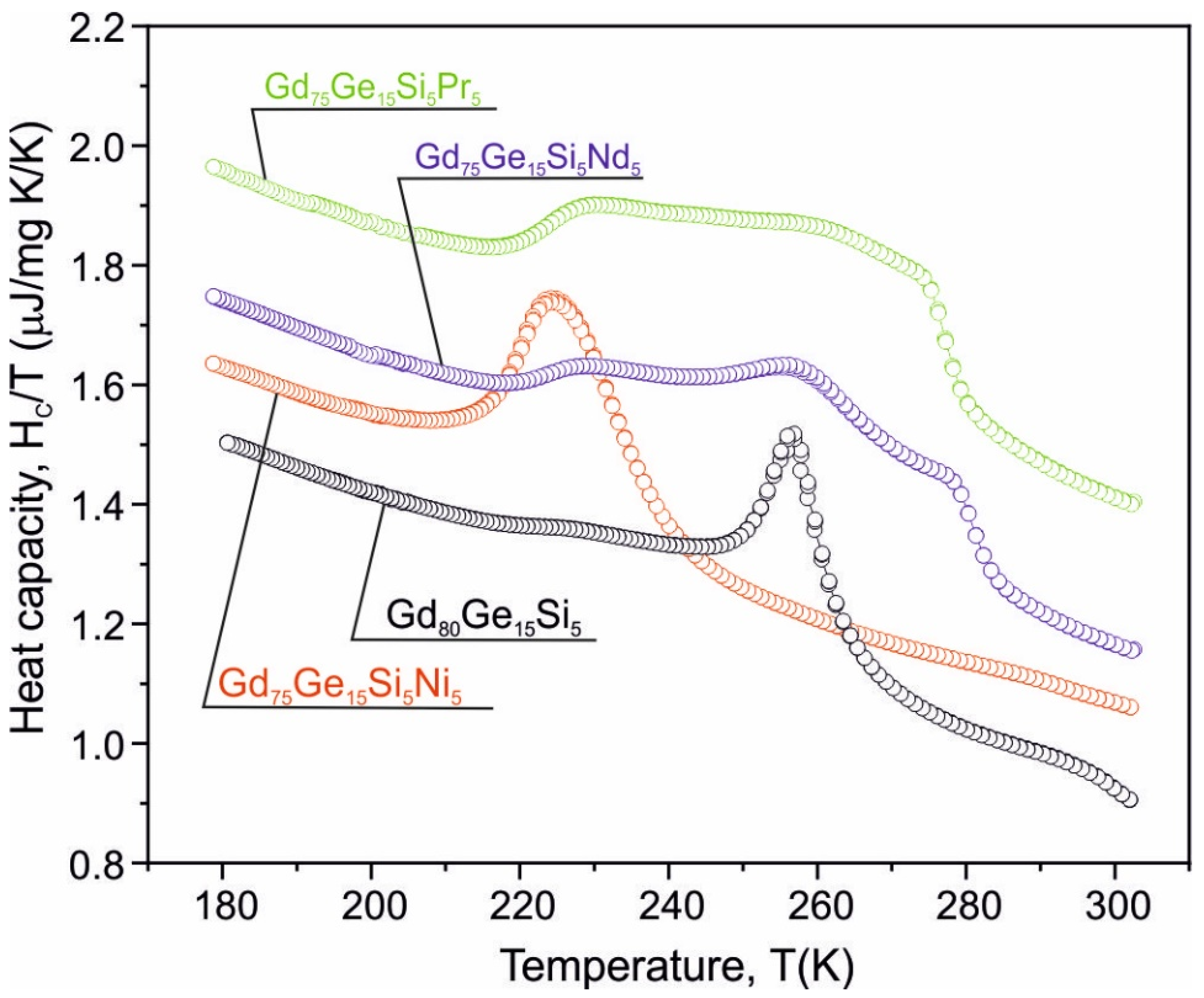
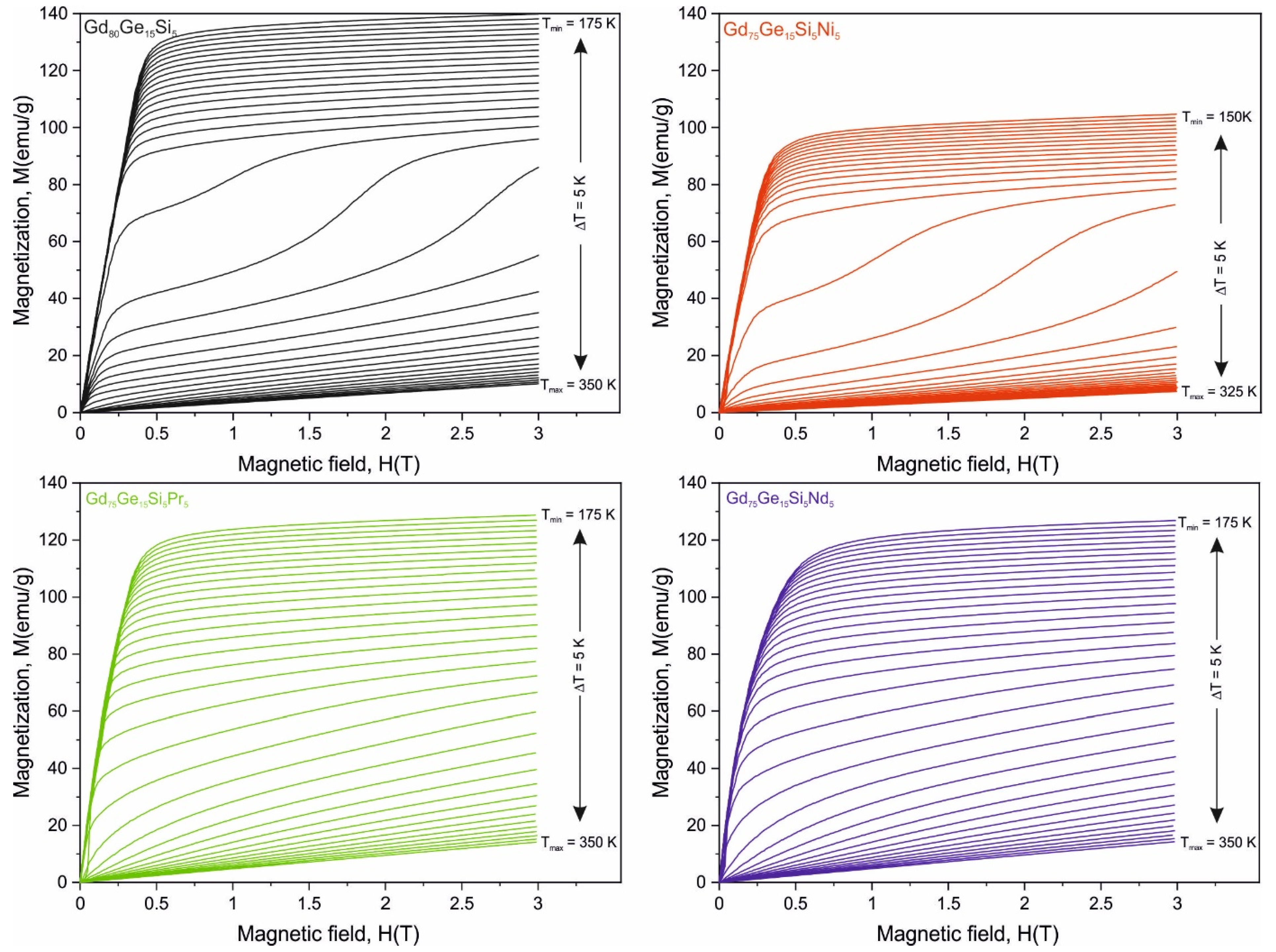

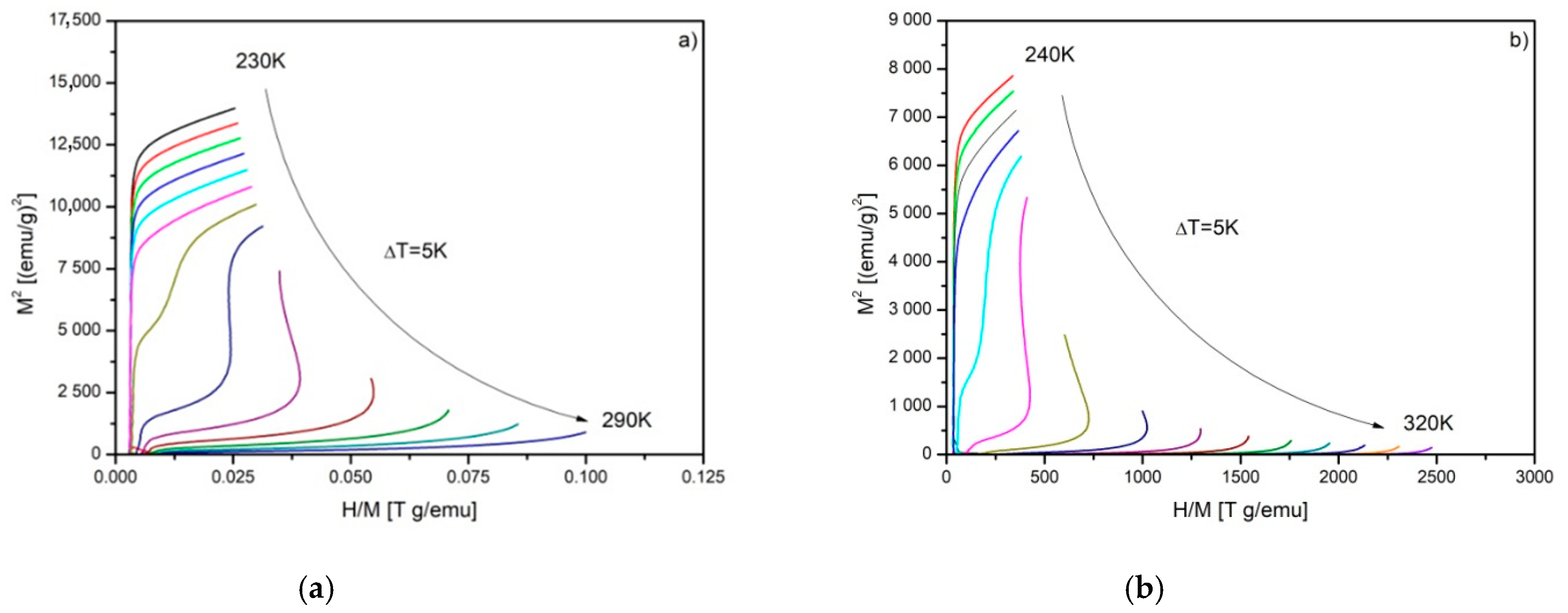
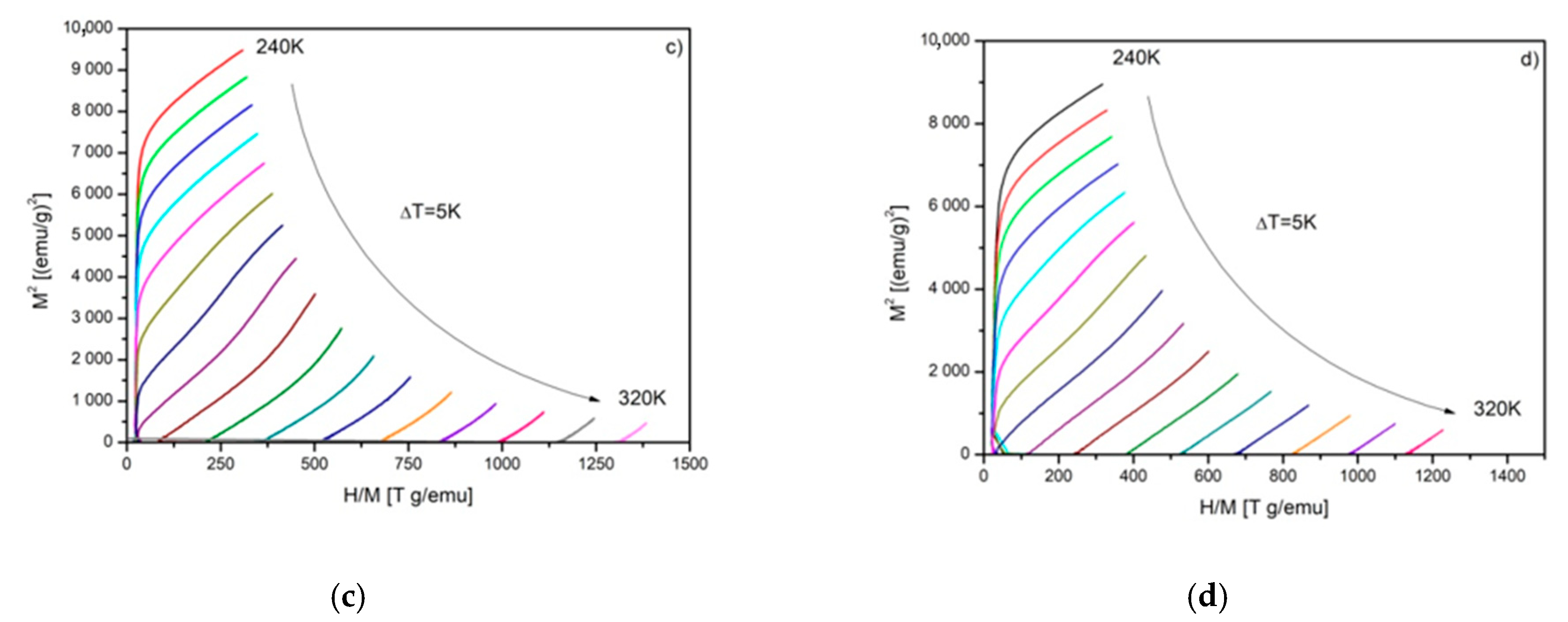
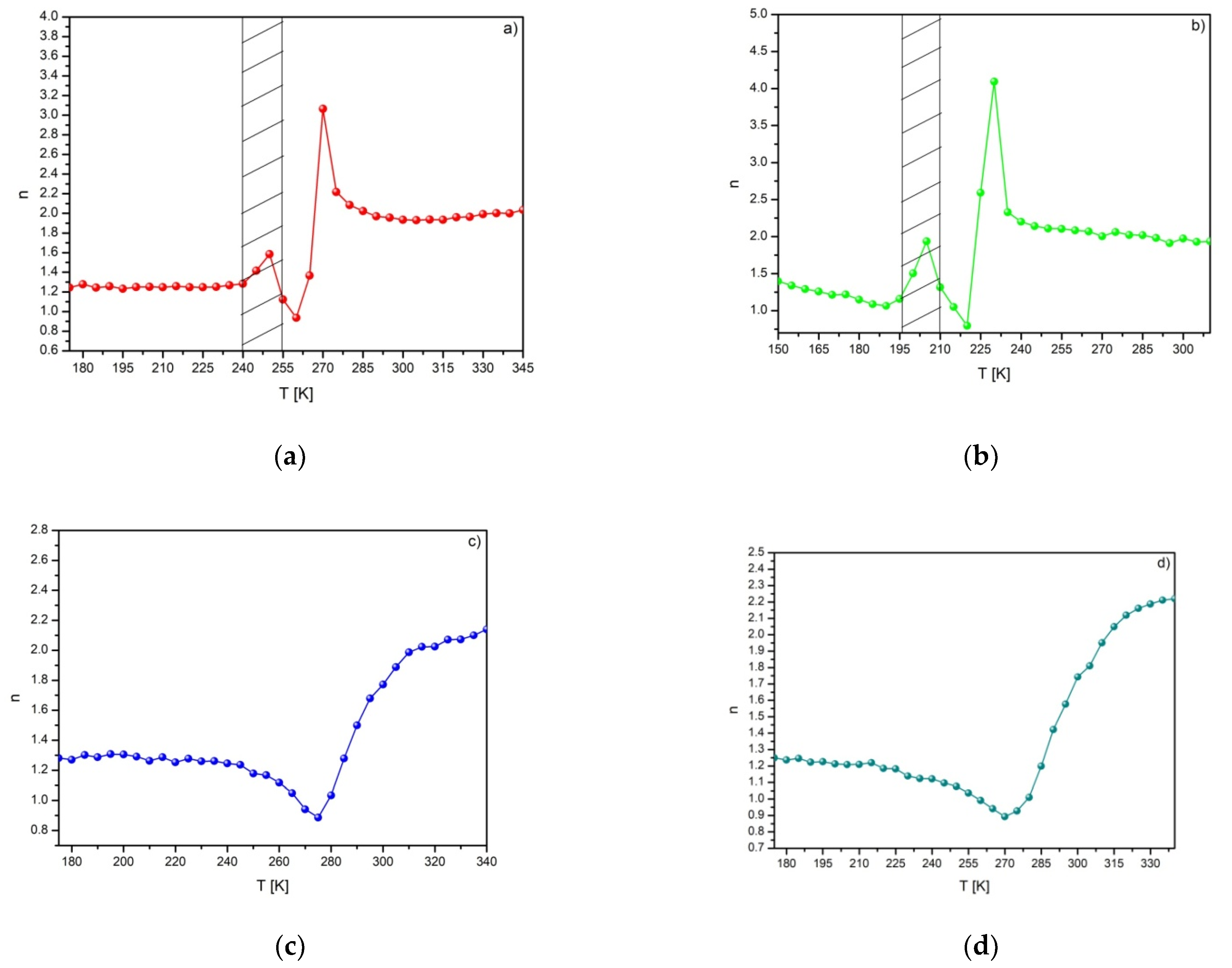
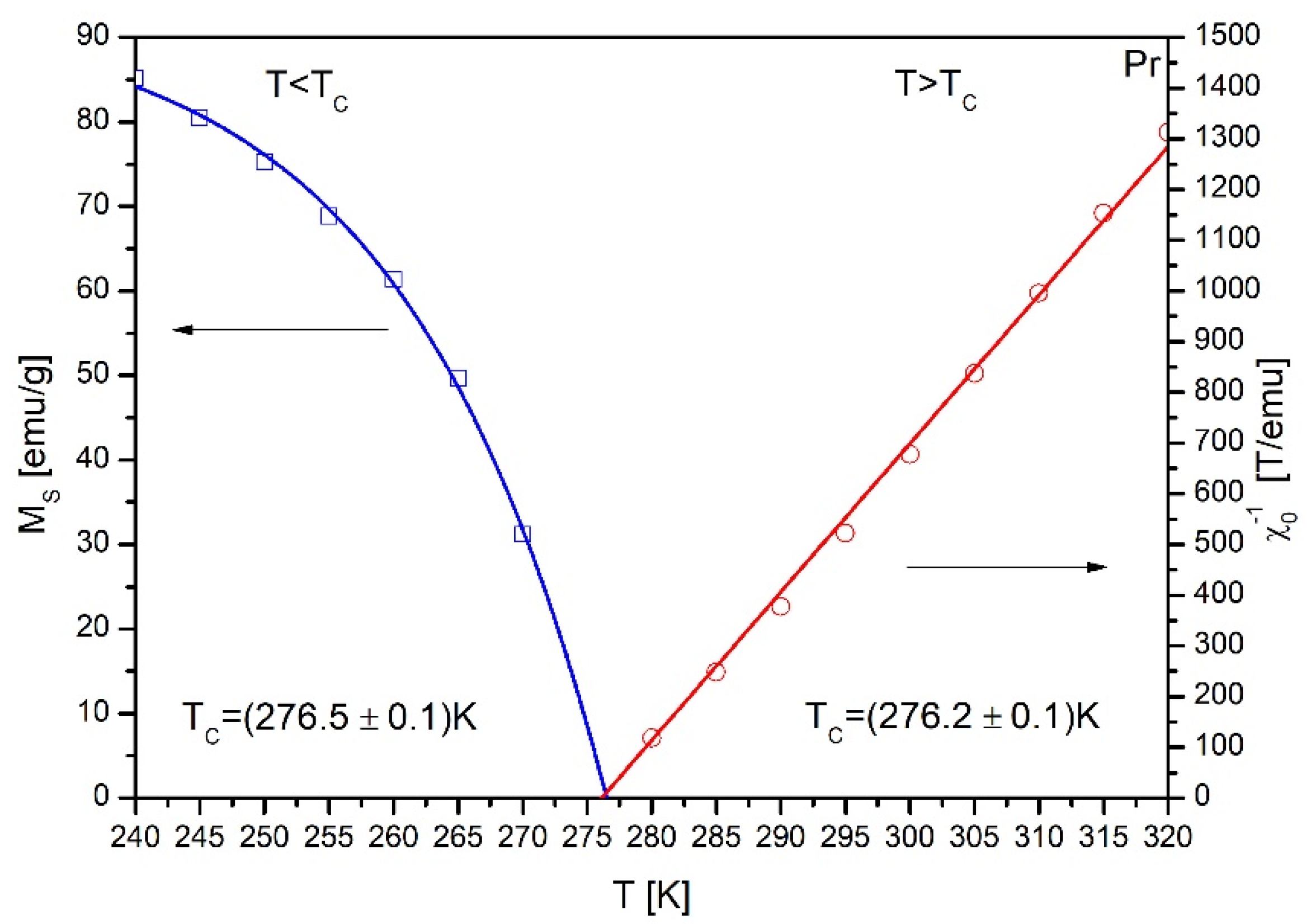


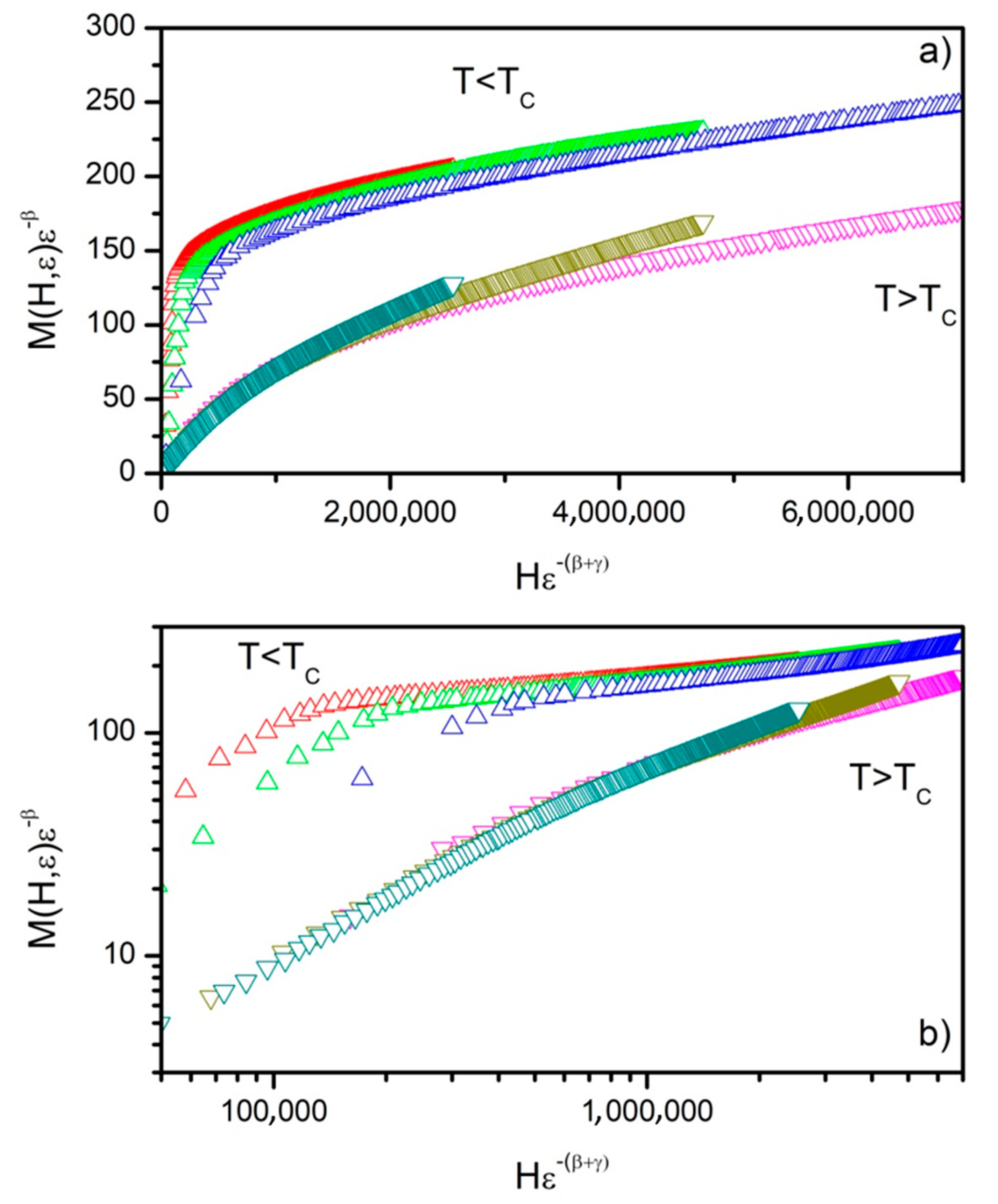
| Alloy | μ0H [T] | -SM [J/(kg K)] | RC [J/kg] |
|---|---|---|---|
| Gd80Ge15Si5 | 0.5 | 2.05 | 16 |
| 1 | 5.06 | 38 | |
| 1.5 | 8.18 | 60 | |
| 2 | 10.71 | 102 | |
| 3 | 11.91 | 164 | |
| Gd75Ge15Si5Ni5 | 0.5 | 2.00 | 20 |
| 1 | 4.54 | 38 | |
| 1.5 | 7.13 | 66 | |
| 2 | 9.78 | 84 | |
| 3 | 12.11 | 140 | |
| Gd75Ge15Si5Pr5 | 0.5 | 1.05 | 22 |
| 1 | 1.95 | 42 | |
| 1.5 | 2.98 | 72 | |
| 2 | 3.77 | 103 | |
| 3 | 5.08 | 160 | |
| Gd75Ge15Si5Nd5 | 0.5 | 0.92 | 21 |
| 1 | 1.86 | 52 | |
| 1.5 | 2.53 | 76 | |
| 2 | 3.38 | 108 | |
| 3 | 4.71 | 140 |
| Alloy | Ref. | β | γ | δ | TC [K] | nexp | ntheor | nW |
|---|---|---|---|---|---|---|---|---|
| Gd75Ge15Si5Pr5 = Gd4.8Pr0.4Ge2.0Si1.8 | TW | 0.353 | 1.174 | 4.252 4.326 (W) | 276.2 ± 0.1 | 0.8863 | 0.8716 | 0.8739 |
| Gd75Ge15Si5Nd5 = Gd4.8Nd0.4Ge2.0Si1.8 | TW | 0.324 | 1.119 | 4.167 4.456 (W) | 277.6 ± 0.1 | 0.8933 | 0.8849 | 0.8924 |
| Gd75Ge15Si5Ce5 = Gd4.8Ce0.4Si2.0Ge1.8 | [11] | 0.376 | 1.032 | 3.385 3.745 (W) | 275.8 | - | 0.822 | 0.8214 |
| pure Gd | [22] | 0.381 | 1.196 | 4.139 | 296 | - | 0.8513 | - |
| Gd5Si2Ge1.9Cu0.1 | [23] | 0.38 | 1.15 | 4.03 | - | - | 0.8479 | - |
| Gd5Si2Ge1.9Mn0.1 | [23] | 0.41 | 1.05 | 3.56 | - | - | 0.8047 | - |
| Gd5Si2Ge1.9Ga0.1 | [23] | 0.34 | 1.17 | 4.44 | - | - | 0.884 | - |
| Gd5Si2Ge1.9Al0.1 | [23] | 0.38 | 1.08 | 3.84 | - | - | 0.8403 | - |
| Mean-field | [25] | 0.5 | 1 | 3 | - | - | 2/3 | - |
| 3D-Heisenberg | [25] | 0.365 | 1.386 | 4.797 | - | - | 0.8802 | - |
| 3D-Ising | [25] | 0.325 | 1.24 | 4.82 | - | - | 0.9001 | - |
| Tricritical mean-field | [26] | 0.25 | 1 | 5 | - | - | 0.9333 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gębara, P.; Hasiak, M. Determination of Phase Transition and Critical Behavior of the As-Cast GdGeSi-(X) Type Alloys (Where X = Ni, Nd and Pr). Materials 2021, 14, 185. https://doi.org/10.3390/ma14010185
Gębara P, Hasiak M. Determination of Phase Transition and Critical Behavior of the As-Cast GdGeSi-(X) Type Alloys (Where X = Ni, Nd and Pr). Materials. 2021; 14(1):185. https://doi.org/10.3390/ma14010185
Chicago/Turabian StyleGębara, Piotr, and Mariusz Hasiak. 2021. "Determination of Phase Transition and Critical Behavior of the As-Cast GdGeSi-(X) Type Alloys (Where X = Ni, Nd and Pr)" Materials 14, no. 1: 185. https://doi.org/10.3390/ma14010185
APA StyleGębara, P., & Hasiak, M. (2021). Determination of Phase Transition and Critical Behavior of the As-Cast GdGeSi-(X) Type Alloys (Where X = Ni, Nd and Pr). Materials, 14(1), 185. https://doi.org/10.3390/ma14010185






