Basalt Fibre Reinforcement of Bent Heterogeneous Glued Laminated Beams
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specifications of Materials Used in Glulam Beams
2.2. Preparation of BFRP Reinforcement
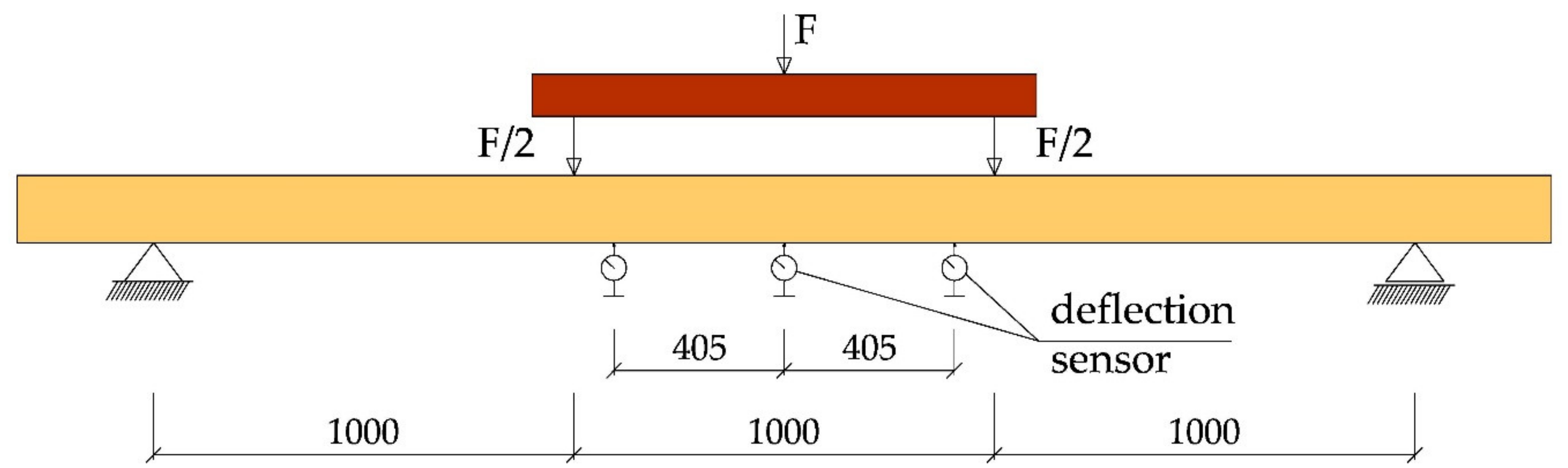
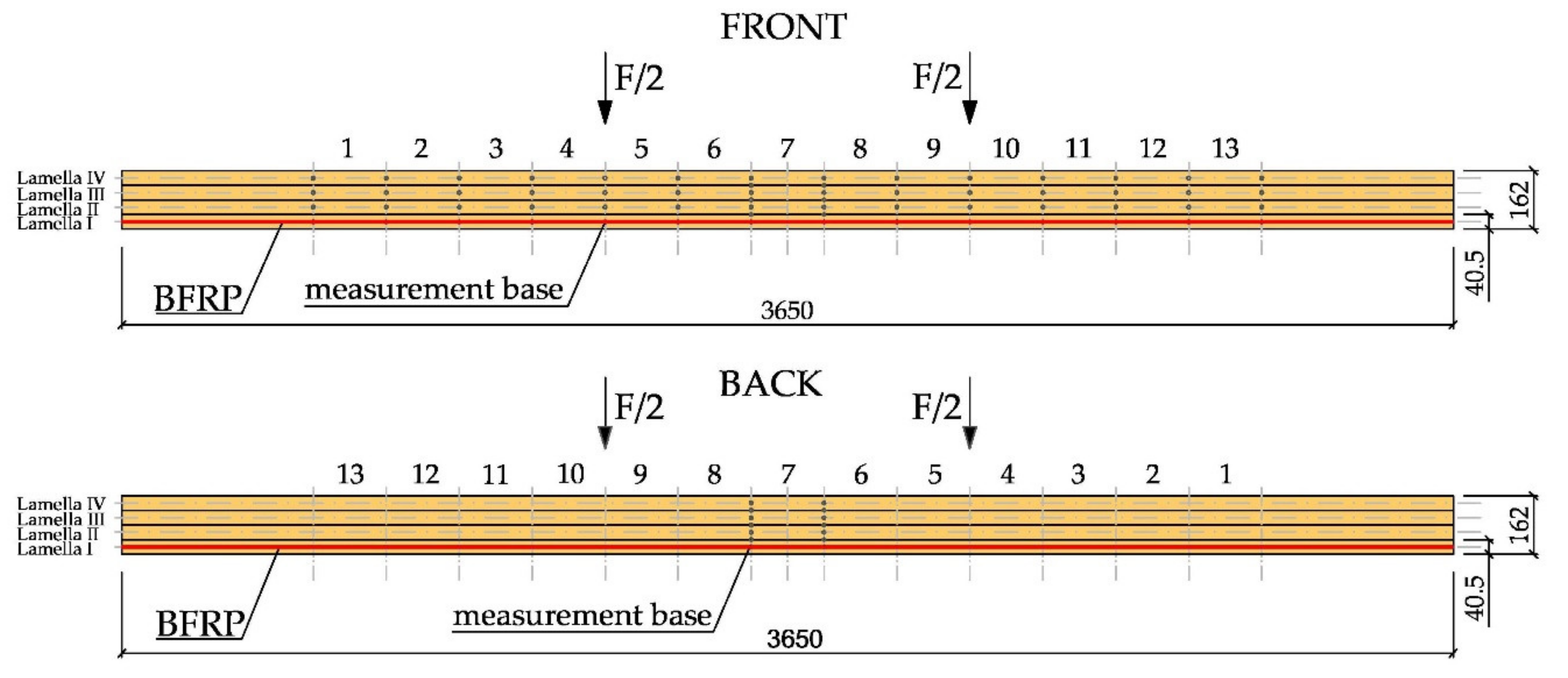
2.3. Tests
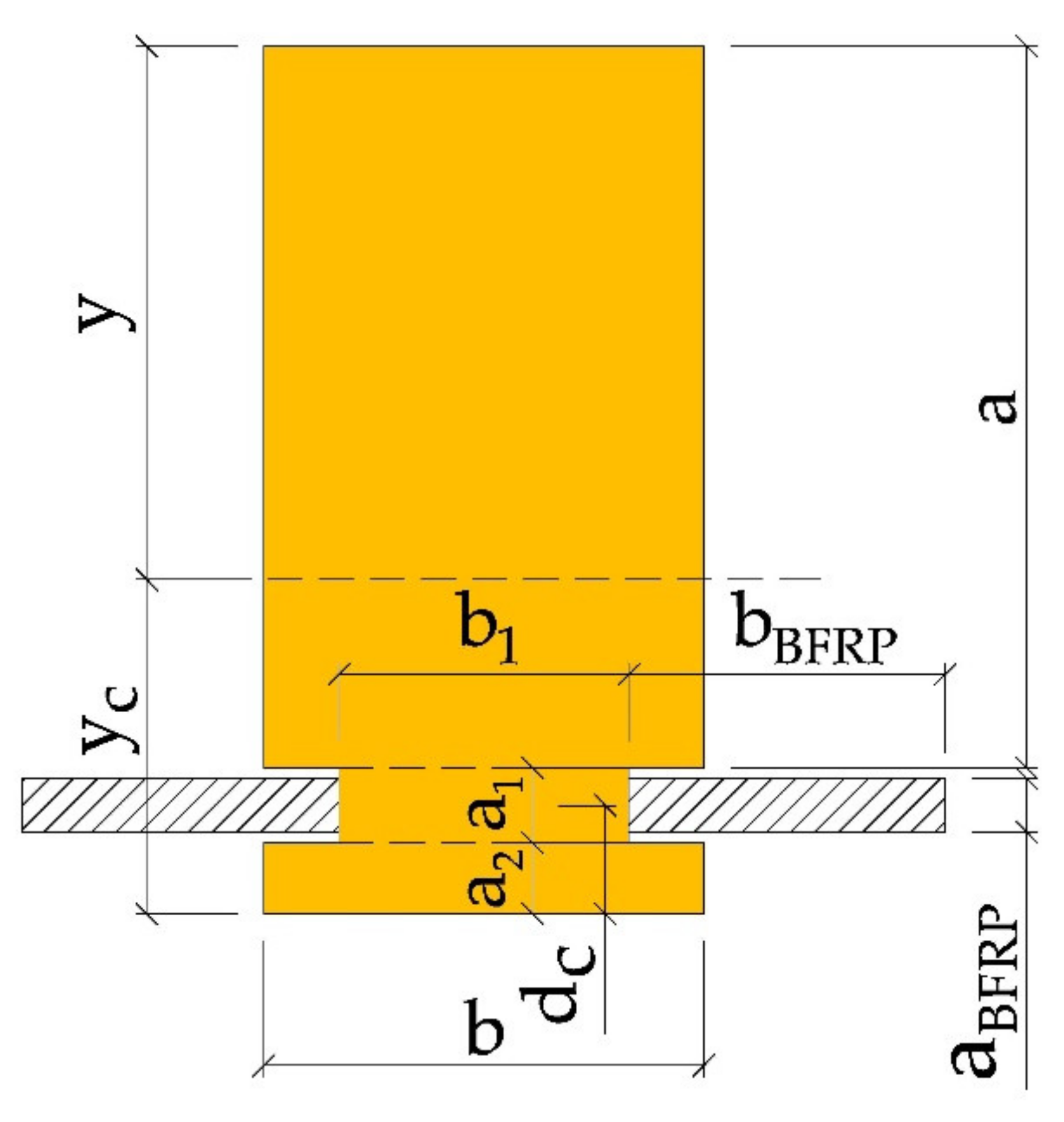
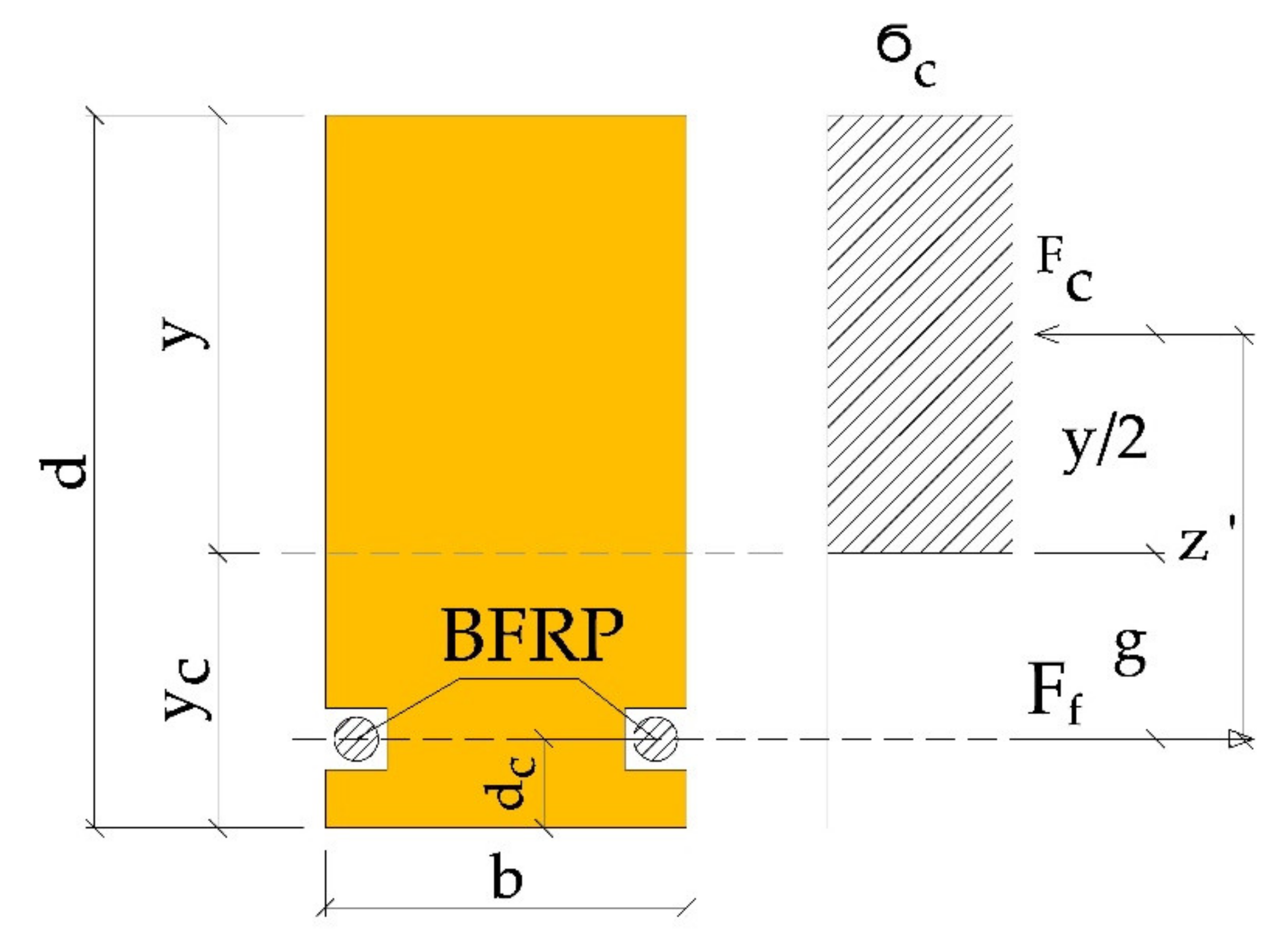
2.4. Analytical Procedure
- the moduli of wood elasticity along the fibres in compression and in tension were distinguished,
- the modulus of elasticity of wood under tension was reduced to the modulus of elasticity of wood compressed along the fibres with the coefficient:
- the modulus of elasticity of the BFRP fibres in tension was reduced to the modulus of elasticity of the wood compressed along the fibres using the coefficient:where:
- —modulus of elasticity of BFRP fibres in tension,
- —the average modulus of wood elasticity when tensioned along the fibres,
- —the average modulus of wood elasticity in compression along the fibres.
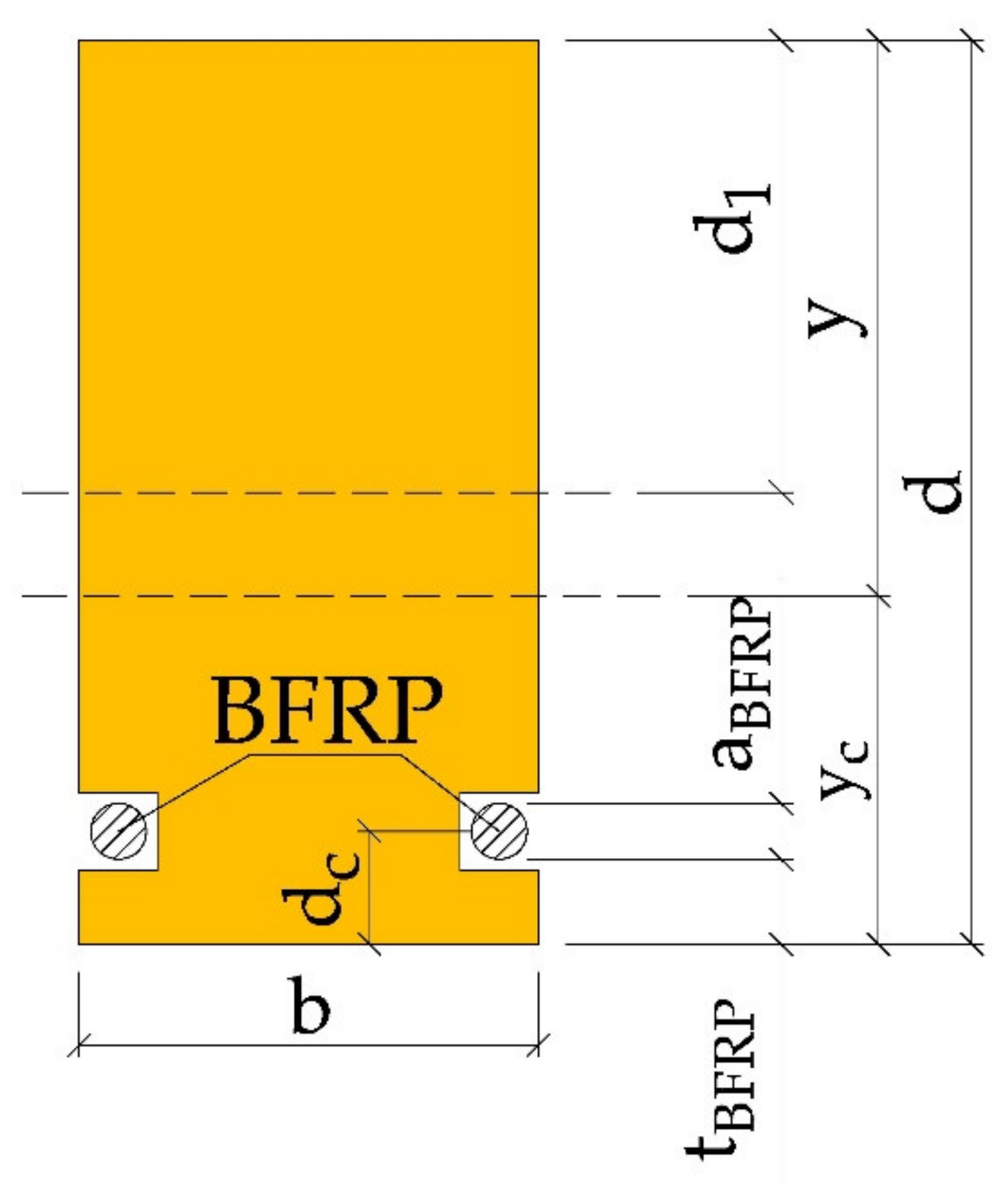
- —adjustment value for reinforcement in tension zone,
- —adjustment value for bumper layer in tension zone,
- —the height of the glued beam,
- —distance of the neutral axis to the beam top before correction for reinforcement,
- —BFRP fibre diameter,
- —thickness of the “cover” of the BFRP fibre,
- —BFRP reinforcement distance to the lower edge of the beam,
- —distance of the neutral axis after reinforcement to the upper edge of the beam,
- —distance of the neutral axis to the lower edge of the beam.
2.5. Numerical Procedure
- wood quality class KS: T13 (C22),
- KG wood quality class: T8 (C14).
3. Results
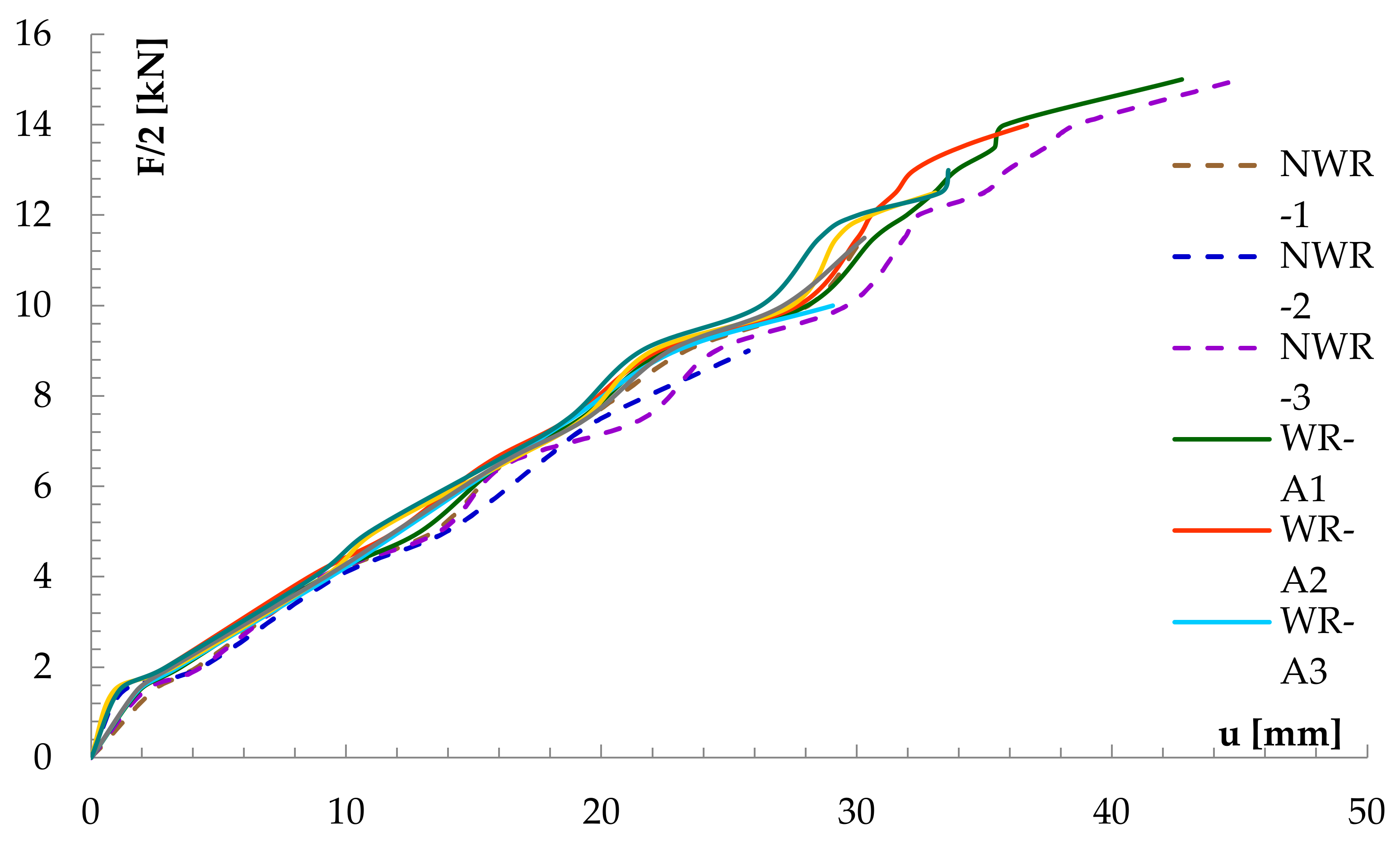
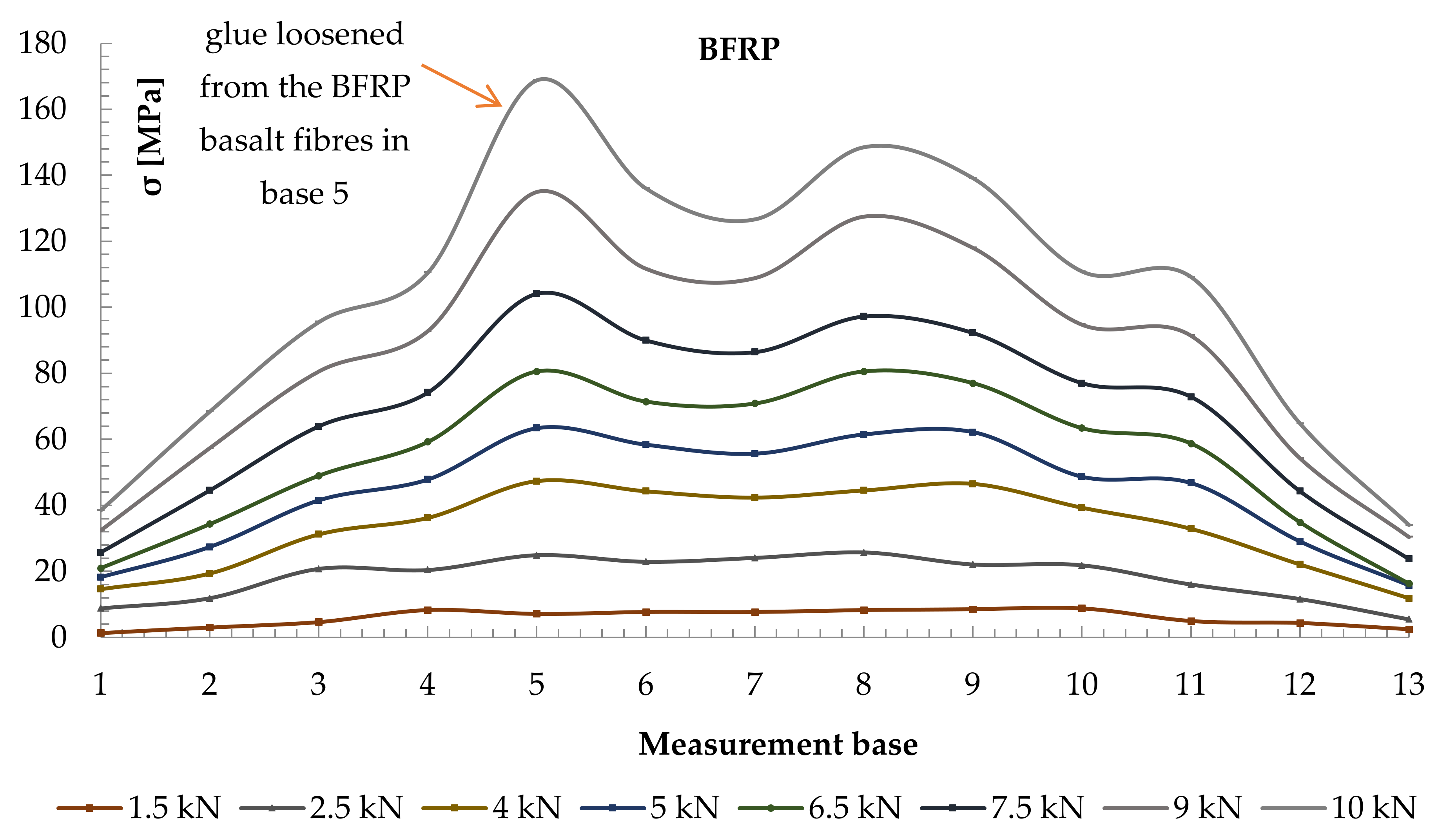
3.1. Force-Bending Relation
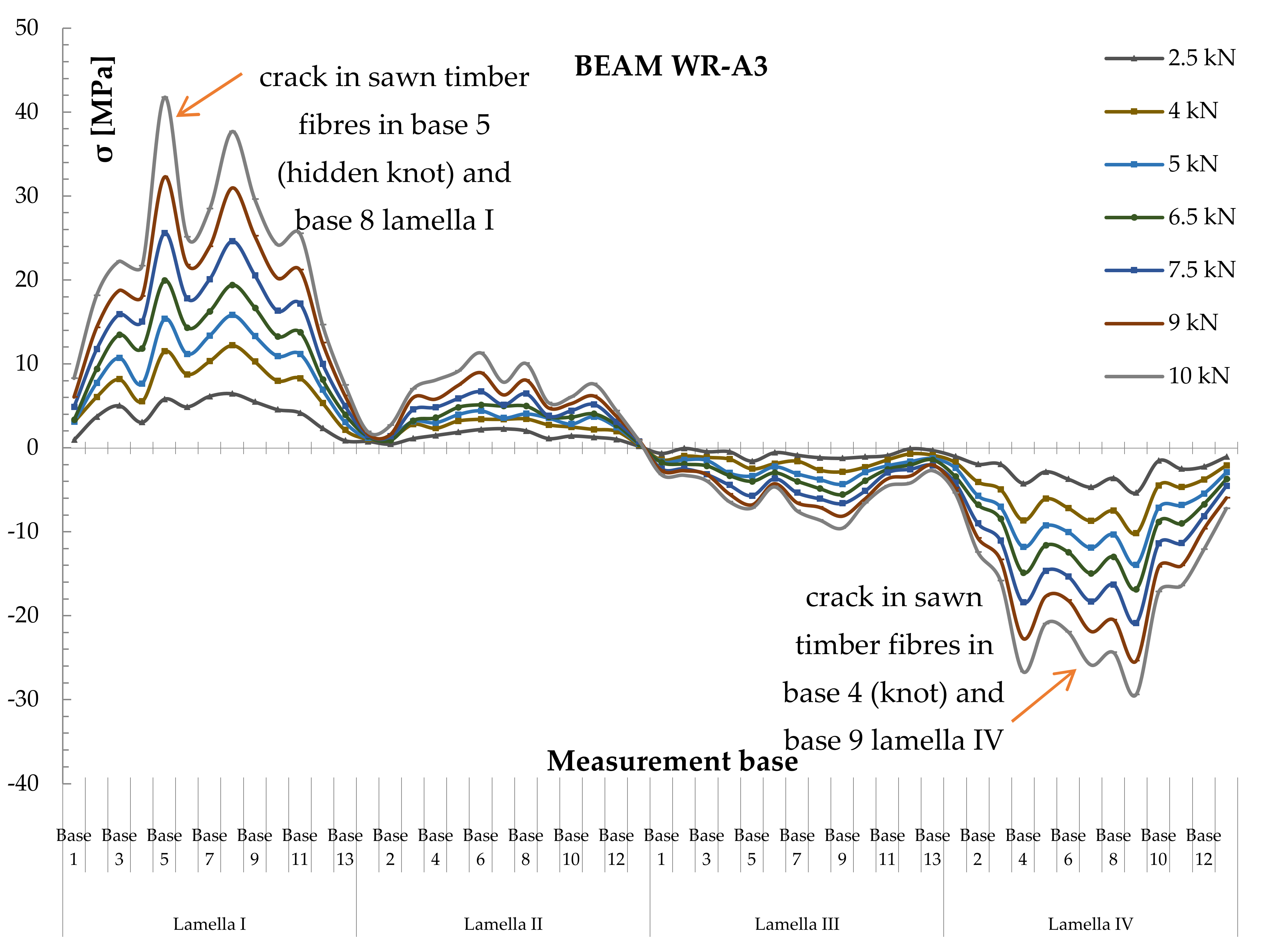
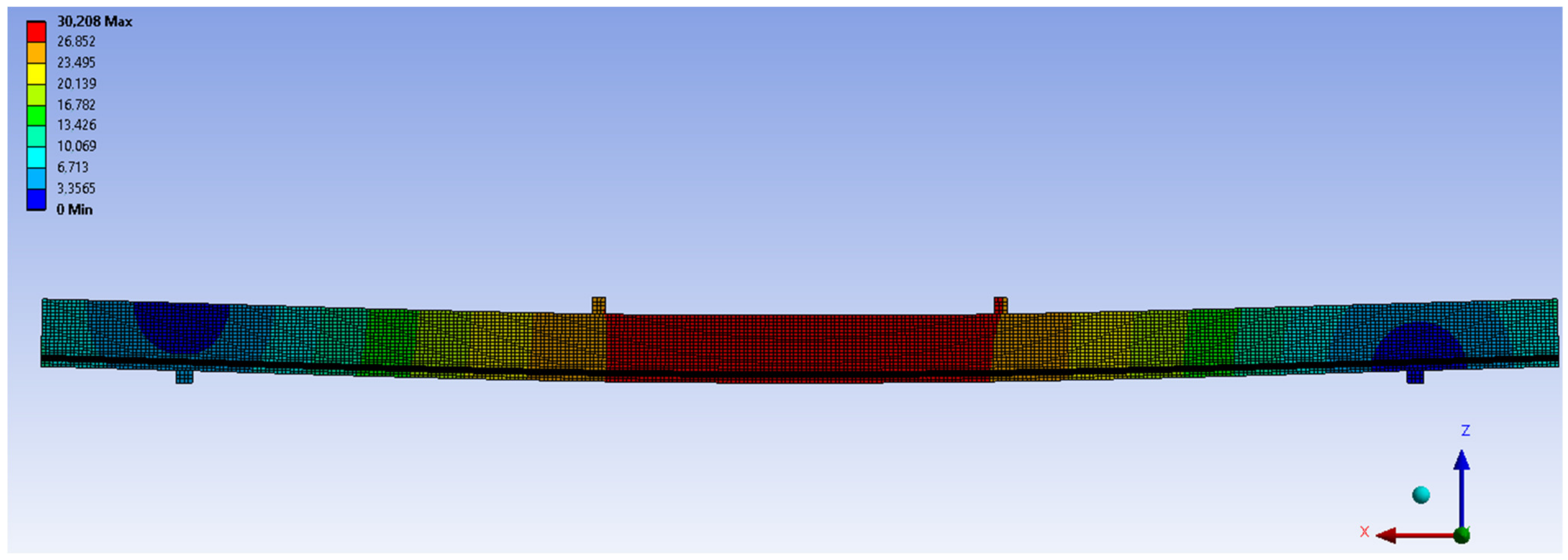
3.2. Analysis of Normal Stresses
3.3. Modes of Failure
3.4. Comparison of Theoretical and Numerical Analysis with Laboratory Tests
4. Conclusions
- It was noted that the failure load significantly increased with an increase in the reinforcement ratio, while maximum bending was slightly reduced. Based on the test result analysis, it was concluded that the load capacity of the WR-A and WR-B was increased by, respectively, 13% and 20%, while their rigidity grew by 9.99% and 17.13%, when compared with reference beams. The tests also demonstrated that application of BFRP reduced variation in the bending strength.
- In the tests, it was found that basalt fibres perfectly compensated for the heterogeneous timber structure, being an ideal application to timber of poor and average quality. BFRP fibres inhibit or limit the propagation of cracks, neutralizing local defects in the wood. An important conclusion is that glulam beams made mostly of sawn timber of poor and average quality and reinforced with basalt fibres have better strength and rigidity parameters, and their failure modes show an increase in the elastic phase.
- It should be remembered that BFRP reinforcement in glulam beams can be applied both on-site and in the beam manufacturing process. Timber gluing is an effective method that allows for obtaining more uniform stress distribution between reinforcement and timber. The 2 mm thick epoxy layer, located directly between reinforcement and timber, maintained good quality during the entire test period. No premature delamination between the FRP composite material and timber was detected before complete timber failure.
- Theoretical analysis is important for the designer to select the appropriate type of reinforcement when designing new reinforcement techniques. For the adopted computational model of BFRP fibre composites reinforced beams in bending, the values of normal stresses of BFRP fibres were slightly higher than in laboratory or numerical tests.
- Displacements, normal stresses of wood and BFRP basalt fibres were determined with reasonable accuracy. A three-dimensional FE model was consistent with the experimental studies. The findings can be useful for further analysis of the reinforcement and repair system employing BFRP fibres. The numerical analysis can be applied to reinforced elements when designing various reinforcement schemes, with particular emphasis put on the configuration of wood quality classes. However, it is necessary to carry out material tests of the analysed elements on individual basis, and to determine the mean values for each quality class of structural timber. The determination of Poisson’s ratios for particular strength classes would allow for conducting analysis of structures with advanced computational systems at the stage of structure design.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Donadon, B.F.; Mascia, N.T.; Vilela, R.; Trautwein, L.M. Experimental Investigation of Glued-Laminated Timber Beams with Vectran-FRP Reinforcement. Eng. Struct. 2020, 202, 109818. [Google Scholar] [CrossRef]
- Wood Handbook—Wood as an Engineering Material; Forest Products Laboratory, Department of Agriculture: Madison, WI, USA, 2010.
- Fossetti, M.; Minafò, G.; Papia, M. Flexural Behaviour of Glulam Timber Beams Reinforced with FRP Cords. Constr. Build. Mater. 2015, 95, 54–64. [Google Scholar] [CrossRef]
- Raftery, G.M.; Rodd, P.D. FRP Reinforcement of Low-Grade Timber Bonded with Wood Adhesive. Constr. Build. Mater. 2015, 91, 116–125. [Google Scholar] [CrossRef]
- Gilfillan, J.R.; Gilbert, S.G.; Patrick, G.R.H. The Use of CFRP Composites in Enhancing the Structural Behaviour of Timber Beams. J. Reinf. Plast. Compos. 2003, 22, 1373–1388. [Google Scholar] [CrossRef]
- Buell, T.W.; Saadatmanesh, P.E. Strengthening Timber Beams Using Carbon Fiber. J. Struct. Eng. 2005, 131, 173–187. [Google Scholar] [CrossRef]
- André, A.; Kliger, R. Strengthening of Timber Beams Using FRP, with Emphasis on Compression Strength: A State of the Art Review. In Proceedings of the Second Official International Conference of International Institute for FRP in Construction for Asia-Pacific Region APFIS, Seoul, Korea, 9–11 December 2009. [Google Scholar]
- Svecova, D.; Eden, R.J. Flexural and Shear Strengthening of Timber Beams Using Glass Fibre Reinforced Polymer Bars—An Experimental Investigation. Can. J. Civ. Eng. 2004, 31, 45. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Grazini, A. A Method for Flexural Reinforcement of Old Wood Beams with CFRP Materials. Compos. Part B 2005, 36, 143–153. [Google Scholar] [CrossRef]
- Brol, J.; Wdowiak, A. The Use of Glass and Aramid Fibres for the Strengthening of Timber Structures. Ann. Wars. Univ. Life Sci. For. Wood Technol. 2017, 100, 128–138. [Google Scholar]
- Brol, J.; Nowak, T.; Wdowiak, A. Numerical Analysis and Modelling of Timber Elements Strengthened with FRP Materials. Ann. Wars. Univ. Life Sci. For. Wood Technol. 2018, 104, 274–282. [Google Scholar]
- Wdowiak, A. Assessment of Technical Condition of Wooden Structures. In Proceedings of the 11th European Conference of Young Researchers and Scientist, Zilina, Slovakia, 22–24 June 2015; Volume 7, pp. 326–332. [Google Scholar]
- Wdowiak, A. Analysis of Bent Timber Beam Reinforcement with the Application of Composite Materials. Struct. Environ. 2016, 8, 10–16. [Google Scholar]
- Wdowiak, A. Structural and Strength Properties of Bent Wooden Beams Reinforced with Fibre Composites. Ph.D. Thesis, Kielce University of Technology, Kielce, Poland, 12 April 2019. [Google Scholar]
- Wdowiak, A.; Brol, J. Effectiveness of Reinforcing Bent Non-Uniform Pre-Stressed Glulam Beams with Basalt Fibre Reinforced Polymers Rods. Materials 2019, 12, 3141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brol, J.; Wdowiak-Postulak, A. Old Timber Reinforcement with FRP. Materials 2019, 12, 4197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wdowiak-Postulak, A. Natural Fibre as Reinforcement for Vintage Wood. Materials 2020, 13, 4799. [Google Scholar] [CrossRef] [PubMed]
- Wdowiak-Postulak, A.; Brol, J. Ductility of the Tensile Zone in Bent Wooden Beams Strengthened with CFRP Materials. Materials 2020, 13, 5451. [Google Scholar] [CrossRef]
- Rudzinski, L.; Wdowiak, A. Strength and Structural Properties of Structural Timber. Struct. Environ. 2016, 8, 103–108. [Google Scholar]
- Wdowiak, A. Using the Visual Method to Sort Polish Pine Structural Sawn Timber with Respect to Strength. Czas. Tech. 2016, 113, 219–224. [Google Scholar]
- Wdowiak, A. Defects in Structural Timber. Struct. Environ. 2017, 9, 112–122. [Google Scholar]
- Wdowiak, A.; Brol, J. Methods of Strength Grading of Structural Timber—Comparative Analysis of Visual and Machine Grading on the Example of Scots Pine Timber from Four Natural Forest Regions of Poland. Struct. Environ. 2019, 11, 210–224. [Google Scholar] [CrossRef]
- Wdowiak, A. Examination of Structural and Geometric Characteristics during the Strength Sorting of Construction Timber by Visual Method. Przeglad Bud. 2017, 88, 42–46. [Google Scholar]
- Wdowiak, A. Structure of Construction Timber. J. Civil. Eng. Environ. Archit. 2017, 34, 365–380. [Google Scholar]
- Raftery, G.M.; Kelly, F. Basalt FRP Rods for Reinforcement and Repair of Timber. Compos. Part B Eng. 2015, 70, 9–19. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Speranzini, E. Bending Tests on Natural Fiber Reinforced Fir Wooden Elements. Adv. Mat. Res. 2013, 778, 537–544. [Google Scholar] [CrossRef]
- Speranzini, E.; Tralascia, S. Engineered Sawn Timber: LVL and Solid Wood Reinforced with Natural Fibres. In Proceedings of the World Conference on Timber Engineering (WCTE 2010), Riva del Garda, Italy, 20–24 June 2010. Paper 798. [Google Scholar]
- Speranzini, E.; Agnetti, S. Structural Performance of Natural Fibers REINFORCED timber Beams. In Proceedings of the 6th International Conference on FRP Composites in Civil Engineering (CICE 2012), Rome, Italy, 13–15 June 2012. [Google Scholar]
- Lopresto, V.; Leone, C.; De Iorio, I. Mechanical Characterisation of Basalt Fibre Reinforced Plastic. Compos. Part B 2011, 42, 717–723. [Google Scholar] [CrossRef]
- Kromer, K.H. Physical Properties of Flax Fibre for Non-Textile-Use. Res. Agr. Eng. 2009, 55, 52–61. [Google Scholar] [CrossRef] [Green Version]
- Corradi, S.; Isidori, T.; Corradi, M.; Soleri, F.; Olivari, L. Composite Boat Hulls with Bamboo Natural Fibres. Int. J. Mater. Prod. Technol. 2009, 36, 73–89. [Google Scholar] [CrossRef]
- De la Rosa García, P.; Cobo Escamilla, A.; Nieves González Garcia, M. Bending Reinforcement of Timber Beams with Composite Carbon Fiber and Basalt Fiber Materials. Compos. Part B Eng. 2013, 55, 528–536. [Google Scholar] [CrossRef] [Green Version]
- Gand, A.K.; Yeboah, D.; Khorami, M.; Olubanwo, A.O.; Lumor, R. Behaviour of Strengthened Timber Beams Using Near Surface Mounted Basalt Fibre Reinforced Polymer (BFRP) Rebars. Eng. Solid Mech. 2018, 6, 341–352. [Google Scholar] [CrossRef]
- Righetti, L.; Corradi, M.; Borri, A. Strengthening of Timber Beams with Unbonded FRP. In Proceedings of the 16th European Bridge Conference, Edinburgh, UK, 23–25 June 2015. [Google Scholar]
- Yeboah, D.; Taylor, S.; McPolin, D.; Gilfillan, R. Pull-Out Behaviour of Axially Loaded Basalt Fibre Reinforced Polymer (BFRP) Rods Bonded Perpendicular to the Grain of Glulam Elements. Constr. Build. Mater. 2013, 38, 962–969. [Google Scholar] [CrossRef] [Green Version]
- McConnell, E.; McPolin, D.; Taylor, S. Post-Tensioning Glulam Timber Beams with Basalt FRP Tendons. Proc. ICE Constr. Mater. 2015, 168, 232–240. [Google Scholar] [CrossRef] [Green Version]
- Kelly, F. Basalt FRP Rods for Strengthening and Repair of Glued Laminated Timber. Master’s Thesis, National University of Ireland, Galway, UK, 2012. [Google Scholar]
- Zachary, C.; Kavan, S. Feasibility of Strengthening Glulam Beams with Prestressed Basalt Fibre Reinforced Polymers. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2012. [Google Scholar]
- Sim, J.; Park, C.; Young Moon, D. Characteristics of Basalt Fiber as a Strengthening Material for Concrete Structures. Compos. Part B Eng. 2005, 36, 504–515. [Google Scholar] [CrossRef]
- Wei, B.; Cao, H.; Song, S. Degradation of Basalt Fibre and Glass Fibre/Epoxy Resin Composites in Seawater. Corros. Sci. 2011, 53, 426–431. [Google Scholar] [CrossRef]
- Tan, K.H.; Zhou, Y. Performance of FRP Strengthened Beams Subjected to Elevated Temperatures. J. Compos. Constr. 2011, 15, 304–311. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.T.; Wu, Z.S.; Liu, H.Y.; Ren, Y. Experimental Study on the Fatigue Behaviour of Steel Beams Strengthened with Different Fiber-Reinforced Composite Plates. J. Compos. Constr. 2012, 16, 127–137. [Google Scholar] [CrossRef]
- Barbero, E.; Davalos, J.; Munipalle, U. Bond Strength of FRP–Wood Interface. J. Reinf. Plast. Compos. 1994, 13, 835–854. [Google Scholar] [CrossRef]
- Raftery, G.M.; Harte, A.M.; Rodd, P.D. Bond Quality at the FRP–Wood Interface Using Wood-Laminating Adhesives. Int. J. Adhes. Adhes. 2009, 29, 101–110. [Google Scholar] [CrossRef]
- Tlustochowicz, G.; Serrano, E.; Steiger, R. State-of-the-Art Review on Timber Connections with Glued-in Steel Rods. Mater. Struct. 2011, 44, 997–1020. [Google Scholar] [CrossRef]
- Steiger, R.; Serrano, E.; Stepinac, S.; Rajčić, V.; O’Neill, C.; McPolin, D.; Widmann, R. Strengthening of Timber Structures with Glued-in Rods. Constr. Build. Mater. 2015, 97, 90–105. [Google Scholar] [CrossRef] [Green Version]
- Harvey, K.; Ansell, M.P. Improved Timber Connections Using Bonded-in GRRP Rods. In Proceedings of the 6th World Conference on Timber Engineering, WCTE, Whistler, BC, Canada, 31 July–3 August 2000. [Google Scholar]
- O’Neill, C.; McPolin, D.O.; Harte, A.M.; Taylor, S.E. Influence of Embedded Length on Strength of BFRP Rods Bonded Parallel to the Grain in Low Grade Timber by Pullout-Bending Tests. In Proceedings of the Civil Engineering Research in Ireland, Belfast, UK, 28–29 August 2014. [Google Scholar]
- Moisture Content of a Piece of Sawn Timber—Part 2: Estimation by Electrical Resistance Method; PN-EN 13183-2:2002; Polish Committee for Standardization: Warsaw, Poland, 2002.
- Moisture Content of a Piece of Sawn Timber—Part 3: Estimation by Capacitance Method; PN-EN 13183-3:2007; Polish Committee for Standardization: Warsaw, Poland, 2007.
- Softwood Structural Sawn Timber Sorted Using Strength Methods; PN-D-94021:2013-10; Polish Committee for Standardization: Warsaw, Poland, 2013.
- Timber Structures—Glued Laminated Timber and Structural Glued Solid Timber—Requirements; PN-EN 14080:2013-07; Polish Committee for Standardization: Warsaw, Poland, 2013.
- Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties; PN-EN 408+A1:2012; Polish Committee for Standardization: Warsaw, Poland, 2012.
- US Standard ICBO/Uniform Building Code; 5100; Accredited by the American National Standards Institute; American National Standards Institute: Washington, DC, USA, 1985.
- US Standard ICBO/Uniform Building Code; 6046; Accredited by the American National Standards Institute; American National Standards Institute: Washington, DC, USA, 1991.
- Neuhaus, H. Timber Construction; Polish Technical Publishing House: Rzeszów, Poland, 2006. [Google Scholar]
- Structural Timber—Strength Classes; PN-EN 338:2016-06; Polish Committee for Standardization: Warsaw, Poland, 2016.




| Properties | According to PN-EN 14080:2013-07 | According to PN-EN 408 + A1:2012 |
|---|---|---|
| Bending strength (MPa) | 20 | 23.31 |
| Tensile strength (MPa) | ||
| along the fibres | 15 | - |
| across the fibres | 0.5 | - |
| Compressive strength (MPa) | ||
| along the fibres | 18.5 | - |
| across the fibres | 2.5 | - |
| Modulus of elasticity (MPa) | ||
| along the fibres | 10,400 | 10,300 |
| Shear-modulus (MPa) | 650 | - |
| Density (kg/m3) | 355 | 420.09 |
| Beam Type | Description |
|---|---|
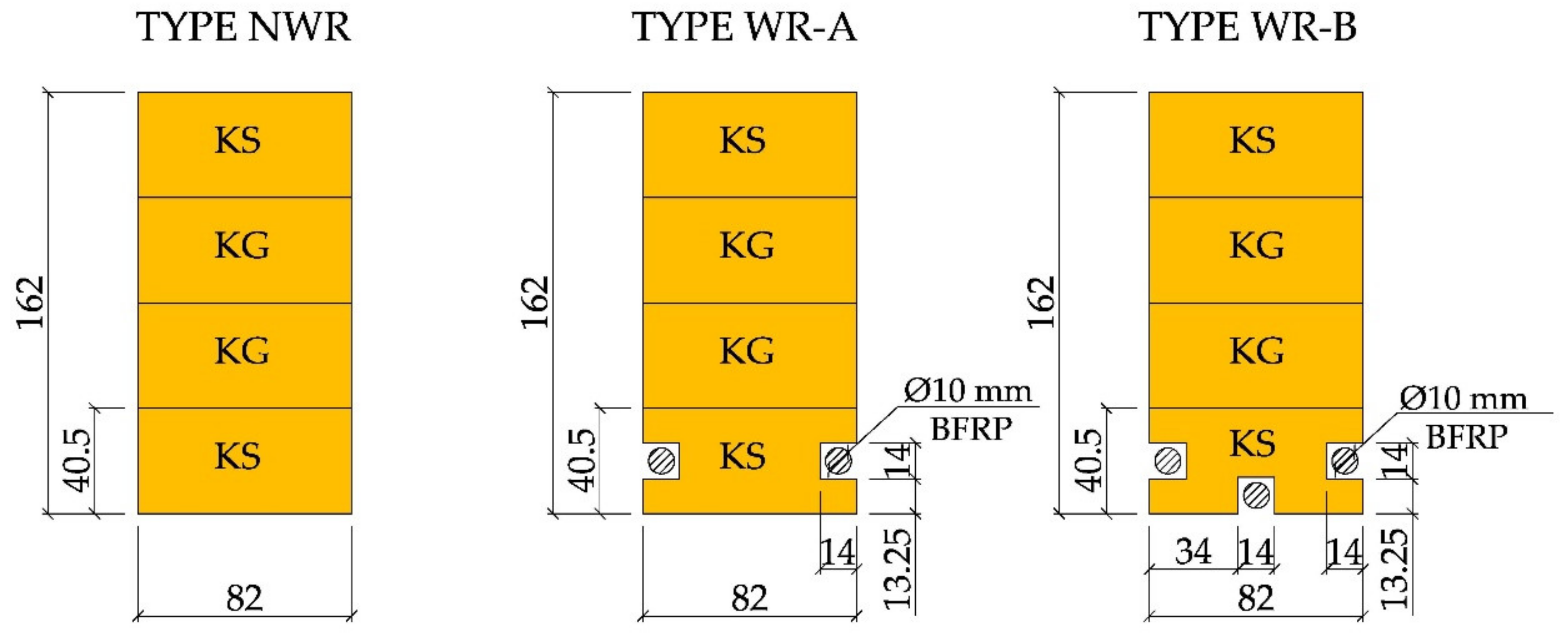
| NWR | non-reinforced beams made of glulam timber of average (KS) and poor (KG) quality |
| WR–A | reinforced beams made of glulam timber of average (KS) and poor quality (KG), reinforced with BFRP, reinforcement ratio: 1.18% |
| WR–B | reinforced beams made of glulam timber of average (KS) and poor quality (KG), reinforced with BFRP, reinforcement ratio: 1.76% |
| Feature | BFRP | Epoxy Glue |
|---|---|---|
| Materials properties | anisotropic | - |
| Density | 1.9 ÷ 2.10 g/cm3 | - |
| Tensile strength | do 1.45 GPa | - |
| Flexural strength | - | 0.11 ÷ 0.12 GPa |
| Modulus of elasticity | do 78 GPa | 2.7 ÷ 3.3 GPa |
| Linear expansion coefficient | 2.2% | - |
| Material Parameters | Young’s Modulus (GPa) | Poisson’s Ratio | Shear Modulus (GPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X Axis (the Longitudinal Direction) | Y Axis (the Radial Direction) | Z Axis (the Tangential Direction) | XY Axis (for a Radial Surface) | YZ Axis (for the Face) | XZ Axis (for the Tangent Surface) | XY Axis (for a Radial Surface) | YZ Axis (for the Face) | XZ Axis (for a Radial Surface) | |
| Lamella KS | 10 | 0.33 | 0.33 | 0.54 | 0.027 | 0.54 | 0.63 | 0.063 | 0.63 |
| Lamella KG | 7 | 0.23 | 0.23 | 0.54 | 0.027 | 0.54 | 0.44 | 0.044 | 0.44 |
| BFRP | 56.30 | 9.38 | 9.38 | 0.26 | 0.026 | 0.26 | 1.9 | 0.19 | 1.9 |
| Material Parameters | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|
| Epoxy glue | 3 | 0.30 |
| BEAM | F/2 [kN] | Compressive Stresses σc [MPa] | Tensile Stresses σt [MPa] | Stresses in BFRP Fibres σBFRP [MPa] | Displacements u [mm] |
|---|---|---|---|---|---|
| NWR-A1 | 5 | −13.12 | 8.54 | - | 13.42 |
| NWR-A2 | 5 | −10.63 | 15.97 | - | 13.92 |
| NWR-A3 | 5 | −8.34 | 10.22 | - | 13.64 |
| Mean | −10.70 | 11.58 | - | 13.66 | |
| Standard deviation | 2.39 | 3.90 | - | 0.25 | |
| WR-A1 | 5 | −12.00 | 13.07 | 58.74 | 12.89 |
| WR-A2 | 5 | −6.92 | 11.60 | 44.88 | 11.91 |
| WR-A3 | 5 | −11.90 | 13.38 | 55.69 | 12.09 |
| Mean | −10.27 | 12.68 | 53.10 | 12.30 | |
| Standard deviation | 2.90 | 0.95 | 7.28 | 0.52 | |
| WR-A1 | 10 | −26.60 | 26.65 | 117.75 | 28.05 |
| WR-A2 | 10 | −17.95 | 22.68 | 97.53 | 27.7 |
| WR-A3 | 10 | −25.85 | 28.48 | 126.62 | 29.06 |
| Mean | −23.47 | 25.94 | 113.97 | 28.27 | |
| Standard deviation | 4.79 | 2.97 | 14.91 | 0.70 |
| Beam | F/2 [kN] | Experimental Results | Theoretical Results | Numerical Results | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σc [MPa] | σt [MPa] | σBFRP [MPa] | u [mm] | σBFRP [MPa] | σc [MPa] | σt [MPa] | σBFRP [MPa] | u [mm] | ||
| NWR (Mean) | 5 | −10.70 | 11.58 | - | 13.66 | - | −9.86 | 10.57 | - | 16.30 |
| WR-A (Mean) | 5 | −10.27 | 12.68 | 53.10 | 12.30 | 82.34 | −8.55 | 8.65 | 48.83 | 15.10 |
| WR-A (Mean) | 10 | −23.47 | 25.94 | 113.97 | 28.27 | 164.68 | −18.49 | 17.00 | 100.04 | 30.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wdowiak-Postulak, A. Basalt Fibre Reinforcement of Bent Heterogeneous Glued Laminated Beams. Materials 2021, 14, 51. https://doi.org/10.3390/ma14010051
Wdowiak-Postulak A. Basalt Fibre Reinforcement of Bent Heterogeneous Glued Laminated Beams. Materials. 2021; 14(1):51. https://doi.org/10.3390/ma14010051
Chicago/Turabian StyleWdowiak-Postulak, Agnieszka. 2021. "Basalt Fibre Reinforcement of Bent Heterogeneous Glued Laminated Beams" Materials 14, no. 1: 51. https://doi.org/10.3390/ma14010051





