Strengthening Effect of Nb on Ferrite Grain Boundary in X70 Pipeline Steel
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
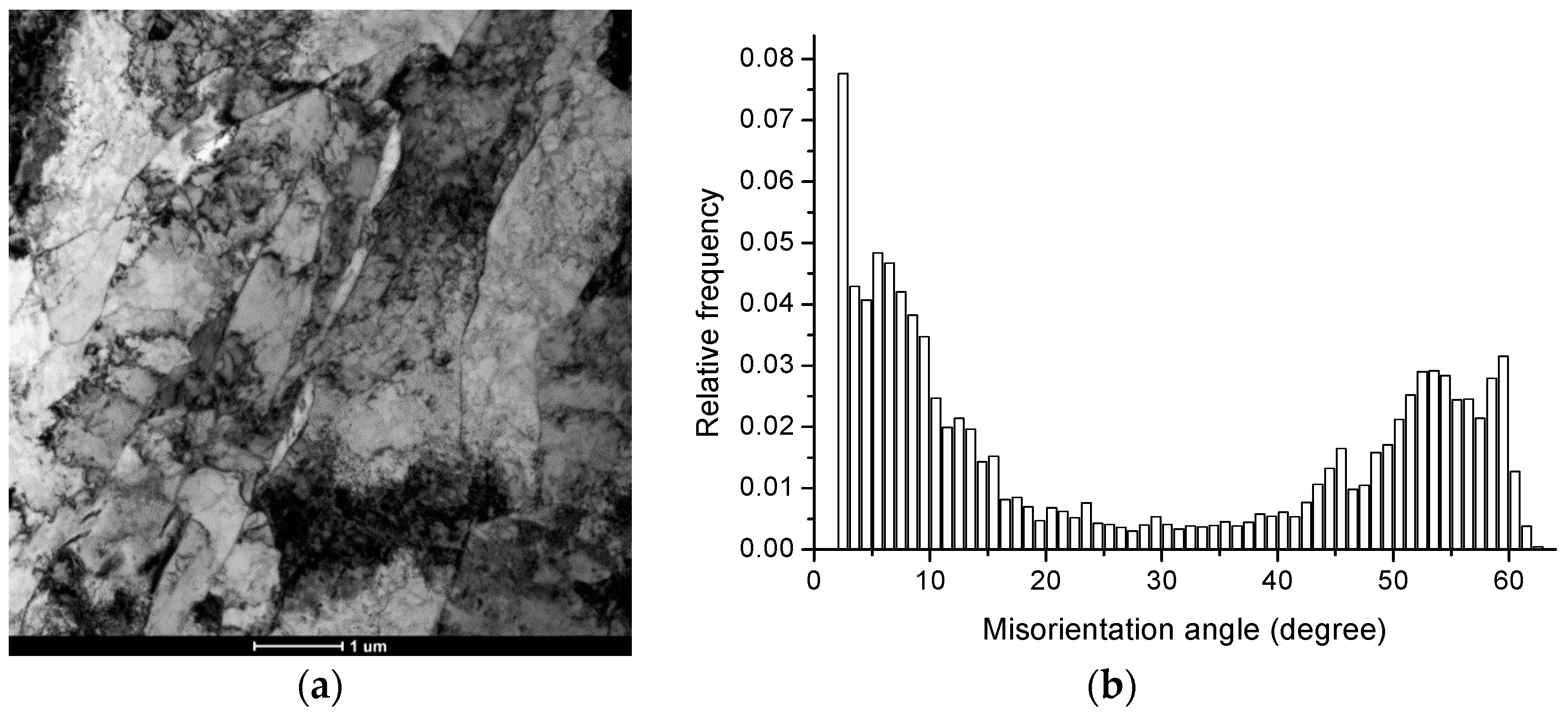
2.2. Microstructure Analysis
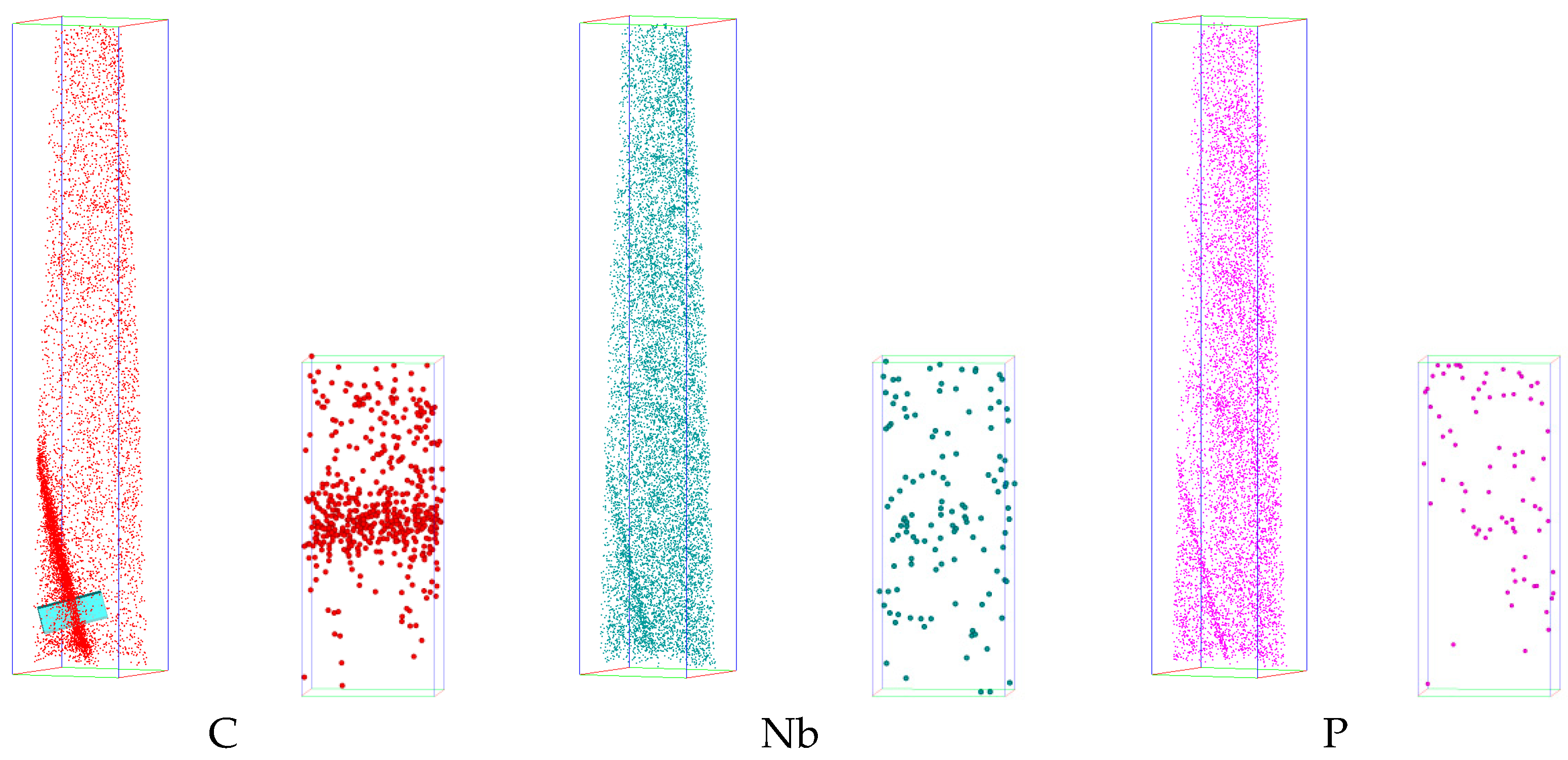
2.3. Three-Dimensional Atom Probe Test
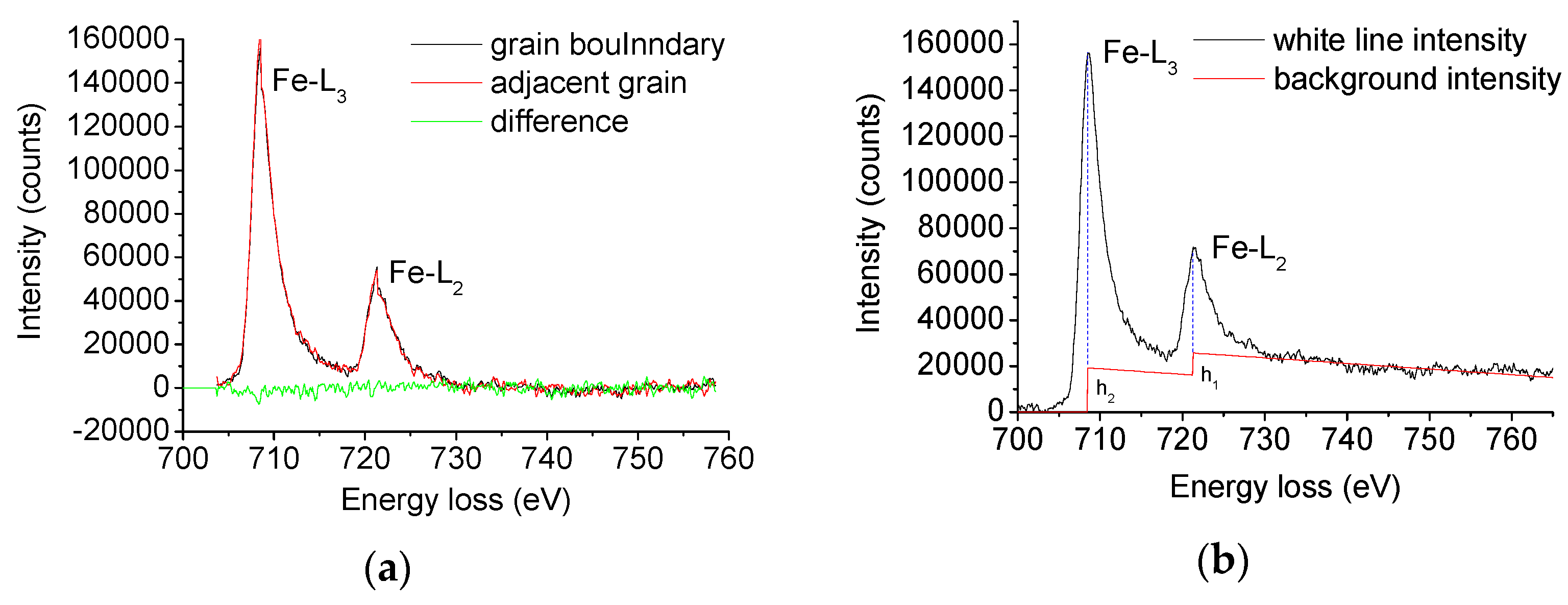
2.4. Electron Energy Loss Spectrum Measurement
2.5. First-Principles Calculation
3. Results and Discussion
3.1. Grain Boundary Characteristics
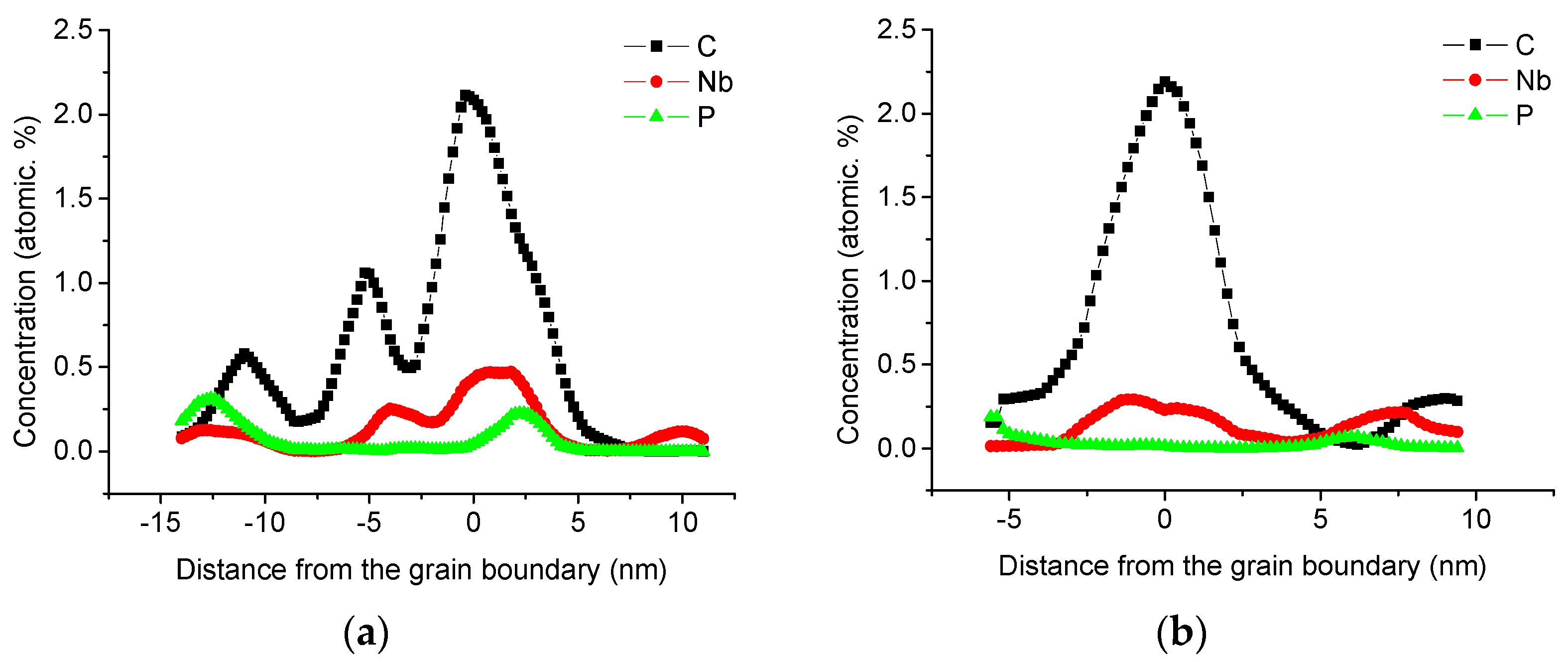
3.2. Elements Distribution Near Grain Boundaries
3.3. Electron Energy Loss Spectrum and Charges in the Occupancy of Fe 3d State
3.4. Segregation Energy
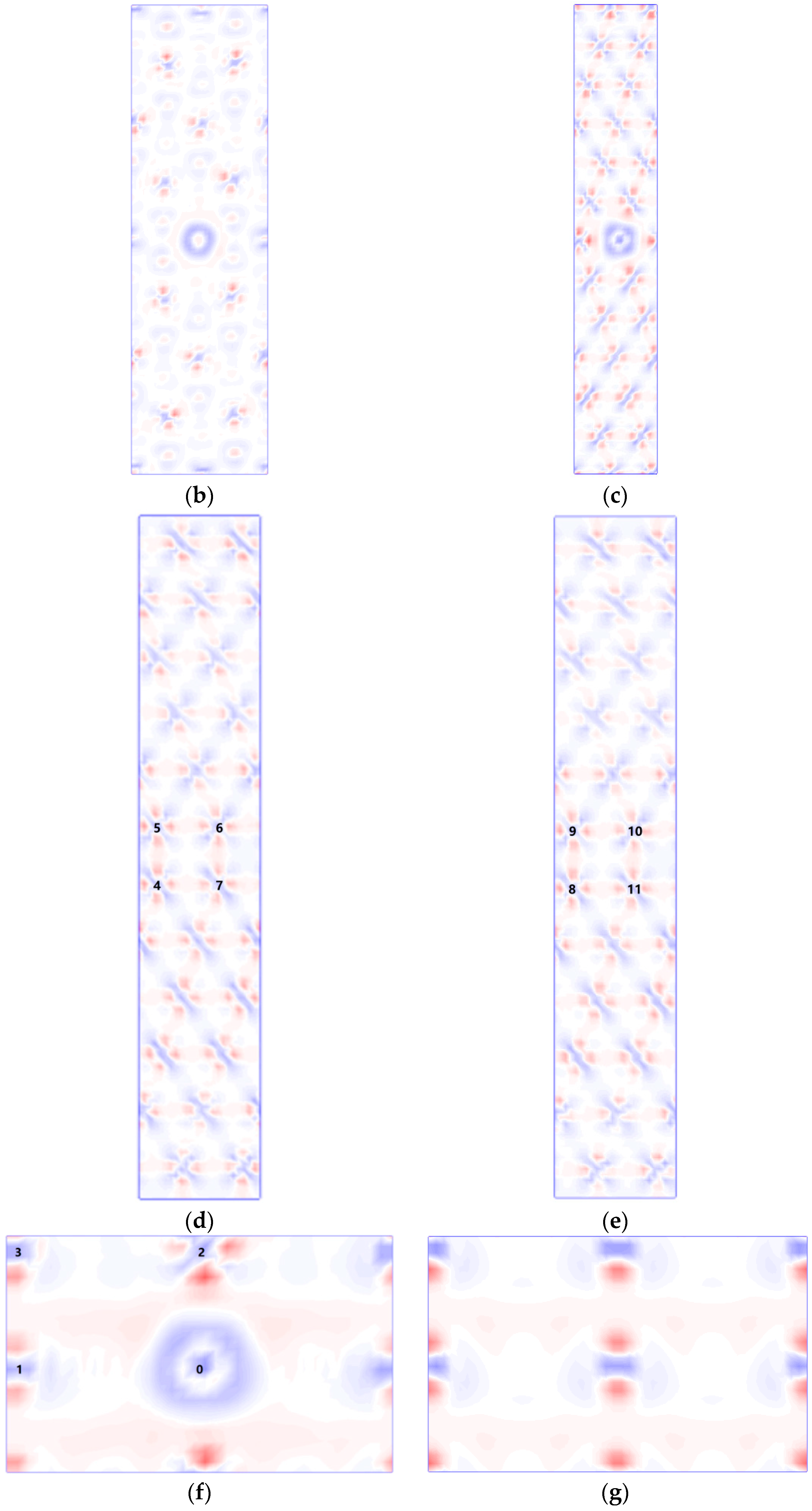
3.5. Charge Distribution
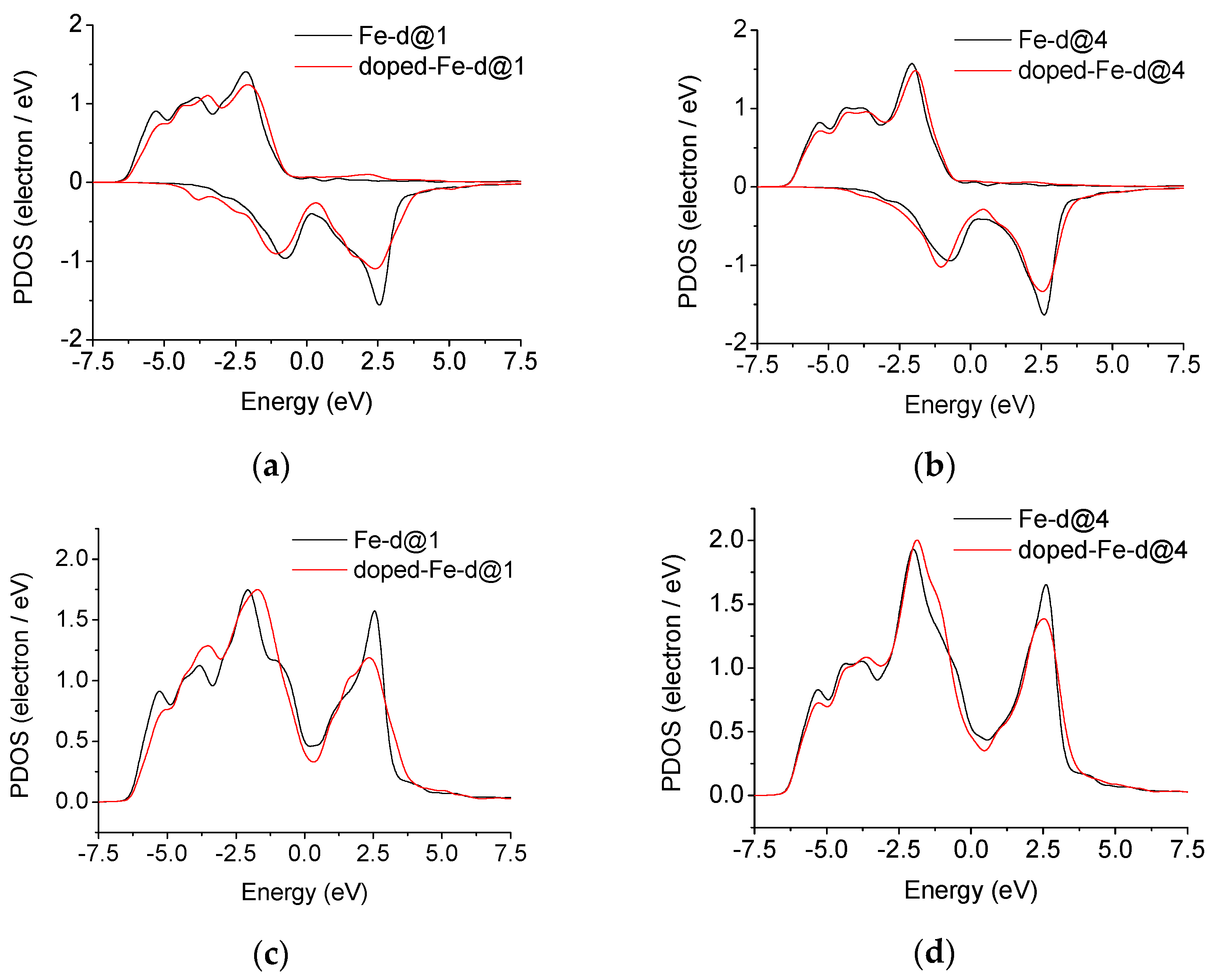
3.6. Electronic Density of State
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Bureau of Statistics. China Statistical Yearbook 2019; China Statistics Press: Beijing, China, 2019.
- Wang, X.X. Overview of the construction of super-large transportation capacity natural gas pipelines at home and abroad. Welded Pipe Tube 2019, 42, 1–9. [Google Scholar] [CrossRef]
- Jiang, Y.W.; Niu, T.; An, C.G.; Wu, X.L.; Zhang, C.X.; Dai, X.L. Strain aging behavior of X70 pipeline steel. Chin. J. Mater. Res. 2016, 30, 767–772. [Google Scholar] [CrossRef]
- Ji, L.K.; Li, H.L.; Zhao, W.Z.; Wang, H.T.; Chen, H.Y.; Li, Y. Microstructure and strain-hardening performance analysis for X70 high strain line pipe. J. Xi’An Jiao-tong Univ. 2012, 46, 108–113. [Google Scholar]
- Li, Z.Y.; Hu, X.W.; Li, W.S.; Tian, W.H.; Liu, D.L. Microstructure and properties of low yield strength ratio X70M steel. Trans. Mater. Heat Treat. 2016, 37, 135–140. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Thibaux, P.; Houbaert, Y. Recrystallization-precipitation interaction during austenite hot deformation of a Nb microalloyed steel. Mater. Sci. Eng. A 2011, 528, 5519–5528. [Google Scholar] [CrossRef]
- Dorin, T.; Wood, K.; Taylor, A.; Hodgson, P.; Stanford, N. Effect of coiling treatment on microstructural development and precipitate strengthening of a strip cast steel. Acta Mater. 2016, 115, 167–177. [Google Scholar] [CrossRef]
- Maruyama, N.; Uemori, R.; Sugiyama, M. The role of niobium in the retardation of the early stage of austenite recovery in hot-deformed steels. Mater. Sci. Eng. A 1998, 250, 2–7. [Google Scholar] [CrossRef]
- Hutchinson, C.R.; Zurob, H.S.; Sinclair, C.W.; Brechet, Y.J.M. The comparative effectiveness of Nb solute and NbC precipitates at impeding grain-boundary motion in Nb steels. Scr. Mater. 2008, 59, 635–637. [Google Scholar] [CrossRef]
- Jia, T.; Militzer, M. The effect of solute Nb on the austenite-to-ferrite transformation. Metall. Mater. Trans. A 2015, 46, 614–621. [Google Scholar] [CrossRef]
- Deardo, A.J. Niobium in modern steels. Int. Mater. Rev. 2013, 48, 371–402. [Google Scholar] [CrossRef]
- Shrestha, S.L.; Xie, K.Y.; Ringer, S.P.; Carpenter, K.R.; Smith, D.R.; Killmore, C.R.; Cairney, J.M. The effect of clustering on the mobility of dislocations during aging in Nb-microalloyed strip cast steels: In situ heating TEM observation. Scr. Mater. 2013, 69, 481–484. [Google Scholar] [CrossRef]
- Li, X.L.; Wu, P.; Yang, R.J.; Zhao, S.T.; Zhang, S.P.; Chen, S.; Cao, X.Z.; Wang, X.M. Nb segregation at prior austenite grain boundaries and defects in high strength low alloy steel during cooling. Mater. Design 2017, 115, 165–169. [Google Scholar] [CrossRef]
- Messmer, R.P.; Briant, C.L. The role of chemical bonding in grain boundary embrittlement. Acta Metall. 1982, 30, 457–467. [Google Scholar] [CrossRef]
- Wachowicz, E.; Kiejna, A. Effect of impurities on grain boundary cohesion in bcc iron. Comput. Mater. Sci. 2008, 43, 736–743. [Google Scholar] [CrossRef]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Olson, G.B. Effect of Mo and Pd on the grain boundary cohesion of Fe. Phys. Rev. B 2000, 62, 6208–6214. [Google Scholar] [CrossRef]
- Shang, J.X.; Zhao, D.L.; Wang, C.Y. Effect of titanium on bcc Fe grain boundary cohesion. Acta Metall. Sin. 2001, 37, 893–896. [Google Scholar] [CrossRef]
- Muller, D.A.; Singh, D.J.; Silcox, J. Connections between the electron energy loss spectra, the local electronic structure, and the physical properties of a material: A study of nickel aluminum alloys. Phys. Rev. B 1998, 57, 8181–8202. [Google Scholar] [CrossRef]
- Pearson, D.H.; Ahn, C.C.; Fultz, B. Measurements of 3d occupancy from Cu L2,3 electron-energy-loss spectra of rapidly quenched CuZr, CuTi, CuPd, CuPt, and CuAu. Phys. Rev. B 1994, 50, 12969–12972. [Google Scholar] [CrossRef]
- Reaz, M.; Haque, A.; Cornelison, D.M.; Wanekaya, A.; Delong, R.; Ghosh, K. Magneto-luminescent zinc/iron oxide core-shell nanoparticles with tunable magnetic properties. Phys. E 2020, 123, 114090. [Google Scholar] [CrossRef]
- Reaz, M.; Haque, A.; Ghosh, K. Synthesis, characterization, and optimization of magnetoelectric BaTiO3-Iron oxide core-shell nanoparticles. Nanomaterials 2020, 10, 563. [Google Scholar] [CrossRef]
- Pearson, D.H.; Ahn, C.C.; Fultz, B. White lines and d-electron occupancies for the 3d and 4d transition metals. Phys. Rev. B 1993, 47, 8471–8478. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.Q.; Wang, L.H.; Liu, Y. Computer simulation of the materials behaviour at the electronic and atomic scale. Chin. J. Mater. Res. 1998, 12, 1–19. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Pickard, M.J.P.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Wang, H.Y.; Gao, X.Y.; Ren, H.P.; Zhang, H.W.; Tan, H.J. First-principles characterization of lanthanum occupying tendency in α-Fe and effect on grain boundaries. Acta Phys. Sin. 2014, 63, 148101. [Google Scholar] [CrossRef]
- Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-principles study on the interaction of H interstitials with grain boundaries in α-Fe and γ-Fe. Phys. Rev. B 2011, 84, 144121. [Google Scholar] [CrossRef]
- Gao, N.; Fu, C.C.; Samaras, M.; Schäublin, R.; Victoria, M.; Hoffelner, W. Multiscale modelling of bi-crystal grain boundaries in bcc iron. J. Nucl. Mater. 2009, 385, 262–267. [Google Scholar] [CrossRef]
- Kohlhaas, R.; Dunner, P.; Schmitz-Prange, N.; Angew, Z. The temperature dependence of the lattice parameters of iron, cobalt, and nickel in the high temperature range. Physics 1967, 23, 245. [Google Scholar]
- Díaz-Fuentes, M.; Iza-Mendia, A.; Gutiérrez, I. Analysis of different acicular ferrite microstructures in low-carbon steels by electron backscattered diffraction. Metall. Mater. Trans. A 2003, 34, 2505–2516. [Google Scholar] [CrossRef]
- Gourgues, A.F.; Flower, H.M.; Lindley, T.C. Electron backscattering diffraction study of acicular ferrite, bainite, and martensite steel microstructures. Mater. Sci. Technol. 2000, 16, 26–40. [Google Scholar] [CrossRef]
- Wang, J.; Janisch, R.; Madsen, G.K.H.; Drautz, R. First-principles study of carbon segregation in bcc iron symmetrical tilt grain boundaries. Acta Mater. 2016, 115, 259–268. [Google Scholar] [CrossRef]
- Park, H.S.; Kang, J.S.; Yoo, J.Y.; Park, C.G. In-situ TEM and APT analysis on the dislocations associated with solute carbons in strain-aged low carbon pipeline steels. Mater. Sci. Forum 2010, 654–656, 122–125. [Google Scholar] [CrossRef]
- Zhang, D.B.; Wu, C.D.; Yang, R. Grain boundary segregation of P in Fe-P and Fe-P-Ce alloys and effect on their brittleness. Acta Metall. Sin. 1991, 27, A111–A114. [Google Scholar]
- Rice, J.R.; Wang, J.S. Embrittlement of interfaces by solute segregation. Mater. Sci. Eng. A 1989, 107, 23–40. [Google Scholar] [CrossRef]
- Peng, H.; Xie, Y.Q.; Wang, C.Y.; Wang, S.Y.; Peng, Q. Comparison between DV-Xαmethod and single2atom theory for calculating electronic structure and physical properties of pure Fe. Chin. J. Nonferrous Met. 2001, 11, 477–480. [Google Scholar]
- Cheng, L.Q.; Yu, T.; Xia, C.F.; Qiu, Z.C. Electronic structure and doping effect of kink in edge dislocation of body-centred cubic iron. Acta Phys. Sin. 2009, 58, S235–S239. [Google Scholar] [CrossRef]
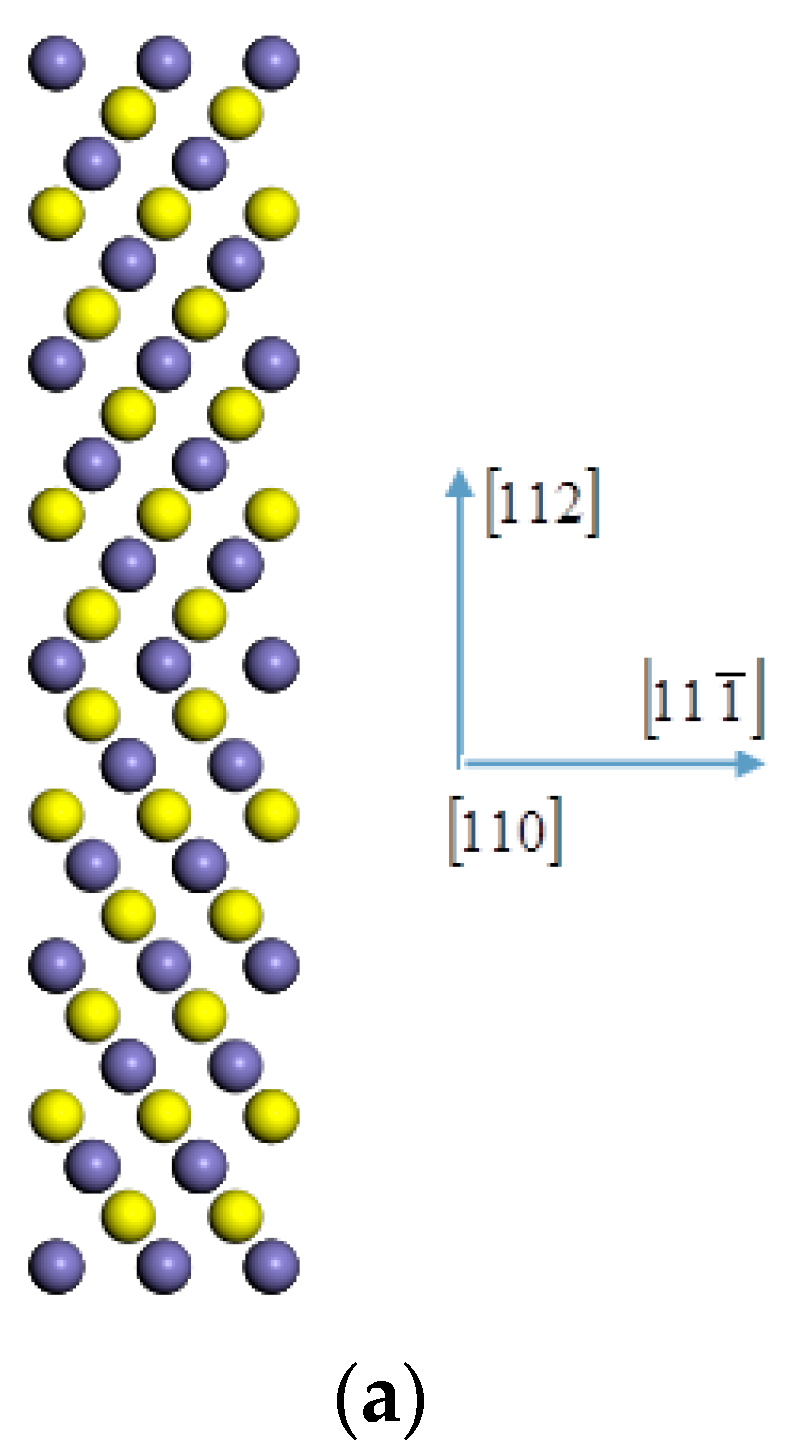

| Element | C | Si | Mn | P | Nb |
|---|---|---|---|---|---|
| Composition (wt.%) | 0.065 | 0.20 | 1.55 | 0.016 | 0.065 |
| Composition (at.%) | 0.300 | 0.39 | 1.57 | 0.029 | 0.039 |
| APT result inside grain (at.%) | 0.153 | 0.56 | 1.49 | 0.034 | 0.032 |
| Maximum concentration of sample 1 (at.%) | 2.110 | 1.27 | 2.50 | 0.220 | 0.466 |
| Maximum concentration of sample 2 (at.%) | 2.160 | 1.29 | 1.99 | 0.188 | 0.294 |
| Position | Grain Boundary | Adjacent Grain1 | Adjacent Grain2 |
|---|---|---|---|
| 1 | 7.25 | 7.22 | 7.24 |
| 2 | 7.57 | 7.44 | 7.18 |
| 3 | 7.29 | 7.24 | 7.05 |
| −377.46 | −178.38 | −376.98 | −370.30 | −178.34 | −20.74 | −13.63 | −20.26 | −7.12 | −6.64 | −0.04 |
| Bond | 0–1 | 4–5 | 7–6 | 8–9 | 11–10 | 4–8 | 5–9 | 6–10 | 7–11 |
|---|---|---|---|---|---|---|---|---|---|
| undoped | 2.482 | 2.420 | 2.420 | 2.420 | 2.420 | 2.482 | 2.482 | 2.482 | 2.482 |
| Nb-doped | 2.461 | 2.396 | 2.388 | 2.387 | 2.385 | 2.453 | 2.462 | 2.462 | 2.468 |
| Atom | Orbital | Fe (Nb) | Fe1 | Fe4 | Fe8 |
|---|---|---|---|---|---|
| Undoped | 4s | 0.62 | 0.62 | 0.62 | 0.62 |
| 4p | 0.83 | 0.83 | 0.79 | 0.79 | |
| 3d | 6.57 | 6.57 | 6.59 | 6.59 | |
| total | 8.03 | 8.03 | 8.0 | 8.0 | |
| Charge/e | −0.03 | −0.03 | 0 | 0 | |
| Nb-doped | 4s (5s) | 2.8 | 0.71 | 0.69 | 0.64 |
| 4p (4p) | 4.94 | 0.77 | 0.73 | 0.73 | |
| 3d (4d) | 4.01 | 6.68 | 6.66 | 6.62 | |
| Total | 11.75 | 8.16 | 8.08 | 7.99 | |
| Charge/e | 1.25 | −0.16 | −0.08 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, Z.; Tian, W. Strengthening Effect of Nb on Ferrite Grain Boundary in X70 Pipeline Steel. Materials 2021, 14, 61. https://doi.org/10.3390/ma14010061
Li Z, Li Z, Tian W. Strengthening Effect of Nb on Ferrite Grain Boundary in X70 Pipeline Steel. Materials. 2021; 14(1):61. https://doi.org/10.3390/ma14010061
Chicago/Turabian StyleLi, Zhongyi, Zhipeng Li, and Wenhuai Tian. 2021. "Strengthening Effect of Nb on Ferrite Grain Boundary in X70 Pipeline Steel" Materials 14, no. 1: 61. https://doi.org/10.3390/ma14010061
APA StyleLi, Z., Li, Z., & Tian, W. (2021). Strengthening Effect of Nb on Ferrite Grain Boundary in X70 Pipeline Steel. Materials, 14(1), 61. https://doi.org/10.3390/ma14010061






