Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting
Abstract
:1. Introduction
2. Model Approaches
2.1. Heat Transfer and Molten Pool Flow Control Equations
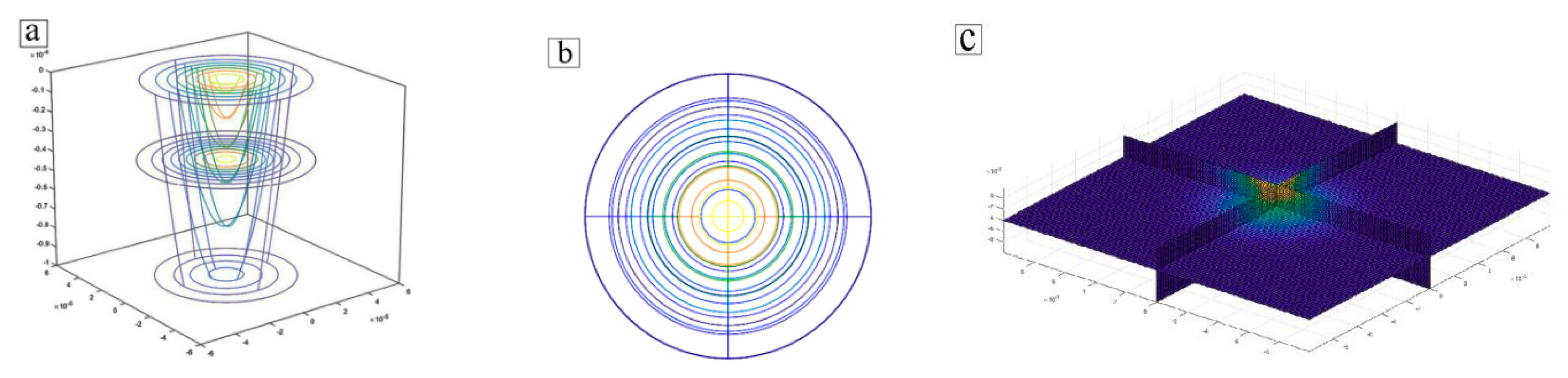
2.2. Heat Source
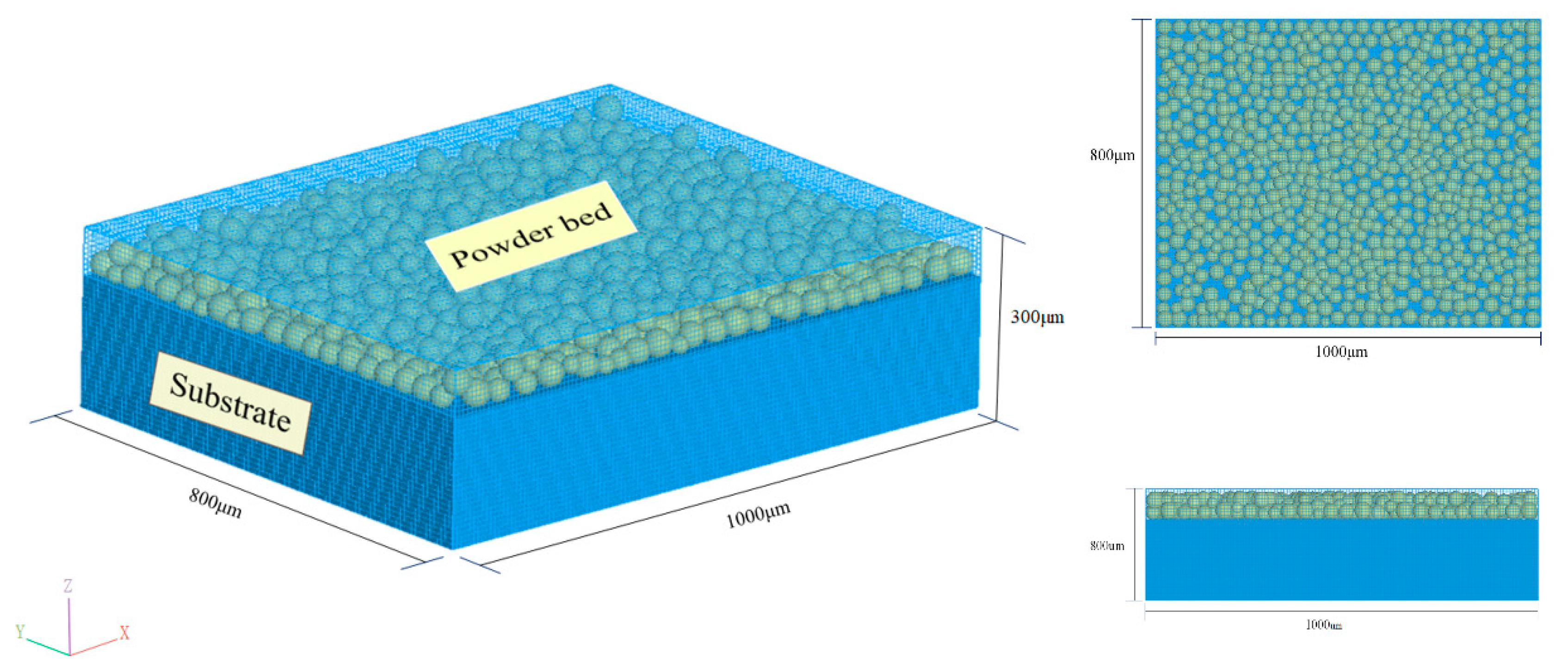
2.3. Model Computing Domain and Power Bed Model
2.4. Boundary Conditions
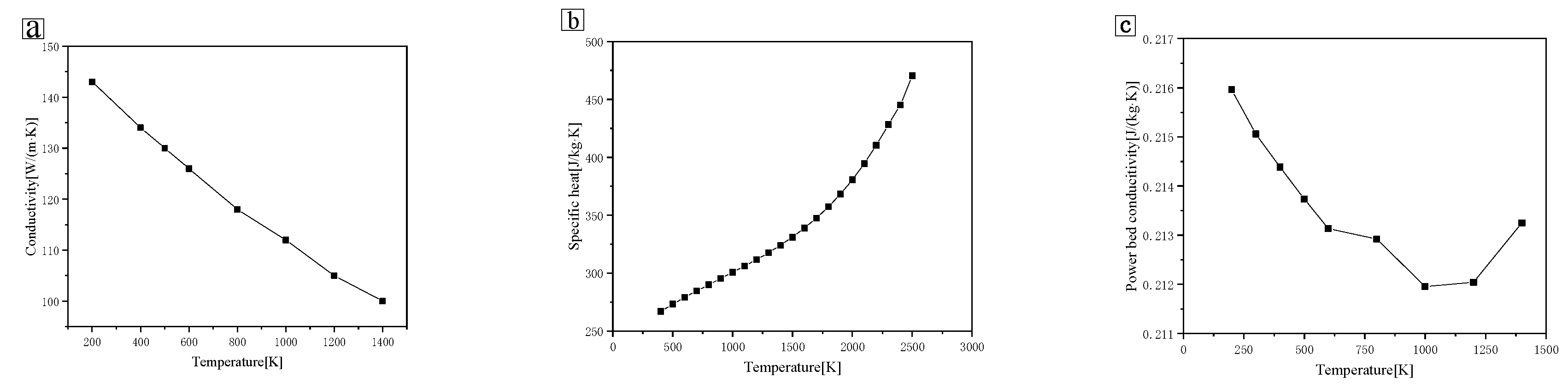
2.5. Thermal Properties of Materials
3. Selective Laser Melting Experiment
4. Results and Discussion
4.1. Optical Microscope (OM) and Simulation Morphology Diagram of Single Track
4.2. Melt Pool Structure and Powder Spatter over Time
4.3. Impact of Marangoni Flow on Defect Suppression
4.4. The Effect of Laser Interaction Time
5. Conclusions
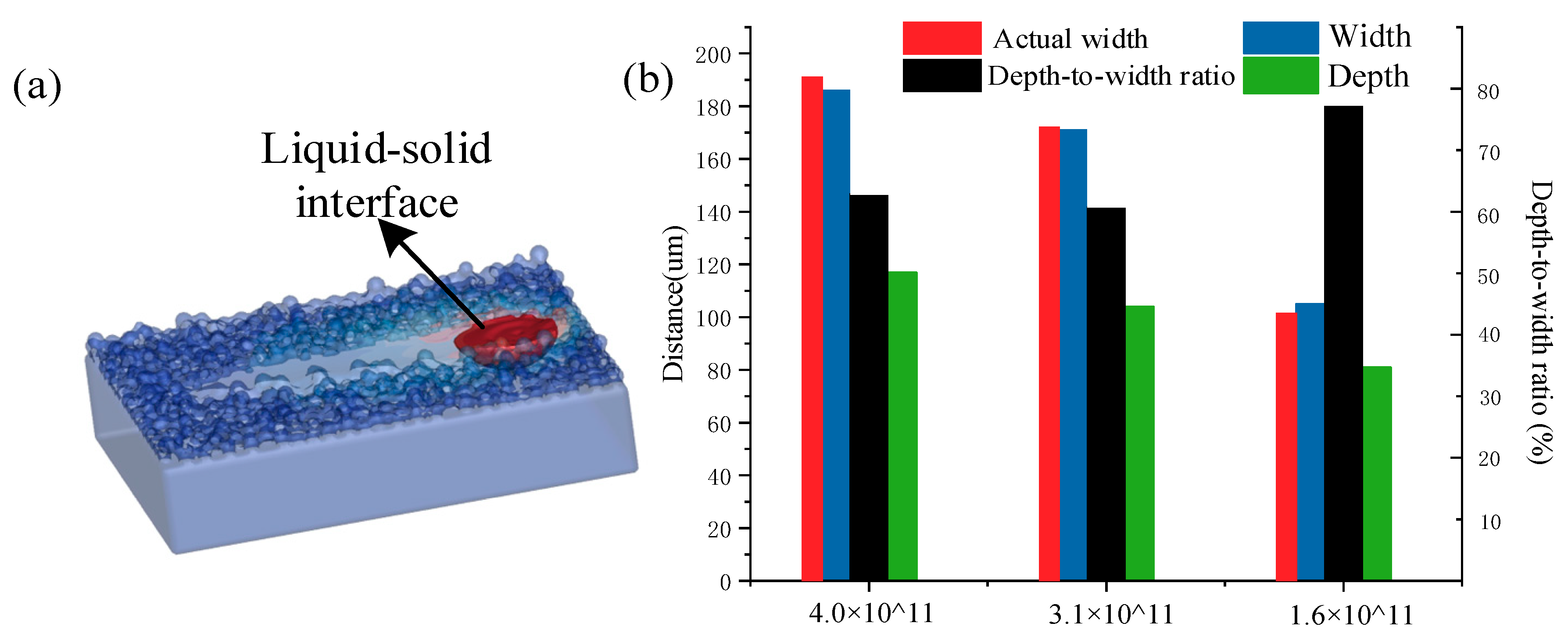
- According to the simulation and experiments results of the pure molybdenum single track, it was concluded that keeping the energy density in the range of 3.1 × 1011–4.0 × 1011 J/m3 maintained appropriate melt channel depth and width. Otherwise, over-melting or insufficient melting would occur and layer-by-layer printing would cause the defects to be enlarged.
- In the process of printing pure molybdenum, the occurrence of laser melting defects was related to molten pool convection and surface ripples. The Marangoni flow backflow helped to fuse the pores and inhibit the generation of defects, while higher energy input was likely to cause unsteady oscillations at the edge of the molten pool, where it was easy for defects to be produced.
- The laser interaction time tmelt and tvapor values were used to measure the time to reach the melting and evaporation points under each laser parameter in the simulation. Considering the solidification/spreading competition mechanism and the range of laser parameters at a suitable density, the processing window for the droplet to maintain better spreading behavior was obtained, which proved that the molten droplet could better complete the spreading behavior when the laser action time was higher than the equilibrium point. This provides a simulation theory guide from the perspective of laser interaction time for the future additive manufacturing of molybdenum alloys.
Author Contributions
Funding
Conflicts of Interest
References and Note
- Dimiduk, D.M.; Perepezko, J.H. Mo-Si-B Alloys: Developing a Revolutionary Turbine-Engine Material. Mrs Bull. 2003, 28, 639–645. [Google Scholar] [CrossRef]
- Andreev, D.E.; Vdovin, Y.S.; Yukhvid, V.I.; Sachkova, N.V.; Kovalev, I.D. Centrifugal SHS-Metallurgy of Composite Materials Mo–Si–B. Russ. J. Phys. Chem. B 2020, 14, 261–265. [Google Scholar] [CrossRef]
- Makineni, S.K.; Kini, A.R.; Jägle, E.A.; Springer, H.; Raabe, D.; Gault, B. Synthesis and stabilization of a new phase regime in a Mo-Si-B based alloy by laser-based additive manufacturing. Acta Mater. 2018, 151, 31–40. [Google Scholar] [CrossRef]
- Lin, J.Z.; Ru, Y.M.; Yan, B.Z.; Qian, G.; Chen, H.W.; Jian, X.Z.; Suck, J.N. Investigation on dissimilar laser beam welding of molybdenum to zirconium via pure titanium interlayer. Opt. Laser Technol. 2020, 131, 106327. [Google Scholar]
- Liverani, E.; Fortunato, A.; Leardini, A.; Belvedere, C.; Siegler, S.; Ceschini, L.; Ascari, A. Fabrication of Co–Cr–Mo endoprosthetic ankle devices by means of Selective Laser Melting (SLM). Mater. Des. 2016, 106, 60–68. [Google Scholar] [CrossRef]
- Anonymous. BUYINS.NET: F, FRE, SLM, MO, HAL, EMC With Highest Daily Short Volume on NYSE Wednesday. M2 Presswire 2009.
- Liang, X.L.; Sridhar, N.; Yong, W.Z. Phase field simulation of powder bed-based additive manufacturing. Acta Mater. 2018, 144, 801–809. [Google Scholar]
- Wang, D.; Yu, C.; Ma, J.; Liu, W.; Shen, Z. Densification and crack suppression in selective laser melting of pure molybdenum. Mater. Des. 2017, 129, 44–52. [Google Scholar] [CrossRef]
- Maamoun, A.H.; Xue, Y.F.; Elbestawi, M.A.; Veldhuis, S.C. Effect of Selective Laser Melting Process Parameters on the Quality of Al Alloy Parts: Powder Characterization, Density, Surface Roughness and Dimensional Accuracy. Materials 2018, 11, 2343. [Google Scholar] [CrossRef] [Green Version]
- Saprykin, A.A.; Sharkeev, Y.P.; Saprykina, N.A.; Saprykina, E.A.; Ibragimov, N.A. The Mechanism of Forming Coagulated Particles in Selective Laser Melting of Cobalt-Chromium-Molybdenum Powder. Key Eng. Mater. 2020, 839, 79–85. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.S.; Zhang, W. Modeling of heat transfer, fluid flow and solidification microstructure of nickel-base superalloy fabricated by laser powder bed fusion. Addit. Manuf. 2016, 12, 178–188. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Bai, P.K.; Li, Y.X. Preparation and Selective Laser Sintering Mechanism of 78Polymer-Coated Mo Powder. Adv. Mater. Res. 2010, 148, 511–514. [Google Scholar] [CrossRef]
- Kruth, J.P.; Mercelis, P.; Vaerenbergh, J.V.; Froyen, L.J.; Rombouts, M. Binding Mechanisms in Selective Laser Sintering and Selective Laser Melting. Rapid Prototyp. J. 2005, 11, 26–36. [Google Scholar] [CrossRef] [Green Version]
- Louvis, E.; Fox, P.; Sutcliffe, C.J. Selective laser melting of aluminium components. J. Mater. Process. Technol. 2011, 211, 275–284. [Google Scholar] [CrossRef]
- Gürtler, F.-J.; Karg, M.; Leitz, K.H.; Schmidt, M. Simulation of Laser Beam Melting of Steel Powders using the Three-Dimensional Volume of Fluid Method. Phys. Procedia 2013, 41, 874–879. [Google Scholar] [CrossRef] [Green Version]
- Schopp, H.; Sperl, A.; Kozakov, R.; Gtt, G. Temperature and emissivity determination of liquid steel S235. J. Phys. D Appl. Phys. 2012, 45, 235203. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Dongyun, Z.; Pudan, Z.; Zhen, L.; Zhe, F.; Chengjie, W.; Yanwu, G. Thermofluid field of molten pool and its effects during selective laser melting (SLM) of Inconel 718 alloy. Addit. Manuf. 2018, 21, 567–578. [Google Scholar]
- King, W.E.; Anderson, A.T.; Ferencz, R.M.; Kamath, C.; Khairallah, S.A.; Rubenchik, A.M. Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Appl. Phys. Rev. 2015, 2, 44–6270. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, D.; Liu, X.; Zhang, D.; Qu, S.; Ma, J.; London, G.; Shen, Z.; Liu, W. 3D-imaging of selective laser melting defects in a Co–Cr–Mo alloy by synchrotron radiation micro-CT. Acta Mater. 2015, 98, 1–16. [Google Scholar] [CrossRef]
- Krivilyov, M.D.; Mesarovic, S.D.; Sekulic, D.P. Phase-field model of interface migration and powder consolidation in additive manufacturing of metals. Mat. Sci. 2017, 52, 4155–4163. [Google Scholar] [CrossRef]
- Zinoviev, A.; Zinovieva, O.; Ploshikhia, V.; Romanova, V.; Balokhonov, R. Evolution of grain structure during laser additive manufacturing. Simulation by a cellular automata method. Mat. Des. 2016, 106, 321–329. [Google Scholar]
- Schiaffino, S.; Sonin, A.A. Molten droplet deposition and solidification at low Weber numbers. Phys. Fluids 1997, 9, 3172–3187. [Google Scholar] [CrossRef]
- Wayne, E.K.; Barth, H.D.; Castillo, V.M.; Gallegos, G.F.; Gibbs, J.W.; Hahn, D.E.; Kamath, C.; Rubenchik, A.M. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J. Mat. Proc. Technol. 2014, 214, 2915–2925. [Google Scholar]
- King, W.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E. Overview of modelling and simulation of metal powder bed fusion process at Lawrence Livermore National Laboratory. Mater. Sci. Technol. 2015, 31, 957–968. [Google Scholar] [CrossRef]








| [kg/m3] | 10.2·103 |
| Viscosity [Pas] | 7.5·10−3 |
| Surface tension [Nm] | 2.27 |
| Temperature coefficient [(Nm)/T] | −0.0001 |
| Absorption coefficient A [-] | 0.34 |
| Melting temperature Tm [K] | 2873 |
| Evaporation temperature Tv [K] | 4912 |
| Melting enthalpy Hm [J/kg] | 2.9·105 |
| Emissivity [-] | 0.8 |
| Convective heat transfer coefficient [W/m2] | 80 |
| Evaporation enthalpy Hv [J/kg] | 5.6·106 |
| Molar mass of metal vapor M [kg/mol] | 0.096 |
| Parameters | 4.0 × 1011 J/m3 | 3.1 × 1011 J/m3 | 1.6 × 1011 J/m3 | 9.0 × 1011 J/m3 |
|---|---|---|---|---|
| Laser power | 400 W | 310 W | 400 W | 450 W |
| Scanning speed | 400 m/s | 400 m/s | 1000 m/s | 200 m/s |
| Powder thickness | 50 μm | 50 μm | 50 μm | 50 μm |
| Laser diameter | 100 μm | 100 μm | 100 μm | 100 μm |
| Energy Densities | |
|---|---|
| 4.0 × 1011 J/m3 | 136 |
| 3.1 × 1011 J/m3 | 125 |
| 1.6 × 1011 J/m3 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Wang, L.; Wang, C.; Ding, X.; Liu, J. Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting. Materials 2021, 14, 75. https://doi.org/10.3390/ma14010075
Guo Z, Wang L, Wang C, Ding X, Liu J. Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting. Materials. 2021; 14(1):75. https://doi.org/10.3390/ma14010075
Chicago/Turabian StyleGuo, Zhenping, Lei Wang, Cheng Wang, Xiangyu Ding, and Jichao Liu. 2021. "Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting" Materials 14, no. 1: 75. https://doi.org/10.3390/ma14010075
APA StyleGuo, Z., Wang, L., Wang, C., Ding, X., & Liu, J. (2021). Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting. Materials, 14(1), 75. https://doi.org/10.3390/ma14010075




