Hydrogen Transportation Behaviour of V–Ni Solid Solution: A First-Principles Investigation
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Structural Stability of V–Ni Solid Solution
3.2. Stability of H Atoms near Multiple Ni Atoms
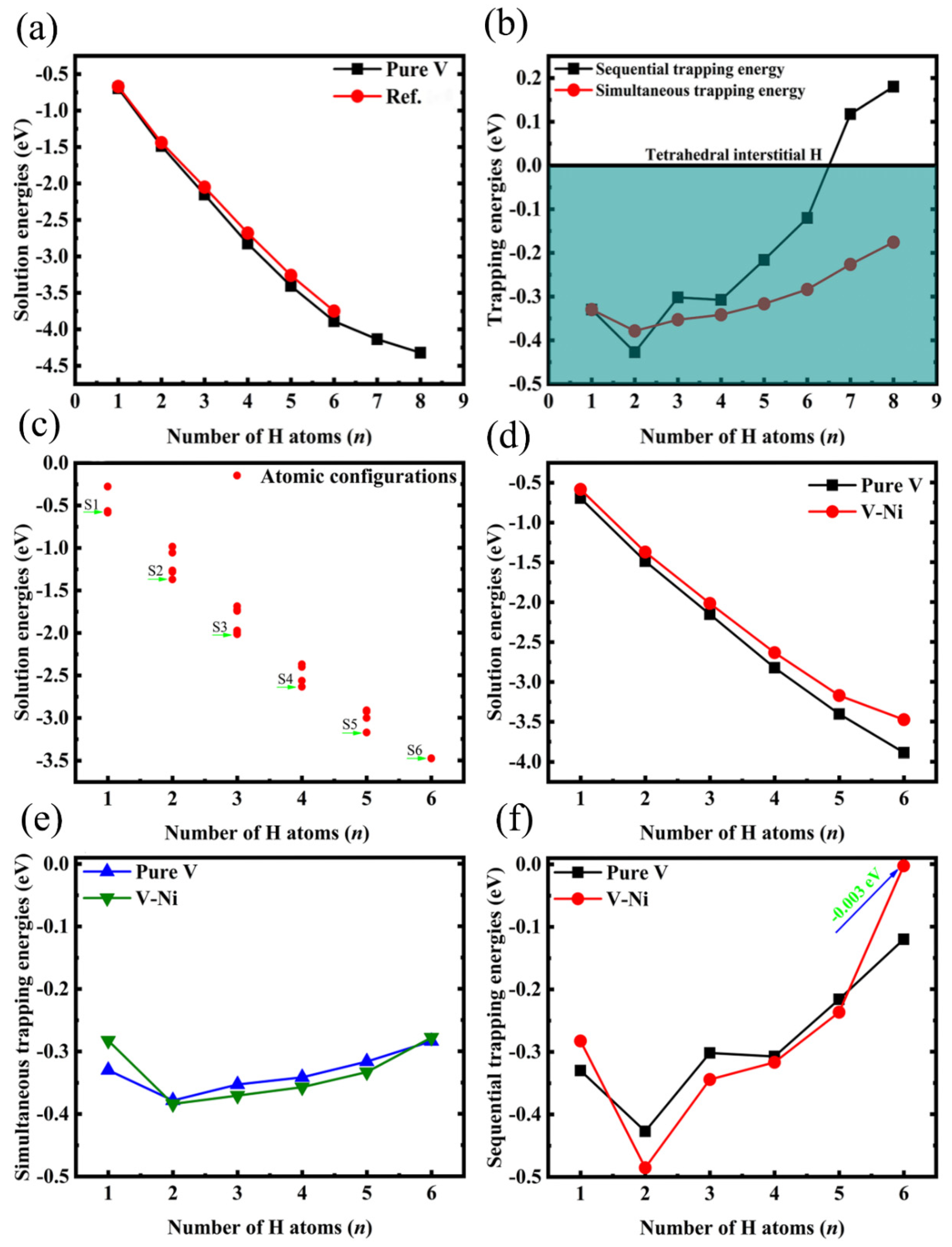
3.3. Interactions between Monovacancies and Multiple H Atoms
3.4. Monovacancy and Vac-nH Cluster Concentrations
3.5. H Diffusion in Interstitials and Vacancies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thomas, J.M.; Edwards, P.P.; Dobson, P.J.; Owen, G.P. Decarbonising energy: The developing international activity in hydrogen technologies and fuel cells. J. Energy Chem. 2020, 51, 405–415. [Google Scholar] [CrossRef]
- Yartys, V.A.; Baricco, M.; Colbe, J.B.V.; Blanchard, D.; Zlotea, C. Materials for hydrogen-based energy storage: Past, recent progress and future outlook. J. Alloys Compd. 2020, 827, 153548. [Google Scholar]
- Cassone, G. Nuclear quantum effects largely influence molecular dissociation and proton transfer in liquid water under an electric field. J. Phys. Chem. Lett. 2020, 11, 8983–8988. [Google Scholar]
- Lu, G.; Kaxiras, E. Hydrogen embrittlement of aluminum: The crucial role of vacancies. Phys. Rev. Lett. 2005, 94, 155501. [Google Scholar] [CrossRef] [Green Version]
- Abe, J.O.; Popoola, A.P.I.; Ajenifuja, E.; Popoola, O.M. Hydrogen energy, economy and storage: Review and recommendation. Int. J. Hydrog. Energy 2019, 44, 15072–15086. [Google Scholar] [CrossRef]
- Xing, W.W.; Chen, X.Q.; Li, X.B.; Ma, Y.C.; Chen, B.; Liu, K. First-principles study of hydrogen trapping behavior in face centered cubic metals (M = Ni, Cu and Al) with monovacancy. Int. J. Hydrog. Energy 2020, 45, 25555–25566. [Google Scholar] [CrossRef]
- Al-Mufachi, N.A.; Rees, N.V.; Steinberger-Wilkens, R. Hydrogen selective membranes: A review of palladium-based dense metal membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Yun, S.; Oyama, S.T. Correlations in palladium membranes for hydrogen separation: A review. J. Membr. Sci. 2011, 375, 28–45. [Google Scholar] [CrossRef]
- Dolan, M.D. Non-Pd, BCC alloy membranes for industrial hydrogen separation. J. Membr. Sci. 2010, 362, 12–28. [Google Scholar] [CrossRef]
- Peng, J.; Song, G.S.; Daniel, L.; Wu, W.P.; Hua, T.S. Vanadium-based alloy membranes for hydrogen purification. Rare Met. Mater. Eng. 2017, 46, 857–863. [Google Scholar]
- Phair, J.W.; Donelson, R. Developments and design of novel (Non-Palladium-Based) metal membranes for hydrogen separation. Ind. Eng. Chem. Res. 2006, 16, 5657–5674. [Google Scholar] [CrossRef]
- Hua, J.; Liu, Y.L.; Zhao, M.W.; Liu, X.D. Effects of Cr on H and He trapping and vacancy complexes in V in a fusion environment: A first-principles study. Eur. Phys. J. B 2017, 90, 119. [Google Scholar] [CrossRef]
- Zhang, P.B.; Zhao, J.J.; Wen, B. Trapping of multiple hydrogen atoms in a vanadium monovacancy: A first-principles study. J. Nucl. Mater. 2012, 429, 216–220. [Google Scholar] [CrossRef]
- Zhang, P.B.; Zou, T.T.; Feng, S.B.; Zhao, J.J. First principles investigations of hydrogen interaction with vacancy-oxygen complexes in vanadium alloys. Int. J. Hydrog. Energy 2019, 44, 26637–26645. [Google Scholar] [CrossRef]
- Akiba, E.; Iba, H. Hydrogen absorption by Laves phase related BCC solid solution. Intermetallics 1998, 6, 461–470. [Google Scholar] [CrossRef]
- Tsukahara, M.; Kamiya, T.; Takahashi, K. Hydrogen storage and electrode properties of V-based solid solution type alloys prepared by a thermic process. J. Electrochem. Soc. 2000, 147, 2941–2944. [Google Scholar] [CrossRef]
- Li, D.; Lou, Y.W.; Du, J.L.; Pu, C.H.; Huang, T.S.; Li, Z.L.; Wu, Z. Research progress of Vanadium-based hydrogen storage alloy. Mater. Rep. 2015, 29, 92–97. [Google Scholar]
- Kumar, S.; Jain, A.; Ichikawa, T.; Kojima, Y.; Dey, G.K. Development of vanadium based hydrogen storage material: A review. Renew. Sustain. Energy Rev. 2017, 72, 791–800. [Google Scholar] [CrossRef]
- Yukawa, H.; Teshima, A.; Yamashita, D.; Ito, S.; Yamaguchi, S.; Morinaga, M. Alloying effects on the hydriding properties of vanadium at low hydrogen pressures. J. Alloys Compd. 2002, 337, 264–268. [Google Scholar] [CrossRef]
- Kim, K.H.; Shim, J.H.; Lee, B.J. Effect of alloying elements (Al, Co, Fe, Ni) on the solubility of hydrogen in vanadium: A thermodynamic calculation. Int. J. Hydrog. Energy 2012, 9, 7836–7847. [Google Scholar] [CrossRef]
- Dolan, M.D.; Kellam, M.E.; Mclennan, K.G.; Liang, D.; Song, G. Hydrogen transport properties of several vanadium-based binary alloys. Int. J. Hydrog. Energy 2013, 23, 9794–9799. [Google Scholar] [CrossRef]
- Amano, M.; Komaki, M.; Nishimura, C. Hydrogen permeation characteristics of palladium-plated V-Ni alloy membranes. J. Less-Common Met. 1991, 172, 727–731. [Google Scholar] [CrossRef]
- Nishimura, C.; Komaki, M.; Amano, M. Hydrogen permeation characteristics of vanadium-nickel alloys. Mater. Trans. 1991, 32, 501. [Google Scholar] [CrossRef] [Green Version]
- Jiang, P.; Sun, B.L.; Wang, H.C.; Peng, G.S.; Ma, Y.Z.; Song, G.S.; Dolan, M. Effect of partial Ni substitution in V85Ni15 by Ti on microstructure, mechanical properties and hydrogen permeability of V-based bcc alloy membranes. Mater. Res. Express 2020, 7, 066505. [Google Scholar] [CrossRef]
- Rusman, N.A.A.; Dahari, M. A review on the current progress of metal hydrides material for solid-state hydrogen storage applications. Int. J. Hydrog. Energy 2016, 41, 12108–12126. [Google Scholar] [CrossRef]
- Fan, K.; Chen, H.; Ji, Y.; Huang, H.; Claesson, P.M. Nicke-vanadium monolayer double hydroxide for efficient electrochemical water oxidation. Nat. Commun. 2016, 7, 11981. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.Y.; Wang, Z.M.; Wang, D.H.; Wang, F.; Yan, X.F.; Zhong, Y.; Hu, C.H.; Zhou, H.Y. First-principle investigation of hydrogen solubility and diffusivity in transition metal-doped vanadium membranes and their mechanical properties. J. Alloys Compd. 2019, 805, 747–756. [Google Scholar] [CrossRef]
- Zhang, P.B.; Zou, T.T.; Zhao, J.J.; Zheng, P.F.; Chen, J.M. Diffusion and retention of hydrogen in vanadium in presence of Ti and Cr: First-principles investigations. J. Nucl. Mater. 2016, 484, 276–282. [Google Scholar] [CrossRef]
- Lee, Y.S.; Ouyang, C.; Suh, J.Y.; Fleury, E.; Cho, Y.W.; Shim, J.H. Role of alloying elements in vanadium-based binary alloy membranes for hydrogen separation. J. Membr. Sci. 2012, 51, 332–341. [Google Scholar] [CrossRef]
- Wang, Z.M.; Qin, J.Y.; Hu, Q.; Wang, D.H.; Wang, F.; Zhong, Y.; Zhang, J.X.; Zhou, H.Y.; Dong, M.Y.; Hu, C.H.; et al. Theoretical investigation of molybdenum/tungsten-vanadium solid solution alloy membranes: Thermodynamic stability and hydrogen permeation. J. Membr. Sci. 2020, 608, 118200. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab-initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1998, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henkelman, G.; Uberuaga, B.P.; Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Gui, L.J.; Liu, Y.L.; Wang, W.T.; Jin, S.; Zhang, Y.; Lu, G.H.; Yao, J.E. First-principles investigation on vacancy trapping behaviors of hydrogen in vanadium. J. Nucl. Mater. 2013, 442, S688–S693. [Google Scholar] [CrossRef]
- Maroevic, P.; Mclellan, R.B. Equilibrium vacancy concentration in Pd–H solid solutions. Acta Mater. 1998, 46, 5593–5597. [Google Scholar] [CrossRef]
- Rao, J.P.; Ouyang, C.Y.; Lei, M.S.; Jiang, F.Y. Vacancy and H Interactions in Nb. Chin. Phys. Lett. 2011, 28, 127101–127104. [Google Scholar] [CrossRef]
- Zhang, P.; Zou, T.; Liu, W.; Yin, Y.; Zhao, J. Stability of X-C-vacancy complexes (X = H, He) in vanadium from first principles investigations. J. Nucl. Mater. 2018, 505, 119–126. [Google Scholar] [CrossRef]
- Luo, J.; Zhou, H.B.; Liu, Y.L.; Gui, L.J.; Jin, S.; Zhang, Y.; Lu, G.H. Dissolution, diffusion and permeation behavior of hydrogen in vanadium: A first-principles investigation. J. Phys. Condens. Matter 2011, 23, 135501. [Google Scholar] [CrossRef]
- Janot, C.; George, B.; Delcroix, P. Point defects in vanadium investigated by mossbauer spectroscopy and positron annihilation. J. Phys. F Met. Phys. 1982, 12, 47–57. [Google Scholar] [CrossRef]
- Myers, S.M.; Richards, P.M.; Wampler, W.R.; Besenbacher, F. Ion-beam studies of hydrogen-metal interactions. J. Nucl. Mater. 1989, 165, 9–64. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Yukawa, H.; Nambu, T. Quantitative evaluation of hydrogen embrittlement of metal membrane defected by in-situ small punch test under hydrogen permeation. Metall. J. 2010, 63, 74–78. [Google Scholar]
- Qin, J.Y.; Hao, C.Y.; Wang, D.H.; Wang, F.; Yan, X.F.; Zhong, Y.; Wang, Z.M.; Hu, C.H.; Wang, X.T. Investigation of adsorption, dissociation, and diffusion properties of hydrogen on the V (100) surface and in the bulk: A first-principles calculation. J. Adv. Res. 2020, 21, 25–34. [Google Scholar] [CrossRef] [PubMed]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Liu, Z.; Zhao, W.; Wang, D.; Zhang, Y.; Zhong, Y.; Zhang, X.; Wang, Z.; Hu, C.; Liu, J. Hydrogen Transportation Behaviour of V–Ni Solid Solution: A First-Principles Investigation. Materials 2021, 14, 2603. https://doi.org/10.3390/ma14102603
Qin J, Liu Z, Zhao W, Wang D, Zhang Y, Zhong Y, Zhang X, Wang Z, Hu C, Liu J. Hydrogen Transportation Behaviour of V–Ni Solid Solution: A First-Principles Investigation. Materials. 2021; 14(10):2603. https://doi.org/10.3390/ma14102603
Chicago/Turabian StyleQin, Jiayao, Zhigao Liu, Wei Zhao, Dianhui Wang, Yanli Zhang, Yan Zhong, Xiaohui Zhang, Zhongmin Wang, Chaohao Hu, and Jiangwen Liu. 2021. "Hydrogen Transportation Behaviour of V–Ni Solid Solution: A First-Principles Investigation" Materials 14, no. 10: 2603. https://doi.org/10.3390/ma14102603






