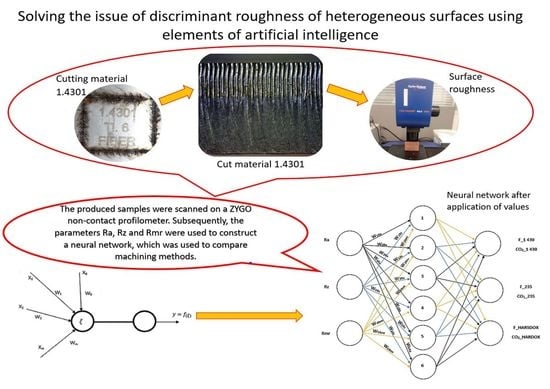
Solving the Issue of Discriminant Roughness of Heterogeneous Surfaces Using Elements of Artificial Intelligence
Abstract
:1. Introduction
2. Materials and Methods
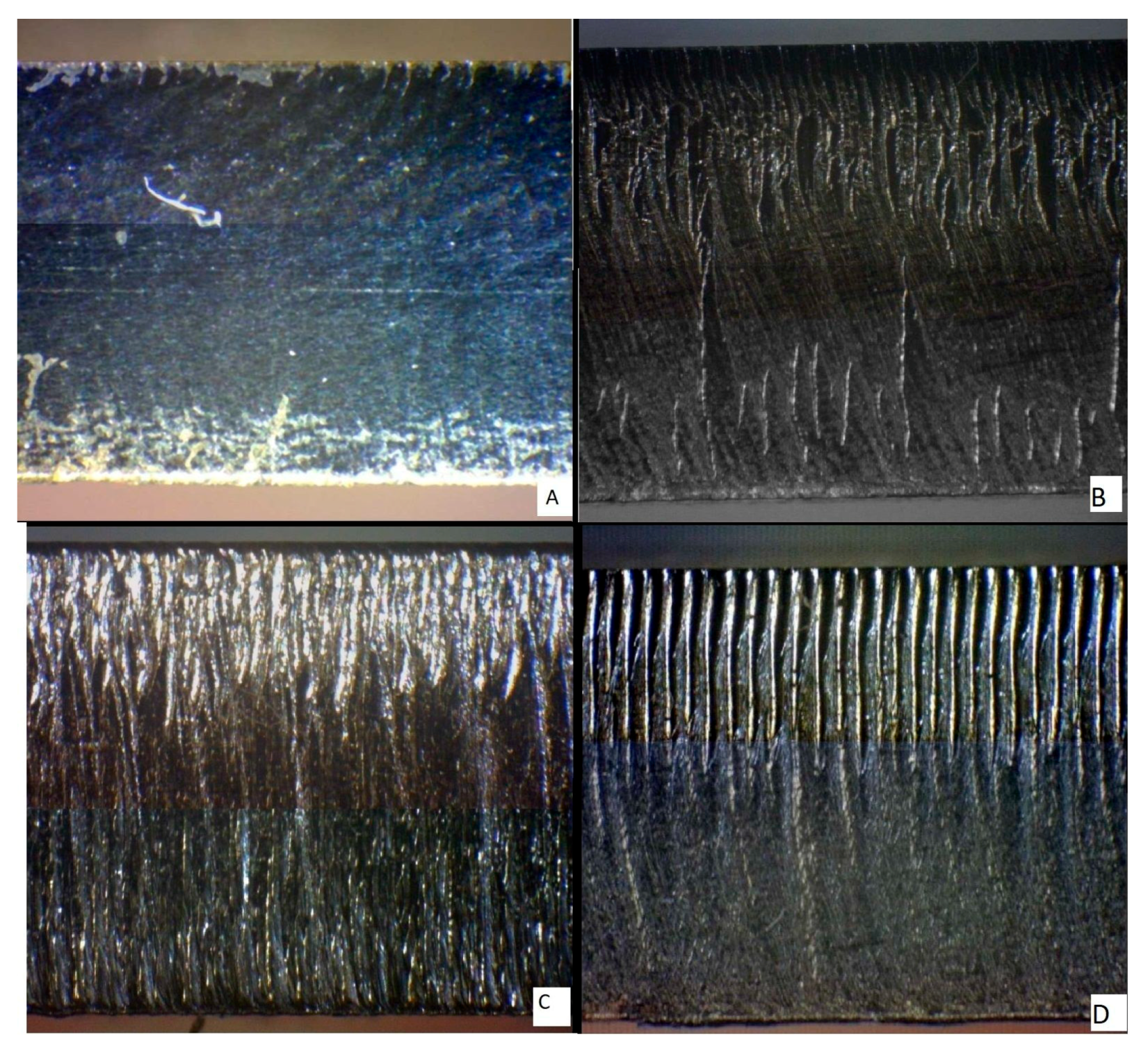
2.1. Studied Materials and Their Machining
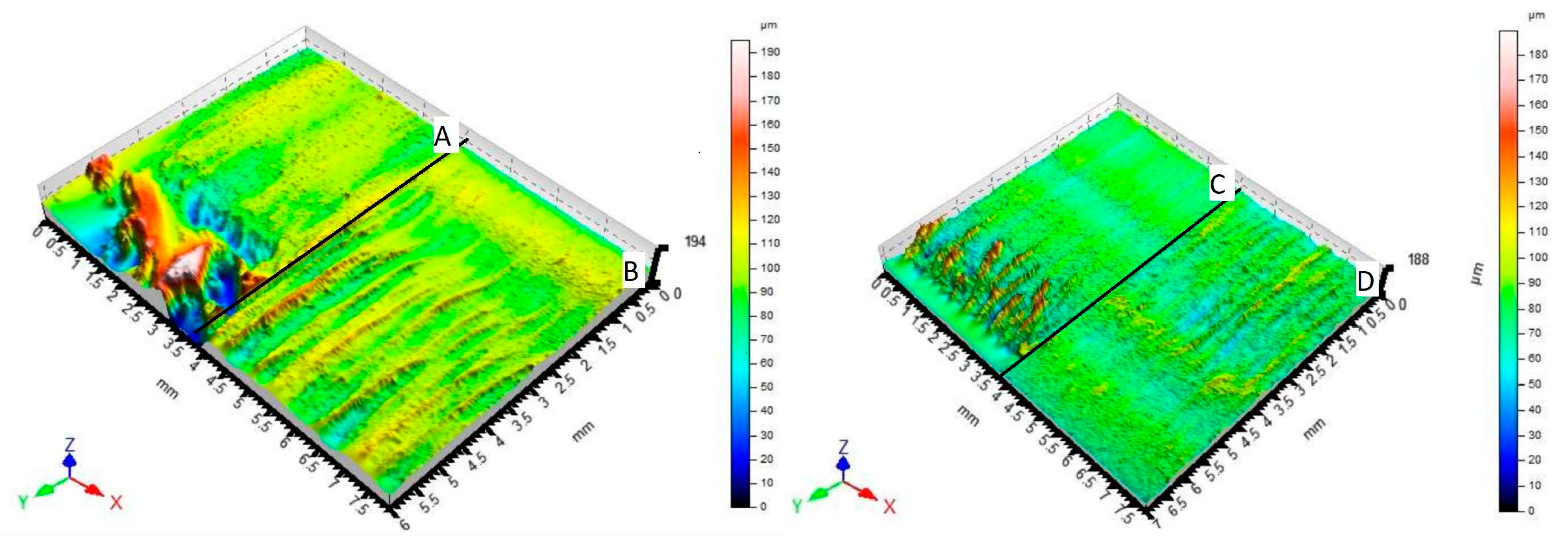
2.2. Surface Quality
2.3. Statistical Tools for Data Evaluation
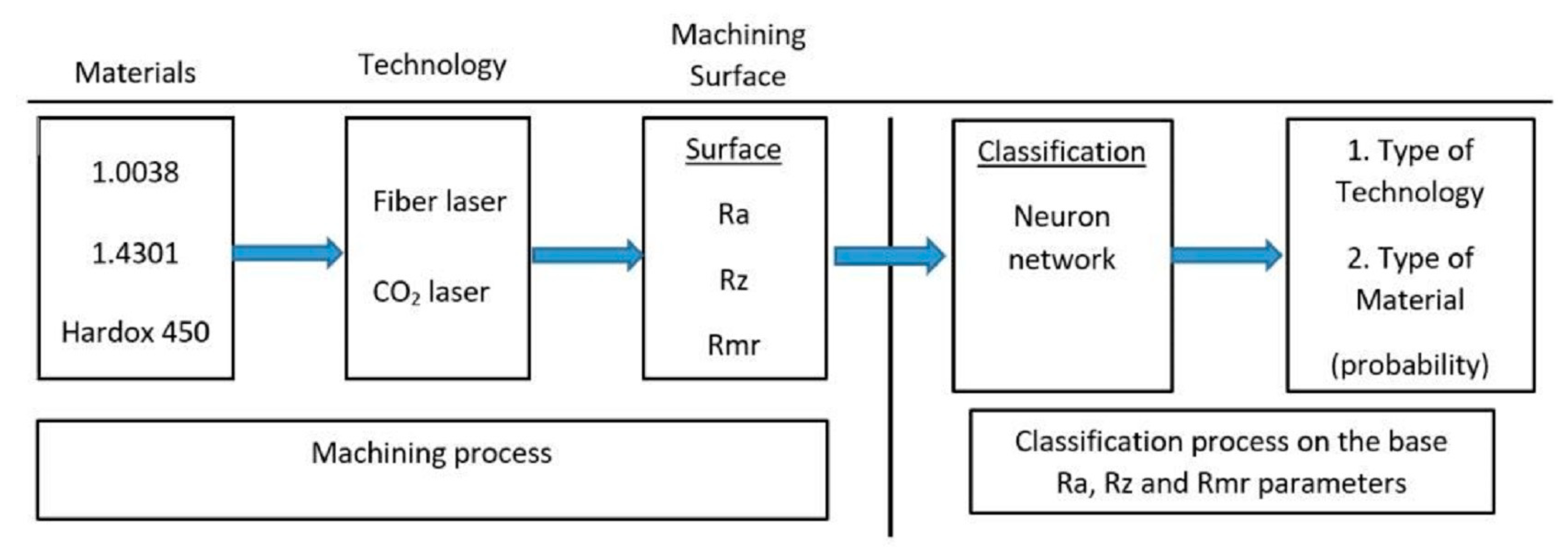
2.4. Data Classification
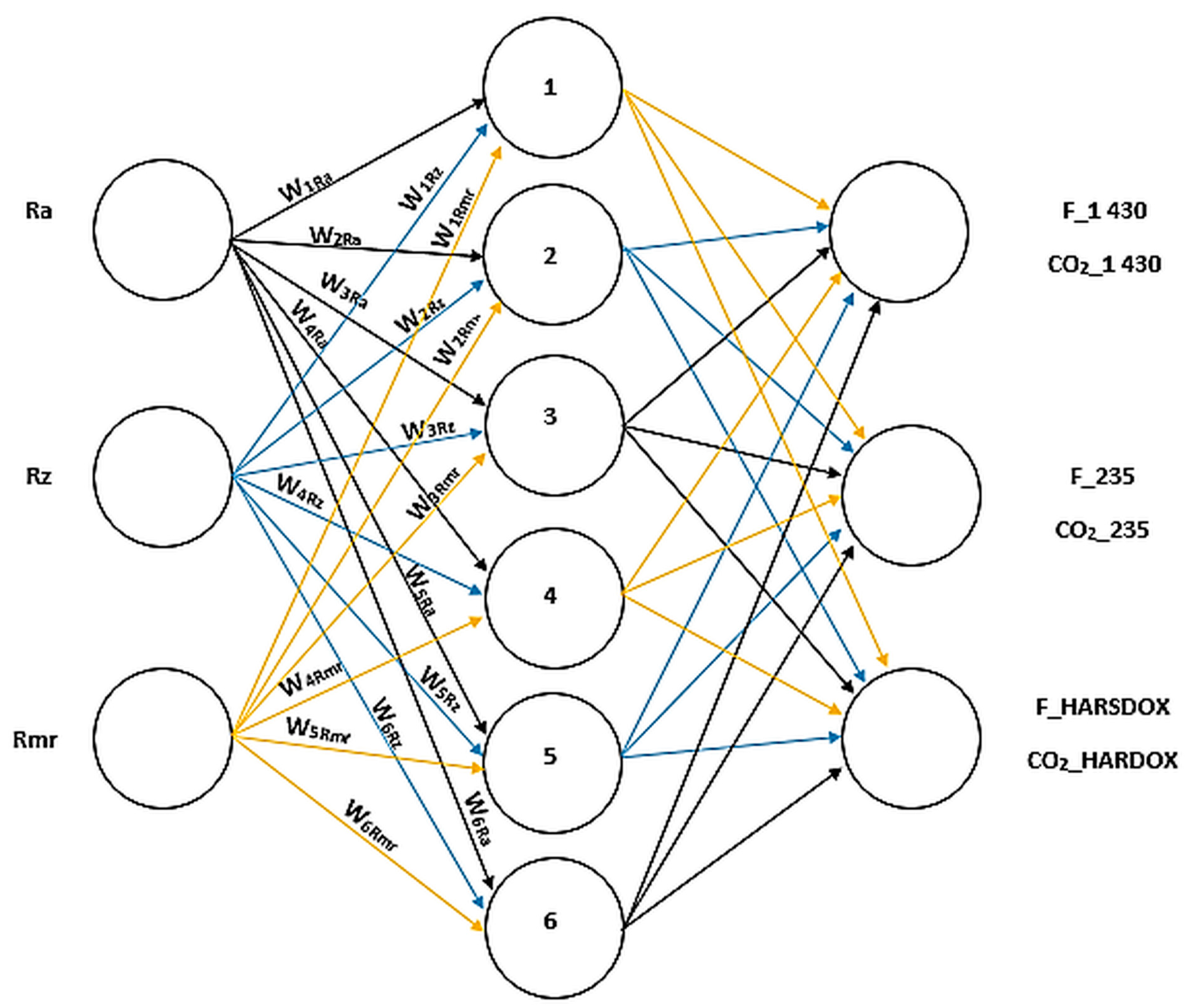
2.5. Mathematical Model of the Neuron
3. Results and Discussion
3.1. Materials
3.2. Evaluation of Surface Roughness
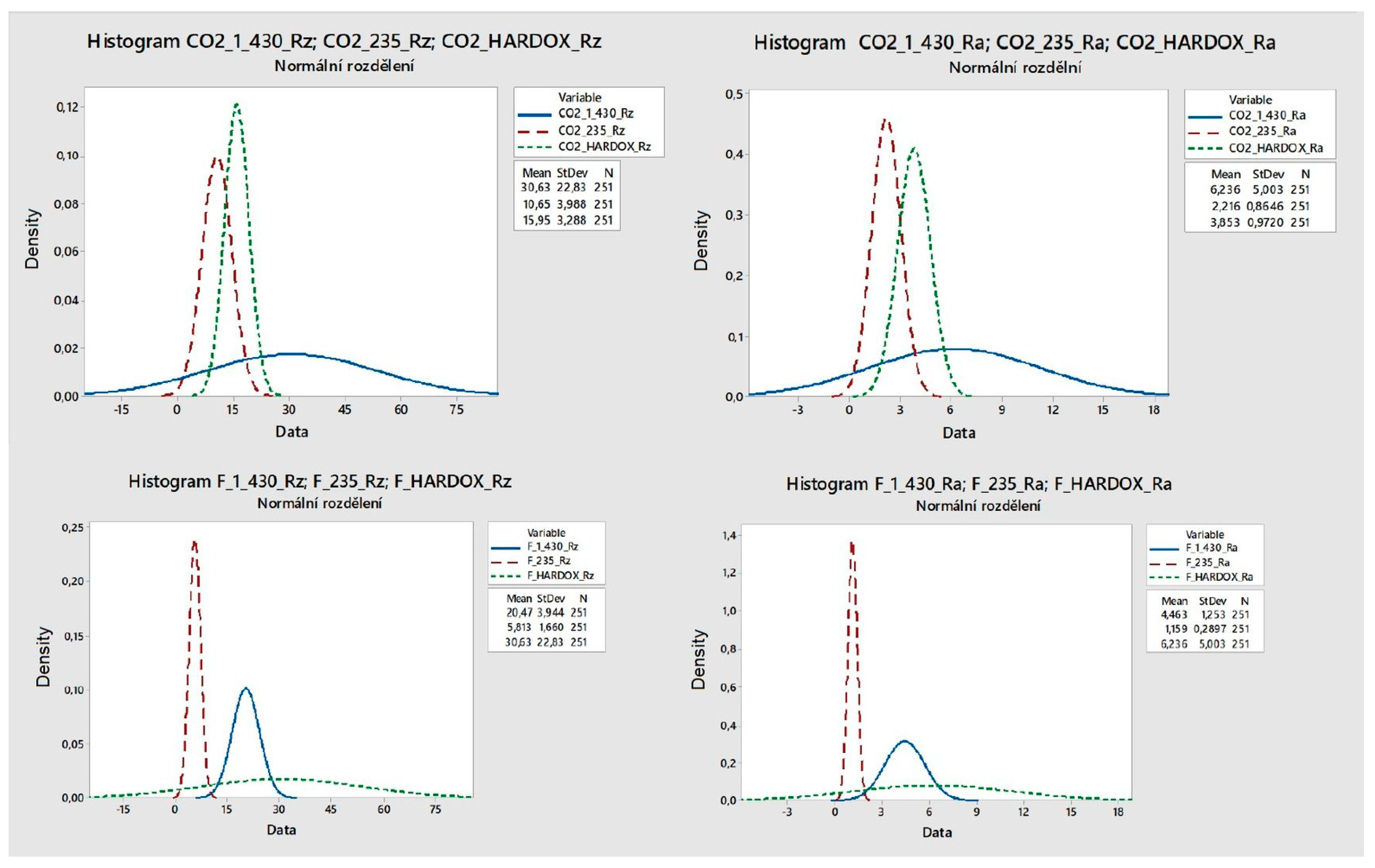
3.3. Statistical Evaluation
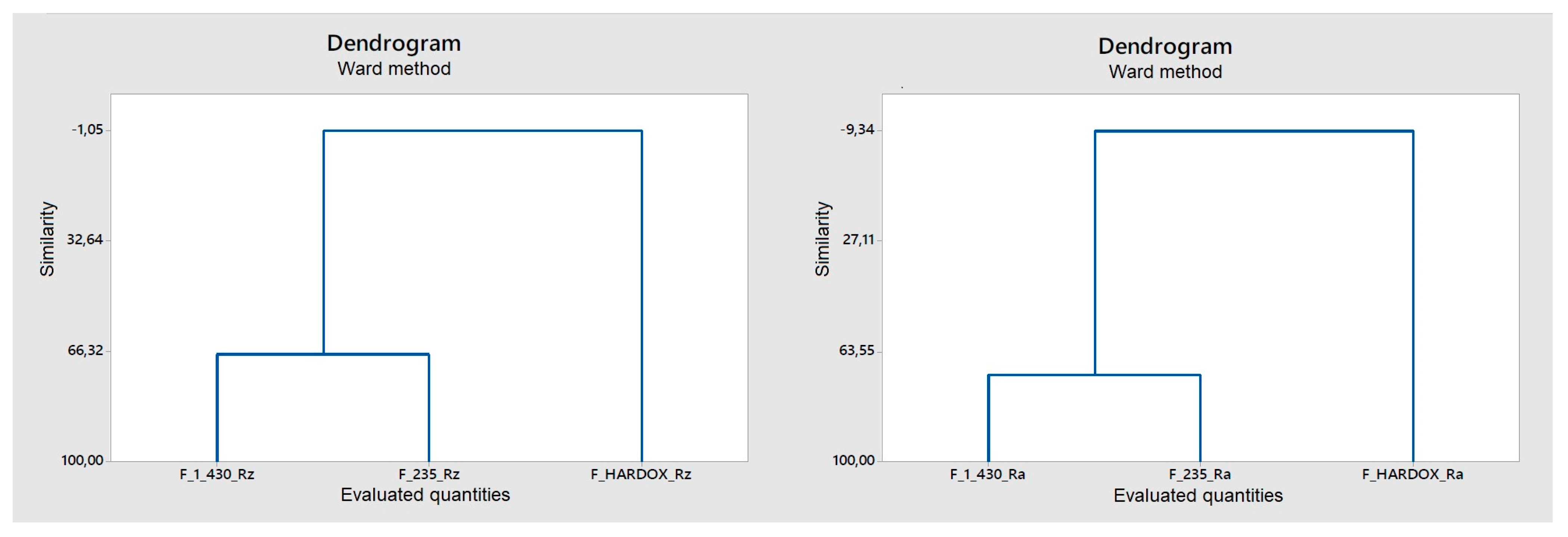
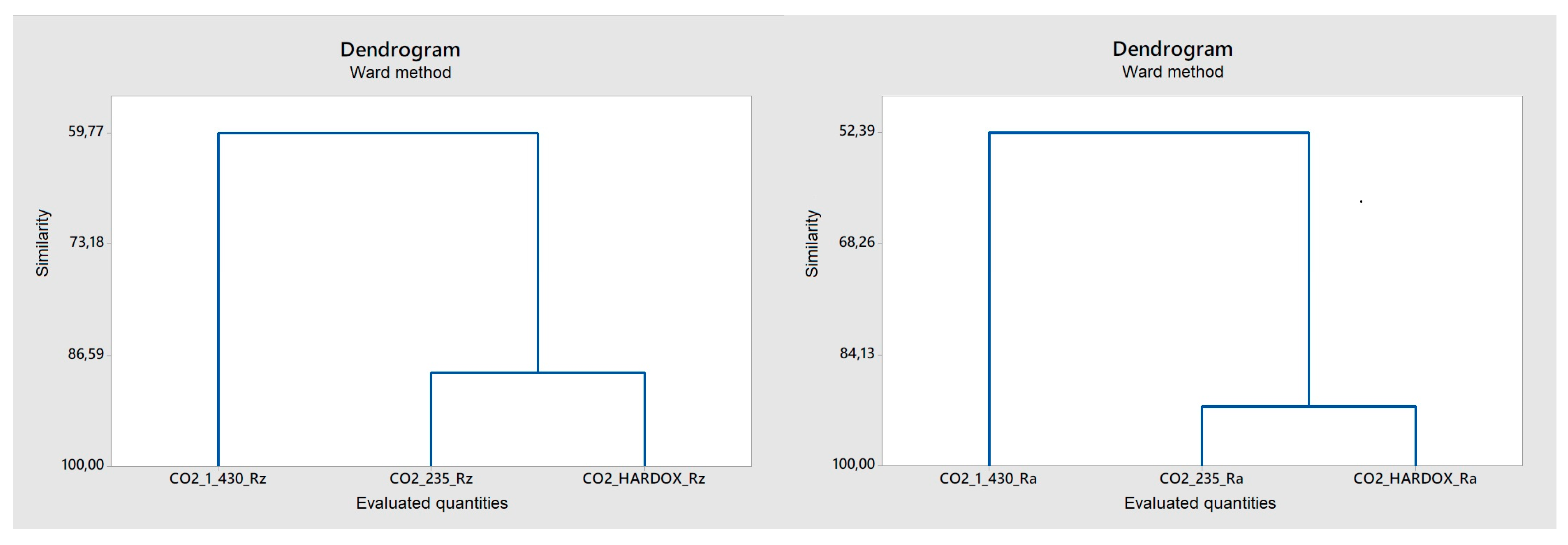
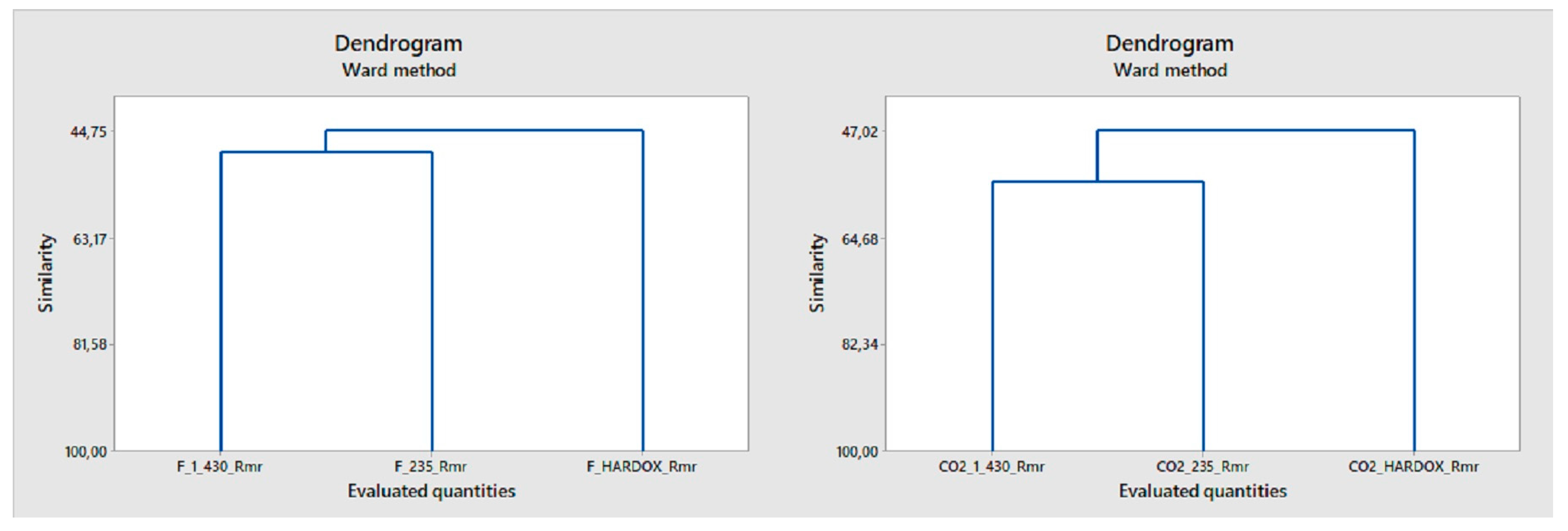
3.4. Classification of Evaluated Data and Cluster Analysis
3.5. Neuron Network
- NNH is the number of neurons in the hidden layer
- n1 is the number of neurons in the input layer
- n2 is the number of neurons in the output layer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitehouse, D.J. Handbook of Surface and Nanometrology, 2nd ed.; CRC Press: London, UK, 2011. [Google Scholar]
- Murat, D.; Ensarioglu, C. Surface Roughness Analysis of Greater Cutting Depths During Hard Turning. Mater. Test. 2017, 59, 795–802. [Google Scholar] [CrossRef]
- Fu, G.; Sun, P.; Zhu, W.; Yang, J.; Cao, Y.; Yang, M.; Cao, Y. A Deep-Learning-Based Approach for Fast and Robust Steel Surface Defects Classification. Opt. Lasers Eng. 2019, 121, 397–405. [Google Scholar] [CrossRef]
- Yida, L.; Gao, T. Local Defects in Colloidal Quantum Dot Thin Films Measured Via Spatially Resolved Multi-Modal Optoelectronic Spectroscopy. Adv. Mater. 2020, 31, 105–119. [Google Scholar]
- Patel, A.; Bhavsar, S.N. Experimental investigation to optimize laser cutting process parameters for difficult to cut die alloy steel using response surface methodology. Mater. Today Proc. 2021, 43, 28–35. [Google Scholar] [CrossRef]
- Giudice, F.; Missori, S. Parameterised multipoint-line analytical modeling of a mobile heat source for thermal field prediction in laser beam welding. Int. J. Adv. Manuf. Technol. 2021, 112, 1339–1358. [Google Scholar] [CrossRef]
- Neslušan, M.; Minárik, P. Non-destructive evaluation of the railway wheel surface damage after long-term operation via Barkhausen noise technique. Wear 2019, 420–421, 195–206. [Google Scholar] [CrossRef]
- Abonyi, J.; Feil, B. Cluster Analysis for Data Mining and System Identification, 1st ed.; Birkhäuser Basel: Basel, Switzerland, 2007. [Google Scholar]
- Yadav, N.; Yadav, A. An Introduction to Neural Network Methods for Differential Equations; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Patterson, D.W. Artificial Neural Networks: Theory and Applications; Prentice Hall: New York, NY, USA, 1996. [Google Scholar]
- Muthuramalingam, T.; Akash, R. Surface quality measures analysis and optimization on machining titanium alloy using CO2 based laser beam drilling process. J. Manuf. Process. 2021, 62, 1–6. [Google Scholar] [CrossRef]
- Mayuet Ares, P.; Vázquez Martínez, J. Experimental Study of Macro and Microgeometric Defects in Drilled Carbon Fiber Reinforced Plastics by Laser Beam Machining. Materials 2018, 11, 1466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, A.R.; Bhavsar, S.N. Laser Machining of Die Steel (EN-31): An. Experimental Approach to Optimize Process. Parameters using Response Surface Methodology. Int. J. Automot. Mech. Eng. 2021, 18, 8563. [Google Scholar] [CrossRef]
- Kumar, U.; Gope, D. Experimental and Numerical Assessment of Temperature Field and Analysis of Microstructure and Mechanical Properties of Low Power Laser Annealed Welded Joints. Materials 2018, 11, 1514. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Domokos, E.-K.; Bálint, C. Definition of user groups applying Ward’s method. Transp. Res. Procedia 2017, 22, 25–34. [Google Scholar]
- Erdenechimeg, K.; Jeong, H.-I. A Study on the Laser-Assisted Machining of Carbon Fiber Reinforced Silicon Carbide. Materials 2019, 12, 2061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Callus, E.; the Approach-IS consortium and the International Society for Adult Congenital Heart Disease (ISACHD); Pagliuca, S.; Boveri, S.; Ambrogi, F.; Luyckx, K.; Kovacs, A.H.; Apers, S.; Budts, W.; Enomoto, J.; et al. Phenotypes of adults with congenital heart disease around the globe: A cluster analysis. Health Qual. Life Outcomes 2021, 19, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Guarino, S.; Ponticelli, G.S. Environmental assessment of Selective Laser Melting compared with Laser Cutting of 316L stainless steel: A case study for flat washers’ production. CIRP J. Manuf. Sci. Technol. 2020, 31, 525–538. [Google Scholar] [CrossRef]
- Quondam Antonio, S.; Riganti Fulginei, F. An effective neural network approach to reproduce magnetic hysteresis in electrical steel under arbitrary excitation waveforms. J. Magn. Magn. Mater. 2021, 528, 167735. [Google Scholar] [CrossRef]







| Machining Type | Material Type | Material Thickness [mm] | Cutting Gas | Gas Pres. [Bar] | Cutting Jet Diam. [mm] | Focal Length [mm] | Cutting Speed [mm min−1] | Power [W] |
|---|---|---|---|---|---|---|---|---|
| Fiber laser | 1.0038 | 6 | Oxygen | 0.73 | 1.2 | 4.4 | 2600 | 3080 |
| Fiber laser | 1.0038 | 8 | Oxygen | 0.5 | 1.2 | 4 | 1700 | 3050 |
| Fiber laser | Hardox | 6 | Oxygen | 0.73 | 1.2 | 4.4 | 1300 | 3080 |
| Fiber laser | Hardox | 8 | Oxygen | 0.5 | 1.2 | 4 | 900 | 3050 |
| Fiber laser | 1.4301 | 6 | Nitrogen | 17 | 2.5 | −5.7 | 2100 | 3080 |
| Fiber laser | 1.4301 | 8 | Nitrogen | 19.3 | 2.5 | −7.3 | 1200 | 3080 |
| CO2 laser | 1.0038 | 6 | Oxygen | 0.7 | 1 | 0.7 | 2700 | 4000 |
| CO2 laser | 1.0038 | 8 | Oxygen | 0.4 | 1.5 | 1.5 | 2100 | 4000 |
| CO2 laser | Hardox | 6 | Oxygen | 0.7 | 1 | 0.7 | 2700 | 4000 |
| CO2 laser | Hardox | 8 | Oxygen | 0.4 | 1.5 | 1.5 | 2100 | 4000 |
| CO2 laser | 1.4301 | 6 | Nitrogen | 13 | 2 | −6.5 | 1350 | 4000 |
| CO2 laser | 1.4301 | 8 | Nitrogen | 14 | 2.5 | −9 | 1000 | 4000 |
| Indication | Pattern |
|---|---|
| F_1_430 | steel 1.0043 Fiber laser machining |
| CO2_1_430 | laser-treated CO2 steel 1.0043 |
| F_235 | steel 1.0038 Fiber laser machining |
| CO2_235 | laser-treated CO2 steel 1.0038 |
| F_HARDOX | steel HARDOX 450 Fiber laser machining |
| CO2_HARDOX | laser-treated CO2 steel HARDOX 450 |
| Cluster | F_1_430 | F_235 F_HARDOX |
|---|---|---|
| Similarity Levels [%] | Similarity Levels [%] | |
| Rz | 67.3 | −1.05 |
| Ra | 71.5 | −9.3 |
| Cluster | CO2_1_430 | CO2_235 CO2_HARDOX |
|---|---|---|
| Similarity Levels [%] | Similarity Levels [%] | |
| Rz | 59.8 | 88.7 |
| Ra | 52.4 | 91.6 |
| Fiber Laser | CO2 Laser | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rz [µm] | Ra [µm] | Rmr | Recognized | % | Rz [µm] | Ra [µm] | Rmr | Recognized | % |
| 20.30 | 4.80 | 0.60 | F_1_430 | 0.99850 | 13.40 | 2.60 | 0.62 | CO2_1_430 | 0.6122 |
| 18.50 | 4.60 | 1.80 | F_1_430 | 0.99980 | 11.30 | 2.50 | 1.80 | CO2_1_430 | 0.8978 |
| 20.32 | 4.70 | 1.20 | F_1_430 | 0.99850 | 11.90 | 2,52 | 1,86 | CO2_1_430 | 0,7229 |
| 20,98 | 4,78 | 2,40 | F_1_430 | 0,99820 | 11,70 | 2,54 | 1,24 | CO2_1_430 | 0,5873 |
| 19,40 | 4,48 | 3,10 | F_1_430 | 0,99820 | 12,40 | 2,40 | 1,20 | CO2_1_430 | 0.8348 |
| 20.40 | 4.90 | 1.80 | F_1_430 | 0.99900 | 11.60 | 2.10 | 0.60 | CO2_1_430 | 0.8873 |
| 19.20 | 5.00 | 2.40 | F_1_430 | 0.99930 | 10.70 | 2.12 | 0.62 | CO2_1_430 | 0.6611 |
| 21.80 | 5.20 | 1.80 | F_1_430 | 0.99910 | 11.40 | 2.62 | 1.80 | CO2_1_430 | 0.4669 |
| 22.27 | 5.60 | 0.60 | F_1_430 | 0.99940 | 11.20 | 2.43 | 0.62 | CO2_1_430 | 0.5175 |
| 21.20 | 5.20 | 1.20 | F_1_430 | 0.99920 | 11.60 | 2.30 | 0.62 | CO2_1_430 | 0.7579 |
| 7.50 | 1.40 | 3.70 | F_235 | 0.99998 | 8.70 | 1.40 | 1.80 | CO2_235 | 0.4242 |
| 6.80 | 1.30 | 3.70 | F_235 | 0.99998 | 5.00 | 1.20 | 13.60 | CO2_235 | 0.9849 |
| 6.70 | 1.26 | 1.20 | F_235 | 0.99940 | 7.30 | 1.44 | 4.30 | CO2_235 | 0.9134 |
| 6.60 | 1.41 | 1.24 | F_235 | 0.99270 | 6.20 | 1.10 | 3.70 | CO2_235 | 0.9307 |
| 6.20 | 1.25 | 0.60 | F_235 | 0.99880 | 7.50 | 1.40 | 3.10 | CO2_235 | 0.8222 |
| 7.20 | 1.31 | 1.86 | F_235 | 0.99970 | 6.70 | 1.30 | 3.00 | CO2_235 | 0.9085 |
| 5.90 | 1.20 | 8.07 | F_235 | 1.00000 | 6.00 | 1.10 | 3.70 | CO2_235 | 0.9419 |
| 6.00 | 1.42 | 3.10 | F_235 | 0.95950 | 6.60 | 1.20 | 0.60 | CO2_235 | 0.9165 |
| 7.20 | 1.49 | 1.20 | F_235 | 0.98950 | 7.10 | 1.18 | 2.50 | CO2_235 | 0.8538 |
| 6.95 | 1.41 | 0.60 | F_235 | 0.99640 | 6.30 | 1.22 | 8.00 | CO2_235 | 0.9607 |
| 13.30 | 2.60 | 0.62 | F_HARDOX | 0.88750 | 16.60 | 3.70 | 1.80 | CO2_HARDOX | 0.6329 |
| 11.20 | 2.50 | 1.86 | F_HARDOX | 0.99999 | 14.10 | 3.50 | 1.20 | CO2_HARDOX | 0.9273 |
| 11.90 | 2.52 | 1.80 | F_HARDOX | 0.99940 | 15.10 | 3.60 | 1.80 | CO2_HARDOX | 0.9074 |
| 11.80 | 2.54 | 1.24 | F_HARDOX | 0.99900 | 15.00 | 3.70 | 0.62 | CO2_HARDOX | 0.9745 |
| 12.40 | 2.41 | 1.24 | F_HARDOX | 0.86100 | 14.44 | 3.60 | 1.10 | CO2_HARDOX | 0.9728 |
| 11.40 | 2.10 | 0.62 | F_HARDOX | 0.87560 | 14.80 | 3.50 | 1.80 | CO2_HARDOX | 0.7229 |
| 10.80 | 2.12 | 0.62 | F_HARDOX | 0.99880 | 14.60 | 3.55 | 1.24 | CO2_HARDOX | 0.8973 |
| 11.50 | 2.62 | 1.80 | F_HARDOX | 0.99970 | 14.20 | 3.70 | 0.60 | CO2_HARDOX | 0.9937 |
| 11.29 | 2.40 | 0.60 | F_HARDOX | 0.99880 | 15.00 | 3.50 | 4.30 | CO2_HARDOX | 0.8853 |
| 11.64 | 2.30 | 0.62 | F_HARDOX | 0.99870 | 13.30 | 3.40 | 3.70 | CO2_HARDOX | 0.9415 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubišová, M.; Pata, V.; Měřínská, D.; Škrobák, A.; Marcaník, M. Solving the Issue of Discriminant Roughness of Heterogeneous Surfaces Using Elements of Artificial Intelligence. Materials 2021, 14, 2620. https://doi.org/10.3390/ma14102620
Kubišová M, Pata V, Měřínská D, Škrobák A, Marcaník M. Solving the Issue of Discriminant Roughness of Heterogeneous Surfaces Using Elements of Artificial Intelligence. Materials. 2021; 14(10):2620. https://doi.org/10.3390/ma14102620
Chicago/Turabian StyleKubišová, Milena, Vladimír Pata, Dagmar Měřínská, Adam Škrobák, and Miroslav Marcaník. 2021. "Solving the Issue of Discriminant Roughness of Heterogeneous Surfaces Using Elements of Artificial Intelligence" Materials 14, no. 10: 2620. https://doi.org/10.3390/ma14102620
APA StyleKubišová, M., Pata, V., Měřínská, D., Škrobák, A., & Marcaník, M. (2021). Solving the Issue of Discriminant Roughness of Heterogeneous Surfaces Using Elements of Artificial Intelligence. Materials, 14(10), 2620. https://doi.org/10.3390/ma14102620