Factorial Analysis of Fiber Laser Fusion Cutting of AISI 304 Stainless Steel: Evaluation of Effects on Process Performance, Kerf Geometry and Cut Edge Roughness
Abstract
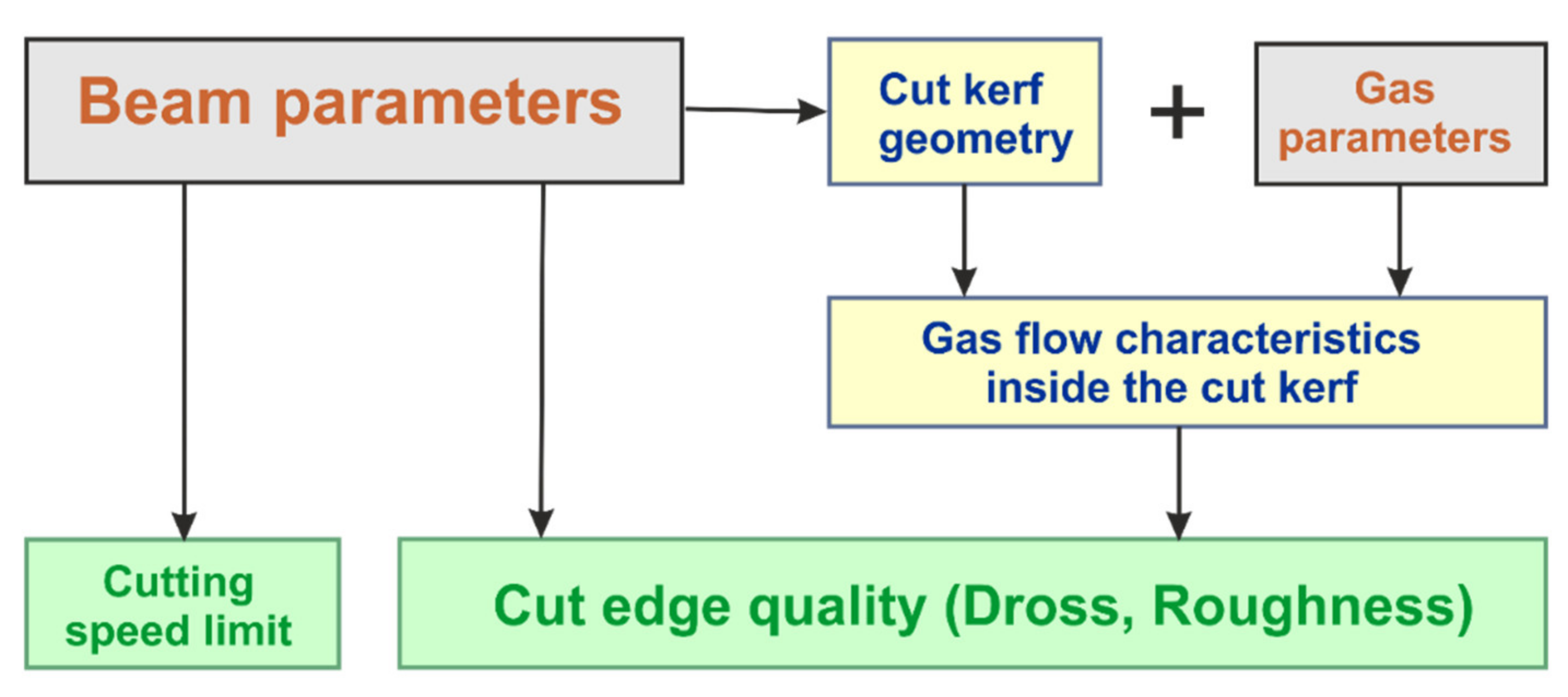
1. Introduction
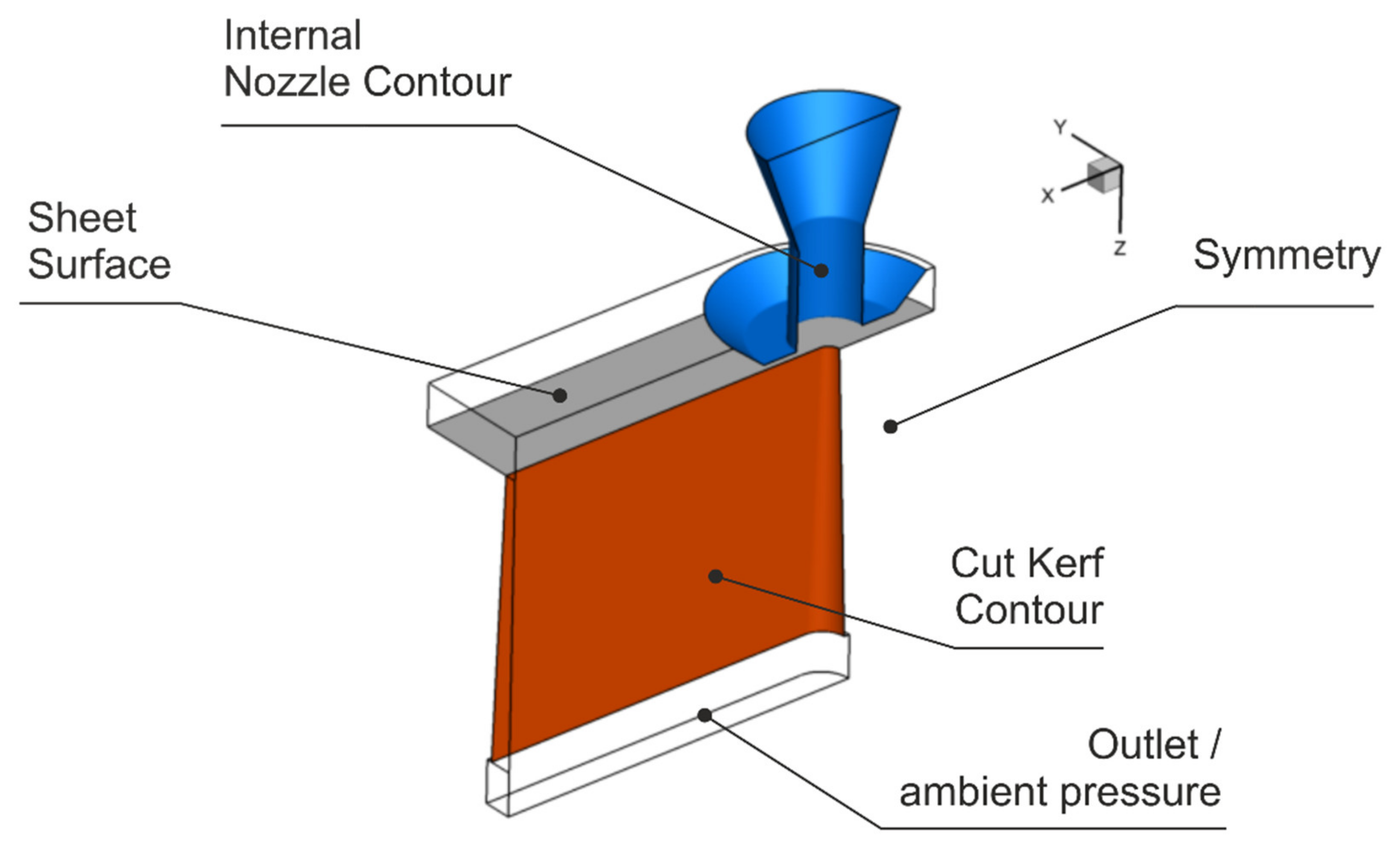
2. Materials and Methods
3. Results and Discussion
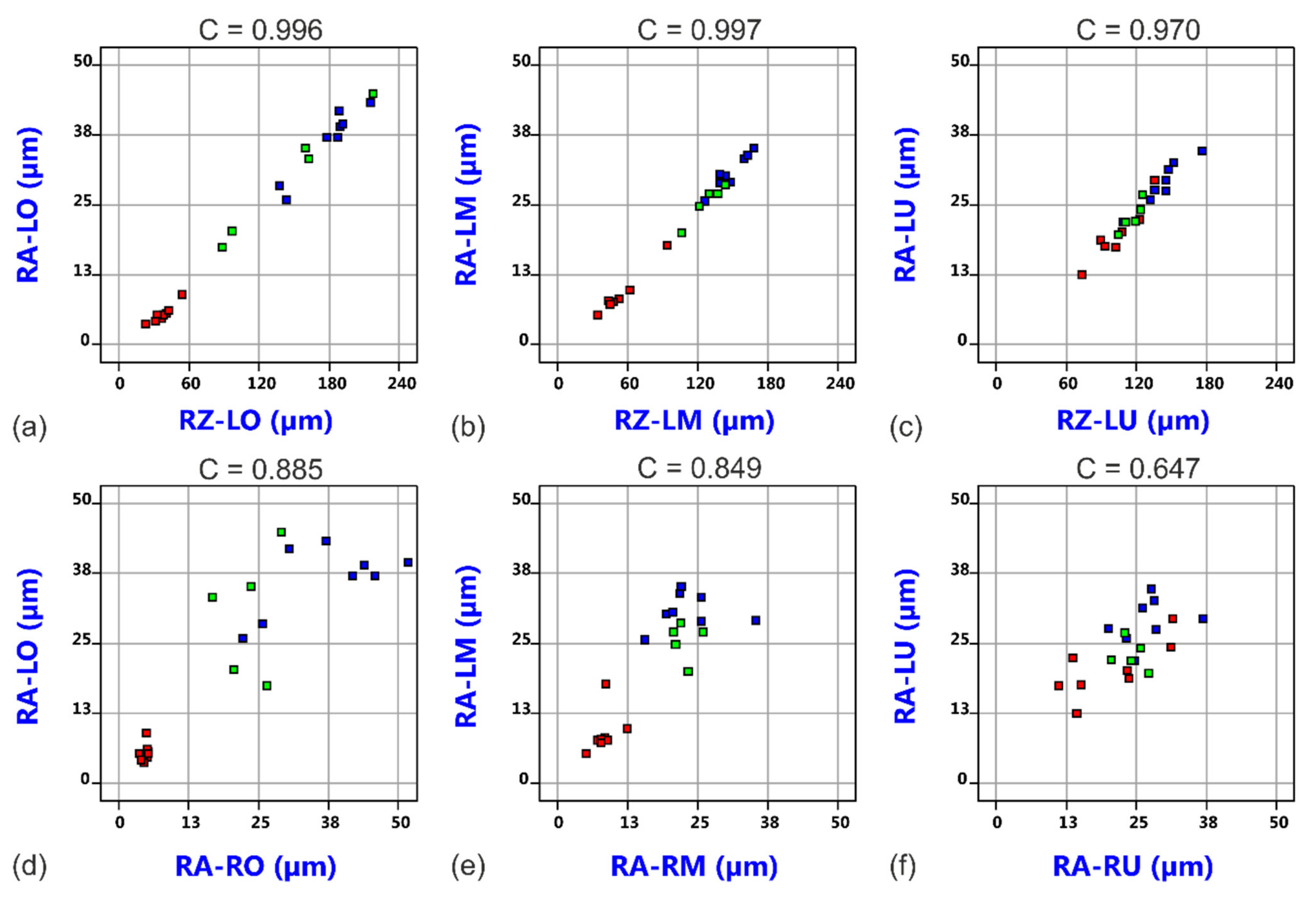
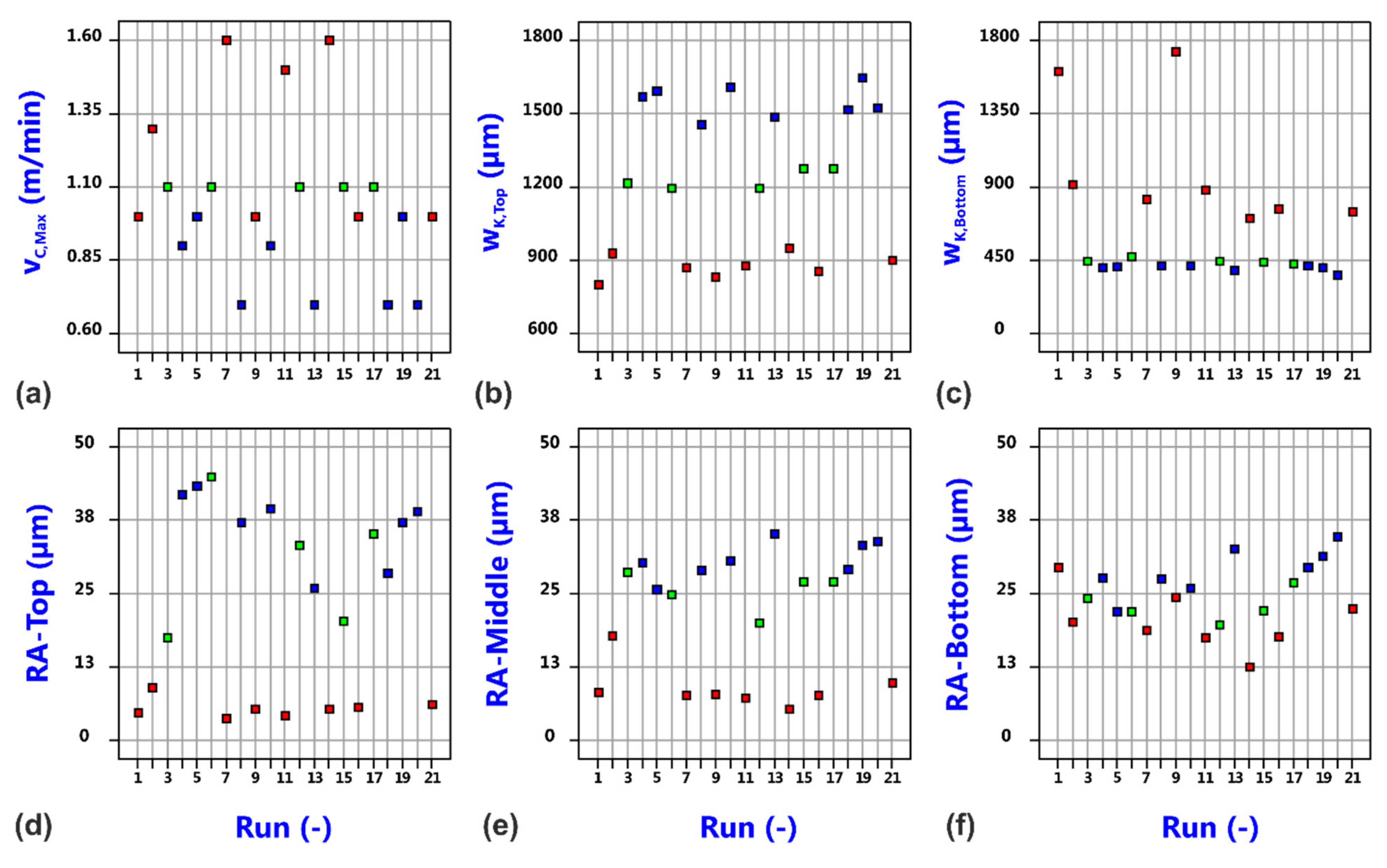
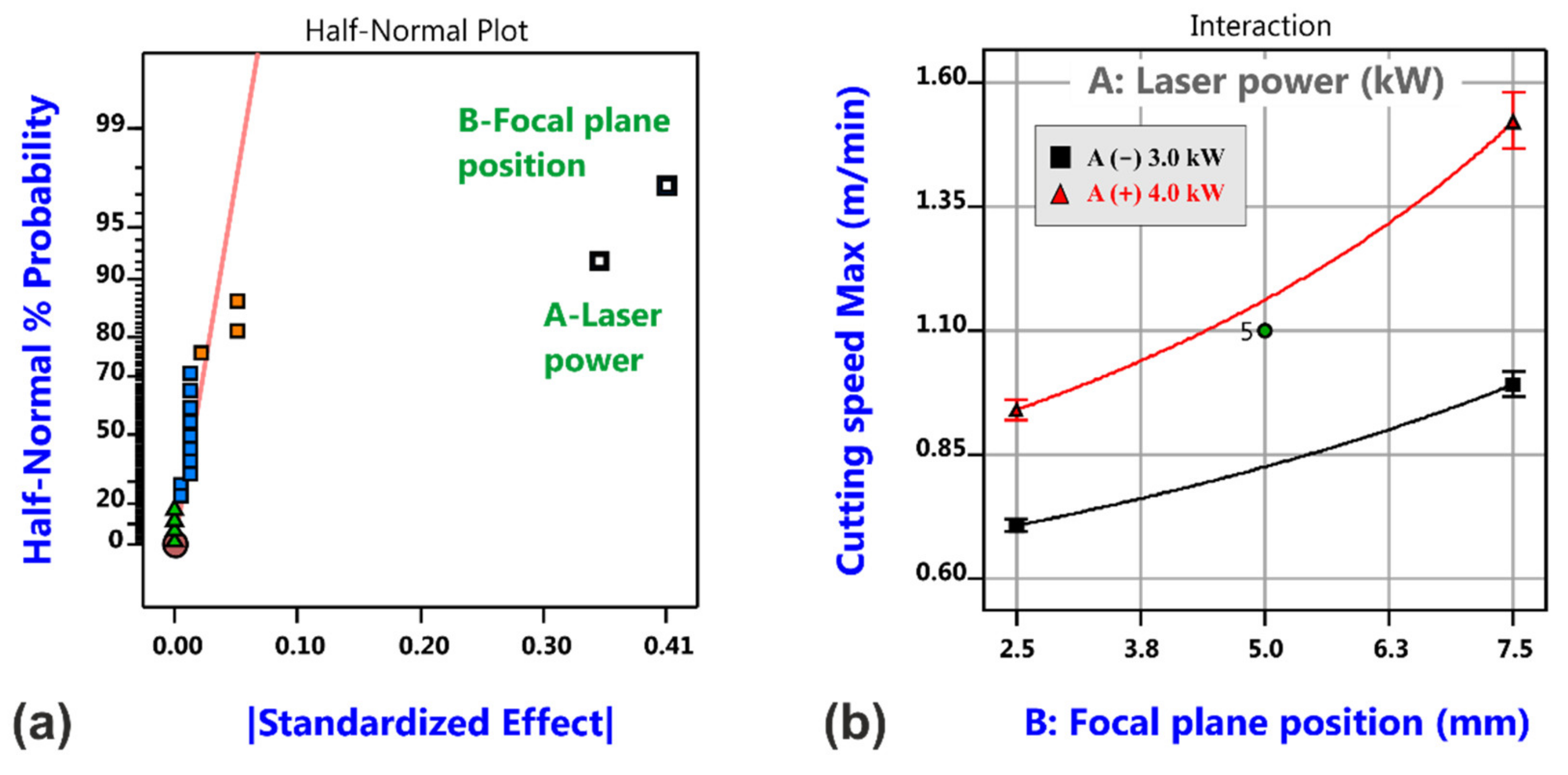
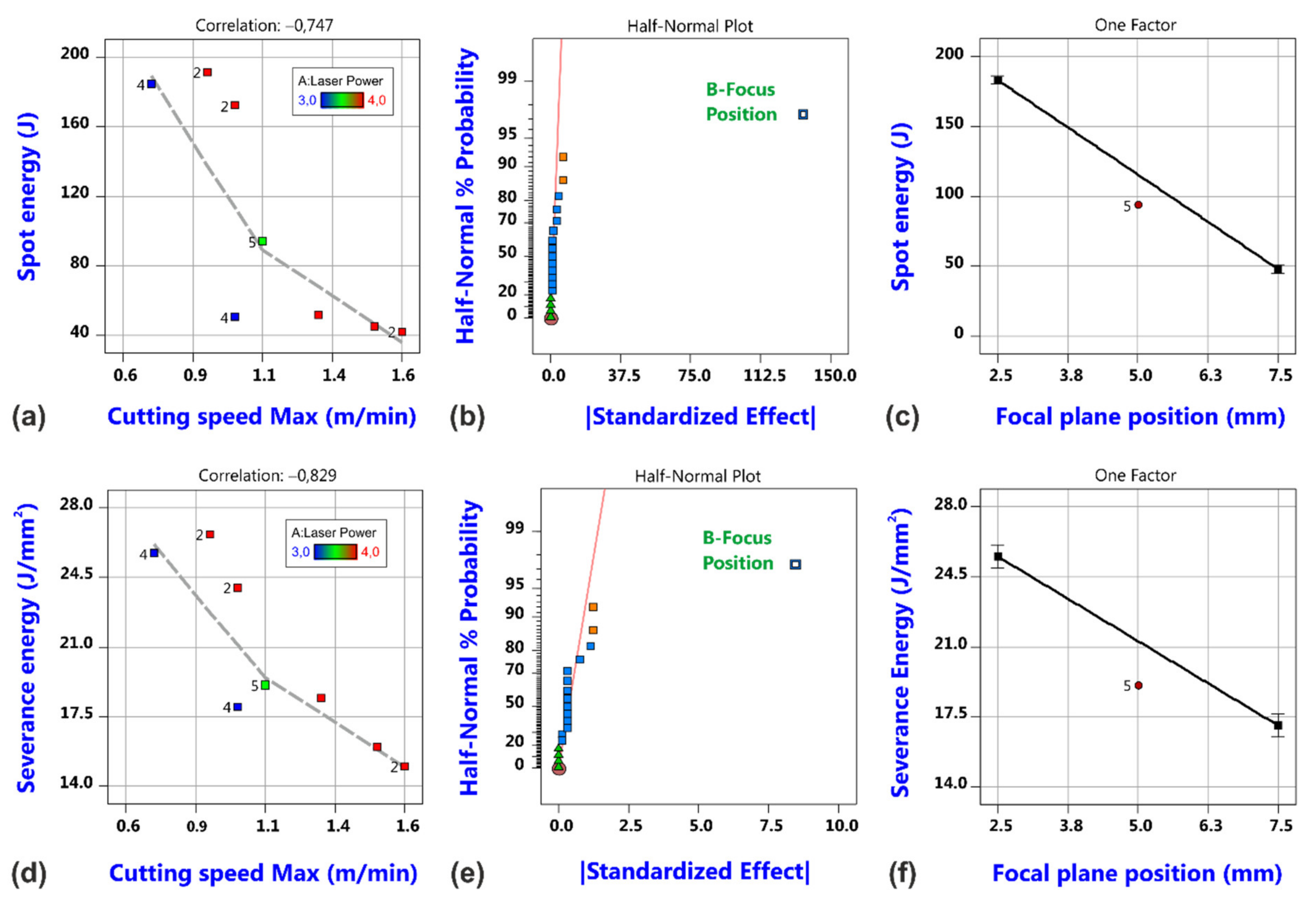
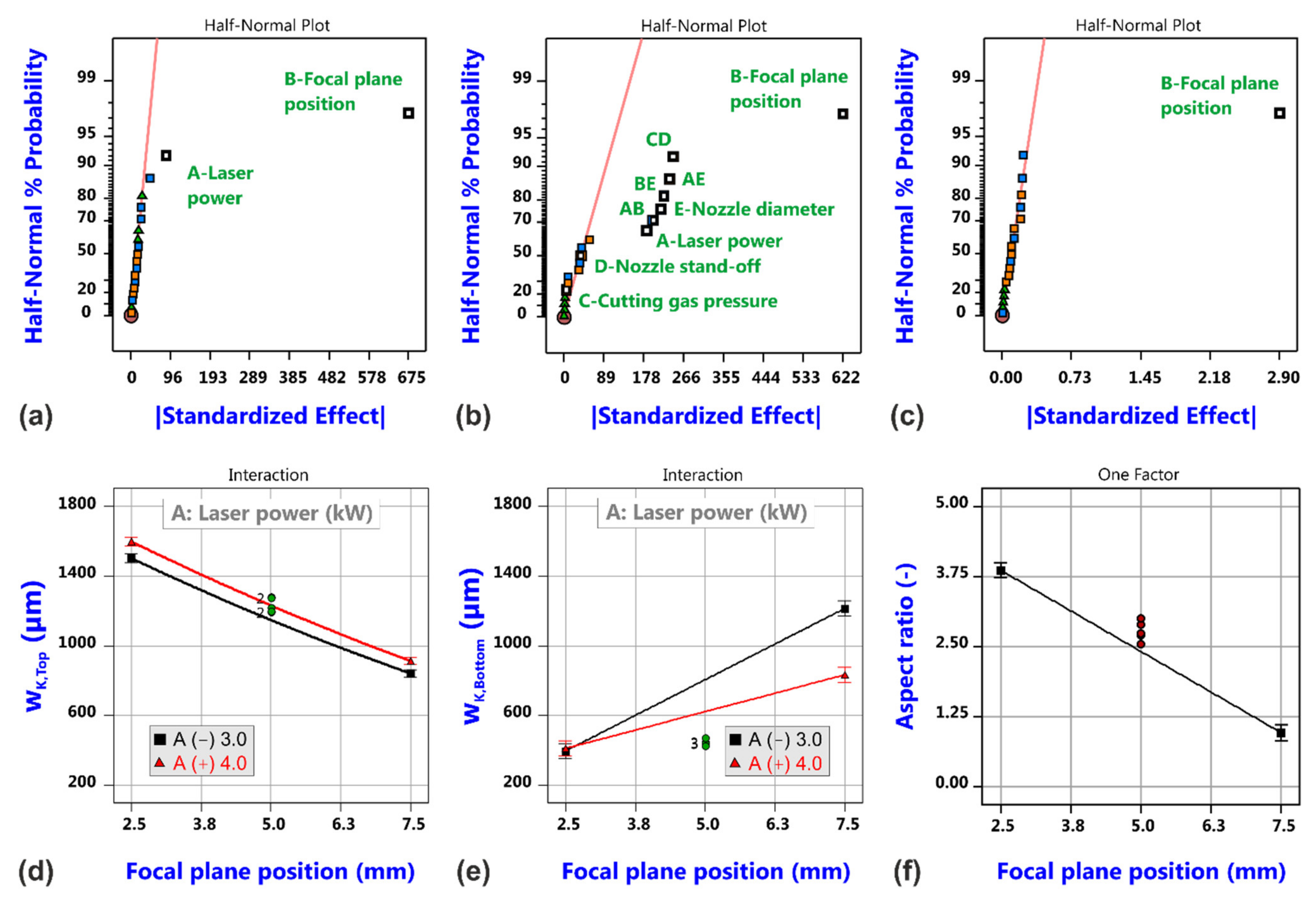
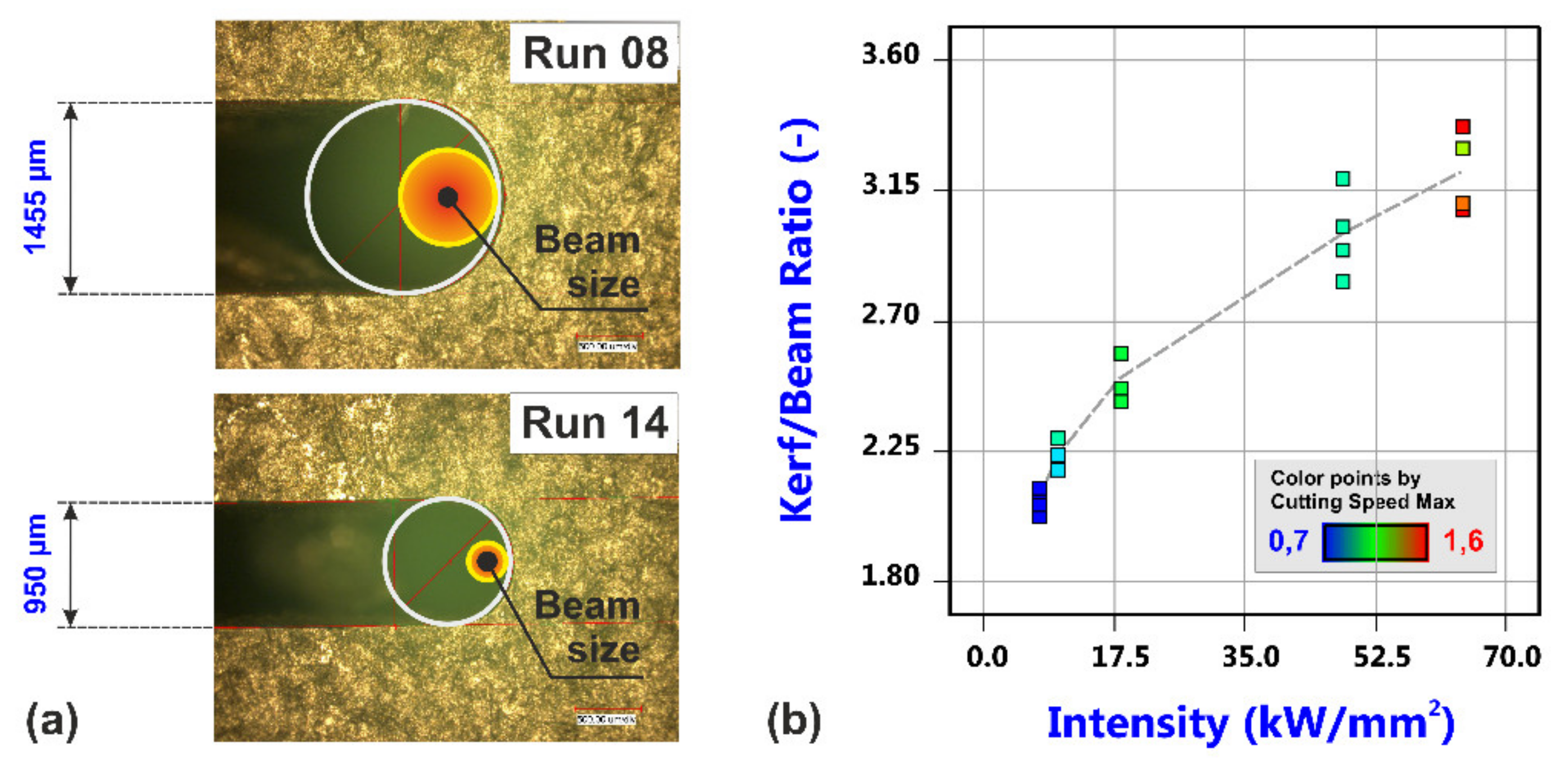
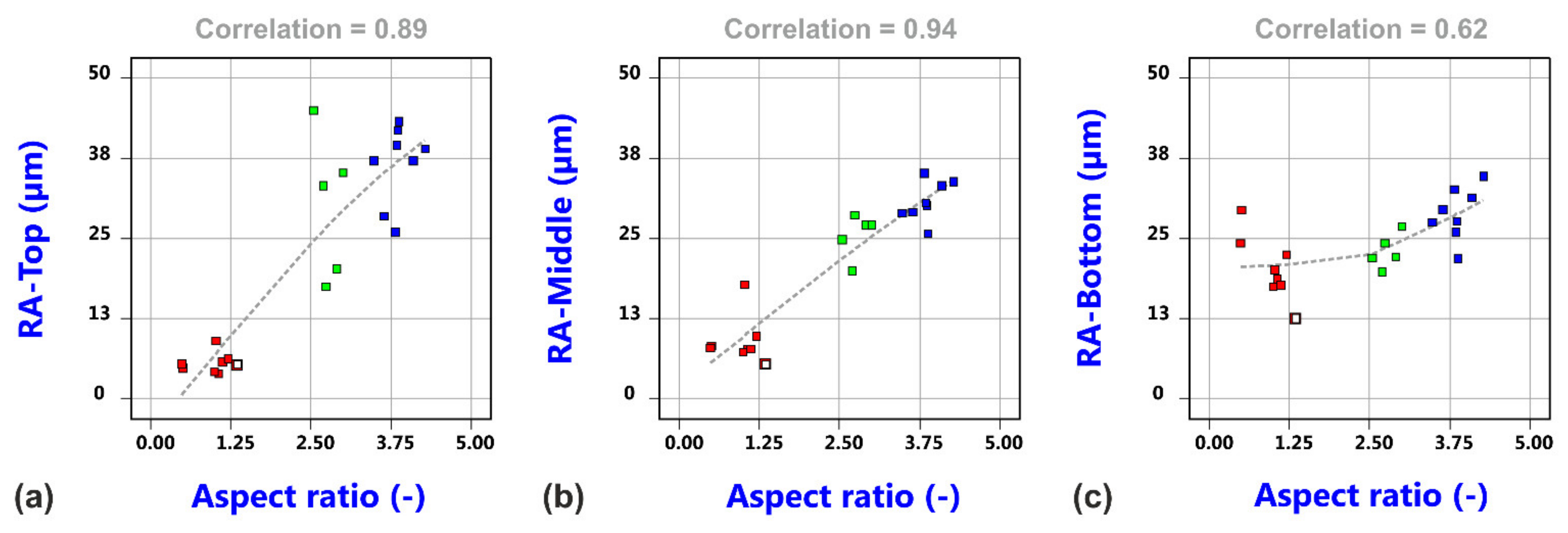
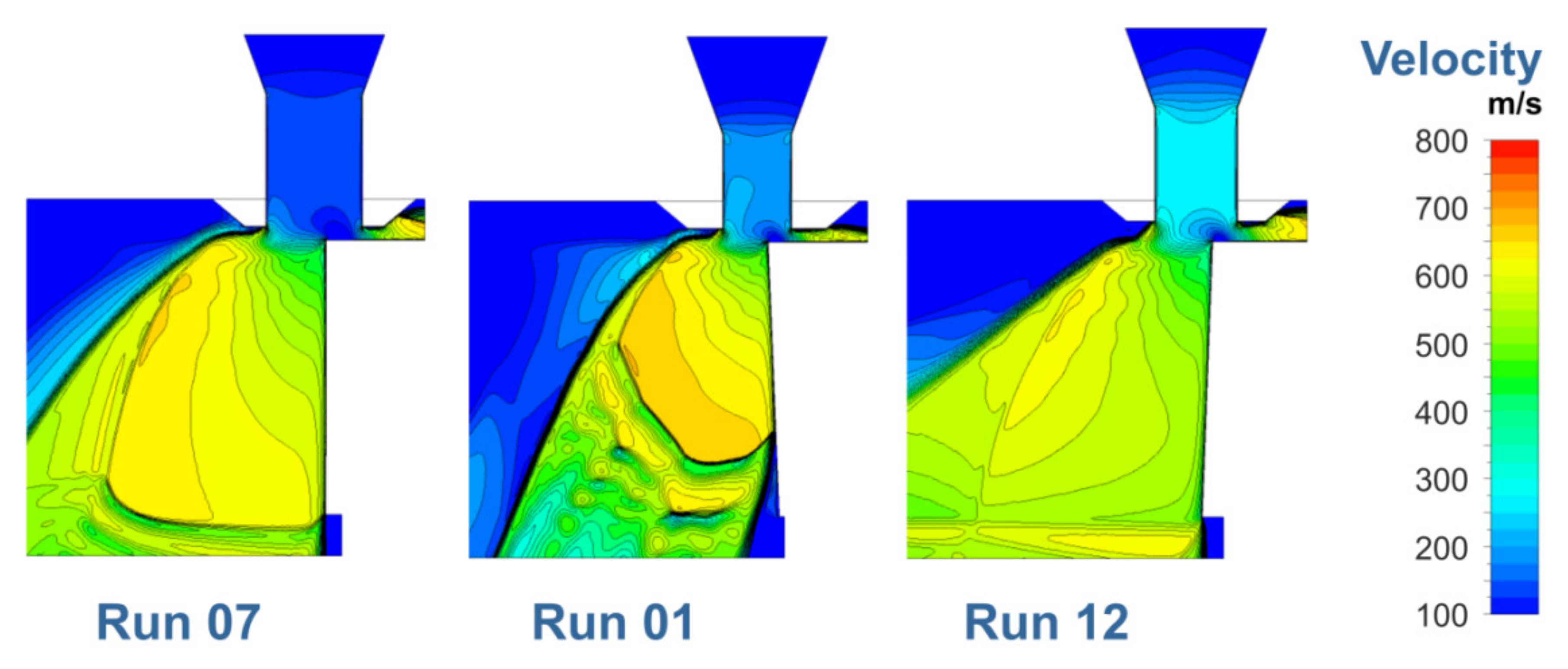
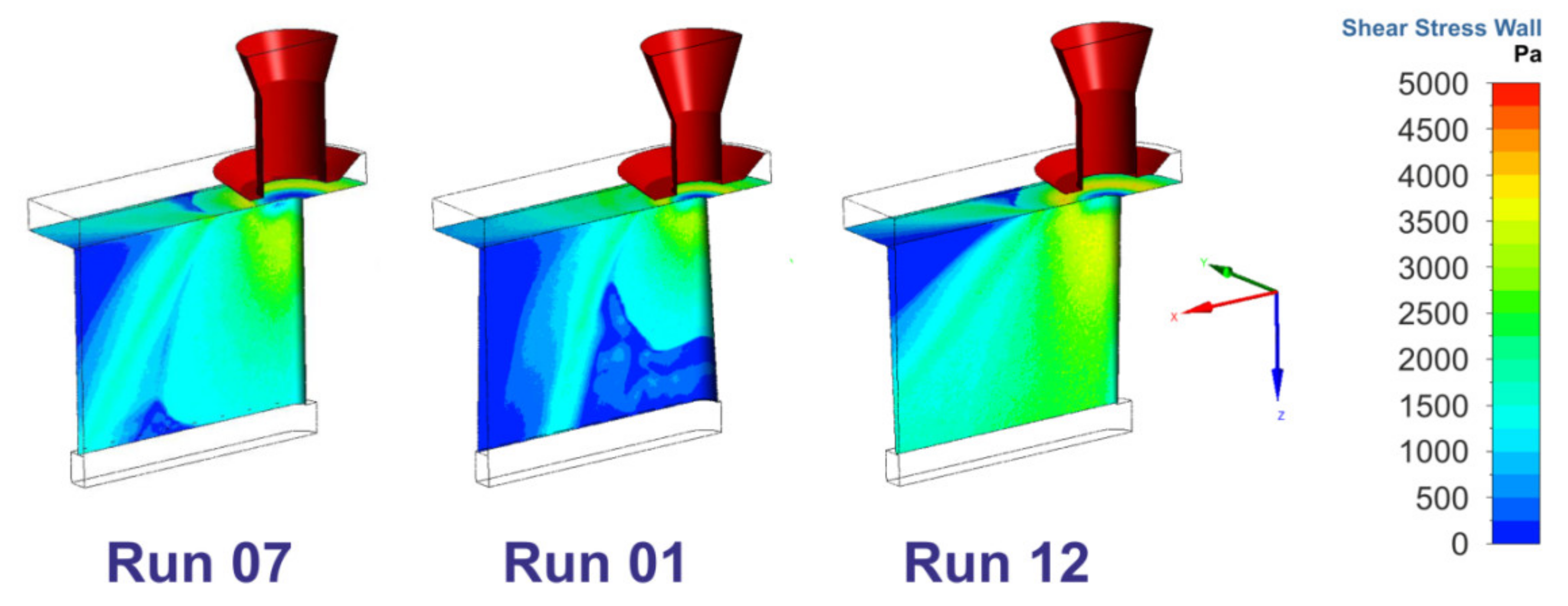
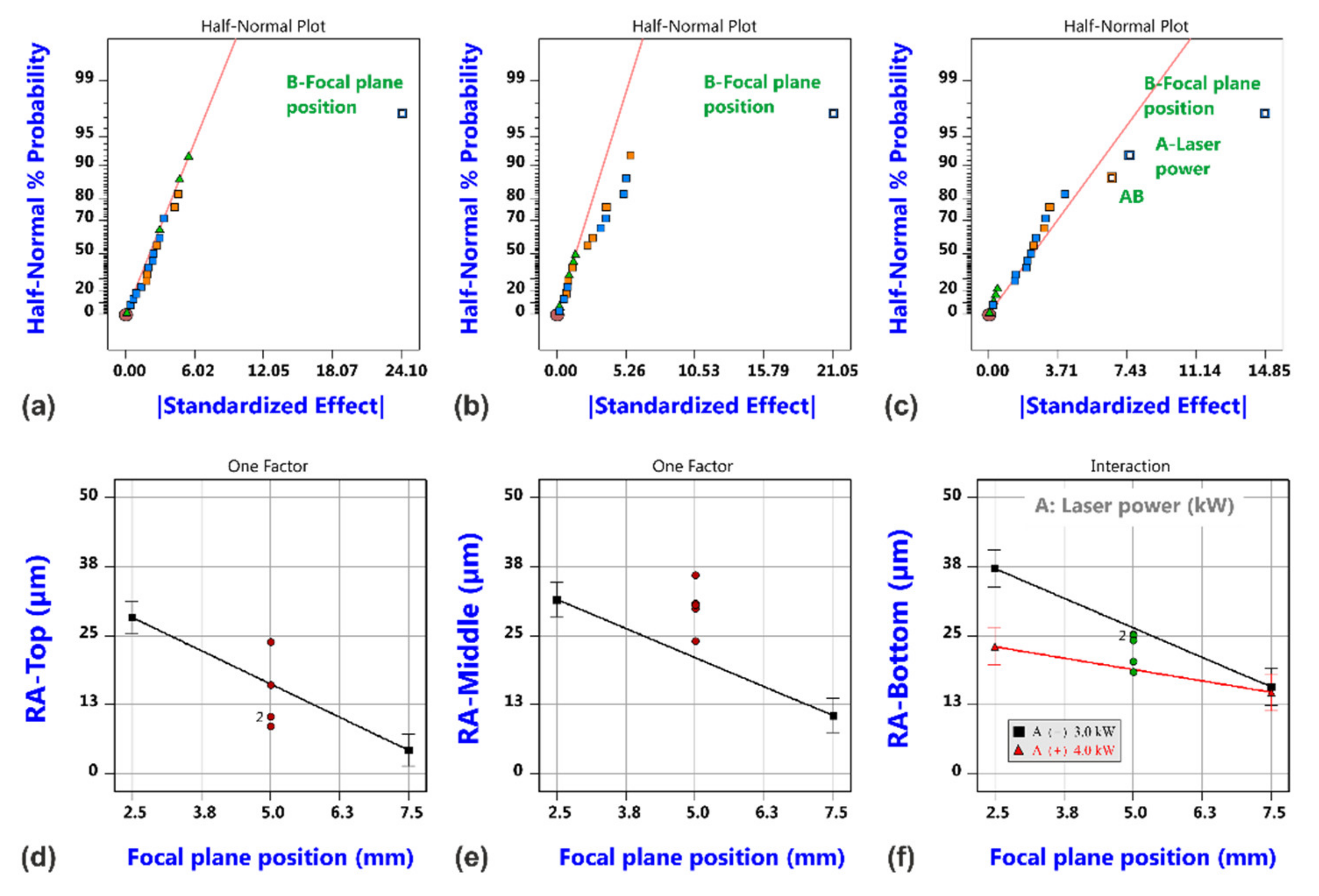
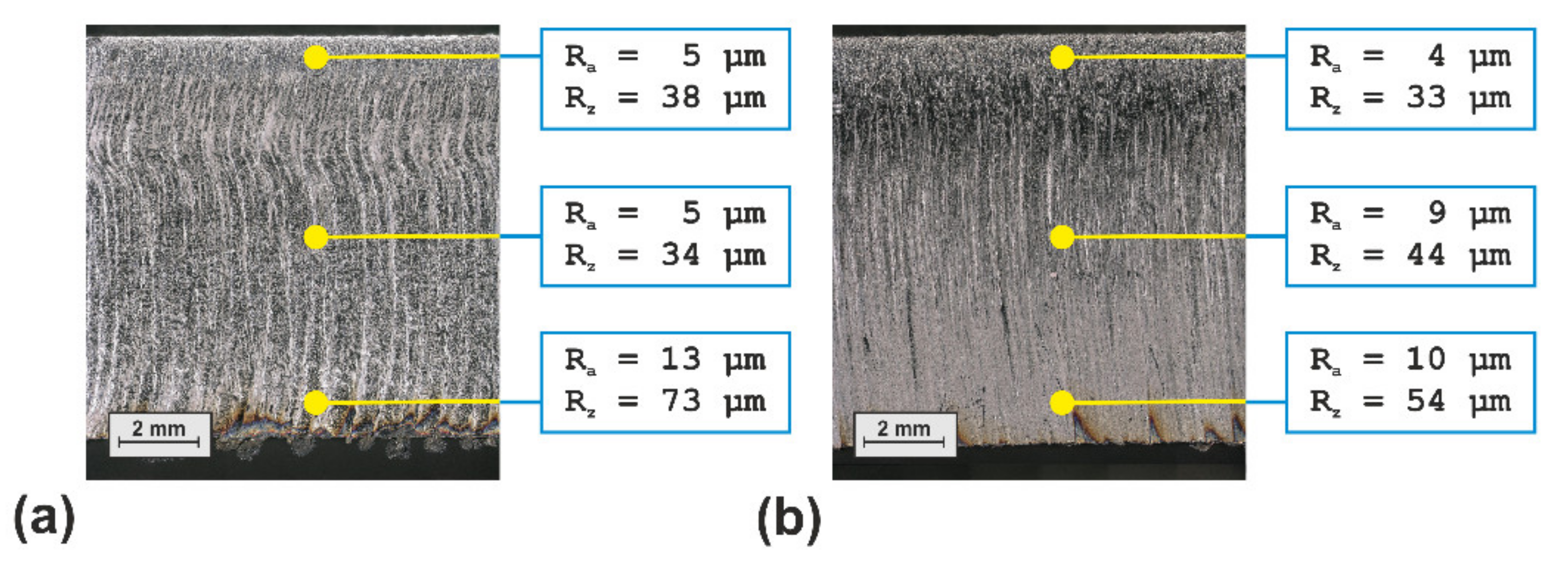
3.1. Factorial Analysis of Conventional Cutting
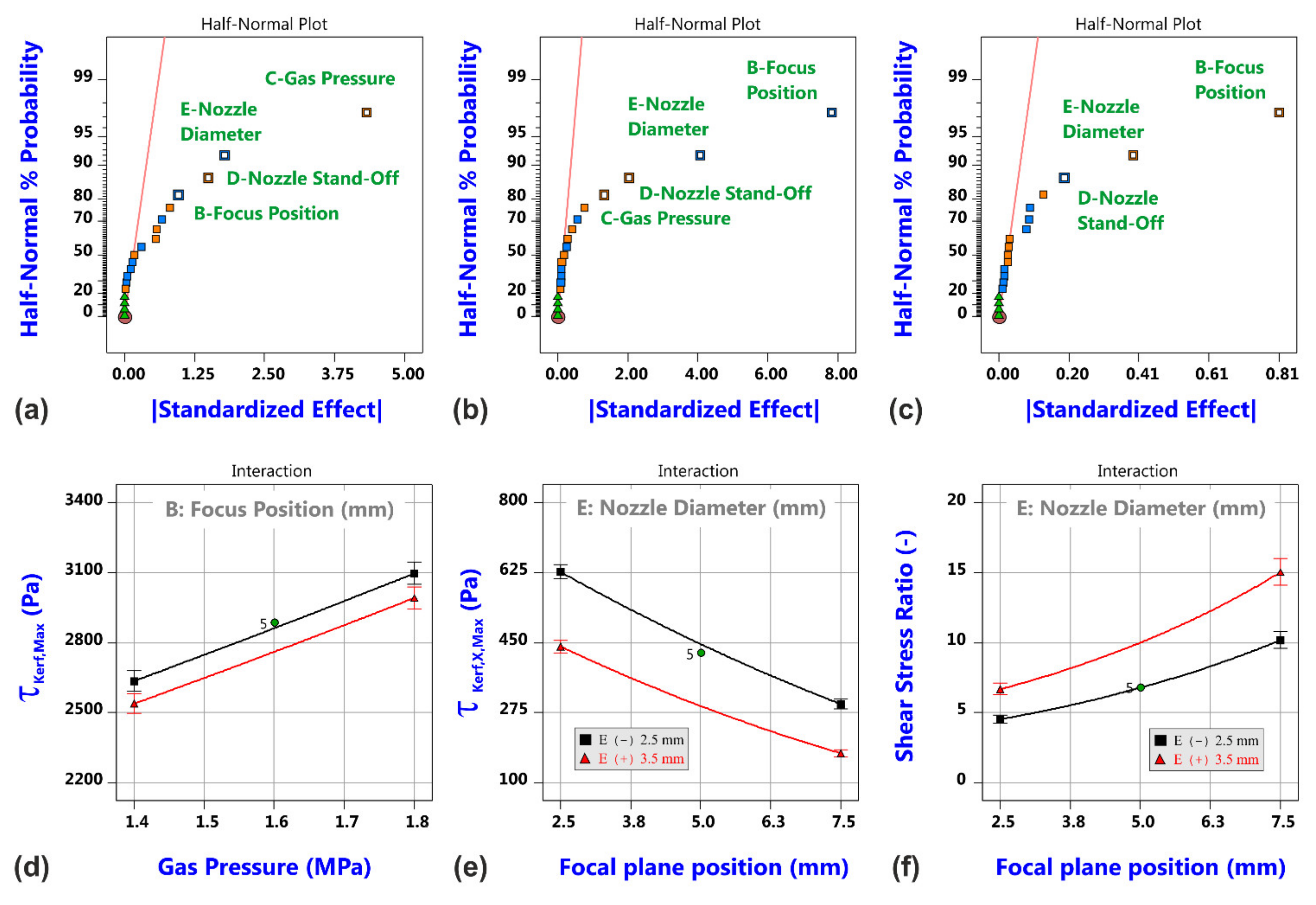
3.2. Factorial Analysis of Cutting Gas Flow
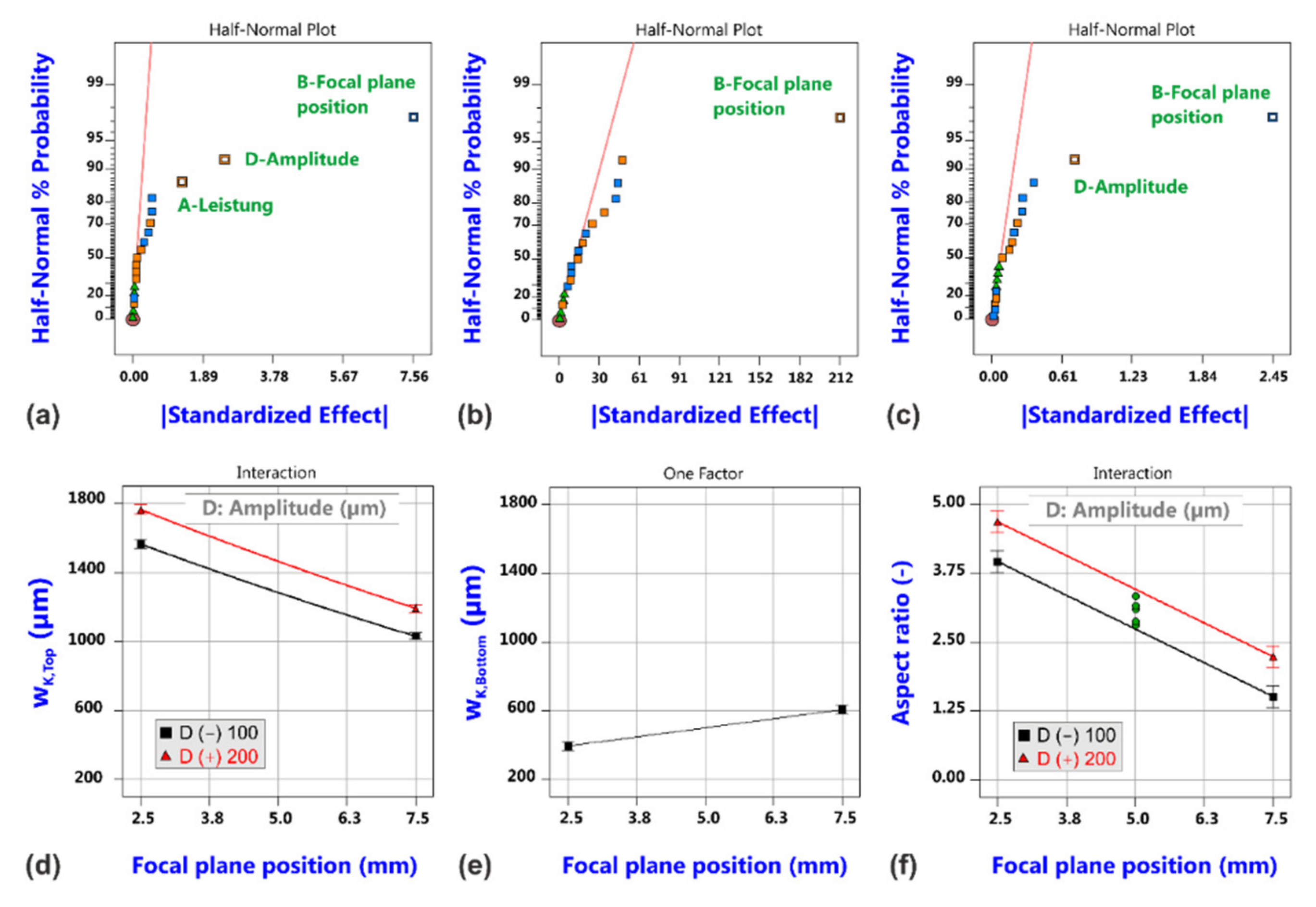
3.3. Factorial Analysis of Beam Oscillation Laser Cutting
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Powell, J. CO2 Laser Cutting, 2nd ed.; Springer: London, UK, 1998. [Google Scholar]
- Steen, W.M.; Mazumder, J. Laser Material Processing, 4th ed.; Springer: London, UK, 2010; pp. 156–198. [Google Scholar]
- Wandera, C.; Salminen, A.; Olsen, F.O.; Kujanpää, V. Cutting of stainless steel with fiber and disk laser. In Proceedings of the 25th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2006), Scottsdale, AZ, USA, 30 October–2 November 2006; Paper 404. pp. 211–220. [Google Scholar]
- Himmer, T.; Pinder, T.; Morgenthal, L.; Beyer, E. High-brightness lasers in cutting applications. In Proceedings of the 26th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2007), Orlando, FL, USA, 29 October–1 November 2007; Paper 206. pp. 87–91. [Google Scholar]
- Hilton, P.A. Cutting stainless steel with disc and CO2 lasers. In Proceedings of the 5th International Congress on Laser Advanced Materials Processing (LAMP 2009), Kobe, Japan, 29 June–2 July 2009. [Google Scholar]
- Scintilla, L.D.; Tricarico, L.; Mahrle, A.; Wetzig, A.; Himmer, T.; Beyer, E. A comparative study on fusion cutting with disk and CO2 lasers. In Proceedings of the 29th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2010), Anaheim, CA, USA, 26–30 September 2010; Paper 704. pp. 249–258. [Google Scholar]
- Scintilla, L.D.; Tricarico, L.; Wetzig, A.; Mahrle, A.; Beyer, E. Primary losses in disk and CO2 laser beam inert gas fusion cutting. J. Mater. Process. Technol. 2011, 211, 2050–2061. [Google Scholar] [CrossRef]
- Scintilla, L.D.; Tricarico, L.; Mahrle, A.; Wetzig, A.; Himmer, T.; Beyer, E. Fusion cutting of steel with disk and CO2 lasers. Laser User 2011, 62, 24–26. [Google Scholar]
- Petring, D.; Schneider, F.; Wolf, N.; Nazery, V. The relevance of brightness for high power laser cutting and welding. In Proceedings of the 27th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2008), Temecula, CA, USA, 20–23 October 2008; Paper 206. pp. 95–103. [Google Scholar]
- Mahrle, A.; Bartels, F.; Beyer, E. Theoretical aspects of the process efficiency in laser beam cutting with fiber lasers. In Proceedings of the 27th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2008), Temecula, CA, USA, 20–23 October 2008; Paper 2006. pp. 703–712. [Google Scholar]
- Mahrle, A.; Beyer, E. Theoretical aspects of fibre laser cutting. J. Phys. D Appl. Phys. 2009, 42, 1175507. [Google Scholar] [CrossRef]
- Petring, D. Calculable laser cutting. In Proceedings of the 5th International Conference on Lasers in Manufacturing (LIM 2009), Munich, Germany, 15–18 June 2009; pp. 209–214. [Google Scholar]
- Mahrle, A.; Beyer, E. Theoretical estimation of achievable travel rates in inert-gas fusion cutting with fibre and CO2 lasers. In Proceedings of the 5th International Conference on Lasers in Manufacturing (LIM 2009), Munich, Germany, 15–18 June 2009; p. 6. [Google Scholar]
- Mahrle, A.; Beyer, E. Thermodynamic evaluation of inert-gas laser beam fusion cutting with CO2, disk and fiber lasers. In Proceedings of the 28th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2009), Orlando, FL, USA, 2–5 November 2009; Paper 1404. p. 10. [Google Scholar]
- Olsen, F.O. Fundamental mechanisms of cutting front formation in laser cutting. Proc. SPIE 1994, 2207, 402–413. [Google Scholar]
- Sparkes, M.; Gross, M.; Celotto, S.; Zhang, T.; O’Neill, W. Inert cutting of medium section stainless steel using a 2.2 kW high brightness fibre laser. In Proceedings of the 25th International Congress on Applications of Lasers & Electro-Optics (ICALEO 2006), Scottsdale, AZ, USA, 30 October–2 November 2006; Paper 402. pp. 197–205. [Google Scholar]
- Sparkes, M.; Gross, M.; Celotto, S.; Zhang, T.; O’Neill, W. Practical and theoretical investigations into inert-gas cutting of 304 stainless steel using a high brightness fiber laser. J. Laser Appl. 2008, 20, 59–67. [Google Scholar] [CrossRef]
- Wandera, C.; Kujanpää, V. Characterization of the melt removal rate in laser cutting of thick section stainless steel. J. Laser Appl. 2010, 22, 62–70. [Google Scholar] [CrossRef]
- Wandera, C.; Kujanpää, V. Optimization of parameters for fibre laser cutting of a 10 mm stainless steel plate. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2010, 225, 641–649. [Google Scholar] [CrossRef]
- Goppold, C.; Zenger, K.; Herwig, P.; Wetzig, A.; Mahrle, A.; Beyer, E. Experimental analysis for improvements of process efficiency and cut edge quality of fusion cutting with 1 µm laser radiation. Phys. Procedia 2014, 56, 892–900. [Google Scholar] [CrossRef]
- Goppold, C.; Pinder, T.; Herwig, P. Dynamic beam shaping for thick sheet metal cutting. In Proceedings of the Lasers in Manufacturing Conference (LIM 2017), Munich, Germany, 26–29 June 2017; p. 9. [Google Scholar]
- Pang, H.; Haecker, T. Laser cutting with annular intensity distribution. Procedia CIRP 2020, 94, 481–486. [Google Scholar] [CrossRef]
- Hirano, K.; Fabbro, R. Experimental observation of hydrodynamics of melt layer and striation generation during laser cutting of steel. Phys. Procedia 2011, 12, 555–564. [Google Scholar] [CrossRef]
- Hirano, K.; Fabbro, R. Study on striation generation process during laser cutting of steel. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics (ICALEO 2011), Orlando, FL, USA, 23–27 October 2011; Paper 106. pp. 50–59. [Google Scholar]
- Hirano, K.; Fabbro, R. Experimental investigation of hydrodynamics of melt layer during laser cutting of steel. J. Phys. D Appl. Phys. 2011, 44, 12. [Google Scholar] [CrossRef]
- Ermolaev, G.V.; Yudin, P.V.; Briand, F.; Zaitsev, A.V.; Kovalev, O.B. Fundamental study of CO2 and fibre laser cutting of steel plates with high speed visualization technique. J. Laser Appl. 2014, 26, 9. [Google Scholar] [CrossRef]
- Arntz, D.; Petring, D.; Stoyanov, S.; Quiring, N.; Poprawe, R. Quantitative study of melt flow dynamics inside laser cutting kerfs by in-situ high-speed video-diagnostics. Procedia CIRP 2018, 74, 640–644. [Google Scholar] [CrossRef]
- Arntz, D.; Petring, D.; Stoyanov, S.; Jansen, U.; Schneider, F.; Poprawe, R. In-situ visualization of multiple reflections on the cut flank during laser cutting with 1 µm wavelength. J. Laser Appl. 2018, 30, 10. [Google Scholar] [CrossRef]
- Petring, D. Virtual laser cutting simulation for real parameter optimization. In Proceedings of the 84th Laser Materials Processing Conference (JLPS), Nagoya, Japan, 19–20 January 2016; pp. 11–20. [Google Scholar]
- Amara, E.H.; Kheloufi, K.; Tamsaout, T. Wavelength effect on striation formation during metal laser cutting. In Proceedings of the 34th International Congress on Applications of lasers & Electro-Optics (ICALEO 2015), Atlanta, GA, USA, 18–22 October 2015; Paper 2006. pp. 950–954. [Google Scholar]
- Tamsaout, T.; Amara, E.H.; Bouabdallah, A. Numerical approach for hydrodynamic behavior in the kerf with a quasi-complete model of laser cutting process. J. Opt. Soc. Am. 2020, 37, 9. [Google Scholar] [CrossRef]
- Fieret, J.; Terry, M.J.; Ward, B.A. Aerodynamic interactions during laser cutting. Proc. SPIE 1986, 668, 53–62. [Google Scholar]
- Fieret, J.; Terry, M.J.; Ward, B.A. Overview of flow dynamics in gas-assisted laser cutting. Proc. SPIE 1987, 801, 243–250. [Google Scholar]
- Petring, D.; Abels, P.; Beyer, E.; Herziger, G. Werkstoffbearbeitung mit Laserstrahlung, Teil 10: Schneiden von metallischen Werkstoffen mit CO2 Hochleistungslasern. Feinw. Messtech. 1988, 96, 364–372. [Google Scholar]
- Brandt, A.D.; Scroggs, S.D.; Settles, G.S. Effects of nozzle orientation on the gas dynamics of inert-gas laser cutting of mild steel. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics (ICALEO 1996), Detroit, MA, USA, 14–17 October 1996; Section C. pp. 10–19. [Google Scholar]
- Brandt, A.D.; Settles, G.S. Effect of nozzle orientation on the gas dynamics of inert-gas laser cutting of mild steel. J. Laser Appl. 1997, 9, 269–277. [Google Scholar] [CrossRef]
- Chen, K.; Yao, L.; Modi, V. Gas dynamic effects on laser cut quality. J. Manuf. Process. 2001, 3, 38–49. [Google Scholar] [CrossRef]
- Man, H.C.; Duan, J.; Yue, T.M. Analysis of the dynamic characteristics of gas flow inside a laser cut kerf under high cut-assist gas pressure. J. Phys. D Appl. Phys. 1999, 32, 1460–1477. [Google Scholar] [CrossRef]
- Riveiro, A.; Quintero, F.; Boutinguiza, M.; del Val, J.; Comesana, R.; Lusquinos, F.; Pou, J. Laser cutting: A review on the influence of assist gas. Materials 2019, 12, 157. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.J.; Whitcomb, P.J. DOE Simplified, 3rd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2015; p. 252. [Google Scholar]
- Anderson, M.J.; Whitcomb, P.J. RSM Simplified; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2005; p. 292. [Google Scholar]
- Son, S.; Lee, D. The effect of laser parameters on cutting metallic materials. Materials 2020, 13, 4596. [Google Scholar] [CrossRef]
- Huehnlein, K.; Tschirpke, K.; Hellmann, R. Optimization of laser cutting processes using design of experiments. Physics Procedia 2010, 5, 243–252. [Google Scholar] [CrossRef][Green Version]
- Eltawahni, H.A.; Hagino, M.; Benyounis, K.Y.; Inoue, T.; Olabi, A.G. Effect of CO2 laser cutting process parameters on edge quality and operating cost of AISI316L. Opt. Laser Technol. 2012, 44, 1068–1082. [Google Scholar] [CrossRef]
- Tahir, A.F.M.; Aquida, S.N. An investigation of laser cutting quality of 22MnB5 ultra high strength steel using response surface methodology. Opt. Laser Technol. 2017, 92, 142–149. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Ninikas, K.; Petousis, M.; Vidakis, N.; Vaxevanidis, N. An investigation of surface quality characteristics of 3D printed PLA plates cut by CO2 laser using experimental design. Mater. Manuf. Process. 2021. [Google Scholar] [CrossRef]
- Sharma, A.; Yadava, V. Optimization of cut quality characteristics during Nd:YAG laser straight cutting of Ni-based superalloy thin sheet using grey relational analysis with entropy measurement. Mater. Manuf. Process. 2011, 26, 1522–1529. [Google Scholar] [CrossRef]
- Mukherjee, I.; Ray, P.K. A review of optimization techniques in metal cutting processes. Comput. Ind. Eng. 2006, 50, 15–34. [Google Scholar] [CrossRef]
- Hashemzadeh, M.; Suder, W.; Williams, S.; Powell, J.; Kaplan, A.F.H.; Voisey, K.T. The application of specific point energy analysis to laser cutting with 1 µm laser radiation. Phys. Procedia 2014, 56, 909–918. [Google Scholar] [CrossRef]
- Steen, W.M. Laser Material Processing, 2nd ed.; Springer: London, UK, 1998; pp. 109–115. [Google Scholar]
- Borkmann, M.; Mahrle, A.; Beyer, E.; Leyens, C. Cut edge structures and gas boundary layer characteristics in laser beam fusion cutting. In Proceedings of the Lasers in Manufacturing Conference (LIM 2019), Munich, Germany, 24–27 June 2019; p. 11. [Google Scholar]
- Borkmann, M.; Mahrle, A.; Beyer, E.; Leyens, C. Laser fusion cutting: Evaluation of gas boundary layer flow state, momentum and heat transfer. Mater. Res. Express 2021, 8, 036513. [Google Scholar] [CrossRef]








| Element | M% |
|---|---|
| Carbon (C) | 0.019 |
| Silicon (Si) | 0.556 |
| Manganese (Mn) | 1.042 |
| Phosphorous (P) | 0.0296 |
| Sulphur (S) | 0.0255 |
| Chromium (Cr) | 18.206 |
| Nickel (Ni) | 8.103 |
| Molybdenum (Mo) | 0.398 |
| Cobalt (Co) | 0.106 |
| Nitrogen (N) | 0.081 |
| Copper (Cu) | 0.432 |
| Iron (Fe) | Balance |
| Run | Factor A | Factor B | Factor C | Factor D | Factor E | Category |
|---|---|---|---|---|---|---|
| Laser Power | Focal Plane Position | Cutting Gas Pressure | Nozzle Stand-Off | Nozzle Diameter | ||
| - | (kW) | (mm) | (MPa) | (mm) | (mm) | - |
| 1 | 3.0 | 7.5 | 1.4 | 0.50 | 2.5 | 2 |
| 2 | 4.0 | 7.5 | 1.4 | 1.00 | 2.5 | 2 |
| 3 | 3.5 | 5.0 | 1.6 | 0.75 | 3.0 | 3 |
| 4 | 4.0 | 2.5 | 1.4 | 1.00 | 3.5 | 3 |
| 5 | 4.0 | 2.5 | 1.8 | 0.50 | 3.5 | 3 |
| 6 | 3.5 | 5.0 | 1.6 | 0.75 | 3.0 | 3 |
| 7 | 4.0 | 7.5 | 1.4 | 0.50 | 3.5 | 1 |
| 8 | 3.0 | 2.5 | 1.8 | 0.50 | 2.5 | 3 |
| 9 | 3.0 | 7.5 | 1.8 | 1.00 | 2.5 | 2 |
| 10 | 4.0 | 2.5 | 1.8 | 1.00 | 2.5 | 3 |
| 11 | 4.0 | 7.5 | 1.8 | 1.00 | 3.5 | 2 |
| 12 | 3.5 | 5.0 | 1.6 | 0.75 | 3.0 | 3 |
| 13 | 3.0 | 2.5 | 1.8 | 1.00 | 3.5 | 3 |
| 14 | 4.0 | 7.5 | 1.8 | 0.50 | 2.5 | 1 |
| 15 | 3.5 | 5.0 | 1.6 | 0.75 | 3.0 | 3 |
| 16 | 3.0 | 7.5 | 1.8 | 0.50 | 3.5 | 1 |
| 17 | 3.5 | 5.0 | 1.6 | 0.75 | 3.0 | 3 |
| 18 | 3.0 | 2.5 | 1.4 | 0.50 | 3.5 | 3 |
| 19 | 4.0 | 2.5 | 1.4 | 0.50 | 2.5 | 3 |
| 20 | 3.0 | 2.5 | 1.4 | 1.00 | 2.5 | 3 |
| 21 | 3.0 | 7.5 | 1.4 | 1.00 | 3.5 | 1 |
| Response | Unit | Minimum | Maximum | Ratio | Mean |
|---|---|---|---|---|---|
| Cutting Speed Max | m/min | 0.70 | 1.60 | 2.28 | 1.05 |
| Kerf width Top | µm | 800 | 1650 | 2.06 | 1218 |
| Kerf width Bottom | µm | 816 | 1685 | 2.06 | 1240 |
| Aspect ratio | - | 0.48 | 4.28 | 8.92 | 2.5 |
| RA-LO (Ra (left side, top)) | µm | 4 | 45 | 11.2 | 23 |
| RA-LM (Ra (left side, middle)) | µm | 5 | 35 | 7.00 | 21 |
| RA-LU (Ra (left side, bottom)) | µm | 13 | 35 | 2.69 | 24 |
| RA-RO (Ra (right side, top)) | µm | 4 | 52 | 13.0 | 22 |
| RA-RM (Ra (right side, middle)) | µm | 5 | 35 | 7.00 | 17 |
| RA-RU (Ra (right side, bottom)) | µm | 11 | 37 | 3.36 | 24 |
| RZ-LO (Rz (left side, top)) | µm | 23 | 218 | 9.48 | 117 |
| RZ-LM (Rz (left side, middle)) | µm | 34 | 168 | 4.94 | 107 |
| RZ-LU (Rz (left side, bottom)) | µm | 73 | 176 | 2.41 | 122 |
| RZ-RO (Rz (right side, top)) | µm | 25 | 216 | 8.64 | 101 |
| RZ-RM (Rz (right side, middle)) | µm | 31 | 163 | 5.26 | 92 |
| RZ-RU (Rz (right side, bottom)) | µm | 59 | 181 | 3.07 | 118 |
| Response | Unit | Minimum | Maximum | Ratio | Mean |
|---|---|---|---|---|---|
| Shear stress τFront,Max (Front Max) | Pa | 2194 | 3402 | 1.55 | 2757 |
| Shear stress τKerf,Max (Kerf Max) | Pa | 2375 | 3277 | 1.38 | 2834 |
| X Shear stress τKerf,X,Max (Kerf Max) | Pa | 120 | 708 | 5.91 | 395 |
| Shear stress ratio τKerf,Max/τKerf,X,Max | - | 4.52 | 20.0 | 4.42 | 9 |
| Shear stress τFront,Mean (Front Mean) | Pa | 1722 | 2578 | 1.50 | 2135 |
| Shear stress τKerf,Mean (Kerf Mean) | Pa | 1840 | 2750 | 1.49 | 2272 |
| X Shear stress τKerf,X,Mean (Kerf Mean) | Pa | 51 | 449 | 8.84 | 242 |
| Run | Factor A | Factor B | Factor C | Factor D | Cut Edge Category |
|---|---|---|---|---|---|
| Laser Power | Focal Plane Position | Oscillation Frequency | Oscillation Amplitude | ||
| - | (kW) | (mm) | (Hz) | (µm) | - |
| 1 | 3.5 | 5.0 | 2000 | 150 | 3 |
| 2 | 4.0 | 7.5 | 2800 | 200 | 1 |
| 3 | 3.0 | 7.5 | 2800 | 100 | 2 |
| 4 | 3.0 | 2.5 | 2800 | 100 | 3 |
| 5 | 3.0 | 7.5 | 1200 | 200 | 1 |
| 6 | 3.0 | 2.5 | 1200 | 100 | 3 |
| 7 | 3.5 | 5.0 | 2000 | 150 | 3 |
| 8 | 3.0 | 7.5 | 2800 | 200 | 1 |
| 9 | 4.0 | 2.5 | 2800 | 100 | 3 |
| 10 | 4.0 | 7.5 | 1200 | 200 | 1 |
| 11 | 4.0 | 7.5 | 1200 | 100 | 1 |
| 12 | 4.0 | 2.5 | 2800 | 200 | 3 |
| 13 | 4.0 | 2.5 | 1200 | 200 | 3 |
| 14 | 3.5 | 5.0 | 2000 | 150 | 3 |
| 15 | 3.0 | 2.5 | 2800 | 200 | 3 |
| 16 | 3.5 | 5.0 | 2000 | 150 | 3 |
| 17 | 4.0 | 7.5 | 2800 | 100 | 1 |
| 18 | 4.0 | 2.5 | 1200 | 100 | 3 |
| 19 | 3.5 | 5.0 | 2000 | 150 | 3 |
| 20 | 3.0 | 2.5 | 1200 | 200 | 3 |
| 21 | 3.0 | 7.5 | 1200 | 100 | 1 |
| Response | Unit | Minimum | Maximum | Ratio | Mean |
|---|---|---|---|---|---|
| Cutting Speed Max | m/min | 0.60 | 1.50 | 2.50 | 0.99 |
| Kerf width Top | µm | 944 | 1836 | 1.94 | 1408 |
| Kerf width Bottom | µm | 331 | 671 | 2.03 | 491 |
| Aspect ratio | - | 1.41 | 5.15 | 3.65 | 3.10 |
| RA-LO (Ra (left side, top)) | µm | 4 | 40 | 10.0 | 17 |
| RA-LM (Ra (left side, middle)) | µm | 5 | 43 | 8.60 | 23 |
| RA-LU (Ra (left side, bottom)) | µm | 10 | 34 | 3.40 | 23 |
| RA-RO (Ra (right side, top)) | µm | 3 | 38 | 12.7 | 16 |
| RA-RM (Ra (right side, middle)) | µm | 5 | 38 | 7.60 | 20 |
| RA-RU (Ra (right side, bottom)) | µm | 10 | 41 | 4.10 | 23 |
| RZ-LO (Rz (left side, top)) | µm | 26 | 170 | 6.54 | 89 |
| RZ-LM (Rz (left side, middle)) | µm | 31 | 217 | 7.00 | 117 |
| RZ-LU (Rz (left side, bottom)) | µm | 56 | 160 | 2.86 | 121 |
| RZ-RO (Rz (right side, top)) | µm | 21 | 187 | 8.90 | 78 |
| RZ-RM (Rz (right side, middle)) | µm | 30 | 206 | 6.87 | 107 |
| RZ-RU (Rz (right side, bottom)) | µm | 54 | 193 | 3.57 | 117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahrle, A.; Borkmann, M.; Pfohl, P. Factorial Analysis of Fiber Laser Fusion Cutting of AISI 304 Stainless Steel: Evaluation of Effects on Process Performance, Kerf Geometry and Cut Edge Roughness. Materials 2021, 14, 2669. https://doi.org/10.3390/ma14102669
Mahrle A, Borkmann M, Pfohl P. Factorial Analysis of Fiber Laser Fusion Cutting of AISI 304 Stainless Steel: Evaluation of Effects on Process Performance, Kerf Geometry and Cut Edge Roughness. Materials. 2021; 14(10):2669. https://doi.org/10.3390/ma14102669
Chicago/Turabian StyleMahrle, Achim, Madlen Borkmann, and Peer Pfohl. 2021. "Factorial Analysis of Fiber Laser Fusion Cutting of AISI 304 Stainless Steel: Evaluation of Effects on Process Performance, Kerf Geometry and Cut Edge Roughness" Materials 14, no. 10: 2669. https://doi.org/10.3390/ma14102669
APA StyleMahrle, A., Borkmann, M., & Pfohl, P. (2021). Factorial Analysis of Fiber Laser Fusion Cutting of AISI 304 Stainless Steel: Evaluation of Effects on Process Performance, Kerf Geometry and Cut Edge Roughness. Materials, 14(10), 2669. https://doi.org/10.3390/ma14102669







