Broadband RCS Reduction by a Quaternionic Metasurface
Abstract
:1. Introduction
2. Design Principle of Metasurface
3. Results and Discussion
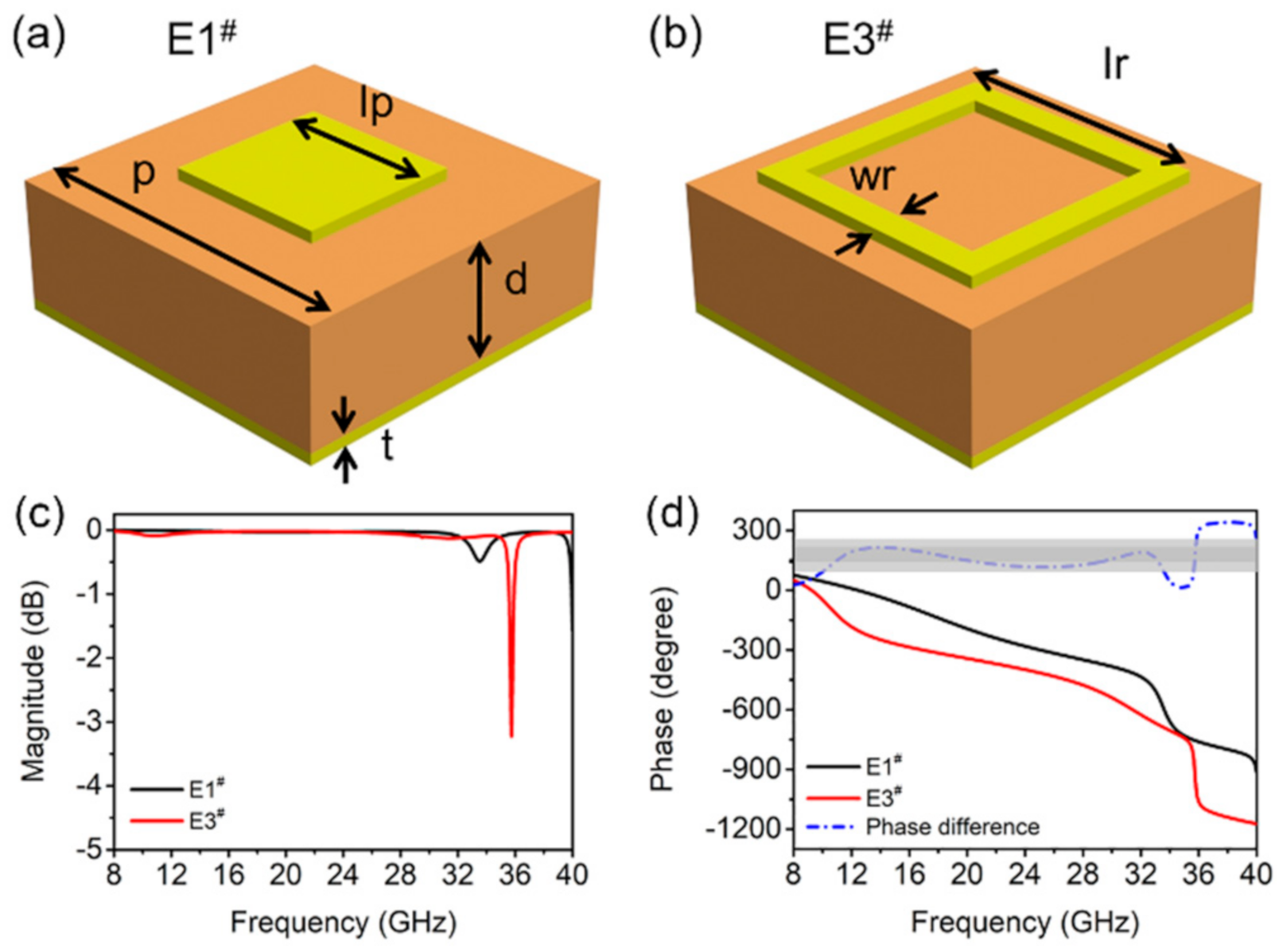
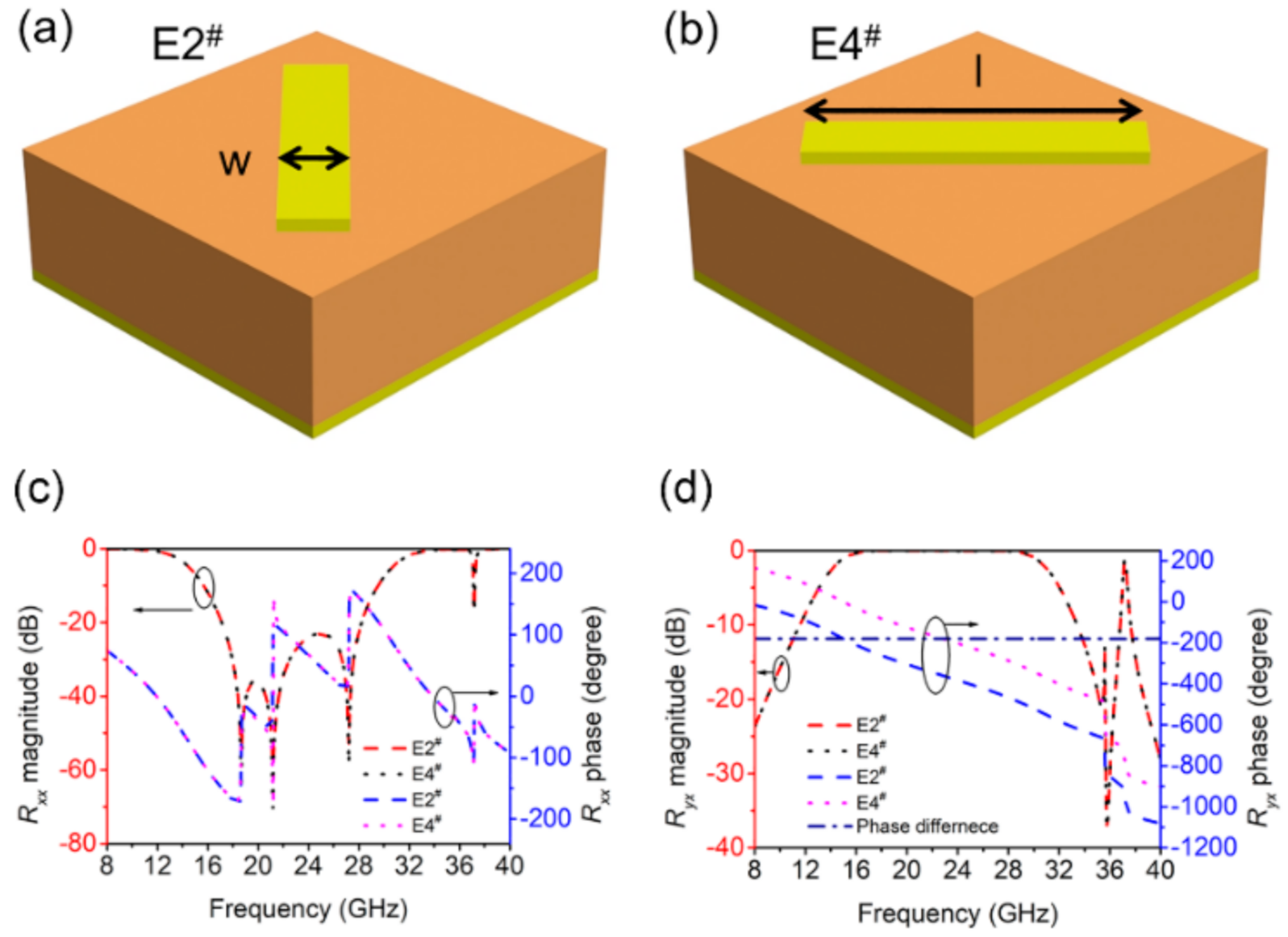
3.1. Anti-Phase Unit Cells
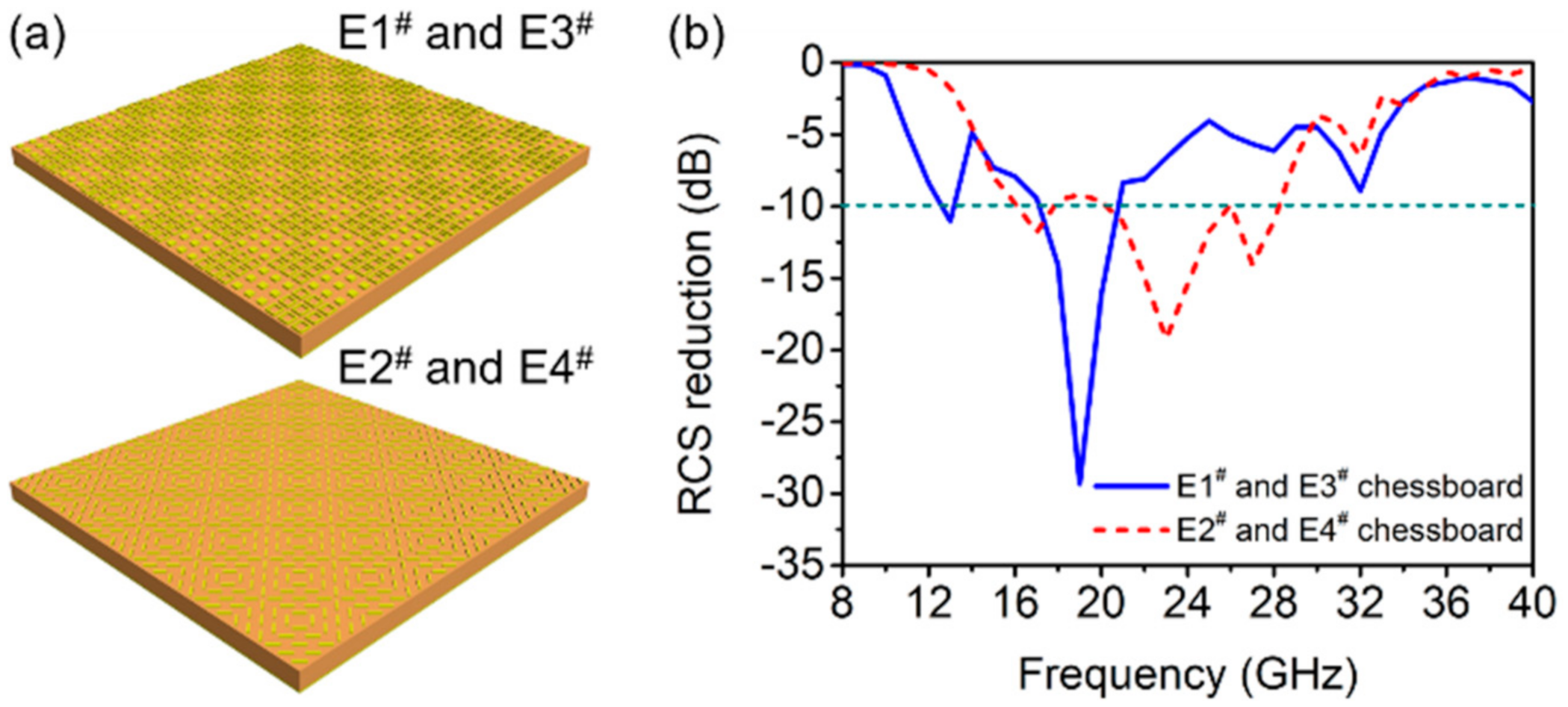
3.2. Binary Metasurface
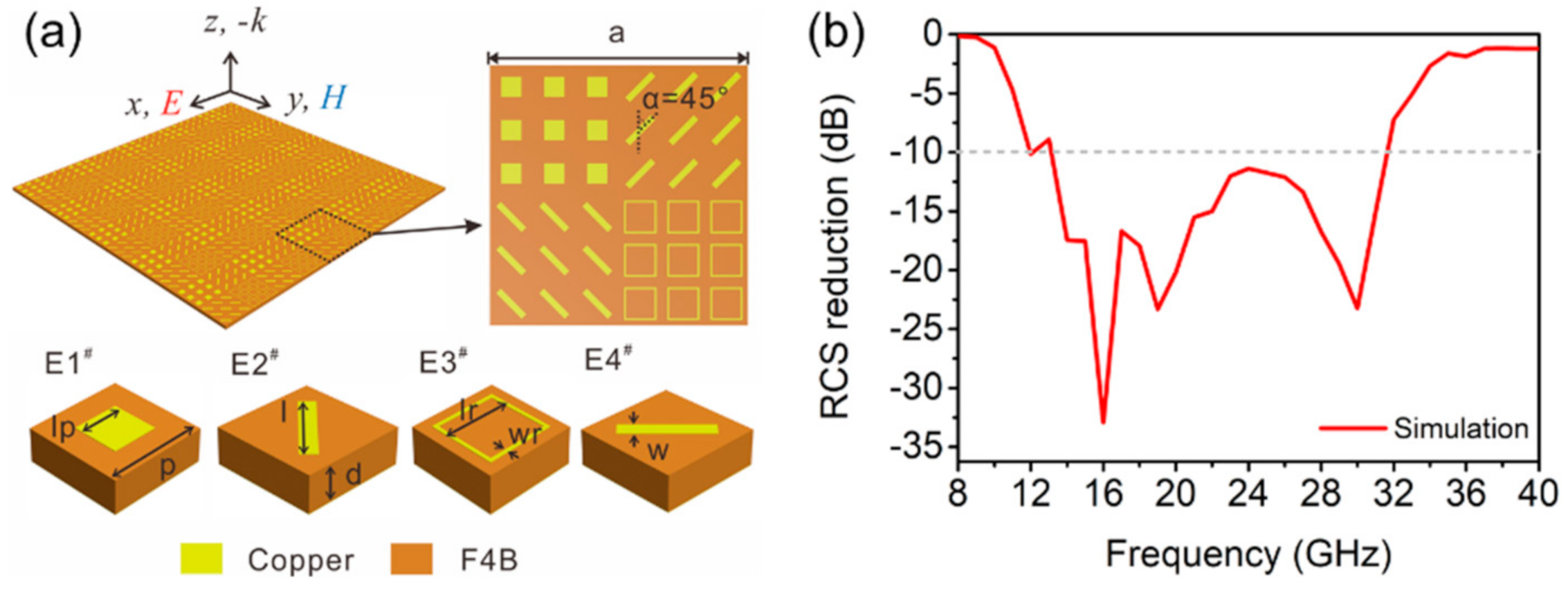
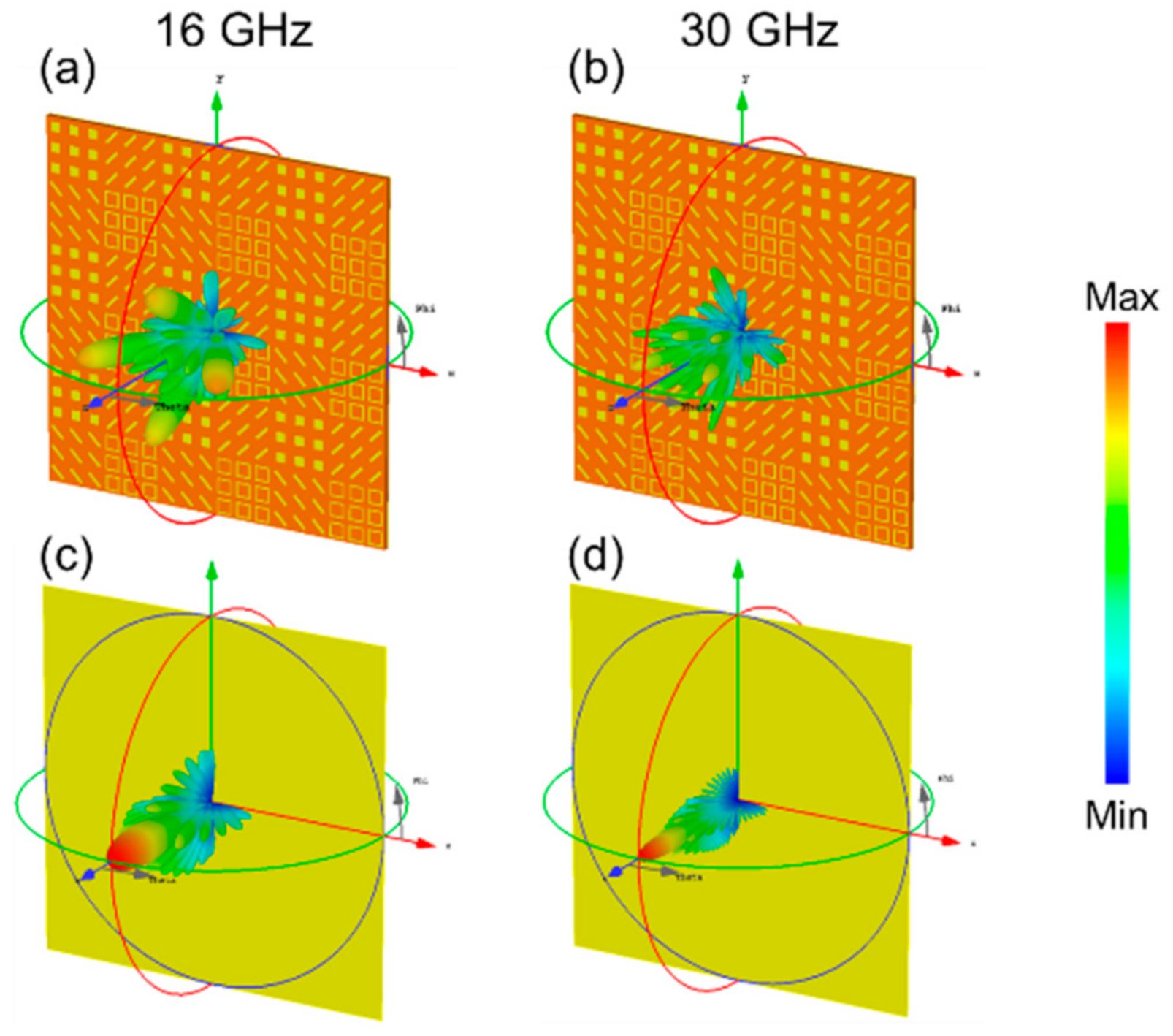
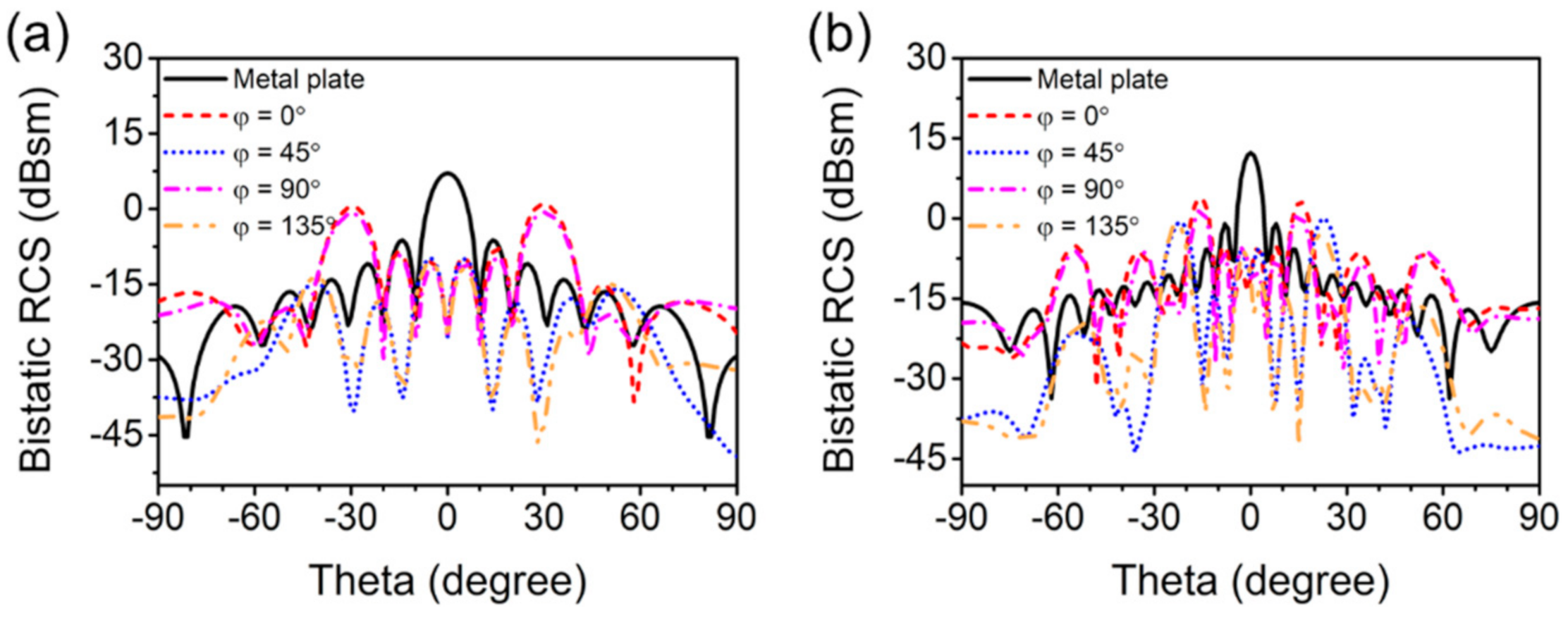
3.3. Quaternionic Metasurface
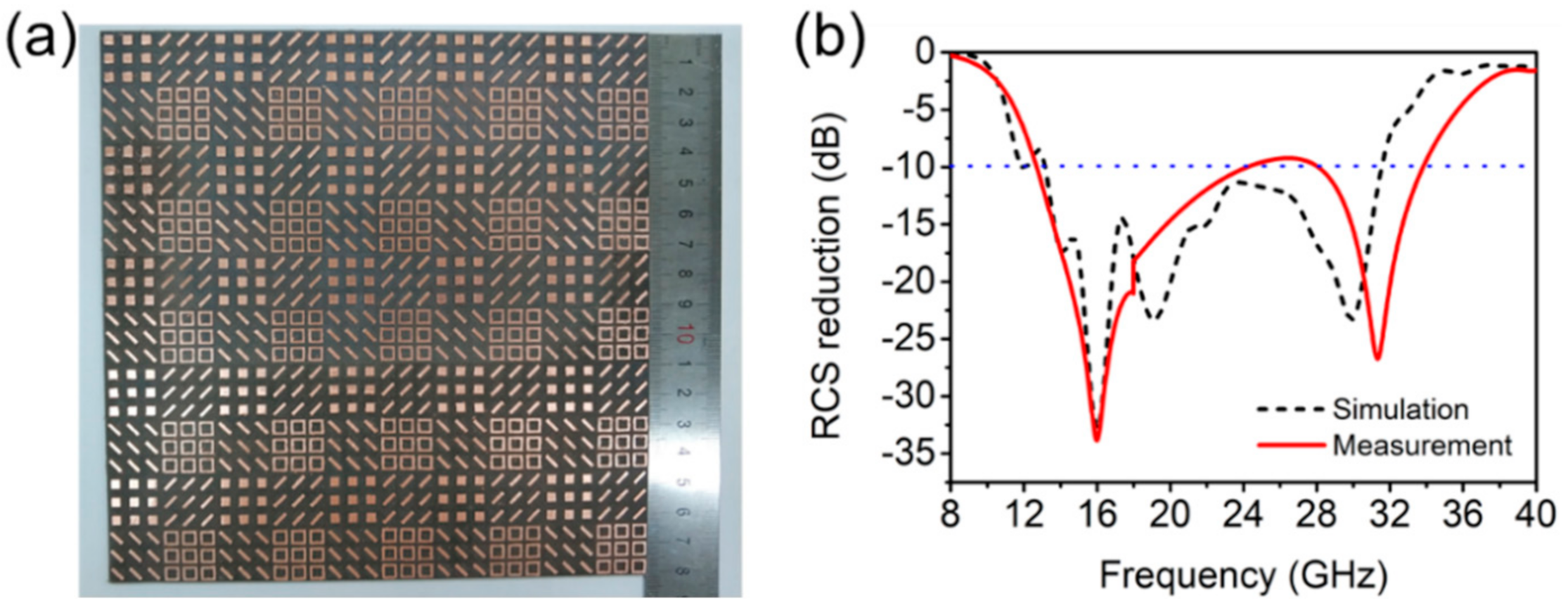
3.4. Fabrication and Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Lu, W.; Hang, Z.; Chen, H.; Hou, B.; Lai, Y.; Chan, C.T. Arbitrary control of electromagnetic flux in inhomogeneous anisotropic media with near-zero index. Phys. Rev. Lett. 2014, 112, 073903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfeiffer, C.; Grbic, A. Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 2013, 110, 197401. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Han, X.; Cao, W.-P.; Li, H.O.; Ma, H.F.; Cui, T.J. Ultrawideband and high-efficiency linear polarization converter based on double V-shaped metasurface. IEEE Trans. Antennas Propag. 2015, 63, 3522–3530. [Google Scholar] [CrossRef]
- Chen, H.-T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.; Wang, G.M.; Xu, H.X.; Tang, S.W.; Li, H.; Liang, J.G.; Zhuang, Y.Q. Bifunctional Pancharatnam-Berry Metasurface with High-Efficiency Helicity-Dependent Transmissions and Reflections. Annalen Phys. 2018, 530, 1700321. [Google Scholar] [CrossRef]
- Ishikawa, A.; Tanaka, T. Metamaterial Absorbers for Infrared Detection of Molecular Self-Assembled Monolayers. Sci. Rep. 2015, 5, 12570. [Google Scholar] [CrossRef]
- Wang, B.-Y.; Liu, S.-B.; Bian, B.-R.; Mao, Z.-W.; Liu, X.-C.; Ma, B.; Chen, L. A novel ultrathin and broadband microwave metamaterial absorber. J. Appl. Phys. 2014, 116, 094504. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, H. Design, simulation, and measurement of metamaterial absorber. J. Appl. Phys. 2010, 108, 034906. [Google Scholar] [CrossRef]
- Yoo, Y.J.; Ju, S.; Park, S.Y.; Kim, Y.J.; Bong, J.; Lim, T.; Kim, K.W.; Rhee, J.Y.; Lee, Y. Metamaterial absorber for electromagnetic waves in periodic water droplets. Sci. Rep. 2015, 5, 14018. [Google Scholar] [CrossRef] [Green Version]
- Kowerdziej, R.; Jaroszewicz, L. Tunable dual-band liquid crystal based near-infrared perfect metamaterial absorber with high-loss metal. Liq. Cryst. 2019, 46, 1568–1573. [Google Scholar] [CrossRef]
- Bilal, R.; Saeed, M.; Choudhury, P.; Baqir, M.; Kamal, W.; Ali, M.M.; Rahim, A.A. Elliptical metallic rings-shaped fractal metamaterial absorber in the visible regime. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- Qin, F.; Chen, Z.; Chen, X.; Yi, Z.; Yao, W.; Duan, T.; Wu, P.; Yang, H.; Li, G.; Yi, Y. A tunable triple-band near-infrared metamaterial absorber based on Au nano-cuboids array. Nanomaterials 2020, 10, 207. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, J.; Qu, S.; Wang, J.; Chen, H.; Xu, Z.; Zhang, A. Wideband radar cross section reduction using two-dimensional phase gradient metasurfaces. Appl. Phys. Lett. 2014, 104, 221110. [Google Scholar] [CrossRef]
- Chen, W.; Balanis, C.A.; Birtcher, C.R. Checkerboard EBG surfaces for wideband radar cross section reduction. IEEE Trans. Antennas Propag. 2015, 63, 2636–2645. [Google Scholar] [CrossRef]
- Wen, Q.-Y.; Zhang, H.-W.; Xie, Y.-S.; Yang, Q.-H.; Liu, Y.-L. Dual band terahertz metamaterial absorber: Design, fabrication, and characterization. Appl. Phys. Lett. 2009, 95, 241111. [Google Scholar] [CrossRef]
- Sellier, A.; Teperik, T.V.; de Lustrac, A. Resonant circuit model for efficient metamaterial absorber. Opt. Express 2013, 21 (Suppl. 6), A997–A1006. [Google Scholar] [CrossRef]
- Shen, X.; Cui, T.J.; Zhao, J.; Ma, H.F.; Jiang, W.X.; Li, H. Polarization-independent wide-angle triple-band metamaterial absorber. Opt. Express 2011, 19, 9401–9407. [Google Scholar] [CrossRef]
- Ding, F.; Cui, Y.; Ge, X.; Jin, Y.; He, S. Ultra-broadband microwave metamaterial absorber. Appl. Phys. Lett. 2012, 100, 103506. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.; Long, C.; Li, J.; Zhu, H.; Chen, L.; Guan, J.; Li, X. Ultra-wideband microwave absorber by connecting multiple absorption bands of two different-sized hyperbolic metamaterial waveguide arrays. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Long, C.; Yin, S.; Wang, W.; Li, W.; Zhu, J.; Guan, J. Broadening the absorption bandwidth of metamaterial absorbers by transverse magnetic harmonics of 210 mode. Sci. Rep. 2016, 6, 21431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Wu, T.; Wang, W.; Zhai, P.; Guan, J. Broadband patterned magnetic microwave absorber. J. Appl. Phys. 2014, 116, 044110. [Google Scholar] [CrossRef]
- Chen, K.; Cui, L.; Feng, Y.; Zhao, J.; Jiang, T.; Zhu, B. Coding metasurface for broadband microwave scattering reduction with optical transparency. Opt. Express 2017, 25, 5571–5579. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Zhang, C.; Yang, J.; Sun, B.; Zhao, B.; Luo, X. Reconfigurable metasurface for multifunctional control of electromagnetic waves. Adv. Opt. Mater. 2017, 5, 1700485. [Google Scholar] [CrossRef]
- Zhao, J.; Sima, B.; Jia, N.; Wang, C.; Zhu, B.; Jiang, T.; Feng, Y. Achieving flexible low-scattering metasurface based on randomly distribution of meta-elements. Opt. Express 2016, 24, 27849–27857. [Google Scholar] [CrossRef] [PubMed]
- Al-Nuaimi, M.K.T.; Hong, W.; He, Y. Backscattered EM-wave manipulation using low cost 1-bit reflective surface at W-band. J. Phys. D Appl. Phys. 2018, 51, 145105. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Q.; Wang, X.K.; Yuan, M.J.; Zhou, X.; Fu, X.J.; Qi, M.Q.; Liu, S.; Chen, H.B.; Zhang, Y. Controlling the bandwidth of terahertz low-scattering metasurfaces. Adv. Opt. Mater. 2016, 4, 1773–1779. [Google Scholar] [CrossRef]
- Moccia, M.; Liu, S.; Wu, R.Y.; Castaldi, G.; Andreone, A.; Cui, T.J.; Galdi, V. Coding metasurfaces for diffuse scattering: Scaling laws, bounds, and suboptimal design. Adv. Opt. Mater. 2017, 5, 1700455. [Google Scholar] [CrossRef]
- Paquay, M.; Iriarte, J.-C.; Ederra, I.; Gonzalo, R.; de Maagt, P. Thin AMC structure for radar cross-section reduction. IEEE Trans. Antennas Propag. 2007, 55, 3630–3638. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, C.; Cheng, Q.; Yang, J.; Cui, T.J. An optically transparent metasurface for broadband microwave antireflection. Appl. Phys. Lett. 2018, 112, 073504. [Google Scholar] [CrossRef]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Mattelin, A. Method for Manufacturing Printed Circuit. Boards.U.S. Patent No. 4,943,346, 24 July 1990. [Google Scholar]
- Knott, E.F.; Schaeffer, J.F.; Tulley, M.T. Radar Cross Section; SciTech Publishing: Raleigh, NC, USA, 2004. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, Y.; Wu, T.; Chen, S.; Li, W.; Guan, J. Broadband RCS Reduction by a Quaternionic Metasurface. Materials 2021, 14, 2787. https://doi.org/10.3390/ma14112787
Zhang Z, Zhang Y, Wu T, Chen S, Li W, Guan J. Broadband RCS Reduction by a Quaternionic Metasurface. Materials. 2021; 14(11):2787. https://doi.org/10.3390/ma14112787
Chicago/Turabian StyleZhang, Zhao, Yazhong Zhang, Tianlong Wu, Shaowen Chen, Wei Li, and Jianguo Guan. 2021. "Broadband RCS Reduction by a Quaternionic Metasurface" Materials 14, no. 11: 2787. https://doi.org/10.3390/ma14112787
APA StyleZhang, Z., Zhang, Y., Wu, T., Chen, S., Li, W., & Guan, J. (2021). Broadband RCS Reduction by a Quaternionic Metasurface. Materials, 14(11), 2787. https://doi.org/10.3390/ma14112787







