Identification of Mode Shapes of a Composite Cylinder Using Convolutional Neural Networks
Abstract
1. Introduction
2. Formulation of the Problem
2.1. Solution of the Vibration Problem
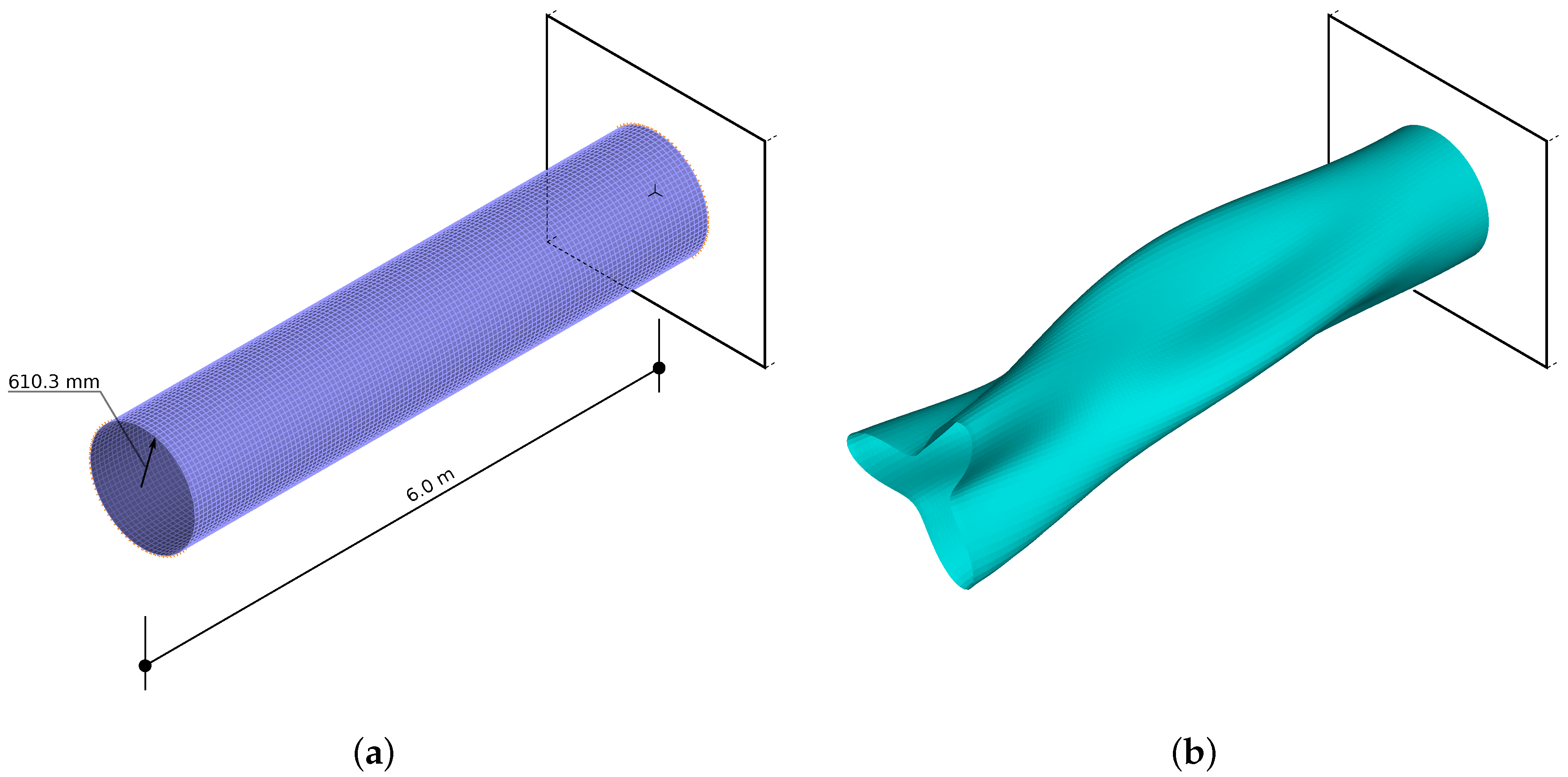
2.2. Investigated Structure and Its Finite Element Model
2.3. Convolutional Neural Networks
3. Mode Shapes Identification
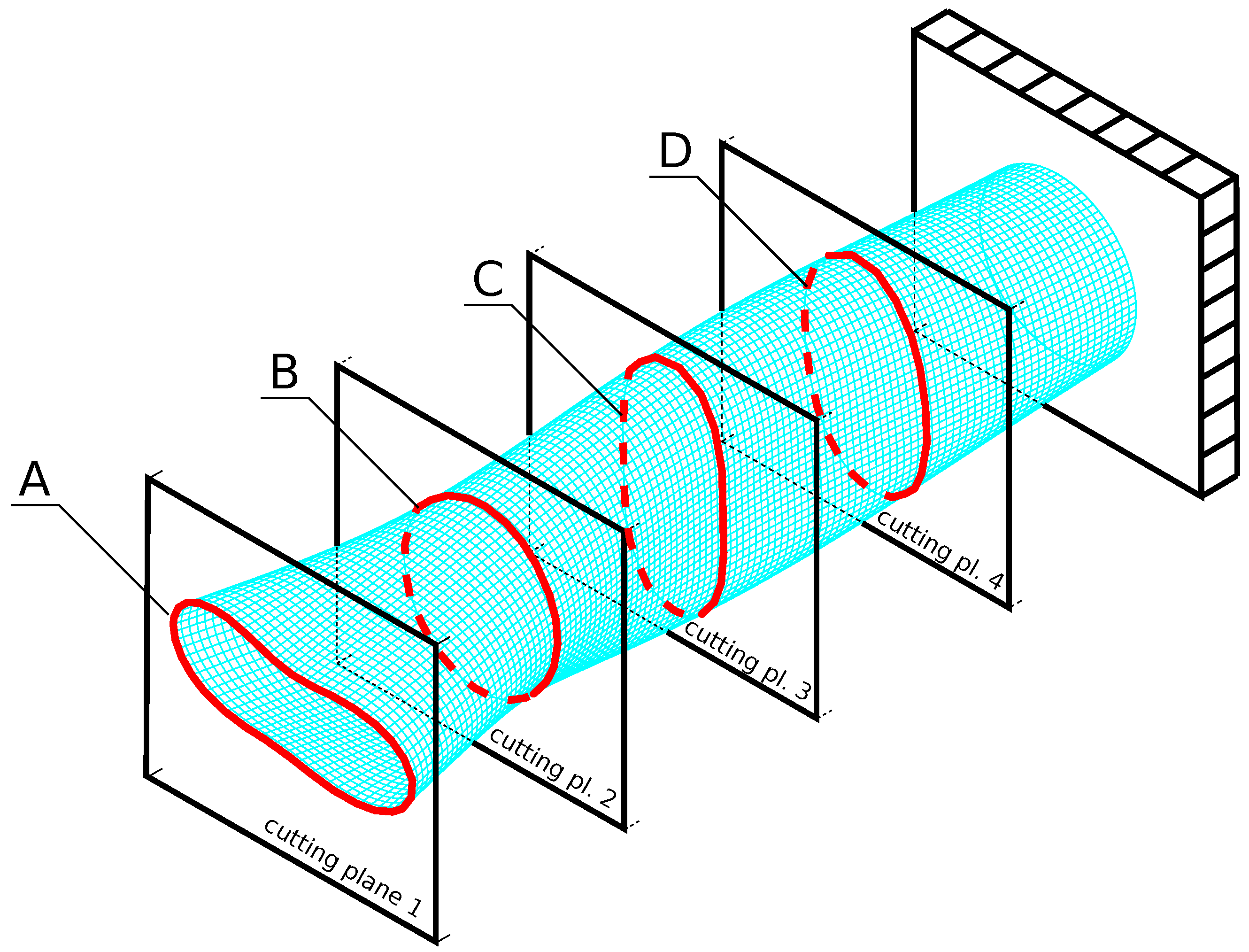
3.1. The Analytical Approach
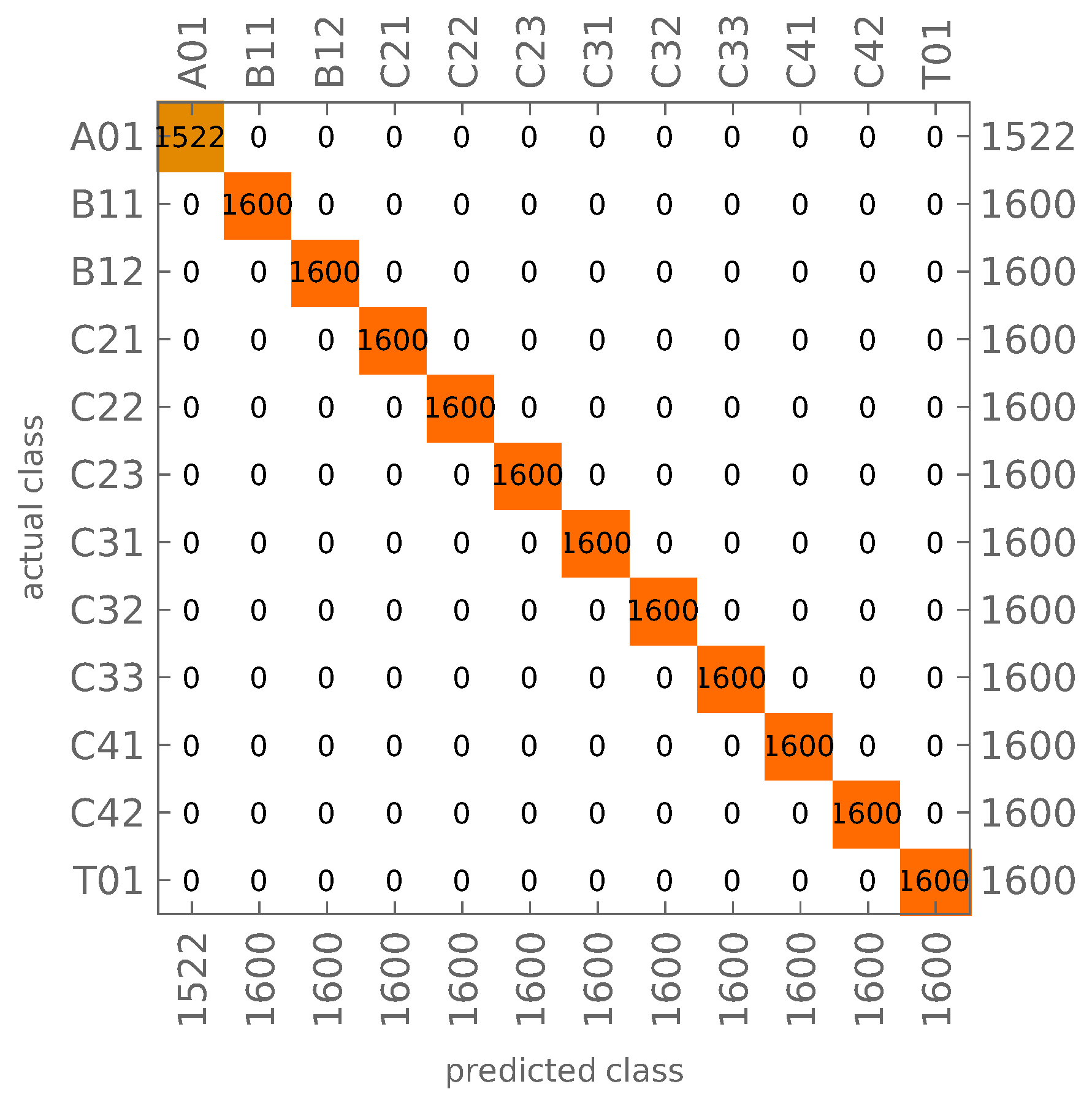
3.2. Neural Network Based Mode Shapes Identification
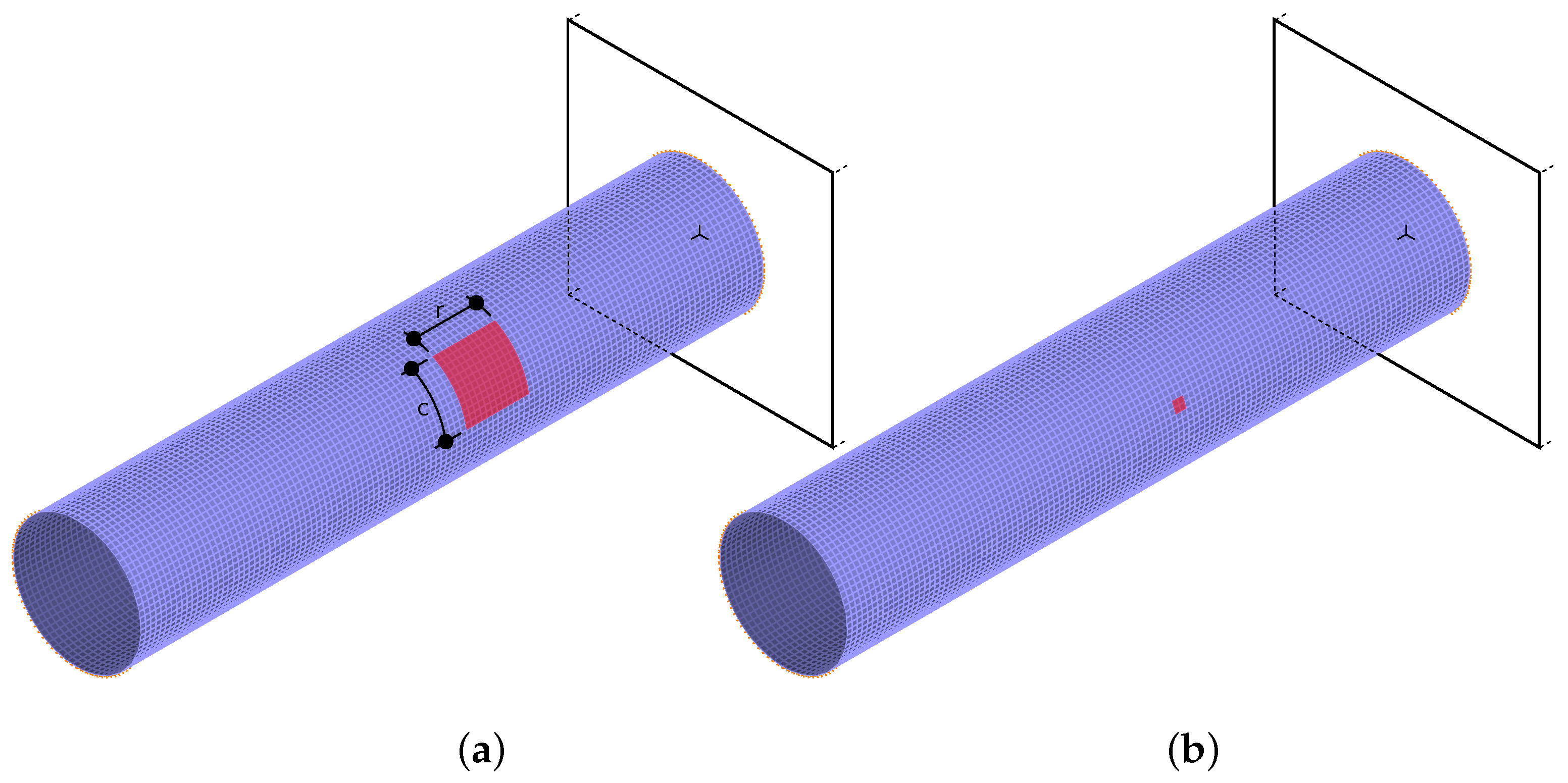
- each of the four cross-sections was shifted by a random vector (the same for the whole cross-section),
- each node on each of the four cross-sections was shifted by a random vector (unique for each node),
- the accuracy of each mode shape element was truncated to l significant digits.
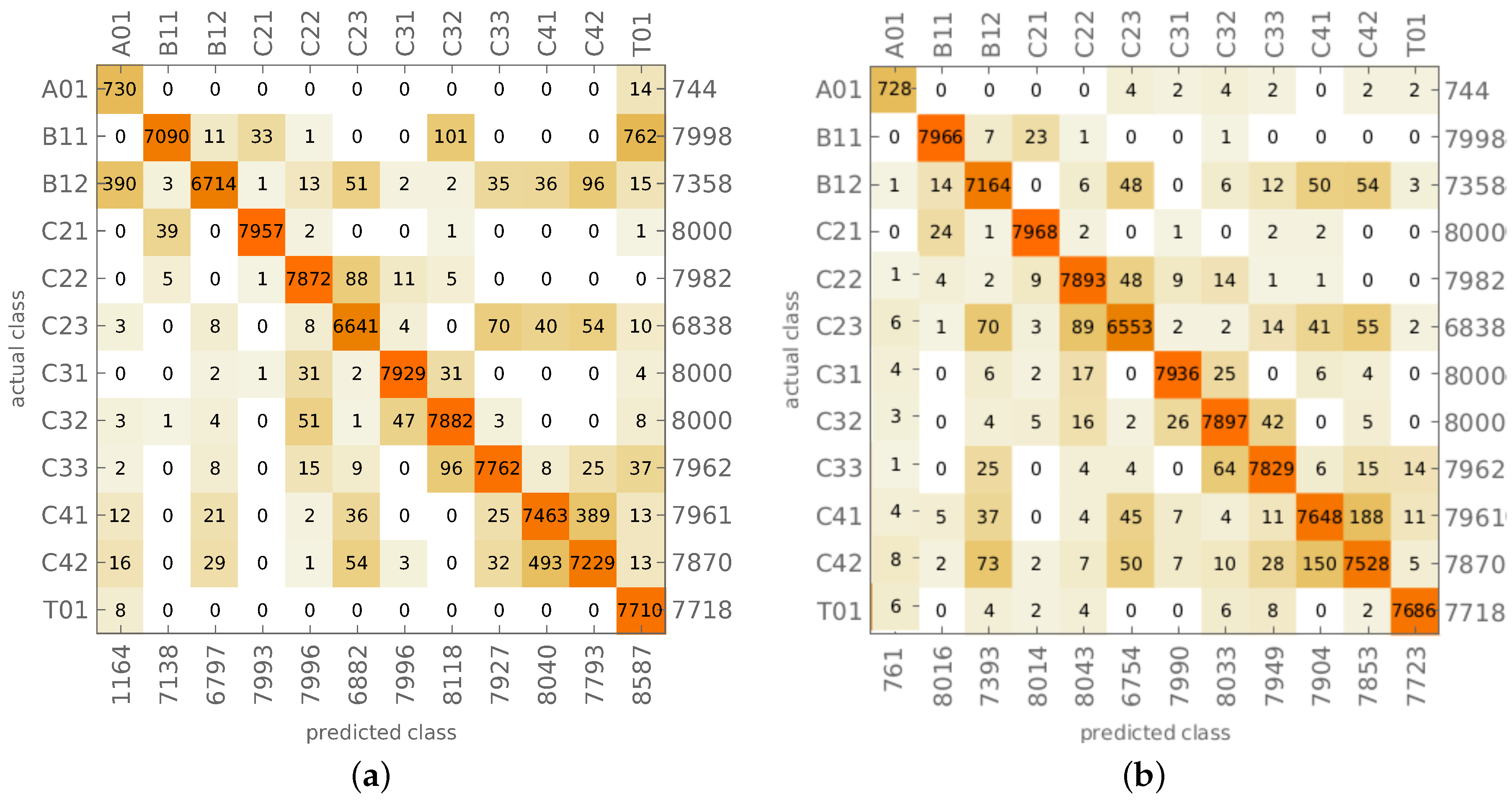
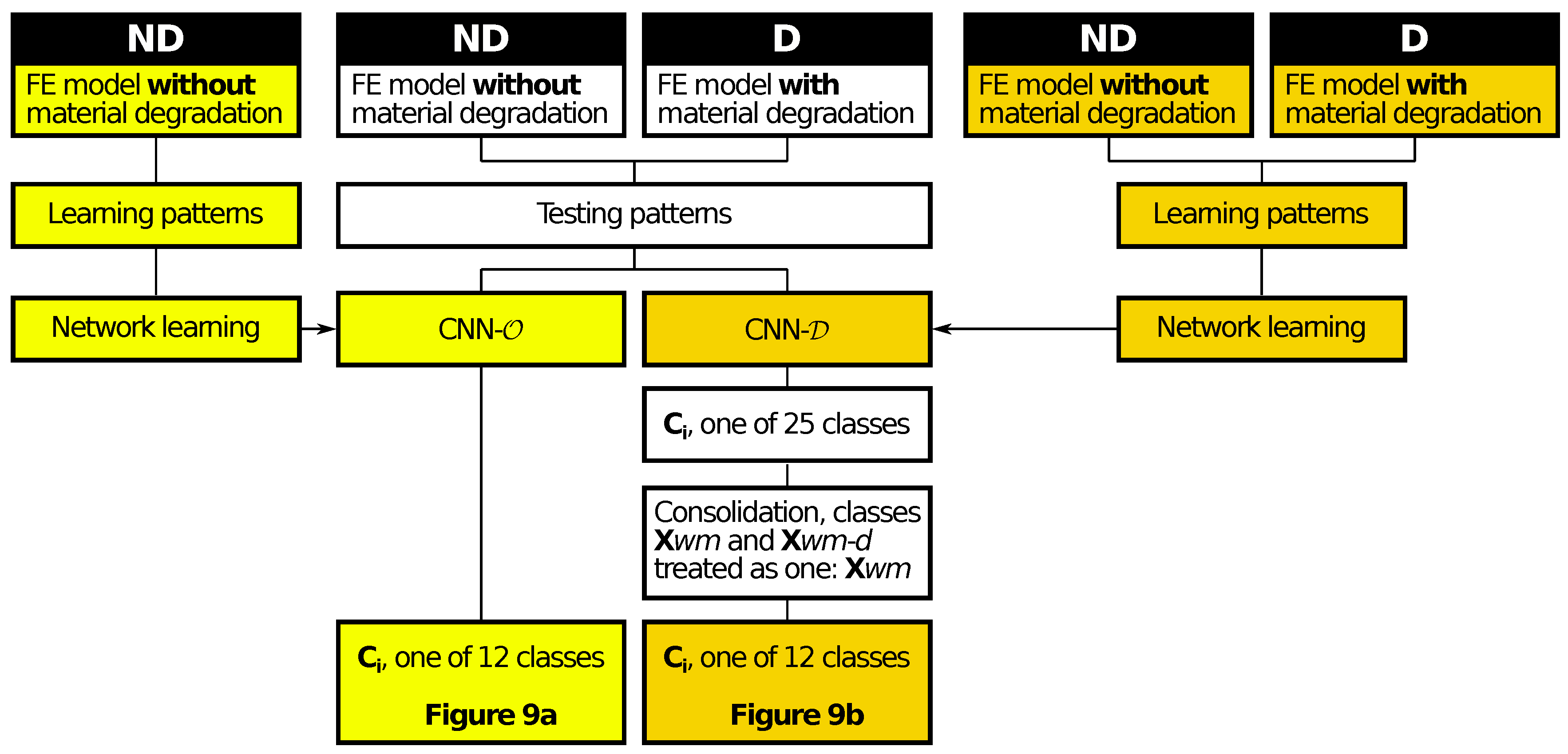
3.3. Identification of Mode Shapes Obtained from the Model with Material Degradation
- 24 classes: both the mode shape and the state of the structure (with or without material degradation); the number of mode shapes classes being identified was equal to 24, the additional ones were A01d, B11d, B12d, C21d, C22d, C23d, C31d, C32d, C33d, C41d, C42d and T01d (where d stands for material degradation),
- 25 classes: both the mode shape and the state of the structure (with or without material degradation) with an additional 25th class for unrecognized mode shapes; the additional class corresponds to cases where the analytical procedure failed to recognize the mode shape,
- 25 classes (two stage CNN learning): stage I: learning on patterns without material degradation, stage II: additional learning on patterns with material degradation; such approach is suggested for this kind of networks [41], the obtained network is called CNN- in what follows.
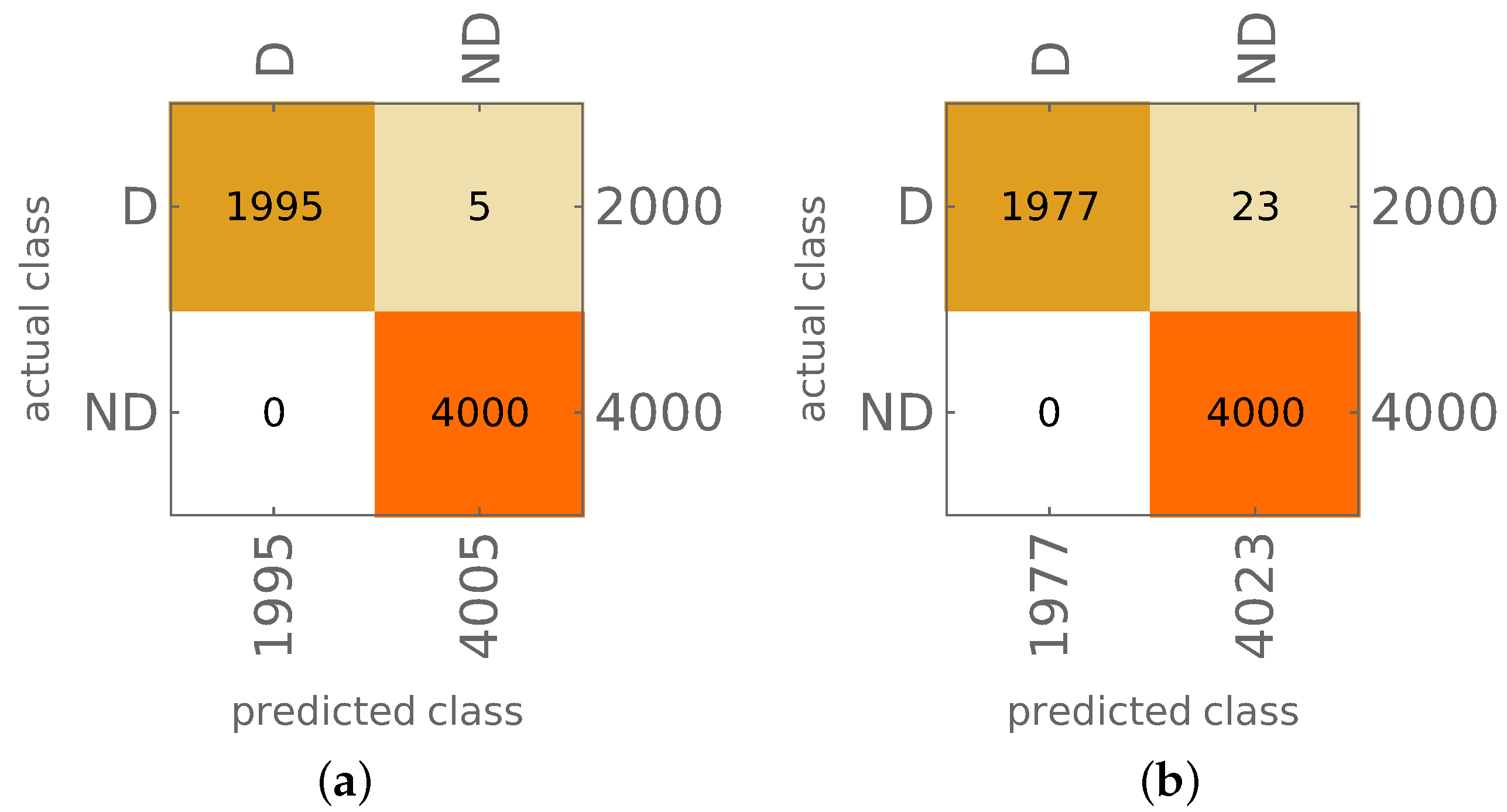
4. Identification of Models with Material Degradation
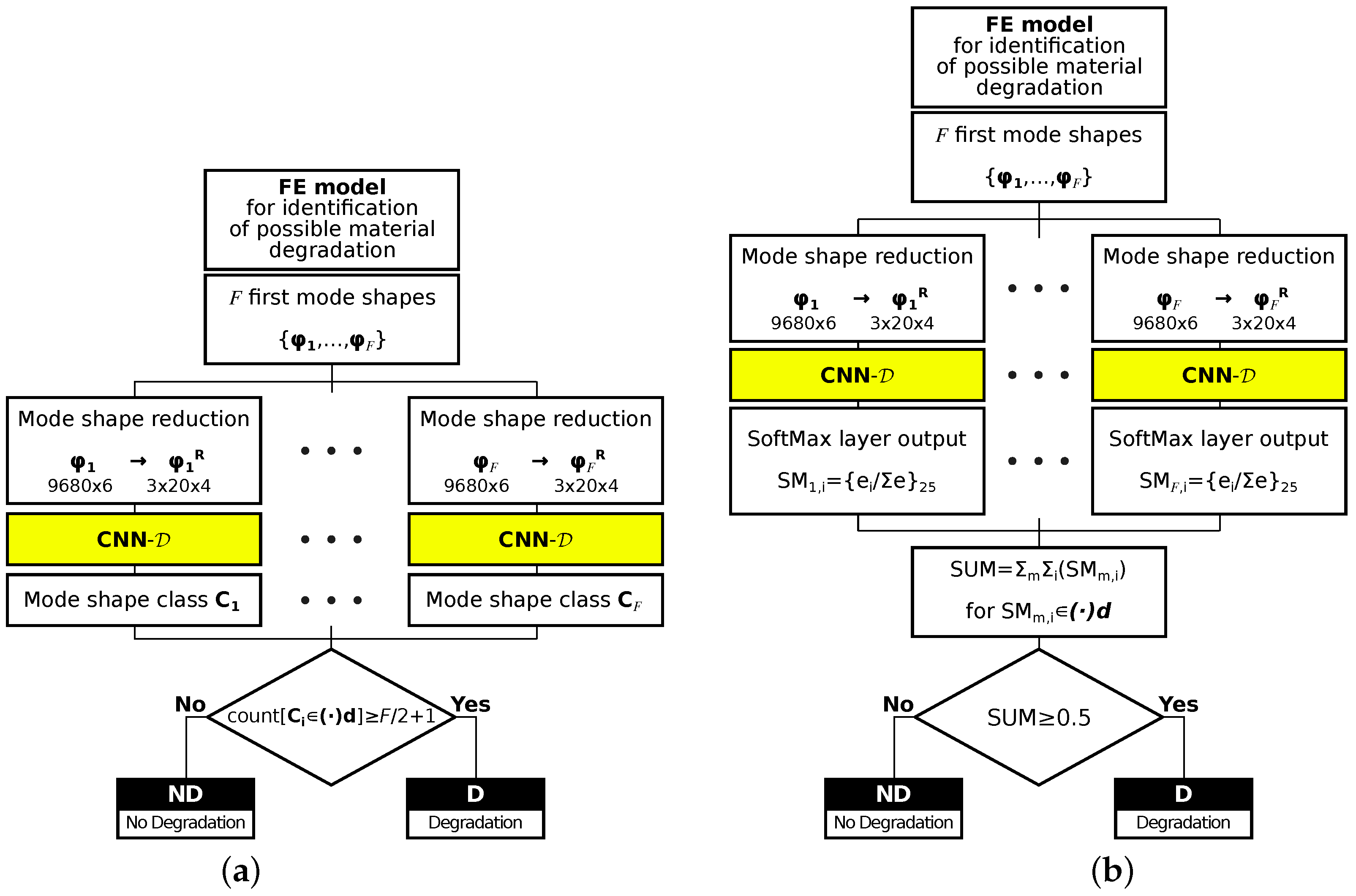
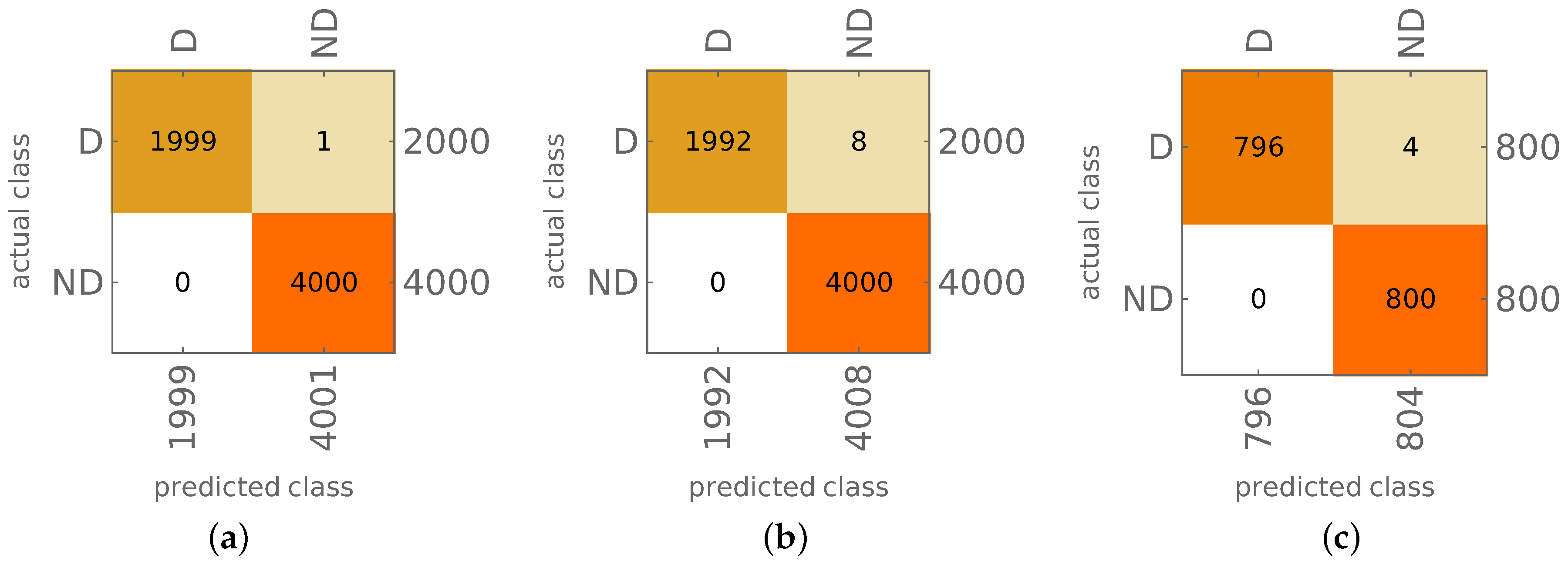
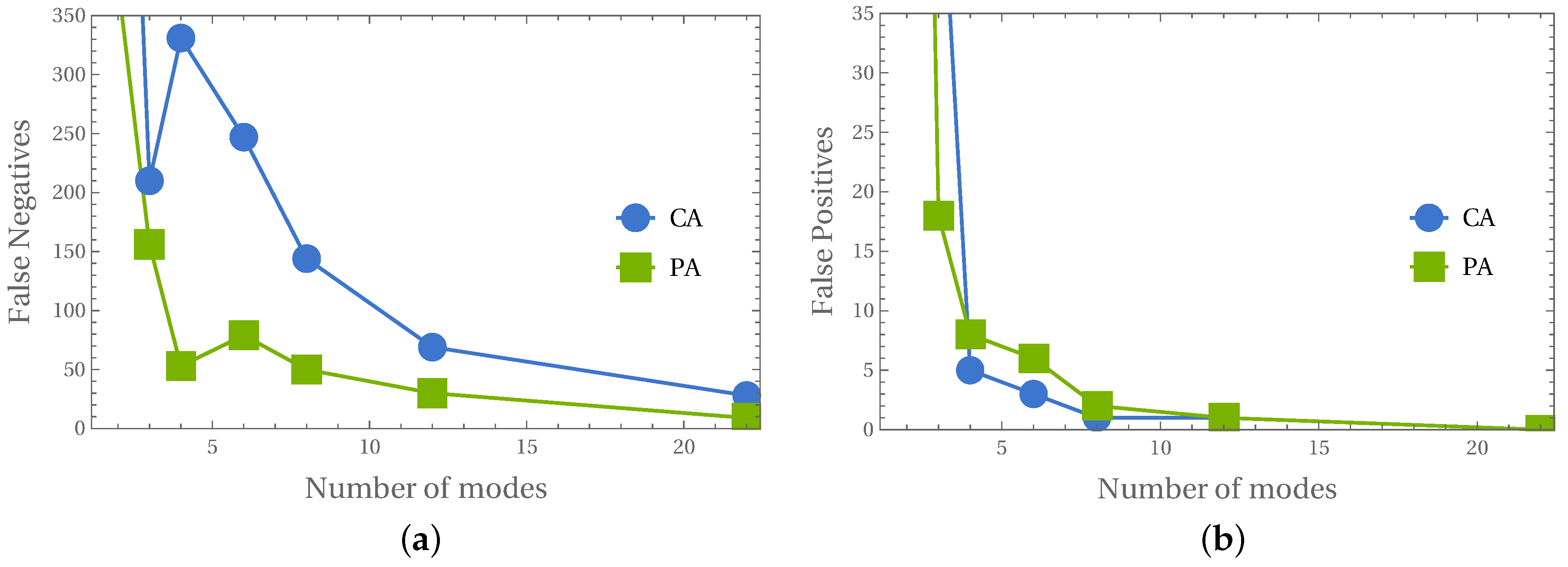
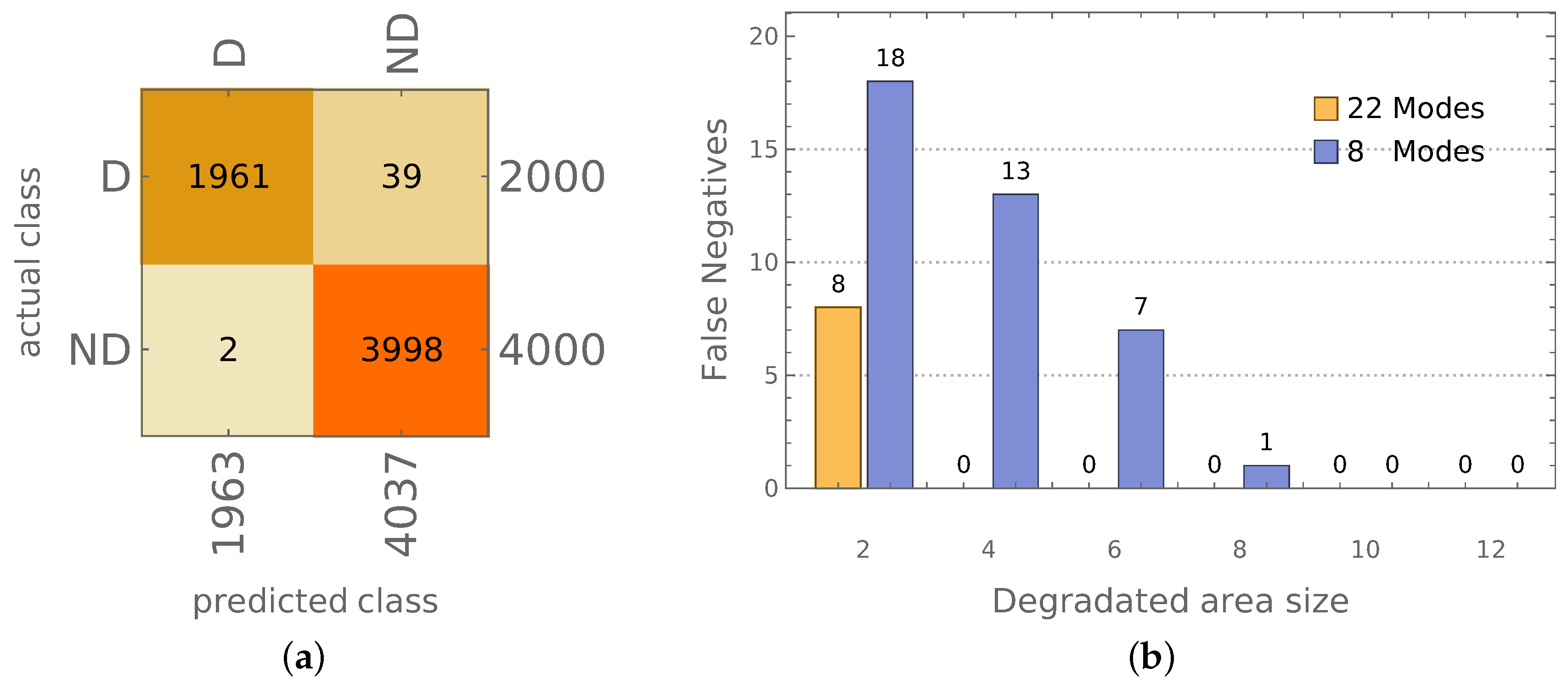
- For each of 24 classes (12 mode shapes with and d states), with the 25th class ignored, for each model, 22 first mode shapes are calculated and cases are counted when the identified mode shape belongs to a group of degradated modes (d state), when the number of identified degradated modes is equal or higher than 12 the whole model is considered as a model with material degradation; this approach is called in what follows the counting approach (CA); see Figure 11a;
- As it was mentioned earlier, apart from the name of the identified mode shape, CNNs can also return a more elaborate response in the form of a vector composed of probabilities that the analyzed mode shape belongs to considered classes; the probabilities corresponding to degradated modes are summed and divided by the sum of all probabilities when the obtained value is higher than 0.5. The whole model is considered as a model with material degradation; this approach is called in what follows the probability approach (PA) (see Figure 11b).
5. Discussion of Results
6. Conclusions
- application of graphical images to represent mode shapes rather than numerical data,
- application of the proposed method of mode shape identification in optimization tasks,
- identification of the location of the area of local material degradation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional neural network |
| FFNN | Feedforward neural network |
| FE | Finite element |
| FEM | Finite element method |
| PA | Probability approach |
| CA | Counting approach |
| TP | True positives |
| TN | True negatives |
| FP | False positives |
| FN | False negatives |
References
- Reddy, J. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Qatu, M.S.; Sullivan, R.W.; Wang, W. Recent research advances on the dynamic analysis of composite shells: 2000–2009. Compos. Struct. 2010, 93, 14–31. [Google Scholar] [CrossRef]
- Serhat, G.; Basdogan, I. Multi-objective optimization of composite plates using lamination parameters. Mater. Des. 2019, 180, 107904. [Google Scholar] [CrossRef]
- Lopatin, A.; Morozov, E. Fundamental frequency of a cantilever composite cylindrical shell. Compos. Struct. 2015, 119, 638–647. [Google Scholar] [CrossRef]
- An, H.; Chen, S.; Huang, H. Multi-objective optimal design of hybrid composite laminates for minimum cost and maximum fundamental frequency and frequency gaps. Compos. Struct. 2019, 209, 268–276. [Google Scholar] [CrossRef]
- Miller, B.; Ziemiański, L. Optimization of Dynamic and Buckling Behavior of Thin-Walled Composite Cylinder, Supported by Nature-Inspired Agorithms. Materials 2020, 13, 5414. [Google Scholar] [CrossRef] [PubMed]
- Kalantari, M.; Dong, C.; Davies, I.J. Multi-objective robust optimisation of unidirectional carbon/glass fibre reinforced hybrid composites under flexural loading. Compos. Struct. 2016, 138, 264–275. [Google Scholar] [CrossRef]
- Topal, U. Multiobjective optimization of laminated composite cylindrical shells for maximum frequency and buckling load. Mater. Des. 2009, 30, 2584–2594. [Google Scholar] [CrossRef]
- Ruiz, D.; Bellido, J.; Donoso, A. Eigenvector sensitivity when tracking modes with repeated eigenvalues. Comput. Methods Appl. Mech. Eng. 2017, 326, 338–357. [Google Scholar] [CrossRef]
- Bunting, G.; Miller, S.T.; Walsh, T.F.; Dohrmann, C.R.; Aquino, W. Novel strategies for modal-based structural material identification. Mech. Syst. Signal Process. 2021, 149, 107295. [Google Scholar] [CrossRef]
- Miller, B.; Ziemiański, L. Optimization of dynamic behavior of thin-walled laminated cylindrical shells by genetic algorithms and deep neural networks supported by modal shape identification. Adv. Eng. Softw. 2020, 147, 102830. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.E.; Mares, C. Mode-shape recognition and finite element model updating using the Zernike moment descriptor. Mech. Syst. Signal Process. 2009, 23, 2088–2112. [Google Scholar] [CrossRef]
- Zang, C.; Lan, H.B.; Jiang, D.D.; Friswell, M.I. Mode Shape Description and Model Updating of Axisymmetric Structures Using Radial Tchebichef Moment Descriptors. Shock Vib. 2021. [Google Scholar] [CrossRef]
- Zhong, K.; Teng, S.; Liu, G.; Chen, G.; Cui, F. Structural Damage Features Extracted by Convolutional Neural Networks from Mode Shapes. Appl. Sci. 2020, 10, 4247. [Google Scholar] [CrossRef]
- Morlier, J.; Bergh, M.; Mevel, L. Modeshapes Recognition Using Fourier Descriptors: A Simple SHM Example. In Topics in Modal Analysis II; Allemang, R., De Clerck, J., Niezrecki, C., Blough, J., Eds.; Springer: New York, NY, USA, 2012; Volume 6, pp. 195–204. [Google Scholar] [CrossRef]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.E.; Mares, C. Vibration mode shape recognition using image processing. J. Sound Vib. 2009, 326, 909–938. [Google Scholar] [CrossRef]
- Abubakar, I.; Mehrabi, H.; Morton, R. Classifying Turbomachinery Blade Mode Shapes Using Artificial Neural Networks. Int. J. Mech. Mechatron. Eng. 2020, 14, 300–303. [Google Scholar]
- Porter, R.; Hepworth, A.; Jensen, C.G. Application of machine learning and parametric NURBS geometry to mode shape identification. Comput. Aided Des. Appl. 2016, 13, 184–198. [Google Scholar] [CrossRef]
- La, A.; Salmon, J.; Ellingson, J. Identifying Mode Shapes of Turbo-Machinery Blades Using Principal Component Analysis and Support Vector Machines. In Structural Health Monitoring, Photogrammetry & DIC; Niezrecki, C., Baqersad, J., Eds.; Springer International Publishing: Cham, Switherland, 2019; Volume 6, pp. 23–26. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Poggio, T.; Mhaskar, H.; Rosasco, L.; Miranda, B.; Liao, Q. Why and when can deep-but not shallow-networks avoid the curse of dimensionality: A review. Int. J. Autom. Comput. 2017, 14, 503–519. [Google Scholar] [CrossRef]
- Chen, W.; Shi, K. A deep learning framework for time series classification using Relative Position Matrix and Convolutional Neural Network. Neurocomputing 2019, 359, 384–394. [Google Scholar] [CrossRef]
- Oishi, A.; Yagawa, G. Computational mechanics enhanced by deep learning. Comput. Methods Appl. Mech. Eng. 2017, 327, 327–351. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Modarres, C.; Astorga, N.; Droguett, E.L.; Meruane, V. Convolutional neural networks for automated damage recognition and damage type identification. Struct. Control. Health Monit. 2018, 25, e2230. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, Z.; Bao, Y.; Li, H. Convolutional neural network-based data anomaly detection method using multiple information for structural health monitoring. Struct. Control. Health Monit. 2019, 26, e2296. [Google Scholar] [CrossRef]
- Teng, S.; Chen, G.; Gong, P.; Liu, G.; Cui, F. Structural damage detection using convolutional neural networks combining strain energy and dynamic response. Meccanica 2020, 55, 945–959. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.E.; Ihle, A.; Siebert, T.; Reinhard Schubach, H. Finite element model updating from full-field vibration measurement using digital image correlation. J. Sound Vib. 2011, 330, 1599–1620. [Google Scholar] [CrossRef]
- Molina-Viedma, Á.J.; López-Alba, E.; Felipe-Sesé, L.; Díaz, F.A. Full-field modal analysis during base motion excitation using high-speed 3D digital image correlation. Meas. Sci. Technol. 2017, 28, 105402. [Google Scholar] [CrossRef]
- Stanbridge, A.B.; Martarelli, M.; Ewins, D.J. Measuring area vibration mode shapes with a continuous-scan LDV. Measurement 2004, 35, 181–189. [Google Scholar] [CrossRef]
- Tawfik, M.; Bishay, P.; Sadek, E.A. Neural Network-Based Second Order Reliability Method (NNBSORM) for Laminated Composite Plates in Free Vibration. Comput. Model. Eng. Sci. 2018, 115, 105–129. [Google Scholar] [CrossRef]
- Bathe, K. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Vo, T.P.; Lee, J.; Ahn, N. On sixfold coupled vibrations of thin-walled composite box beams. Compos. Struct. 2009, 89, 524–535. [Google Scholar] [CrossRef][Green Version]
- Bathe, K. ADINA: Theory and Modeling Guide Volume I: ADINA Solids & Structures; ADINA R&D, Inc.: Watertown, NY, USA, 2016. [Google Scholar]
- Miller, B.; Ziemiański, L. Chapter Numerical Analysis of Free Vibrations of a Tube Shaped Laminated Cantilever. In Proceedings of the 11th International Conference Shell Structures: Theory and Applications, (SSTA 2017), Gdansk, Poland, 11–13 October 2017; Pietraszkiewicz, W., Witkowski, W., Eds.; CRC Press: London, UK, 2018; Volume 4, pp. 309–312. [Google Scholar] [CrossRef]
- Miller, B.; Ziemiański, L. Maximization of Eigenfrequency Gaps in a Composite Cylindrical Shell Using Genetic Algorithms and Neural Networks. Appl. Sci. 2019, 9, 2754. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Mathematica, Version 12.0; Wolfram Research, Inc.: Champaign, IL, USA, 2019.




| Layer | Input | Kernel | Kernel | Dimension | Activation |
|---|---|---|---|---|---|
| Number | Type | Number | Size | of Data | Function |
| 1 | Convolution | 33 | {2,5} | 33 × 2 × 16 | |
| 2 | Batch normalization | 33 × 2 × 16 | |||
| 3 | Activation | 33 × 2 × 16 | ReLU | ||
| 4 | Convolution | 66 | {2,5} | 66 × 1 × 12 | |
| 5 | Batch normalization | 66 × 1 × 12 | |||
| 6 | Activation | 66 × 1 × 12 | ReLU | ||
| 7 | Convolution | 33 | {1,3} | 33 × 1 × 10 | |
| 8 | Batch normalization | 33 × 1 × 10 | |||
| 9 | Activation | 33 × 1 × 10 | ReLU | ||
| 10 | Pooling | {1,2} | 33 × 1 × 5 | ||
| 11 | Flatten | 165 | |||
| 12 | MLP | 75 | |||
| 13 | MLP | 25 | |||
| 14 | SoftMax | 25 | Softmax | ||
| Output “class” |
| Learning | Testing | |
|---|---|---|
| CNN- mode shapes identification (Figure 5) | 7 (96,000) | 3 (96,000) |
| Testing for a different material (Figure 6) | — | 0 (19,200) |
| Noised mode shapes, and | 8 (96,000) | 6 (96,000) |
| Noised mode shapes, and | 9 (96,000) | 16 (96,000) |
| Noised mode shapes, and (Figure 7) | 12 (96,000) | 20 (96,000) |
| Learning | Testing | |
|---|---|---|
| FFNN mode shapes identification | 62 (96,000) | 17 (96,000) |
| Noised mode shapes, and | 164 (96,000) | 162 (96,000) |
| Learning | Testing | |||
|---|---|---|---|---|
| n = 4 | n = 16 | n = 8 | n = 32 | |
| 24 classes | ||||
| Patterns with no material degradation | 95.4% | 98.2% | 94.3% | 96.8% |
| Resultant accuracy | 96.8% | 95.6% | ||
| Patterns with material degradation | 80.9% | 84.7% | 75.6% | 80.0% |
| Resultant accuracy | 82.8% | 77.8% | ||
| Overall accuracy, with and without material degradation | 91.6% | 89.0% | ||
| 25 classes | ||||
| Patterns with no material degradation | 95.5% | 97.2% | 93.0% | 97.1% |
| Resultant accuracy | 96.4% | 95.1% | ||
| Patterns with material degradation | 87.9% | 89.2% | 80.1% | 80.7% |
| Resultant accuracy | 88.6% | 80.4% | ||
| Overall accuracy, with and without material degradation | 93.3% | 89.7% | ||
| 5 classes, two stage learning; CNN- | ||||
| Patterns with no material degradation | 97.2% | 98.2% | 93.8% | 95.9% |
| Resultant accuracy | 97.7% | 94.9% | ||
| Patterns with material degradation | 92.2% | 93.3% | 81.4% | 85.8% |
| Resultant accuracy | 92.8% | 83.6% | ||
| Overall accuracy, with and without material degradation | 95.9% | 90.7% | ||
| Models without Material Degradation | With Degradation | ||||||
|---|---|---|---|---|---|---|---|
| CNN- | CNN- | CNN- | CNN- | CNN- | |||
| Learn | Test | New Material | Learn | Test | Figure 9a | Figure 9b | |
| Macro-Precision | 0.9999 | 0.9999 | 1.0000 | 0.9998 | 0.9997 | 0.8453 | 0.8985 |
| Macro-Recall | 0.9999 | 0.9998 | 1.0000 | 0.9996 | 0.9998 | 0.8006 | 0.9149 |
| Macro-F1 | 0.9997 | 0.9998 | 1.0000 | 0.9997 | 0.9997 | 0.8223 | 0.9066 |
| Accuracy | 0.9999 | 1.0000 | 1.0000 | 0.9996 | 0.9998 | 0.9601 | 0.9811 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, B.; Ziemiański, L. Identification of Mode Shapes of a Composite Cylinder Using Convolutional Neural Networks. Materials 2021, 14, 2801. https://doi.org/10.3390/ma14112801
Miller B, Ziemiański L. Identification of Mode Shapes of a Composite Cylinder Using Convolutional Neural Networks. Materials. 2021; 14(11):2801. https://doi.org/10.3390/ma14112801
Chicago/Turabian StyleMiller, Bartosz, and Leonard Ziemiański. 2021. "Identification of Mode Shapes of a Composite Cylinder Using Convolutional Neural Networks" Materials 14, no. 11: 2801. https://doi.org/10.3390/ma14112801
APA StyleMiller, B., & Ziemiański, L. (2021). Identification of Mode Shapes of a Composite Cylinder Using Convolutional Neural Networks. Materials, 14(11), 2801. https://doi.org/10.3390/ma14112801






