Crash Response of Laser-Welded Energy Absorbers Made of Docol 1000DP and Docol 1200M Steels
Abstract
1. Introduction
2. Materials and Experimental Methods
2.1. Materials
2.2. Mechanical Testing Procedure
2.3. Square Tube Absorber Fabrication
2.4. Crash Tests Procedure
3. Results and Discussion
3.1. Microstructure and Microhardness
3.2. Quasi-Static and High Strain Rate Behavior
3.3. Quasi-Static Crush Response
3.4. Dynamic Crush Response
3.5. Mechnical Energy Absorption Capability
4. Conclusions
- Docol 1000DP steel demonstrates a higher strain rate sensitivity than that of Docol 1200M steel. The strain rate loading condition increases the ductility of both steel grades.
- A well-made laser-welded butt joint does not adversely affect the crushing process of the absorber; in most absorbers, no cracks in the welded joints were noticed.
- Laser welding technology enables the production of high-strength welded joints, which are crucial in the crash performance of column energy absorbers.
- The use of a more durable method to connect the tube absorber and the protective discs would increase the stability of the absorber crushing process. Welding should be more reliable than adhesive glue connection.
- The influence of the strain rate and inertia forces on the energy absorption and the crushing process were observed. The difference is mainly due to the material strain rate sensitivity.
- Under quasi-static and impact loading conditions, SEA is greater for Docol 1200M in comparison in Docol 1200M, whereas CFE is more favorable for Docol 1000DP. In engineering, column energy absorbers are more preferred with greater CFE; for that reason, Docol 1000DP is the more preferred material used in design axial crash energy absorbers.
- The use of the DIH method may be an appropriate approach for investigation of the crushing behavior of model tube absorbers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boyes, E.; Stanisstreet, M. The Environmental Impact of Cars: Children’s ideas and reasoning. Environ. Educ. Res. 1997, 3, 269–282. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2019—Scaling up the Transition to Electric Mobility, IEA (2019), “Global EV Outlook 2019”; IEA: Paris France, 2019. Available online: https//www.iea.org/reports/global-ev-outlook-2019 (accessed on 6 September 2020).
- Greene, D.L.; DeCicco, J. Engineering-economic analyses of automotive fuel economy potential in the United States. Annu. Rev. Energy Environ. 2000, 25, 477–535. [Google Scholar] [CrossRef]
- Fontaras, G.; Franco, V.; Dilara, P.; Martini, G.; Manfredi, U. Development and review of Euro 5 passenger car emission factors based on experimental results over various driving cycles. Sci. Total Environ. 2014, 468–469, 1034–1042. [Google Scholar] [CrossRef] [PubMed]
- Nia, A.A.A.; Hamedani, J.H.H. Comparative analysis of energy absorption and deformations of thin walled tubes with various section geometries. Thin Walled Struct. 2010, 48, 946–954. [Google Scholar] [CrossRef]
- Nagel, G.M.M.; Thambiratnam, D.P.P. Computer simulation and energy absorption of tapered thin-walled rectangular tubes. Thin Walled Struct. 2005, 43, 1225–1242. [Google Scholar] [CrossRef]
- Pirmohammad, S.; Marzdashti, S.E. Crushing behavior of new designed multi-cell members subjected to axial and oblique quasi-static loads. Thin Walled Struct. 2016, 108, 291–304. [Google Scholar] [CrossRef]
- Zhao, X.-L.; van Binh, D.; Al-Mahaidi, R.; Tao, Z. Stub column tests of fabricated square and triangular sections utilizing very high strength steel tubes. J. Constr. Steel Res. 2004, 60, 1637–1661. [Google Scholar] [CrossRef]
- Wågström, L.; Thomson, R.; Pipkorn, B. Structural adaptivity in frontal collisions: Implications on crash pulse characteristics. Int. J. Crashworthiness 2005, 10, 371–378. [Google Scholar] [CrossRef]
- Abedrabbo, N.; Mayer, R.; Thompson, A.; Salisbury, C.; Worswick, M.; van Riemsdijk, I. Crash response of advanced high-strength steel tubes: Experiment and model. Int. J. Impact Eng. 2009, 36, 1044–1057. [Google Scholar] [CrossRef]
- Cora, Ö.N.; Koç, M. Promises and Problems of Ultra/Advanced High Strength Steel (U/AHSS) Utilization in Automotive Industry. In Proceedings of the 7th Automotive Technologies Congress, (OTEKON 2014), Bursa, Turkey, 26 – 27 May 2014; pp. 1–8. Available online: http://www.otekon.org/eng/default.asp%5Cn; http://www.otekon.org/bildiriler/B238.pdf (accessed on 13 July 2020).
- Dahmen, M.; Gerhards, B.; Lindner, S. Alloyed Ultra-High Strength Steels Properties, benefits and challenges with laser beam welding. Laser Tech. J. 2016, 13, 48–52. [Google Scholar] [CrossRef]
- Kędzierski, P.; Morka, A.; Sławiński, G.; Niezgoda, T. Optimization of two-component armour. Bull. Polish Acad. Sci. Tech. Sci. 2015, 63, 173–179. [Google Scholar] [CrossRef]
- Kurzawa, D.; Pyka, K.; Jamroziak, M.; Bocian, P.; Kotowski, P.; Widomski, P. Analysis of ballistic resistance of composites based on EN AC-44200 aluminum alloy reinforced with Al2O3 particles. Compos. Struct. 2018, 201, 834–844. [Google Scholar] [CrossRef]
- Kurzawa, D.; Pyka, K.; Jamroziak, M.; Bajkowski, M.; Bocian, M.; Magier, M.; Koch, J. Assessment of the impact resistance of a composite material with EN AW-7075 matrix reinforced with α-Al2O3 particles using a 7.62 × 39 mm projectile. Materials 2020, 13, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Rudd, C.D. Composites for Automotive Applications. Rapra Rev. Rep. 2000, 11, 8–9. [Google Scholar]
- Morka, P.; Kędzierski, P.; Muzolf, P. Optimization of the structure of a ceramic-aluminum alloy composite subjected to the impact of hard steel projectiles. Mech. Compos. Mater. 2016, 52, 333–346. [Google Scholar] [CrossRef]
- Rowe, J. Advanced Materials in Automotive Engineering, 1st ed.; Woodhead Publishing Limited: Philadelphia, PA, USA, 2012. [Google Scholar] [CrossRef]
- Wang, W.; Li, M.; He, C.; Wei, X.; Wang, D.; Du, H. Experimental study on high strain rate behavior of high strength 600-1000MPa dual phase steels and 1200MPa fully martensitic steels. Mater. Des. 2013, 47, 510–521. [Google Scholar] [CrossRef]
- Han, H.; Taheri, F.; Pegg, N. Quasi-static and dynamic crushing behaviors of aluminum and steel tubes with a cutout. Thin Walled Struct. 2007, 45, 283–300. [Google Scholar] [CrossRef]
- Langseth, M.; Hopperstad, O.S. Static and dynamic axial crushing of square thin-walled aluminium extrusions. Int. J. Impact Eng. 1996, 18, 949–968. [Google Scholar] [CrossRef]
- Gronostajski, Z.; Polak, S. Quasi-static and dynamic deformation of double-hat thin-walled elements of vehicle controlled body crushing zones joined by clinching. Arch. Civ. Mech. Eng. 2008, 8, 57–65. [Google Scholar] [CrossRef]
- Kohar, C.P.; Cherkaoui, M.; el Kadiri, H.; Inal, K. Numerical modeling of TRIP steel in axial crashworthiness. Int. J. Plast. 2015, 84, 224–254. [Google Scholar] [CrossRef]
- Oliver, S.; Jones, T.B.; Fourlaris, G. Dual phase versus TRIP strip steels: Microstructural changes as a consequence of quasi-static and dynamic tensile testing. Mater. Charact. 2007, 58, 390–400. [Google Scholar] [CrossRef]
- Ying, L.; Zhao, X.; Dai, M.; Zhang, S.; Hu, P. Crashworthiness design of quenched boron steel thin-walled structures with functionally graded strength. Int. J. Impact Eng. 2016, 95, 72–88. [Google Scholar] [CrossRef]
- Ma, J. Energy Absorption of Thin-Walled Square Tubes with a Prefolded Origami Pattern—Part I: Geometry and Numerical Simulation. J. Appl. Mech. 2014, 81, 1–11. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, S.; Zhang, Z. Energy absorption properties of non-convex multi-corner thin-walled columns. Thin-Walled Struct. 2012, 51, 112–120. [Google Scholar] [CrossRef]
- Mamalis, A.G.; Manolakos, D.E.; Demosthenous, G.A.; Ioannidis, M.B. Crash Worthiness of Composite Thin-Walled Structural Components; CRC Press: Boca Raton, FA, USA, 1998. [Google Scholar] [CrossRef]
- Wu, S.; Zheng, G.; Sun, G.; Liu, Q.; Li, G.; Li, Q. On design of multi-cell thin-wall structures for crashworthiness. Int. J. Impact Eng. 2016, 88, 102–117. [Google Scholar] [CrossRef]
- Larour, P.; Lackner, J.; Wagner, L. Influence of single hat crash box flange triggering and impactor top plate welding strategy on axial crash foldability of AHSS & UHSS sheets. IOP Conf. Ser. Mater. Sci. Eng. 2019, 651, 012023. [Google Scholar] [CrossRef]
- Rusiński, E.; Kopczyński, A.; Czmochowski, J. Tests of thin-walled beams joined by spot welding. J. Mater. Process. Technol. 2004, 157, 405–409. [Google Scholar] [CrossRef]
- Liu, W.; Lian, J.; Münstermann, S.; Zeng, C.; Fang, X. Prediction of crack formation in the progressive folding of square tubes during dynamic axial crushing. Int. J. Mech. Sci. 2020, 176, 105534. [Google Scholar] [CrossRef]
- Gedikli, H. Numerical investigation of axial crushing behavior of a tailor welded tube. Mater. Des. 2013, 44, 587–595. [Google Scholar] [CrossRef]
- Yuen, S.C.K.C.K.; Nurick, G.N.N. The energy-absorbing characteristics of tubular structures with geometric and material modifications: An overview. Appl. Mech. Rev. 2008, 61, 208021–2080215. [Google Scholar] [CrossRef]
- Shome, M.; Tumuluru, M. Introduction to welding and joining of advanced high-strength steels (AHSS). In Welding and Joining of Advanced High Strength Steels (AHSS); Elsevier Ltd.: New York, NY, USA, 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, G.; Mei, L.; Zhang, M.; Zhang, Y.; Wang, Z. Research on key influence factors of laser overlap welding of automobile body galvanized steel. Opt. Laser Technol. 2013, 45, 726–733. [Google Scholar] [CrossRef]
- Harooni, M.; Kovacevic, R. Laser Welding of Magnesium Alloys: Issues Laser Welding of Magnesium Alloys: Issues and Remedies. In Magnesium Alloys; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Bambach, M.; Conrads, L.; Daamen, M.; Güvenç, O.; Hirt, G. Enhancing the crashworthiness of high-manganese steel by strain-hardening engineering, and tailored folding by local heat-treatment. Mater. Des. 2016, 110, 157–168. [Google Scholar] [CrossRef]
- Yu, H.; Guo, Y.; Lai, X. Rate-dependent behavior and constitutive model of DP600 steel at strain rate from 10-4 to 103 s-1. Mater. Des. 2009, 30, 2501–2505. [Google Scholar] [CrossRef]
- Qin, J.; Chen, R.; Wen, X.; Lin, Y.; Liang, M.; Lu, F. Mechanical behaviour of dual-phase high-strength steel under high strain rate tensile loading. Mater. Sci. Eng. A. 2013, 586, 62–70. [Google Scholar] [CrossRef]
- Li, Y.; Song, R.; Jiang, L.; Zhao, Z. Deformation response of 1200 MPa grade martensite-ferrite dual-phase steel under high strain rates. Mater. Sci. Eng. A 2019, 750, 40–44. [Google Scholar] [CrossRef]
- Boyce, B.L.; Dilmore, M.F. The dynamic tensile behavior of tough, ultrahigh-strength steels at strain-rates from 0.0002 s−1 to 200 s−1. Int. J. Impact Eng. 2009, 36, 263–271. [Google Scholar] [CrossRef]
- Costa, S.L.; Mendonça, J.P.; Peixinho, N. Study on the impact behaviour of a new safety toe cap model made of ultra-high-strength steels. Mater. Des. 2016, 91, 143–154. [Google Scholar] [CrossRef]
- Yoon, J.-H.; Huh, H.; Kim, S.-H.; Park, S.-H. Comparative Crashworthiness Assessment of the ULSAB-AVC Model with Advance High Strength Steel and with Low Strength Steel. Trans. Korean Soc. Automot. Eng. 2006, 14, 22–27. [Google Scholar]
- Eva, S.; Bohumil, C.; Petr, H. Dynamic Fracture Behavior of the Martensitic High Strength Steel after Spot Welding. Mater. Today Proc. 2016, 3, 1156–1160. [Google Scholar] [CrossRef]
- SSAB EMEA AB. Materials Certificates Provided by the Manufacturer with the Delivery of the Material (according EN 10204-3.1). 2017. Available online: https://www.ssab.com/brands-and-products/docol (accessed on 19 April 2020).
- EN ISO 6507-1. Metallic Materials—Vickers Hardness Test—Part1: Test Method; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Nicholas, T. Tensile testing of materials at high rates of strain. Exp. Mech. 1981, 21, 177–185. [Google Scholar] [CrossRef]
- Verleysen, P.; Degrieck, J.; Verstraete, T.; van Slycken, J. Influence of specimen geometry on split hopkinson tensile bar tests on sheet materials. Exp. Mech. 2008, 48, 587–598. [Google Scholar] [CrossRef]
- Chen, W.W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Ion, J. Laser Processing of Engineering Materials: Principles, Procedure and Industrial Application; Elsevier: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Liu, J.; He, S.; Zhao, H.; Li, G.; Wang, M. Experimental investigation on the dynamic behaviour of metal foam: From yield to densification. Int. J. Impact Eng. 2018, 114, 69–77. [Google Scholar] [CrossRef]
- Kucewicz, M.; Baranowski, P.; Małachowski, J.; Popławski, A.; Płatek, P. Modelling, and characterization of 3D printed cellular structures. Mater. Des. 2018, 142, 177–189. [Google Scholar] [CrossRef]
- Baroutaji; Sajjia, M.; Olabi, A.G. On the crashworthiness performance of thin-walled energy absorbers: Recent advances and future developments. Thin Walled Struct. 2017, 118, 137–163. [Google Scholar] [CrossRef]
- EN ISO 13919-1. Electron and Laser-Beam Welded Joints—Requirements and Recommendations on Quality Levels for Imperfections—Part 1: Steel, Nickel, Titanium and Their Alloys; ISO: Geneva, Switzerland, 2020. [Google Scholar]
- Górka, J.; Ozgowicz, A. The study of laser welding low alloy high strength steel with a martensitic structure. Weld. Technol. Rev. 2016, 88, 24–27. [Google Scholar]
- Nowacki, J. Microstructure and mechanical properties of advanced High—Strength steels (AHSS). Weld. Technol. Rev. 2011, 83, 22–27. [Google Scholar]
- Kumar, V.S.; Manikandaraja, G. Numerical study on energy absorbing characteristics of thin-walled tube under axial and oblique impact. Alexandria Eng. J. 2016, 55, 187–192. [Google Scholar] [CrossRef]





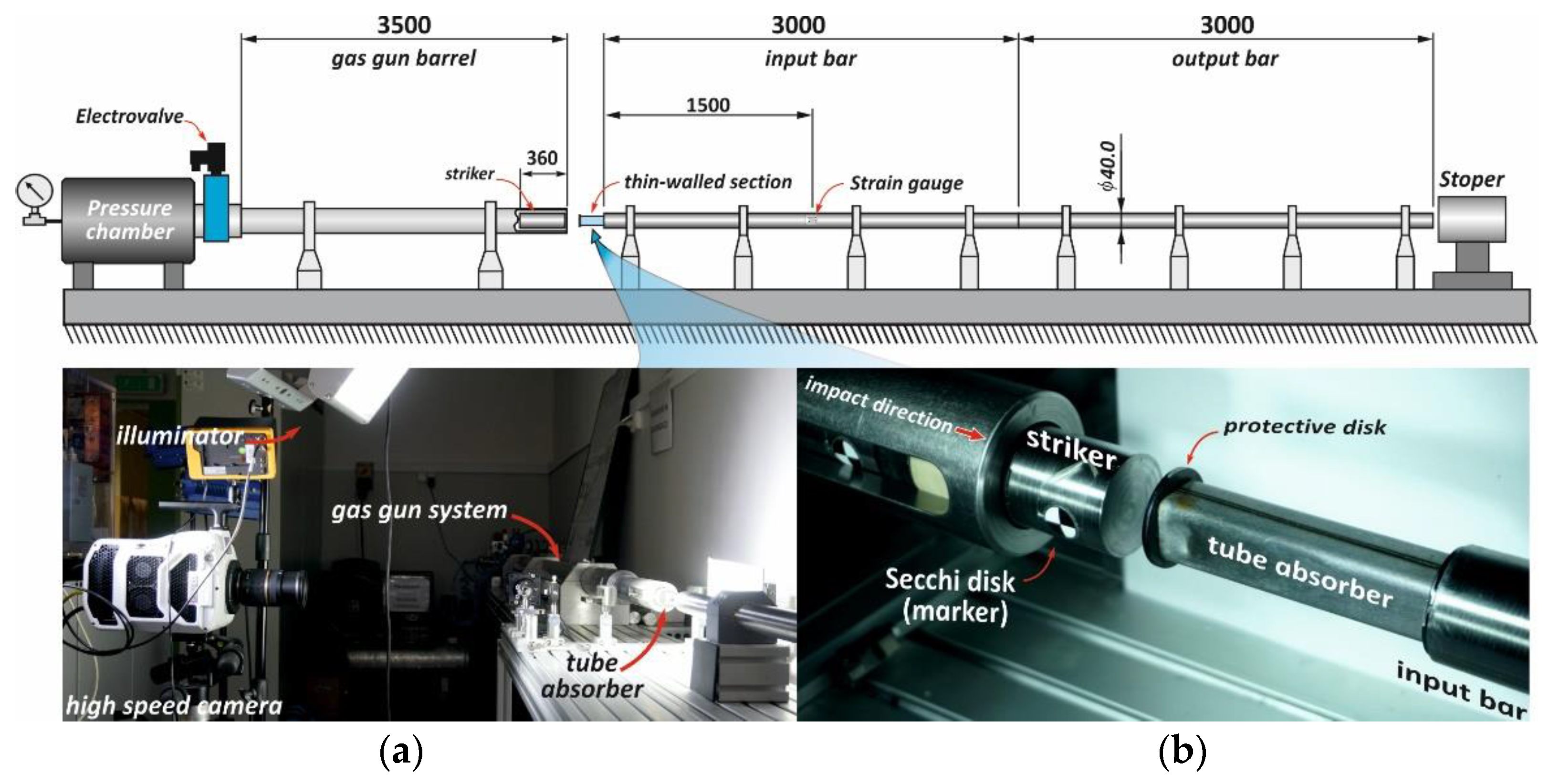





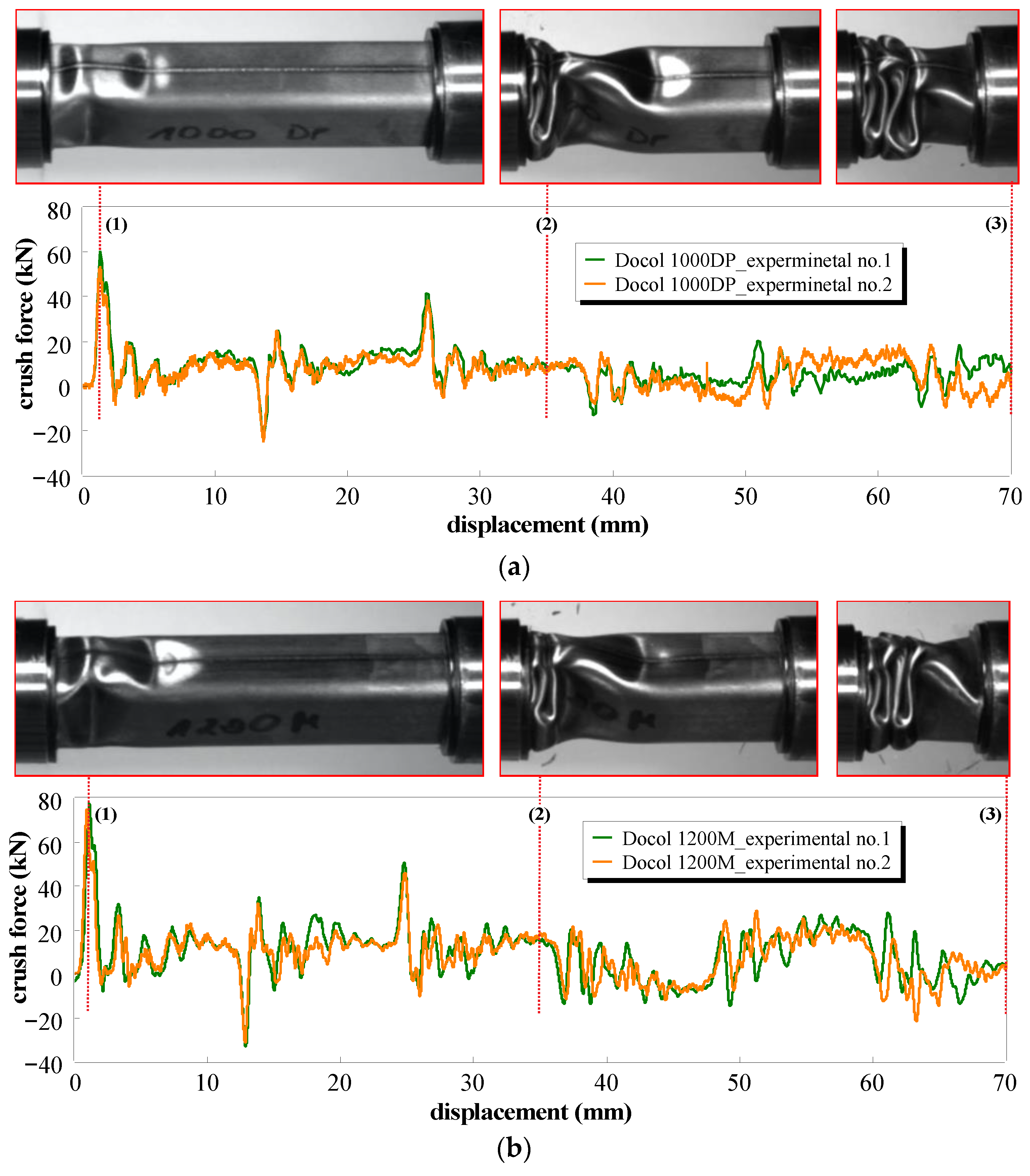

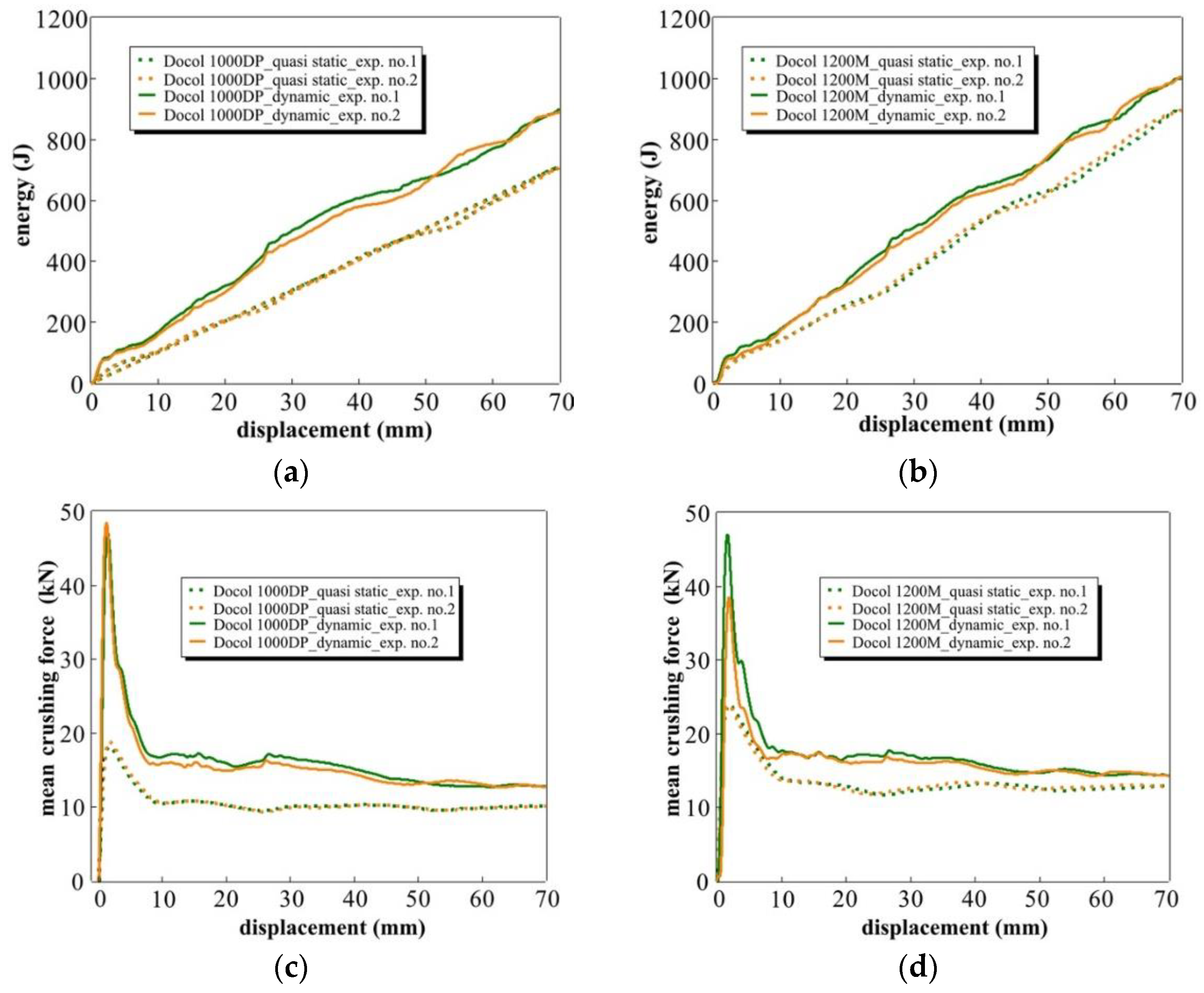
| Material | C | Si | Mn | P | Cr | Ni | Al | Cu | Nb | V |
|---|---|---|---|---|---|---|---|---|---|---|
| Docol 1000DP | 0.130 | 0.21 | 1.47 | 0.011 | 0.02 | 0.03 | 0.047 | 0.01 | 0.017 | 0.01 |
| Docol 1200M | 0.111 | 0.21 | 1.59 | 0.009 | 0.02 | 0.04 | 0.04 | 0.01 | 0.000 | 0.02 |
| Parameter | Value | |
|---|---|---|
| Beam power | (W) | 450 |
| Fiber diameter | (µm) | 50 |
| Spot diameter | (µm) | 100 |
| Wobble mode | Circle | |
| Wobble frequency | (Hz) | 250 |
| Wobble diameter | (mm) | 0.5 |
| Focal length (mm) | 200 | |
| Welding speed | (mm/s) | 37.5 |
| Joint type | Butt | |
| Sheet thickness | (mm) | 0.6 |
| Material | ||||||
|---|---|---|---|---|---|---|
| Docol 1000DP | 0.23 | 0.16 | 0.19 | 0.11 | 0.26 | 0.18 |
| Docol 1200M | 0.21 | 0.09 | 0.19 | 0.09 | 0.20 | 0.15 |
| Material | Absorbed Energy at 70 mm [J] | Peak Force [kN] | Mean Force [kN] | CFE | SEA [kJ/kg] |
|---|---|---|---|---|---|
| Quasi-static conditions | |||||
| 1000DP_Exp. No. 1 | 710 | 26.1 | 10.2 | 0.40 | 18.9 |
| 1000DP_Exp. No. 2 | 707 | 25.3 | 10.1 | 0.40 | 18.8 |
| 1200M_Exp. No. 1 | 902 | 35.1 | 13.5 | 0.38 | 24.0 |
| 1200M_Exp. No. 2 | 897 | 34.2 | 12.9 | 0.38 | 23.9 |
| Dynamic conditions | |||||
| 1000DP_Exp. No. 1 | 905 | 60.4 | 13.1 | 0.22 | 24.0 |
| 1000DP_Exp. No. 2 | 935 | 53.6 | 13.8 | 0.26 | 24.9 |
| 1200M_Exp. No. 1 | 1007 | 79.8 | 14.3 | 0.18 | 26.8 |
| 1200M_Exp. No. 2 | 1009 | 77.6 | 14.3 | 0.18 | 26.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prochenka, P.; Janiszewski, J.; Kucewicz, M. Crash Response of Laser-Welded Energy Absorbers Made of Docol 1000DP and Docol 1200M Steels. Materials 2021, 14, 2808. https://doi.org/10.3390/ma14112808
Prochenka P, Janiszewski J, Kucewicz M. Crash Response of Laser-Welded Energy Absorbers Made of Docol 1000DP and Docol 1200M Steels. Materials. 2021; 14(11):2808. https://doi.org/10.3390/ma14112808
Chicago/Turabian StyleProchenka, Paweł, Jacek Janiszewski, and Michał Kucewicz. 2021. "Crash Response of Laser-Welded Energy Absorbers Made of Docol 1000DP and Docol 1200M Steels" Materials 14, no. 11: 2808. https://doi.org/10.3390/ma14112808
APA StyleProchenka, P., Janiszewski, J., & Kucewicz, M. (2021). Crash Response of Laser-Welded Energy Absorbers Made of Docol 1000DP and Docol 1200M Steels. Materials, 14(11), 2808. https://doi.org/10.3390/ma14112808






