Basic Mechanical Properties of Duplex Stainless Steel Bars and Experimental Study of Bonding between Duplex Stainless Steel Bars and Concrete
Abstract
:1. Introduction
2. Duplex Stainless Steel Bar Room Temperature Tensile Test
2.1. Specimen Design
2.2. Experimental Method and Procedure
2.3. Analysis of Experimental Results
2.3.1. Analysis of the Fracture Position of Duplex Stainless Steel Bars
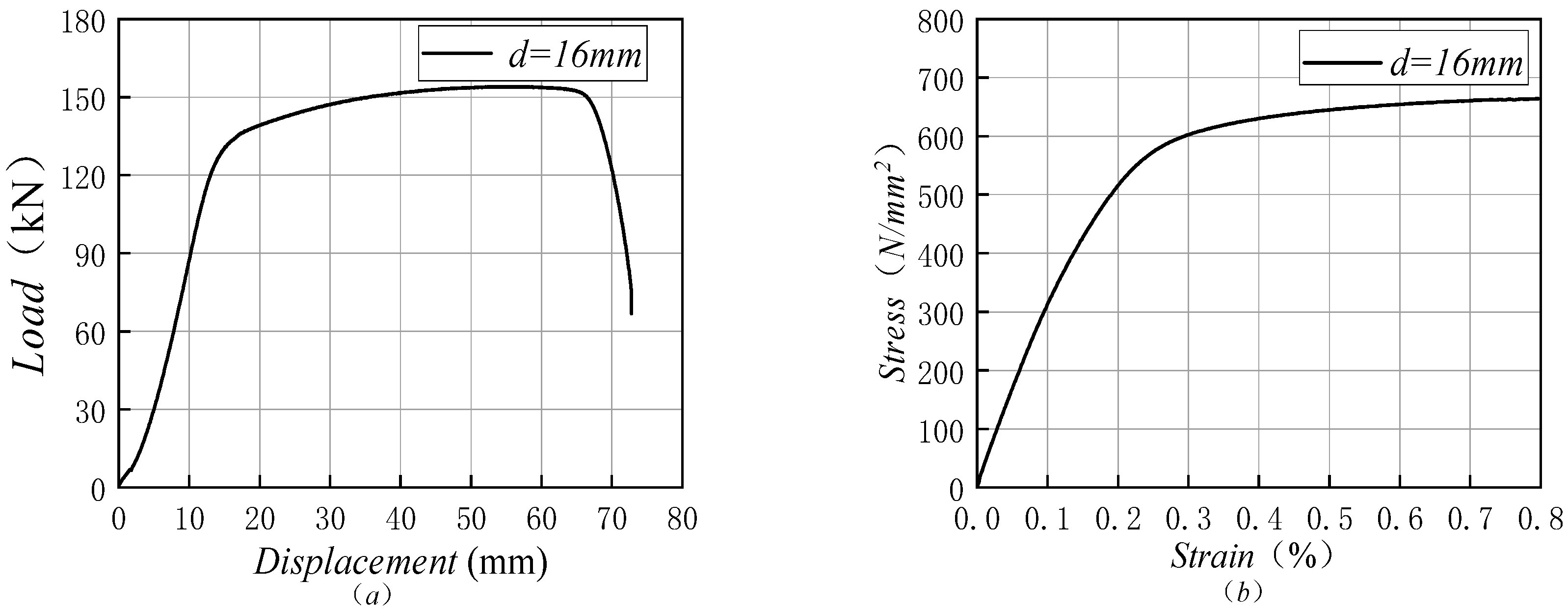
2.3.2. Stress–Strain Curve Analysis of Duplex Stainless Steel Bars
2.3.3. Duplex Stainless Steel Bar Basic Mechanical Properties Index
2.4. Recommendations for the Basic Mechanical Properties of Duplex Stainless Steel Bars
- Hypothesis that : the measured data (random variable ) follows a normal distribution.
- Sort the measured data from smallest to largest and calculate the measured frequency .
- Calculate the theoretical distribution of the distribution function .
- Calculate the theoretical frequency and the theoretical frequency .
- Calculate the value
- Look up the table, calculate , and make statistical judgments: ifwhere:
- k: number of groups; and,
- r: estimate the number of parameters, which is 2 in this article.
3. Bonding Performance Test
3.1. Experimental Overview
3.1.1. Specimen Design and Production
3.1.2. Loading Device
3.2. Analysis of Test Results
3.2.1. Forms of Damage
- Duplex stainless steel bar pull-out damage
- 2.
- Concrete splitting damage
3.2.2. Bond Stress
- : Bond stress;
- : Duplex stainless steel bar diameter (mm);
- : The length of the bonded section of duplex stainless steel bars (mm); and,
- : Test load.
3.2.3. The Influence of Various Factors on the Bonding Performance
- The effect of concrete strength on bonding performance
- 2.
- The effect of duplex stainless steel bar diameter on bonding performance
- 3.
- The influence of the ratio of concrete cover to reinforcing steel diameter on bonding performance
- 4.
- Effect of relative anchorage length on bonding performance
4. Regression Model of Bond Stress
5. Summary and Conclusions
- The tensile process of duplex stainless steel bars is different from that of ordinary steel bars, which can be divided into three stages: elastic stage, strengthening stage, and necking stage. The mechanical properties of duplex stainless steel bars are stable, and their strength is high. Additionally, there is no significant yield strength, but the elastic modulus is low.
- Duplex stainless steel reinforcement center pull-out specimens have two forms of damage, respectively, pull-out damage and concrete splitting damage. In duplex stainless steel bars in the extraction process, its raised ribs will produce squeezing force on the surrounding concrete matrix. The squeezing force causes tension in the surrounding concrete. When this tensile stress exceeds the tensile strength of the concrete, the specimen cracks internally, which involves cracks developing from the inside out. When the tensile strength of the concrete specimen is small, the internal cracks develop to the surface of the specimen and splitting damage occurs. When the tensile strength of concrete is higher, no cracks are visible on the surface of the specimen, the concrete in front of the reinforcing rib is crushed, and the reinforcing bar is pulled out, at which time the specimen undergoes pull-out damage.
- The higher the strength of the concrete, the greater the bond stress between the duplex stainless steel reinforcement and the concrete, and the bond stress is proportional to the square root of the concrete strength. The change in the diameter of duplex stainless steel reinforcement has an effect on the damage form of the specimen: the larger the diameter of duplex stainless steel reinforcement the lower the bond stress. The increase in the ratio of concrete cover to rebar diameter can enhance the crack resistance of the specimen: when the ratio of concrete cover to rebar diameter is less than 4.5 and when the concrete has a small tensile strength, the specimen is prone to splitting damage and the bond stress increases with the ratio of concrete cover to rebar diameter; when the ratio of concrete cover to rebar diameter is greater than 4.5 and when the concrete has a higher tensile strength, the specimen is prone to pull-out damage and bond stress remains basically unchanged. Because the duplex stainless steel reinforcement has higher strength, which greatly enhances the bond strength with concrete and duplex stainless steel reinforcement, bond stress is more uniformly distributed along the anchorage length direction, so that, when the relative anchorage length increases, the mechanical bite between the duplex stainless steel reinforcement and concrete increases, and the bond strength increases accordingly.
- The duplex stainless steel bar bond stress expression that is established by regression analysis can better fit the test value and predicted value for different concrete strengths, the duplex stainless steel bar diameters, the ratio of concrete cover to bar diameter, relative anchorage length, and the formula established, and the test results are in good agreement. It shows that the bond stress formula is scientific and reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Li, C.; Zheng, X.; Zhang, J. Research on Stainless Steel Reinforced Concrete Structure; The People’s Communication Publishing Company: Beijing, China, 2015. [Google Scholar]
- Geng, H. Experimental Study on Mechanical Properties of Stainless Steel Bars and Components for Bridges. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2013. [Google Scholar]
- Rabi, M.; Cashell, K.A.; Shamass, R.; Desnerck, P. Bond behaviour of austenitic stainless steel reinforced concrete. Eng. Struct. 2020, 221, 111027. [Google Scholar] [CrossRef]
- Correia, M.J.; Salta, M.M. Stress corrosion cracking of austenitic stainless steel alloys for reinforced concrete. Mater. Sci. Forum 2006, 514, 1511–1515. [Google Scholar] [CrossRef]
- James, E. New stainless steel alloy with implications for reinforced concrete. Concr. Eng. Int. 2004, 8, 24–25. [Google Scholar]
- Leroy, G. The use of stainless steel in structures. Prog. Struct. Eng. Mater. 2010, 7, 45–55. [Google Scholar]
- Pauletta, M.; Rovere, N.; Randl, N.; Russo, G. Bond-Slip Behavior between Stainless Steel Rebars and Concrete. Materials 2020, 13, 979. [Google Scholar] [CrossRef] [Green Version]
- Ogunsanya, I.G.; Hansson, C.M. Reproducibility of the Corrosion Resistance of UNS S32205 and UNS S32304 Stainless Steel Reinforcing Bars. Corrosion 2020, 76, 114–130. [Google Scholar] [CrossRef]
- Niejenhuis, C.V.; Walbridge, S.; Hansson, C. Life-Cycle Cost Analysis of Concrete Structures Reinforced with Stainless Steel Reinforcing Bars; IABSE Symposium Report; Engineering the Future: Vancouver, BC, Canada, 2017. [Google Scholar]
- Kulessa, G. Stainless steel reinforcement for concrete. Betonw. Fert. Tech./Concr. Precast. Plant Technol. 1988, 54, 58–63. [Google Scholar]
- Bertolini, L.; Pedeferri, P. Laboratory and field experience on the use of stainless steel to improve durability of reinforced concrete. Corros. Rev. 2002, 20, 129–152. [Google Scholar] [CrossRef]
- Cochrane, D. Success for stainless steel-Durable reinforced concrete bridges. Concrete 2003, 37, 26–28. [Google Scholar]
- Yue, L.A.; Tafsirojjaman, T.; Dogar, A.U.R.; Hückler, A. Bond behaviour improvement between infra-lightweight and high strength concretes using FRP grid reinforcements and development of bond strength prediction models—ScienceDirect. Constr. Build. Mater. 2020, 270, 121426. [Google Scholar]
- Freitas, E.; Louro, A.S.; Costa, H.; Cavaco, E.S.; Júlio, E.; Pipa, M. Bond behaviour between steel / stainless-steel reinforcing bars and low binder concrete (LBC). Eng. Struct. 2020, 221, 111072. [Google Scholar] [CrossRef]
- Casanova, A.; Jason, L.; Davenne, L. Bond slip model for the simulation of reinforced concrete structures. Eng. Struct. 2012, 39, 66–78. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, X.; Ying, J. Bond of epoxy-coated steel bars to seawater sea sand recycled concrete. Structures 2021, 30, 866–876. [Google Scholar] [CrossRef]
- Xiong, X.; Xiao, Q. Meso-scale simulation of bond behaviour between retarded-bonded tendons and concrete. Eng. Struct. 2021, 228, 111410. [Google Scholar] [CrossRef]
- Islam, K.; Billah, A.M.; Chowdhury, M.I.; Ahmed, K.S. Exploratory study on bond behavior of plain and sand coated stainless steel rebars in concrete. Structures 2020, 27, 2365–2378. [Google Scholar] [CrossRef]
- Harajli, M.; Hamad, B.; Karam, K. Bond-slip Response of Reinforcing Bars Embedded in Plain and Fiber Concrete. J. Mater. Civ. Eng. 2002, 14, 503–511. [Google Scholar] [CrossRef]
- Ertzibengoa, D.; Matthys, S.; Taerwe, L. Bond characteristics of carbon and stainless steel flat rebars with an alter-nate rib pattern. Mater. Struct. 2013, 46, 1107–1121. [Google Scholar] [CrossRef]
- Carvalho, E.P.; Miranda, M.P.; Fernandes, D.S.; Alves, G.V. Comparison of test methodologies to evaluate steel-concrete bond strength of thin reinforcing bar. Constr. Build. Mater. 2018, 183, 243–252. [Google Scholar] [CrossRef]
- Le, H.A.; Ye, H.; Xu, L.; Chi, Y. A mechanistic model for the nonlinear bond behavior of steel reinforcement in concrete. Eng. Struct. 2021, 231, 111715. [Google Scholar]
- Ming, M. Experimental study of bond-slip performance of steel sections with high-performance fibers for concrete. Eng. Mech. 2020, 37, 148–157. [Google Scholar]
- Ling, H.U. Experimental study on bond and anchorage properties of HRBF500 steel bars in concrete. Ind. Constr. 2009, 39, 13–15. [Google Scholar]
- Billah, A.M.; Alam, M.S. Bond behavior of smooth and sand-coated shape memory alloy (SMA) rebar in concrete. Structures 2016, 5, 186–195. [Google Scholar] [CrossRef]
- Pour, S.M.; Alam, M.S. Investigation of Compressive Bond Behavior of Steel Rebar Embedded in Concrete with Partial Recycled Aggregate Replacement. Structures 2016, 7, 153–164. [Google Scholar] [CrossRef]
- Shen, D.; Shi, X.; Zhang, H.; Duan, X.; Jiang, G. Experimental study of early-age bond behavior between high strength concrete and steel bars using a pull-out test. Constr. Build. Mater. 2016, 113, 653–663. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Xiong, Z.; Lu, Z.; Li, L. Bond performance between fibre-reinforced polymer bars and concrete under pull-out tests. Constr. Build. Mater. 2019, 227, 116803. [Google Scholar] [CrossRef]
- B/T 228-2010. Room Temperature Tensile Test Method for Metallic Materials; National Standards of the People’s Republic of China: Beijing, China, 2010. [Google Scholar]
- GB/T 1499.2-2007. Steel for Reinforced Concrete Part 2 Hot Rolled Ribbed Steel Bars; National Standards of the People’s Republic of China: Beijing, China, 2007. [Google Scholar]
- GB 50153-2008. Uniform Standards for Engineering Structural Reliability Design; National Standards of the People’s Republic of China: Beijing, China, 2008. [Google Scholar]
- Mousavi, S.S.; Guizani, L.; Ouellet-Plamondon, C.M. Simplified analytical model for interfacial bond strength of deformed steel rebars embedded in pre-cracked concrete. J. Struct. Eng. 2020, 146, 04020142. [Google Scholar] [CrossRef]
- Wu, C.; Chen, G. Unified model of local bond between deformed steel rebar and concrete: Indentation analogy theory and validation. J. Eng. Mech. 2015, 141, 04015038. [Google Scholar] [CrossRef]
- Xu, C.; Yuan, Y.; Lu, B.; Guo, Y. Design and reliability analysis of duplex stainless steel reinforcement with concrete anchorage. J. Shenyang Univ. Archit. (Nat. Sci. Ed.) 2019, 35, 445–452. [Google Scholar]











| Model Number | C | Si | Mn | P | S | Ni | Cr | Mo | Cu | N |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.4362 | 0.03 | 1.0 | 2.5 | 0.035 | 0.03 | 3.0–5.5 | 21.5–24.5 | 0.05–0.60 | 0.05–0.60 | 0.05–0.20 |
| Number | Diameter/mm | Original Scale Distance/mm | Total Length/mm | Number of Test Roots |
|---|---|---|---|---|
| L12 | 12 | 60 | 250 | 32 |
| L16 | 16 | 80 | 300 | 35 |
| L25 | 25 | 125 | 450 | 33 |
| L28 | 28 | 140 | 450 | 39 |
| L32 | 32 | 160 | 500 | 38 |
| Diameter (mm) | Number of Specimens | Tensile Strength (MPa) | Yield Strength (MPa) | Elastic Modulus (105 MPa) | Elongation after Break (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | ||
| 12 | 32 | 842 | 9.32 | 636 | 23.92 | 1.56 | 0.06 | 33.00 | 1.43 |
| 16 | 35 | 768 | 5.96 | 531 | 16.67 | 1.56 | 0.08 | 36.39 | 2.43 |
| 25 | 33 | 760 | 9.21 | 542 | 26.94 | 1.40 | 0.11 | 34.13 | 1.25 |
| 28 | 39 | 743 | 9.19 | 514 | 17.21 | 1.38 | 0.09 | 39.53 | 1.21 |
| 32 | 38 | 748 | 4.30 | 527 | 15.48 | 1.39 | 0.13 | 36.89 | 0.75 |
| Rebar Type | Tensile Strength (MPa) | Yield Strength (MPa) | Elongation after Break (%) |
|---|---|---|---|
| 500 MPa grade ordinary carbon steel bars | 630 | 500 | 15 |
| Duplex stainless steel bars | 750 | 514 | 33 |
| Category | Number of Specimens | Test Results | ||
|---|---|---|---|---|
| Tensile strength | 177 | 5.36 | 5.891 | Accepted |
| Elongation after break | 95 | 12.3 | 12.69 | Accepted |
| Modulus of elasticity | 175 | 5.62 | 7.85 | Accepted |
| Yield strength | 175 | 10.33 | 12.92 | Accepted |
| Indicators | Tensile Strength (MPa) | Yield Strength (MPa) | Modulus of Elasticity (×105 MPa) | Elongation after Break (%) |
|---|---|---|---|---|
| Average value | 755 | 529 | 1.43 | 36.74 |
| Standard deviation | 9.82 | 10.02 | 0.07 | 1.92 |
| Coefficient of variation | 0.01 | 0.02 | 0.05 | 0.05 |
| Standard value | 739 | 513 | 1.43 | 33.58 |
| Concrete Strength | Water-Cement Ratio | Sand Rate (%) | Cement (kg/m3) | Water (kg/m3) | Sand (kg/m3) | Coarse Aggregate (kg/m3) | Admixtures |
|---|---|---|---|---|---|---|---|
| C25 | 0.68 | 38 | 287 | 195 | 729 | 1189 | Not used |
| C30 | 0.60 | 37 | 325 | 195 | 696 | 1184 | Not used |
| C40 | 0.49 | 36 | 398 | 195 | 651 | 1156 | Not used |
| Number | Concrete Strength | Concrete Compressive Strength, fc′ (MPa) | Diameterd/mm | c/d | la/d | Specimen Side Length/mm | Number of Test Pieces |
|---|---|---|---|---|---|---|---|
| C25R16T4.5L5 | C25 | 28 | 16 | 4.5 | 5 | 160 | 3 |
| C30R16T4.5L5 | C30 | 38.1 | 16 | 4.5 | 5 | 160 | 3 |
| C40R16T4.5L5 | C40 | 43.7 | 16 | 4.5 | 5 | 160 | 3 |
| C30R12T4.5L5 | C30 | 38.1 | 12 | 4.5 | 5 | 120 | 3 |
| C30R25T4.5L5 | C30 | 38.1 | 25 | 4.5 | 5 | 250 | 3 |
| C30R16T3.3L5 | C30 | 38.1 | 16 | 3.3 | 5 | 120 | 3 |
| C30R16T5.8L5 | C30 | 38.1 | 16 | 5.8 | 5 | 200 | 3 |
| C30R16T7.3L5 | C30 | 38.1 | 16 | 7.3 | 5 | 250 | 3 |
| C30R16T4.5L3 | C30 | 38.1 | 16 | 4.5 | 3 | 160 | 3 |
| C30R16T4.5L4 | C30 | 38.1 | 16 | 4.5 | 4 | 160 | 3 |
| C30R16T4.5L6 | C30 | 38.1 | 16 | 4.5 | 6 | 160 | 3 |
| Number | Form of Damage | Damage Load (KN) | Bond Stress (MPa) |
|---|---|---|---|
| C25R16T4.5L5-1 | Pull-out | 73.3 | 18.2 |
| C25R16T4.5L5-2 | Pull-out | 66.3 | 16.5 |
| C25R16T4.5L5-3 | Pull-out | 70.3 | 17.5 |
| C30R16T4.5L5-1 | Pull-out | 84.0 | 20.9 |
| C30R16T4.5L5-2 | Pull-out | 79.6 | 19.8 |
| C30R16T4.5L5-3 | Pull-out | 80.4 | 20.0 |
| C40R16T4.5L5-1 | Splitting | 88.4 | 22.0 |
| C40R16T4.5L5-2 | Pull-out | 88.8 | 22.1 |
| C40R16T4.5L5-3 | Pull-out | 89.1 | 22.2 |
| C30R12T4.5L5-1 | Pull-out | 44.0 | 19.5 |
| C30R12T4.5L5-2 | Pull-out | 46.9 | 20.7 |
| C30R12T4.5L5-3 | Splitting | 42.0 | 19.6 |
| C30R25T4.5L5-1 | Splitting | 207.1 | 20.1 |
| C30R25T4.5L5-2 | Pull-out | 179.4 | 19.3 |
| C30R25T4.5L5-3 | Splitting | 190.6 | 19.4 |
| C30R16T3.3L5-1 | Splitting | 61.9 | 15.8 |
| C30R16T3.3L5-2 | Splitting | 69.9 | 16.8 |
| C30R16T3.3L5-3 | Splitting | 64.7 | 16.1 |
| C30R16T5.8L5-1 | Pull-out | 81.4 | 20.3 |
| C30R16T5.8L5-2 | Pull-out | 77.7 | 19.3 |
| C30R16T5.8L5-3 | Pull-out | 83.4 | 20.8 |
| C30R16T7.3L5-1 | Pull-out | 80.3 | 20.0 |
| C30R16T7.3L5-2 | Pull-out | 78.9 | 19.6 |
| C30R16T7.3L5-3 | Pull-out | 82.4 | 20.5 |
| C30R16T4.5L3-1 | Pull-out | 45.0 | 18.7 |
| C30R16T4.5L3-2 | Pull-out | 46.6 | 19.3 |
| C30R16T4.5L3-3 | Pull-out | 44.9 | 18.6 |
| C30R16T4.5L4-1 | Pull-out | 66.2 | 19.6 |
| C30R16T4.5L4-2 | Pull-out | 62.4 | 19.4 |
| C30R16T4.5L4-3 | Pull-out | 61.1 | 19.0 |
| C30R16T4.5L6-1 | Pull-out | 101.3 | 21.0 |
| C30R16T4.5L6-2 | Pull-out | 107.1 | 22.2 |
| C30R16T4.5L6-3 | Pull-out | 100.3 | 20.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Cui, Y.; Wang, J. Basic Mechanical Properties of Duplex Stainless Steel Bars and Experimental Study of Bonding between Duplex Stainless Steel Bars and Concrete. Materials 2021, 14, 2995. https://doi.org/10.3390/ma14112995
Li Q, Cui Y, Wang J. Basic Mechanical Properties of Duplex Stainless Steel Bars and Experimental Study of Bonding between Duplex Stainless Steel Bars and Concrete. Materials. 2021; 14(11):2995. https://doi.org/10.3390/ma14112995
Chicago/Turabian StyleLi, Qingfu, Yunqi Cui, and Jinwei Wang. 2021. "Basic Mechanical Properties of Duplex Stainless Steel Bars and Experimental Study of Bonding between Duplex Stainless Steel Bars and Concrete" Materials 14, no. 11: 2995. https://doi.org/10.3390/ma14112995
APA StyleLi, Q., Cui, Y., & Wang, J. (2021). Basic Mechanical Properties of Duplex Stainless Steel Bars and Experimental Study of Bonding between Duplex Stainless Steel Bars and Concrete. Materials, 14(11), 2995. https://doi.org/10.3390/ma14112995





