Experimental and Modelling of Alkali-Activated Mortar Compressive Strength Using Hybrid Support Vector Regression and Genetic Algorithm
Abstract
1. Introduction
2. Description of the Mathematical Background of the Proposed Hybrid Models
2.1. Formulation of Support Vector Regression Algorithm
2.2. Description of Genetic Algorithm
2.3. Acquisition of Experimental Data and Computational Hybridization of the Proposed Models
2.3.1. Experimental Description and Data Acquisition
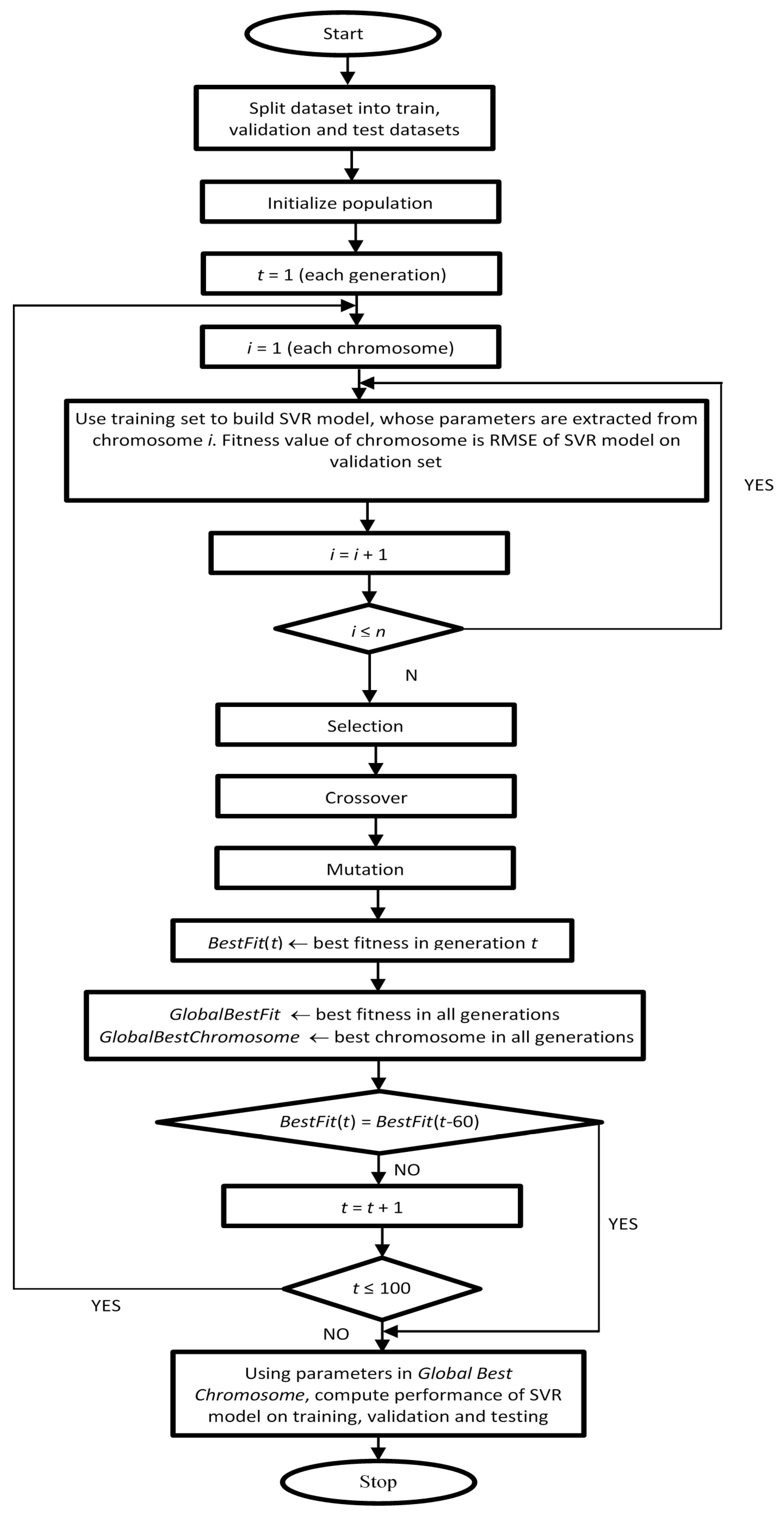
2.3.2. Computational Hybridization of Genetic Algorithm and Support Vector Regression
3. Results and Discussion
3.1. Early Age Compressive Strength Using the Developed Hybrid Models
3.1.1. Optimization of SVR Hyper-Parameters for the Early and 14-Day Compressive Strength Models
3.1.2. Performance of the Developed Early-Age Compressive Strength Models at Each Developmental Stage
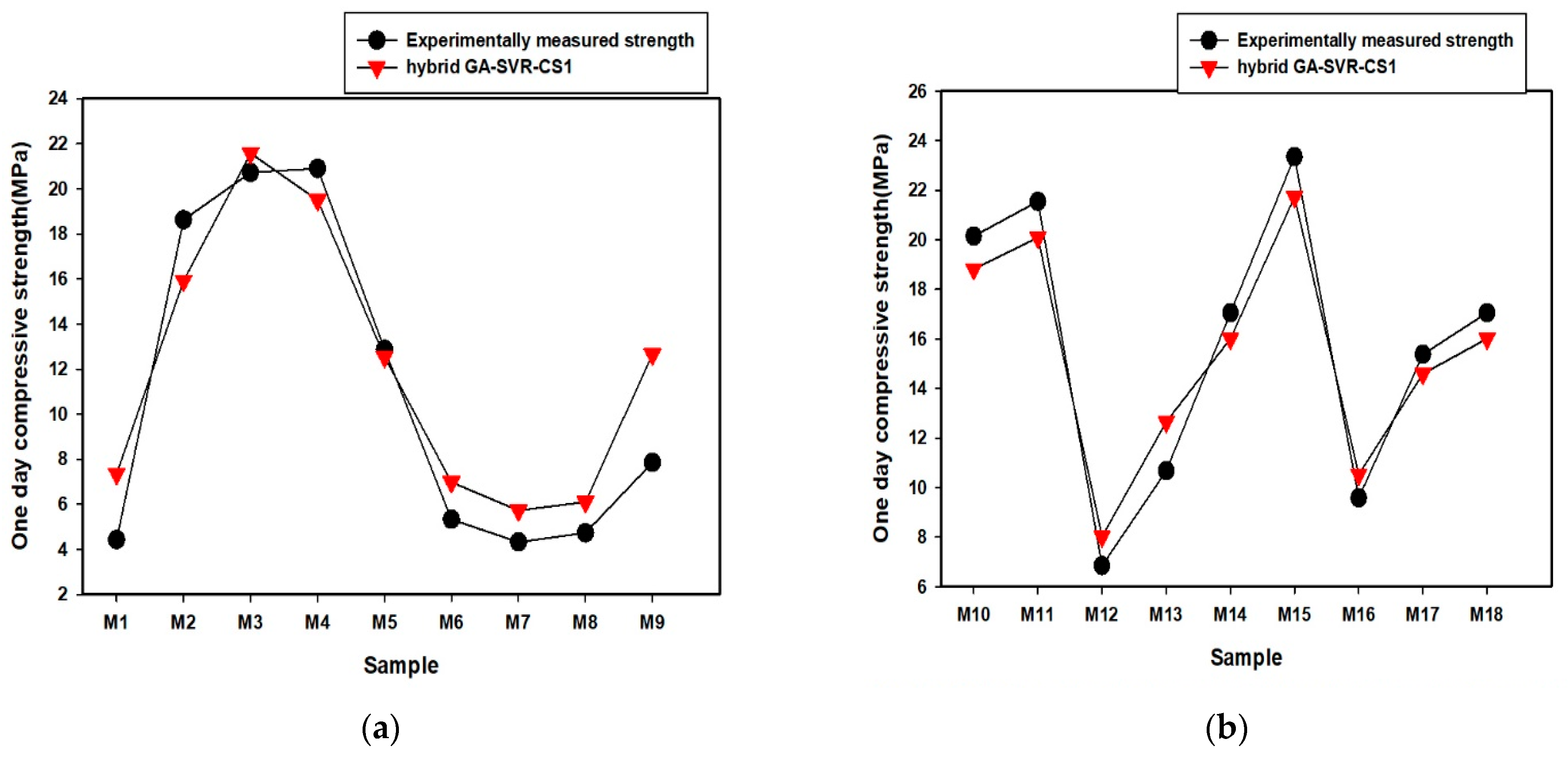
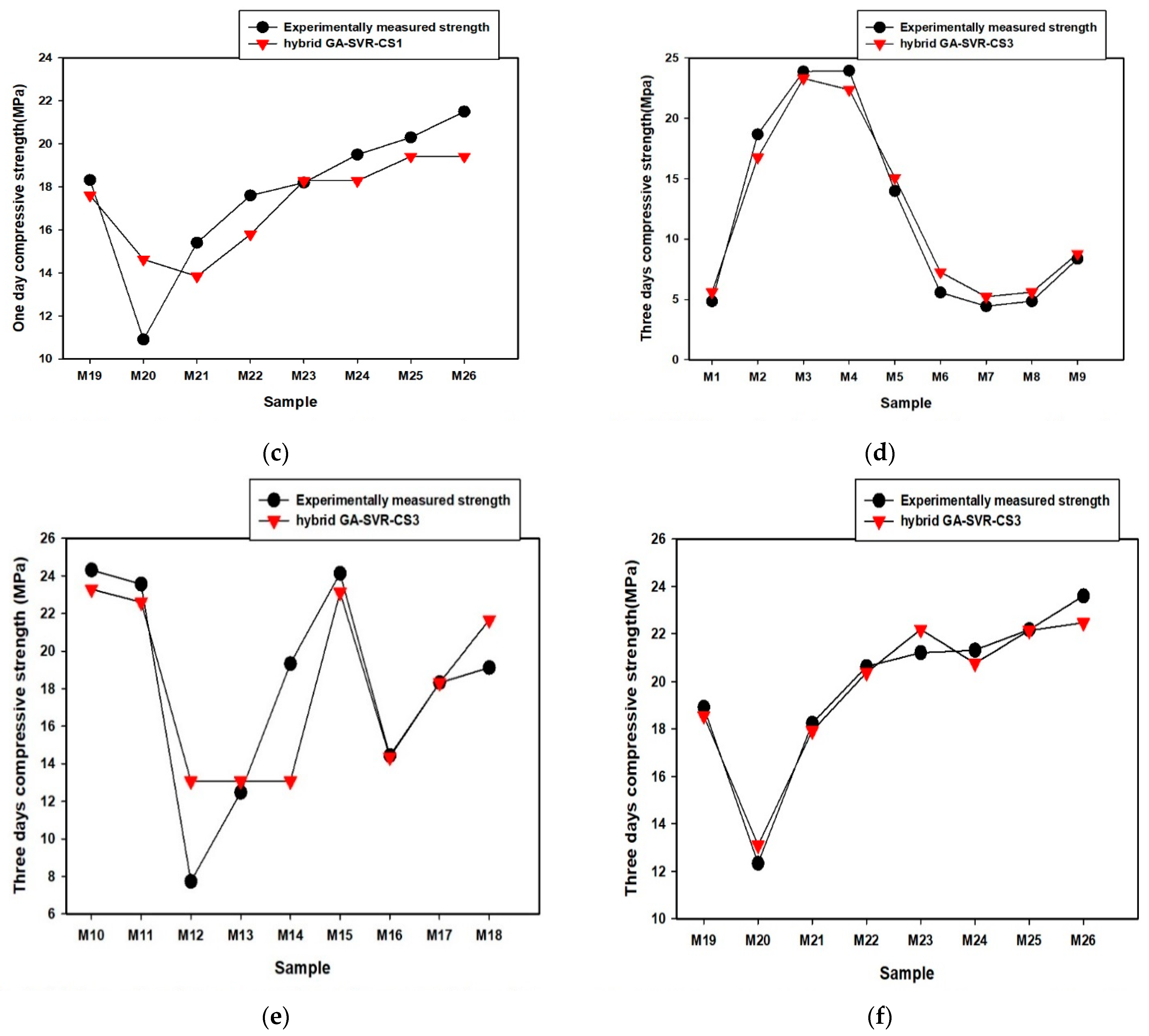
3.1.3. Comparison between the Experimentally-Measured Early and 14-Day Compressive Strength and the Outcomes of the Developed Hybrid Models
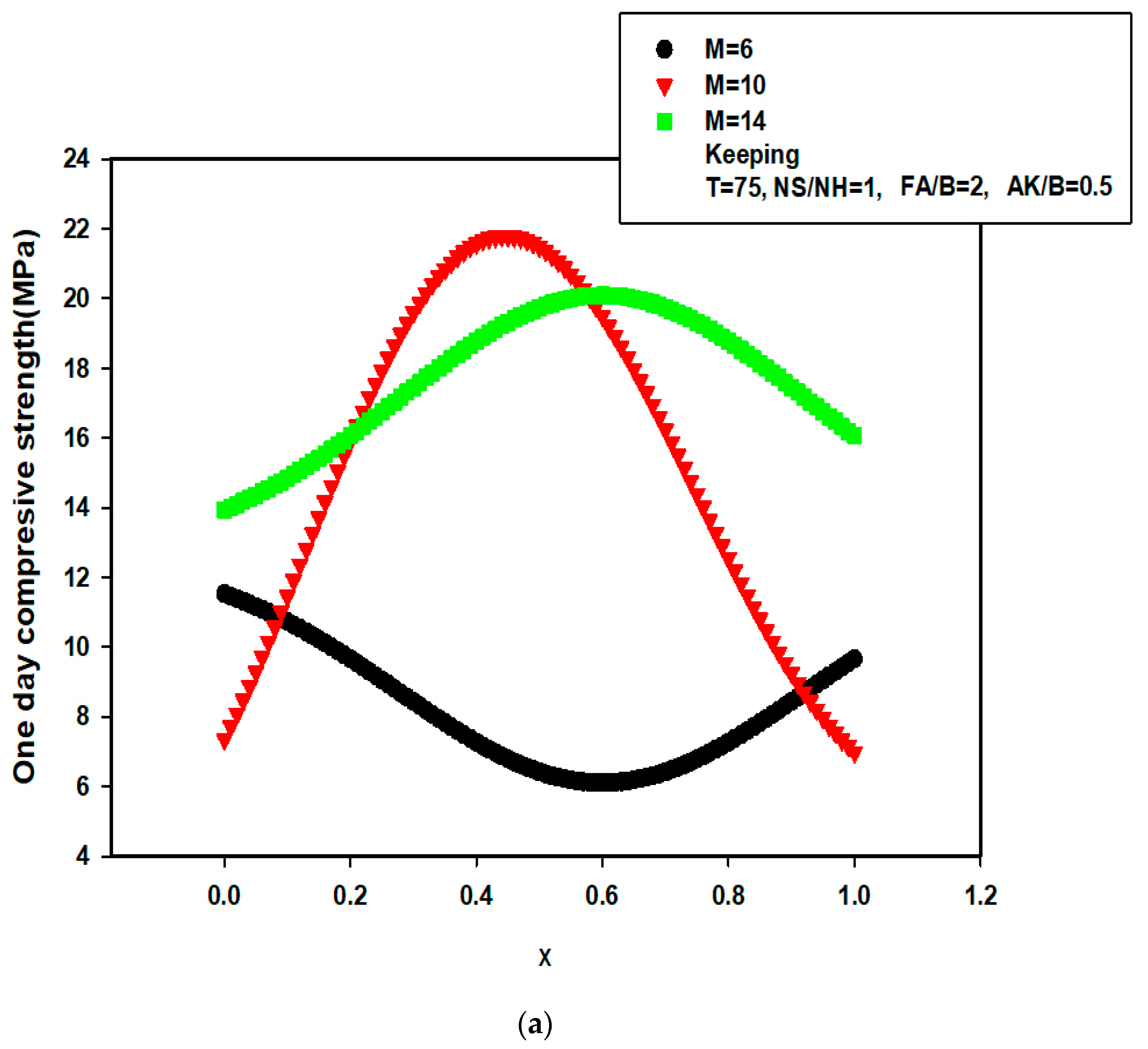
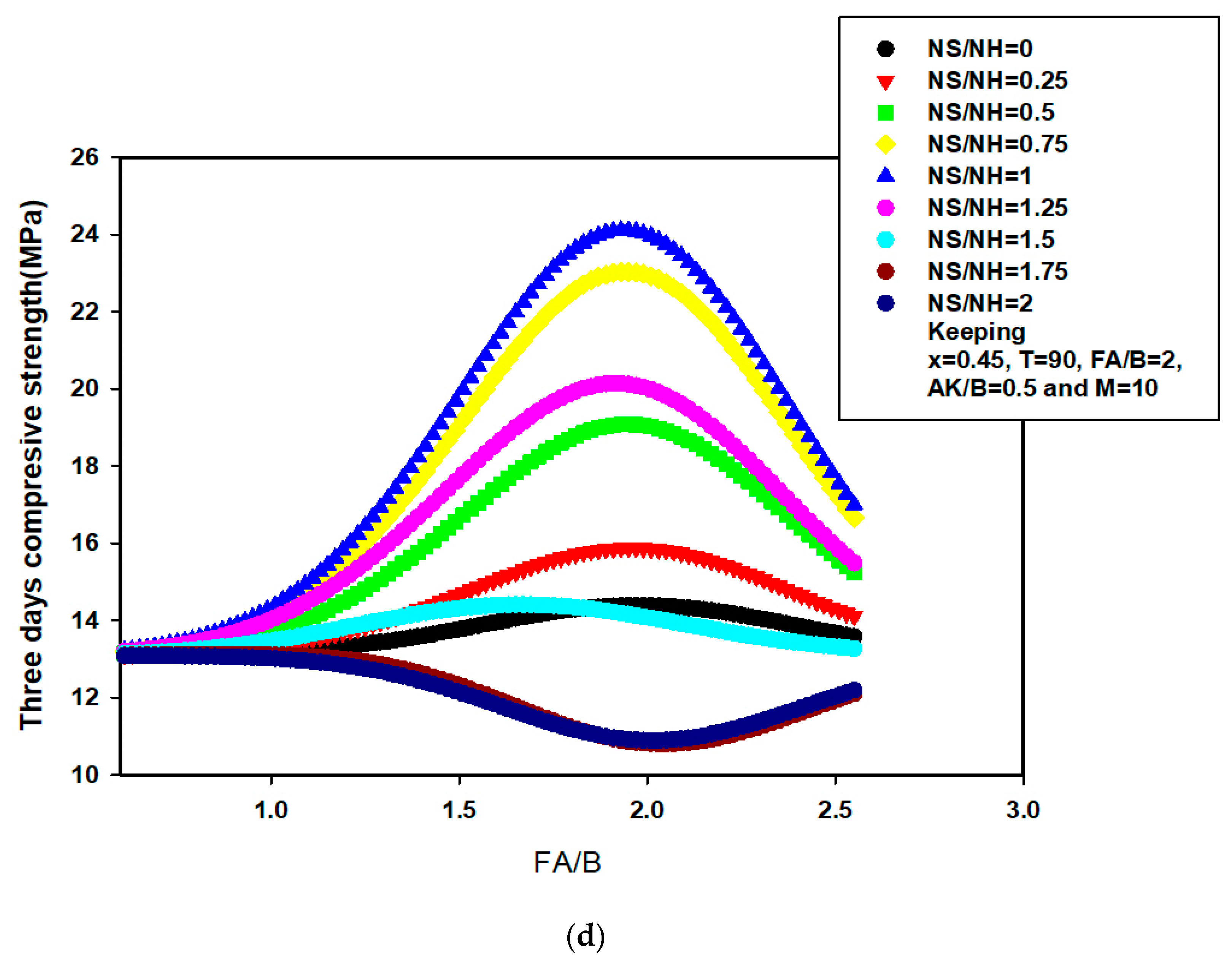
3.2. Modelling the Influence of Constituents of AALNM on the Early-Age and 14-Day Compressive Strength Using the Developed Hybrid Models
3.3. Estimation of 28-Days Compressive Strength Using the Developed Hybrid GA-SVR-CS28 Model
3.3.1. Optimization of SVR Hyper-Parameters for the Developed GA-SVR-CS28 Model
3.3.2. Performance of Hybrid GA-SVR-CS28 at Each Developmental Stage
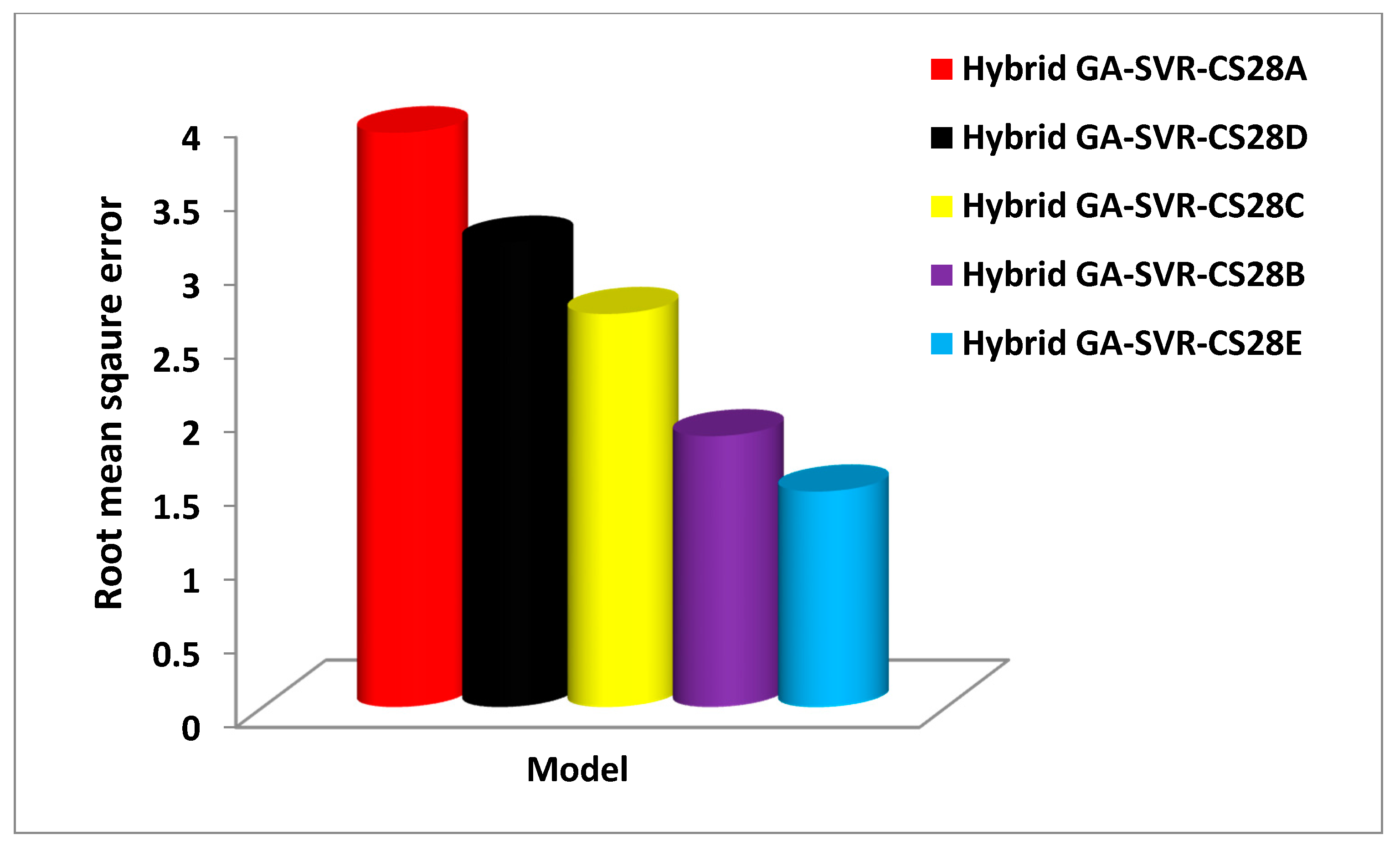
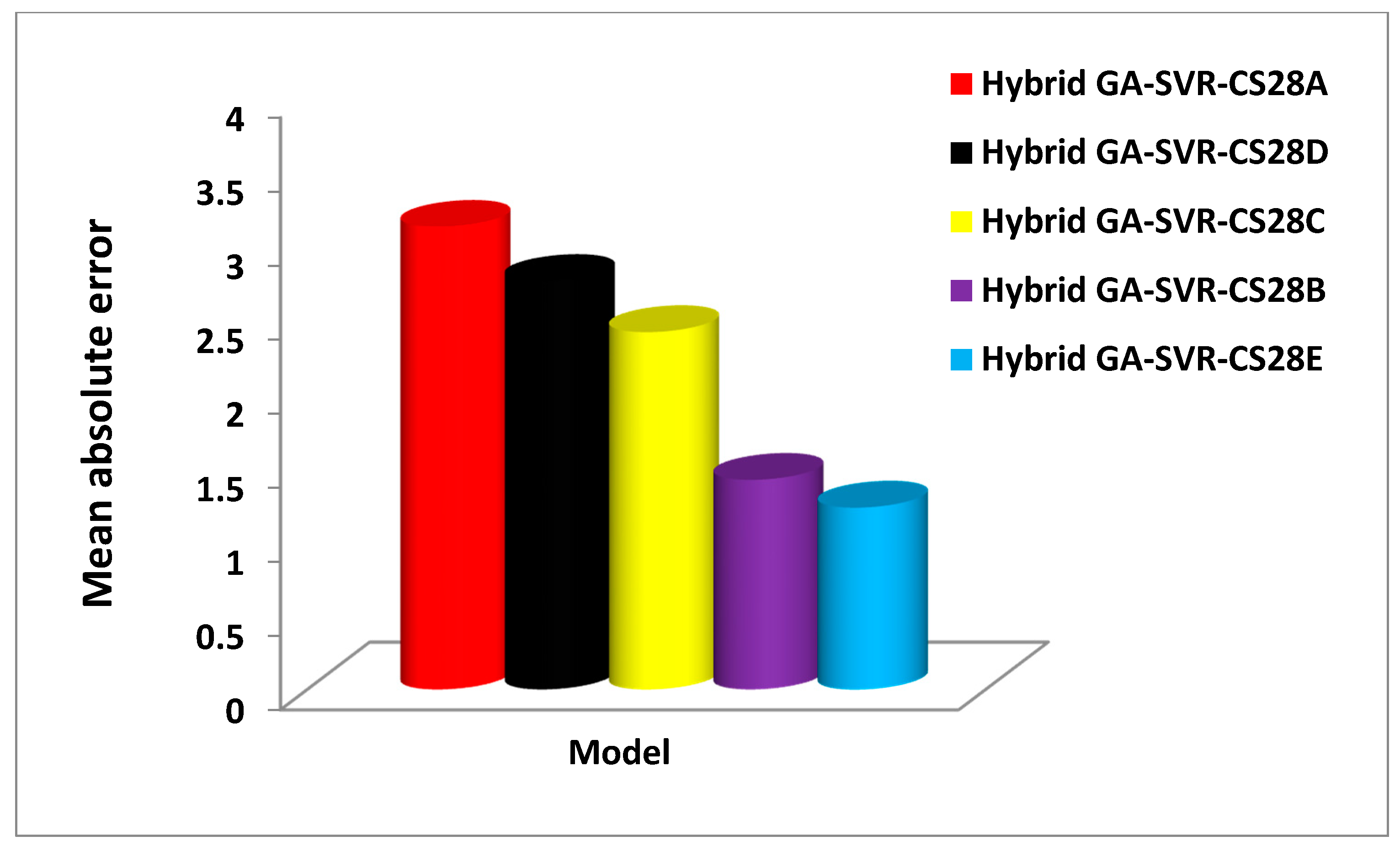
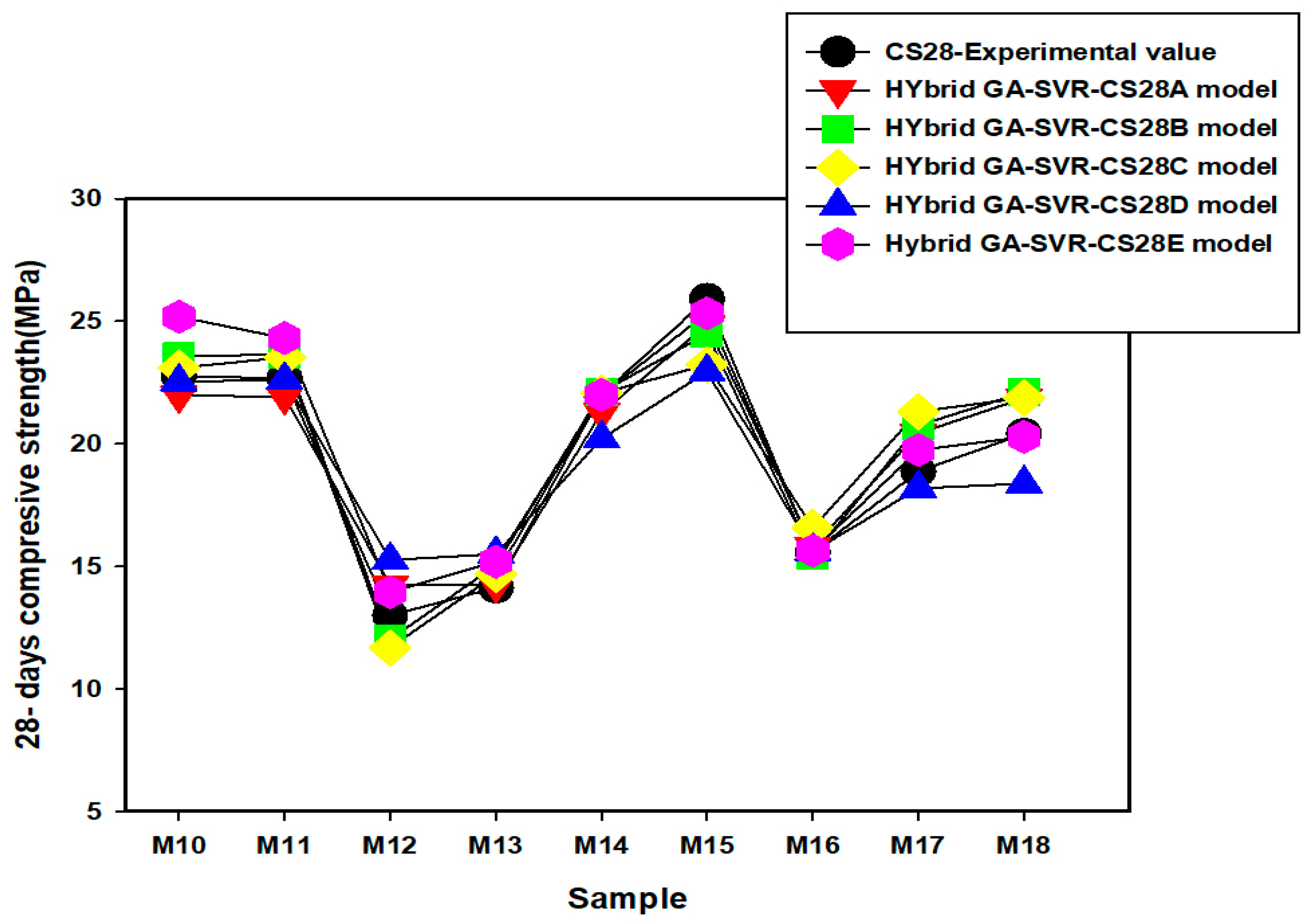
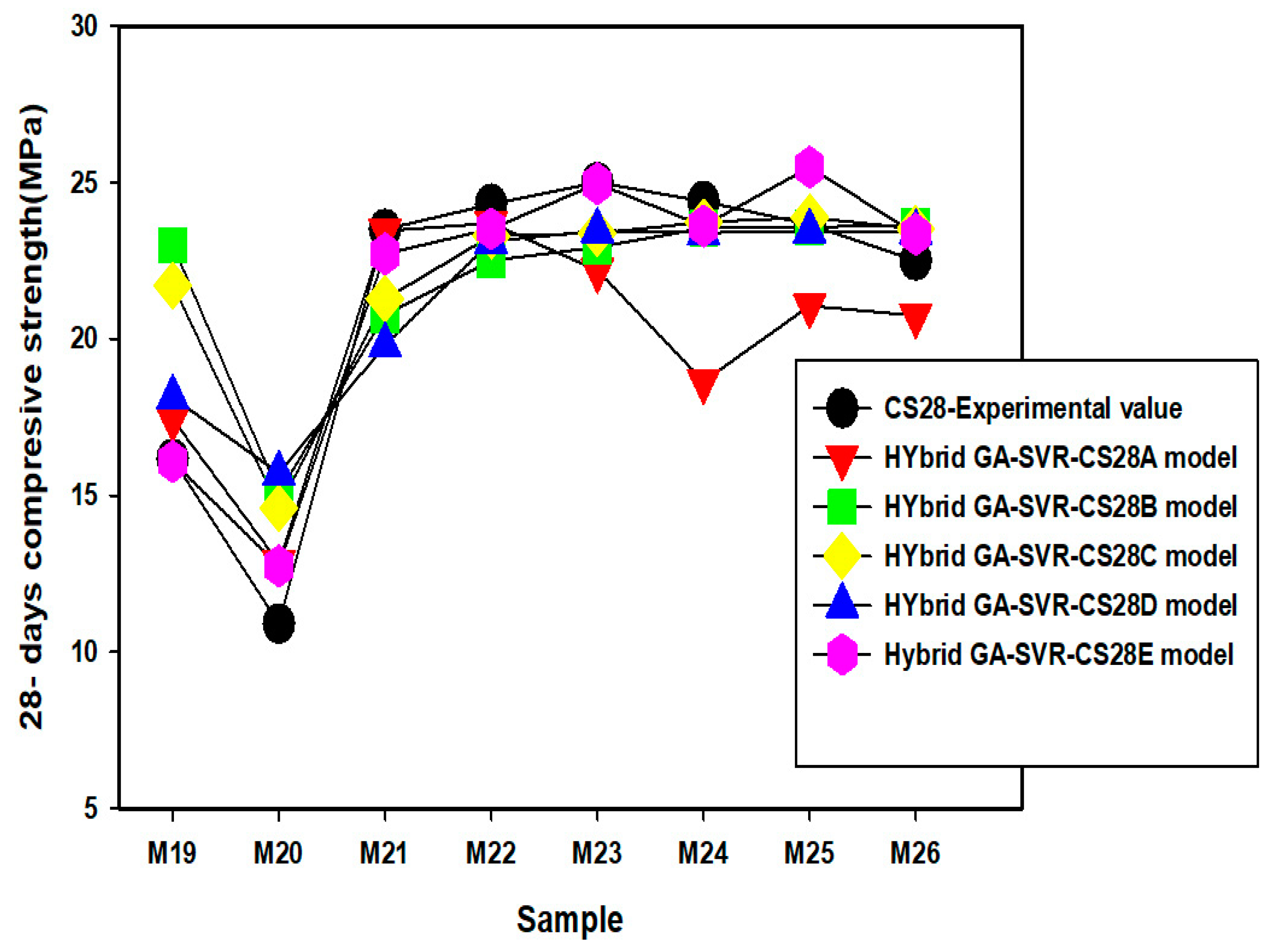
3.4. Comparison between the Experimentally Measured 28-Day Compressive Strength and the Outcomes of the Developed Hybrid GA-SVR-CS28 Model
3.5. Modeling the Influence of Constituents of AALNM on the Compressive Strength Using the Developed Hybrid GA-SVR-CS28A Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Mix | Experimentally Measured CS 1 (MPa) | Hybrid GA-SVR CS1 (Mpa) | Experimentally Measured CS3 (MPa) | Hybrid GA-SVR CS3 (Mpa) | Experimentally Measured CS-14 (MPa) | Hybrid GA-SVR- CS14 (MPa) |
|---|---|---|---|---|---|---|
| M1 | 4.430 | 7.351 | 4.850 | 5.600 | 5.200 | 19.904 |
| M2 | 18.620 | 15.926 | 18.680 | 16.770 | 21.850 | 19.639 |
| M3 | 20.720 | 21.579 | 23.890 | 23.309 | 24.300 | 19.292 |
| M4 | 20.900 | 19.498 | 23.950 | 22.378 | 25.180 | 18.870 |
| M5 | 12.870 | 12.546 | 13.980 | 15.079 | 14.500 | 18.387 |
| M6 | 5.330 | 6.980 | 5.570 | 7.253 | 5.800 | 17.857 |
| M7 | 4.320 | 5.726 | 4.430 | 5.218 | 4.790 | 11.022 |
| M8 | 4.730 | 6.098 | 4.850 | 5.600 | 5.030 | 5.935 |
| M9 | 7.850 | 12.657 | 8.360 | 8.791 | 9.010 | 9.533 |
| M10 | 20.150 | 18.821 | 24.310 | 23.287 | 24.730 | 24.361 |
| M11 | 21.550 | 20.094 | 23.560 | 22.605 | 24.670 | 24.116 |
| M12 | 6.850 | 8.026 | 7.730 | 13.080 | 10.550 | 16.778 |
| M13 | 10.680 | 12.657 | 12.470 | 13.080 | 12.760 | 13.174 |
| M14 | 17.060 | 16.012 | 19.340 | 13.080 | 20.360 | 16.778 |
| M15 | 23.350 | 21.730 | 24.130 | 23.124 | 24.370 | 23.631 |
| M16 | 9.580 | 10.530 | 14.430 | 14.350 | 13.170 | 18.625 |
| M17 | 15.380 | 14.600 | 18.320 | 18.326 | 18.860 | 18.806 |
| M18 | 17.060 | 16.012 | 19.130 | 21.657 | 19.040 | 18.854 |
| M19 | 18.320 | 17.608 | 18.920 | 18.559 | 18.800 | 18.854 |
| M20 | 10.900 | 14.628 | 12.340 | 13.097 | 13.410 | 18.806 |
| M21 | 15.400 | 13.837 | 18.250 | 17.926 | 20.100 | 20.680 |
| M22 | 17.600 | 15.790 | 20.640 | 20.383 | 22.400 | 20.121 |
| M23 | 18.200 | 18.285 | 21.220 | 22.183 | 23.600 | 19.512 |
| M24 | 19.500 | 18.285 | 21.320 | 20.779 | 22.800 | 18.216 |
| M25 | 20.300 | 19.415 | 22.180 | 22.146 | 23.650 | 18.870 |
| M26 | 21.500 | 19.415 | 23.600 | 22.473 | 22.840 | 18.870 |
Appendix B
| Mix | Experimentally Measured CS 28 (MPa) | Hybrid GA-SVR CS-28A (MPa) | Hybrid GA-SVR CS-28B (MPa) | Hybrid GA-SVR CS-28C (MPa) | Hybrid GA-SVR CS-28D (MPa) | Hybrid GA-SVR CS-28E (MPa) |
|---|---|---|---|---|---|---|
| M1 | 8.920 | 14.300 | 8.363 | 8.577 | 14.540 | 8.871 |
| M2 | 22.600 | 19.558 | 23.197 | 21.550 | 22.521 | 22.898 |
| M3 | 25.000 | 22.197 | 22.931 | 23.374 | 23.464 | 24.961 |
| M4 | 27.000 | 20.925 | 23.547 | 23.341 | 21.942 | 25.623 |
| M5 | 15.700 | 16.191 | 17.124 | 15.981 | 16.163 | 16.068 |
| M6 | 6.300 | 9.947 | 8.162 | 9.041 | 14.517 | 6.970 |
| M7 | 6.000 | 6.746 | 8.540 | 8.631 | 14.666 | 7.040 |
| M8 | 7.610 | 8.207 | 8.040 | 8.577 | 14.581 | 6.890 |
| M9 | 11.620 | 11.860 | 14.673 | 12.284 | 15.252 | 11.983 |
| M10 | 22.750 | 21.983 | 23.580 | 23.104 | 22.543 | 25.191 |
| M11 | 22.690 | 21.924 | 23.648 | 23.533 | 22.615 | 24.321 |
| M12 | 13.000 | 14.230 | 12.023 | 11.693 | 15.253 | 13.941 |
| M13 | 14.130 | 14.230 | 15.040 | 14.663 | 15.505 | 15.190 |
| M14 | 22.000 | 21.292 | 22.107 | 22.066 | 20.217 | 22.007 |
| M15 | 25.920 | 24.855 | 24.499 | 23.231 | 22.946 | 25.333 |
| M16 | 15.570 | 15.819 | 15.439 | 16.581 | 15.621 | 15.642 |
| M17 | 18.880 | 20.433 | 20.756 | 21.316 | 18.193 | 19.757 |
| M18 | 20.420 | 21.869 | 22.107 | 21.887 | 18.380 | 20.286 |
| M19 | 16.170 | 17.439 | 23.011 | 21.722 | 18.134 | 16.082 |
| M20 | 10.900 | 12.845 | 15.056 | 14.595 | 15.702 | 12.743 |
| M21 | 23.500 | 23.453 | 20.776 | 21.272 | 19.805 | 22.719 |
| M22 | 24.300 | 23.693 | 22.501 | 23.294 | 23.118 | 23.515 |
| M23 | 25.000 | 22.197 | 22.931 | 23.374 | 23.464 | 24.961 |
| M24 | 24.400 | 18.649 | 23.541 | 23.733 | 23.392 | 23.614 |
| M25 | 23.650 | 21.063 | 23.573 | 23.884 | 23.447 | 25.492 |
| M26 | 22.500 | 20.747 | 23.633 | 23.516 | 23.411 | 23.345 |
References
- UN Environment; Scrivener, K.L.; John, V.M.; Gartner, E.M. Eco-efficient cements: Potential economically viable solutions for a low-CO2 cement-based materials industry. Cem. Concr. Res. 2018, 114, 2–26. [Google Scholar] [CrossRef]
- Van Damme, H. Concrete material science: Past, present, and future innovations. Cem. Concr. Res. 2018, 112, 5–24. [Google Scholar] [CrossRef]
- Imbabi, M.S.; Carrigan, C.; McKenna, S. Trends and developments in green cement and concrete technology. Int. J. Sustain. Built Environ. 2012, 1, 194–216. [Google Scholar] [CrossRef]
- CEMBUREAU. Activity Report 2015; CEMBUREAU: Brussels, Belgium, 2015. [Google Scholar]
- Damtoft, J.S.; Lukasik, J.; Herfort, D.; Sorrentino, D.; Gartner, E.M. Sustainable development and climate change initiatives. Cem. Concr. Res. 2008, 38, 115–127. [Google Scholar] [CrossRef]
- Andrew, R.M. Global CO2 emissions from cement production. Earth Syst. Sci. Data 2017, 10, 1–52. [Google Scholar]
- Rafiei, M.H. Advanced Neural Network and Machine Learning Models for Construction, Materials and Structural Engineering. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2016; p. 228. [Google Scholar]
- Provis, J.L. Alkali avtivated materials. Cem. Concr. Res. 2014, 114, 40–48. [Google Scholar] [CrossRef]
- Najimi, M.; Ghafoori, N.; Sharbaf, M. Alkali-activated natural pozzolan/slag mortars: A parametric study. Constr. Build. Mater. 2018, 164, 625–643. [Google Scholar] [CrossRef]
- Luukkonen, T.; Abdollahnejad, Z.; Yliniemi, J.; Kinnunen, P.; Illikainen, M. One-part alkali-activated materials: A review. Cem. Concr. Res. 2018, 103, 21–34. [Google Scholar] [CrossRef]
- Glasby, T.; Day, J.; Genrich, R.; Aldred, J. EFC geopolymer concrete aircraft pavements at Brisbane West Wellcamp Airport. Concrete 2015, 11, 1–9. [Google Scholar]
- Van Deventer, J.S.J.; Provis, J.L.; Duxson, P. Technical and commercial progress in the adoption of geopolymer cement. Miner. Eng. 2012, 29, 89–104. [Google Scholar] [CrossRef]
- McIntosh, A.; Lawther, S.E.M.; Kwasny, J.; Soutsos, M.N.; Cleland, D.; Nanukuttan, S. Selection and characterisation of geological materials for use as geopolymer precursors. Adv. Appl. Ceram. 2015, 114, 378–385. [Google Scholar] [CrossRef]
- Patel, R.; Kinney, F.; Schumacher, G. Green concrete using 100% fly ash based hydraulic binder. Int. Concr. Sustain. Conf. 2012, 5, 1–15. [Google Scholar]
- Cross, D.; Stephens, J.; Vollmer, J. Structural Applications of 100 Percent Fly Ash Concrete. Available online: https://p2infohouse.org/ref/45/44859.pdf (accessed on 4 April 2021).
- Najimi, M.; Sobhani, J.; Ahmadi, B.; Shekarchi, M. An experimental study on durability properties of concrete containing zeolite as a highly reactive natural pozzolan. Constr. Build. Mater. 2012, 35, 1023–1033. [Google Scholar] [CrossRef]
- Ibrahim, M.; Johari, M.A.M.; Rahman, M.K.; Maslehuddin, M. Effect of alkaline activators and binder content on the properties of natural pozzolan-based alkali activated concrete. Constr. Build. Mater. 2017, 147, 648–660. [Google Scholar] [CrossRef]
- Karim, M.R.; Zain, M.F.M.; Jamil, M.; Lai, F.C. Fabrication of a non-cement binder using slag, palm oil fuel ash and rice husk ash with sodium hydroxide. Constr. Build. Mater. 2013, 49, 894–902. [Google Scholar] [CrossRef]
- Salami, B.A.; Johari, M.A.M.; Ahmad, Z.A.; Maslehuddin, M. Impact of added water and superplasticizer on early compressive strength of selected mixtures of palm oil fuel ash-based engineered geopolymer composites. Constr. Build. Mater. 2016, 109, 198–206. [Google Scholar] [CrossRef]
- Kubba, Z.; Huseien, G.F.; Sam, A.R.M.; Shah, K.W.; Asaad, M.A.; Ismail, M.; Tahir, M.M.; Mirza, J. Impact of curing temperatures and alkaline activators on compressive strength and porosity of ternary blended geopolymer mortars. Case Stud. Constr. Mater. 2018, 9, e00205. [Google Scholar] [CrossRef]
- Salami, B.A.; Johari, M.A.M.; Ahmad, Z.A.; Maslehuddin, M.; Adewumi, A.A. Impact of Al(OH)3 addition to POFA on the compressive strength of POFA alkali-activated mortar. Constr. Build. Mater. 2018, 190, 65–82. [Google Scholar] [CrossRef]
- Yusuf, M.O. Performance of slag blended alkaline activated palm oil fuel ash mortar in sulfate environments. Constr. Build. Mater. 2015, 98, 417–424. [Google Scholar] [CrossRef]
- Najamuddin, S.K.; Johari, M.A.M.; Maslehuddin, M.; Yusuf, M.O. Synthesis of low temperature cured alkaline activated silicomanganese fume mortar. Constr. Build. Mater. 2019, 200, 387–397. [Google Scholar] [CrossRef]
- Deb, P.S.; Nath, P.; Sarker, P.K. The effects of ground granulated blast-furnace slag blending with fly ash and activator content on the workability and strength properties of geopolymer concrete cured at ambient temperature. Mater. Des. 2014, 62, 32–39. [Google Scholar] [CrossRef]
- Criado, M.; Aperador, W.; Sobrados, I. Microstructural and mechanical properties of alkali activated Colombian raw materials. Materials 2016, 9, 158. [Google Scholar] [CrossRef]
- Lee, N.K.; Lee, H.K. Setting and mechanical properties of alkali-activated fly ash/slag concrete manufactured at room temperature. Constr. Build. Mater. 2013, 47, 1201–1209. [Google Scholar] [CrossRef]
- Sinthaworn, S.; Nimityongskul, P. Effects of temperature and alkaline solution on electrical conductivity measurements of pozzolanic activity. Cem. Concr. Compos. 2011, 33, 622–627. [Google Scholar] [CrossRef]
- Topçu, I.B.; Toprak, M.U.; Uygunoǧlu, T. Durability and microstructure characteristics of alkali activated coal bottom ash geopolymer cement. J. Clean. Prod. 2014, 81, 211–217. [Google Scholar] [CrossRef]
- Adesanya, E.; Ohenoja, K.; Luukkonen, T.; Kinnunen, P.; Illikainen, M. One-part geopolymer cement from slag and pretreated paper sludge. J. Clean. Prod. 2018, 185, 168–175. [Google Scholar] [CrossRef]
- Jang, J.G.; Lee, N.K.; Lee, H.K. Fresh and hardened properties of alkali-activated fly ash/slag pastes with superplasticizers. Constr. Build. Mater. 2014, 50, 169–176. [Google Scholar] [CrossRef]
- Adewumi, A.A.; Owolabi, T.O.; Alade, I.O.; Olatunji, S.O. Estimation of physical, mechanical and hydrological properties of permeable concrete using computational intelligence approach. Appl. Soft Comput. J. 2016, 42, 342–350. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Owolabi, T.O. Development of a particle swarm optimization based support vector regression model for titanium dioxide band gap characterization. J. Semicond. 2019, 40, 022803. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Gondal, M.A. Development of hybrid extreme learning machine based chemo-metrics for precise quantitative analysis of LIBS spectra using internal reference pre-processing method. Anal. Chim. Acta 2018, 1030, 33–41. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Gondal, M.A. Quantitative analysis of LIBS spectra using hybrid chemometric models through fusion of extreme learning machines and support vector regression. J. Intell. Fuzzy Syst. 2018, 35, 1–10. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O.; Aldhafferi, N. Ensemble-based support vector regression with gravitational search algorithm optimization for estimating magnetic relative cooling power of manganite refrigerant in magnetic refrigeration application. J. Supercond. Nov. Magn. 2018, 32, 2107–2118. [Google Scholar] [CrossRef]
- Oloore, L.E.; Owolabi, T.O.; Fayose, S.; Adegoke, M.; Akande, K.O.; Olatunji, S.O. Modeling of semiconductors refractive indices using hybrid chemometric model. Model. Meas. Control. A 2018, 91, 95–103. [Google Scholar] [CrossRef]
- Owolabi, T.O.; Akande, K.O.; Olatunji, S.O. Computational intelligence method of estimating solid-liquid interfacial energy of materials at their melting temperatures. J. Intell. Fuzzy Syst. 2016, 31, 519–527. [Google Scholar] [CrossRef]
- Baser, F.; Apaydin, A. Hybrid fuzzy support vector regression analysis. J. Intell. Fuzzy Syst. 2015, 28, 2037–2045. [Google Scholar] [CrossRef]
- Suleiman, M.A.; Owolabi, T.O.; Adeyemo, H.B.; Olatunji, S.O. Modeling of autoignition temperature of organic energetic compounds using hybrid intelligent method. Process. Saf. Environ. Prot. 2018, 120, 79–86. [Google Scholar] [CrossRef]
- Vapnik, V.M. Statistical Learning Theory; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Niu, J.; Chen, J.; Xu, Y. Twin support vector regression with Huber loss. J. Intell. Fuzzy Syst. 2017, 32, 4247–4258. [Google Scholar] [CrossRef]
- Al-Anazi, A.F.; Gates, I.D. Support vector regression to predict porosity and permeability: Effect of sample size. Comput. Geosci. 2012, 39, 64–76. [Google Scholar] [CrossRef]
- Smola, A.; Scholköpf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Owolabi, T.O. Modeling the magnetocaloric effect of manganite using hybrid genetic and support vector regression algorithms. Phys. Lett. A 2019, 383, 1782–1790. [Google Scholar] [CrossRef]
- Crone, S.F.; Guajardo, J.; Weber, R. The impact of preprocessing on support vector regression and neural networks in time series prediction. Conf. Data Min. 2006, 3, 37–42. [Google Scholar]
- Owolabi, T.O. Determination of the velocity of detonation of primary explosives using genetically optimized support vector regression. Propellants Explos. Pyrotech. 2019, 44, 1–12. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Salami, H.O.; Mamman, E.Y. A genetic algorithm for allocating project supervisors to students. Int. J. Intell. Syst. Appl. 2016, 8, 51–59. [Google Scholar] [CrossRef][Green Version]
- ASTM International. ASTM Standard C33, 2003. In Specification for Concrete Aggregates; ASTM International: West Conshohocken, PA, USA, 2003. [Google Scholar]
- American Society of Testing Materials. Standard Specification for Portland Cement; ASTM: West Conshohocken, PA, USA, 2015; Volume 1999, pp. 1–6. [Google Scholar]
- Adewumi, A.A.; Ariffin, M.A.M.; Yusuf, M.O.; Maslehuddin, M.; Ismail, M. Effect of sodium hydroxide concentration on strength and microstructure of alkali-activated natural pozzolan and limestone powder mortar. Constr. Build. Mater. 2021, 271, 121530. [Google Scholar] [CrossRef]







| Mix | X - | M mol/dm3 | T (°C) | NS/NH - | FA/B - | AK/B - | CS-1 (MPa) | CS-3 (MPa) | CS-7 (MPa) | CS-14 (MPa) | CS-28 (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 0 | 10 | 75 | 1 | 2 | 0.5 | 4.4 | 4.9 | 5.2 | 7.4 | 8.9 |
| M2 | 0.2 | 10 | 75 | 1 | 2 | 0.5 | 18.6 | 18.7 | 21.9 | 22.4 | 22.6 |
| M3 | 0.4 | 10 | 75 | 1 | 2 | 0.5 | 20.7 | 23.9 | 24.3 | 24.5 | 25.0 |
| M4 | 0.6 | 10 | 75 | 1 | 2 | 0.5 | 20.9 | 24.0 | 25.2 | 25.3 | 27.0 |
| M5 | 0.8 | 10 | 75 | 1 | 2 | 0.5 | 12.9 | 14.0 | 14.5 | 15.3 | 15.7 |
| M6 | 1 | 10 | 75 | 1 | 2 | 0.5 | 5.3 | 5.6 | 5.8 | 6.0 | 6.3 |
| M7 | 0.6 | 4 | 75 | 1 | 2 | 0.5 | 4.3 | 4.4 | 4.8 | 5.3 | 6.0 |
| M8 | 0.6 | 6 | 75 | 1 | 2 | 0.5 | 4.7 | 4.9 | 5.0 | 5.6 | 7.6 |
| M9 | 0.6 | 8 | 75 | 1 | 2 | 0.5 | 7.9 | 8.4 | 9.0 | 9.8 | 11.6 |
| M10 | 0.6 | 12 | 75 | 1 | 2 | 0.5 | 20.2 | 24.3 | 24.7 | 24.7 | 22.8 |
| M11 | 0.6 | 14 | 75 | 1 | 2 | 0.5 | 21.6 | 23.6 | 24.7 | 24.0 | 22.7 |
| M12 | 0.6 | 10 | 25 | 1 | 2 | 0.5 | 6.85 | 7.73 | 10.55 | 11.68 | 13.00 |
| M13 | 0.6 | 10 | 45 | 1 | 2 | 0.5 | 10.68 | 12.47 | 12.76 | 13.25 | 14.13 |
| M14 | 0.6 | 10 | 60 | 1 | 2 | 0.5 | 17.06 | 19.34 | 20.36 | 20.86 | 22.00 |
| M15 | 0.6 | 10 | 90 | 1 | 2 | 0.5 | 23.35 | 24.13 | 24.37 | 24.84 | 25.92 |
| M16 | 0.6 | 10 | 75 | 0 | 2 | 0.5 | 9.6 | 14.4 | 13.2 | 14.3 | 15.6 |
| M17 | 0.6 | 10 | 75 | 0.5 | 2 | 0.5 | 15.4 | 18.3 | 18.9 | 19.1 | 18.9 |
| M18 | 0.6 | 10 | 75 | 0.75 | 2 | 0.5 | 17.1 | 19.1 | 19.0 | 19.5 | 20.4 |
| M19 | 0.6 | 10 | 75 | 1.25 | 2 | 0.5 | 18.3 | 18.9 | 18.8 | 15.3 | 16.2 |
| M20 | 0.6 | 10 | 75 | 1.5 | 2 | 0.5 | 10.9 | 12.3 | 13.4 | 10.5 | 10.9 |
| M21 | 0.6 | 10 | 75 | 1 | 1.4 | 0.5 | 15.4 | 18.3 | 20.1 | 22 | 23.5 |
| M22 | 0.6 | 10 | 75 | 1 | 1.6 | 0.5 | 17.6 | 20.6 | 22.4 | 23.3 | 24.3 |
| M23 | 0.6 | 10 | 75 | 1 | 1.8 | 0.5 | 18.2 | 21.2 | 23.6 | 24.2 | 25 |
| M24 | 0.6 | 10 | 75 | 1 | 2.2 | 0.5 | 19.5 | 21.3 | 22.8 | 23.4 | 24.4 |
| M25 | 0.6 | 10 | 75 | 1 | 2 | 0.45 | 20.3 | 22.2 | 23.7 | 25.0 | 23.7 |
| M26 | 0.6 | 10 | 75 | 1 | 2 | 0.55 | 21.5 | 23.6 | 22.8 | 23.1 | 22.5 |
| Parameter | Mean | Range | Standard Deviation | CC-1 (MPa) | CC-3 (MPa) | CC-7 (MPa) | CC-14 (MPa) | CC-28 (MPa) |
|---|---|---|---|---|---|---|---|---|
| X | 0.577 | 1 | 0.173 | −0.026 | −0.007 | −0.035 | −0.073 | −0.095 |
| M(mol/dm3) | 9.769 | 10 | 1.728 | 0.578 | 0.605 | 0.609 | 0.589 | 0.545 |
| T (°C) | 71.923 | 65 | 12.006 | 0.329 | 0.308 | 0.255 | 0.236 | 0.226 |
| NS/NH | 0.962 | 1.5 | 0.252 | 0.083 | −0.021 | 0.032 | −0.042 | −0.055 |
| FA/B | 1.962 | 0.8 | 0.150 | −0.055 | −0.102 | −0.144 | −0.189 | −0.225 |
| AK/B | 0.500 | 0.1 | 0.014 | 0.027 | 0.029 | −0.016 | −0.039 | −0.024 |
| CS-1 (MPa) | 14.737 | 19.05 | 6.187 | |||||
| CS-3 (MPa) | 16.556 | 19.9 | 6.871 | |||||
| CS-7 (MPa) | 17.376 | 20.4 | 7.053 | |||||
| CS-14(MPa) | 17.714 | 20 | 7.004 | |||||
| CS-28 (MPa) | 18.328 | 21 | 6.655 |
| Model | Regularization Factor | Epsilon | Kernel Option | Hyper-Parameter Lambda | Kernel Function |
|---|---|---|---|---|---|
| Hybrid GA-SVR-CS1 | 418.5247 | 0.7126 | 0.3201 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS3 | 417.1485 | 0.002 | 0.4056 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS7 | 36.7688 | 0.0539 | 2.0000 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS14 | 457.0419 | 0.002 | 0.2433 | 0.1 | Gaussian |
| Model | Training | Testing | Validation |
|---|---|---|---|
| Hybrid GA-SVR-CS1 | |||
| CC | 0.9315 | 0.9779 | 0.9664 |
| RMSE | 2.1655 | 2.7192 | 1.8432 |
| MAE | 1.5296 | 2.4756 | 1.4143 |
| Hybrid GA-SVR-CS3 | |||
| CC | 0.9952 | 0.6755 | 0.9084 |
| RMSE | 1.1651 | 3.7007 | 1.4896 |
| MAE | 0.9163 | 2.5532 | 1.2969 |
| Hybrid GA-SVR-CS7 | |||
| CC | 0.7039 | 0.8284 | 0.6557 |
| RMSE | 5.2789 | 4.6159 | 5.0503 |
| MAE | 3.108 | 4.0925 | 4.9916 |
| Hybrid GA-SVR-CS14 | |||
| CC | 0.9768 | 0.9541 | 0.934 |
| RMSE | 2.1681 | 2.7784 | 3.4103 |
| MAE | 1.5633 | 2.3586 | 2.7793 |
| Model | Regularization Factor | Epsilon | Kernel Option | Hyper-Parameter Lambda | Kernel Function |
|---|---|---|---|---|---|
| Hybrid GA-SVR-CS28A | 689.1925 | 0.002 | 0.6379 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS28B | 15.124 | 0.5571 | 2 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS28C | 7.7528 | 0.3432 | 2 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS28D | 1.000 | 0.002 | 2 | 0.1 | Gaussian |
| Hybrid GA-SVR-CS28E | 13.7523 | 0.002 | 2 | 0.1 | Gaussian |
| Model | Training | Testing | Validation |
|---|---|---|---|
| Hybrid GA-SVR-CS28A | |||
| CC | 0.9684 | 0.9899 | 0.6548 |
| RMSE | 2.2452 | 0.8442 | 3.8911 |
| MAE | 1.7507 | 0.6908 | 3.1246 |
| Hybrid GA-SVR-CS28B | |||
| CC | 0.9315 | 0.9779 | 0.9664 |
| RMSE | 2.1655 | 2.7192 | 1.8432 |
| MAE | 1.5296 | 2.4756 | 1.4143 |
| Hybrid GA-SVR-CS28C | |||
| CC | 0.9502 | 0.9958 | 0.9288 |
| RMSE | 1.9366 | 1.442 | 2.669 |
| MAE | 1.4209 | 1.1161 | 2.4128 |
| Hybrid GA-SVR-CS28D | |||
| CC | 0.9392 | 0.9539 | 0.9675 |
| RMSE | 4.1867 | 1.0493 | 3.1514 |
| MAE | 3.087 | 0.8511 | 2.7583 |
| Hybrid GA-SVR-CS28E | |||
| CC | 0.9947 | 0.9945 | 0.976 |
| RMSE | 0.7669 | 1.0394 | 1.4688 |
| MAE | 0.5998 | 0.8671 | 1.226 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sodani, K.A.A.; Adewumi, A.A.; Mohd Ariffin, M.A.; Maslehuddin, M.; Ismail, M.; Salami, H.O.; Owolabi, T.O.; Mohamed, H.D. Experimental and Modelling of Alkali-Activated Mortar Compressive Strength Using Hybrid Support Vector Regression and Genetic Algorithm. Materials 2021, 14, 3049. https://doi.org/10.3390/ma14113049
Al-Sodani KAA, Adewumi AA, Mohd Ariffin MA, Maslehuddin M, Ismail M, Salami HO, Owolabi TO, Mohamed HD. Experimental and Modelling of Alkali-Activated Mortar Compressive Strength Using Hybrid Support Vector Regression and Genetic Algorithm. Materials. 2021; 14(11):3049. https://doi.org/10.3390/ma14113049
Chicago/Turabian StyleAl-Sodani, Khaled A. Alawi, Adeshina Adewale Adewumi, Mohd Azreen Mohd Ariffin, Mohammed Maslehuddin, Mohammad Ismail, Hamza Onoruoiza Salami, Taoreed O. Owolabi, and Hatim Dafalla Mohamed. 2021. "Experimental and Modelling of Alkali-Activated Mortar Compressive Strength Using Hybrid Support Vector Regression and Genetic Algorithm" Materials 14, no. 11: 3049. https://doi.org/10.3390/ma14113049
APA StyleAl-Sodani, K. A. A., Adewumi, A. A., Mohd Ariffin, M. A., Maslehuddin, M., Ismail, M., Salami, H. O., Owolabi, T. O., & Mohamed, H. D. (2021). Experimental and Modelling of Alkali-Activated Mortar Compressive Strength Using Hybrid Support Vector Regression and Genetic Algorithm. Materials, 14(11), 3049. https://doi.org/10.3390/ma14113049









