Review and a Theoretical Approach on Pressure Drop Correlations of Flow through Open-Cell Metal Foam
Abstract
1. Introduction
- A high porosity (ε ≥ = 0.85–0.99);
- A low density (e.g., 0.45 kg/m3) and light weight;
- A high interstitial surface area per unit volume, which ranges from 1000 to 3000 m2/m3. Such a value can reach up to 8000 m2/m3 under compressed condition;
- Excellent fluid mixing, due to the tortuous flow paths;
- A high permeability.
2. Governing Equations of Fluid Flow and Geometry Structures of Open-Cell Metal Foams
2.1. Governing Equations
2.2. Geometry Structure
3. Pressure Drop Correlations for Open-Cell Metal Foams
3.1. Permeability and Forchheimer Coefficient
3.2. Friction Factor
4. Discussions
5. Summary and Conclusions
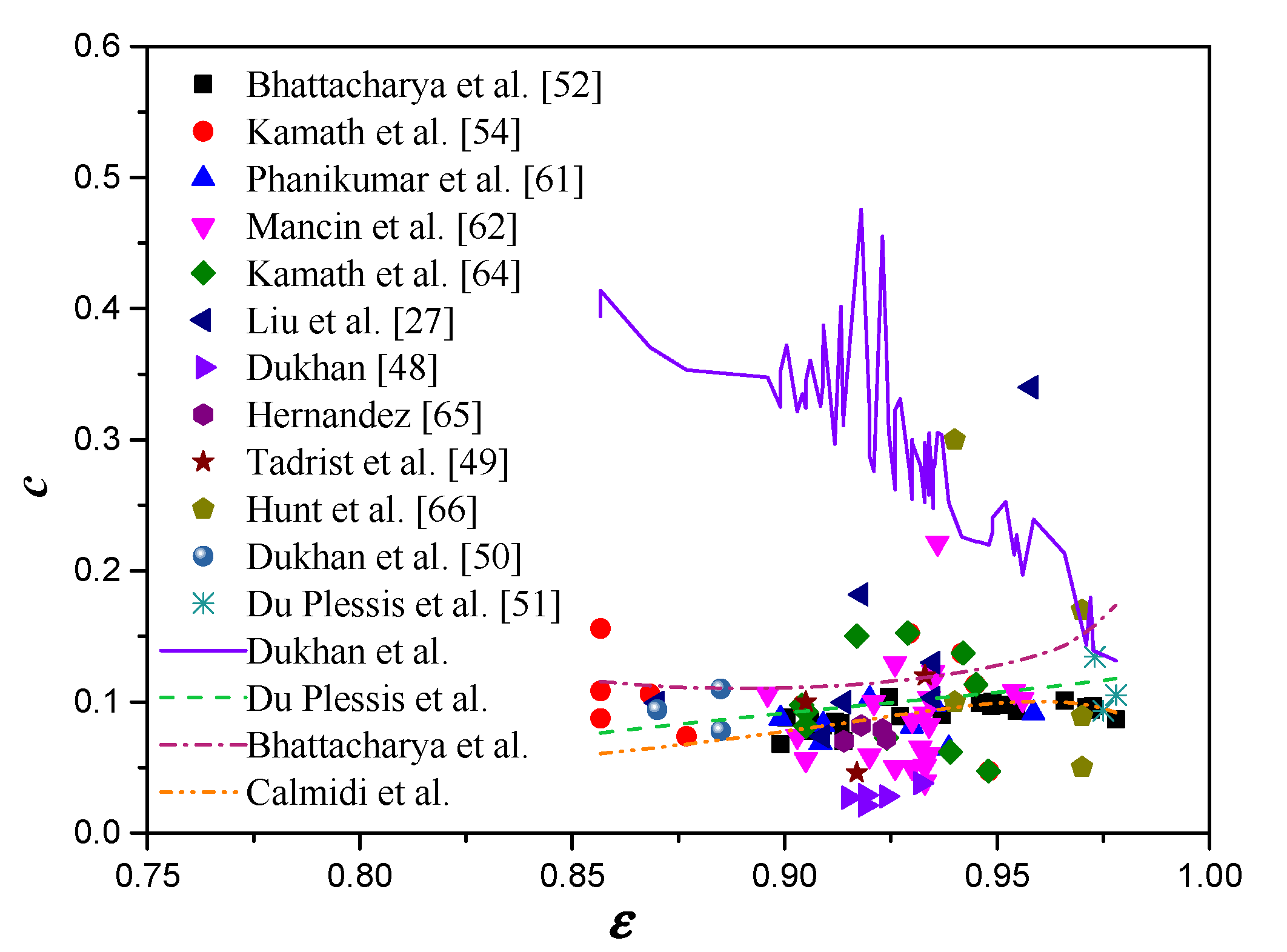
- The pressure drop for turbulent flow through open-cell metal foams can still be described by the Forchheimer equation with different fitting parameters (different permeability and Forchheimer coefficient). Meanwhile, for compressible gas flow, the permeability and Forchheimer coefficient should be obtained using Equation (10).
- There is a significant deviation in the permeability between the predictions from most empirical models (except for Calmidi’s model) and the experimental data available in the literature. Even for Calmidi’s model, an abnormal change of permeability is found for porosities greater than 0.96. However, the empirical Forchheimer coefficient models from Du Plessis et al. and Calmidi were found to yield consistent results with the experimental data.
- By imitating Calmidi’s model for permeability, two empirical correlations of permeability were developed in this study and recommended for open-cell metal foam. Meanwhile, Calmidi’s model is recommended for calculating the Forchheimer coefficient for flow through open-cell metal foam. These three equations together allow calculating the pressure drop through open-cell metal foam as a function of porosity and pore diameter (or strut diameter) for a wide range of porosities ε between 85.7 and 97.8% and pore densities between 10 and 100 PPI.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin symbols | ||
| Acor | cross-section area | m2 |
| C | form drag coefficient | m−1 |
| c | Forchheimer coefficient | |
| Dp | equivalent spherical diameter | m |
| df | strut diameter | m |
| dp | pore diameter | m |
| d | characteristic pore width | m |
| f | friction factor | |
| K | permeability | m2 |
| L | length | m |
| Δp | pressure drop | Pa |
| Q | volume flow rate | m3·s−1 |
| Re | Reynolds number | |
| Sv | surface area per unit volume of solid | m−1 |
| t | time | s |
| u | velocity | m·s−1 |
| uD | Darcy velocity | m·s−1 |
| up | pore velocity | m·s−1 |
| v | velocity vector | m·s−1 |
| V | volume | m3 |
| Greek symbols | ||
| ρ | density | kg·m−3 |
| μ | viscosity | kg·m−1·s−1 |
| σ | surface area per unit volume | m−1 |
| ε | porosity | |
| χ | tortuosity | |
| Subscripts | ||
| s | solid phase | |
| tot | total | |
References
- Tuchinskiy, L. Novel fabrication technology for metal foam. J. Adv. Mater. 2005, 37, 60–65. [Google Scholar]
- Garcia-Moreno, F. Commercial Applications of Metal Foams: Their Properties and Production. Materials 2016, 9, 85. [Google Scholar] [CrossRef]
- Kuruneru, S.T.W.; Sauret, E.; Vafai, K.; Saha, S.C.; Gu, Y.T. Analysis of particle-laden fluid flows, tortuosity and particle-fluid behaviour in metal foam heat exchangers. Chem. Eng. Sci. 2017, 172, 677–687. [Google Scholar] [CrossRef]
- Schampheleire, S.D.; Jaeger, P.D.; Kerpel, K.D.; Ameel, B.; Huisseune, H.; Paepe, M.D. How to Study Thermal Applications of Open-Cell Metal Foam: Experiments and Computational Fluid Dynamics. Materials 2016, 9, 94. [Google Scholar] [CrossRef]
- Veale, J.P. Investigation of the Behaviour of Open Cell Aluminum Foam. Master’s Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2010. [Google Scholar]
- Somasundaram, D.; Mani, A.; Kamaraj, M. Heat and Fluid Flow Characteristics of Copper Metal Foam as Heat Pipe Wick Material. Appl. Mech. Mater. 2015, 787, 112–116. [Google Scholar] [CrossRef]
- Ribeiro, G.B.; Barbosa, J.R.; Prata, A.T. Performance of Microchannel Condensers with Metal Foams on the Air-Side: Application in Small-Scale Refrigeration Systems. Appl. Therm. Eng. 2012, 36, 152–160. [Google Scholar] [CrossRef]
- Qu, J.; Sun, Q.; Wang, H.; Zhang, D.H.; Yuan, J.P. Performance characteristics of flat-plate oscillating heat pipe with porous metal-foam wicks. Int. J. Heat Mass Transf. 2019, 137, 20–30. [Google Scholar] [CrossRef]
- Wang, H.; Guo, L.J. Experimental investigation on pressure drop and heat transfer in metal foam filled tubes under convective boundary condition. Chem. Eng. Sci. 2016, 155, 438–448. [Google Scholar] [CrossRef]
- Yang, H.Z.; Li, Y.Y.; Yang, Y.; Chen, D.; Zhu, Y.G. Effective thermal conductivity of high porosity open-cell metal foams. Int. J. Heat Mass Transf. 2020, 147, 118974. [Google Scholar] [CrossRef]
- Sun, M.R.; Hu, C.Z.; Zha, L.G.; Xie, Z.Y.; Yang, L.; Tang, D.W.; Song, Y.C.; Zhao, J.F. Pore-scale simulation of forced convection heat transfer under turbulent conditions in open-cell metal foam. Chem. Eng. J. 2020, 389, 124427. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, G.H.; Chen, Z.Q.; Dang, C.B. Experimental study of flow condensation heat transfer in tubes partially filled with hydrophobic annular metal foam. Int. J. Heat Mass Transf. 2019, 136, 1265–1272. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Gu, M.W.; Peng, D.H. Heat transfer performance analysis of a solar flat-plate collector with an integrated metal foam porous structure filled with paraffin. Appl. Therm. Eng. 2010, 30, 1967–1973. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Du, Y.P.; Shum, C.; Cai, B.Y.; Le, N.C.H.; Chen, X.; Duck, B.; Fell, C.; Zhu, Y.G.; Gu, M. Efficiently-cooled plasmonic amorphous silicon solar cells integrated with a nano-coated heat-pipe plate. Sci. Rep. 2016, 6, 24972. [Google Scholar] [CrossRef]
- Wang, B.; Cao, B.; Wang, C.; Zhang, Y.; Yao, H.f.; Wang, Y.Q. The Optical and Electrical Performance of CuO Synthesized by Anodic Oxidation Based on Copper Foam. Material 2020, 13, 5411. [Google Scholar] [CrossRef]
- Chen, S.; Bourham, M.; Rabiei, A. Applications of open-cell and closed-cell metal foams for radiation shielding. Procedia Mater. Sci. 2014, 4, 293–298. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer: New York, NY, USA, 1991. [Google Scholar]
- Gorman, J.M.; Zheng, A.; Sparrow, E.M. Bounding wall effects on fluid flow and pressure drop through packed beds of spheres. Chem. Eng. J. 2019, 373, 519–530. [Google Scholar] [CrossRef]
- Calmidi, V.V. Transport Phenomena in High Porosity Metal Foams. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1998. [Google Scholar]
- Zhao, C.Y.; Kim, T.; Lu, T.J.; Hodson, H.P. Thermal Transport in High Porosity Cellular Metal Foams. J. Thermophys. Heat Transf. 2004, 18, 309–317. [Google Scholar] [CrossRef]
- Dyga, R.; Płaczek, M. Influence of Hydrodynamic Conditions on the Type and Area of Occurrence of Gas–Liquid Flow Patterns in the Flow through Open–Cell Foams. Materials 2020, 13, 3254. [Google Scholar] [CrossRef]
- Hutter, C.; Buchi, D.; Zuber, V.; Rohr, P. Heat transfer in metal foams and designed porous media. Chem. Eng. Sci. 2011, 66, 3806–3814. [Google Scholar] [CrossRef]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and Numerical Study of Free-Surface Flows in a Corrugated Pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef]
- Calomino, F.; Tafarojnoruz, A.; De Marchis, M.; Gaudio, R.; Napoli, E. Experimental and Numerical Study on the Flow Field and Friction Factor in a Pressurized Corrugated Pipe. J. Hydraul. Eng. 2015, 141, 04015027. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 2nd ed.; Springer: New York, NY, USA, 1992. [Google Scholar]
- Vafai, K.; Tien, C.L. Boundary and inertia effects on flow and heat transfer in porous media. Int. J. Heat Mass Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Liu, J.F.; Wu, W.T.; Chiu, W.C.; Hsieh, W.H. Measurement and correlation of friction characteristic of flow through foam matrixes. Exp. Therm. Fluid Sci. 2006, 30, 329–336. [Google Scholar] [CrossRef]
- Scheidegger, A.E. The Physics of Flows through Porous Media, 3rd ed.; University of Toronto Press: Toronto, ON, USA, 1974. [Google Scholar]
- Kaviany, M. Principles of Heat Transfer in Porous Media, 2nd ed.; Springer: New York, NY, USA, 1995. [Google Scholar]
- Macdonald, I.F.; Sayed, M.S.; Mow, K.; Dullien, F.A.L. Flow through porous media: The Ergun equation revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Fand, R.M.; Kim, B.Y.K.; Lam, A.C.C.; Phan, R.T. Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres. J. Fluids Eng. 1987, 109, 268–274. [Google Scholar] [CrossRef]
- Kececioglu, I.; Jiang, Y. Flow through porous media of packed spheres saturated with water. J. Fluids Eng. 1994, 116, 164–170. [Google Scholar] [CrossRef]
- Seguin, D.; Montillet, A.; Comiti, J. Experimental characterization of flow regimes in various porous media—I: Limit of laminar flow regime. Chem. Eng. Sci. 1998, 53, 3751–3761. [Google Scholar] [CrossRef]
- Skjetne, E.; Auriault, J.L. High-velocity laminar and turbulent flow in porous media. Transp. Porous Media 1999, 36, 131–147. [Google Scholar] [CrossRef]
- Bağcı, Ö.; Dukhan, N. Experimental hydrodynamics of high-porosity metal foam: Effect of pore density. Int. J. Heat Mass Transf. 2016, 103, 879–885. [Google Scholar] [CrossRef]
- Dukhan, N.; Bağcı, Ö.; Özdemir, M. Metal foam hydrodynamics: Flow regimes from pre-Darcy to turbulent. Int. J. Heat Mass Transf. 2014, 77, 114–123. [Google Scholar] [CrossRef]
- Bonnet, J.B.; Topin, F.; Tadrist, L. Flow laws in metal foams: Compressibility and pore size effects. Transp. Porous Media 2008, 73, 233–254. [Google Scholar] [CrossRef]
- Geertsma, J. Estimating the coefficient of inertial resistance in fluid flow through porous media. Soc. Pet. Eng. J. 1974, 10, 445–450. [Google Scholar] [CrossRef]
- Richardson, J.T.; Peng, Y.; Remue, D. Properties of ceramic foam catalyst supports: Pressure drop. Appl. Catal. Gen. 2000, 204, 19–32. [Google Scholar] [CrossRef]
- Cunsolo, S.; Oliviero, M.; Harris, W.M.; Andreozzi, A.; Bianco, N.; Chiu, W.K.; Naso, V. Monte Carlo determination of radiative properties of metal foams: Comparison between idealized and real cell structures. Int. J. Therm. Sci. 2015, 87, 94–102. [Google Scholar] [CrossRef]
- Veyhl, C.; Belova, I.; Murch, G.; Fiedler, T. Finite element analysis of the mechanical properties of cellular aluminum based on micro-computed tomography. Mater. Sci. Eng. A Struct. 2011, 528, 4550–4555. [Google Scholar] [CrossRef]
- Jaeger, P.D.; TJoen, C.; Huisseune, H.; Ameel, B.; Paepe, M.D. An experimentally validated and parameterized periodic unit-cell reconstruction of open-cell foams. J. Appl. Phys. 2011, 109, 103519. [Google Scholar] [CrossRef]
- Fourie, J.G.; Du Plessis, J.P. Pressure drop modelling in cellular metallic foams. Chem. Eng. Sci. 2002, 57, 2781–2789. [Google Scholar] [CrossRef]
- Huu, T.T.; Lacroix, M.; Huu, C.P.; Schweich, D.; Edouard, D. Towards a more realistic modeling of solid foam: Use of the pentagonal dodecahedron geometry. Chem. Eng. Sci. 2009, 64, 5131–5142. [Google Scholar] [CrossRef]
- Kumar, P.; Topin, F. Investigation of fluid flow properties in open cell foams: Darcy and weak inertia regimes. Chem. Eng. Sci. 2014, 116, 793–805. [Google Scholar] [CrossRef]
- Krishnan, S.; Murthy, J.Y.; Garimella, S.V. Direct Simulation of Transport in Open-Cell Metal Foams. J. Heat Transf. 2006, 128, 793–799. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Dukhan, N. Correlations for the pressure drop for flow through metal foam. Exp. Fluids 2006, 41, 665–672. [Google Scholar] [CrossRef]
- Tadrist, L.; Miscevic, M.; Rahli, O.; Topin, F. About the use of fibrous materials in compact heat exchangers. Exp. Therm. Fluid Sci. 2004, 28, 193–199. [Google Scholar] [CrossRef]
- Dukhan, N.; Picón-Feliciano, R.; Álvarez-Hernández, Á. Air flow through compressed and uncompressed aluminum foam: Measurements and correlations. J. Fluids Eng. 2006, 128, 1004–1012. [Google Scholar] [CrossRef]
- Du Plessis, P.; Montillet, A.; Comiti, J.; Legrand, J. Pressure drop prediction for flow through high porosity metallic foams. Chem. Eng. Sci. 1994, 49, 3545–3553. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Calmidi, V.; Mahajan, R. Thermophysical properties of high porosity metal foams. Int. J. Heat Mass Transf. 2002, 45, 1017–1031. [Google Scholar] [CrossRef]
- Yang, X.H.; Lu, T.J.; Kim, T. An analytical model for permeability of isotropic porous media. Phys. Lett. A 2014, 378, 2308–2311. [Google Scholar] [CrossRef]
- Kamath, M.P.; Balaji, C.; Venkateshan, S.P. Convection heat transfer from aluminium and copper foams in a vertical channel-An experimental study. Int. J. Therm. Sci. 2013, 64, 1–10. [Google Scholar] [CrossRef]
- Paek, J.W.; Kang, B.H.; Kim, S.Y.; Hyun, J.M. Effective thermal conductivity and permeability of aluminum foam materials. Int. J. Thermophys. 2000, 21, 453–464. [Google Scholar] [CrossRef]
- Noh, N.S.; Lee, K.B.; Lee, C.G. Pressure loss and forced convective heat transfer in an annulus filled with aluminum foam. Int. Commun. Heat Mass Transf. 2006, 33, 434–444. [Google Scholar] [CrossRef]
- Beavers, G.S.; Sparrow, E.M. Non-Darcy Flow through Fibrous Porous Media. J. Appl. Mech. 1969, 36, 711–715. [Google Scholar] [CrossRef]
- Hamaguchi, K.; Takahashi, S.; Miyabe, H. Pressure drop and heat transfer characteristics of regenerator matrix. JSME 1983, 49, 1991–1999. (In Japanese) [Google Scholar]
- Hwang, J.J.; Hwang, G.J.; Yeh, R.H.; Chao, C.H. Measurement of interstitial convective heat transfer and frictional drag for flow across metal foams. J. Heat Transf. 2002, 124, 120–129. [Google Scholar] [CrossRef]
- Dukhan, N.; Patel, P. Equivalent particle diameter and length scale for pressure drop in porous metals. Exp. Therm. Fluid Sci. 2008, 32, 1059–1067. [Google Scholar] [CrossRef]
- Phanikumar, M.S.; Mahajan, R.L. Non-Darcy natural convection in high porosity metal foams. Int. J. Heat Mass Transf. 2002, 45, 3781–3793. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Cavallini, A.; Rossetto, L. Pressure drop during air flow in aluminum foams. Int. J. Heat Mass Transf. 2010, 53, 3121–3130. [Google Scholar] [CrossRef]
- Kim, S.Y.; Paek, J.W.; Kang, B.H. Flow and heat transfer correlations for porous fin in plate-fin heat exchanger. J. Heat Transf. 2000, 122, 572–578. [Google Scholar] [CrossRef]
- Kamath, P.M.; Balaji, C.; Venkateshan, S.P. Heat transfer studies in a vertical channel filled with a porous medium. Tech Sci. Press 2013, 9, 111–126. [Google Scholar]
- Hernández, Á.R.Á. Combined Flow and Heat Transfer Characterization of Open Cell Aluminum Foams. Master’s Thesis, University of Puerto Rico, San Juan, Puerto Rico, 2005. [Google Scholar]
- Hunt, M.L.; Tien, C.L. Effects of thermal dispersion on forced convection in fibrous media. Int. J. Heat Mass Transf. 1988, 31, 301–309. [Google Scholar] [CrossRef]
- Boomsma, K.; Poulikakos, D. The effects of compression and pore size variations on the liquid flow characteristics of metal foams. ASME J. Fluid Eng. 2002, 124, 263–272. [Google Scholar] [CrossRef]







| References | Unit Cell | Geometric Relationships | Comments |
|---|---|---|---|
| Fourie and Du Plessis [43] |  Cubic | , , and | Requires the porosity ε and pore diameter dp as the inputs, and tortuosity χ is the important variable |
| Huu et al. [44] |  Dodecahedron | , , , , , and | For equilateral triangular struts and very high porosity, requires the porosity ε and strut diameter ds (or pore diameter a) as the inputs, and Φ is cell diameter, c is side of the perfect pentagon length and ls is strut length |
| Kumar and Topin [45] | 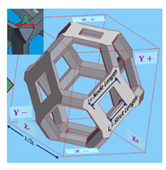 tetrakaidecahedron | ,
, , and | For equilateral triangular struts and porosity in the range of 80–95%, requires the porosity ε and side length of strut A (or strut length Ls) as the inputs, and L is node length, Vligament is the volume of the ligament and Vnode is the volume of the node |
| Krishnan et al. [46] |  body-centered-cubic | , , , and | Porosity higher than 94%, requires the porosity ε and the unit cell length a (or radius of sphere R) as the inputs, and Ain,f is inlet face area, Vint is the intersection volume between two overlapping spheres and Vsc is the volume occupied by the spherical cap |
| Reference | Expression | Comments |
|---|---|---|
| Dukhan [48] | , | c1, c2, c3, and c4 are curve-fit constants that depend on the type of foam. |
| Richardson et al. [39] | , , where , and | Requires the porosity ε and pore diameter dp as the inputs. |
| Tadrist et al. [49] | , | A =100–865, B = 0.65–2.6. However, it is unclear how the final values of A and B are selected. |
| Dukhan et al. [50] | , | Applicable to uncompressed foam, requires the porosity ε and strut diameter df as the inputs. |
| Du Plessis et al. [51] | , , where , and | Developed based on cubic model, requires the porosity ε and pore diameter dp as the inputs. |
| Fouriea and Du Plessis [43] | where ,
, | Developed based on cubic model, requires the porosity ε, pore diameter dp, and pore velocity up as the inputs. |
| Bhattacharya et al. [52] | , where , , (0.85 < ε < 0.97) and G=0.5831 (ε ≥ 0.97) | Only requires the porosity ε as the input. |
| Calmidi [19] | , , where and | Requires the porosity ε and pore diameter dp (or strut diameter df ) as the inputs. |
| Yang et al. [53] | , where , | Requires the porosity ε and pore diameter dp as the inputs, applicable for porosity ε = 55–98% and pore density between 5–100 PPI. |
| Reference | Expression | Comments |
|---|---|---|
| Kamath et al. [54] | , where , | cF = 0.129 for Al; cF = 0.147 for Cu |
| Hwang et al. [59] | , where , | Only valid for 10 PPI, a and b vary for different porosities |
| Dukhan and Petal [60] | where , | Requires the surface area per unit volume as the input, A and B vary with different foam |
| Liu et al. [27] | , , , , , where , , , and | Requires the porosity ε and pore diameter dp as the input, valid for porosity ε ranging from 80.2–95.8% and pore density between 5–65 PPI. |
| Reference | RSM × 107 |
|---|---|
| Richardson et al. [39] | 1.91 |
| Improved Richardson et al. | 1.35 |
| Tadrist et al. [49] | 1.82 |
| Improved Tadrist et al. | 1.27 |
| Dukhan et al. [50] | 2.14 |
| Improved Dukhan et al. | 1.59 |
| Du Plessis et al. [51] | 1.36 |
| Calmidi [19] | 1.37 |
| Yang et al. [53] | 4.58 |
| Proposed Equation (20) | 0.94 |
| Proposed Equation (21) | 1.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Li, Y.; Ma, B.; Zhu, Y. Review and a Theoretical Approach on Pressure Drop Correlations of Flow through Open-Cell Metal Foam. Materials 2021, 14, 3153. https://doi.org/10.3390/ma14123153
Yang H, Li Y, Ma B, Zhu Y. Review and a Theoretical Approach on Pressure Drop Correlations of Flow through Open-Cell Metal Foam. Materials. 2021; 14(12):3153. https://doi.org/10.3390/ma14123153
Chicago/Turabian StyleYang, Huizhu, Yongyao Li, Binjian Ma, and Yonggang Zhu. 2021. "Review and a Theoretical Approach on Pressure Drop Correlations of Flow through Open-Cell Metal Foam" Materials 14, no. 12: 3153. https://doi.org/10.3390/ma14123153
APA StyleYang, H., Li, Y., Ma, B., & Zhu, Y. (2021). Review and a Theoretical Approach on Pressure Drop Correlations of Flow through Open-Cell Metal Foam. Materials, 14(12), 3153. https://doi.org/10.3390/ma14123153









