The Influence of Background Ultrasonic Field on the Strength of Adhesive Zones under Dynamic Impact Loads
Abstract
:1. Introduction
2. Delamination Criterion
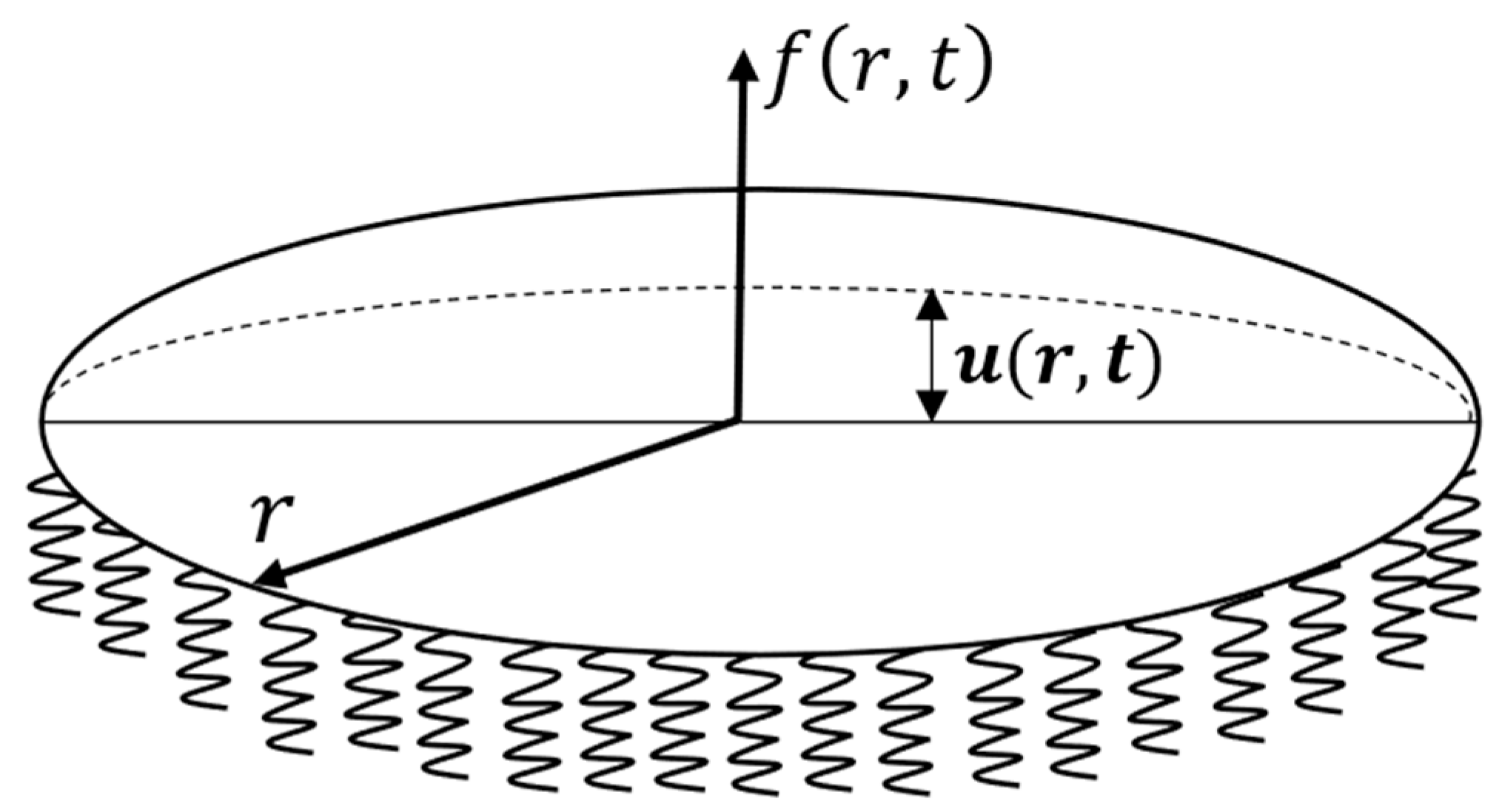
3. Membrane Approximation
3.1. Constant Load
3.2. Pulse Load
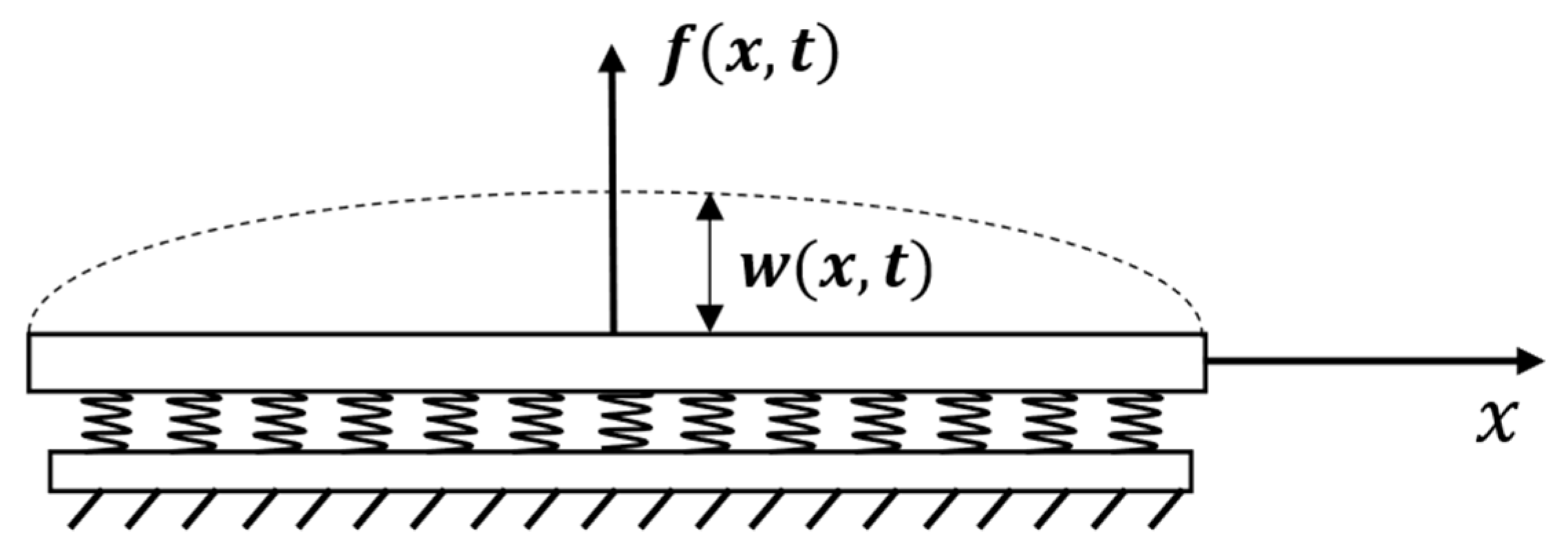
4. Beam Approximation
- Hinged ends of the beam:
- Clamped ends of the beam:
- Beam with free ends:
4.1. Constant Load
4.2. Pulse Load
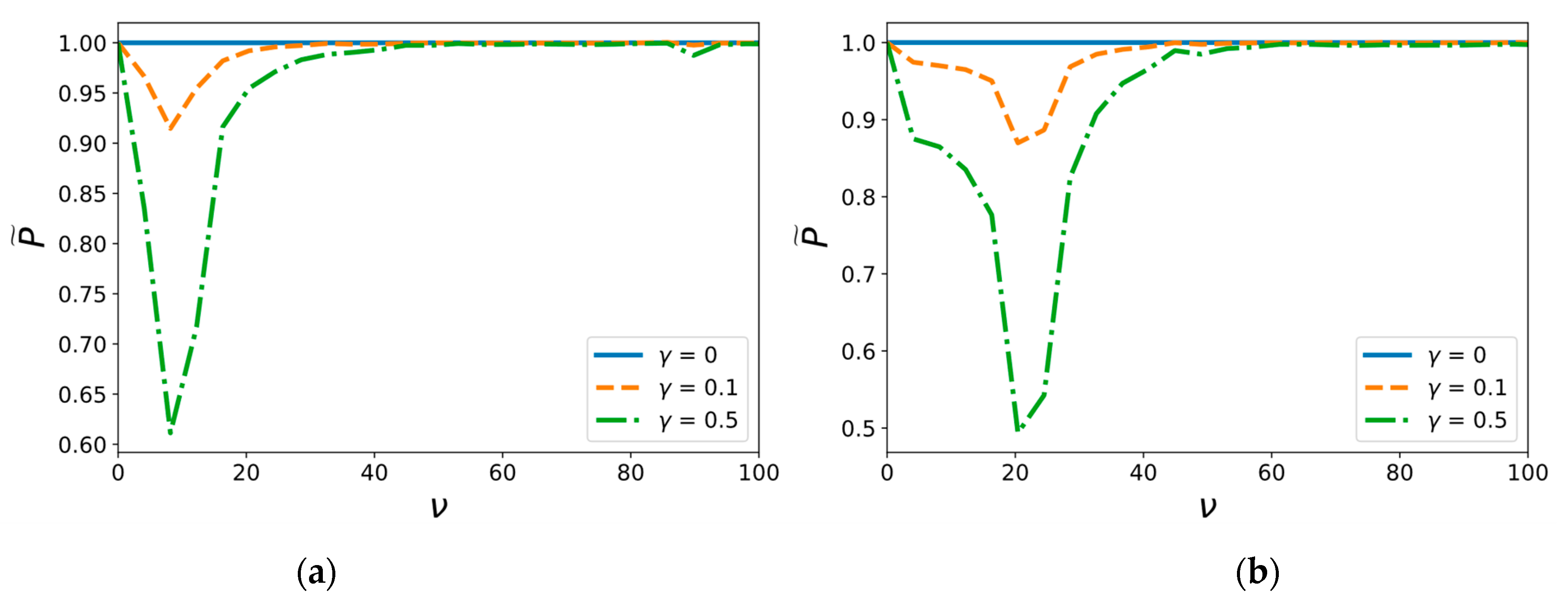
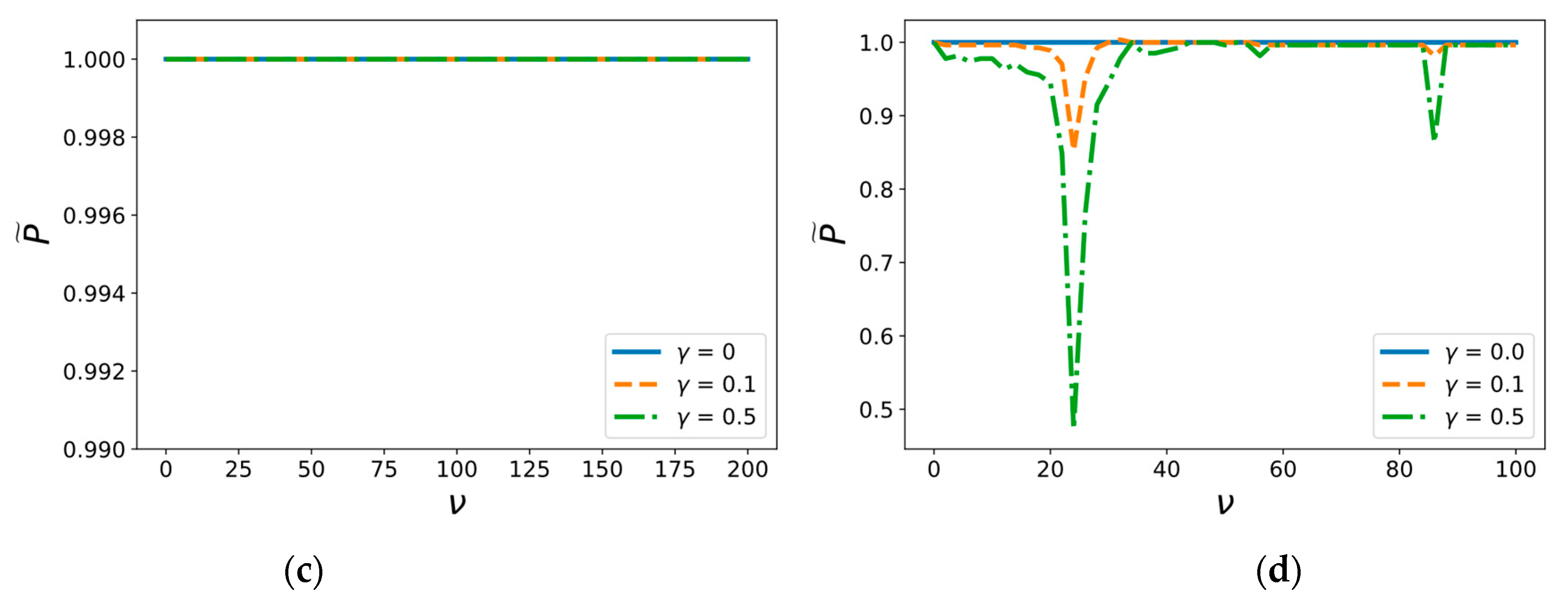
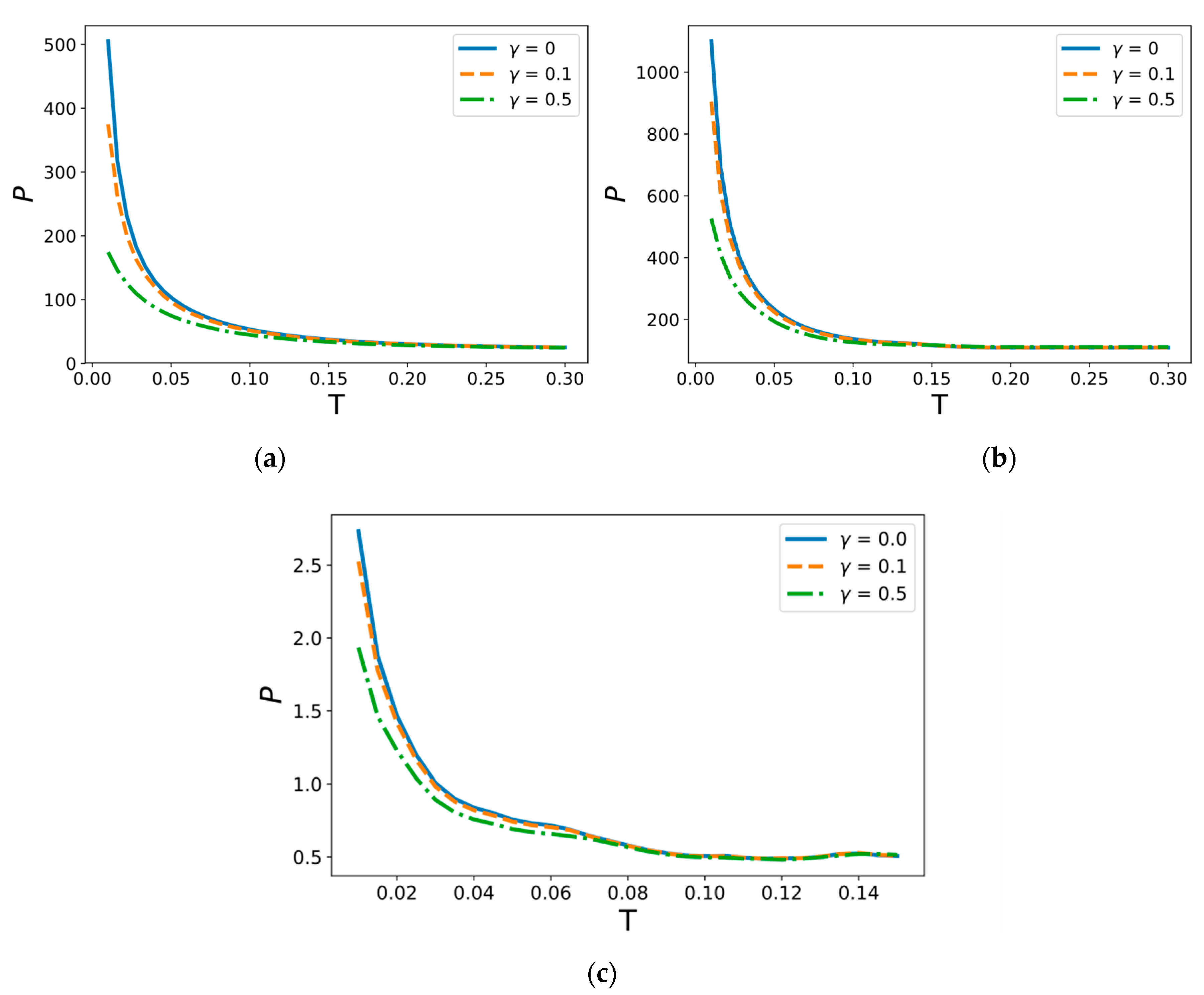
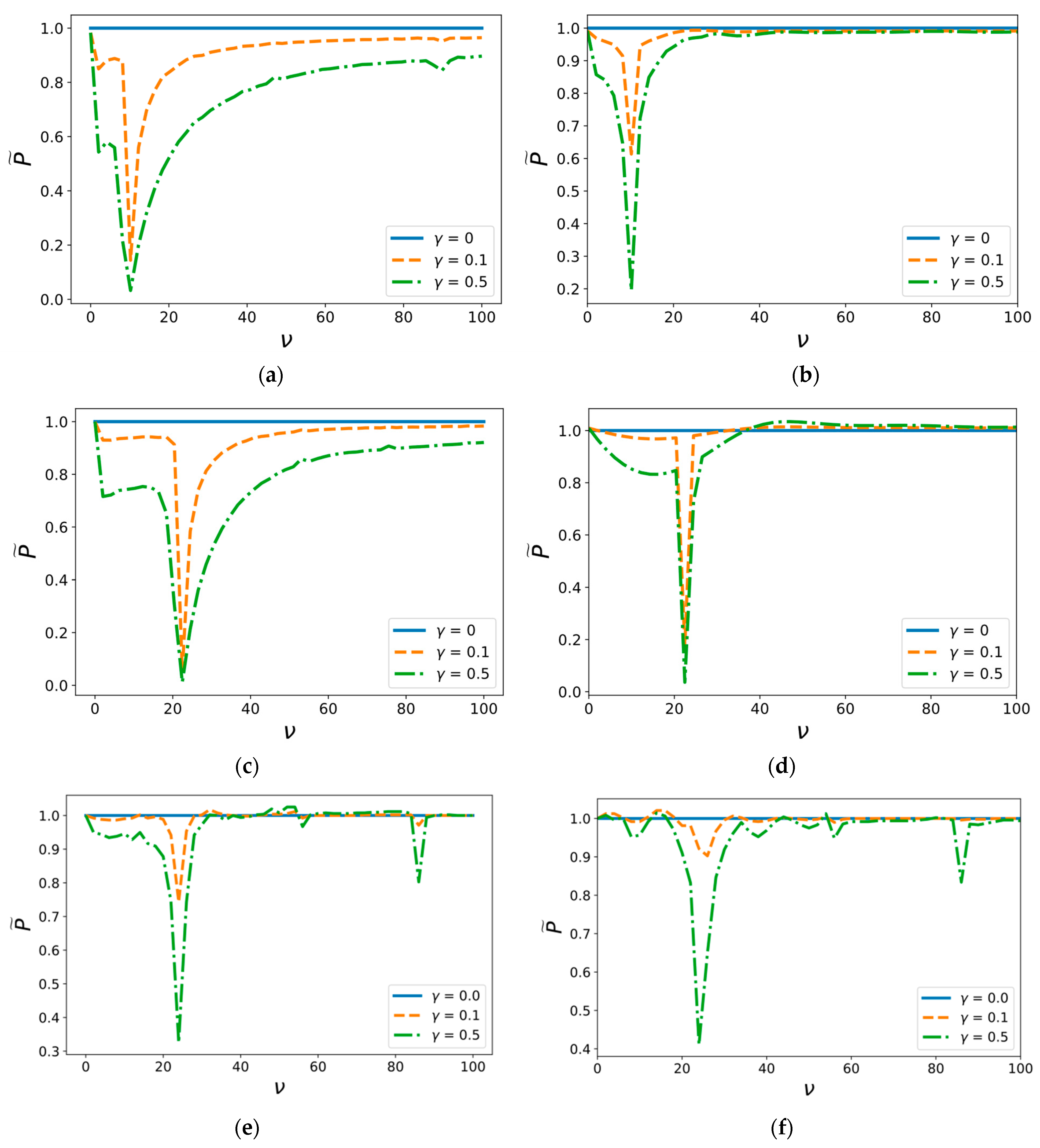
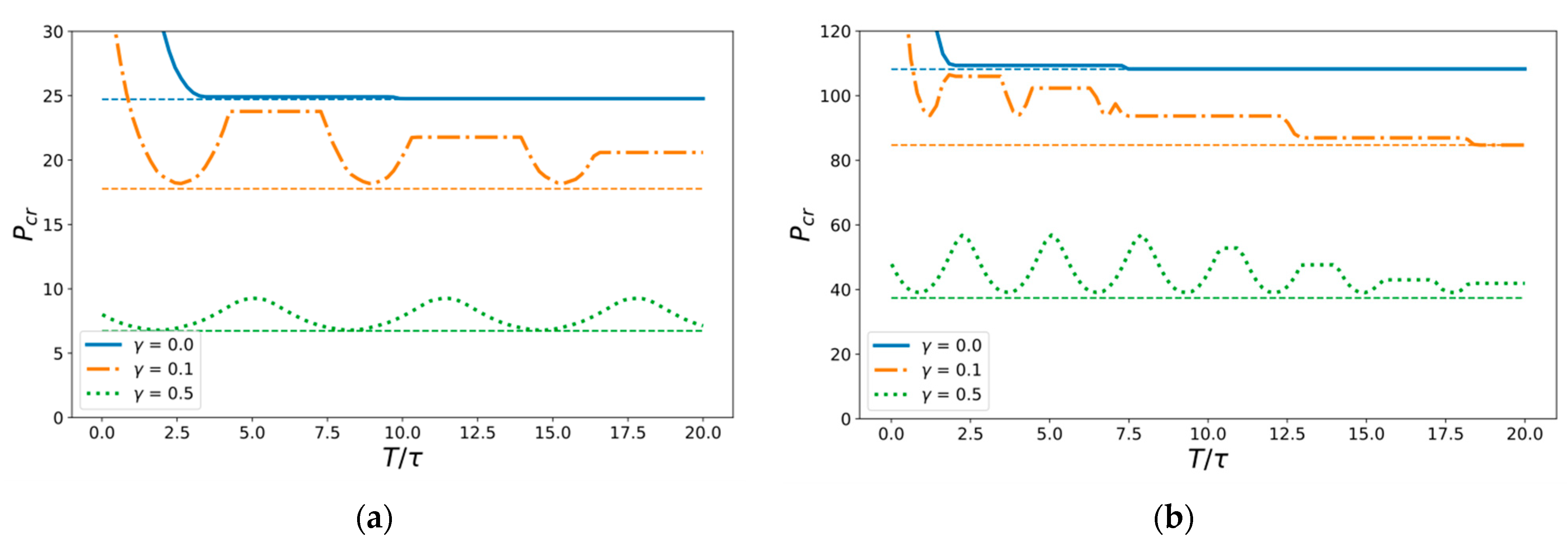
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Solution to the Problem Using the Fourier Method
Appendix A.2. Calculation of the Green Function
Appendix A.3. Solution for the Beam Model
| Condition | ||
|---|---|---|
| Hinged beam | ||
| Clamped beam | Roots of | |
| Free ends | Roots of |
Nomenclature
| [-] | zeros of the zero-order Bessel function | |
| [] | wave velocity | |
| [-] | relative intensity of the background vibration field | |
| [-] | Dirac delta function | |
| [Pa] | Young’s modulus | |
| [] | external force | |
| [-] | Green’s function | |
| [-] | Heaviside step function | |
| [] | area moment of inertia | |
| [-] | zero-order and first-order Bessel function | |
| [Pa] | modulus elastic foundation | |
| [-] | Krylov’s functions | |
| [m] | beam length | |
| [] | frequency of the background vibration field | |
| [-] | concentrated constant force | |
| [-] | relative critical force | |
| [m] | radius of the circular membrane | |
| [m2] | cross-sectional area | |
| [kg/m3] | density | |
| [s] | pulse duration | |
| [s] | upper border of the considered time period | |
| [s] | incubation time | |
| [m] | displacement | |
| [m] | displacement limit under quasistatic loading | |
| [m] | vertical deflection of the beam | |
| ω | [] | characteristic of the elastic foundation rigidity |
| [] | critical frequencies |
References
- Eisenhaure, J.; Kim, S. A review of the state of dry adhesives: Biomimetic structures and the alternative designs they inspire. Micromachines 2017, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Kasar, A.K.; Ramachandran, R.; Menezes, P.L. Natural Adhesion System Leads to Synthetic Adhesives. J. Bio- Tribo-Corros. 2018, 4, 1–17. [Google Scholar] [CrossRef]
- Li, X.; Tao, D.; Lu, H.; Bai, P.; Liu, Z.; Ma, L.; Meng, Y.; Tian, Y. Recent developments in gecko-inspired dry adhesive surfaces from fabrication to application. Surf. Topogr. Metrol. Prop. 2019, 7. [Google Scholar] [CrossRef]
- Hu, S.; Xia, Z.; Dai, L. Advanced gecko-foot-mimetic dry adhesives based on carbon nanotubes. Nanoscale 2013, 5, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Autumn, K. Frictional adhesion: A new angle on gecko attachment. J. Exp. Biol. 2006, 209, 3569–3579. [Google Scholar] [CrossRef] [Green Version]
- Parness, A.; Soto, D.; Esparza, N.; Gravish, N.; Wilkinson, M.; Autumn, K.; Cutkosky, M. A microfabricated wedge-shaped adhesive array displaying gecko-like dynamic adhesion, directionality and long lifetime. J. R. Soc. Interface 2009, 6, 1223–1232. [Google Scholar] [CrossRef] [Green Version]
- Shui, L.; Jia, L.; Li, H.; Guo, J.; Guo, Z.; Liu, Y.; Liu, Z.; Chen, X. Rapid and continuous regulating adhesion strength by mechanical micro-vibration. Nat. Commun. 2020, 11. [Google Scholar] [CrossRef]
- Loh, O.Y.; Espinosa, H.D. Nanoelectromechanical contact switches. Nat. Nanotechnol. 2012, 7, 283–295. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y. A precise model for the shape of an adhered microcantilever. Sens. Actuators A Phys. 2011, 171, 381–390. [Google Scholar] [CrossRef] [Green Version]
- Volkov, G.A.; Petrov, Y.V.; Gruzdkov, A.A. Acoustic strength of water and effect of ultrasound on the liquid-vapor phase diagram. Tech. Phys. 2015, 60, 753–756. [Google Scholar] [CrossRef]
- Herbert, E.; Balibar, S.; Caupin, F. Cavitation pressure in water. Phys. Rev. E 2006, 74, 041603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volkov, G.A.; Bratov, V.A.; Gruzdkov, A.A.; Babitsky, V.I.; Petrov, Y.V.; Silberschmidt, V.V. Energy-based analysis of ultrasonically assisted turning. Shock Vib. 2011, 18, 333–341. [Google Scholar] [CrossRef]
- Bai, W.; Roy, A.; Guo, L.; Xu, J.; Silberschmidt, V.V. Analytical prediction of shear angle and frictional behaviour in vibration-assisted cutting. J. Manuf. Process. 2021, 62, 37–46. [Google Scholar] [CrossRef]
- Gorbushin, N.; Petrov, Y.; Zhao, Y.-P.; Zhang, Y. Threshold characteristics of short-pulsed loads combined with the ultrasound field causing dynamic delamination of adhesive joints. Theor. Appl. Mech. Lett. 2018, 8, 28–31. [Google Scholar] [CrossRef]
- Dillard, D.A.; Mukherjee, B.; Karnal, P.; Batra, R.C.; Frechette, J. A review of Winkler’s foundation and its profound influence on adhesion and soft matter applications. Soft Matter 2018, 14, 3669–3683. [Google Scholar] [CrossRef]
- Godara, R.K.; Joglekar, M.M. Suppression of contact bounce in beam-type microelectromechanical switches using a feedforward control scheme. JVC/J. Vib. Control 2018, 24, 5502–5513. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Tavallaeinejad, M. Stability and nonlinear dynamical analysis of functionally graded microplates. Microsyst. Technol. 2018, 24, 2109–2121. [Google Scholar] [CrossRef]
- Darvishvand, A.; Zajkani, A. A new model for permanent flexural deflection of cantilever MEMS actuator by conventional mechanism-based strain gradient plasticity framework. Microsyst. Technol. 2019, 25, 4277–4289. [Google Scholar] [CrossRef]
- Więckowski, Z.; Świątkiewicz, P. Stress-Based FEM in the Problem of Bending of Euler–Bernoulli and Timoshenko Beams Resting on Elastic Foundation. Materials 2021, 14, 460. [Google Scholar] [CrossRef]
- Panettieri, E.; Fanteria, D.; Danzi, F. Delaminations growth in compression after impact test simulations: Influence of cohesive elements parameters on numerical results. Compos. Struct. 2016, 137, 140–147. [Google Scholar] [CrossRef]
- Liu, P.F.; Gu, Z.P.; Peng, X.Q.; Zheng, J.Y. Finite element analysis of the influence of cohesive law parameters on the multiple delamination behaviors of composites under compression. Compos. Struct. 2015, 131, 975–986. [Google Scholar] [CrossRef]
- Rozylo, P. Experimental-numerical study into the stability and failure of compressed thin-walled composite profiles using progressive failure analysis and cohesive zone model. Compos. Struct. 2021, 257, 113303. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Morozov, N.F. On the Modeling of Fracture of Brittle Solids. J. Appl. Mech. 1994, 61, 710–712. [Google Scholar] [CrossRef]
- Bragov, A.M.; Karihaloo, B.L.; Petrov, Y.V.; Konstantinov, A.Y.; Lamzin, D.A.; Lomunov, A.K.; Smirnov, I.V. High-rate deformation and fracture of fiber reinforced concrete. J. Appl. Mech. Tech. Phys. 2012, 53, 926–933. [Google Scholar] [CrossRef]
- Ou, Z.-C.; Duan, Z.-P.; Huang, F.-L. Analytical approach to the strain rate effect on the dynamic tensile strength of brittle materials. Int. J. Impact Eng. 2010, 37, 942–945. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Smirnov, I.V.; Volkov, G.A.; Abramian, A.K.; Bragov, A.M.; Verichev, S.N. Dynamic failure of dry and fully saturated limestone samples based on incubation time concept. J. Rock Mech. Geotech. Eng. 2017, 9, 125–134. [Google Scholar] [CrossRef]
- Gorbushin, N.; Vitucci, G.; Volkov, G.; Mishuris, G. Influence of fracture criteria on dynamic fracture propagation in a discrete chain. Int. J. Fract. 2018, 209, 131–142. [Google Scholar] [CrossRef] [Green Version]
- Shockey, D.A.; Erlich, D.C.; Kalthoff, J.F.; Homma, H. Short-pulse fracture mechanics. Eng. Fract. Mech. 1986, 23, 311–319. [Google Scholar] [CrossRef]
- Kimberley, J.; Ramesh, K.T.; Daphalapurkar, N.P. A scaling law for the dynamic strength of brittle solids. Acta Mater. 2013, 61, 3509–3521. [Google Scholar] [CrossRef]
- Cadoni, E.; Forni, D.; Bonnet, E.; Dobrusky, S. Experimental study on direct tensile behaviour of UHPFRC under high strain-rates. Constr. Build. Mater. 2019, 218, 667–680. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations; A CRC Press Company: Boca Raton, FL, USA, 2004; ISBN 1584883553. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volkov, G.; Logachev, A.; Granichin, N.; Zhao, Y.-P.; Zhang, Y.; Petrov, Y. The Influence of Background Ultrasonic Field on the Strength of Adhesive Zones under Dynamic Impact Loads. Materials 2021, 14, 3188. https://doi.org/10.3390/ma14123188
Volkov G, Logachev A, Granichin N, Zhao Y-P, Zhang Y, Petrov Y. The Influence of Background Ultrasonic Field on the Strength of Adhesive Zones under Dynamic Impact Loads. Materials. 2021; 14(12):3188. https://doi.org/10.3390/ma14123188
Chicago/Turabian StyleVolkov, Grigory, Andrey Logachev, Nikolai Granichin, Ya-Pu Zhao, Yin Zhang, and Yuri Petrov. 2021. "The Influence of Background Ultrasonic Field on the Strength of Adhesive Zones under Dynamic Impact Loads" Materials 14, no. 12: 3188. https://doi.org/10.3390/ma14123188






