Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses
Abstract
:1. Introduction
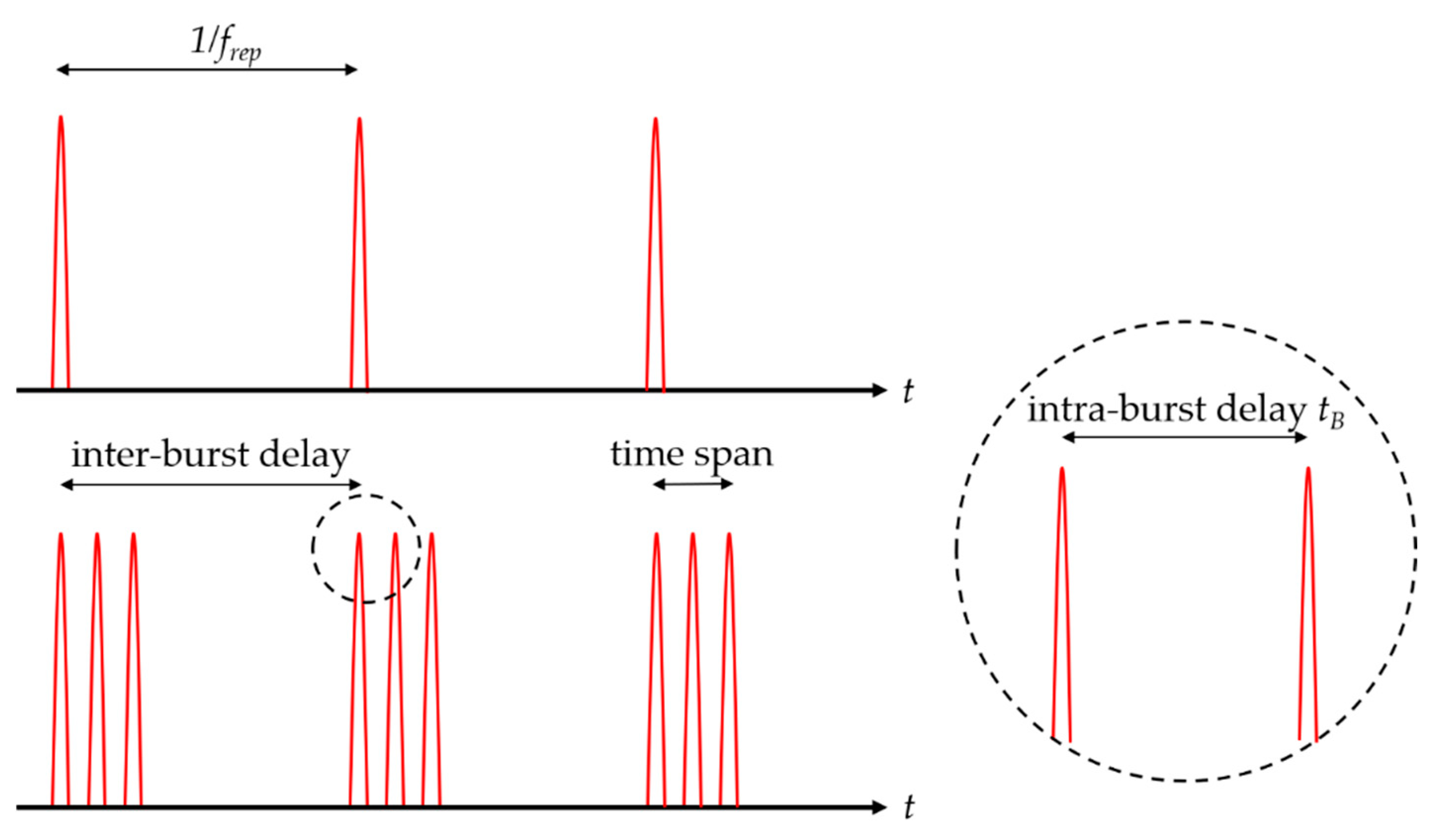
Processing Strategies and Definitions
2. Physics of Ultra-Short Burst Pulse Ablation of Metals
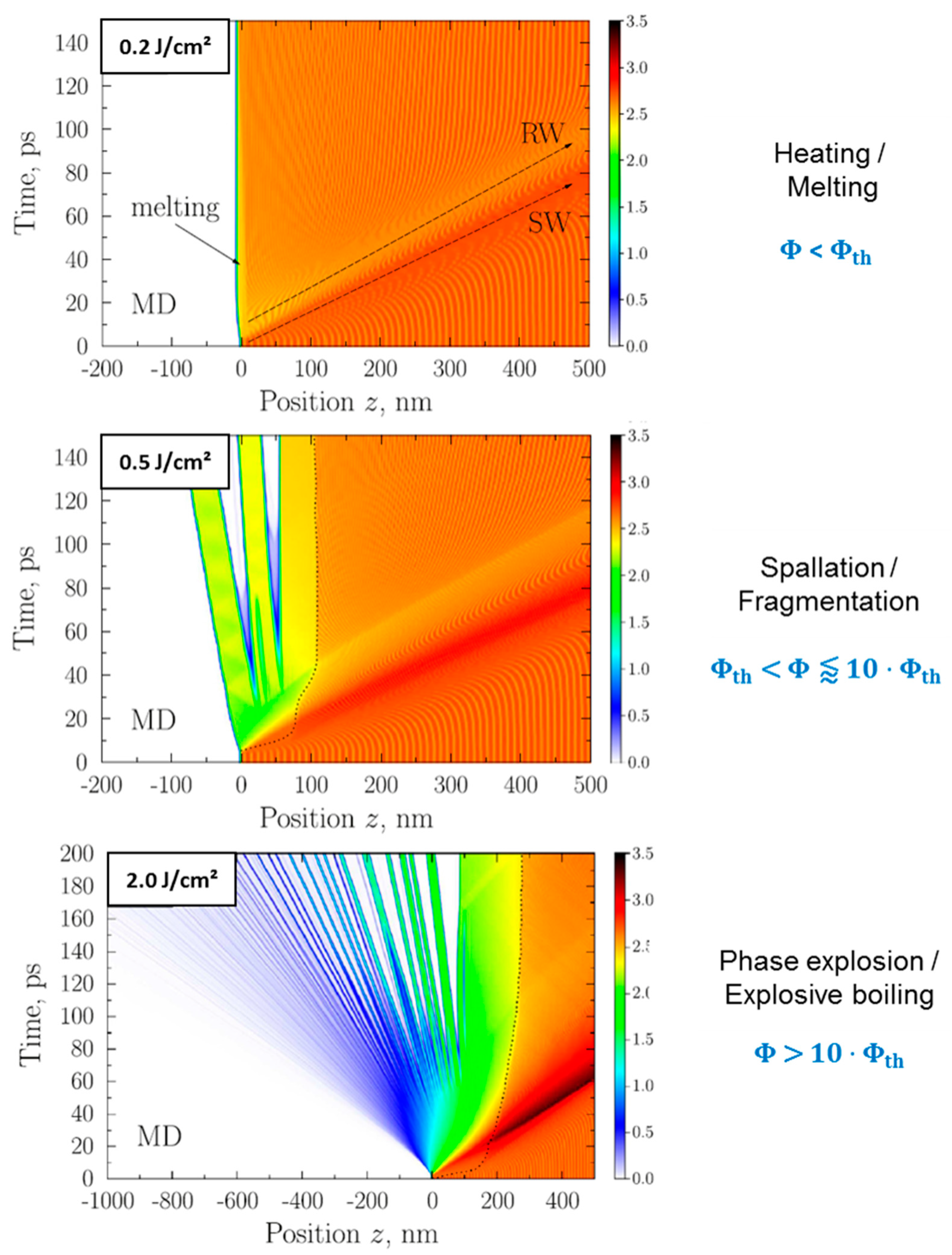
2.1. Single Pulse Laser Ablation
- heating of the metal surface;
- melting of the metal surface;
- spallation of surface layers (rupture of material when the fluence is above the ablation threshold);
- phase explosion (explosive boiling of the surface with the generation of vapor and plasma).
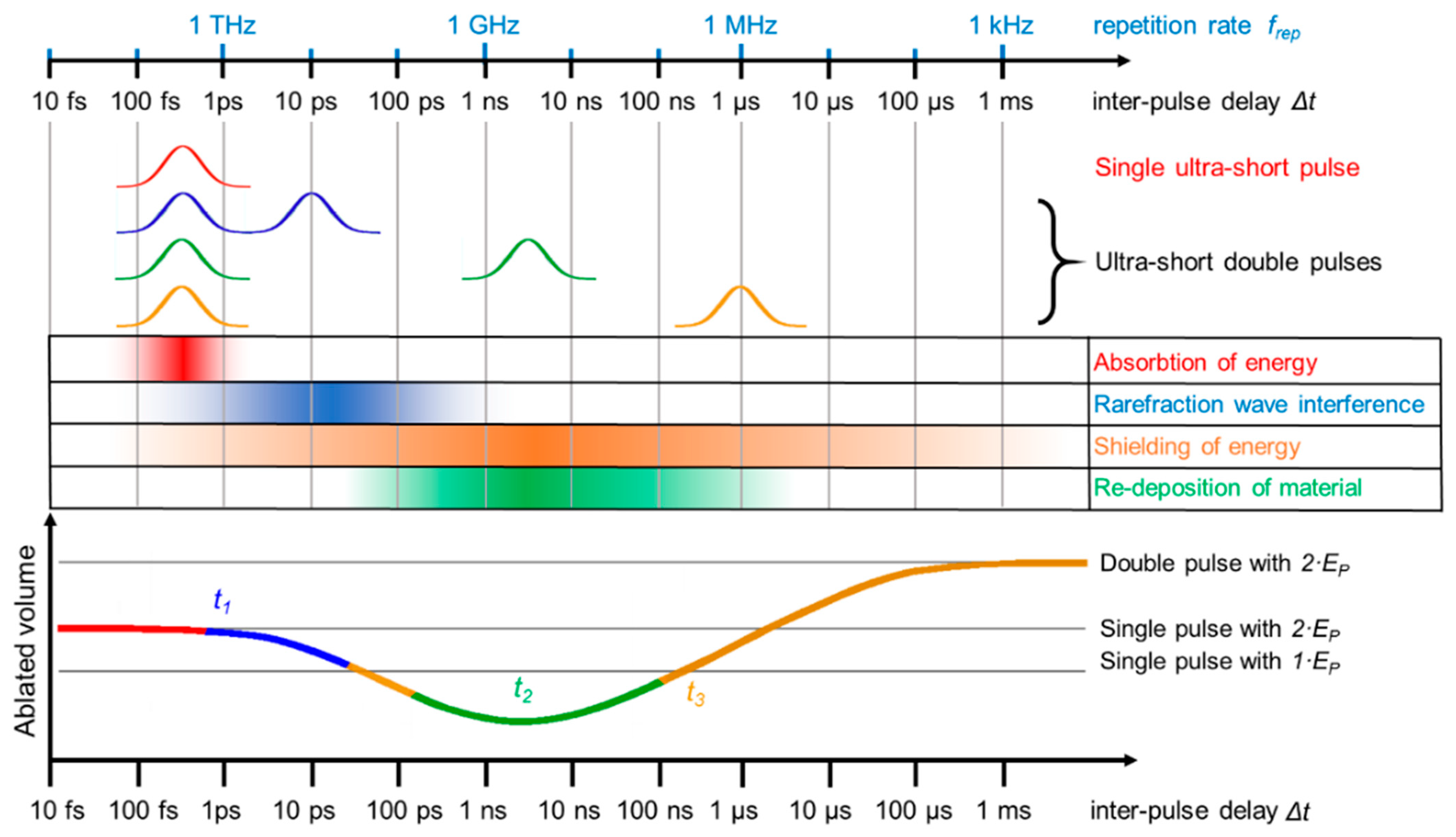
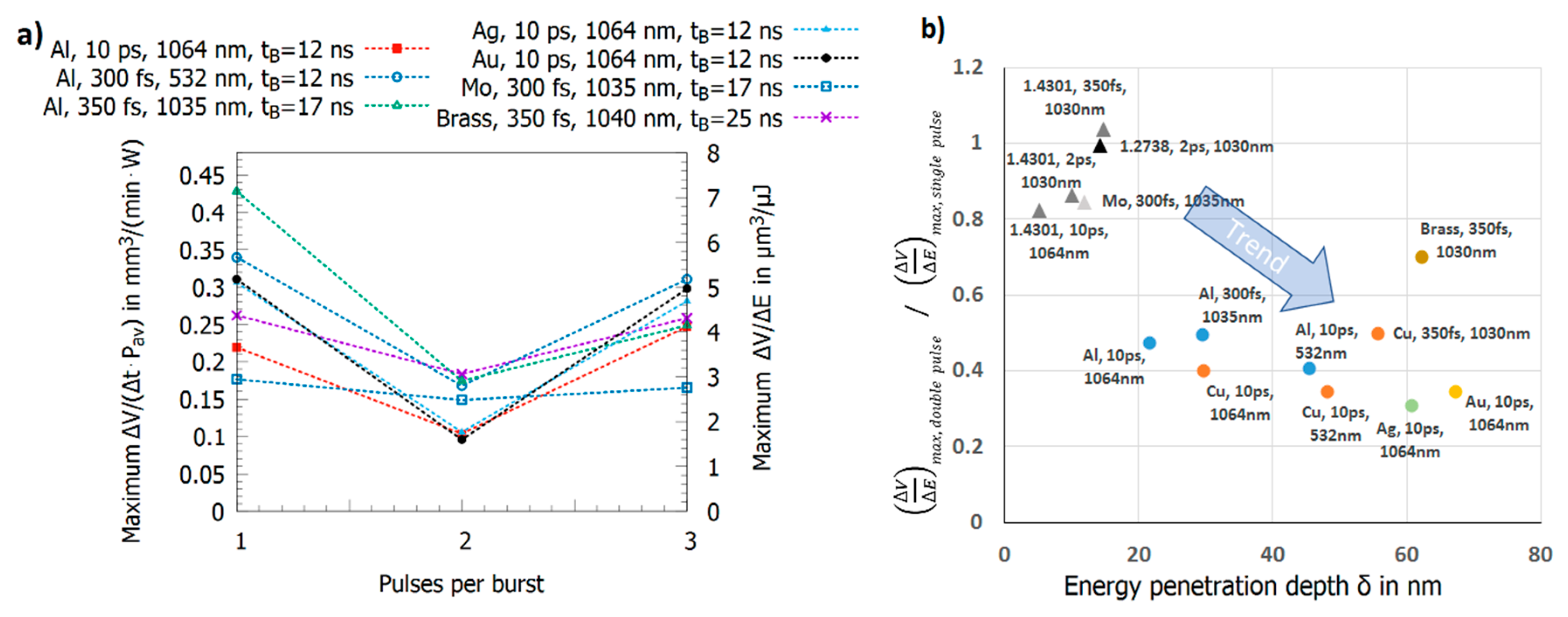
2.2. Double Pulses: Pulse-to-Pulse Interaction
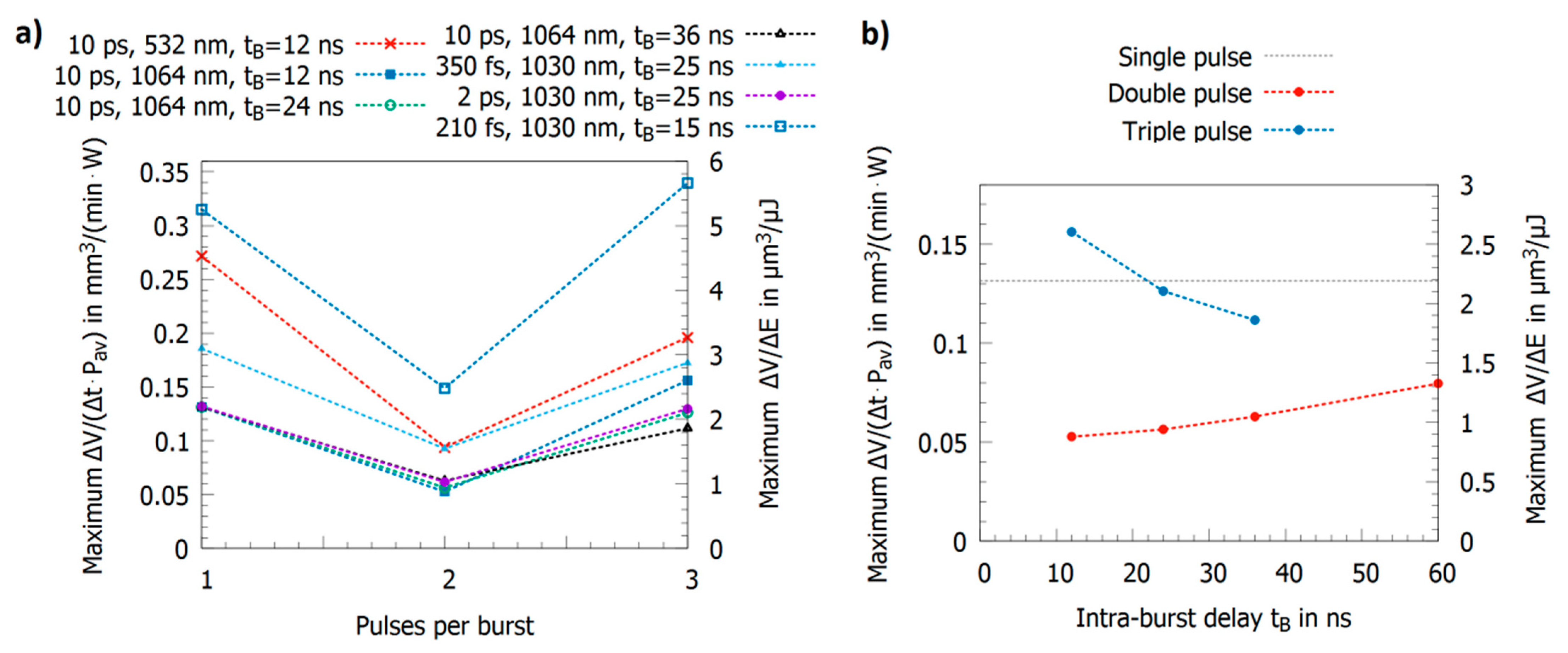
2.3. Triple Pulses with Intra-Burst Delays in the Range of Tens of Nanoseconds
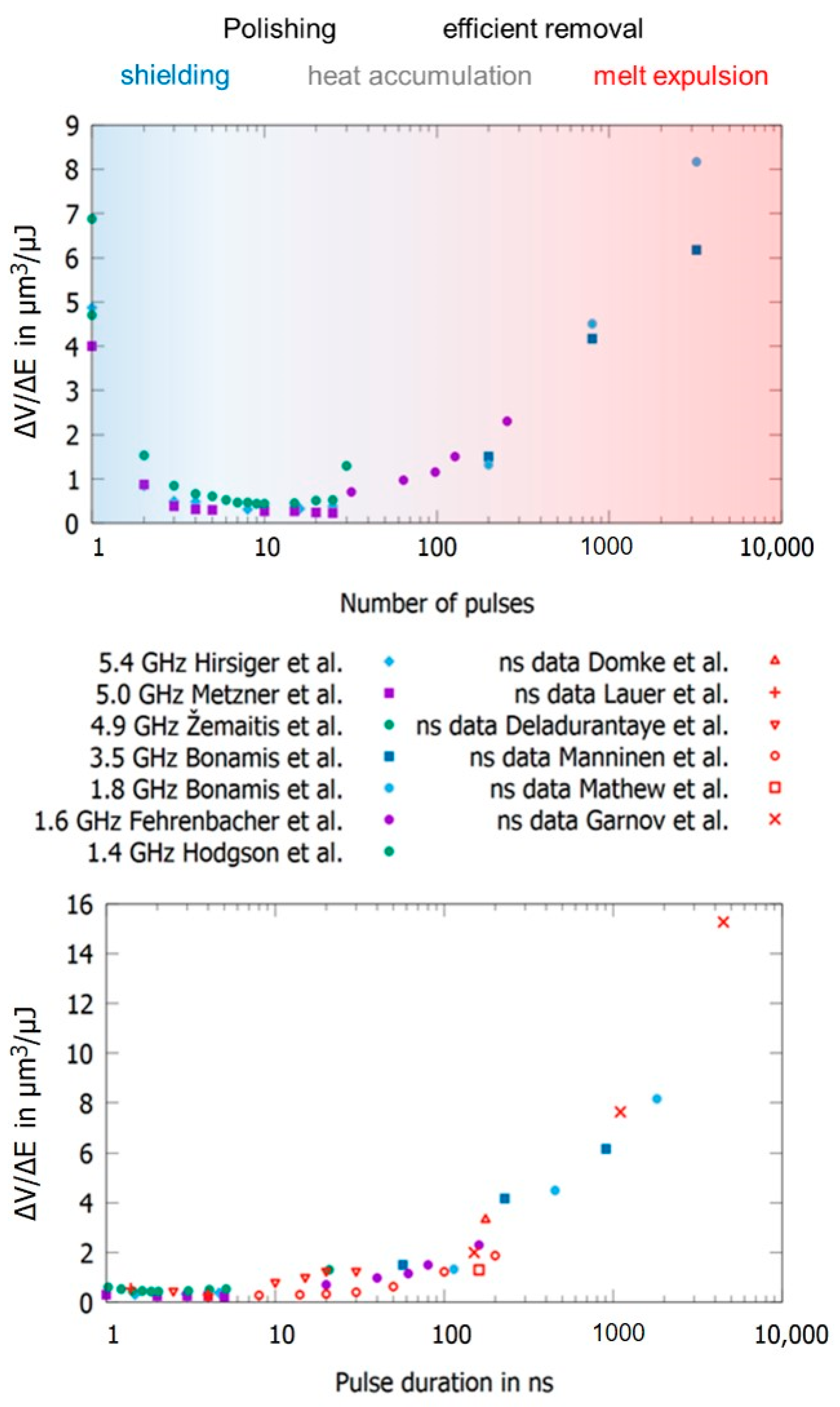
2.4. Multi-Pulse Bursts with Intra-Burst Repetition Rates in the MHz Range
2.5. Multi-Pulse Bursts with Intra-Burst Repetition Rates in the GHz Range
3. Applications Using Burst Pulses
3.1. Punching and Drilling
3.2. Scribing and Cutting
3.3. Surface Structures
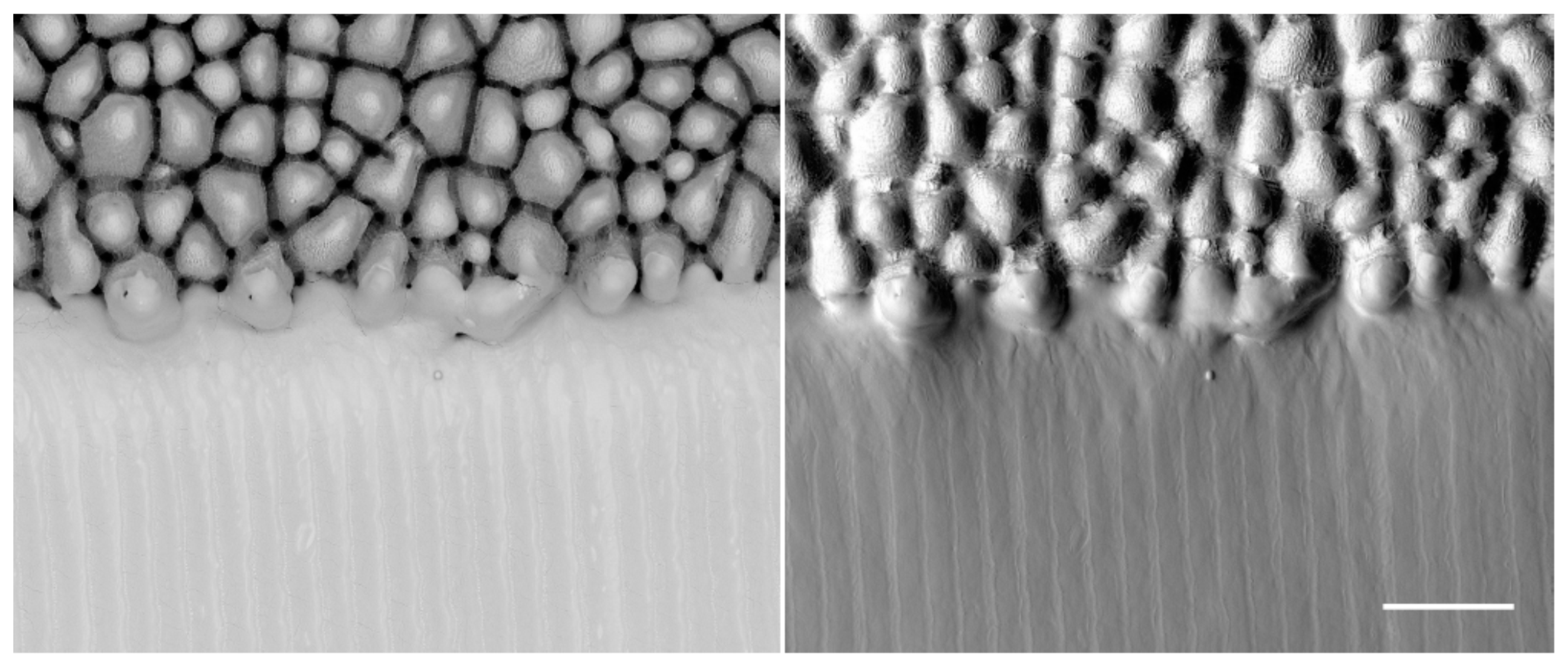
3.3.1. Polishing/Smoothing
3.3.2. Coloring
3.3.3. Laser-Induced Periodic Surface Structures (LIPSS)
3.4. Milling
3.5. Further Applications
3.5.1. Laser-Ablative Space Propulsion
3.5.2. Laser-Induced Breakdown Spectroscopy
3.5.3. Generation of Particle Beams and X-rays
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Negel, J.-P.; Voss, A.; Ahmed, M.A.; Bauer, D.; Sutter, D.; Killi, A.; Graf, T. 11 kW average output power from a thin-disk multipass amplifier for ultrashort laser pulses. Opt. Lett. 2013, 38, 5442–5445. [Google Scholar] [CrossRef] [PubMed]
- Negel, J.-P.; Loescher, A.; Bauer, D.; Sutter, D.; Killi, A.; Ahmed, M.A.; Graf, T. Second Generation Thin-Disk Multipass Amplifier Delivering Picosecond Pulses with 2 kW of Average Output Power. In Advanced Solid State Lasers, Proceedings of the Lasers Congress 2016 (ASSL, LSC, LAC), Boston, MA, USA, 30 October–3 November 2016; The Optical Society of America: Washington, DC, USA, 2016; p. ATu4A.5. [Google Scholar]
- Nubbemeyer, T.; Kaumanns, M.; Ueffing, M.; Gorjan, M.; Alismail, A.; Fattahi, H.; Brons, J.; Pronin, O.; Barros, H.G.; Major, Z.; et al. 1 kW, 200 mJ picosecond thin-disk laser system. Opt. Lett. 2017, 42, 1381–1384. [Google Scholar] [CrossRef] [PubMed]
- Gaida, C.; Gebhardt, M.; Heuermann, T.; Stutzki, F.; Jauregui, C.; Limpert, J. Ultrafast thulium fiber laser system emitting more than 1 kW of average power. Opt. Lett. 2018, 43, 5853–5856. [Google Scholar] [CrossRef]
- Schnitzler, C.; Mans, T.G.; Dolkemeyer, J.; Dittmann, P. High Power, High Energy, and High Flexibility: Powerful Ultrafast Lasers Based on InnoSlab Technology. In High-Power Laser Materials Processing: Applications, Diagnostics, and Systems VIII, Proceedings of the SPIE LASE, 2019, San Francisco, CA, USA, 2–7 February 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; p. 1091103. [Google Scholar]
- Müller, M.; Aleshire, C.; Klenke, A.; Haddad, E.; Légaré, F.; Tünnermann, A.; Limpert, J. 104 kW coherently combined ultrafast fiber laser. Opt. Lett. 2020, 45, 3083–3086. [Google Scholar] [CrossRef] [PubMed]
- Semerok, A.; Dutouquet, C. Ultrashort double pulse laser ablation of metals. Thin Solid Films 2004, 453, 501–505. [Google Scholar] [CrossRef]
- Donnelly, T.; Lunney, J.G.; Amoruso, S.; Bruzzese, R.; Wang, X.; Ni, X. Double pulse ultrafast laser ablation of nickel in vacuum. J. Appl. Phys. 2009, 106, 013304. [Google Scholar] [CrossRef] [Green Version]
- Povarnitsyn, M.E.; Itina, T.E.; Khishchenko, K.V.; Levashov, P.R. Suppression of Ablation in Femtosecond Double-Pulse Experiments. Phys. Rev. Lett. 2009, 103, 195002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Povarnitsyn, M.E.; Fokin, V.B.; Levashov, P.R.; Itina, T.E. Molecular dynamics simulation of subpicosecond double-pulse laser ablation of metals. Phys. Rev. B 2015, 92, 174104. [Google Scholar] [CrossRef]
- Hartmann, C.; Gillner, A.; Aydin, U.; Noll, R.; Fehr, T.; Gehlen, C.; Poprawe, R. Investigation on laser micro ablation of metals using ns-multi-pulses. J. Physics Conf. Ser. 2007, 59, 440–444. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Shin, Y.C.; King, G. Modeling of multi-burst mode pico-second laser ablation for improved material removal rate. Appl. Phys. A 2009, 98, 407–415. [Google Scholar] [CrossRef]
- Hernandez-Rueda, J.; Siegel, J.; Galvan-Sosa, M.; De La Cruz, A.R.; Solis, J. Surface structuring of fused silica with asymmetric femtosecond laser pulse bursts. J. Opt. Soc. Am. B 2013, 30, 1352–1356. [Google Scholar] [CrossRef] [Green Version]
- Neuenschwander, B.; Kramer, T.; Lauer, B.; Jaeggi, B. Burst Mode with Ps- and Fs-Pulses: Influence on the Removal Rate, Surface Quality, and Heat Accumulation. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XX, Proceedings of the SPIE LASE, San Francisco, CA, USA, 9–12 February 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9350, p. 93500U. [Google Scholar]
- Kerse, C.; Kalaycıoglu, H.; Elahi, P.; Cetin, B.; Kesim, D.K.; Akcaalan, O.; Yavas, S.; Asik, M.D.; Oktem, B.; Hoogland, H.; et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 2016, 537, 84–88. [Google Scholar] [CrossRef] [PubMed]
- Jäggi, B.; Förster, D.J.; Weber, R.; Neuenschwander, B. Residual heat during laser ablation of metals with bursts of ultra-short pulses. Adv. Opt. Technol. 2018, 7, 175–182. [Google Scholar] [CrossRef]
- Neuenschwander, B.; Jaeggi, B.; Foerster, D.J.; Kramer, T.; Remund, S. Influence of the burst mode onto the specific removal rate for metals and semiconductors. J. Laser Appl. 2019, 31, 022203. [Google Scholar] [CrossRef]
- Zemaitis, A.; Gecys, P.; Barkauskas, M.; Raciukaitis, G.; Gedvilas, M. Highly-efficient laser ablation of copper by bursts of ultrashort tuneable (fs–ps) pulses. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Bornschlegel, B.; Finger, J. In-Situ Analysis of Ultrashort Pulsed Laser Ablation with Pulse Bursts. JLMN 2019, 14, 88–94. [Google Scholar]
- Gaudiuso, C.; Kämmer, H.; Dreisow, F.; Ancona, A.; Tünnermann, A.; Nolte, S. Ablation of Silicon with Bursts of Femtosecond Laser Pulses. In Frontiers in Ultrafast Optics: Biomedical, Scientific, and Industrial Applications XVI, Proceedings of the SPIE LASE, San Francisco, CA, USA, 13–18 February 2016; Heisterkamp, A., Herman, P.R., Meunier, M., Nolte, S., Eds.; SPIE: Bellingham, WA, USA, 2016; p. 974017. [Google Scholar]
- Metzner, D.; Lickschat, P.; Weißmantel, S. High-quality surface treatment using GHz burst mode with tunable ultrashort pulses. Appl. Surf. Sci. 2020, 531, 147270. [Google Scholar] [CrossRef]
- Hodgson, N.; Allegre, H.; Starodoumov, A.; Bettencourt, S. Femtosecond Laser Ablation in Burst Mode as a Function of Pulse Fluence and Intra-Burst Repetition Rate. JLMN 2020, 15. [Google Scholar] [CrossRef]
- Hodgson, N.; Steinkopff, A.; Heming, S.; Allegre, H.; Haloui, H.; Lee, T.S.; Laha, M.; van Nunen, J. Ultrafast Laser Machining: Process Optimization and Applications. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXVI, Proceedings of the SPIE LASE, San Francisco, CA, USA, 6–12 March 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11673, p. 1167308. [Google Scholar]
- Žemaitis, A.; Gaidys, M.; Gečys, P.; Barkauskas, M.; Gedvilas, M. Femtosecond laser ablation by bibursts in the MHz and GHz pulse repetition rates. Opt. Express 2021, 29, 7641–7653. [Google Scholar] [CrossRef]
- Führa, B.; Russ, S.; Hammers-Weber, P.; Diego-Vallejo, D.; Kahmann, M.; Andreev, A.; Hesse, T. High precision drilling with ultra-short laser pulses. In Proceedings of the Lasers in Manufacturing Conference 2017, Munich, Germany, 26–29 June 2017. [Google Scholar]
- Žemaitis, A.; Gaidys, M.; Brikas, M.; Gečys, P.; Raciukaitis, G.; Gedvilas, M. Advanced laser scanning for highly-efficient ablation and ultrafast surface structuring: Experiment and model. Sci. Rep. 2018, 8, 17376. [Google Scholar] [CrossRef]
- Jaeggi, B.; Neuenschwander, B.; Meier, T.; Zimmermann, M.; Hennig, G. High Precision Surface Structuring with Ultra-Short Laser Pulses and Synchronized Mechanical Axes. Phys. Procedia 2013, 41, 319–326. [Google Scholar] [CrossRef] [Green Version]
- Kramer, T.; Remund, S.; Gafner, M.; Zwygart, D.; Neuenschwander, B.; Holtz, R.; Witte, R.; Dury, N. Novel strategy for ultrafast pulsed laser micromachining of rotational symmetric metallic parts. Procedia CIRP 2018, 74, 611–617. [Google Scholar] [CrossRef]
- Bruening, S.; Hennig, G.; Eifel, S.; Gillner, A. Ultrafast Scan Techniques for 3D-μm Structuring of Metal Surfaces with high repetitive ps-laser pulses. Phys. Procedia 2011, 12, 105–115. [Google Scholar] [CrossRef]
- Liu, X.; Du, D.; Mourou, G. Laser ablation and micromachining with ultrashort laser pulses. IEEE J. Quantum Electron. 1997, 33, 1706–1716. [Google Scholar] [CrossRef]
- Shirk, M.D.; Molian, P.A. A review of ultrashort pulsed laser ablation of materials. J. Laser Appl. 1998, 10, 18–28. [Google Scholar] [CrossRef]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef]
- Perry, M.D.; Stuart, B.C.; Banks, P.S.; Feit, M.D.; Yanovsky, V.; Rubenchik, A.M. Ultrashort-pulse laser machining of electric materials. J. Appl. Phys. 1999, 85, 6803–6810. [Google Scholar] [CrossRef] [Green Version]
- Krüger, J.; Kautek, W. Ultrashort Pulse Laser Interaction with Dielectrics and Polymers. In Advances in Polymer Science; Springer Science and Business Media: New York, NY, USA, 2012; Volume 168, pp. 247–290. [Google Scholar]
- Bulgakova, N.M.; Zhukov, V.P.; Collins, A.R.; Rostohar, D.; Derrien, T.J.-Y.; Mocek, T. How to optimize ultrashort pulse laser interaction with glass surfaces in cutting regimes? Appl. Surf. Sci. 2015, 336, 364–374. [Google Scholar] [CrossRef]
- Samant, A.N.; Dahotre, N.B. Laser machining of structural ceramics—A review. J. Eur. Ceram. Soc. 2009, 29, 969–993. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, C.; Shang, S.; Liu, D.; Perrie, W.; Dearden, G.; Watkins, K. A review of ultrafast laser materials micromachining. Opt. Laser Technol. 2013, 46, 88–102. [Google Scholar] [CrossRef]
- Mishra, S.; Yadava, V. Laser Beam MicroMachining (LBMM)—A review. Opt. Lasers Eng. 2015, 73, 89–122. [Google Scholar] [CrossRef]
- Lei, S.; Zhao, X.; Yu, X.; Hu, A.; Vukelic, S.; Jun, M.B.G.; Joe, H.-E.; Yao, Y.L.; Shin, Y.C. Ultrafast Laser Applications in Man-ufacturing Processes: A State-of-the-Art Review. J. Manuf. Sci. Eng. 2020, 142, 031005. [Google Scholar] [CrossRef]
- Momma, C.; Nolte, S.; Chichkov, B.; Tunnermann, A.; Von Alvensleben, F. Precise Laser Ablation with Ultra-Short Pulses. In Proceedings of the European Meeting on Lasers and Electro-Optics CLEOE-96, Hamburg, Germany, 8–13 September 1996. [Google Scholar]
- Zhigilei, L. Dynamics of the plume formation and parameters of the ejected clusters in short-pulse laser ablation. Appl. Phys. A 2003, 76, 339–350. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, D.S.; Zhigilei, L. Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films. Phys. Rev. B 2003, 68, 064114. [Google Scholar] [CrossRef] [Green Version]
- Povarnitsyn, M.E.; Andreev, N.E.; Apfelbaum, E.M.; Itina, T.E.; Khishchenko, K.; Kostenko, O.F.; Levashov, P.R.; Veysman, M.E. A wide-range model for simulation of pump-probe experiments with metals. Appl. Surf. Sci. 2012, 258, 9480–9483. [Google Scholar] [CrossRef]
- Wu, C.; He, M. Microscopic mechanisms of laser spallation and ablation of metal targets from large-scale molecular dynamics simulations. Appl. Phys. A 2014, 114, 11–32. [Google Scholar] [CrossRef]
- Povarnitsyn, M.E.; Fokin, V.B.; Levashov, P.R. Microscopic and macroscopic modeling of femtosecond laser ablation of metals. Appl. Surf. Sci. 2015, 357, 1150–1156. [Google Scholar] [CrossRef]
- Breitling, D.; Ruf, A.; Dausinger, F. Fundamental Aspects in Machining of Metals with Short and Ultrashort Laser Pulses. In Photon Processing in Microelectronics and Photonics III—Fundamental Aspects in Machining of Metals with Short and Ultrashort Laser Pulses, Proceedings of the SPIE Lasers and Applications in Science and Engineering, San Jose, CA, USA, 25 January 2004; SPIE: Bellingham, WA, USA, 2004; p. 49. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Wright, O.B. Ultrafast nonequilibrium stress generation in gold and silver. Phys. Rev. B 1994, 49, 9985–9988. [Google Scholar] [CrossRef]
- Hüttner, B.; Rohr, G. On the theory of ps and sub-ps laser pulse interaction with metals I. Surface temperature. Appl. Surf. Sci. 1996, 103, 269–274. [Google Scholar] [CrossRef]
- Nedialkov, N.N.; Imamova, S.E.; Atanasov, P.A. Ablation of metals by ultrashort laser pulses. J. Phys. D Appl. Phys. 2004, 37, 638–643. [Google Scholar] [CrossRef]
- Wellershoff, S.-S.; Hohlfeld, J.; Güdde, J.; Matthias, E. The role of electron–phonon coupling in femtosecond laser damage of metals. Appl. Phys. A 1999, 69, S99–S107. [Google Scholar]
- Lin, Z.; Zhigilei, L.; Celli, V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys. Rev. B 2008, 77, 075133. [Google Scholar] [CrossRef] [Green Version]
- Foumani, A.A.; Förster, D.J.; Ghorbanfekr-Kalashami, H.; Weber, R.; Graf, T.; Niknam, A.R. Atomistic simulation of ultra-short pulsed laser ablation of metals with single and double pulses: An investigation of the re-deposition phenomenon. Appl. Surf. Sci. 2021, 537, 147775. [Google Scholar] [CrossRef]
- Amoruso, S.; Bruzzese, R.; Pagano, C.; Wang, X. Features of plasma plume evolution and material removal efficiency during femtosecond laser ablation of nickel in high vacuum. Appl. Phys. A 2007, 89, 1017–1024. [Google Scholar] [CrossRef] [Green Version]
- Düsing, J.F.; Hwang, D.J.; Grigoropoulos, C.; Ostendorf, A.; Kling, R. Optical emission imaging and spectroscopy during femtosecond laser ablation of thin metal films on flexible polymer substrates. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics, Orlando, FL, USA, 2–5 November 2009; p. 888. [Google Scholar]
- Förster, D.J.; Faas, S.; Gröninger, S.; Bauer, F.; Michalowski, A.; Weber, R.; Graf, T. Shielding effects and re-deposition of material during processing of metals with bursts of ultra-short laser pulses. Appl. Surf. Sci. 2018, 440, 926–931. [Google Scholar] [CrossRef]
- König, J.; Nolte, S.; Tünnermann, A. Plasma evolution during metal ablation with ultrashort laser pulses. Opt. Express 2005, 13, 10597. [Google Scholar] [CrossRef]
- Neuenschwander, B.; Jaeggi, B.; Schmid, M.; Hennig, G. Surface Structuring with Ultra-short Laser Pulses: Basics, Limitations and Needs for High Throughput. Phys. Procedia 2014, 56, 1047–1058. [Google Scholar] [CrossRef] [Green Version]
- Kramer, T.; Zhang, Y.; Remund, S.; Jaeggi, B.; Michalowski, A.; Grad, L.; Neuenschwander, B. Increasing the Specific Removal Rate for Ultra Short Pulsed Laser-Micromachining by Using Pulse Bursts. JLMN 2017, 12, 107–114. [Google Scholar] [CrossRef]
- Jaeggi, B.; Cangueiro, L.; Bruneel, D.; de Campos, J.A.R.; Hairaye, C.; Neuenschwander, B. Micromachining using pulse bursts: Influence of the pulse duration and the number of pulses in the burst on the specific removal rate. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10519, p. 1051905. [Google Scholar]
- Neuenschwander, B.; Jaeggi, B.; Schmid, M.; Rouffiange, V.; Martin, P.-E. Optimization of the Volume Ablation Rate for Metals at Different Laser Pulse-Durations from ps to fs. In Proceedings of the SPIE LASE, San Francisco, CA, USA, 15 February 2012; p. 824307. [Google Scholar]
- Schille, J.; Schneider, L.; Loeschner, U. Process optimization in high-average-power ultrashort pulse laser microfabrication: How laser process parameters influence efficiency, throughput and quality. Appl. Phys. A 2015, 120, 847–855. [Google Scholar] [CrossRef]
- Domke, M.; Matylitsky, V.; Stroj, S. Surface ablation efficiency and quality of fs lasers in single-pulse mode, fs lasers in burst mode, and ns lasers. Appl. Surf. Sci. 2020, 505, 144594. [Google Scholar] [CrossRef]
- Raciukaitis, G.; Brikas, M.; Gecys, P.; Voisat, B.; Gedvilas, M. Use of High Repetition Rate and High Power Lasers in Microfabrication: How to Keep the Efficiency High? JLMN 2009, 4, 186–191. [Google Scholar] [CrossRef]
- Gillner, A.; Hartmann, C.; Dohrn, A. High Quality Micro Machining with Tailored Short and Ultra Short Laser Pulses. In Proceedings of the Pacific International Conference on Applications of Lasers and Optics; Laser Institute of America: Orlando, FL, USA, 2008; Volume 2008, p. 685. [Google Scholar]
- Knappe, R.; Haloui, H.; Seifert, A.; Weis, A.; Nebel, A. Scaling ablation rates for picosecond lasers using burst micromachining. In Laser-Based Micro- and Nanopackaging and Assembly IV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 23–28 January 2010; SPIE: Bellingham, WA, USA, 2010; Volume 7585, p. 75850H. [Google Scholar]
- Vorobyev, A.Y.; Guo, C. Direct observation of enhanced residual thermal energy coupling to solids in femtosecond laser ablation. Appl. Phys. Lett. 2005, 86, 011916. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Enhanced absorptance of gold following multipulse femtosecond laser ablation. Phys. Rev. B 2005, 72, 195422. [Google Scholar] [CrossRef] [Green Version]
- Vorobyev, A.Y.; Guo, C. Enhanced energy coupling in femtosecond laser-metal interactions at high intensities. Opt. Express 2006, 14, 13113–13119. [Google Scholar] [CrossRef]
- Vorobyev, A.; Kuzmichev, V.; Kokody, N.; Kohns, P.; Dai, J.; Guo, C. Residual thermal effects in Al following single ns- and fs-laser pulse ablation. Appl. Phys. A 2005, 82, 357–362. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Thermal response and optical absorptance of metals under femtosecond laser irradiation. Nat. Sci. 2011, 03, 488–495. [Google Scholar] [CrossRef] [Green Version]
- Bauer, F.; Michalowski, A.; Kiedrowski, T.; Nolte, S. Heat accumulation in ultra-short pulsed scanning laser ablation of metals. Opt. Express 2015, 23, 1035–1043. [Google Scholar] [CrossRef]
- Förster, D.J.; Weber, R.; Graf, T. Residual heat during ultrashort laser drilling of metals. In Proceedings of the LPM2017—The 18th International Symposium on Laser Precision Microfabrication, Toyama, Japan, 5–8 June 2017. [Google Scholar]
- Bauer, F. Grundlegende Untersuchungen zum Abtragen von Stahl mit Ultrakurzen Laserpulsen. Ph.D. Thesis, Friedrich-Schiller-Universität Jena, Jena, Germany, 2018. [Google Scholar]
- Bornschlegel, B.; Koller, J.; Finger, J. In-Situ Analysis of Heat Accumulation during Ultrashort Pulsed Laser Ablation. JLMN 2020, 15, 56–62. [Google Scholar]
- Wu, B.; Deng, L.; Liu, P.; Zhang, F.; Duan, J.; Zeng, X. Effects of picosecond laser repetition rate on ablation of Cr12MoV cold work mold steel. Appl. Surf. Sci. 2017, 409, 403–412. [Google Scholar] [CrossRef]
- Metzner, D.; Lickschat, P.; Weißmantel, S. Influence of heat accumulation during laser micromachining of CoCrMo alloy with ultrashort pulses in burst mode. Appl. Phys. A 2020, 126, 84. [Google Scholar] [CrossRef]
- Martan, J.; Prokešová, L.; Moskal, D.; de Faria, B.F.; Honner, M.; Lang, V. Heat accumulation temperature measurement in ultrashort pulse laser micromachining. Int. J. Heat Mass Transf. 2021, 168, 120866. [Google Scholar] [CrossRef]
- Weber, R.; Graf, T.; Berger, P.; Onuseit, V.; Wiedenmann, M.; Freitag, C.; Feuer, A. Heat accumulation during pulsed laser materials processing. Opt. Express 2014, 22, 11312–11324. [Google Scholar] [CrossRef] [Green Version]
- Weber, R.; Graf, T.; Freitag, C.; Feuer, A.; Kononenko, T.; Konov, V.I. Processing constraints resulting from heat accumulation during pulsed and repetitive laser materials processing. Opt. Express 2017, 25, 3966–3979. [Google Scholar] [CrossRef]
- Di Niso, F.; Gaudiuso, C.; Sibillano, T.; Mezzapesa, F.P.; Ancona, A.; Lugarà, P.M. Role of heat accumulation on the incubation effect in multi-shot laser ablation of stainless steel at high repetition rates. Opt. Express 2014, 22, 12200–12210. [Google Scholar] [CrossRef] [PubMed]
- Raciukaitis, G.; Brikas, M.; Gecys, P.; Gedvilas, M. Accumulation Effects in Laser Ablation of Metals with High-Repetition-Rate Lasers. In High-Power Laser Ablation VII, Proceedings of the SPIE LASE, San Francisco, CA, USA, 23–28 January 2008; SPIE: Bellingham, WA, USA, 2008. [Google Scholar]
- Faas, S.; Bielke, U.; Weber, R.; Graf, T. Prediction of the surface structures resulting from heat accumulation during processing with picosecond laser pulses at the average power of 420 W. Appl. Phys. A 2018, 124, 612. [Google Scholar] [CrossRef] [Green Version]
- St-Onge, L.; Sabsabi, M.; Cielo, P. Analysis of solids using laser-induced plasma spectroscopy in double-pulse mode. Spectrochim. Acta Part B At. Spectrosc. 1998, 53, 407–415. [Google Scholar] [CrossRef]
- Mao, S.; Mao, X.; Greif, R.; Russo, R.E. Influence of preformed shock wave on the development of picosecond laser ablation plasma. J. Appl. Phys. 2001, 89, 4096–4098. [Google Scholar] [CrossRef]
- Corsi, M.; Cristoforetti, G.; Giuffrida, M.; Hidalgo, M.; Legnaioli, S.; Palleschi, V.; Salvetti, A.; Tognoni, E.; Vallebona, C. Three-dimensional analysis of laser induced plasmas in single and double pulse configuration. Spectrochim. Acta Part B At. Spectrosc. 2004, 59, 723–735. [Google Scholar] [CrossRef]
- Scuderi, D.; Albert, O.; Moreau, D.; Pronko, P.P.; Etchepare, J. Interaction of a laser-produced plume with a second time delayed femtosecond pulse. Appl. Phys. Lett. 2005, 86, 071502. [Google Scholar] [CrossRef]
- Hanada, Y.; Sugioka, K.; Miyamoto, I.; Midorikawa, K. Double-pulse irradiation by laser-induced plasma-assisted ablation (LIPAA) and mechanisms study. Appl. Surf. Sci. 2005, 248, 276–280. [Google Scholar] [CrossRef]
- Le Harzic, R.; Breitling, D.; Sommer, S.; Föhl, C.; König, K.; Dausinger, F.; Audouard, E. Processing of metals by double pulses with short laser pulses. Appl. Phys. A 2005, 81, 1121–1125. [Google Scholar] [CrossRef]
- Babushok, V.; DeLucia, F.; Gottfried, J.; Munson, C.; Miziolek, A. Double pulse laser ablation and plasma: Laser induced breakdown spectroscopy signal enhancement. Spectrochim. Acta Part B At. Spectrosc. 2006, 61, 999–1014. [Google Scholar] [CrossRef]
- Suttmann, O.; Wojakowski, B.; Klug, U.; Kling, R.; Ostendorf, A. Picosecond double-pulse ablation in silicon and aluminium with variable delay. J. Laser Appl. 2008, 42. [Google Scholar] [CrossRef]
- Bogaerts, A.; Chen, Z.; Autrique, D. Double pulse laser ablation and laser induced breakdown spectroscopy: A modeling investigation. Spectrochim. Acta Part B At. Spectrosc. 2008, 63, 746–754. [Google Scholar] [CrossRef]
- Singha, S.; Hu, Z.; Gordon, R.J. Ablation and plasma emission produced by dual femtosecond laser pulses. J. Appl. Phys. 2008, 104, 113520. [Google Scholar] [CrossRef]
- Noel, S.; Hermann, J. Reducing nanoparticles in metal ablation plumes produced by two delayed short laser pulses. Appl. Phys. Lett. 2009, 94, 53120. [Google Scholar] [CrossRef]
- Wojakowski, B.; Suttmann, O.; Klug, U.; Kling, R. Micromachining with Picosecond Double Pulses on Silicon and Aluminium. In Laser-Based Micro- and Nanopackaging and Assembly III, Proceedings of the SPIE LASE: Lasers and Applications in Science and Engineering, San Jose, CA, USA, 24 January 2009; SPIE: Bellingham, WA, USA, 2009; p. 72020O. [Google Scholar]
- Roberts, D.; du Plessis, A.; Botha, L. Femtosecond laser ablation of silver foil with single and double pulses. Appl. Surf. Sci. 2010, 256, 1784–1792. [Google Scholar] [CrossRef]
- Deladurantaye, P.; Cournoyer, A.; Drolet, M.; Desbiens, L.; Lemieux, D.; Briand, M.; Taillon, Y. Material Micromachining Using Bursts of High Repetition Rate Picosecond Pulses from a Fiber Laser Source. In Fiber Lasers VIII: Technology, Systems, and Applications, Proceedings of the SPIE LASE San Francisco, CA, USA, 22–27 January 2011; SPIE: Bellingham, WA, USA, 2011; Volume 7914, p. 791404. [Google Scholar]
- Axente, E.; Mihailescu, I.N.; Itina, T.; Hermann, J. Probing electron-phonon coupling in metals via observations of ablation plumes produced by two delayed short laser pulses. Appl. Phys. Lett. 2011, 99, 081502. [Google Scholar] [CrossRef] [Green Version]
- Sailer, M.; Bauer, F.; Kleiner, J.; Kaiser, M. Scaling of ablation rates. Ablation efficiency and quality aspects of “Burstmode”—Micromachining of metals. In Proceedings of the Lasers in Manufacturing Conference, Munich, Germany, 22–25 June 2015; p. 8. [Google Scholar]
- Hänel, N.; Stolze, M.; Herrmann, T.R.W.; Lhuillier, J.A. Fundamental Investigations of ps-Laser Burst-Mode on Common Metals for an Enhanced Ablation Process. In Laser-Based Micro- and Nanoprocessing IX, Proceedings of the SPIE LASE San Francisco, CA, USA, 7–12 February 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9351, p. 93510E. [Google Scholar]
- Kramer, T.; Neuenschwander, B.; Jäggi, B.; Remund, S.; Hunziker, U.; Zürcher, J. Influence of Pulse Bursts on the Specific Removal Rate for Ultra-fast Pulsed Laser Micromachining of Copper. Phys. Procedia 2016, 83, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Schille, J.; Schneider, L.; Kraft, S.; Hartwig, L.; Loeschner, U. Experimental study on double-pulse laser ablation of steel upon multiple parallel-polarized ultrashort-pulse irradiations. Appl. Phys. A 2016, 122, 644. [Google Scholar] [CrossRef]
- Finger, J. Puls-zu-Puls-Wechselwirkungen beim Ultrakurzpuls-Laserabtrag mit hohen Repetitionsraten. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2017. [Google Scholar]
- Lickschat, P.; Demba, A.; Weissmantel, S. Ablation of steel using picosecond laser pulses in burst mode. Appl. Phys. A 2017, 123, 137. [Google Scholar] [CrossRef]
- Mayerhofer, R. Ultrashort-pulsed laser material processing with high repetition rate burst pulses. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXII, Proceedings of the SPIE LASE, 2017, San Francisco, CA, USA, 28 January–2 February 2017; SPIE: Bellingham, WA, USA, 2017; p. 100910. [Google Scholar]
- Jaeggi, B.; Remund, S.; Zhang, Y.; Kramer, T.; Neuenschwander, B. Optimizing the Specific Removal Rate with the Burst Mode Under Varying Conditions. JLMN 2017, 12, 107–114. [Google Scholar]
- Rosenfeld, A.; Höhm, S.; Krüger, J.; Bonse, J. Dynamics of Ultrashort Double-Pulse Laser Ablation of Solid Surfaces. In Encyclopedia of Interfacial Chemistry; Elsevier: Amsterdam, The Netherlands, 2018; pp. 338–347. [Google Scholar]
- Hashida, M.; Masuno, S.; Furukawa, Y.; Kusaba, M.; Inoue, S.; Sakabe, S.; Sakagami, H.; Tsukamoto, M. Suppression of ablation by double-pulse femtosecond laser irradiation. In Frontiers in Ultrafast Optics: Biomedical, Scientific, and Industrial Applications XVIII, Proceedings of the SPIE LASE, San Francisco, CA, USA, 27 January–1 February 2018; SPIE: Bellingham, WA, USA, 2018; p. 105220. [Google Scholar]
- Zhang, K.; Zhang, J.; Jiang, L.; Li, X.; Liu, Y.; Li, B.; Lu, Y. Ablation enhancement of metal in ultrashort double-pulse experiments. Appl. Phys. Lett. 2018, 112, 261906. [Google Scholar] [CrossRef]
- Takenaka, K.; Tsukamoto, M.; Hashida, M.; Masuno, S.; Sakagami, H.; Kusaba, M.; Sakabe, S.; Inoue, S.; Furukawa, Y.; Asai, S. Ablation suppression of a titanium surface interacting with a two-color double-pulse femtosecond laser beam. Appl. Surf. Sci. 2019, 478, 882–886. [Google Scholar] [CrossRef]
- Bruening, S.; Du, K.; Gillner, A. Micro processing with ultrafast bursts of pulses. Procedia CIRP 2020, 94, 856–862. [Google Scholar] [CrossRef]
- Lin, Z.; Ji, L.; Hong, M. Enhancement of femtosecond laser-induced surface ablation via temporal overlapping double-pulse irradiation. Photon Res. 2020, 8, 271. [Google Scholar] [CrossRef]
- Förster, D.J.; Faas, S.; Weber, R.; Graf, T. Thrust enhancement and propellant conservation for laser propulsion using ultra-short double pulses. Appl. Surf. Sci. 2020, 510, 145391. [Google Scholar] [CrossRef]
- Cheng, C.-W.; Chen, J.-K. Drilling of Copper Using a Dual-Pulse Femtosecond Laser. Technologies 2016, 4, 7. [Google Scholar] [CrossRef] [Green Version]
- Förster, G.D.; Lewis, L.J. Numerical study of double-pulse laser ablation of Al. Phys. Rev. B 2018, 97, 224301. [Google Scholar] [CrossRef]
- Roth, J.; Krauß, A.; Lotze, J.; Trebin, H.-R. Simulation of laser ablation in aluminum: The effectivity of double pulses. Appl. Phys. A 2014, 117, 2207–2216. [Google Scholar] [CrossRef] [Green Version]
- Povarnitsyn, M.E.; Itina, T.E.; Levashov, P.R.; Khishchenko, K. Simulation of ultrashort double-pulse laser ablation. Appl. Surf. Sci. 2011, 257, 5168–5171. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Samokhvalov, A.A.; Golubev, Y.D.; Ivanov, D.S.; Garcia, M.E.; Veiko, V.P.; Rethfeld, B.; Mikhailovskii, V.Y. Dynamic all-optical control in ultrashort double-pulse laser ablation. Appl. Surf. Sci. 2021, 537, 147940. [Google Scholar] [CrossRef]
- Spellauge, M.; Winter, J.; Rapp, S.; McDonnell, C.; Sotier, F.; Schmidt, M.; Huber, H.P. Influence of stress confinement, particle shielding and re-deposition on the ultrashort pulse laser ablation of metals revealed by ultrafast time-resolved experiments. Appl. Surf. Sci. 2021, 545, 148930. [Google Scholar] [CrossRef]
- Ackerl, N. Laser Surface Functionalization from Fundamentals to Application. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2020. [Google Scholar]
- Börner, P. Ultra-Short Pulsed Laser Ablation of Diamond. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2019. [Google Scholar]
- Furukawa, Y.; Inoue, S.; Hashida, M. Temporal change in laser penetration length of titanium and platinum for double-pulse ablation measured by a novel ablation method. J. Laser Appl. 2021, 33, 012023. [Google Scholar] [CrossRef]
- Lauer, B.; Jaeggi, B.; Zhang, Y.; Neuenschwander, B. Measurement of the maximum specific removal rate: Unexpected influence of the experimental method and the spot size. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics, Atlanta, GA, USA, 18–22 October 2015; Laser Institute of America: Orlando, FL, USA, 2015; Volume 2015, p. 146. [Google Scholar]
- Kramer, T.; Remund, S.; Jäggi, B.; Schmid, M.; Neuenschwander, B. Ablation dynamics—From absorption to heat accumulation/ultra-fast laser matter interaction. Adv. Opt. Technol. 2018, 7, 129–144. [Google Scholar] [CrossRef]
- Winter, J.; Rapp, S.; Schmidt, M.; Huber, H.P. Ultrafast laser processing of copper: A comparative study of experimental and simulated transient optical properties. Appl. Surf. Sci. 2017, 417, 2–15. [Google Scholar] [CrossRef]
- Neuenschwander, B.; Bucher, G.F.; Nussbaum, C.; Joss, B.; Muralt, M.; Hunziker, U.W.; Schuetz, P. Processing of metals and dielectric materials with ps-laser pulses: Results, strategies, limitations and needs. In Laser Applications in Microelectronic and Optoelectronic Manufacturing XV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 12 March 2010; 75840R-SPIE; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Osbild, M.; Brenner, A.; Röther, L.; Finger, J. Ultrashort pulse laser micro polishing of steel—Investigation of the melt pool depth. Procedia CIRP 2020, 94, 936–941. [Google Scholar] [CrossRef]
- Remund, S.; Kramer, T.; Neuenschwander, B.; Jäggi, B. Method for Producing an Implant, and Implant Produced by Said Method. U.S. Patent WO/2020/038925, 27 February 2020. [Google Scholar]
- Brenner, A.; Röther, L.; Osbild, M.; Finger, J. Laser Polishing Using Ultrashort Pulse Laser. In Laser-Based Micro- and Nanoprocessing XIV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 1–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11268, p. 112680. [Google Scholar]
- Metzner, D.; Lickschat, P.; Weißmantel, S. Optimization of the ablation process using ultrashort pulsed laser radiation in different burst modes. J. Laser Appl. 2021, 33, 012057. [Google Scholar] [CrossRef]
- Metzner, D.; Lickschat, P.; Weißmantel, S. Surface treatment on cobalt and titanium alloys using picosecond laser pulses in burst mode. Appl. Phys. A 2021, 127, 1–9. [Google Scholar] [CrossRef]
- Matsumoto, H.; Lin, Z.; Kleinert, J. Ultrafast Laser Ablation of Copper with ~GHz Bursts. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXIII (International Society for Optics and Photonics, Proceedings of the SPIE LASE, San Francisco, CA, USA, 29–31 January 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10519, p. 1051902. [Google Scholar]
- Povarnitsyn, M.E.; Levashov, P.R.; Knyazev, D.V. Simulation of ultrafast bursts of subpicosecond pulses: In pursuit of efficiency. Appl. Phys. Lett. 2018, 112, 051603. [Google Scholar] [CrossRef]
- Bonamis, G.; Audouard, E.; Hoenninger, C.; Lopez, J.; Mishchik, K.; Mottay, E.; Manek-Hönninger, I. Systematic study of laser ablation with GHz bursts of femtosecond pulses. Opt. Express 2020, 28, 27702. [Google Scholar] [CrossRef]
- Bonamis, G.; Mishchick, K.; Audouard, E.; Hönninger, C.; Mottay, E.; Lopez, J.; Manek-Hönninger, I. High efficiency femtosecond laser ablation with gigahertz level bursts. J. Laser Appl. 2019, 31, 022205. [Google Scholar] [CrossRef]
- Butkus, S.; Jukna, V.; Paipulas, D.; Barkauskas, M.; Sirutkaitis, V. Micromachining of Invar Foils with GHz, MHz and kHz Femtosecond Burst Modes. Micromachines 2020, 11, 733. [Google Scholar] [CrossRef] [PubMed]
- Hendow, S.T.; Takahashi, H.; Yamaguchi, M.; Xu, J. Enhanced Ablation Using GHz-Pulsed fs Laser. In Laser-Based Micro- and Nanoprocessing XIV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 1–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11268, p. 1126809. [Google Scholar]
- Hirsiger, T.; Gafner, M.; Remund, S.M.; Chaja, M.W.; Urniezius, A.; Butkus, S.; Neuenschwander, B. Machining Metals and Silicon with GHz Bursts: Surprising Tremendous Reduction of the Specific Removal Rate for Surface Texturing Applications. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 1–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11267, p. 112670T. [Google Scholar]
- Cheng, C.-W.; Chen, J.-K. Ultrafast laser ablation of copper by GHz bursts. Appl. Phys. A 2020, 126, 1–7. [Google Scholar] [CrossRef]
- Fehrenbacher, A.; Sailer, M.; Fuehra, B.; Jansen, F.; Tan, C.; Baumbach, S.; Flaig, R.; Eberhardt, C.; Ruebling, S.; Quentin, U.; et al. New generation TruMicro Series 2000: Micromachining Versatility by GHz-burst, Higher Average Power, Flexible Pulse on Demand and Integrated Hollow-Core Fiber Interface. In Laser-Based Micro- and Nanoprocessing XV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 6–11 March 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11674, p. 116740U. [Google Scholar]
- Nyenhuis, F.; Michalowski, A.; L’Huillier, J.A. Surface Treatment with GHz-Bursts. In Laser-Based Micro- and Nanoprocessing XIV, Proceedings of the SPIE LASE, San Francisco, CA, USA, 1–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11268, p. 112680B. [Google Scholar]
- Michalowski, A.; Nyenhuis, F.; Kunz, G. Smooth Surfaces by Pulsed Laser Processing with Bursts. Photonics Views 2020, 17, 42–45. [Google Scholar] [CrossRef]
- Obata, K.; Caballero-Lucas, F.; Sugioka, K. Material Processing at GHz Burst Mode by Femtosecond Laser Ablation. JLMN 2021, 16, 5. [Google Scholar]
- Manninen, M.; Hirvimäki, M.; Poutiainen, I.; Salminen, A. Effect of Pulse Length on Engraving Efficiency in Nanosecond Pulsed Laser Engraving of Stainless Steel. Met. Mater. Trans. A 2015, 46, 2129–2136. [Google Scholar] [CrossRef]
- Mathew, M.M.; Bathe, R.N.; Padmanabham, G.; Padmanaban, R.; Thirumalini, S. A study on the micromachining of molybdenum using nanosecond and femtosecond lasers. Int. J. Adv. Manuf. Technol. 2017, 104, 3239–3249. [Google Scholar] [CrossRef]
- Garnov, S.; Konov, V.; Kononenko, T.; Pashinin, V.; Sinyavsky, M. Microsecond laser material processing at 1.06 µm. Laser Phys. 2004, 14, 910–915. [Google Scholar]
- Mur, J.; Petkovšek, R. Precision and resolution in laser direct microstructuring with bursts of picosecond pulses. Appl. Phys. A 2018, 124, 62. [Google Scholar] [CrossRef]
- Gaudiuso, C.; Giannuzzi, G.; Volpe, A.; Lugarà, P.M.; Choquet, I.; Ancona, A. Incubation during laser ablation with bursts of femtosecond pulses with picosecond delays. Opt. Express 2018, 26, 3801–3813. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Ji, P.; He, M.; Zhang, Y.; Tang, Y. Multiscale Investigation of Femtosecond Laser Pulses Processing Aluminum in Burst Mode. Nanoscale Microscale Thermophys. Eng. 2018, 22, 324–347. [Google Scholar] [CrossRef]
- Mur, J.; Petkovšek, R. Near-THz bursts of pulses—Governing surface ablation mechanisms for laser material processing. Appl. Surf. Sci. 2019, 478, 355–360. [Google Scholar] [CrossRef]
- Wang, A.; Das, A.; Grojo, D. Ultrafast Laser Writing Deep inside Silicon with THz-Repetition-Rate Trains of Pulses. Research 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Ancona, A.; Gaudiuso, C.; Giannuzzi, G.; Choquet, I.; Lugarà, P.M. Incubation Effect In Burst Mode Fs-Laser Ablation Of Stainless Steel Samples. In Laser-Based Micro- and Nanoprocessing XII, Proceedings of the SPIE LASE, San Francisco, CA, USA, 27 January–1 February 2020; SPIE: Bellingham, WA, USA, 2018; Volume 10520, p. 105200A. [Google Scholar]
- Förster, D.J.; Weber, R.; Holder, D.; Graf, T. Estimation of the depth limit for percussion drilling with picosecond laser pulses. Opt. Express 2018, 26, 11546–11552. [Google Scholar] [CrossRef] [Green Version]
- Holder, D.; Weber, R.; Graf, T.; Onuseit, V.; Brinkmeier, D.; Förster, D.J.; Feuer, A. Analytical model for the depth progress of percussion drilling with ultrashort laser pulses. Appl. Phys. A 2021, 127, 1–8. [Google Scholar] [CrossRef]
- Lapczyna, M.; Chen, K.; Herman, P.; Tan, H.; Marjoribanks, R. Ultra high repetition rate (133 MHz) laser ablation of aluminum with 1.2-ps pulses. Appl. Phys. A 1999, 69, S883–S886. [Google Scholar] [CrossRef]
- Esser, D.; Rezaei, S.; Li, J.; Herman, P.R.; Gottmann, J. Time dynamics of burst-train filamentation assisted femtosecond laser machining in glasses. Opt. Express 2011, 19, 25632–25642. [Google Scholar] [CrossRef]
- Kammer, H.; Dreisow, F.; Tünnermann, A. Analysis of the Hole Shape Evolution in fs-Pulse Percussion Drilling with Bursts. In Frontiers in Ultrafast Optics: Biomedical, Scientific, and Industrial Applications XVI, Proceedings of the SPIE LASE, San Francisco, CA, USA, 13–18 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9740, p. 974012. [Google Scholar]
- Wang, Q.; Luo, S.; Chen, Z.; Qi, H.; Deng, J.; Hu, Z. Drilling of aluminum and copper films with femtosecond double-pulse laser. Opt. Laser Technol. 2016, 80, 116–124. [Google Scholar] [CrossRef]
- Balachninaitė, O.; Tamulienė, V.; Eičas, L.; Vaičaitis, V. Laser micromachining of steel and copper using femtosecond laser pulses in GHz burst mode. Results Phys. 2021, 22, 103847. [Google Scholar] [CrossRef]
- Schille, J.; Loeschner, U.; Ebert, R.; Scully, P.; Goddard, N.; Exner, H. Laser micro processing using a high repetition rate femto second laser. J. Laser Appl. 2010, 1491–1499. [Google Scholar] [CrossRef]
- Tsukamoto, M.; Kayahara, T.; Nakano, H.; Hashida, M.; Katto, M.; Fujita, M.; Tanaka, M.; Abe, N. Microstructures formation on titanium plate by femtosecond laser ablation. J. Physics Conf. Ser. 2007, 59, 666–669. [Google Scholar] [CrossRef]
- Herrmann, T.; Harth, F.; Henrich, B.; L’Huillier, J.; Hajri, M. How to Improve Efficiency in USP Laser Micromachining. Laser Tech. J. 2016, 13, 16–19. [Google Scholar] [CrossRef]
- Nyenhuis, F.; Michalowski, A.; L’Huillier, J. Dual Process Strategy to Increase the Usable Power for Laser-Milling. JLMN 2020. [Google Scholar] [CrossRef]
- Sassmannshausen, A.; Brenner, A.; Finger, J. Ultrashort pulse laser polishing by continuous surface melting. J. Mater. Process. Technol. 2021, 293, 117058. [Google Scholar] [CrossRef]
- Kažukauskas, E.; Butkus, S.; Tokarski, P.; Jukna, V.; Barkauskas, M.; Sirutkaitis, V. Micromachining of Transparent Biocompatible Polymers Applied in Medicine Using Bursts of Femtosecond Laser Pulses. Micromachines 2020, 11, 1093. [Google Scholar] [CrossRef] [PubMed]
- Antończak, A.J.; Stępak, B.; Kozioł, P.E.; Abramski, K.M. The influence of process parameters on the laser-induced coloring of titanium. Appl. Phys. A 2013, 115, 1003–1013. [Google Scholar] [CrossRef] [Green Version]
- Veiko, V.; Odintsova, G.; Ageev, E.; Karlagina, Y.; Loginov, A.; Skuratova, A.; Gorbunova, E. Controlled oxide films formation by nanosecond laser pulses for color marking. Opt. Express 2014, 22, 24342–24347. [Google Scholar] [CrossRef]
- Lecka, K.M.; Wojcik, M.R.; Antonczak, A.J. Laser-Induced Color Marking of Titanium: A Modeling Study of the Interference Effect and the Impact of Protective Coating. Math. Probl. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lin, W.; Hong, M. Surface coloring by laser irradiation of solid substrates. APL Photon. 2019, 4, 051101. [Google Scholar] [CrossRef] [Green Version]
- Vorobyev, A.Y.; Guo, C. Colorizing metals with femtosecond laser pulses. Appl. Phys. Lett. 2008, 92, 041914. [Google Scholar] [CrossRef]
- Dusser, B.; Sagan, S.; Soder, H.; Faure, N.; Colombier, J.-P.; Jourlin, M.; Audouard, E. Controlled nanostructrures formation by ultra fast laser pulses for color marking. Opt. Express 2010, 18, 2913–2924. [Google Scholar] [CrossRef] [Green Version]
- Ackerl, N.; Gugger, P.; Warhanek, M.; Gysel, J.; Wegener, K. Ultra-Short Pulsed Laser Marking and Coloration of Metals with Segmented Pixel Parameter Transformation. JLMN 2020, 15. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Direct femtosecond laser surface nano/microstructuring and its applications: Direct femtosecond laser surface nano/microstructuring and its applications. Laser Photonics Rev. 2013, 7, 385–407. [Google Scholar] [CrossRef]
- Guay, J.-M.; Lesina, A.C.; Cote, G.; Charron, M.; Poitras, D.; Ramunno, L.; Berini, P.; Weck, A. Laser-induced plasmonic colours on metals. Nat. Commun. 2017, 8, 16095. [Google Scholar] [CrossRef]
- Berini, P.; Guay, J.-M.; Lesina, A.C.; Walia, J.; Ramunno, L.; Weck, A.; Krupin, O.; Warren, M. Plasmonic Colours on Bulk Metals: Laser Coloring of Large Areas Exhibiting High Topography. In Frontiers in Ultrafast Optics: Biomedical, Scientific, and Industrial Applications XVIII, Proceedings of the SPIE LASE, San Francisco, CA, USA, 27 January–1 February 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10522, p. 105220G. [Google Scholar]
- Lumentum. FlexBurstTM—Picosecond Micromachining Lasers Offer “Burst Mode” with Full User Control of Intra-Burst Pulse Energy Distribution; Lumentum: San Jose, CA, USA, 2016. [Google Scholar]
- Guay, J.-M.; Lesina, A.C.; Baxter, J.; Killaire, G.; Ramunno, L.; Berini, P.; Weck, A. Topography Tuning for Plasmonic Color Enhancement via Picosecond Laser Bursts. Adv. Opt. Mater. 2018, 6, 1800189. [Google Scholar] [CrossRef] [Green Version]
- Stratakis, E.; Bonse, J.; Heitz, J.; Siegel, J.; Tsibidis, G.; Skoulas, E.; Papadopoulos, A.; Mimidis, A.; Joel, A.-C.; Comanns, P.; et al. Laser engineering of biomimetic surfaces. Mater. Sci. Eng. R Rep. 2020, 141, 100562. [Google Scholar] [CrossRef]
- Masato, D.; Sorgato, M.; Batal, A.; Dimov, S.; Lucchetta, G. Thin-wall injection molding of polypropylene using molds with different laser-induced periodic surface structures. Polym. Eng. Sci. 2019, 59, 1889–1896. [Google Scholar] [CrossRef]
- Florian, C.; Kirner, S.V.; Krüger, J.; Bonse, J. Surface functionalization by laser-induced periodic surface structures. J. Laser Appl. 2020, 32, 022063. [Google Scholar] [CrossRef]
- Piccolo, L.; Sorgato, M.; Batal, A.; Dimov, S.; Lucchetta, G.; Masato, D. Functionalization of Plastic Parts by Replication of Variable Pitch Laser-Induced Periodic Surface Structures. Micromachines 2020, 11, 429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonse, J.; Höhm, S.; Kirner, S.V.; Rosenfeld, A.; Krüger, J. Laser-Induced Periodic Surface Structures—A Scientific Evergreen. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 9000615. [Google Scholar] [CrossRef]
- Bonse, J.; Graf, S. Maxwell Meets Marangoni—A Review of Theories on Laser-Induced Periodic Surface Structures. Laser Photonics Rev. 2020, 14, 2000215. [Google Scholar] [CrossRef]
- Bonse, J. Quo Vadis LIPSS? Recent and Future Trends on Laser-Induced Periodic Surface Structures. Nanomaterials 2020, 10, 1950. [Google Scholar] [CrossRef]
- Bonse, J.; Kirner, S.V.; Krüger, J. Laser-Induced Periodic Surface Structures (LIPSS). In Handbook of Laser Micro- and Nano-Engineering; Sugioka, K., Ed.; Springer International Publishing: New York, NY, USA, 2021; pp. 1–59. [Google Scholar]
- Fraggelakis, F.; Mincuzzi, G.; Lopez, J.; Manek-Hönninger, I.; Kling, R. Controlling 2D laser nano structuring over large area with double femtosecond pulses—ScienceDirect. Appl. Surf. Sci. 2019, 470, 677–686. [Google Scholar] [CrossRef]
- Hashida, M.; Furukawa, Y.; Inoue, S.; Sakabe, S.; Masuno, S.; Kusaba, M.; Sakagami, H.; Tsukamoto, M. Uniform LIPSS on titanium irradiated by two-color double-pulse beam of femtosecond laser. J. Laser Appl. 2020, 32, 022054. [Google Scholar] [CrossRef]
- Hashida, M. Periodic Grating Structures on Metal Self-organized by Double-pulse Irradiation. J. Laser Micro Nanoeng. 2014, 9, 234–237. [Google Scholar] [CrossRef]
- Hashida, M.; Nishii, T.; Miyasaka, Y.; Sakagami, H.; Shimizu, M.; Inoue, S.; Sakabe, S. Orientation of periodic grating structures controlled by double-pulse irradiation. Appl. Phys. A 2016, 122, 1–5. [Google Scholar] [CrossRef]
- Giannuzzi, G.; Gaudiuso, C.; Di Franco, C.; Scamarcio, G.; Lugarà, P.M.; Ancona, A. Large area laser-induced periodic surface structures on steel by bursts of femtosecond pulses with picosecond delays. Opt. Lasers Eng. 2019, 114, 15–21. [Google Scholar] [CrossRef]
- Giannuzzi, G.; Gaudiuso, C.; Cinquino, M.; Di Mundo, R.; Mirenghi, L.; Di Franco, C.; Scamarcio, G.; Lugarà, P.M.; Ancona, A. 1-D and 2-D Surface Structuring of Steel by Bursts of Femtosecond Laser Pulses. In Laser-Based Micro- and Nanoprocessing XIII, Proceedings of the SPIE LASE, San Francisco, CA, USA, 4 February 2019; SPIE: Bellingham, WA, USA, 2019; Volume 10906, p. 109060O. [Google Scholar]
- Wang, X.; Li, C.; Ma, C.; Feng, J.; Hong, W.; Zhang, Z. Formation of laser induced periodic structures on stainless steel using multi-burst picosecond pulses. Opt. Express 2018, 26, 6325–6330. [Google Scholar] [CrossRef]
- Fraggelakis, F.; Giannuzzi, G.; Gaudiuso, C.; Manek-Hönninger, I.; Mincuzzi, G.; Ancona, A.; Kling, R. Double- and Multi-Femtosecond Pulses Produced by Birefringent Crystals for the Generation of 2D Laser-Induced Structures on a Stainless Steel Surface. Materials 2019, 12, 1257. [Google Scholar] [CrossRef] [Green Version]
- Höhm, S.; Rosenfeld, A.; Krüger, J.; Bonse, J. Area dependence of femtosecond laser-induced periodic surface structures for varying band gap materials after double pulse excitation. Appl. Surf. Sci. 2013, 278, 7–12. [Google Scholar] [CrossRef]
- Höhm, S.; Herzlieb, M.; Rosenfeld, A.; Krüger, J.; Bonse, J. Femtosecond laser-induced periodic surface structures on silicon upon polarization controlled two-color double-pulse irradiation. Opt. Express 2015, 23, 61–71. [Google Scholar] [CrossRef]
- Jaeggi, B.; Neuenschwander, B.; Zimmermann, M.; Zecherle, M.; Boeckler, E.W. Time-Optimized Laser Micro Machining by Using a New High Dynamic and High Precision Galvo Scanner. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXI, Proceedings of the SPIE LASE, San Francisco, CA, USA, 13–18 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9735, p. 973513. [Google Scholar]
- Häfner, T.; Heberle, J.; Holder, D.; Schmidt, M. Adjustment of surface energy on steel surfaces due to CLP generation by picosecond laser processing. In Proceedings of the Lasers in Manufacturing Conference, Munich, Germany, 22–25 June 2015; pp. 1–10. [Google Scholar]
- Jaeggi, B.; Neuenschwander, B.; Hunziker, U.; Zuercher, J.; Meier, T.; Zimmermann, M.; Selbmann, K.H.; Hennig, G. Ultra-High-Precision Surface Structuring by Synchronizing a Galvo Scanner with an Ultra-Short-Pulsed Laser System in MOPA Arrangement. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XVII, Proceedings of the SPIE LASE, San Francisco, CA, USA, 21–26 January 2012; 82430K; SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Loeschner, U.; Schille, J.; Streek, A.; Knebel, T.; Hartwig, L.; Hillmann, R.; Endisch, C. High-rate laser microprocessing using a polygon scanner system. J. Laser Appl. 2015, 27, S29303. [Google Scholar] [CrossRef]
- Schille, J.; Schneider, L.; Mauersberger, S.; Szokup, S.; Höhn, S.; Pötschke, J.; Reiß, F.; Leidich, E.; Löschner, U. High-Rate Laser Surface Texturing for Advanced Tribological Functionality. Lubricants 2020, 8, 33. [Google Scholar] [CrossRef] [Green Version]
- Jaeggi, B.; Remund, S.; Streubel, R.; Goekce, B.; Barcikowski, S.; Neuenschwander, B. Laser Micromachining of Metals with Ultra-Short Pulses: Factors Limiting the Scale-Up Process. JLMN 2017, 12, 267–273. [Google Scholar]
- Brenner, A.; Zecherle, M.; Verpoort, S.; Schuster, K.; Schnitzler, C.; Kogel-Hollacher, M.; Reisacher, M.; Nohn, B. Efficient production of design textures on large-format 3D mold tools. J. Laser Appl. 2020, 32, 012018. [Google Scholar] [CrossRef] [Green Version]
- Phipps, C.; Luke, J. Diode Laser-Driven Microthrusters: A New Departure for Micropropulsion. AIAA J. 2002, 40, 310–318. [Google Scholar] [CrossRef] [Green Version]
- Phipps, C.; Birkan, M.; Bohn, W.; Eckel, H.-A.; Horisawa, H.; Lippert, T.; Michaelis, M.; Rezunkov, Y.; Sasoh, A.; Schall, W.; et al. Review: Laser-Ablation Propulsion. J. Propuls. Power 2010, 26, 609–637. [Google Scholar] [CrossRef]
- Phipps, C.R.; Baker, K.L.; Libby, S.; Liedahl, D.A.; Olivier, S.S.; Pleasance, L.D.; Rubenchik, A.; Trebes, J.E.; George, E.V.; Marcovici, B.; et al. Removing orbital debris with lasers. Adv. Space Res. 2012, 49, 1283–1300. [Google Scholar] [CrossRef] [Green Version]
- Scharring, S.; Lorbeer, R.A.; Karg, S.; Pastuschka, L.; Förster, D.J.; Eckel, H.A. The MICROLAS Concept: Precise Thrust Generation in the Micronewton Range by Laser Ablation. In Technology for Small Satellite Research: Payloads and Subsystem Technologies Small Satellite Applications, Missions, and In-Orbit Experiences; International Academy of Astronautics: Stockholm, Sweden, 2016; pp. 27–34. [Google Scholar]
- Phipps, C.R. Laser Ablation Propulsion and Its Applications in Space. In Superconductivity; Springer Science and Business Media: New York, NY, USA, 2018; Volume 274, pp. 217–246. [Google Scholar]
- Levchenko, I.; Bazaka, K.; Mazouffre, S.; Xu, S. Prospects and physical mechanisms for photonic space propulsion. Nat. Photon. 2018, 12, 649–657. [Google Scholar] [CrossRef]
- Lorbeer, R.-A.; Zwilich, M.; Zabic, M.; Scharring, S.; Eisert, L.; Wilken, J.; Schumacher, D.; Roth, M.; Eckel, H.-A. Experimental verification of high energy laser-generated impulse for remote laser control of space debris. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Cremers, D.A.; Knight, A.K. Laser-Induced Breakdown Spectroscopy. In Encyclopedia of Analytical Chemistry; Meyers, R.A., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000; p. a5110t. [Google Scholar]
- Song, K.; Lee, Y.-I.; Sneddon, J. Recent developments in instrumentation for laser induced breakdown spectroscopy. Appl. Spectrosc. Rev. 2002, 37, 89–117. [Google Scholar] [CrossRef]
- Miziolek, A.W.; Palleschi, V.; Schechter, I. Laser-Induced Breakdown Spectroscopy (LIBS): Fundamentals and Applications; Cambridge University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kim, B.-M.; Feit, M.; Rubenchik, A.; Mammini, B.; Da Silva, L. Optical feedback signal for ultrashort laser pulse ablation of tissue. Appl. Surf. Sci. 1998, 127-129, 857–862. [Google Scholar] [CrossRef] [Green Version]
- Margetic, V.; Pakulev, A.; Stockhaus, A.; Bolshov, M.; Niemax, K.; Hergenröder, R. A comparison of nanosecond and femtosecond laser-induced plasma spectroscopy of brass samples. Spectrochim. Acta Part B At. Spectrosc. 2000, 55, 1771–1785. [Google Scholar] [CrossRef]
- Burgio, L.; Melessanaki, K.; Doulgeridis, M.; Clark, R.; Anglos, D. Pigment identification in paintings employing laser induced breakdown spectroscopy and Raman microscopy. Spectrochim. Acta Part B At. Spectrosc. 2001, 56, 905–913. [Google Scholar] [CrossRef]
- Serifaki, K.; Boke, H.; Yalcin, S.; Ipekoglu, B. Characterization of materials used in the execution of historic oil paintings by XRD, SEM-EDS, TGA and LIBS analysis. Mater. Charact. 2009, 60, 303–311. [Google Scholar] [CrossRef] [Green Version]
- Borba, F.D.S.L.; Cortez, J.; Asfora, V.K.; Pasquini, C.; Pimentel, M.F.; Pessis, A.-M.; Khoury, H.J. Multivariate treatment of LIBS data of prehistoric paintings. J. Braz. Chem. Soc. 2012, 23, 958–965. [Google Scholar] [CrossRef]
- Dikmelik, Y.; McEnnis, C.; Spicer, J.B. Femtosecond and nanosecond laser-induced breakdown spectroscopy of trinitrotoluene. Opt. Express 2008, 16, 5332–5337. [Google Scholar] [CrossRef] [PubMed]
- Gottfried, J.L.; De Lucia, F.C.; Munson, C.A.; Miziolek, A.W. Laser-induced breakdown spectroscopy for detection of explosives residues: A review of recent advances, challenges, and future prospects. Anal. Bioanal. Chem. 2009, 395, 283–300. [Google Scholar] [CrossRef]
- Shaik, A.K.; Epuru, N.R.; Syed, H.; Byram, C.; Soma, V.R. Femtosecond laser induced breakdown spectroscopy based standoff detection of explosives and discrimination using principal component analysis. Opt. Express 2018, 26, 8069–8083. [Google Scholar] [CrossRef]
- Gurevich, E.L.; Hergenröder, R. Femtosecond Laser-Induced Breakdown Spectroscopy: Physics, Applications, and Perspectives. Appl. Spectrosc. 2007, 61, A233–A242. [Google Scholar] [CrossRef]
- Malvezzi, A.M. Laser–Matter Interaction in LIBS Experiments. In Laser-Induced Breakdown Spectroscopy; Musazzi, S., Perini, U., Eds.; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2014; Volume 182, pp. 3–29. [Google Scholar]
- Labutin, T.A.; Lednev, V.N.; Ilyin, A.A.; Popov, A. Femtosecond laser-induced breakdown spectroscopy. J. Anal. At. Spectrom. 2015, 31, 90–118. [Google Scholar] [CrossRef]
- Piñon, V.; Fotakis, C.; Nicolas, G.; Anglos, D. Double pulse laser-induced breakdown spectroscopy with femtosecond laser pulses. Spectrochim. Acta Part B At. Spectrosc. 2008, 63, 1006–1010. [Google Scholar] [CrossRef]
- Lu, Y.; Zorba, V.; Mao, X.; Zheng, R.; Russo, R.E. UV fs–ns double-pulse laser induced breakdown spectroscopy for high spatial resolution chemical analysis. J. Anal. At. Spectrom. 2013, 28, 743–748. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Khoroshkov, V.S. Feasibility of using laser ion accelerators in proton therapy. Plasma Phys. Rep. 2002, 28, 453–456. [Google Scholar] [CrossRef]
- Ditmire, T.; Donnelly, T.; Rubenchik, A.M.; Falcone, R.W.; Perry, M.D. Interaction of intense laser pulses with atomic clusters. Phys. Rev. A 1996, 53, 3379–3402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malka, V.; Fritzler, S. Electron and proton beams produced by ultra short laser pulses in the relativistic regime. Laser Part. Beams 2004, 22, 399–405. [Google Scholar] [CrossRef]
- Neely, D.; Foster, P.; Robinson, A.; Lindau, F.; Lundh, O.; Persson, A.; Wahlström, C.-G.; McKenna, P. Enhanced proton beams from ultrathin targets driven by high contrast laser pulses. Appl. Phys. Lett. 2006, 89, 021502. [Google Scholar] [CrossRef]
- Andreev, A.; Sonobe, R.; Kawata, S.; Miyazaki, S.; Sakai, K.; Miyauchi, K.; Kikuchi, T.; Platonov, K.; Nemoto, K. Effect of a laser prepulse on fast ion generation in the interaction of ultra-short intense laser pulses with a limited-mass foil target. Plasma Phys. Control. Fusion 2006, 48, 1605–1619. [Google Scholar] [CrossRef]
- Passoni, M.; Bertagna, L.; Zani, A. Target normal sheath acceleration: Theory, comparison with experiments and future perspectives. New J. Phys. 2010, 12, 045012. [Google Scholar] [CrossRef]
- Daido, H.; Nishiuchi, M.; Pirozhkov, A. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 2012, 75, 056401. [Google Scholar] [CrossRef]
- Fourmaux, S.; Buffechoux, S.; Albertazzi, B.; Capelli, D.; Levy, A.; Gnedyuk, S.; Lecherbourg, L.; Lassonde, P.; Payeur, S.; Antici, P.; et al. Investigation of laser-driven proton acceleration using ultra-short, ultra-intense laser pulses. Phys. Plasmas 2013, 20, 013110. [Google Scholar] [CrossRef] [Green Version]
- Barberio, M.; Veltri, S.; Scisciò, M.; Antici, P. Laser-Accelerated Proton Beams as Diagnostics for Cultural Heritage. Sci. Rep. 2017, 7, 40415. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barberio, M.; Scisciò, M.; Vallières, S.; Cardelli, F.; Chen, S.N.; Famulari, G.; Gangolf, T.; Revet, G.; Schiavi, A.; Senzacqua, M.; et al. Laser-accelerated particle beams for stress testing of materials. Nat. Commun. 2018, 9, 372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torrisi, L.; Cutroneo, M.; Torrisi, A.; Silipigni, L.; Costa, G.; Rosinski, M.; Badziak, J.; Wołowski, J.; Zaraś-Szydłowska, A.; Parys, P. Protons accelerated in the target normal sheath acceleration regime by a femtosecond laser. Phys. Rev. Accel. Beams 2019, 22, 021302. [Google Scholar] [CrossRef] [Green Version]
- Bulanov, S.; Esirkepov, T.; Khoroshkov, V.; Kuznetsov, A.; Pegoraro, F. Oncological hadrontherapy with laser ion accelerators. Phys. Lett. A 2002, 299, 240–247. [Google Scholar] [CrossRef]
- Malka, V.; Faure, J.; Gauduel, Y.A. Ultra-short electron beams based spatio-temporal radiation biology and radiotherapy. Mutat. Res. Mutat. Res. 2010, 704, 142–151. [Google Scholar] [CrossRef]
- Schardt, D.; Elsaesser, T.; Schulz-Ertner, D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev. Mod. Phys. 2010, 82, 383–425. [Google Scholar] [CrossRef]
- Döppner, T.; Fennel, T.; Diederich, T.; Tiggesbäumker, J.; Meiwes-Broer, K.H. Controlling the Coulomb Explosion of Silver Clusters by Femtosecond Dual-Pulse Laser Excitation. Phys. Rev. Lett. 2005, 94, 013401. [Google Scholar] [CrossRef]
- Markey, K.; McKenna, P.; Brenner, C.M.; Carroll, D.C.; Günther, M.M.; Harres, K.; Kar, S.; Lancaster, K.; Nürnberg, F.; Quinn, M.N.; et al. Spectral Enhancement in the Double Pulse Regime of Laser Proton Acceleration. Phys. Rev. Lett. 2010, 105, 195008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uryupina, D.S.; Ivanov, K.A.; Brantov, A.; Savel’Ev, A.B.; Bychenkov, V.Y.; Povarnitsyn, M.E.; Volkov, R.V.; Tikhonchuk, V.T. Femtosecond laser-plasma interaction with prepulse-generated liquid metal microjets. Phys. Plasmas 2012, 19, 13104. [Google Scholar] [CrossRef]


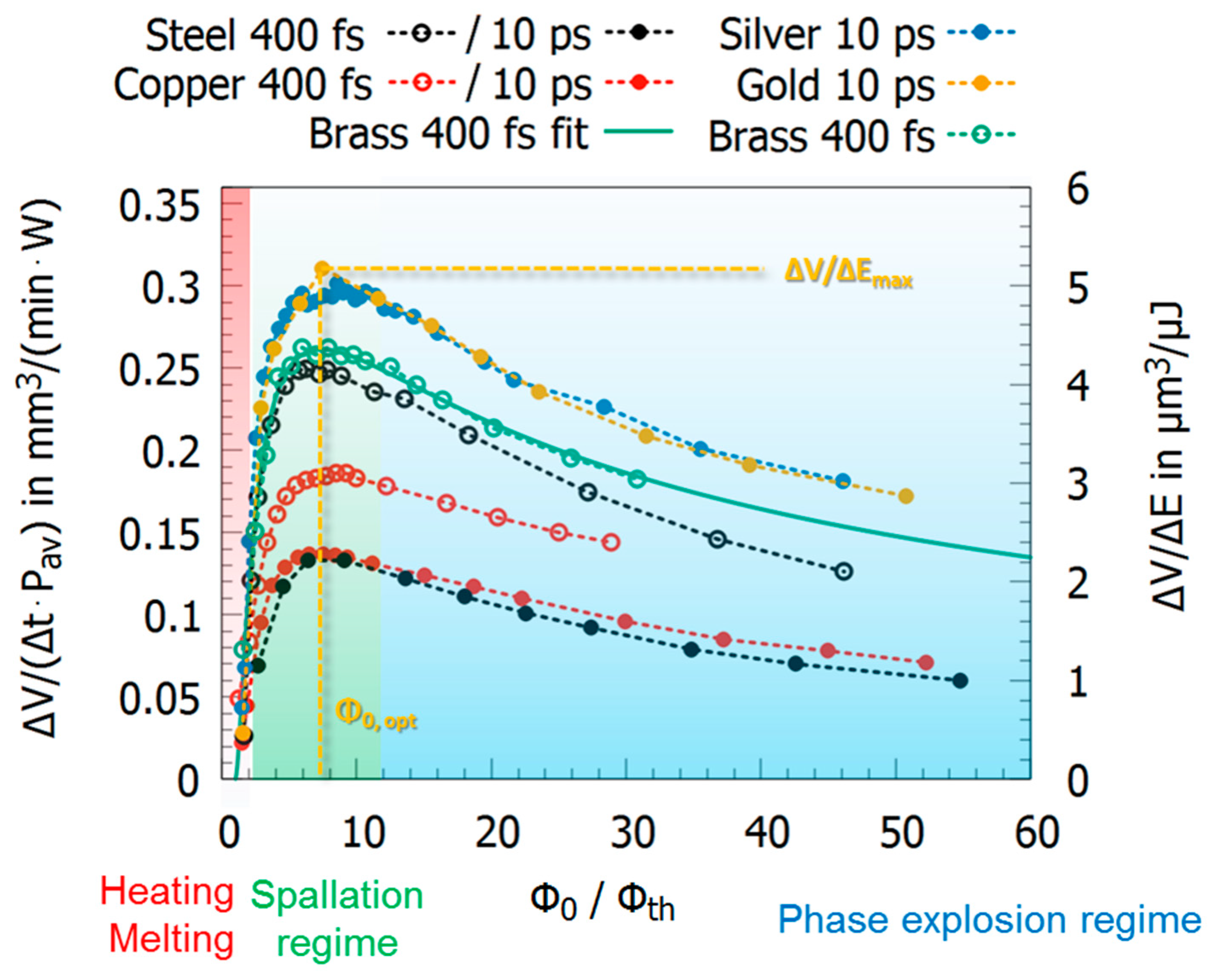






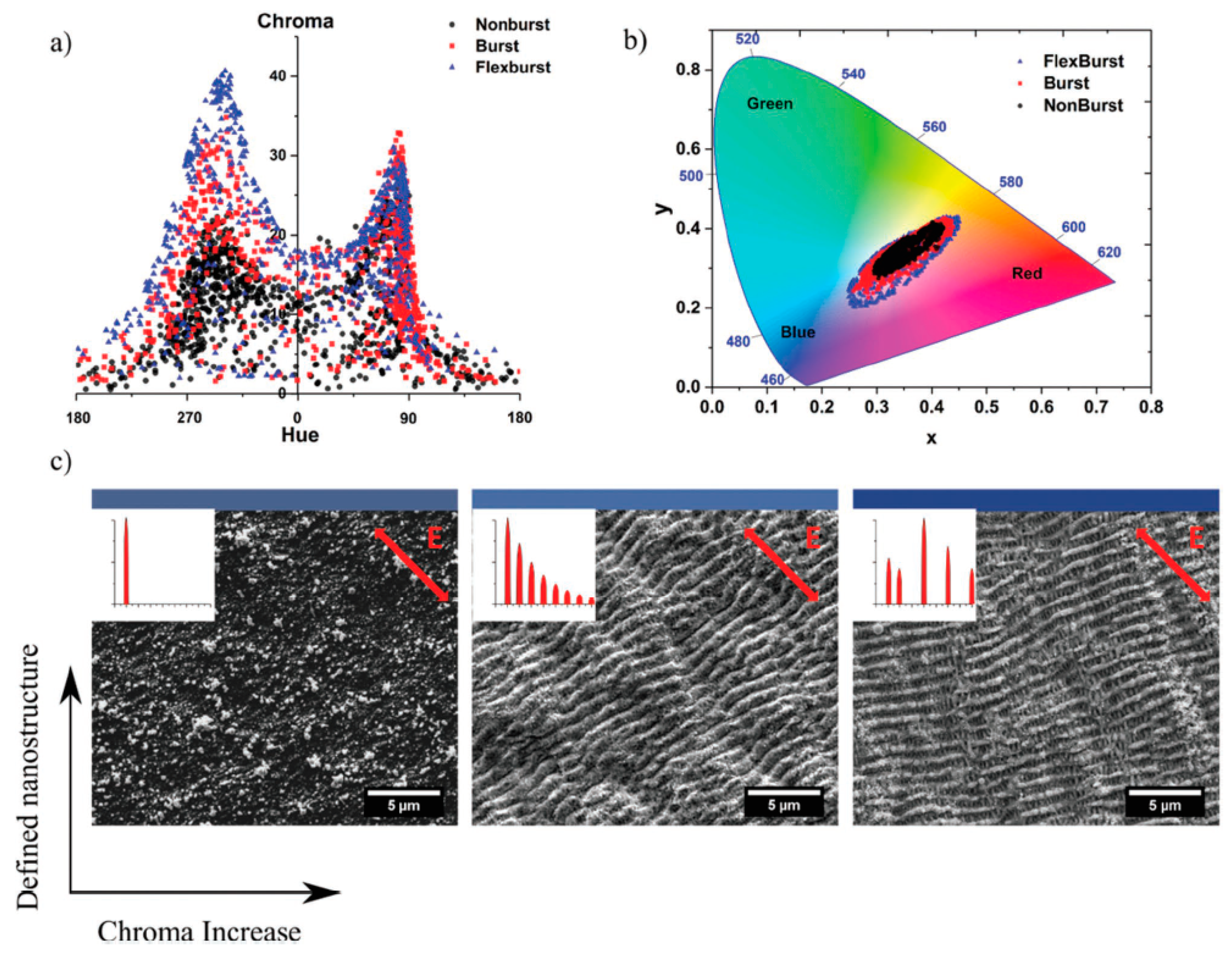

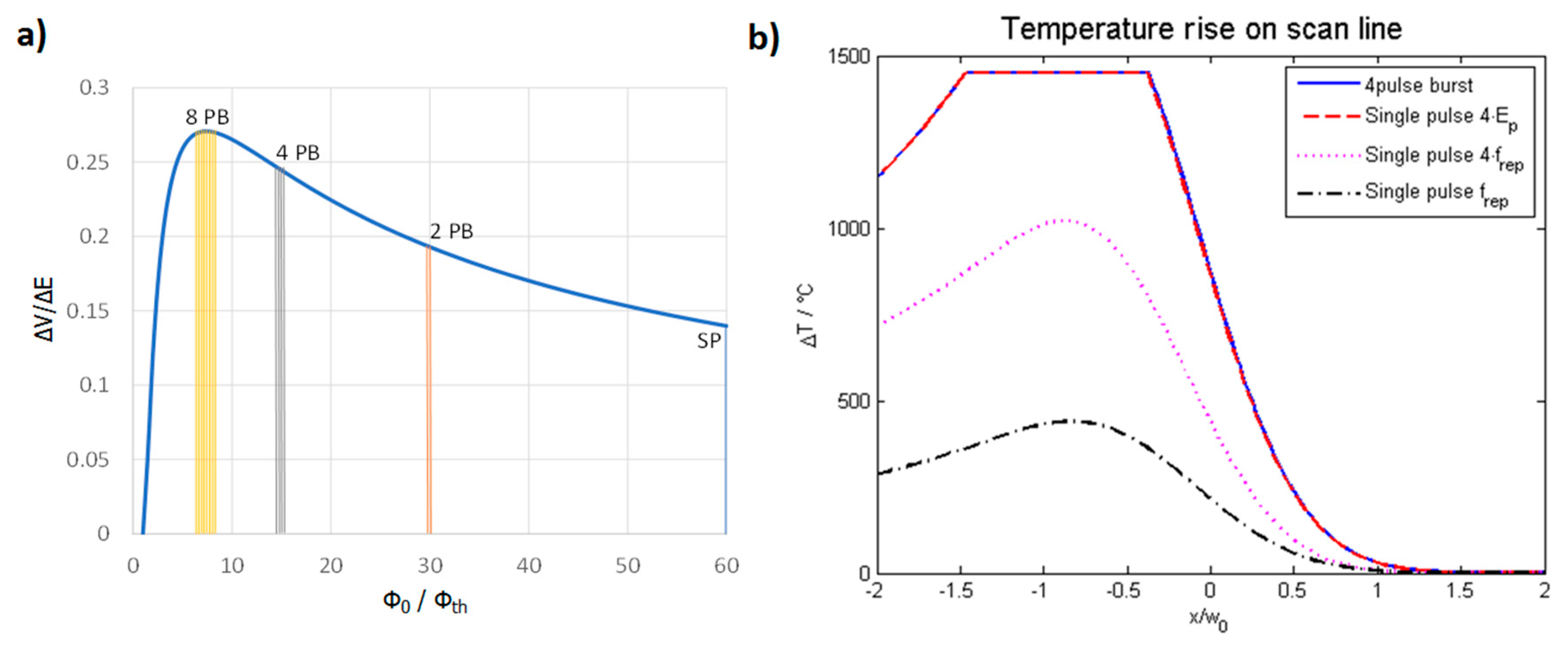

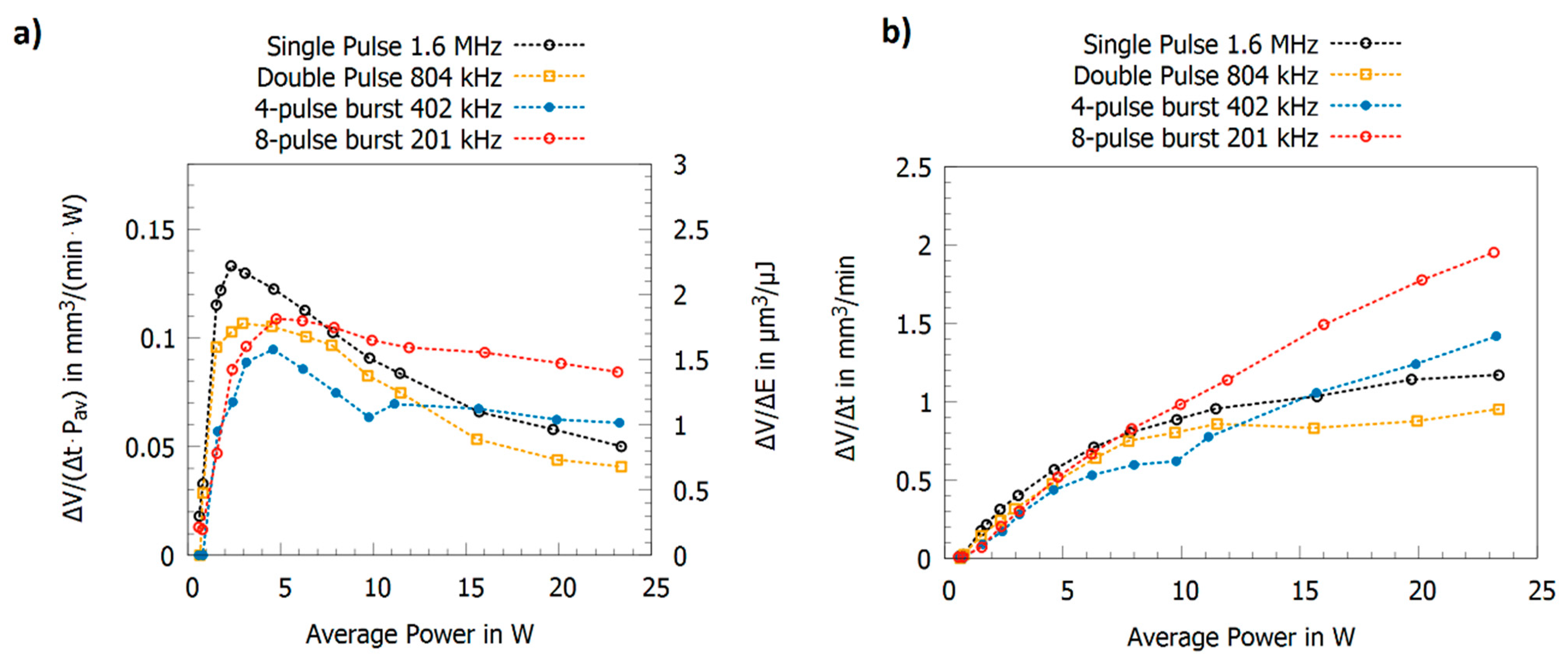

| Material | Ag | Al | Au | Cu | Fe | Mb | Ni | Pt | Ti | W |
|---|---|---|---|---|---|---|---|---|---|---|
| τel-phon in ps | 84.3 1 | 4.5 1 | 115.5 1 | 57.5 2 | 1.3 3 | 2.2 4 | 1.1 4 | 2.2 5 | 1.9 5 | 12.1 5 |
| Quantity | Brass 1 | Copper 1 | Copper 2 | Gold 2 | Silver 2 | Steel 1 | Steel 2 | |
|---|---|---|---|---|---|---|---|---|
| nm | 1030 | 1030 | 1064 | 1064 | 1064 | 1030 | 1064 | |
| ps | 0.4 | 0.4 | 10 | 10 | 10 | 0.4 | 10 | |
| (fit) | nm | 62.3 | 55.7 | 29.1 | 64.8 | 67.2 | 13.9 | 4.5 |
| (fit) | J/cm2 | 0.39 | 0.49 | 0.35 | 0.35 | 0.36 | 0.09 | 0.06 |
| mm3/W/min | 0.26 | 0.19 | 0.14 | 0.30 | 0.30 | 0.25 | 0.13 | |
| µm3/µJ | 4.3 | 3.1 | 2.3 | 5.0 | 5.0 | 4.2 | 2.2 | |
| J/cm2 | 2.7 | 4.5 | 2.2 | 2.4 | 2.7 | 0.5 | 0.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Förster, D.J.; Jäggi, B.; Michalowski, A.; Neuenschwander, B. Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses. Materials 2021, 14, 3331. https://doi.org/10.3390/ma14123331
Förster DJ, Jäggi B, Michalowski A, Neuenschwander B. Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses. Materials. 2021; 14(12):3331. https://doi.org/10.3390/ma14123331
Chicago/Turabian StyleFörster, Daniel J., Beat Jäggi, Andreas Michalowski, and Beat Neuenschwander. 2021. "Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses" Materials 14, no. 12: 3331. https://doi.org/10.3390/ma14123331
APA StyleFörster, D. J., Jäggi, B., Michalowski, A., & Neuenschwander, B. (2021). Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses. Materials, 14(12), 3331. https://doi.org/10.3390/ma14123331







