2. Numerical Subroutine for Predicting the Direction of Crack Propagation
A subroutine is a program code written in Fortran that can replace a fragment of the Abaqus solver algorithm. In this work, it was necessary to perform three different subroutines, each with a different task. The implementation of these subroutines enabled the use of any failure criterion.
To explain how the subroutines work, we start by explaining the algorithm of the Abaqus system during the calculations. Calculations in a solver that uses Abaqus are divided into individual stages. The largest stage is the step, which is the stage of the calculation given by the user. The steps are divided into increments. They allow for a smooth linear load increase so that at the post-processing stage, it is possible to read the results appearing during the model loading. The increments are divided into iterations. In each iteration, displacements at all integration points in all finite elements of the model are calculated. The X-FEM in Abaqus allows for the use of only four-node elements; however, it is possible to choose between a regular four-node plane stress element with four integration points (CPS4) and the same element with reduced integration, i.e., with one integration point (CPS4R). It was decided that the created subroutines would only work with the CPS4 elements, because four times as many data points will produce more accurate results. Similarly, for an axially symmetric task, 4-node axisymmetric elements (CAX4) are used.
As shown in the algorithm in
Figure 1 the program starts the user subroutine to generate element output (UVARM) subroutine and then the UDMGINI subroutine after each calculation of displacement at each integration point. Before each increment, Abaqus saves the selected results to the results file (a selection of the data is saved in the appropriate place in the input file by the user). The data are then read from the results file by the user subroutine to read the results file (URDFIL) subroutine. The UVARM and UDMGINI subroutines are launched many times more than the URDFIL subroutine. Theoretically, the whole process could be performed without the URDFIL subroutine, but the computation would take incomparably longer. It was decided that the most important calculations would be performed in the URDFIL subroutine to reduce the simulation time. Additionally, there is a place in the computer’s memory called the common block. It is a memory common to all subroutines, and it allows the results of calculations to be transferred between subroutines.
UVARM is used to read the results available for the currently analyzed integration point. The UDMGINI subroutine is used to define the direction of the crack propagation and the value of the material effort. The URDFIL subroutine is responsible for reading the results file before each load increment and using the common block for transmitting these results to other subroutines. In this case, it was also used to calculate the crack propagation angle α from the read results.
Abaqus works very simply in the default method of determining the direction of fracture propagation using the criterion of maximum principal stresses, without the use of subroutines. It reads the stresses at each integration point that belongs to an element with an enrichment function. These are all elements at the beginning of the simulation, and after the fracture is formed, the three elements closest to the crack tip are included. Then, these stresses are rotated to the principal stresses. The rotation angle of these stresses is the angle of the fracture propagation for its next increment. A crack occurs when the material effort is greater than 1. Material effort in this case is the maximum principal stresses found in the model divided by the user-specified tensile strength value. Unfortunately, in the case of a four-node element, Abaqus averages the value of the four integration points in one element. Most often, the stresses at one integration point exceed the tensile strength, but the average does not yet, which is a misconception. Additionally, Abaqus averages the four rotation vectors of the stress tensor, which also means that the direction of propagation is often incorrect. The tensor rotation is significantly influenced by shear stresses, which are often disturbed near the crack tip. The method described below is a solution to all the problems mentioned above.
When the UDMGINI subroutine is performed for the first three integration points in an element, the program only collects data and remembers them until it reaches the last integration point in the element. For the first three elements, the criterion value and the crack propagation direction vector are defined as 0. As Abaqus averages the values of the crack propagation direction vector from four integration points, it was found that the average of one determined vector for the fourth integration point and three zero vectors will provide a vector directed in the same direction. Similarly, for the maximum principal stress criterion, the algorithm finds the maximum principal stresses at the four integration points, and while processing the fourth point, it selects the largest value of the four (the integration point with the highest effort) and then multiplies it by 4, so that the program (when calculating the arithmetic mean) obtains the real value closest to the crack tip. The crack propagation direction vector for this method is counted in the URDFIL subroutine and only the final value is passed to the UDMGINI subroutine.
We assumed that around the hypothetical crack in any model, the stress field would be close to the Westergaard solution for the Griffith fracture (
Figure 2). This task is symmetrical along the initial crack, which means that the crack should propagate at an angle of 0°. The stresses around the crack tip in the polar coordinate system for Mode I of loading are as follows (assuming the stress intensity factor = 1):
By substituting the radius
r of any value (e.g., 1) and converting the above formulas to the principal stresses, for an angle of 0°, there is a local minimum value of the principal stresses in a certain range of angles (adopted from −60° to 60°), as shown in
Figure 3.
The absolute conditions that must be met by the angle of the crack propagation were determined:
It must be zero for the first derivative of the function (because this point is the extreme),
The second derivative of the function must be positive (because it is the minimum), and
This is the value closest to the angle found in the previous load increment (since sometimes two angle values meet the above two conditions).
The URDFIL subroutine first reads the following data from the results file: node coordinates, node displacements, integration point coordinates, integration point stresses, and the values of
φ function of the level set method (PHILSM). In Abaqus, it is not possible to read the crack tip coordinates directly from the results file. Therefore, before the operation of the crack propagation algorithm will be presented, the data from Abaqus, named PHILSM, should be explained. PHILSM is a result that occurs only on cracked finite elements. On one side of the crack, it has positive values; on the other, it has negative values. With a linear fit, the crack is where the PHILSM takes the value of 0 (
Figure 4). Knowing the PHILSM values in the nodes and their coordinates, the algorithm determines the coordinates of the crack tip.
Based on the figure above, we found that the crack tip localized in an element that had one node with a negative PHILSM value, one node with a positive PHILSM value, and two nodes without a PHILSM value. Based on the linear interpolation of the coordinates of the nodes with PHILSM values, the coordinates of the crack tip are searched.
Based on changes in the PHILSM value, the algorithm also checks whether a crack is already present in the model and whether there has been an increase in the crack propagation in the analyzed increment. The program searches the direction of the crack propagation only in increments when in the previous increment there was an increase in the crack length. This saves computation time.
After finding the crack tip coordinates, the origin of the coordinate system is transferred to the crack tip, and the angle of the last crack propagation is set to 0°. Next, the algorithm searches for several dozen integration points around the crack tip; it reads the stresses at these points and then counts the values of the maximum principal stresses at these points. There should be enough points (no less than 30 were set) to obtain an accurate graph of a function similar to the Westergaard function. There must not be too many points (no more than 300 were set) so that points too far from the crack tip are not considered and so that the other stress concentration points in the model do not interfere with the results.
In the next step, these stresses are reduced to a unit radius, as shown in
Figure 3. Following Equation (1), for this purpose, the stresses are multiplied by
, where
r is the distance of the crack tip from the analyzed integration point.
Based on these values, it is possible to create a plot of the maximum principal stress versus the angle around the crack tip, which should be similar to the plot in
Figure 3. The sixth-degree polynomial is fitted to these points using the least-squares method. Then, a point that meets three conditions is searched, i.e., the zero of the derivative of this polynomial is searched by the bisection method (the closest to the angle of the crack propagation from the previous increment). The value obtained is the next crack propagation angle, which is passed to the UDMGINI subroutine.
The operation of this algorithm is shown in
Figure 5. In
Figure 5a, the values of the principal stresses are inserted around the crack tip in an exemplary calculation step. In
Figure 5b, these stresses are divided by
, and in
Figure 5c, the polynomial is fitted and the minimum is found near the previous crack propagation angle (0°). This angle is the new crack propagation angle
α, which is transferred to the UDMGINI subroutine.
None of the above steps can work when the crack has not yet appeared in the model. The difficulty in locating the initial fracture is a known problem in the X-FEM. In such a case, it was decided that the coordinates of the crack tip are taken as the coordinates of the integration point where the highest maximum principal stresses occur, while the direction of the crack propagation from the previous increment was assumed as the direction from the outside of the model to the inside, so this can help to find the first crack propagation direction in the simulation.
The criterion of the minimum gradient of the effort function for the Ottosen–Podgórski (O–P) failure criterion [
11,
12] was implemented very similarly. The O–P failure criterion is expressed as a relationship of three alternative stress tensor invariants:
where
P(
J) is a function describing the cross-section of the boundary surface by a deviator plane
σ0 = const., and is given by the equation
;
α,
β,
C0,
C1, and
C2 are material constants that can be obtained from the formulas presented in [
12,
13].
In this case, instead of the maximum principal stresses around the crack tip, the values of the material effort function
μ is calculated as:
where
σ0 and
τ0 are the normal and tangential octahedral stresses determined at the tested point around the crack tip in the polar system, respectively; and
σf and
τf are the values of critical stresses proportional to
σ0 and
τ0, respectively [
13].
By inserting the Westergaard’s stresses as data around the crack tip, the material effort
μ also takes a local minimum in the direction of the crack propagation, which can be seen in
Figure 6.
The algorithm differs in two places from the criterion of the maximum principal stresses. The calculation of the crack propagation angle in the URDFIL subroutine is calculated using the material effort instead of the principal stresses. In the UDMGINI subroutine, the decision of crack initiation is made when the material effort is greater than 1.
The novel criterion, called the minimum displacement criterion, was created next. It is based on the distribution of displacements around Griffith’s crack, which in Mode I of the crack loading is described by the following formulas:
ux and
uy are horizontal and vertical displacements at any point in the polar system around the crack tip, respectively, assuming that the crack tip does not move (e.g., due to the movement of the entire model under load). The diagram of these displacements is shown in
Figure 7. After rotating these displacements by angle
θ into displacements
ur and
uθ, in the crack propagation direction:
Displacements along the radius ur take the minimum value;
Displacements perpendicular to the radius uθ = 0 or d2u/dθ 2 = 0 (min duθ);
The resultant displacements u have a minimum value;
We decided to use the third condition. This situation is illustrated in
Figure 8.
The difference between the subroutines is that the stresses at the integration points are not read, but the displacements at the nodes are. In the URDFIL subroutine, the resultant displacements are read for at least 30 points around the crack tip, then the displacements are shifted so that at the crack tip, as in the Westergaard’s formula, the displacements are zero (because the model usually moves during the simulation). The displacements are reduced to a unit radius according to the relationship described in Equation (4). A 6th-order polynomial is fitted and the minimum is found.
Unfortunately, using this criterion, it is not possible to determine the crack initiation condition. Thus, the criterion of maximum principal stresses was used in the UDMGINI subroutine. Only the direction of the crack is defined by the displacements.
The last criterion modeled is the maximum circumferential tensile stress (MTS) criterion [
14]. It is a criterion based on stress intensity factors. In this case, the fracture occurs in the direction for which the graph described by the formula below reaches the local minimum:
The formula shows that as the values of the stress intensity factors
KI and
KII for the crack are known, it is not necessary to read any further data from the model. We attempted to find the stress intensity factors using the direct method:
To find the direction of the crack propagation, it is not necessary to find the exact values of the coefficients
KI and
KII, only the relations between them. For this reason, the constant values and the influence of the distance from the crack tip can be removed. Hence, the values of the coefficients take a simple form:
where
ux and
uy are the differences in displacements on both sides of the crack along the crack and perpendicular to the crack, respectively. Thus, in
Figure 9, they are
and
, respectively.
The values for u1θ, u2θ, u1r, and u2r are found from the displacement plots ur and uθ by reading these values at the nodes around the crack tip during the simulation. Polynomials are fitted to the displacement plots, and the values for the angles of 180° and −180° are read. Unfortunately, it is not possible to accurately fit a polynomial from an angle of 0° in most cases. The values of displacements very close to the crack calculated during the simulation are often inaccurate and distorted by the crack. For this reason, as will be shown in the next section, the obtained values of KI and KII are far from reality; therefore, the direction of the crack propagation is less precise than for the previous criteria.
Since the KI and KII values are calculated with the unit values of μ and κ in Equation (6), this criterion cannot be used to determine crack initiation in the UDMGINI subroutine. Again, in this case, the criterion of maximum principal stresses was used.
The comparison of the applied criteria predicting the direction of the crack propagation with the maximum energy release rate (MERR) criterion [
15,
16] in the case of unidirectional tensile state is shown in
Figure 10. As can be seen, the criteria based on stresses give practically identical values of the propagation angle in this case. The differences between these criteria become apparent only in the case of two-directional stress states. The criteria based on the analysis of displacements around the crack tip give results that are significantly different from the stress criteria, which becomes very visible for larger slopes of the crack.
3. Laboratory and “In Situ” Tests to Verify the Implemented Subroutine
In order to verify the correctness of the implemented method of predicting the crack propagation path, two laboratory tests were simulated: three-point bending of a beam with a notch and an anchor pull-out test. These results were compared with the results of tests carried out in the laboratory and under “in situ” conditions.
The adopted material was sandstone, and the material parameters of which were taken from previous author’s work [
17]:
Compressive strength fc = 92.563 MPa,
Tensile strength ft = 3.069 MPa,
Young’s modulus E = 13.727 GPa,
Poisson’s ratio ν = 0.148,
Critical strain energy release rate in mode I GIC = 47.946 N/m.
The above results were obtained on the basis of our own laboratory tests. The average compressive strength was obtained from the uniaxial compression test of 12 cubic samples. Before the samples were destroyed, the Young’s modulus and Poisson’s ratio were determined from the compression test of samples with four strain gauges glued in the horizontal and vertical directions on the edges of the sample. The tensile strength was obtained from the three-point bending test of four beams and the "Brazilian" test of 9 cubic samples. Critical fracture energy
GIC in the I mode was determined on the basis of a three-point bending test of three notched beams. The energy value was determined using the method of Brown and Srawley formula [
18].
The description of computer simulations without and with the use of the novel proprietary method of crack propagation with a comparison of the implemented failure criteria are presented below. The failure criterion selected for simulation without the novel method is one of the default criteria recommended in the Abaqus documentation, the maximum principal stress (MAXPS) criterion. As previously described, this criterion rotates the stresses at the integration points into principal stresses and leads the crack according to the rotation vector of the stress tensor when the maximum stresses exceed the tensile strength.
The first test chosen was a three-point beam bending with a notch. The test scheme is shown in
Figure 11a. This test was ideal to carry out first because the fracture line is very predictable, even without simulation. The task is axially symmetrical, so the fracture will certainly run vertically from the cut to the point where the load is applied.
The dimensions of the sample were assumed to be the same as for one of the beams in the laboratory test described in [
17], i.e.,
h = 93.7 mm,
b = 90.22 mm,
l = 320 mm, and
a = 25 mm. The model was constructed in a plane stress state. The mesh size varied from 2 to 15 mm, and the mesh is presented in
Figure 11b. To reduce the dependence of the crack path on the mesh, it was generated chaotically in the area of the planned crack path.
Another test for which simulations were performed was the anchor pull-out test. An attempt to pull out a self-undercutting anchor embedded in sandstone was simulated. In the analyzed study, an anchor was used that was blocked by the wings at the end of the anchor and not by the side surface. The crack simulation in this study has been extensively described in the literature [
19,
20].
Figure 12a shows the anchor prepared for mounting, and
Figure 12b shows a used anchor with folded wings.
To compare the results, a series of in situ tests of pulling out an anchor embedded in a sandstone block were performed. 31 tests were performed for different anchorage depths. The diagram of the relationship between the maximum force and the anchorage depth is presented in
Figure 13. The results of these studies come from the work carried out by the teams of the Institute of Mining Technology in Gliwice and the Lublin University of Technology as part of the project financed by the Polish National Science Center: RODEST No. 2015/19 / B / ST10 / 02817 [
21].
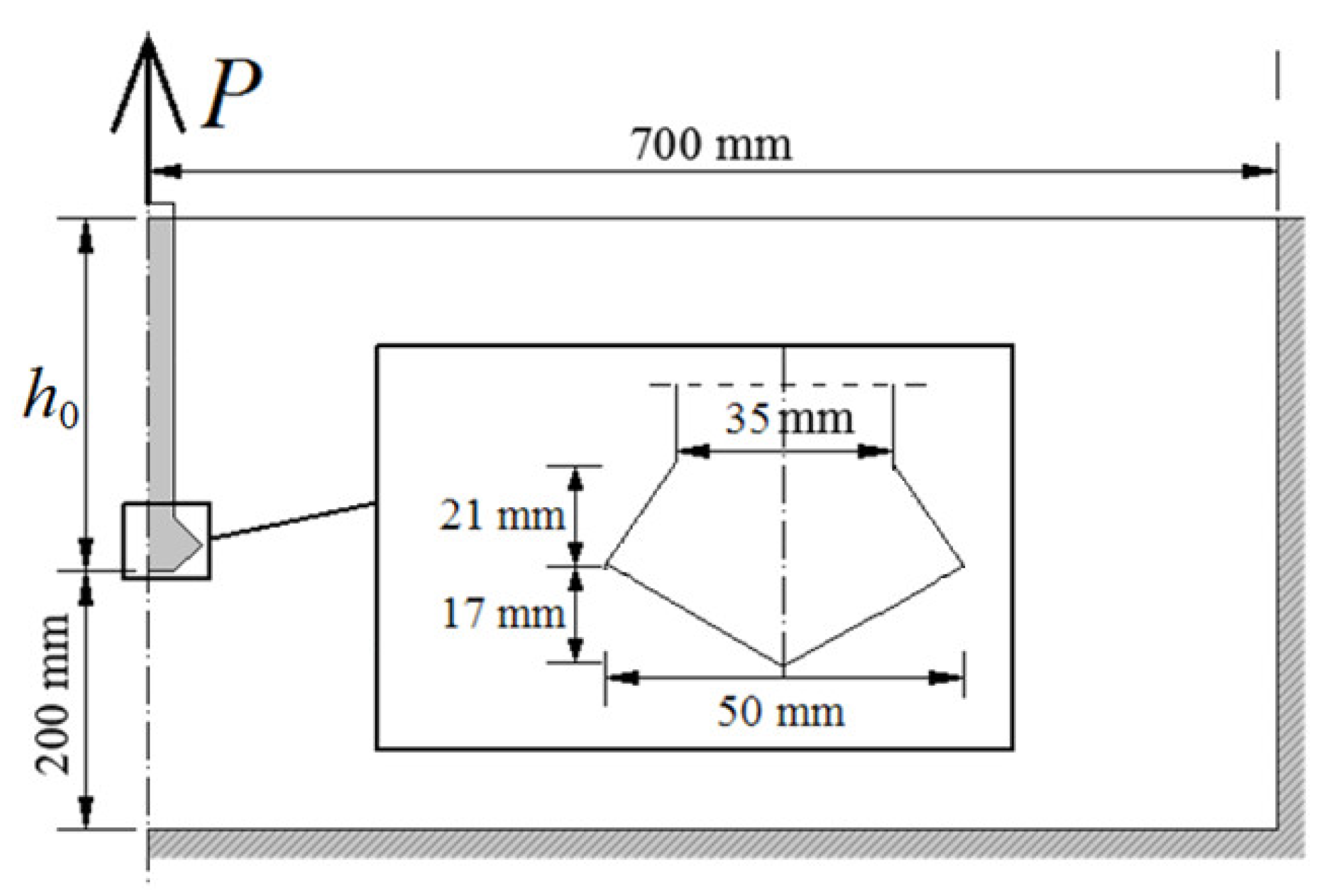
It is a 2D axially symmetric test, the diagram of which is shown in
Figure 14. A large reserve of the model dimensions was assumed so that the boundary conditions did not have a large impact on the result.
In
Figure 14,
P is the pulling-out force and
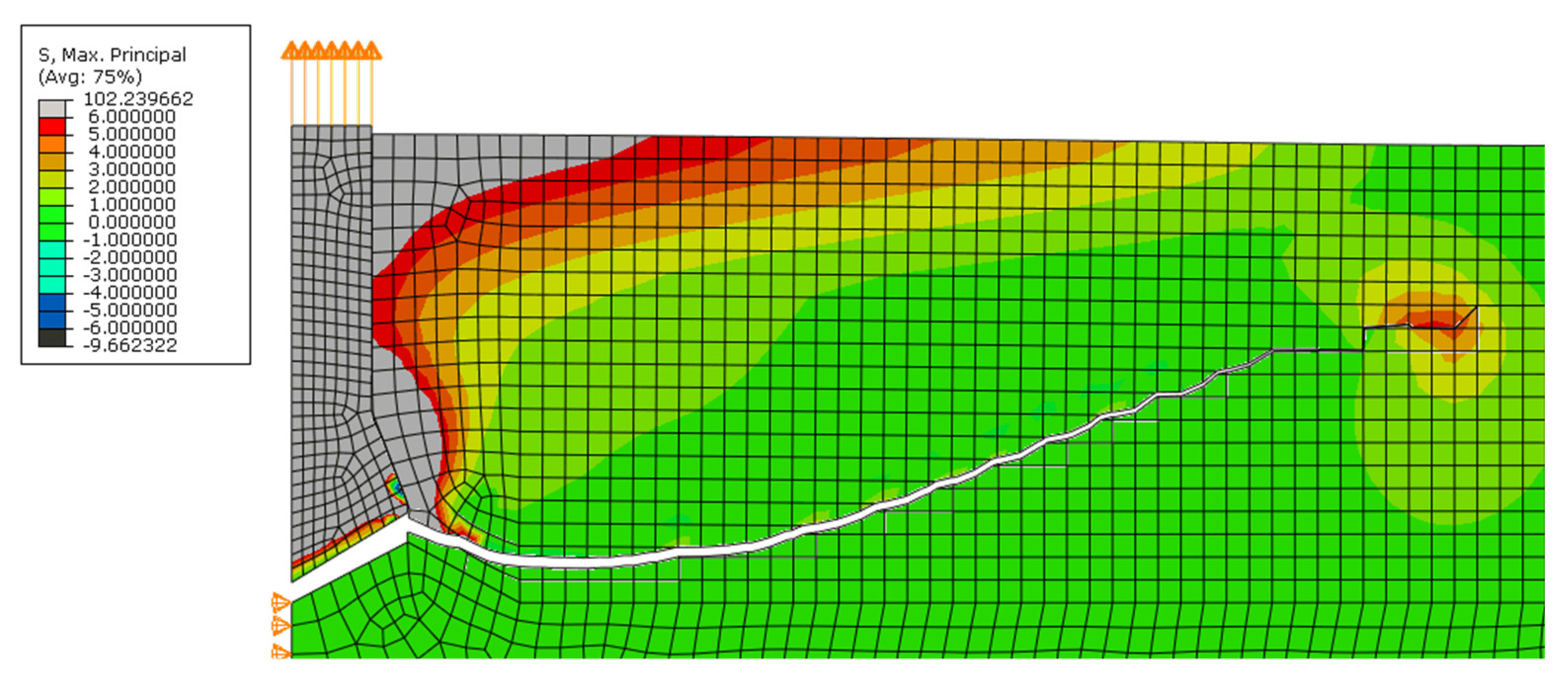
h0 is the anchorage depth. In the computer simulation, the load on the material is transferred through contact at the undercut. In this case, the same material used in the previous study was adopted. The material of the anchor was steel, and the friction coefficient between the materials was 0.1. So far, many simulations with different anchorage depths, material parameters, different mesh, etc., have been performed. For this study, the size of the finite element mesh was from 5 to 25 mm, as shown in
Figure 15. An anchorage depth of 10 cm was assumed.