Influence of Boundary Migration Induced Softening on the Steady State of Discontinuous Dynamic Recrystallization
Abstract
:1. Introduction
- -
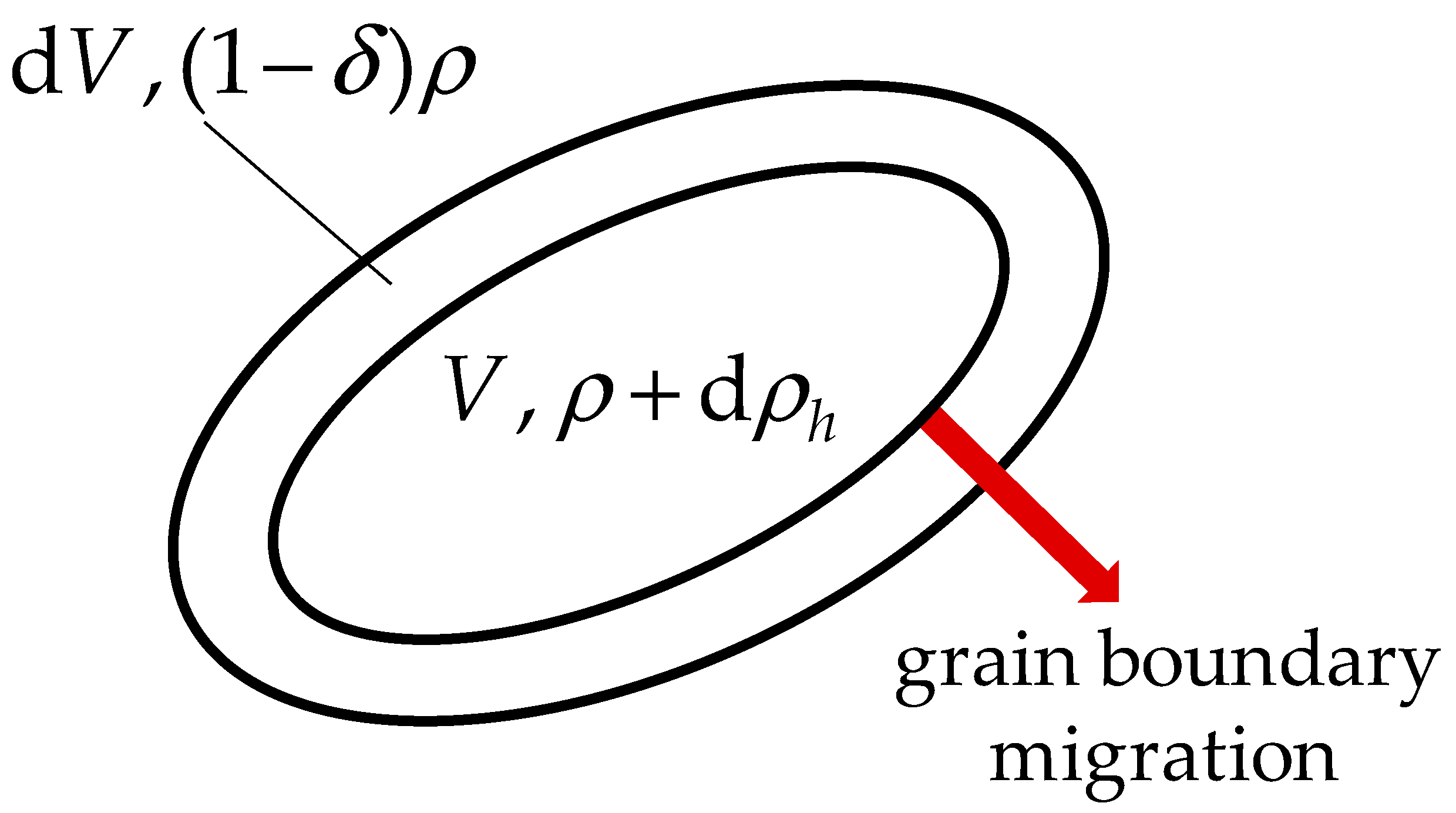
- In SRX, the main softening effect is due to the migration of grain boundaries of the (recrystallized) growing grains, towards regions containing high dislocation densities: it is generally considered that dislocations are completely or almost completely annihilated by their interactions with moving grain boundaries. This mechanism can be referred to as boundary migration induced softening (BMIS). Static recovery within the regions not yet recrystallized constitutes a secondary softening process during SRX. In this way, the material transforms from an initial state of high dislocation density due to prior deformation to a final state with very low dislocation density . This makes SRX very similar to a phase change.
- -
- In DDRX, a more complex situation arises, because the recrystallized grains undergo strain-hardening during their growth. There are then three mechanisms that counterbalance the increase in dislocation density: (1) Dynamic recovery, which takes place in growing as well as shrinking grains; (2) The substitution of “younger” grains for “older” grains with higher dislocation content, whatever the interaction between dislocations and moving boundaries, which is merely a geometric effect, and (3) The annihilation of dislocations by grain boundary migration (BMIS), which is a physical effect. Note that mechanisms (2) and (3) are closely interrelated, although they can be clearly distinguished in theory. At large strain (von Mises equivalent strains of the order of 1), DDRX leads to a steady state where the material behaves as a dissipative structure that converts the mechanical energy input into heat.
2. Basic Equations
2.1. General Formulation of BMIS
2.2. Grain Growth and Strain Hardening Equations
2.3. Introduction of Non-Dimensional Variables
3. Derivation of the Steady State Flow Stress and Grain Size
3.1. Steady State Condition
3.2. Average Steady State Grain Size
3.3. Grain Size and Dislocation Density Changes Along the Lifetime of a Grain
4. Constitutive Parameters
4.1. Microscopic Constitutive Parameters
4.2. Macroscopic Strain Rate Sensitivity and Activation Energy
4.3. Derby Exponent
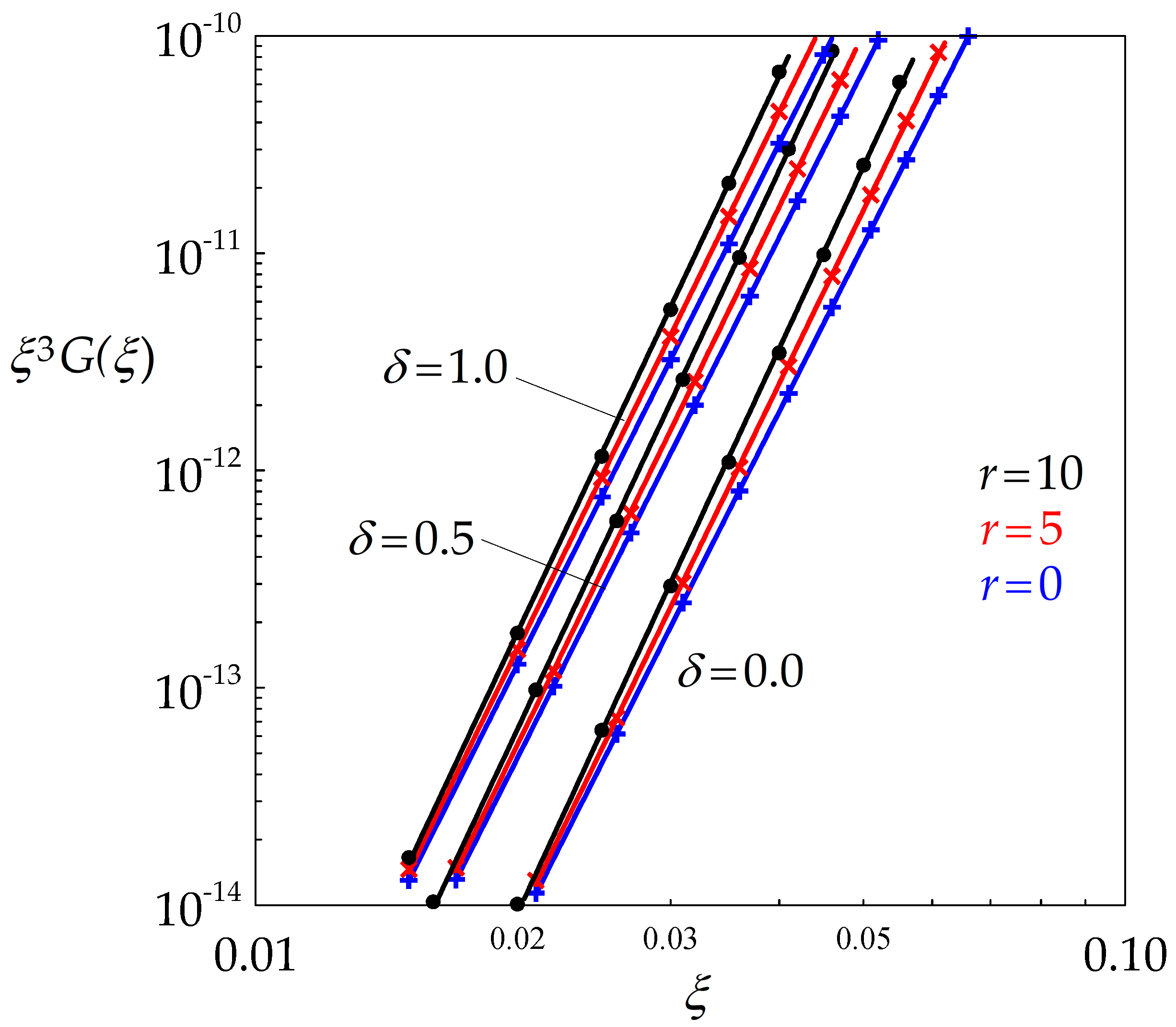
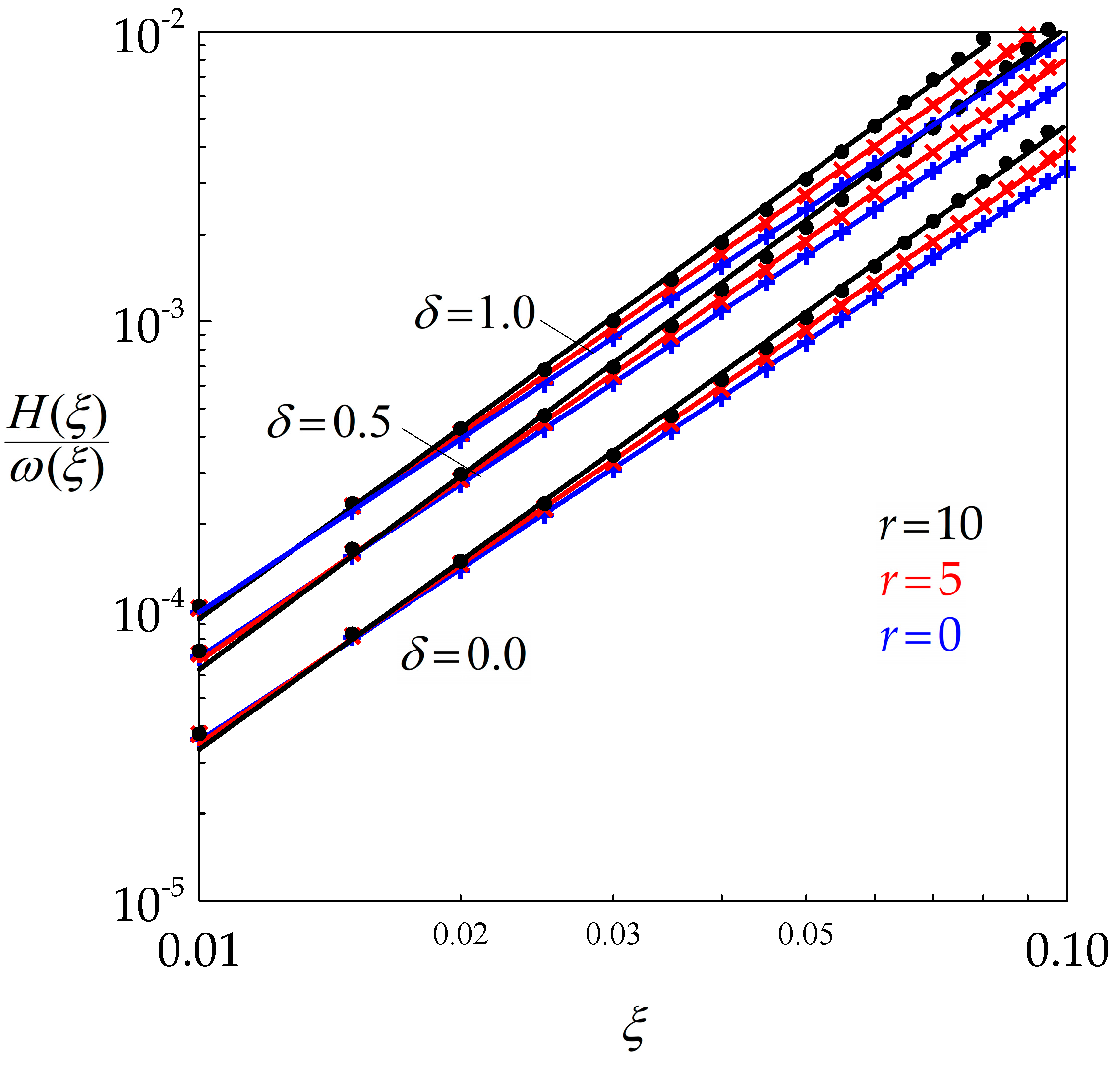
4.4. Estimation of and from the Experimental Data
5. Conclusions and Future Developments
- (i).
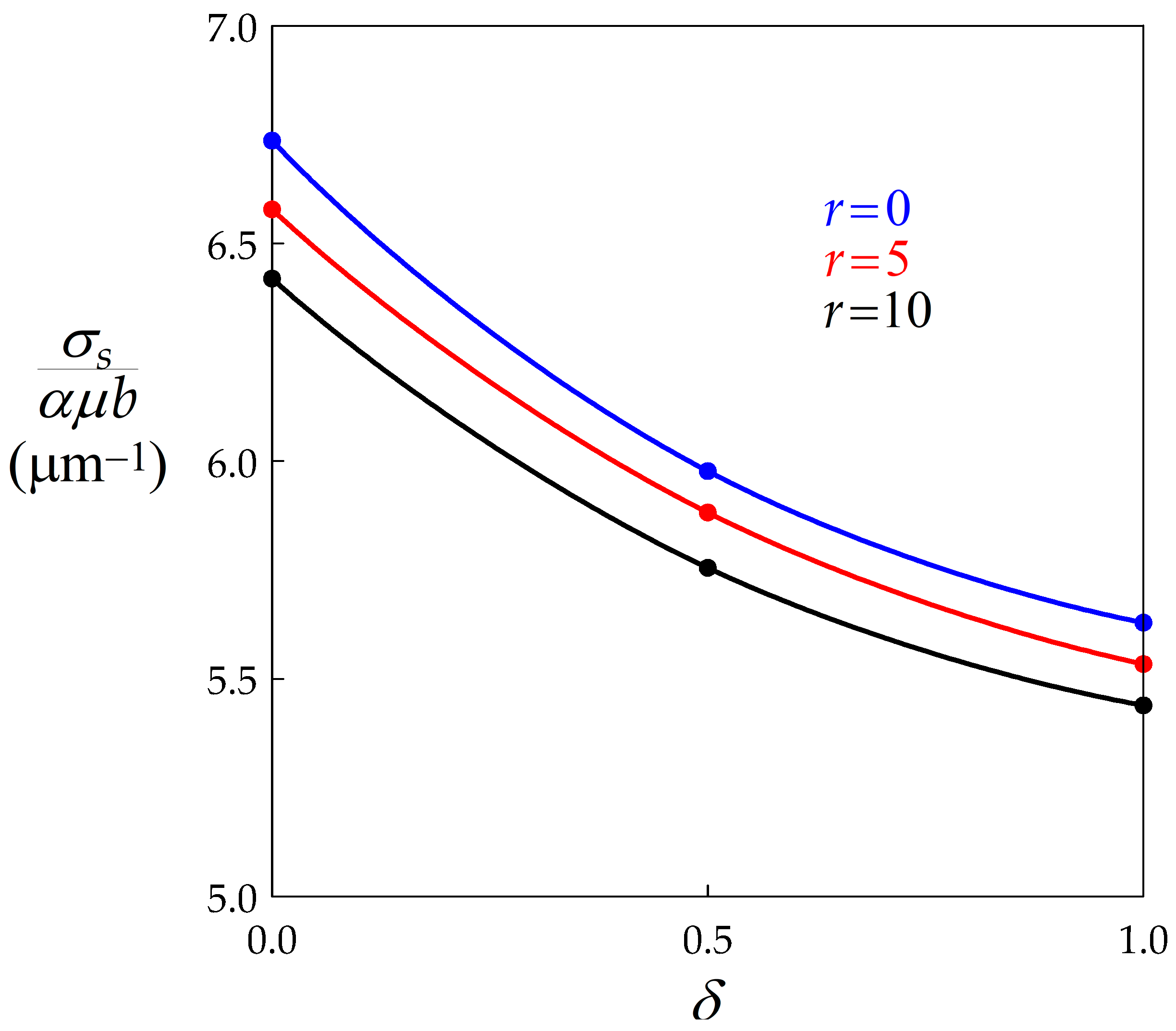
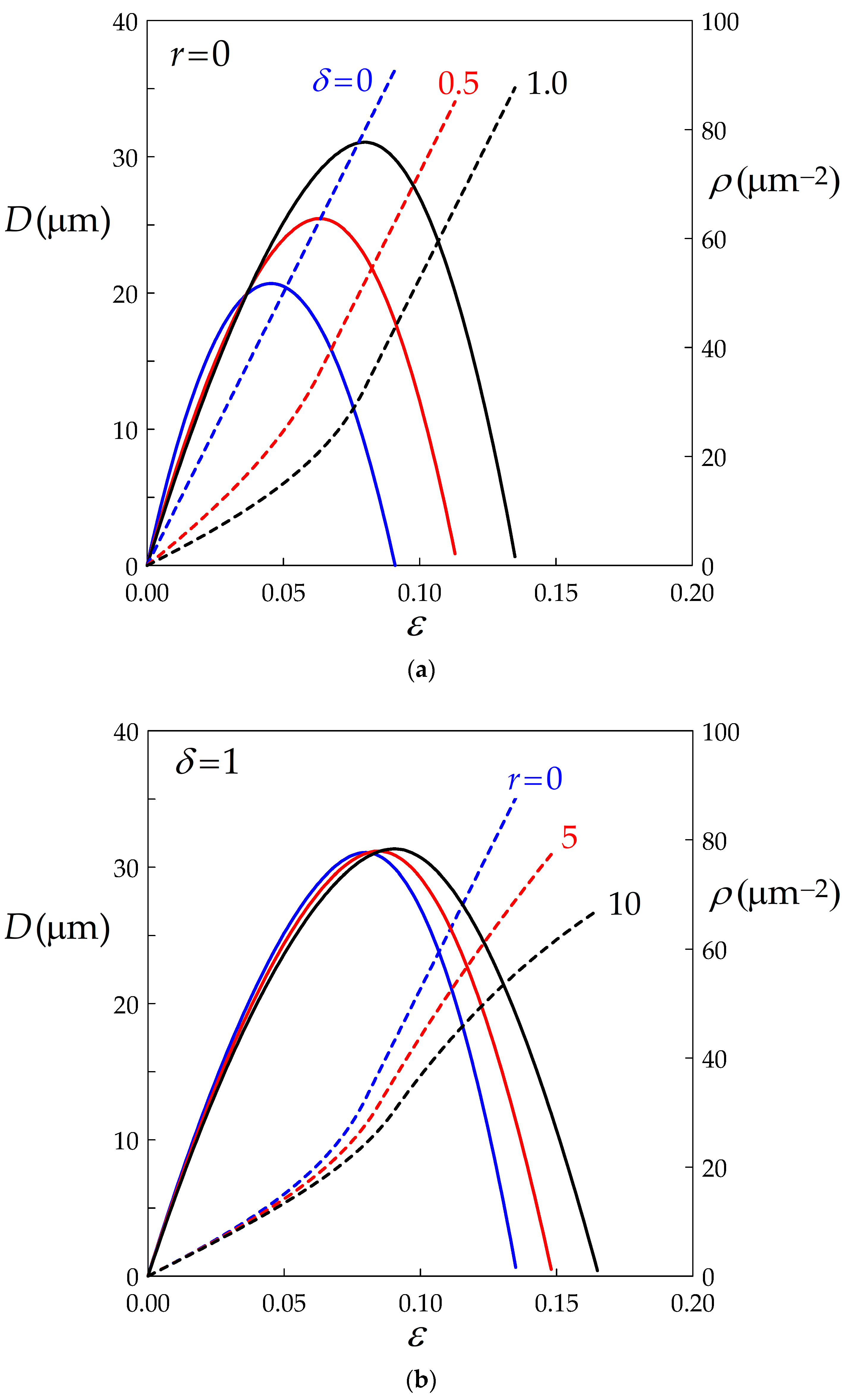
- As expected, BMIS induces significant flow softening. For r values ranging between 0 and 10, typical of materials undergoing DDRX, BMIS is even more efficient than dynamic recovery.
- (ii).
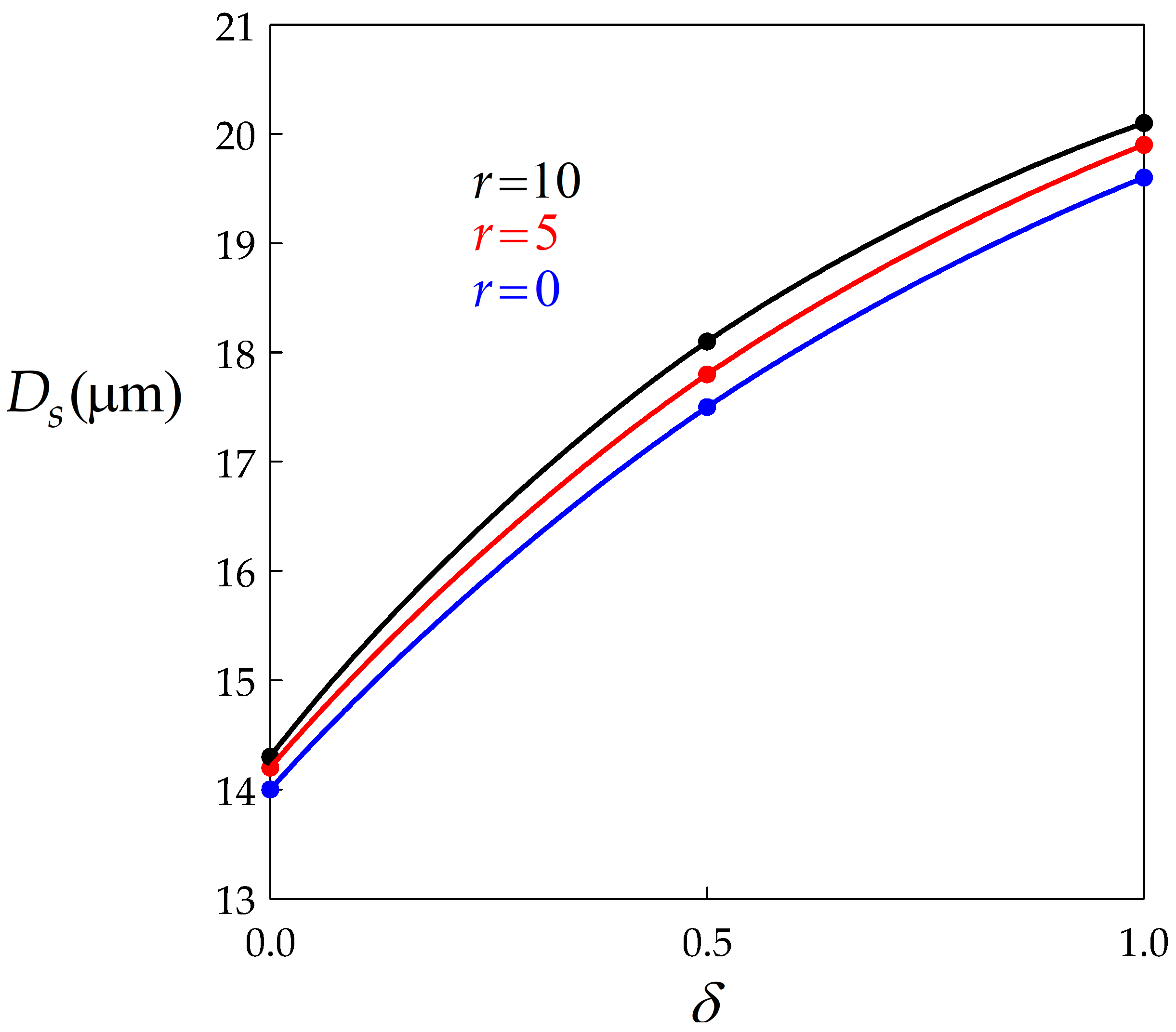
- The second major effect of BMIS is to promote average grain size growth, while the influence of dynamic recovery is weak.
- (iii).
- The lifetime of a grain, and thus the strain at the time of disappearance, is increased by BMIS. The aspect ratio of the grains nevertheless remains sufficiently close to unity for them to be considered as approximately equiaxed.
- (iv).
- By contrast, the macroscopic strain rate sensitivity and apparent activation energy are not considerably modified by BMIS.
- (v).
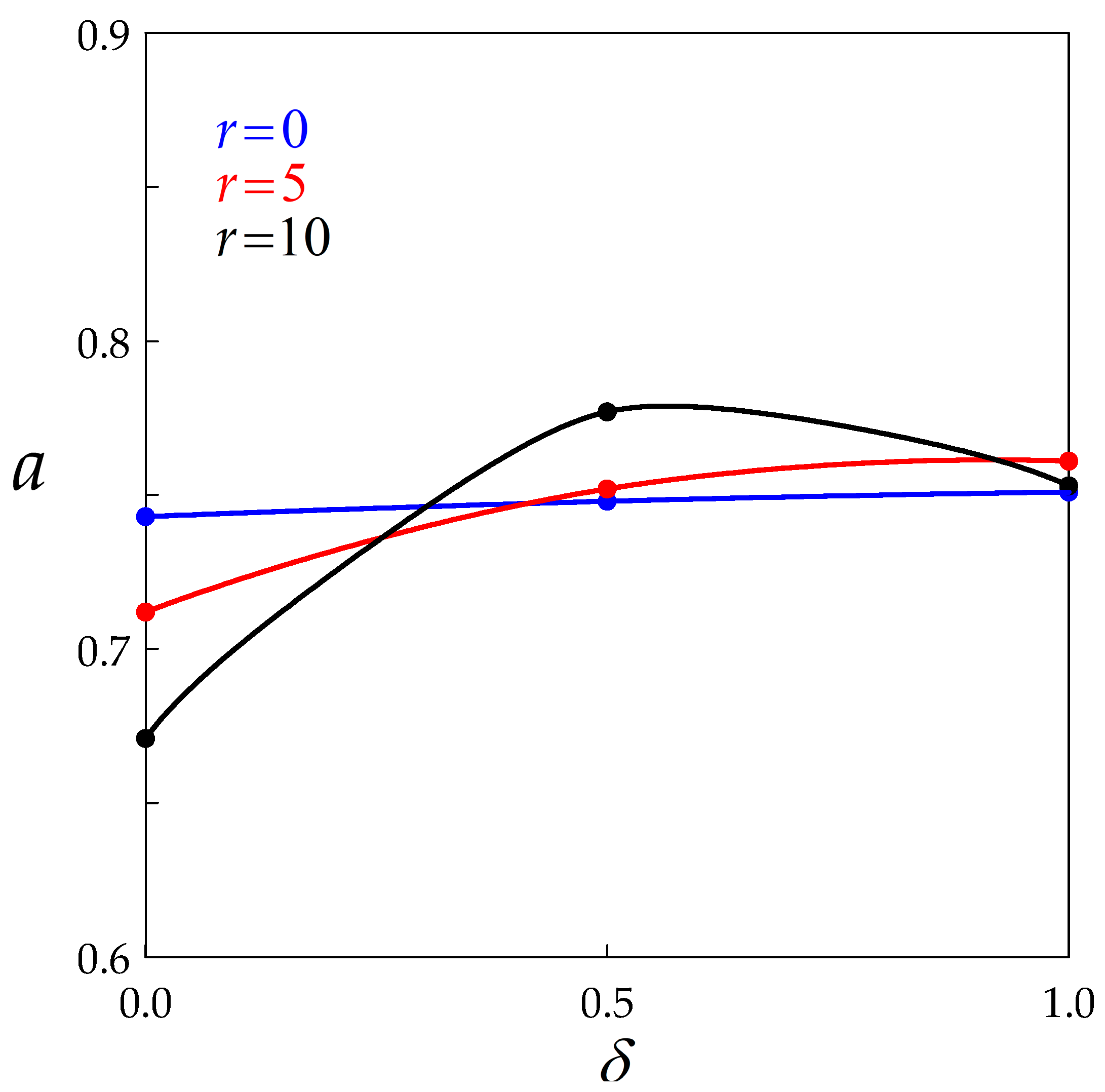
- The classical Derby equation relating the flow stress to the average grain size was found by the model. The Derby exponent a is globally increased by BMIS. For full BMIS (), it takes a value close to 0.75 whatever the level of dynamic recovery.
- (vi).
- Finally, the present approach shows that whenever the grain boundary migration parameter and the nucleation rate parameter are estimated from the data with the mesoscale model, they can be both overestimated if BMIS is neglected.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jonas, J.J. Dynamic recrystallization−Scientific curiosity or industrial tool? Mater. Sci. Eng. A 1994, 184, 155–165. [Google Scholar] [CrossRef]
- McQueen, H.J.; Jonas, J.J. Recovery and recrystallization during high temperature deformation. In Treatise on Materials Science and Technology; Arsenault, R.J., Ed.; Academic Press: New York, NY, USA, 1975; Volume 6, pp. 394–493. [Google Scholar]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef] [Green Version]
- Stüwe, H.P.; Ortner, B. Recrystallization in hot working and creep. Met. Sci. 1974, 8, 161–167. [Google Scholar] [CrossRef]
- Sandström, R.; Lagneborg, R. A model for hot working occurring by recrystallization. Acta Metall. 1975, 23, 387–398. [Google Scholar] [CrossRef]
- Hallberg, H. Approaches to modeling of recrystallization. Metals 2011, 1, 16–48. [Google Scholar] [CrossRef] [Green Version]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Madej, L.; Sitko, M.; Pietrzyk, M. Perceptive comparison of mean and full field dynamic recrystallization models. Archiv. Civ. Mech. Eng. 2016, 16, 569–589. [Google Scholar] [CrossRef]
- Montheillet, F.; Lurdos, O.; Damamme, G. A grain scale approach for modeling steady state discontinuous dynamic recrystallization. Acta Mater. 2009, 57, 1602–1612. [Google Scholar] [CrossRef]
- Montheillet, F.; Jonas, J.J. Models of recrystallization. In Fundamentals of Modeling for Metals Processing; Furrer, D.U., Semiatin, S.L., Eds.; ASM International: Metals Park, OH, USA, 2009; Volume 22A, pp. 220–231. [Google Scholar]
- Maire, L.; Fausty, J.; Bernacki, M.; Bozzolo, N.; De Micheli, P.; Moussa, C. A new topological approach for the mean field modeling of dynamic recrystallization. Mater. Des. 2018, 146, 194–207. [Google Scholar] [CrossRef]
- Rollett, A.D.; Luton, M.J.; Srolovitz, D.J. Microstructural simulation of dynamic recrystallization. Acta Metall. Mater. 1992, 40, 43–55. [Google Scholar] [CrossRef] [Green Version]
- Luton, M.J.; Peczak, P. Monte Carlo modeling of dynamic recrystallization: Recent developments. Mater. Sci. Forum 1993, 113–115, 67–80. [Google Scholar]
- Peczak, P. A Monte Carlo study of influence of deformation temperature on dynamic recrystallization. Acta Metall. Mater. 1995, 43, 1279–1291. [Google Scholar] [CrossRef]
- Hesselbarth, H.W.; Göbel, I.R. Simulation of recrystallization by cellular automata. Acta Metall. Mater. 1991, 39, 2135–2143. [Google Scholar] [CrossRef]
- Goetz, R.L.; Seetharaman, V. Modeling dynamic recrystallization using cellular automata. Scripta Mater. 1998, 38, 405–413. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M. A new cellular automaton method coupled with a rate-dependent (CARD) model for predicting dynamic recrystallization behavior. Metall. Mater. Trans. 2018, 49, 1916–1930. [Google Scholar] [CrossRef]
- De Jaeger, J.; Solas, D.; Fandeur, O.; Schmitt, J.−H.; Rey, C. 3D numerical modeling of dynamic recrystallization under hot working: Application to Inconel 718. Mater. Sci. Eng. A 2015, 646, 33–44. [Google Scholar] [CrossRef]
- Maire, L.; Scholtes, B.; Moussa, C.; Bozzolo, N.; Pino Muñoz, D.; Settefrati, A.; Bernacki, M. Modeling of dynamic and post-dynamic recrystallization by coupling a full field approach to phenomenological laws. Mater. Des. 2017, 133, 498–519. [Google Scholar] [CrossRef]
- Montheillet, F.; Piot, D. Influence of strain-hardening and dynamic recovery on DDRX steady state. In Proceedings of the 11th International Conference on Processing & Manufacturing of Advanced Materials (Thermec’2021), Virtual Conference, 9−14 May 2021; Ionescu, M., Sommitsch, C., Poletti, C., Kozeschnik, E., Chandra, T., Eds.; Materials Science Forum. Trans Tech Publications: Stafa-Zurich, Switzerland, 2021; Volume 1016, pp. 194–199. [Google Scholar]
- Montheillet, F.; Piot, D.; Matougui, N.; Fares, M.L. A critical assessment of three usual equations for strain hardening and dynamic recovery. Metall. Mater. Trans. A 2014, 45, 4324–4332. [Google Scholar] [CrossRef]
- Matougui, N.; Piot, D.; Fares, L.; Montheillet, F.; Semiatin, S.L. Influence of niobium solutes on the mechanical behaviour of nickel during hot working. Mater. Sci. Eng. A 2013, 586, 350–357. [Google Scholar] [CrossRef]
- Montheillet, F. Déformation à chaud des métaux. Physique et Mécanique; Ellipses: Paris, France, 2019; pp. 142–144. [Google Scholar]
- Damamme, G.; Piot, D.; Montheillet, F.; Semiatin, S.L. A model of discontinuous dynamic recrystallization and its application for nickel alloys. In Proceedings of the 6th International Conference on Processing & Manufacturing of Advanced Materials (Thermec’2009), Berlin, Germany, 25−29 August 2009; Chandra, T., Wanderka, N., Reimers, W., Ionescu, M., Eds.; Materials Science Forum. Trans Tech Publications: Stafa-Zurich, Switzerland, 2010; Volumes 638−642, pp. 2543–2548. [Google Scholar]
- Twiss, R.J. Theory and applicability of a recrystallized grain size paleopiezometer. Pure Appl. Geophys. 1977, 115, 227–244. [Google Scholar] [CrossRef]
- Derby, B. The dependence of grain size on stress during dynamic recrystallization. Acta Metall. Mater. 1991, 39, 955–962. [Google Scholar] [CrossRef]
- Derby, B. Dynamic recrystallization: The steady state grain size. Scr. Mater. 1992, 27, 1581–1586. [Google Scholar] [CrossRef]
- Rossard, C.; Blain, P. Evolution de la structure de l’acier sous l’effet de la déformation plastique à chaud. Mém. Sci. Rev. Métall. 1959, 56, 285–300. [Google Scholar]
- Blaz, L.; Sakai, T.; Jonas, J.J. Effect of initial grain size on the dynamic recrystallization of copper. Met. Sci. 1983, 17, 609–616. [Google Scholar] [CrossRef]
- Graez, K.; Miessen, C.; Gottstein, G. Analysis of steady state dynamic recrystallization. Acta Mater. 2014, 67, 58–66. [Google Scholar] [CrossRef]
- Montheillet, F.; Piot, D. Combined effects of grain boundary convection and migration in dynamic phase transformations. In Proceedings of the 9th International Conference on Processing & Manufacturing of Advanced Materials (Thermec’2016), Gratz, Austria, 29 May−3 June 2016; Sommitsch, C., Ionescu, M., Mishra, B., Kozeschnik, E., Chandra, T., Eds.; Materials Science Forum. Trans Tech Publications: Stafa-Zurich, Switzerland, 2017; Volume 879, pp. 72–77. [Google Scholar]


| BMIS Parameter δ | |||||||
| 0 | 0.5 | 1.0 | |||||
| Dynamic recovery parameter r | 0 | 0.233 | 7.937 | 1.587 | 7.960 | 4.399 | 7.967 |
| 5 | 0.898 | 8.263 | 5.449 | 8.241 | 13.912 | 8.221 | |
| 10 | 5.551 | 9.709 | 25.144 | 8.591 | 60.200 | 8.551 | |
| BMIS Parameter δ | |||||||
| 0 | 0.5 | 1.0 | |||||
| Dynamic recovery parameter r | 0 | 0.314 | 1.973 | 0.647 | 1.985 | 0.944 | 1.990 |
| 5 | 0.443 | 2.052 | 0.976 | 2.082 | 1.416 | 2.083 | |
| 10 | 0.689 | 2.158 | 1.728 | 2.220 | 2.220 | 2.186 | |
| BMIS Parameter δ | |||||||
| 0 | 0.5 | 1.0 | |||||
| Dynamic recovery parameter r | 0 | 0.278 | 10.18 | 0.140 | 6.33 | 0.100 | 5.00 |
| 5 | 0.280 | 10.38 | 0.141 | 6.25 | 0.100 | 5.00 | |
| 10 | 0.282 | 10.37 | 0.140 | 6.16 | 0.100 | 5.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montheillet, F. Influence of Boundary Migration Induced Softening on the Steady State of Discontinuous Dynamic Recrystallization. Materials 2021, 14, 3531. https://doi.org/10.3390/ma14133531
Montheillet F. Influence of Boundary Migration Induced Softening on the Steady State of Discontinuous Dynamic Recrystallization. Materials. 2021; 14(13):3531. https://doi.org/10.3390/ma14133531
Chicago/Turabian StyleMontheillet, Frank. 2021. "Influence of Boundary Migration Induced Softening on the Steady State of Discontinuous Dynamic Recrystallization" Materials 14, no. 13: 3531. https://doi.org/10.3390/ma14133531
APA StyleMontheillet, F. (2021). Influence of Boundary Migration Induced Softening on the Steady State of Discontinuous Dynamic Recrystallization. Materials, 14(13), 3531. https://doi.org/10.3390/ma14133531






