Longitudinal Deformation of Deep Shield Tunnels Caused by Upper Load Reduction
Abstract
:1. Introduction
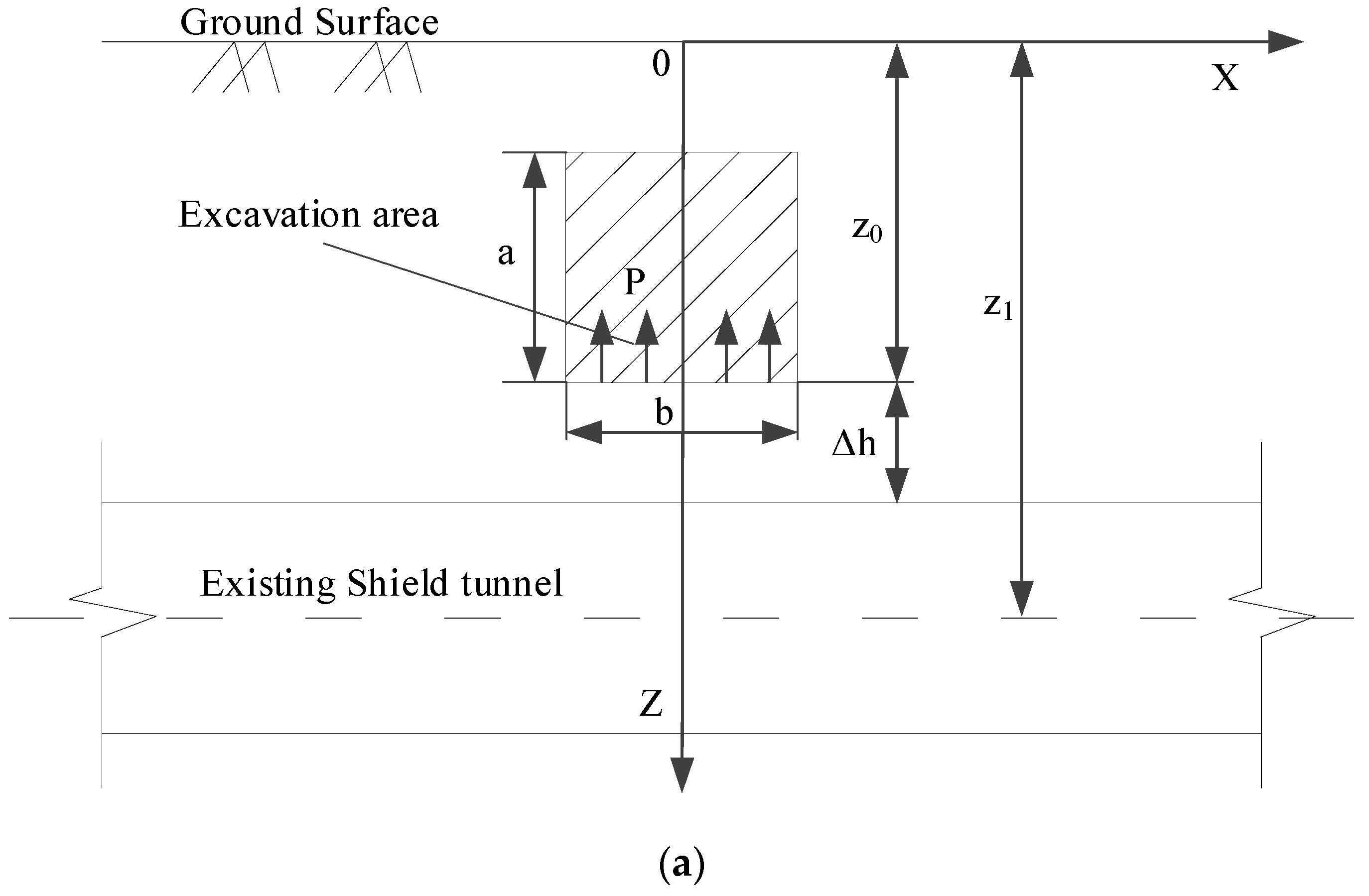
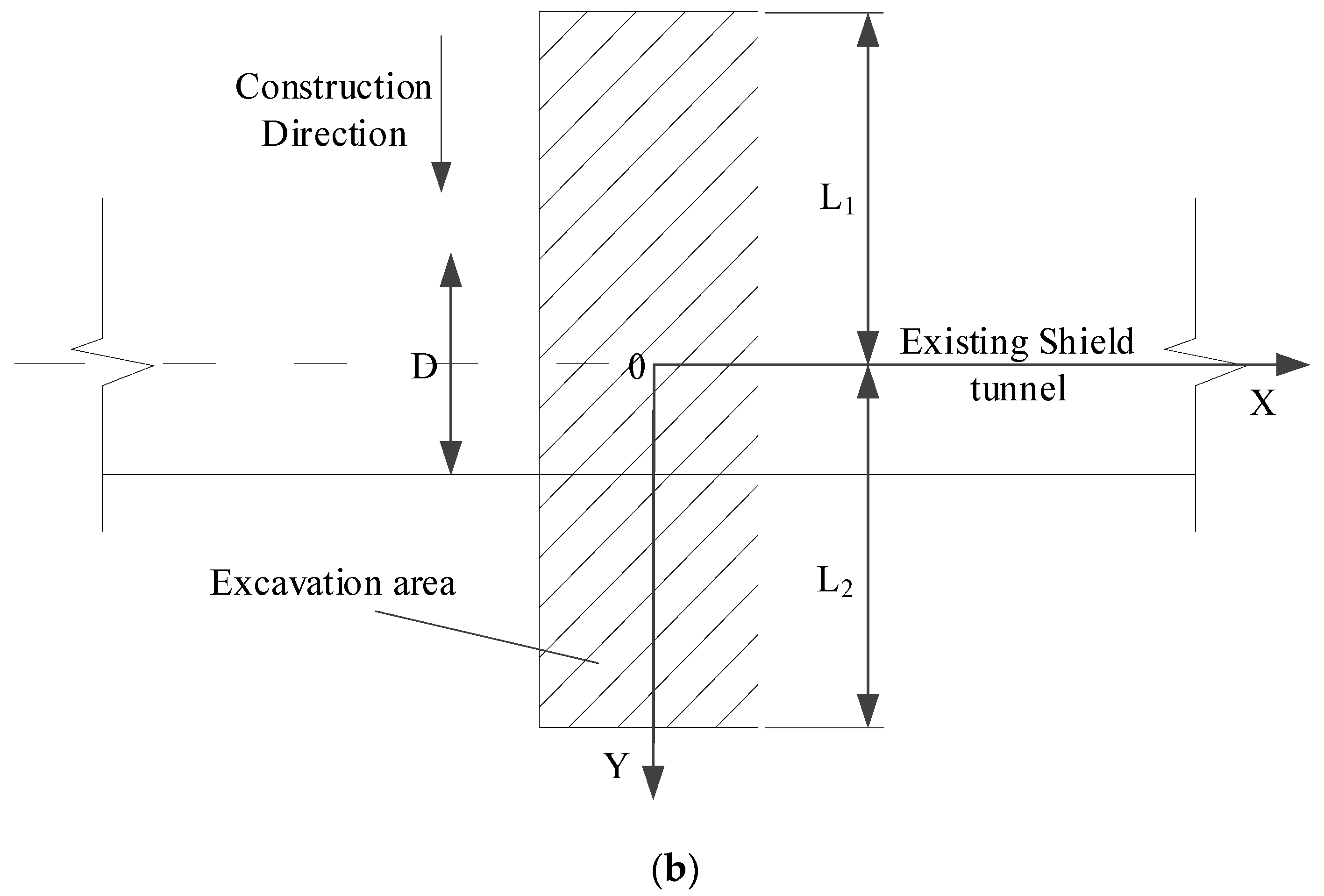
2. Model Analysis
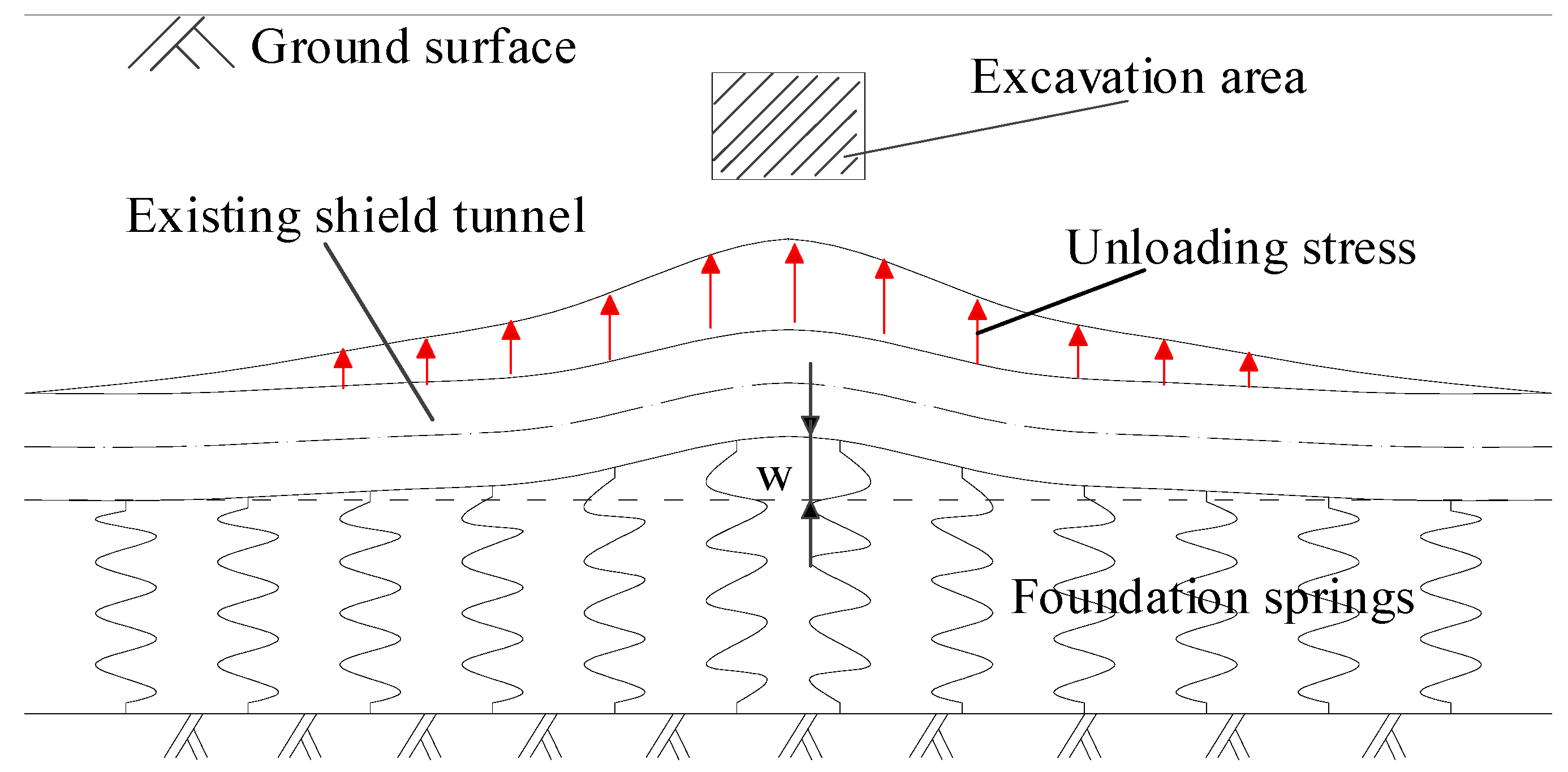
2.1. Longitudinal Deformation Mechanism of Shield Tunnel
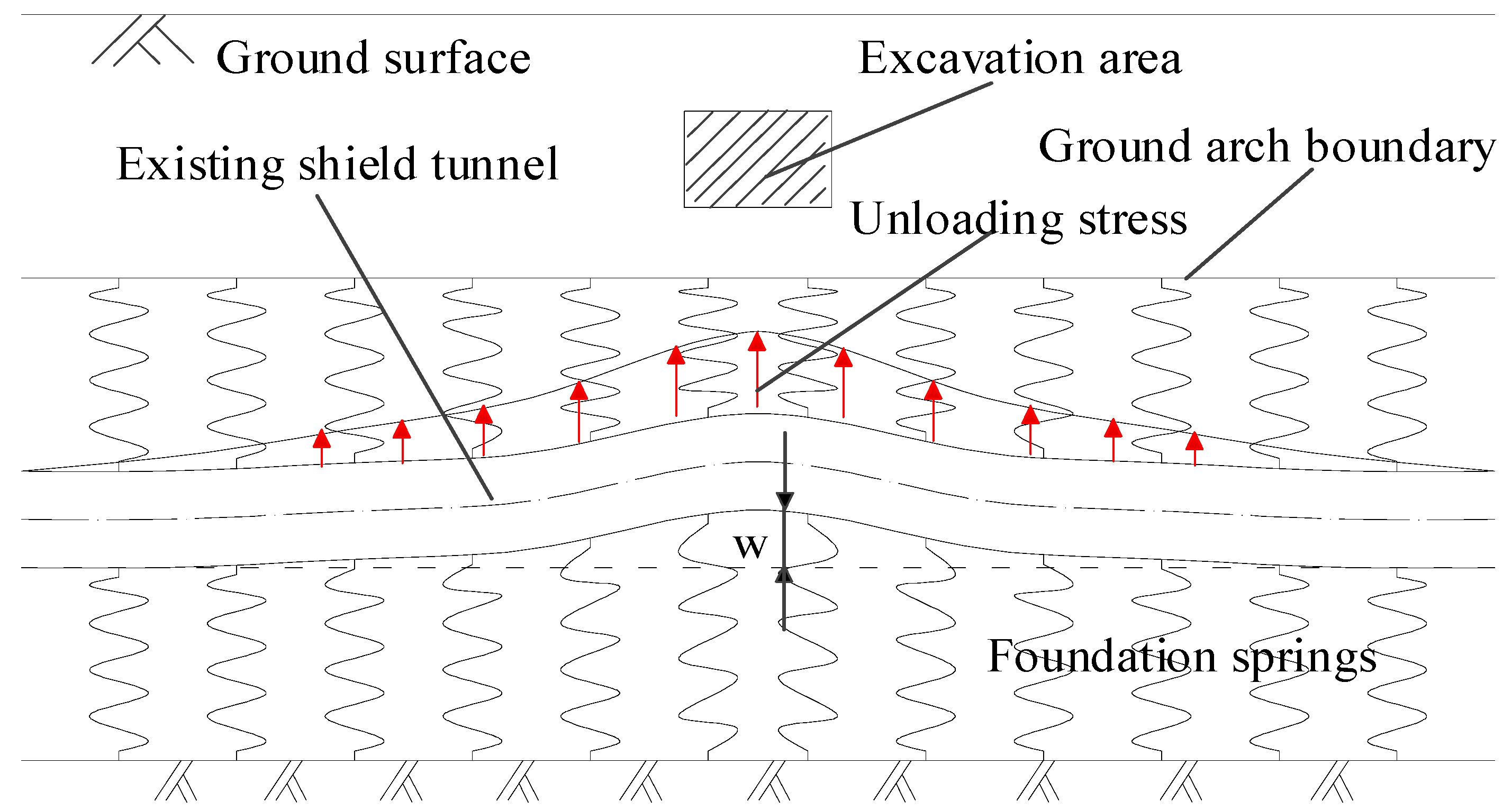
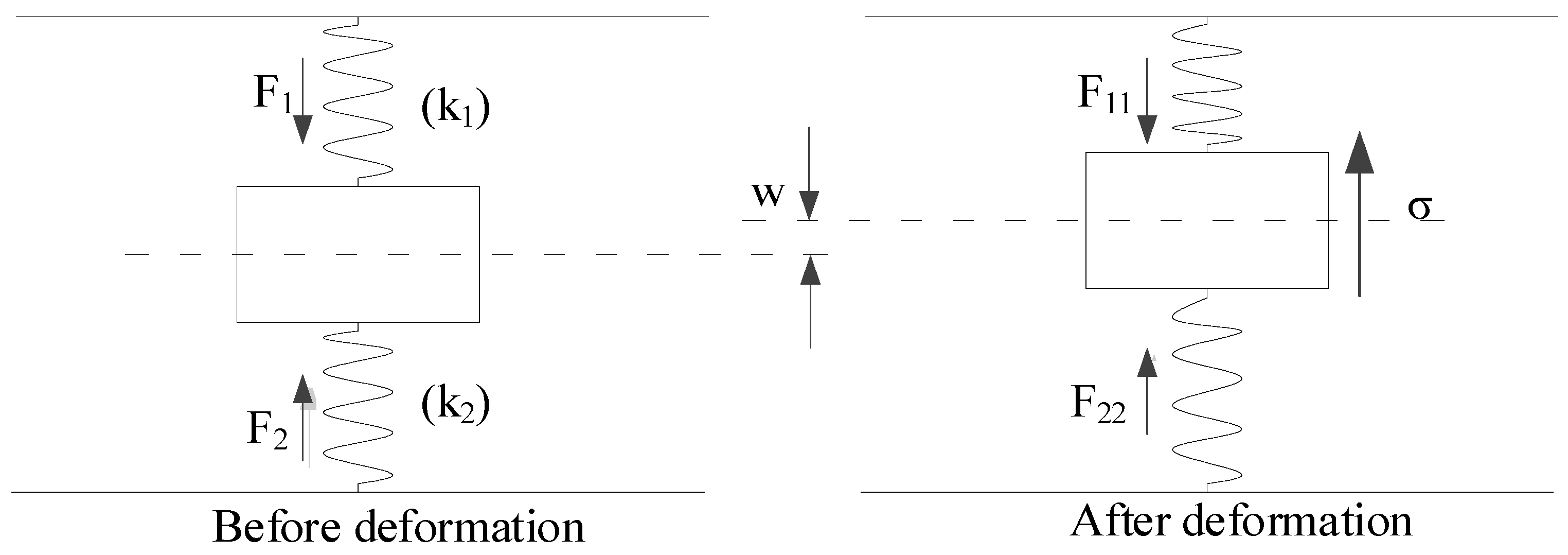
2.2. Force Analysis of Deep Shield Tunnel
2.3. Calculation of Vertical Unloading Stress
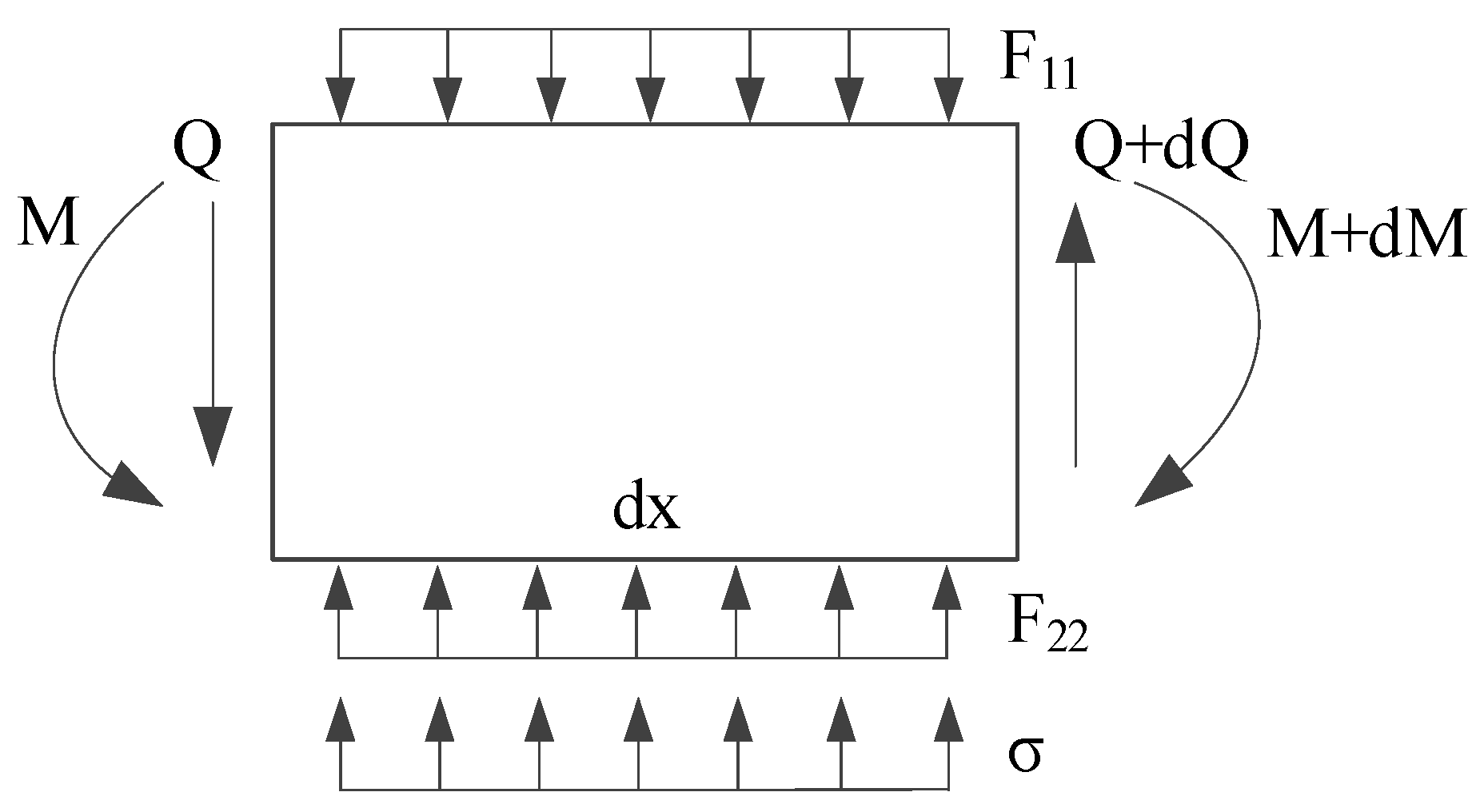
2.4. Solution of Vertical Displacement
3. Determination of Calculation Parameters
3.1. Equivalent Bending Stiffness of Shield Tunnel
3.2. Subgrade Modulus Coefficient
4. Engineering Cases Validation
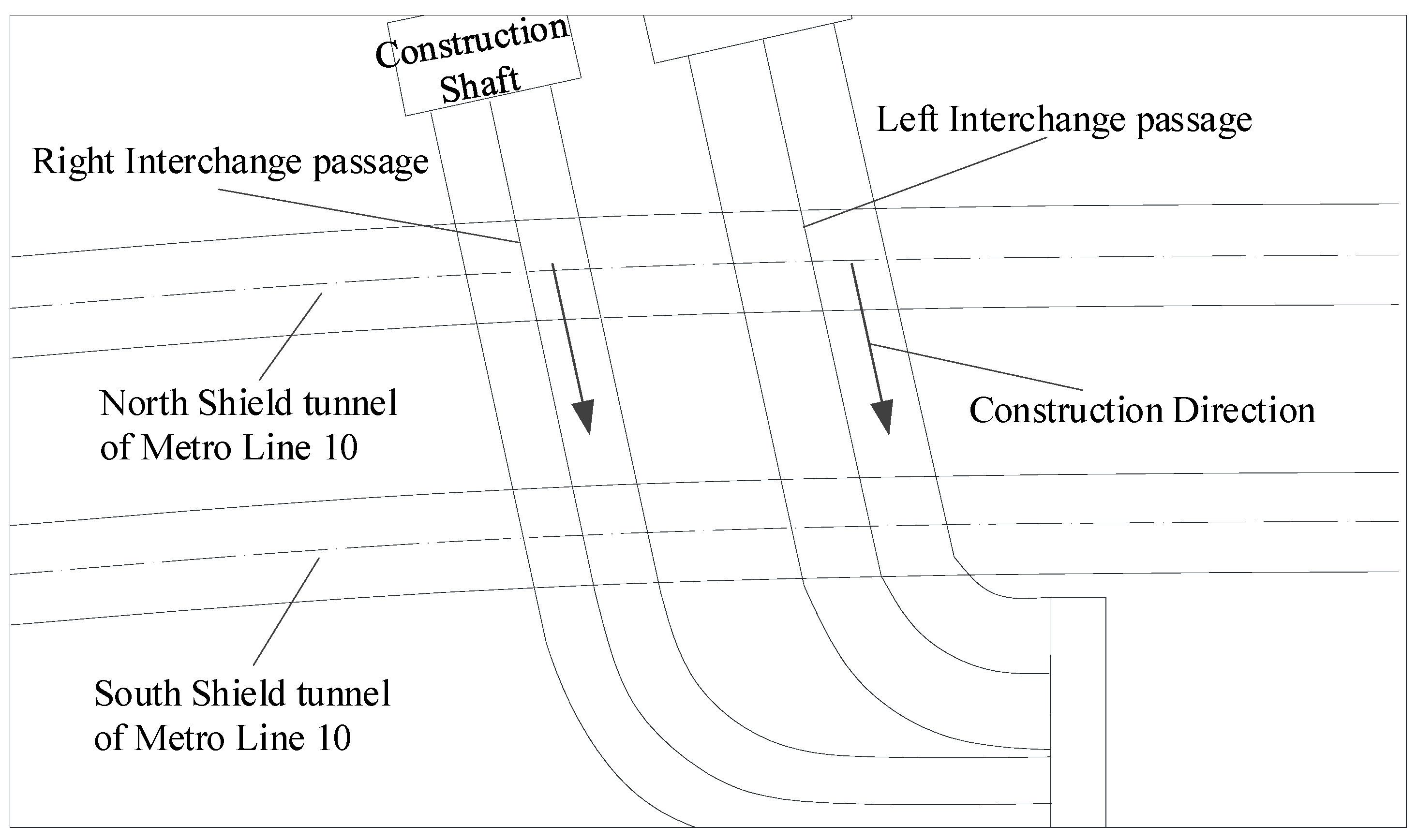
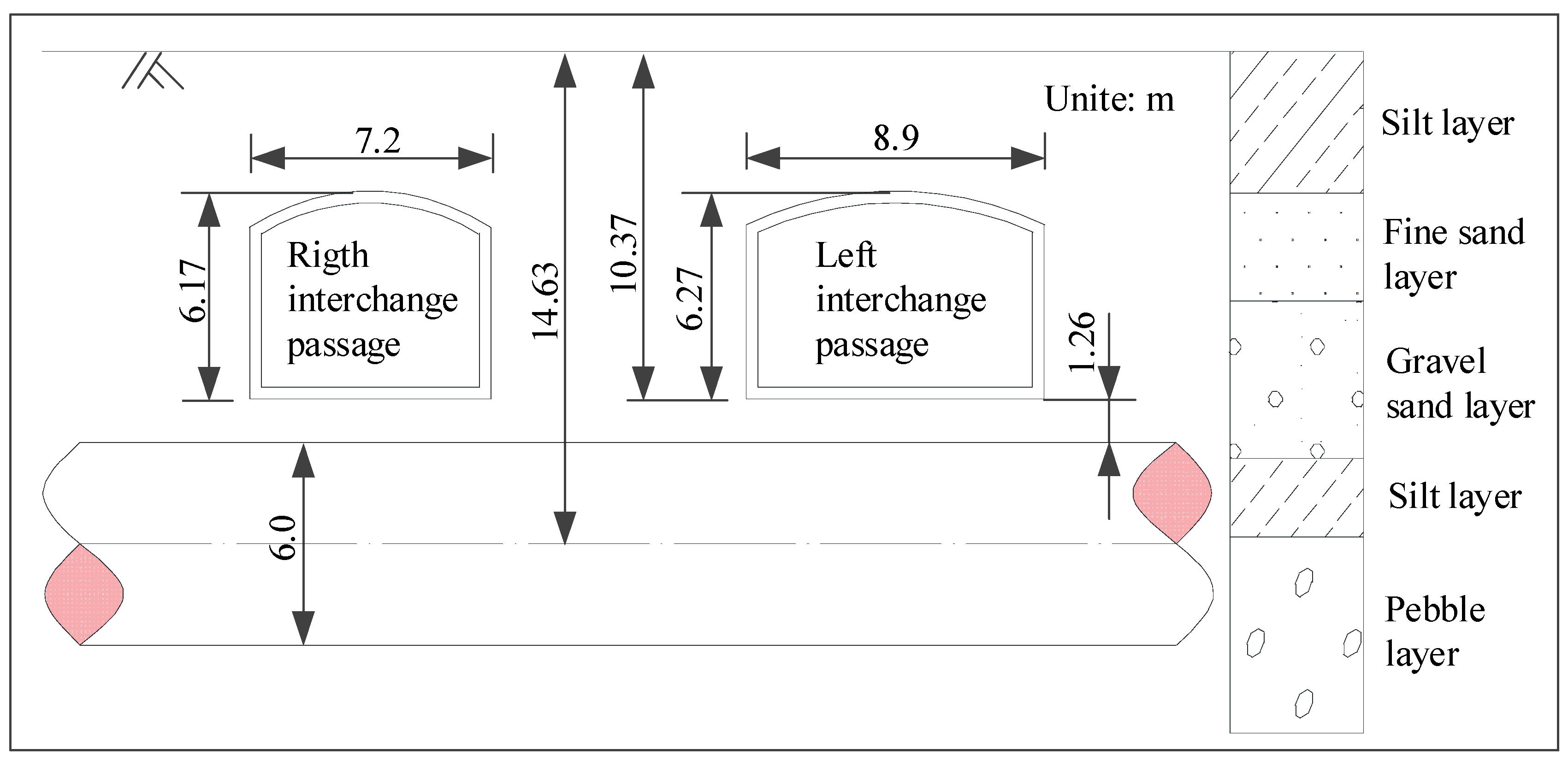
4.1. Interchange Passages of Beijing Daxing International Airport Express Above-Crossing Metro Line 10 Project
4.2. Metro Line 8 Above-Crossing Existing Metro Line 2 Project in Shanghai
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols and Greek Letters | Nomenclature |
| () | the foundation reaction forces before the existing tunnel deformation |
| () | the foundation reaction forces after the existing tunnel deformation |
| () | the subgrade modulus coefficients of strata above and below the tunnel |
| the vertical unloading stress on the existing shield tunnel | |
| the vertical deformation of the existing shield tunnel | |
| the bending moment | |
| the shear force | |
| the gravity of the tunnel microunit | |
| the width of the excavation area | |
| the upward unloading pressure | |
| the Poisson’s ratio | |
| the distance from the axis of the shield tunnel to the surface | |
| the distance from the floor of the excavation area to the surface | |
| the distance from the start of the excavation area to the intersection of the axes | |
| the distance from the intersection of the axes to the end of the excavation area | |
| the elemental nodal vertical displacement vector | |
| the elemental nodal vertical unloading stress vector | |
| the deformation stiffness matrix of the shield tunnel | |
| the upper foundation spring stiffness matrix | |
| the lower foundation spring stiffness matrix | |
| the Young’s modulus | |
| the moment of inertia of the tunnel section | |
| the Young’s modulus of the shield tunnel segments | |
| the outer diameter of the shield tunnel | |
| the inner diameter of the shield tunnel | |
| the Young’s modulus of soils | |
| the width of the beam | |
| the longitudinal equivalent bending stiffness | |
| the undrained shear strength |
Appendix A
References
- He, M.-D.; Liu, J.; Le, G.-P.; Zhang, D.-L.; Wang, M.-S. Deformation analysis for shield tunnel crossing by close range large section passageway. Chin. J. Rock Mech. Eng. 2014, 33, 3682–3691. (In Chinese) [Google Scholar]
- Simpson, B.; Vardanega, P.J. Results of Monitoring at the British Library Excavation. Proc. Inst. Civil Eng. Geotech. Eng. 2014, 167, 99–116. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Liu, G.; Huang, P.; Ng, C.W.W. Interaction between a Large-Scale Triangular Excavation and Adjacent Structures in Shanghai Soft Clay. Tunn. Undergr. Space Technol. 2015, 50, 282–295. [Google Scholar] [CrossRef]
- Chen, L.; Huang, H.; Wang, R. Analysis of the observed longitudinal settlement of a tunnel caused by an adjacent shield tunneling on top. China Civ. Eng. J. 2006, 6, 83–87. (In Chinese) [Google Scholar]
- Chen, J.; Zhu, Y.; Li, M.; Wen, S. Novel excavation and construction method of an underground highway tunnel above operating metro tunnels. J. Aerosp. Eng. ASCE 2015, 28, A4014003. [Google Scholar] [CrossRef]
- Tang, Y.; Xiao, S.; Zhou, J.; Zhan, Y. Three-Dimensional Simplified Method for Predicting Settlement Along Railway Due to Excavation. In Proceedings of the Geo Shanghai 2018 International Conference: Transportation Geotechnics and Pavement Engineering 2018, Shanghai, China, 27–30 May 2018; pp. 100–108. [Google Scholar]
- Chen, R.; Meng, F.; Li, Z.; Ye, Y.; Ye, J. Investigation of Response of Metro Tunnels Due to Adjacent Large Excavation and Protective Measures in Soft Soils. Tunn. Undergr. Space Technol. 2016, 58, 224–235. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Ng, C.W.W.; Chen, Y. Three-Dimensional Numerical Parametric Study of the Influence of Basement Excavation on Existing Tunnel. Comput. Geotech. 2015, 63, 146–158. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, X.; Chen, Y.; Chen, L. Numerical Parametric Study of Countermeasures to Alleviate Basement Excavation Effects on an Existing Tunnel. Tunn. Undergr. Space Technol. 2018, 72, 145–153. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, M.; Wang, F.; Ling, T.; Yang, X. The Failure Mechanism of Surrounding Rock around an Existing Shield Tunnel Induced by an Adjacent Excavation. Comput. Geotech. 2020, 117, 103236. [Google Scholar] [CrossRef]
- Duan, B.; Gong, W.; Ta, G.; Yang, X.; Zhang, X. Influence of Small, Clear Distance Cross-Tunnel Blasting Excavation on Existing Tunnel Below. Adv. Civ. Eng. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Wang, W. Evaluation of Deformation Response for Adjacent Tunnels Due to Soil Unloading in Excavation Engineering. Tunn. Undergr. Space Technol. 2013, 38, 244–253. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Hong, Y.; Yu, F. Effects of Above-Crossing Tunnelling on the Existing Shield Tunnels. Tunn. Undergr. Space Technol. 2016, 58, 159–176. [Google Scholar] [CrossRef]
- Zhang, X.; Ou, X.; Yang, J.; Fu, J. Deformation Response of an Existing Tunnel to Upper Excavation of Foundation Pit and Associated Dewatering. Int. J. Geomech. 2017, 17, 04016112. [Google Scholar] [CrossRef]
- Wu, H.-N.; Shen, S.-L.; Liao, S.-M.; Yin, Z.-Y. Longitudinal Structural Modelling of Shield Tunnels Considering Shearing Dislocation between Segmental Rings. Tunn. Undergr. Space Technol. 2015, 50, 317–323. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Huang, M.; Lin, C. Simplified Analytical Method for Evaluating the Effects of Adjacent Excavation on Shield Tunnel Considering the Shearing Effect. Comput. Geotech. 2017, 81, 167–187. [Google Scholar] [CrossRef]
- Wu, H.-N.; Shen, S.-L.; Yang, J.; Zhou, A. Soil-Tunnel Interaction Modelling for Shield Tunnels Considering Shearing Dislocation in Longitudinal Joints. Tunn. Undergr. Space Technol. 2018, 78, 168–177. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Z.; Han, Y.; Wang, Z.; Zhang, R.; Wang, S. Analytical Solution for the Response of an Existing Tunnel Induced by Above-Crossing Shield Tunneling. Comput. Geotech. 2020, 124, 103624. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, R.; Wu, H.; Meng, F.; Yi, Y. General Solutions for the Longitudinal Deformation of Shield Tunnels with Multiple Discontinuities in Strata. Tunn. Undergr. Space Technol. 2021, 107, 103652. [Google Scholar] [CrossRef]
- Mindlin, R.D. Force at a Point in the Interior of a Semi-Infinite Solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Shiba, Y.; Kawashima, K.; Obinata, N.; Kano, T. An Evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analysis. Proc. Jpn. Soc. Civ. Eng. 1988, 398, 319–327. (In Japanese) [Google Scholar]
- Shiba, Y.; Kawashima, K. Evaluation procedure for seismic stress developed in shield tunnels based on seismic deformation method. Proc. Jpn. Soc. Civil Eng. 1989, 404, 385–394. (In Japanese) [Google Scholar]
- Liao, S.-M.; Peng, F.-L.; Shen, S.-L. Analysis of Shearing Effect on Tunnel Induced by Load Transfer along Longitudinal Direction. Tunn. Undergr. Space Technol. 2008, 23, 421–430. [Google Scholar] [CrossRef]
- Attewell, P.B.; Yeates, J.; Selby, A.R. Soil Movements Induced by Tunnelling and Their Effects on Pipelines and Structures. Tunn. Undergr. Space Technol. 1987, 2, 102. [Google Scholar]
- National Standard of People’s Republic of China. Reinforced Concrete Segments; GB/T 22082-2017; China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
- Gao, Y.; Bao, W.; Lou, K. Laboratory studies on the sensitivity of layer NO.4 soft clay in Shanghai. J. Tongji Univ. Nat. Sci. 2015, 43, 140–145. (In Chinese) [Google Scholar]
- Hashimoto, T.; Nagaya, J.; Konda, T. Prediction of Ground Deformation Due to Shield Excavation in Clayey Soils. Soils Found. 1999, 39, 53–61. [Google Scholar] [CrossRef]
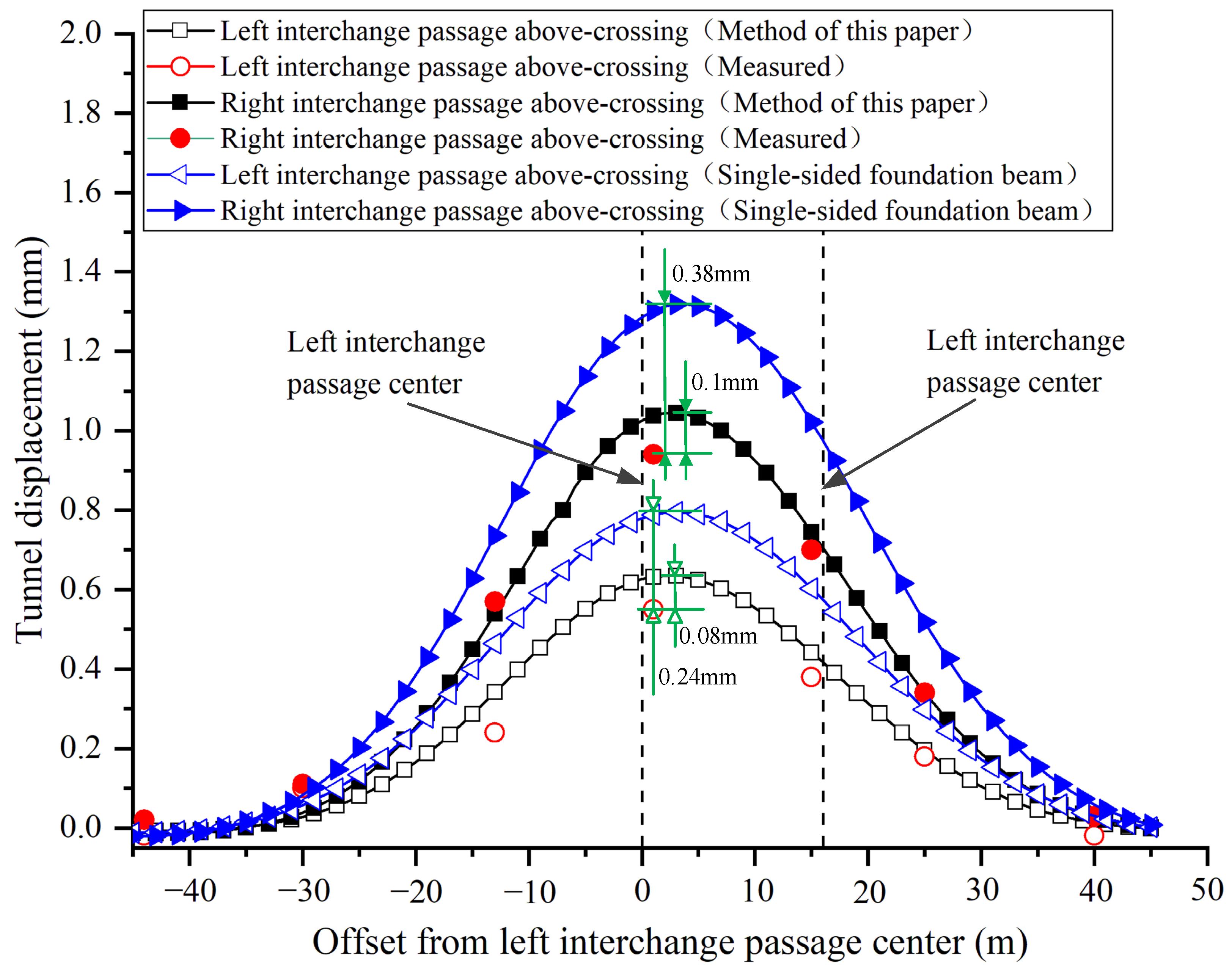
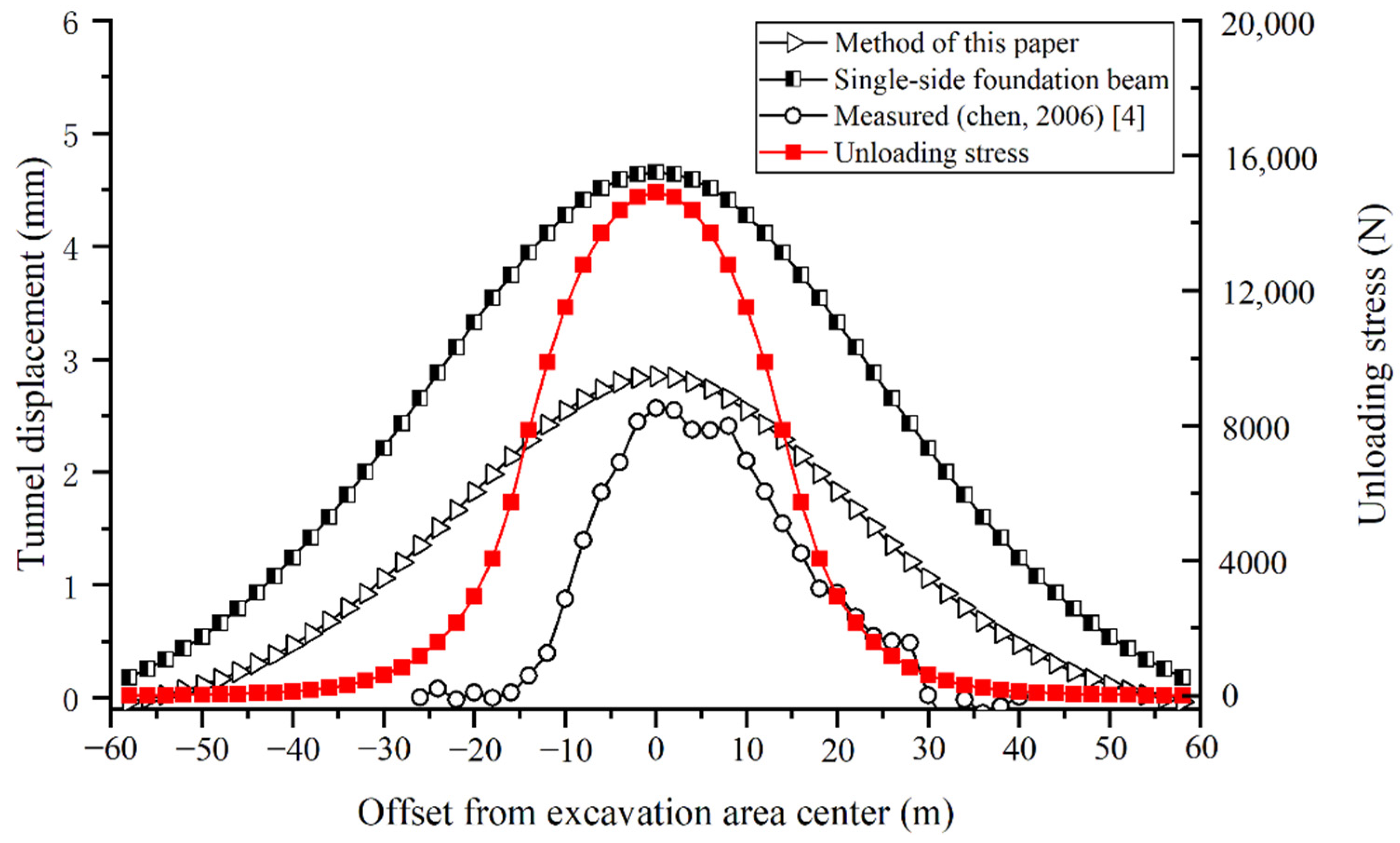
| Parameter | Value |
|---|---|
| shield tunnel segment | [25] |
| longitudinal equivalent bending stiffness | |
| gravel sand layers (k1) | |
| pebble layers (k2) |
| Parameter | Value |
|---|---|
| shield tunnel segment | [25] |
| longitudinal equivalent bending stiffness | |
| Quaternary muddy clay (k1 = k2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; He, S.; Li, Y.; He, J.; He, J. Longitudinal Deformation of Deep Shield Tunnels Caused by Upper Load Reduction. Materials 2021, 14, 3629. https://doi.org/10.3390/ma14133629
Zheng J, He S, Li Y, He J, He J. Longitudinal Deformation of Deep Shield Tunnels Caused by Upper Load Reduction. Materials. 2021; 14(13):3629. https://doi.org/10.3390/ma14133629
Chicago/Turabian StyleZheng, Jinlei, Shaohui He, Yiming Li, Jiaxin He, and Jihua He. 2021. "Longitudinal Deformation of Deep Shield Tunnels Caused by Upper Load Reduction" Materials 14, no. 13: 3629. https://doi.org/10.3390/ma14133629
APA StyleZheng, J., He, S., Li, Y., He, J., & He, J. (2021). Longitudinal Deformation of Deep Shield Tunnels Caused by Upper Load Reduction. Materials, 14(13), 3629. https://doi.org/10.3390/ma14133629










