Development of a Caramel-Based Viscoelastic Reference Material for Cutting Tests at Different Rates
Abstract
:1. Introduction
- Sucrose and glucose syrups are bulk ingredients and sweeteners in caramels as well as in fudge and toffee, giving the products their unique texture and flavor. The ratio of sucrose to glucose syrup, a starch hydrolysis product that also contains small amounts of maltose and larger oligosaccharides, determines the extent of sucrose crystallization during and after production. Glucose syrup prevents graining [23] by increasing bulk viscosity which, in turn, decreases the molecular mobility of sugar crystal seeds [19,24]. Higher levels of glucose syrup are necessary to obtain an ungrained and smooth texture, whereas excessively high levels make products sticky and prone to cold flow [25].
- The rationale behind adding dairy ingredients is to incorporate milk proteins, usually by adding sweetened condensed milk, evaporated milk, or milk powder [25]. Casein, the main milk protein, provides structure by forming a network throughout the sugar matrix upon heating and by stabilizing the fat droplets through the formation of layers on the sugar-fat interface [21]. The whey protein contributes to non-enzymatic browning with reducing sugars, including lactose, bringing up the typical caramel flavor and light brown color [22,26].
- Fat is the third major component that contributes to flavor and texture, gives the product a smooth mouthfeel by reducing stickiness generated by the sugar compounds [19], and provides lubrication for improved machinability, including cutting [27]. This is because fat droplets partly replace the sticky components, namely sugar, on the surface in contact with a tool [28]. As the fat droplets can be regarded as filler in a continuous polymeric matrix, the melting properties of a specific fat also contribute to caramel firmness and product defects such as cold flow [29].
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Experiments on Properties Related to Cooking Temperature and Storage Stability
2.4. Analytical Methods
2.4.1. Moisture Content
2.4.2. Water Activity
2.4.3. Differential Scanning Calorimetry
2.4.4. Compression Tests
2.5. Cutting Experiments
2.6. Statistics
3. Results and Discussion
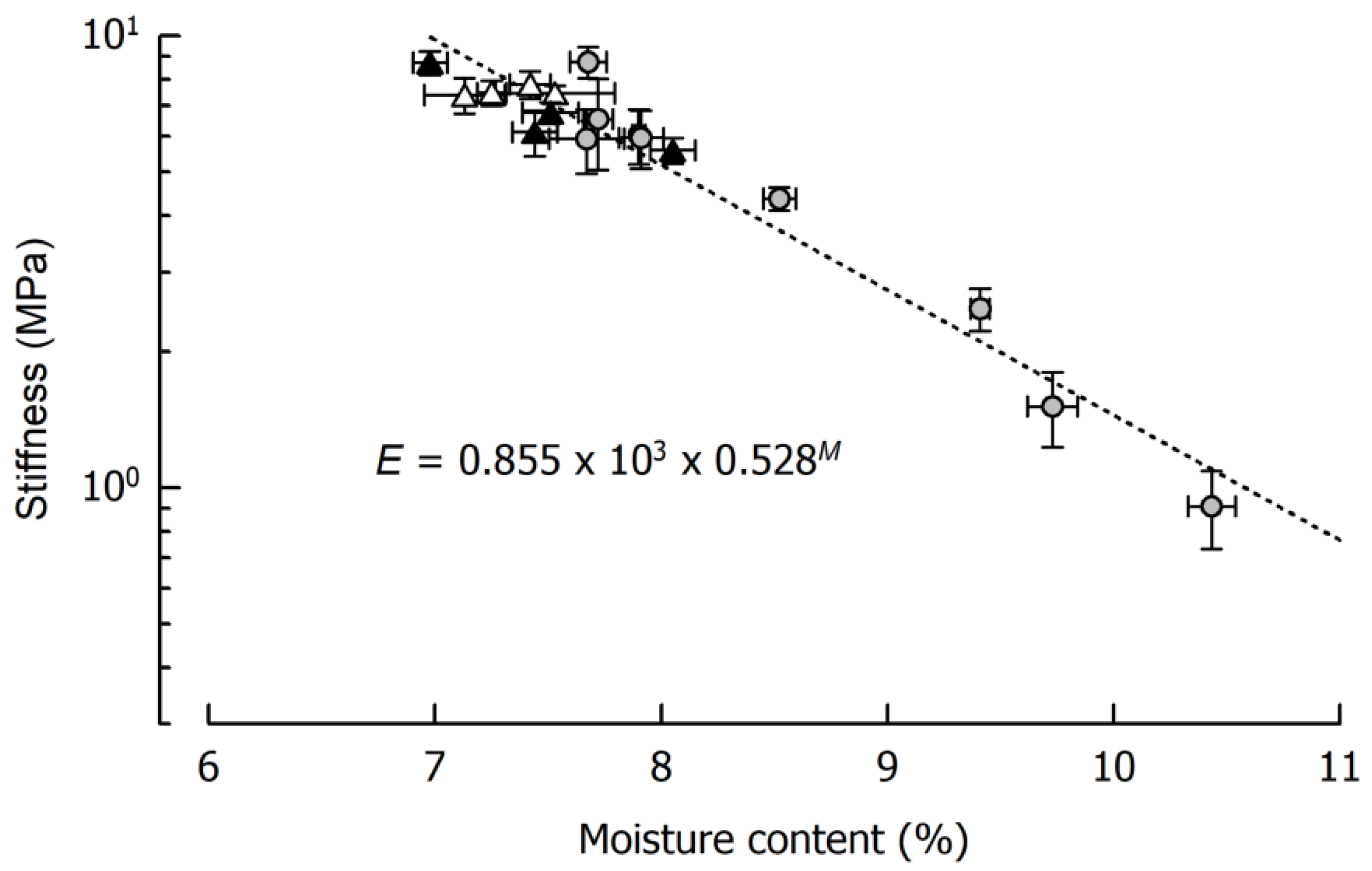
3.1. Impact of Cooking Temperature on Caramel Moisture and Stiffness
3.2. Storage Effects and Reproducibility of the Caramel Model Systems
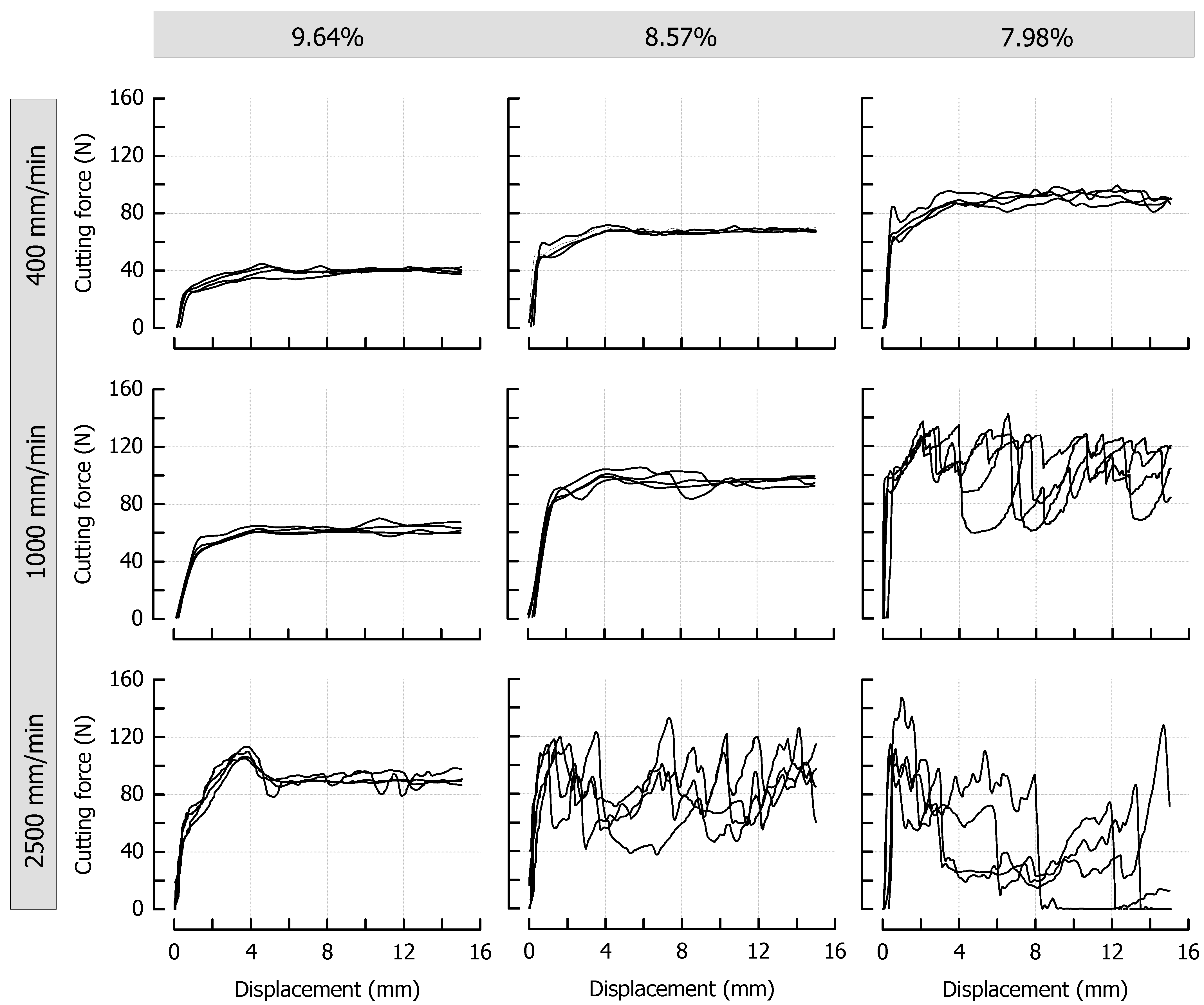
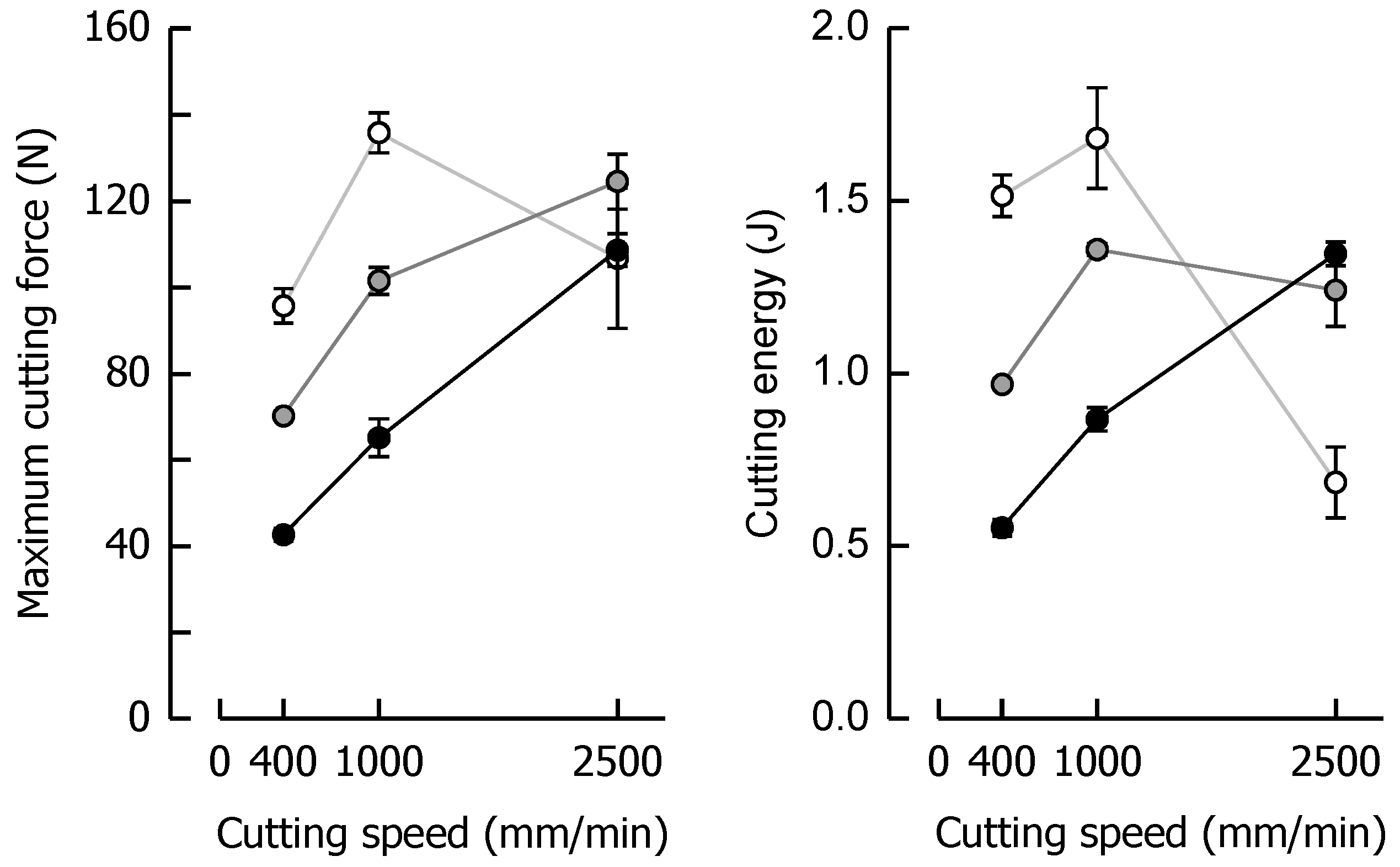
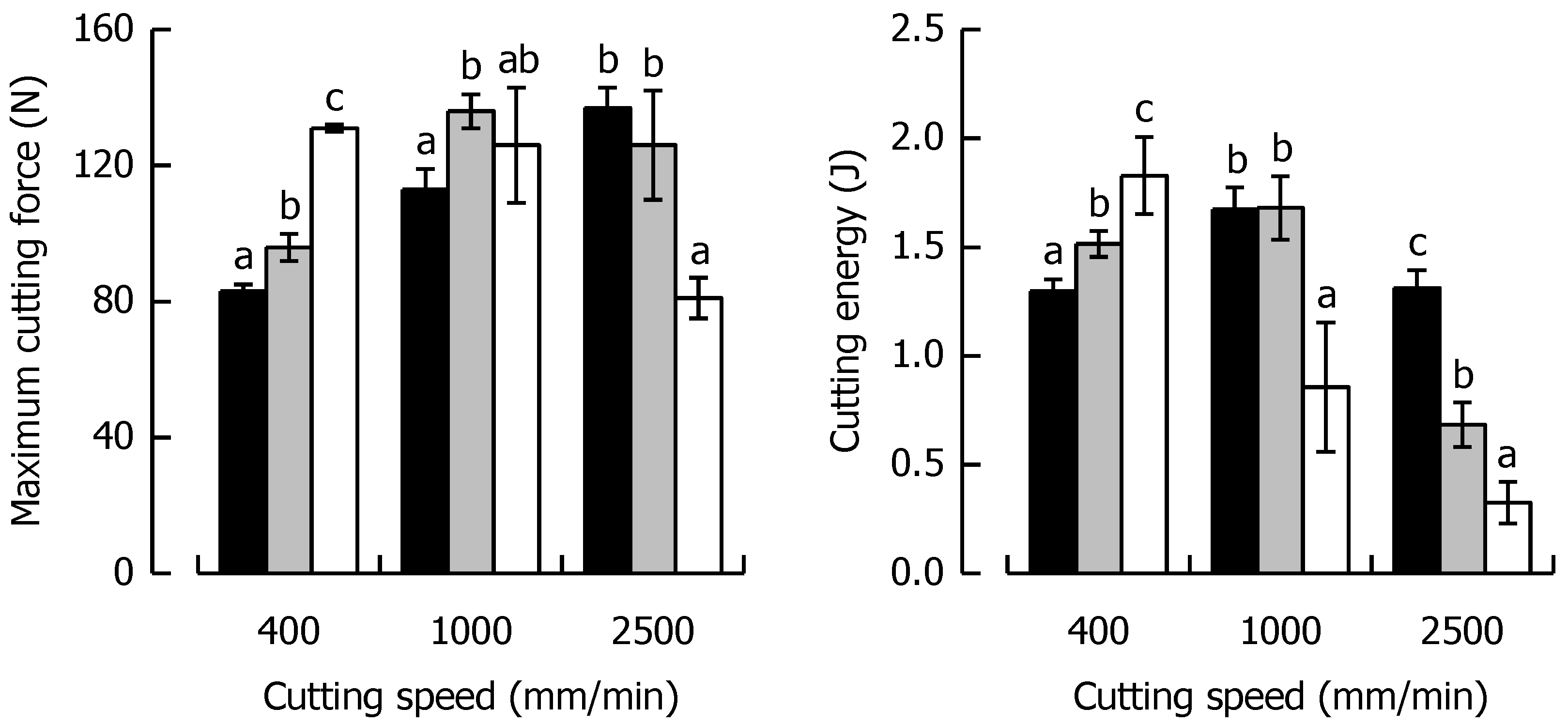
3.3. Effects of Caramel Moisture on Cutting Behavior at Different Cutting Speeds
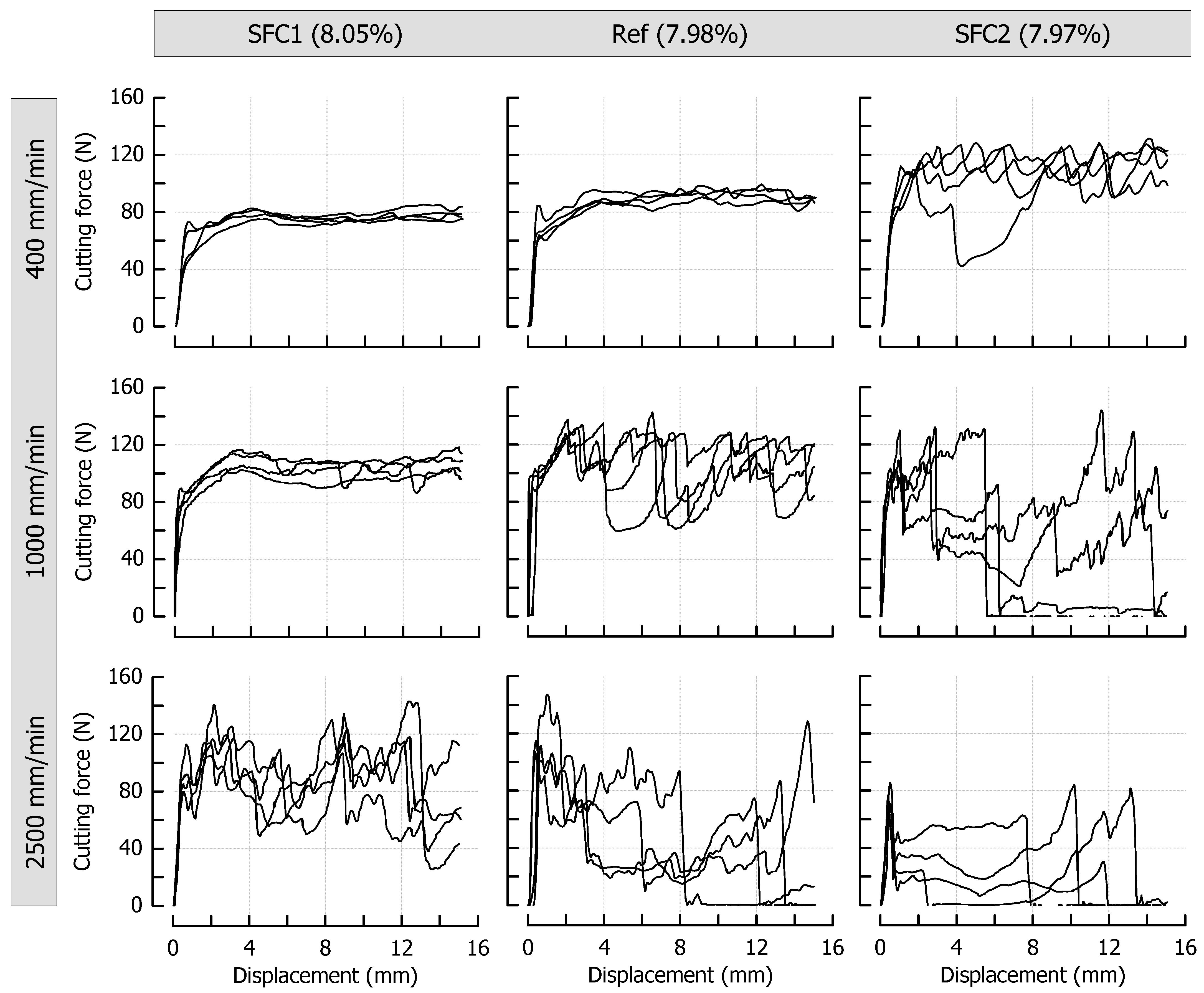
3.4. Effects of Solid Fat Content on Cutting Behavior at Different Cutting Speeds
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnold, G.; Zahn, S.; Legler, A.; Rohm, H. Ultrasonic cutting of foods with inclined moving blades. J. Food Eng. 2011, 103, 394–400. [Google Scholar] [CrossRef]
- Atkins, A.G.; Xu, X.; Jeronimidis, G. Cutting, by ‘pressing and slicing,’ of thin floppy slices of materials illustrated by experiments on cheddar cheese and salami. J. Mater. Sci. 2004, 39, 2761–2766. [Google Scholar] [CrossRef]
- Dowgiallo, A. Cutting force of fibrous materials. J. Food Eng. 2005, 66, 57–61. [Google Scholar] [CrossRef]
- Marsot, J.; Claudon, L.; Jacquin, M. Assessment of knife sharpness by means of a cutting force measuring system. Appl. Ergon. 2007, 38, 83–89. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, C.T.; Hussey, M.; Gilchrist, M.D. On the sharpness of straight edge blades in cutting soft solids: Part I—Indentation experiments. Eng. Fract. Mech. 2007, 74, 2205–2224. [Google Scholar] [CrossRef]
- Schuldt, S.; Arnold, G.; Kowalewski, J.; Schneider, Y.; Rohm, H. Analysis of the sharpness of blades for food cutting. J. Food Eng. 2016, 188, 13–20. [Google Scholar] [CrossRef]
- Schuldt, S.; Boden, L.; Schneider, Y.; Rohm, H. Pre-crack cutting properties of viscoelastic food models. J. Food Eng. 2016, 169, 272–277. [Google Scholar] [CrossRef]
- Schneider, Y.; Kluge, C.; Weiß, U.; Simat, T.; Rohm, H. Packaging materials and equipment. In Technology of Cheesemaking; Law, B.A., Tamime, A.Y., Eds.; Wiley-Blackwell: Oxford, UK, 2010; pp. 413–439. [Google Scholar]
- Steffe, J.F. Rheological Methods in Food Process Engineering; Freeman Press: East Lansing, MI, USA, 1996. [Google Scholar]
- Schuldt, S.; Witt, T.; Schmidt, C.; Schneider, Y.; Nündel, T.; Majschak, J.-P.; Rohm, H. High-speed cutting of foods: Development of a special testing device. J. Food Eng. 2018, 216, 36–41. [Google Scholar] [CrossRef]
- Schuldt, S.; Schneider, Y.; Rohm, H. High-speed cutting of foods: Cutting behavior and initial cutting forces. J. Food Eng. 2018, 230, 55–62. [Google Scholar] [CrossRef]
- Van Vliet, T.; Luyten, H.; Walstra, P. Time dependent fracture behaviour of food. In Food Colloids and Polymers: Stability and Mechanical Properties; Dickinson, E., Walstra, P., Eds.; Royal Society of Chemistry: Cambridge, UK, 1993; pp. 174–189. [Google Scholar]
- Boisly, M.; Schuldt, S.; Kästner, M.; Schneider, Y.; Rohm, H. Experimental characterisation and numerical modelling of cutting processes in viscoelastic solids. J. Food Eng. 2016, 191, 1–9. [Google Scholar] [CrossRef]
- Everard, C.D.; O’Callaghan, D.J.; Howard, T.V.; O’Donnell, C.P.; Sheehan, E.M.; Delahunty, C.M. Relationships between sensory and rheological measurements of texture in maturing commercial cheddar cheese over a range of moisture and pH at the point of manufacture. J. Texture Stud. 2006, 37, 361–382. [Google Scholar] [CrossRef]
- Jaros, D.; Ginzinger, W.; Tschager, E.; Leitgeb, R.; Rohm, H. Application of oilseed feeding to reduce firmness of hard cheeses produced in the winter feeding period. Int. Dairy J. 2001, 11, 611–619. [Google Scholar] [CrossRef]
- Jaros, D.; Petrag, J.; Rohm, H.; Ulberth, F. Influence of milk fat composition on mechanical and rheological properties of processed cheese. Appl. Rheol. 2001, 11, 19–25. [Google Scholar] [CrossRef]
- Wagoner, T.B.; Luck, P.J.; Foegeding, E.A. Caramel as a model system for evaluating the roles of mechanical properties and oral processing on sensory perception of texture. J. Food Sci. 2016, 81, S736–S744. [Google Scholar] [CrossRef]
- Ahmed, J.; Ramaswamy, H.; Pandey, P.K. Dynamic rheological and thermal characteristics of caramels. LWT Food Sci. Technol. 2006, 39, 216–224. [Google Scholar] [CrossRef]
- Steiner, A.E.; Foegeding, E.A.; Drake, M. Descriptive analysis of caramel texture. J. Sens. Stud. 2003, 18, 277–289. [Google Scholar] [CrossRef]
- Mendenhall, H.; Hartel, R.W. Protein content affects caramel processing and properties. J. Food Eng. 2016, 186, 58–68. [Google Scholar] [CrossRef]
- Heathcock, J. Characterisation of milk proteins in confectionery products. Food Struct. 1985, 4, 4. [Google Scholar]
- Sengar, G.; Sharma, H.K. Food caramels: A review. J. Food Sci. Technol. 2014, 51, 1686–1696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhandari, B.R.; Hartel, R.W. Co-crystallization of sucrose at high concentration in the presence of glucose and fructose. J. Food Sci. 2002, 67, 1797–1802. [Google Scholar] [CrossRef]
- Hartel, R.W.; Ergun, R.; Vogel, S. Phase/state transitions of confectionery sweeteners: Thermodynamic and kinetic aspects. Comp. Rev. Food Sci. Food Saf. 2011, 10, 17–32. [Google Scholar] [CrossRef]
- Hartel, R.W.; von Elbe, J.H.; Hofberger, R. Confectionery Science and Technology; Springer: Cham, Germany, 2018; pp. 273–299. [Google Scholar]
- Mohos, F.A. Confectionery and Chocolate Engineering: Principles and Applications; Wiley-Blackwell: Oxford, UK, 2010; pp. 495–524. [Google Scholar]
- Hoseney, R.C.; Smewing, J. Instrumental measurement of stickiness of doughs and other foods. J. Texture Stud. 1999, 30, 123–136. [Google Scholar] [CrossRef]
- Morton, D.N.; Roberts, C.J.; Hey, M.J.; Mitchell, J.R.; Hipkiss, J.; Vercauteren, J. Surface characterization of caramel at the micrometer scale. J. Food Sci. 2003, 68, 1411–1415. [Google Scholar] [CrossRef]
- Mendenhall, H.; Hartel, R.W. Effects of fat content and solid fat content on caramel texture attributes. J. Am. Oil Chem. Soc. 2016, 93, 1191–1199. [Google Scholar] [CrossRef]
- Sritham, E.; Gunasekaran, S. Thermal evaluation of sucrose-maltodextrin-sodium citrate bioglass: Glass transition temperature. Food Hydrocoll. 2016, 60, 589–597. [Google Scholar] [CrossRef]
- Walstra, P. Physical Chemistry of Foods; Marcel Dekker: New York, NY, USA, 2013. [Google Scholar]
- Ergun, R.; Lietha, R.; Hartel, R.W. Moisture and shelf life in sugar confections. Crit. Rev. Food Sci. Nutr. 2010, 50, 162–192. [Google Scholar] [CrossRef]
- Lenz, P.; Hartel, R.W. Empirical models for predicting crystallization in confections. Manuf. Conf. 2005, 85, 55–64. [Google Scholar]
- Miller, E.; Hartel, R.W. Sucrose crystallization in caramel. J. Food Eng. 2015, 153, 28–38. [Google Scholar] [CrossRef]
- Chen, C. Relationship between water activity and moisture content in floral honey. Foods 2019, 8, 30. [Google Scholar] [CrossRef] [Green Version]
- Gleiter, R.; Horn, H.; Isengard, H. Influence of type and state of crystallisation on the water activity of honey. Food Chem. 2006, 96, 441–445. [Google Scholar] [CrossRef]
- Hartel, R.W.; Shastry, A.V. Sugar crystallization in food products. Crit. Rev. Food Sci. Nutr. 1991, 30, 49–112. [Google Scholar] [CrossRef]
- Matveev, Y.I.; Grinberg, V.Y.; Tolstoguzov, V.B. The plasticizing effect of water on proteins, polysaccharides and their mixtures. Glassy state of biopolymers, food and seeds. Food Hydrocoll. 2000, 14, 425–437. [Google Scholar] [CrossRef]
- Zimeri, J.E.; Kokini, J.L. The effect of moisture content on the crystallinity and glass transition temperature of inulin. Carbohydr. Polym. 2002, 48, 299–304. [Google Scholar] [CrossRef]
- Gloria, H.; Sievert, D. Changes in the physical state of sucrose during dark chocolate processing. J. Agric. Food Chem. 2001, 49, 2433–2436. [Google Scholar] [CrossRef]
- Hurtta, M.; Pitkänen, I. Quantification of low levels of amorphous content in maltitol. Thermochim. Acta 2004, 419, 19–29. [Google Scholar] [CrossRef]
- Lappalainen, M.; Pitkänen, I.; Harjunen, P. Quantification of low levels of amorphous content in sucrose by hyperDSC. Int. J. Pharm. 2006, 370, 150–155. [Google Scholar] [CrossRef]
- Yu, X.; Kappes, S.M.; Bello-Perez, L.A.; Schmidt, S.J. Investigating the moisture sorption behavior of amorphous sucrose using a dynamic humidity generating instrument. J. Food Sci. 2008, 73, 25–35. [Google Scholar] [CrossRef] [PubMed]
- Avaltroni, F.; Bouquerand, P.; Normand, V. Maltodextrin molecular weight distribution influence on the glass transition temperature and viscosity in aqueous solutions. Carbohydr. Polym. 2004, 58, 323–334. [Google Scholar] [CrossRef]
- Gibbs, J.H.; DiMarzio, E.A. Nature of the glass transition and the glassy state. J. Chem. Phys. 1958, 28, 373–383. [Google Scholar] [CrossRef]
- Borde, B.; Bizot, H.; Vigier, G.; Buleon, A. Calorimetric analysis of the structural relaxation in partially hydrated amorphous polysaccharides. I. Glass transition and fragility. Carbohydr. Polym. 2002, 48, 83–96. [Google Scholar] [CrossRef]
- Hancock, B.C.; Zografi, G. Characteristics and significance of the amorphous state in pharmaceutical systems. J. Pharm. Sci. 1997, 86, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, J.; Ramaswamy, H.S.; Khan, A.R. Effect of water activity on glass transitions of date pastes. J. Food Eng. 2005, 66, 253–258. [Google Scholar] [CrossRef]
- Mizuno, A.; Mitsuiki, M.; Motoko, M. Glass transition temperature of casein as affected by transglutaminase. J. Food Sci. 1999, 64, 796–799. [Google Scholar] [CrossRef]
- Baik, M.-Y.; Kim, K.-J.; Cheon, K.-C.; Ha, Y.-C.; Kim, W.-S. Recrystallization kinetics and glass transition of rice starch gel system. J. Agric. Food Chem. 1997, 45, 4242–4248. [Google Scholar] [CrossRef]
- Kawai, K.; Hagiwara, T.; Takai, R.; Suzuki, T. Comparative investigation by two analytical approaches of enthalpy relaxation for glassy glucose, sucrose, maltose, and trehalose. Pharm. Res. 2005, 22, 490–495. [Google Scholar] [CrossRef]
- Liu, Y.; Bhandari, B.; Zhou, W. Study of glass transition and enthalpy relaxation of mixtures of amorphous sucrose and amorphous tapioca starch syrup solid by differential scanning calorimetry (DSC). J. Food Eng. 2007, 81, 599–610. [Google Scholar] [CrossRef]
- Mao, C.; Chamarty, S.P.; Pinal, R. Time-dependence of molecular mobility during structural relaxation and its impact on organic amorphous solids: An investigation based on a calorimetric approach. Pharm. Res. 2006, 23, 1906–1917. [Google Scholar] [CrossRef]
- Shamblin, S.L.; Taylor, L.S.; Zografi, G. Mixing behavior of colyophilized binary systems. J. Pharm. Sci. 1998, 87, 694–701. [Google Scholar] [CrossRef]
- Roos, Y.; Karel, M. Water and molecular weight effects on glass transitions in amorphous carbohydrates and carbohydrate solutions. J. Food Sci. 1991, 56, 1676–1681. [Google Scholar] [CrossRef]
- Kasapis, S. Relation between the structure of matrices and their mechanical relaxation mechanisms during the glass transition of biomaterials: A review. Food Hydrocoll. 2012, 26, 464–472. [Google Scholar] [CrossRef]
- Arnold, G.; Leiteritz, L.; Zahn, S.; Rohm, H. Ultrasonic cutting of cheese: Composition affects cutting work reduction and energy demand. Int. Dairy J. 2009, 19, 314–320. [Google Scholar] [CrossRef]
- Bobaru, F.; Zhang, G. Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int. J. Fract. 2015, 196, 59–98. [Google Scholar] [CrossRef]
- Bryan, H.H.; Ahuja, K.K. Review of crack propagation under unsteady loading. AIAA J. 1993, 31, 1077–1089. [Google Scholar] [CrossRef]
- Gdoutos, E.E. Introduction. In Fracture Mechanics: An Introduction, 2nd ed.; Gladwell, G.M.L., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 1–13. [Google Scholar]
- Langer, B.; Seidler, S.; Grellmann, W. Influence of temperature and moisture on toughness behaviour of polyamide. In Deformation Behaviour of Polymers; Grellmann, W., Seidler, S., Eds.; Springer: Berlin, Germany, 2001; pp. 209–228. [Google Scholar]
- Berthaume, M. Food mechanical properties and dietary ecology. Am. J. Phys. Anthropol. 2016, 159, 79–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swackhamer, C.; Bornhost, G.M. Fracture properties of foods: Experimental considerations and applications to mastication. J. Food. Eng. 2019, 263, 213–226. [Google Scholar] [CrossRef]
- Liu, K.; Stieger, M.; van der Linden, E.; van de Velde, F. Fat droplet characteristics affect rheological, tribological and sensory properties of food gels. Food Hydrocoll. 2015, 44, 244–259. [Google Scholar] [CrossRef]


| Day | aW1 (−) | E2 (MPa) | TG,on3 (°C) | TG,end3 (°C) | Δcp 3 (J/g·K) |
|---|---|---|---|---|---|
| Ref_120C_1, moisture 1: 7.64 ± 0.08% | |||||
| 1 | 0.444 ± 0.003 a | n.d. | −5.95 ± 0.09 a | 6.73 ± 0.09 a | 0.43 ± 0.02 a |
| 2 | 0.447 ± 0.001 a | n.d. | −5.93 ± 0.23 a | 6.76 ± 0.08 a | 0.43 ± 0.02 a |
| 3 | 0.448 ± 0.004 a | n.d. | −5.71 ± 0.62 a | 6.61 ± 0.36 a | 0.41 ± 0.02 a |
| 4 | 0.450 ± 0.003 a | n.d. | −5.72 ± 0.42 a | 6.23 ± 0.04 a | 0.39 ± 0.01 a |
| Ref_120C_2, moisture 1: 7.67 ± 0.08% | |||||
| 1 | 0.445 ± 0.003 a | 8.75 ± 0.69 a | −6.06 ± 0.12 b | 6.38 ± 0.16 a | 0.45 ± 0.02 a |
| 2 | 0.446 ± 0.001 ab | 7.51 ± 0.47 a | −5.47 ± 0.10 a | 6.96 ± 0.06 a | 0.42 ± 0.01 a |
| 3 | 0.447 ± 0.002 ab | 8.33 ± 0.43 a | −6.23 ± 0.10 b | 6.44 ± 0.00 a | 0.46 ± 0.01 a |
| 4 | 0.450 ± 0.001 b | 8.72 ± 0.72 a | −5.62 ± 0.14 a | 6.45 ± 0.32 a | 0.42 ± 0.02 a |
| Ref_115C_1, moisture 1: 9.72 ± 0.11% | |||||
| 1 | 0.526 ± 0.003 b | 1.51 ± 0.29 a | −15.46 ± 0.40 a | −1.04 ± 0.72 a | 0.52 ± 0.01 a |
| 2 | 0.529 ± 0.002 b | 1.43 ± 0.21 a | −14.97 ± 0.62 a | −1.59 ± 0.58 a | 0.51 ± 0.02 a |
| 3 | 0.521 ± 0.002 a | 2.09 ± 0.44 b | −15.35 ± 0.27 a | −1.65 ± 0.15 a | 0.52 ± 0.02 a |
| 4 | 0.524 ± 0.002 ab | 2.15 ± 0.12 b | −15.57 ± 0.02 a | −1.86 ± 0.49 a | 0.50 ± 0.01 a |
| Ref_115C_2, moisture 1: 10.42 ± 0.11% | |||||
| 1 | 0.544 ± 0.004 a | 0.91 ± 0.18 a | −17.50 ± 0.23 a | −2.95 ± 0.23 a | 0.52 ± 0.01 a |
| 2 | 0.545 ± 0.002 a | 0.87 ± 0.13 a | −17.95 ± 0.73 a | −3.26 ± 0.73 a | 0.52 ± 0.02 a |
| 3 | 0.542 ± 0.002 a | 0.92 ± 0.13 a | −17.28 ± 0.61 a | −2.28 ± 0.61 a | 0.52 ± 0.00 a |
| 4 | 0.544 ± 0.002 a | 1.02 ± 0.21 a | −16.98 ± 0.30 a | −2.27 ± 0.30 a | 0.50 ± 0.01 a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schab, D.; Zahn, S.; Rohm, H. Development of a Caramel-Based Viscoelastic Reference Material for Cutting Tests at Different Rates. Materials 2021, 14, 3798. https://doi.org/10.3390/ma14143798
Schab D, Zahn S, Rohm H. Development of a Caramel-Based Viscoelastic Reference Material for Cutting Tests at Different Rates. Materials. 2021; 14(14):3798. https://doi.org/10.3390/ma14143798
Chicago/Turabian StyleSchab, Dennis, Susann Zahn, and Harald Rohm. 2021. "Development of a Caramel-Based Viscoelastic Reference Material for Cutting Tests at Different Rates" Materials 14, no. 14: 3798. https://doi.org/10.3390/ma14143798
APA StyleSchab, D., Zahn, S., & Rohm, H. (2021). Development of a Caramel-Based Viscoelastic Reference Material for Cutting Tests at Different Rates. Materials, 14(14), 3798. https://doi.org/10.3390/ma14143798







