Modeling and Solution of Large Amplitude Vibration Problem of Construction Elements Made of Nanocomposites Using Shear Deformation Theory
Abstract
:1. Introduction
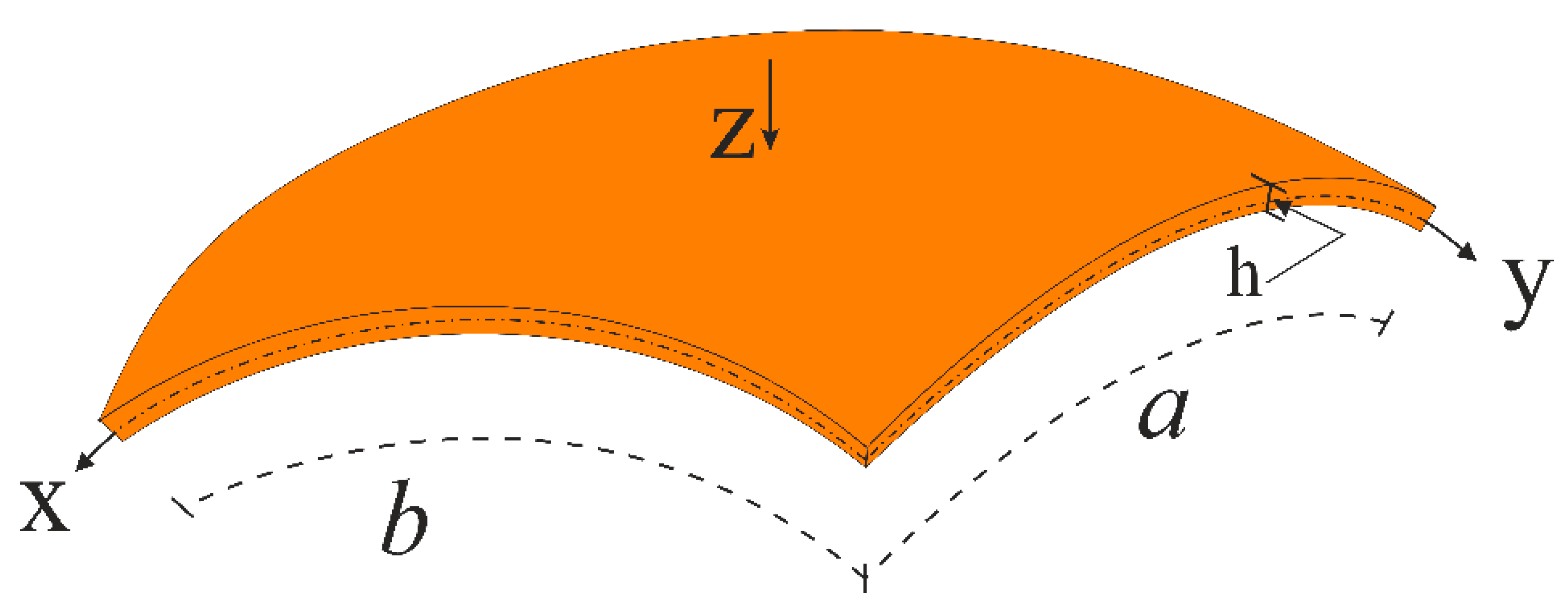
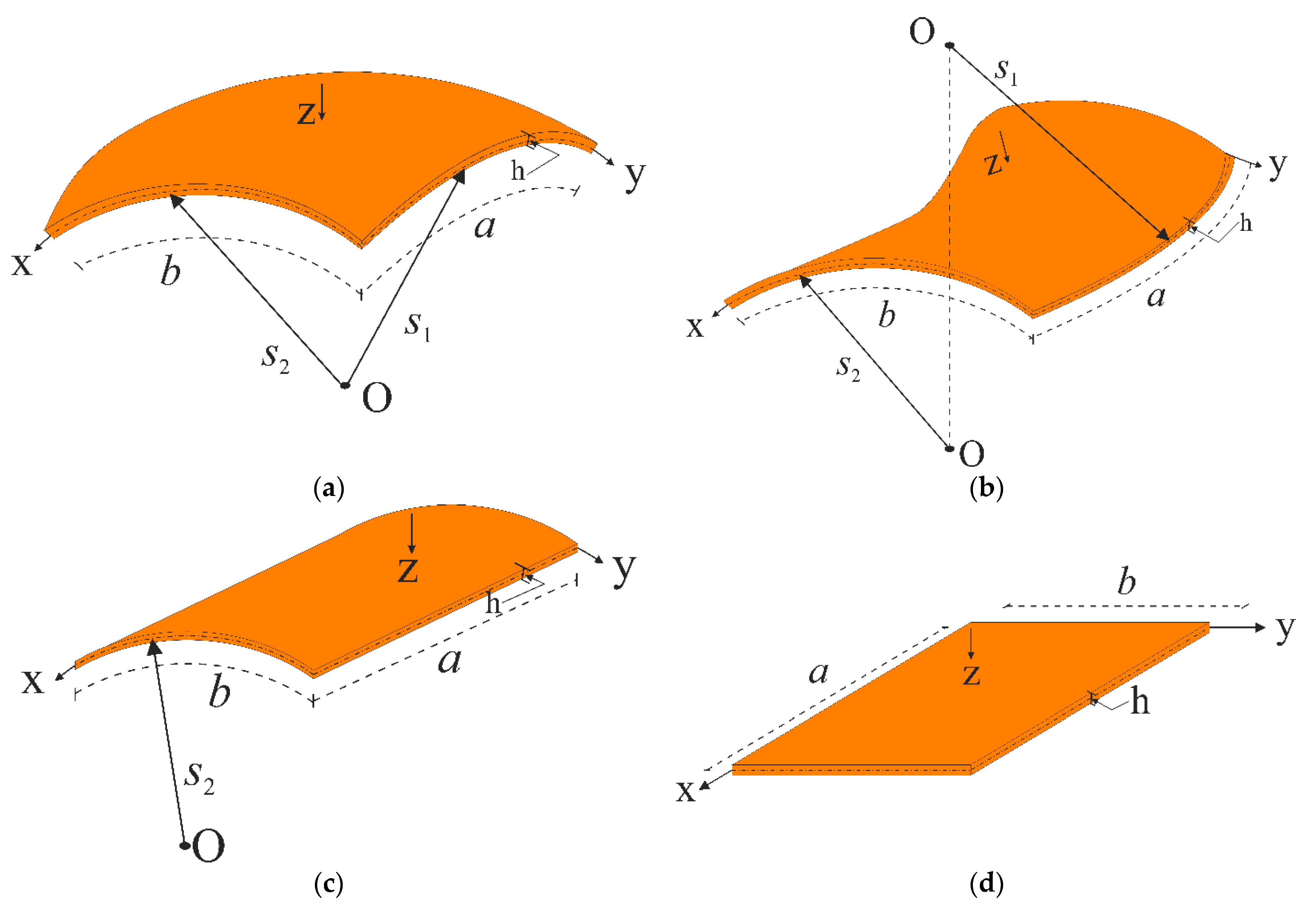
2. Formulation of Problem
3. Basic Relations
4. Basic Equations and Solution
5. Discussion
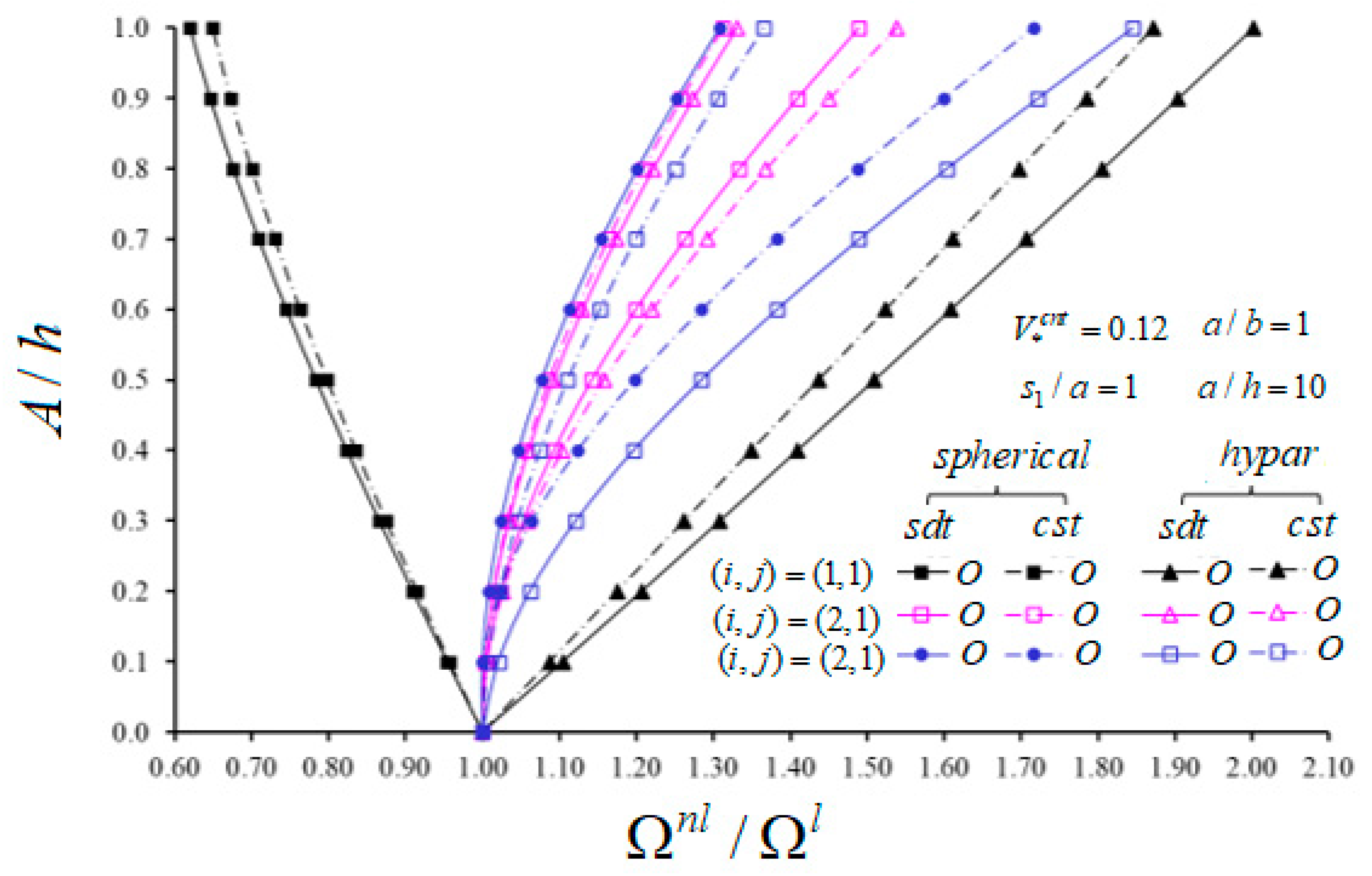
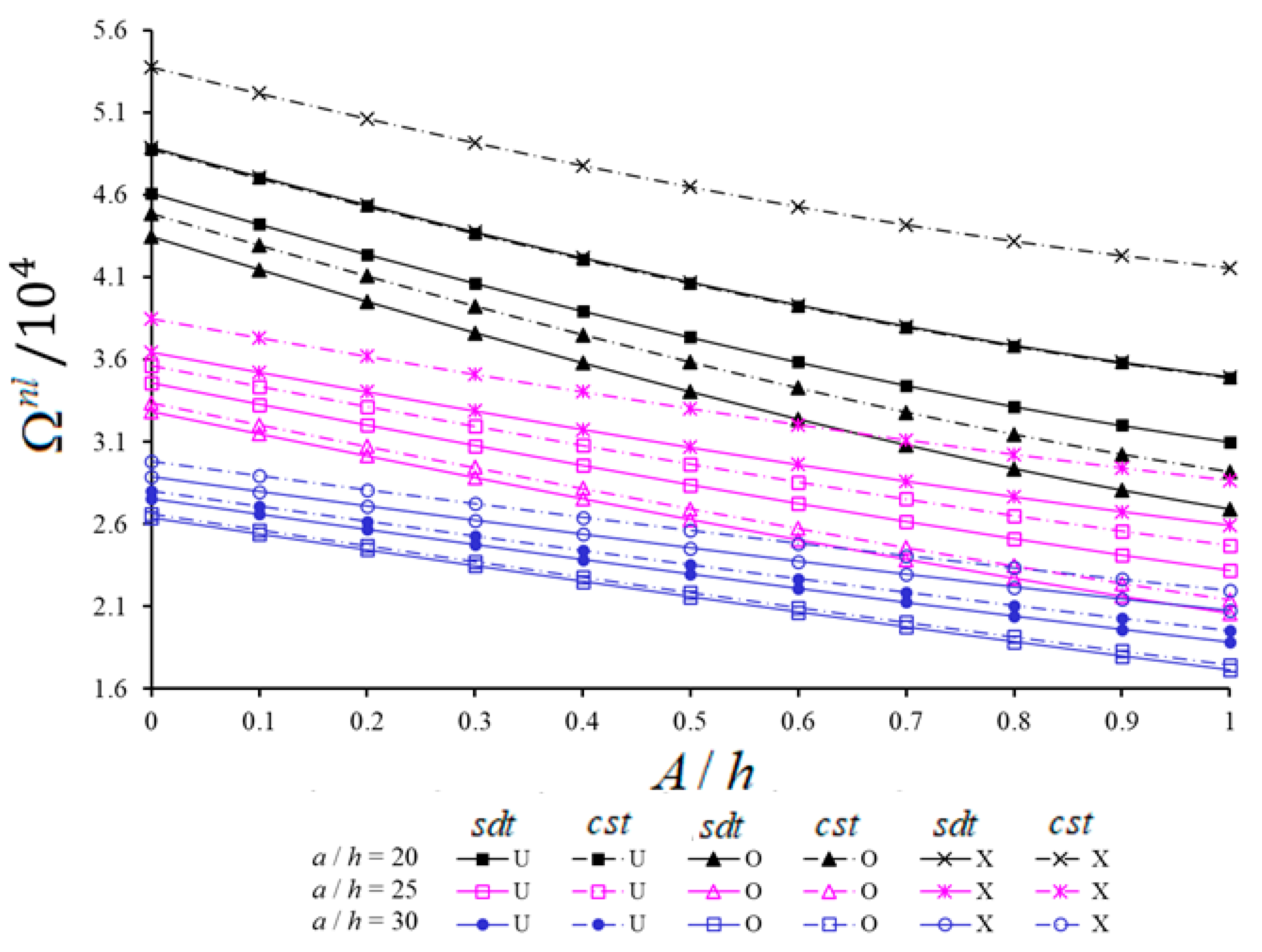
5.1. Comparative Studies
5.2. New Numerical Analyses and Interpretations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Author Agreement
Appendix A
References
- Ambartsumian, S.A. Theory of Anisotropic Shells; TT F-118; NASA: Washington, DC, USA, 1964.
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Viola, E.; Tornabene, F.; Fantuzzi, N. General Higher-Order Shear Deformation Theories for the Free Vibration Analysis of Completely Doubly-Curved Laminated Shells and Panels. Compos. Struct. 2013, 95, 639–666. [Google Scholar] [CrossRef]
- Iijima, S. Single-shell Carbon Nanotubes of 1-nm Diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Salvetat, J.P.; Bonard, J.M.; Thomson, N.H.; Kulik, A.J.; Forró, L.; Benoit, W.; Zuppiroli, L. Mechanical Properties of Carbon Nanotubes. Appl. Phys. 1999, A69, 255–260. [Google Scholar] [CrossRef]
- Harris, P.J.K. Carbon Nanotubes and Related Structures: New Materials for the Twenty-First Century; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Popov, V. Carbon Nanotubes: Properties and Application. Mater. Sci. Eng. R Rep. 2004, 43, 61–102. [Google Scholar] [CrossRef]
- Cooper, C.A.; Ravich, D.; Lips, D.; Mayer, J. Distribution and Alignment of Carbon Nanotubes and Nanofibrils in a Polymer Matrix. Comp. Sci. Tech. 2002, 62, 1105–1112. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, X.; Zhu, Y.; Hui, D.; Qiu, Y. Mechanical, Electrical and Thermal Properties of Aligned Carbon Nanotube/Polyimide Composites. Compos Part B Eng. 2014, 56, 408–412. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale Approach for Three-Phase CNT/Polymer/Fiber Laminated Nanocomposite Structures. Polym. Compos. 2019, 40, E102–E126. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Bacciocchi, M.; Agnelli, J.; Benedetti, D. Three-phase Homogenization Procedure for Woven Fabric Composites Reinforced by Carbon Nanotubes in Thermal Environment. Compos. Struct. 2020, 254, 112840. [Google Scholar] [CrossRef]
- Ulloa-Castillo, N.A.; Martinez-Romero, O.; Hernandez-Maya, R.; Segura-Cárdenas, A.; Elias-Zuniga, A. Spark Plasma Sintering of Aluminum-Based Powders Reinforced with Carbon Nanotubes: Investigation of Electrical Conductivity and Hardness Properties. Materials 2021, 14, 373. [Google Scholar] [CrossRef]
- Esawi, A.M.K.; Farag, M.M. Carbon Nanotube Reinforced Composites: Potential and Current Challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Gohardanı, O.; Elola, M.C.; Elızetxea, C. Potential and Prospective Implementation of Carbon Nanotubes on Next Generation Aircraft and Space Vehicles: A Review of Current and Expected Applications in Aerospace Sciences. Prog. Aerosp. Sci. 2014, 3, 42–68. [Google Scholar] [CrossRef]
- Park, S.H.; Bae, J. Polymer Composite Containing Carbon Nanotubes and Their Applications. Rec. Patent. Nanotech. 2017, 11, 109–115. [Google Scholar] [CrossRef]
- Shen, H.S. Nonlinear Bending of Functionally Graded Carbon Nanotube-Reinforced Composite Plates in Thermal Environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Fazelzadeh, S. Frequency Analysis of Doubly Curved Functionally Graded Carbon Nanotube-Reinforced Composite Panels. Acta Mech. 2016, 227, 2765–2794. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, B.; Shi, D.; Liang, Q. A Semi-Analytical Method for Vibration Analysis of Functionally Graded Carbon Nanotube Reinforced Composite Doubly-Curved Panels and Shells of Revolution. Compos. Struct. 2017, 174, 87–109. [Google Scholar] [CrossRef]
- Wang, Q.; Qin, B.; Shi, D.; Liang, Q. Vibration Analysis of the Functionally Graded Carbon Nanotube Reinforced Composite Shallow Shells with Arbitrary Boundary Conditions. Compos. Struct. 2017, 182, 364–379. [Google Scholar] [CrossRef]
- Braun, M.; Aranda-Ruiz, J.; Rodriguez-Millan, M.; Loya, J.A. On the Bulk Modulus and Natural Frequency of Fullerene and Nanotube Carbon Structures Obtained with a Beam Based Method. Compos. Struct. 2018, 187, 10–17. [Google Scholar] [CrossRef]
- Ansari, M.I.; Kumar, A.; Fic, S.; Barnat-Hunek, D. Flexural and Free Vibration Analysis of CNT-Reinforced Functionally Graded Plate. Materials 2018, 11, 2387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, H.Q.; Tran, M.T.; Vu, V.T. Free Vibration Analysis of Smart Laminated Functionally Graded CNT Reinforced Composite Plates via New Four-Variable Refined Plate Theory. Materials 2019, 12, 3675. [Google Scholar]
- Qin, Z.; Pang, X.; Safaei, B.; Chu, F. Free Vibration Analysis of Rotating Functionally Graded CNT Reinforced Composite Cylindrical Shells with Arbitrary Boundary Conditions. Compos. Struct. 2020, 220, 847–860. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading. Nanomaterials 2020, 10, 419. [Google Scholar] [CrossRef] [Green Version]
- Sofiyev, A.H.; Mammadov, Z.; Dimitri, R.; Tornabene, F. Vibration Analysis of Shear Deformable Carbon Nanotubes-Based Functionally Graded Conical Shells Resting on Elastic Foundations. Math. Meth. Appl. Sci. 2020, 1–15. [Google Scholar] [CrossRef]
- Sofiyev, A.H. On the Vibration and Stability Behaviors of Heterogeneous-CNTRC-Truncated Conical Shells under Axial Load in the Context of FSDT. Thin Wall. Struct. 2020, 151, 106747. [Google Scholar] [CrossRef]
- Azarafza, R.; Davar, A.L.; Fayez, M.S.; Jam, J.E. Free Vibration of Grid-Stiffened Composite Cylindrical Shell Reinforced with Carbon Nanotubes. Mech. Compos. Mater. 2020, 56, 505–522. [Google Scholar] [CrossRef]
- Cornacchia, F.; Fabbrocino, F.; Fantuzzi, N.; Luciano, R.; Penna, R. Analytical Solution of Cross- and Angle-Ply Nano Plates with Strain Gradient Theory for Linear Vibrations and Buckling. Mech. Adv. Mater. Struct. 2021, 28, 1201–1215. [Google Scholar] [CrossRef]
- Vinyas, M.; Harursampath, D.; Kattimani, S.C. On Vibration Analysis of Functionally Graded Carbon Nanotube Reinforced Magneto-Electro-Elastic Plates with Different Electro-Magnetic Conditions Using Higher Order Finite Element Methods. Def. Technol. 2021, 17, 287–303. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Nonlinear Vibration of Nanotube-Reinforced Composite Cylindrical Shells in Thermal Environments. Comput. Methods Appl. Mech. Eng. 2012, 213, 196–205. [Google Scholar] [CrossRef]
- Nguyen, P.D.; Quang, V.D.; Anh, V.T.T.; Duc, N.D. Nonlinear Vibration of Carbon Nanotube Reinforced Composite Truncated Conical Shells in Thermal Environment. Int. J. Struct. Stab. Dyn. 2019, 19, 1950158. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Large Deflection Responses-Based Geometrical Nonlinearity of Nanocomposite Structures Reinforced with Carbon Nanotubes. Appl. Math. Mech. Eng. Edit. 2020, 41, 1227–1250. [Google Scholar] [CrossRef]
- Dat, N.D.; Quan, T.Q.; Vinyas, M.; Duc, N.D. Analytical Solutions for Nonlinear Magneto-Electro-Elastic Vibration of Smart Sandwich Plate with Carbon Nanotube Reinforced Nanocomposite Core in Hygrothermal Environment. Int. J. Mech. Sci. 2020, 186, 105906. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Gao, Y.S.; Zhao, G.Z.; Yu, Y.J.; Chen, M.; Wang, X.F. Geometrically Nonlinear Analysis of CNT-Reinforced Functionally Graded Composite Plates Integrated with Piezoelectric Layers. Compos. Struct. 2020, 234, 111694. [Google Scholar] [CrossRef]
- Huang, X.H.; Yang, J.; Azim, I.; Wang, X.; Ren, X. Geometric Non-Linear Analysis of Auxetic Hybrid Laminated Beams Containing CNT Reinforced Composite Materials. Materials 2020, 13, 3718. [Google Scholar] [CrossRef]
- Avey, M.; Yusufoglu, E. On the Solution of Large-Amplitude Vibration of Carbon Nanotube-Based Doubly-Curved Shallow Shells. Math. Meth. Appl. Sci. 2020, 1–13. [Google Scholar] [CrossRef]
- Yusufoglu, E.; Avey, M. Nonlinear Dynamic Behavior of Hyperbolic Paraboloidal Shells Reinforced by Carbon Nanotubes with Various Distributions. J. Appl. Comput. Mech. 2021, 2, 913–921. [Google Scholar]
- Chakraborty, S.; Dey, T. Non-linear Stability Analysis of CNT Reinforced Composite Cylindrical Shell Panel Subjected to Thermomechanical Loading. Compos. Struct. 2021, 255, 112995. [Google Scholar] [CrossRef]
- Yadav, A.; Amabili, M.; Panda, S.K.; Dey, T.; Kumar, R. Nonlinear Damped Vibrations of Three-Phase CNT-FRC Circular Cylindrical Shell. Compos. Struct. 2021, 255, 112939. [Google Scholar] [CrossRef]
- Liew, K.M.; Pan, Z.; Zhang, L.-W. The Recent Progress of Functionally Graded CNT Reinforced Composites and Structures. Sci. China Phys. Mech. Astron. 2020, 63, 234601. [Google Scholar] [CrossRef] [Green Version]
- Vol’mir, A.S. Nonlinear Dynamics of Plates and Shells; Nauka: Moscow, Russia, 1972. [Google Scholar]
- Grigolyuk, E.I. On Vibrations of a Shallow Circular Cylindrical Panel Experiencing Finite Deflections. Appl. Math. Mech. 1955, 19, 376–382. [Google Scholar]
- Alijani, F.; Amabili, M.; Bakhtiari-Nejad, F. On the Accuracy of the Multiple Scales Method for Non-Linear Vibrations of Doubly Curved Shallow Shells. Int. J. Non-Lin. Mech. 2011, 46, 170–179. [Google Scholar] [CrossRef]
- Bich, D.H.; Duc, N.D.; Quan, T.Q. Nonlinear Vibration of Imperfect Eccentrically Stiffened Functionally Graded Double Curved Shallow Shells Resting on Elastic Foundation Using the First Order Shear Deformation Theory. Int. J. Mech. Sci. 2014, 80, 16–28. [Google Scholar] [CrossRef]




| Construction Elements | |||||||
|---|---|---|---|---|---|---|---|
| U | V | X | |||||
| Ref. [17] | Present Study | Ref. [17] | Present Study | Ref. [17] | Present Study | ||
| Spherical shells | 0.11 | 20.238 | 20.286 | 18.543 | 18.685 | 22.432 | 22.493 |
| 0.14 | 21.655 | 21.756 | 19.779 | 19.966 | 23.997 | 24.064 | |
| 0.17 | 25.021 | 25.158 | 22.951 | 23.165 | 27.883 | 27.893 | |
| Hypar shells | 0.11 | 17.106 | 17.332 | 14.809 | 15.114 | 19.588 | 19.853 |
| 0.14 | 18.626 | 18.924 | 16.181 | 16.544 | 21.225 | 21.512 | |
| 0.17 | 21.093 | 21.423 | 18.225 | 18.645 | 24.274 | 24.524 | |
| Cylindrical panels | 0.11 | 18.126 | 18.116 | 16.060 | 16.150 | 20.548 | 20.545 |
| 0.14 | 19.628 | 19.670 | 17.391 | 17.524 | 22.179 | 22.178 | |
| 0.17 | 22.380 | 22.415 | 19.799 | 19.949 | 25.488 | 25.408 | |
| Rectangular Plates | 0.11 | 18.008 | 17.332 | 15.701 | 15.113 | 20.624 | 19.853 |
| 0.14 | 19.608 | 18.924 | 17.147 | 16.544 | 22.349 | 21.512 | |
| 0.17 | 22.207 | 21.424 | 19.315 | 18.645 | 25.557 | 24.524 | |
| Construction Elements | |||||
|---|---|---|---|---|---|
| Ref. [43]. | Ref. [44]. | Present Study | |||
| Spherical shell | 2 | 2 | 0.0779 | 0.0767 | 0.0769 |
| Rectangular plate | 0.0597 | 0.0581 | 0.0584 | ||
| Cylindrical panel | 2 | 0.0648 | 0.0632 | 0.0636 | |
| 0.12 | 0.137 | 1.022 | 0.715 |
| 0.17 | 0.142 | 1.626 | 1.138 |
| 0.28 | 0.141 | 1.585 | 1.109 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deniz, A.; Fantuzzi, N.; Sofiyev, A.H.; Kuruoglu, N. Modeling and Solution of Large Amplitude Vibration Problem of Construction Elements Made of Nanocomposites Using Shear Deformation Theory. Materials 2021, 14, 3843. https://doi.org/10.3390/ma14143843
Deniz A, Fantuzzi N, Sofiyev AH, Kuruoglu N. Modeling and Solution of Large Amplitude Vibration Problem of Construction Elements Made of Nanocomposites Using Shear Deformation Theory. Materials. 2021; 14(14):3843. https://doi.org/10.3390/ma14143843
Chicago/Turabian StyleDeniz, Ali, Nicholas Fantuzzi, Abdullah Heydaroglu Sofiyev, and Nuri Kuruoglu. 2021. "Modeling and Solution of Large Amplitude Vibration Problem of Construction Elements Made of Nanocomposites Using Shear Deformation Theory" Materials 14, no. 14: 3843. https://doi.org/10.3390/ma14143843
APA StyleDeniz, A., Fantuzzi, N., Sofiyev, A. H., & Kuruoglu, N. (2021). Modeling and Solution of Large Amplitude Vibration Problem of Construction Elements Made of Nanocomposites Using Shear Deformation Theory. Materials, 14(14), 3843. https://doi.org/10.3390/ma14143843







