Experimental Study on the Axial Tensile Properties of FRP Grid-Reinforced ECC Composites
Abstract
:1. Introduction
2. Experiment Design
2.1. Specimen Design
2.2. Test Raw Materials
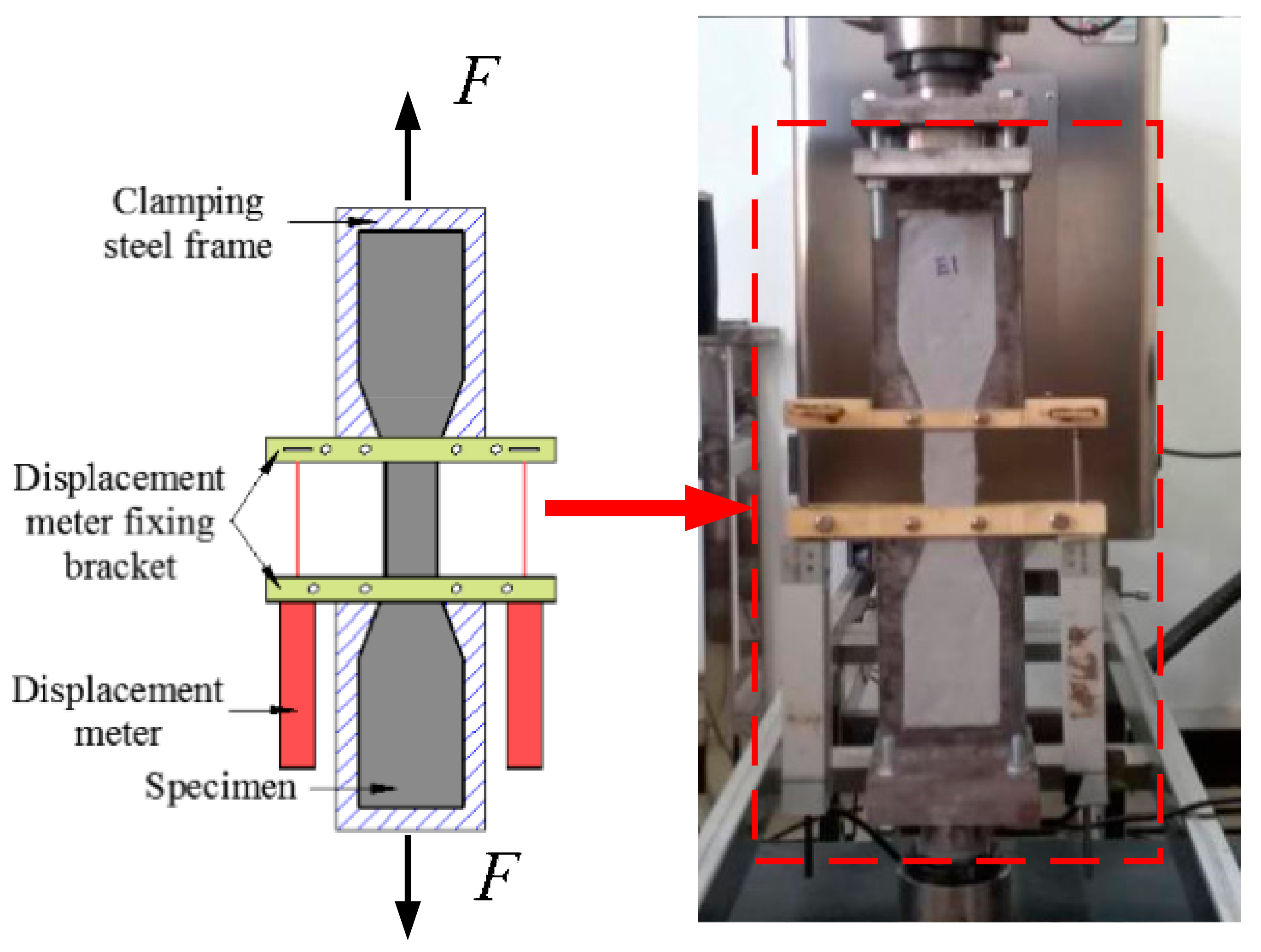
2.3. Test Setup
3. Analysis of Experimental Results
3.1. Experimental Phenomenon
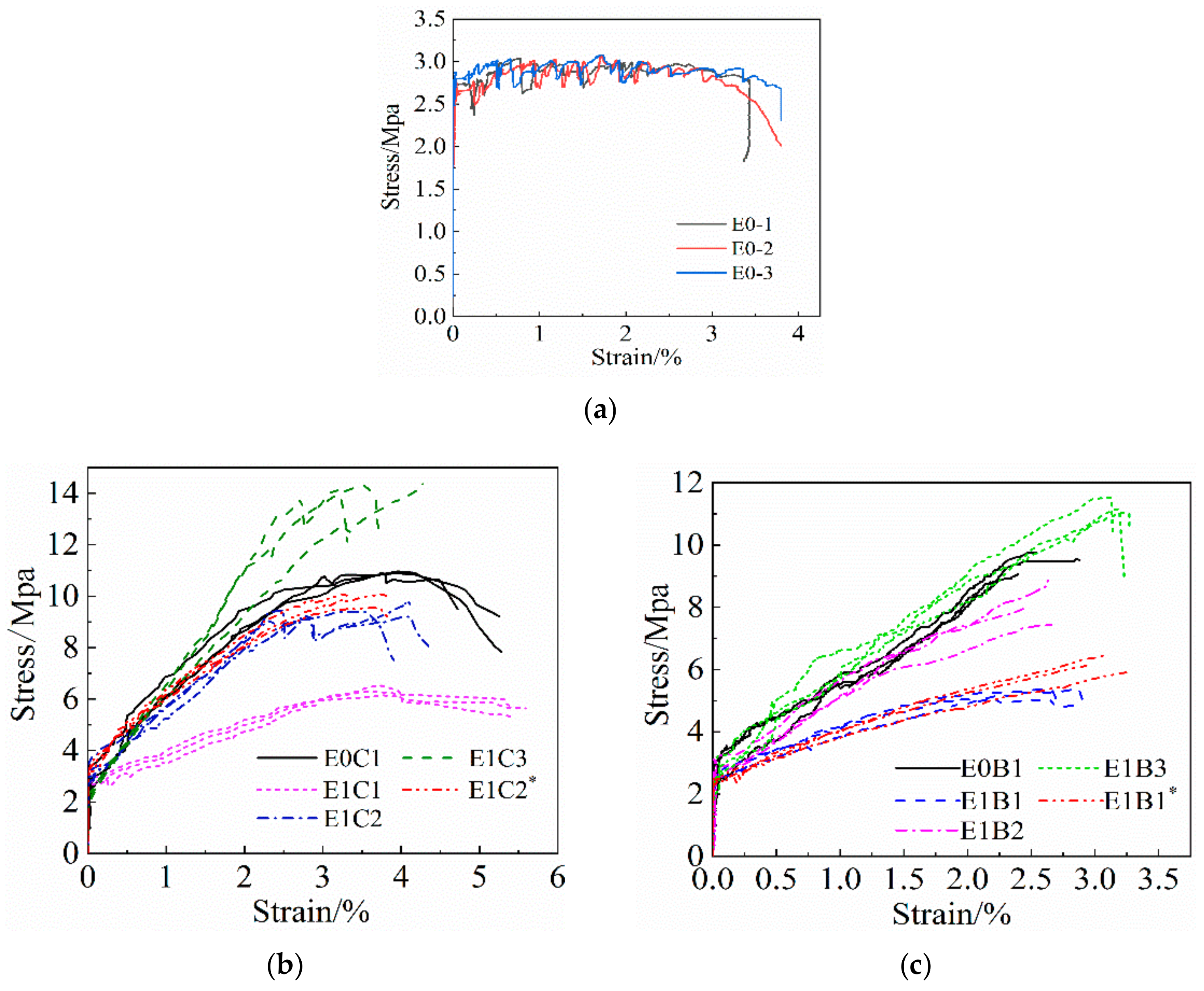
3.2. Stress–Strain Relationship Curve
3.3. Analysis of Influencing Factors
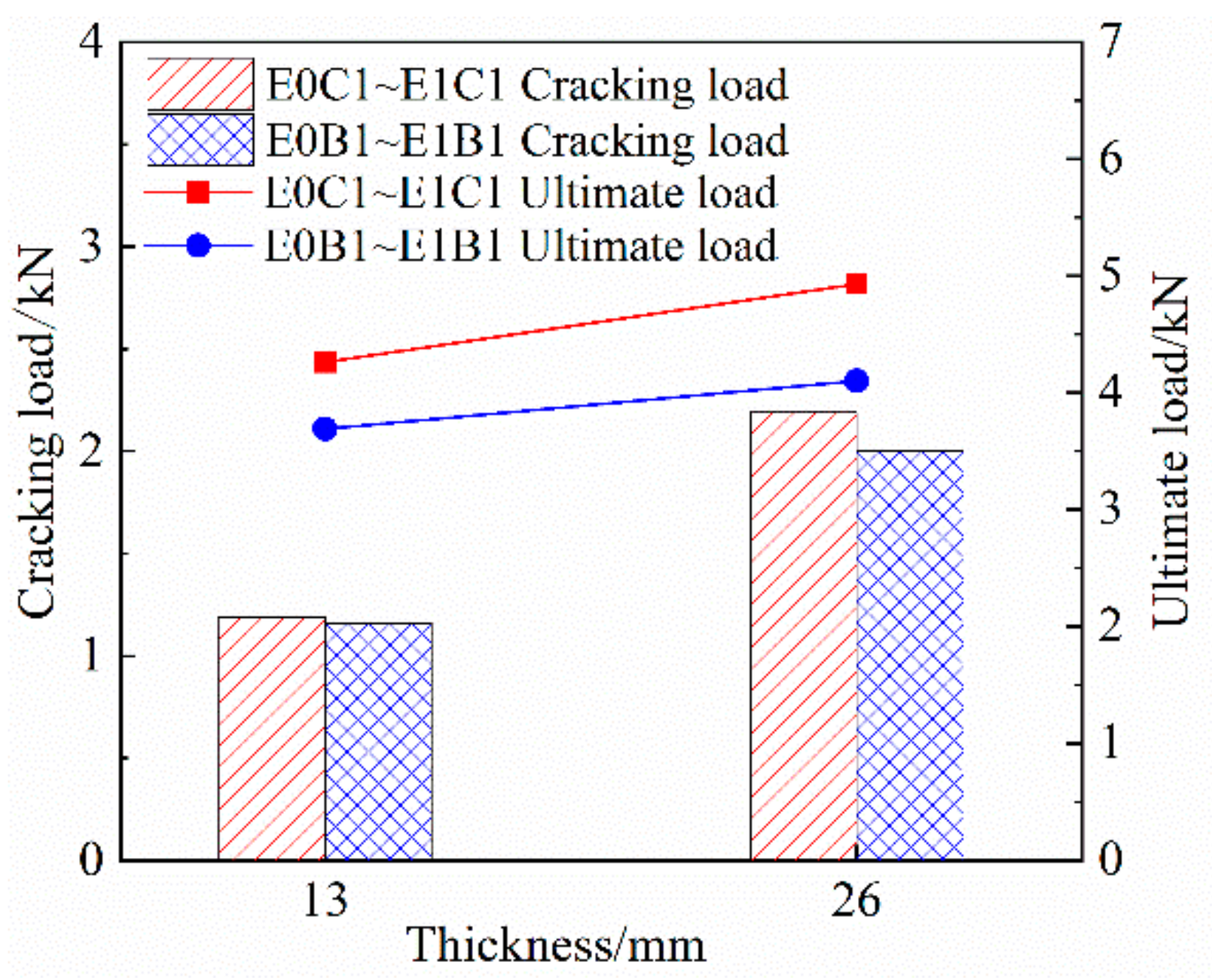
3.3.1. Effect of ECC Substrate Thickness on Tensile Properties of Specimens
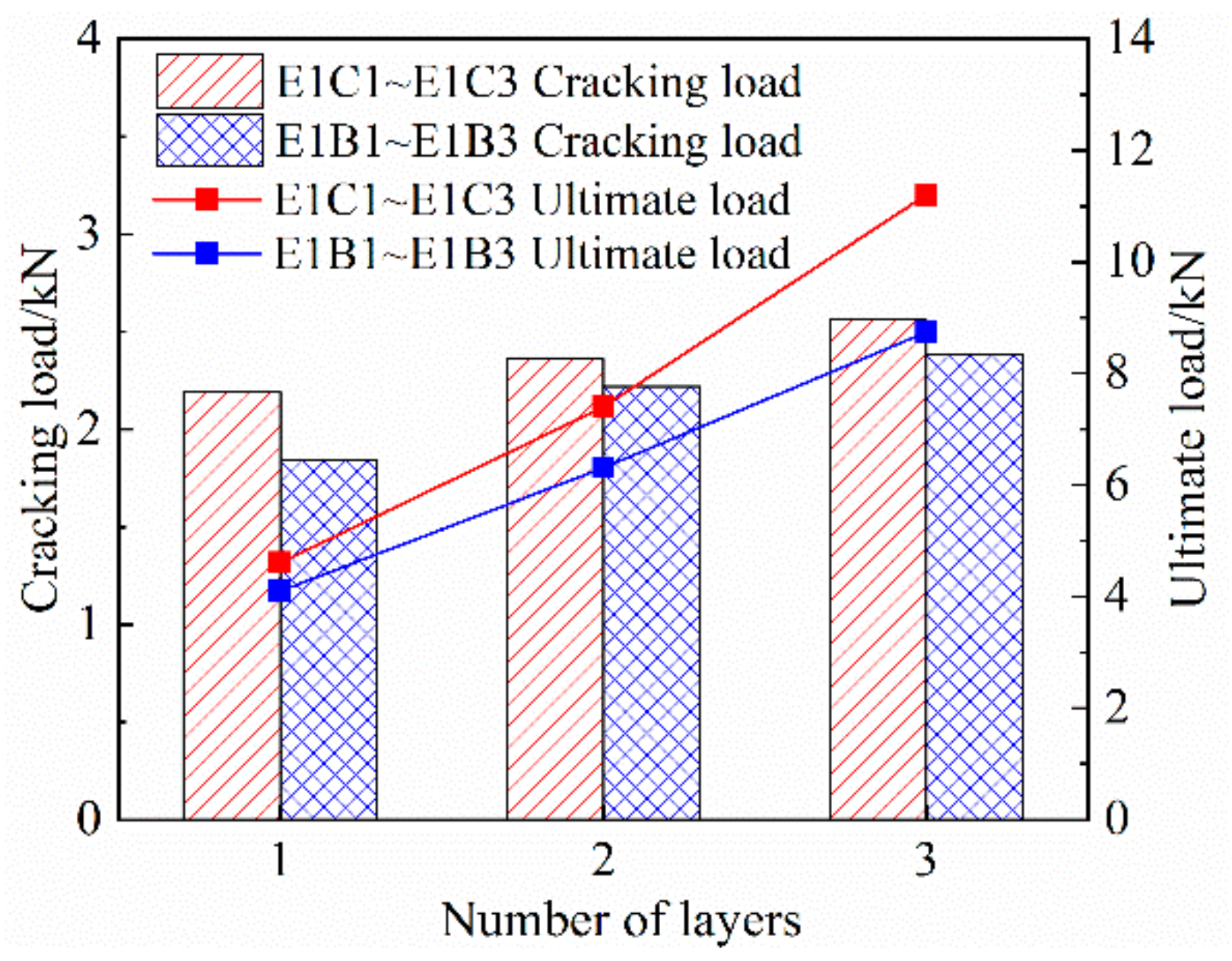
3.3.2. Effect of the Number of Grid Layers on the Tensile Properties of Specimens
3.3.3. Effect of Grid Type on Tensile Properties of Specimens
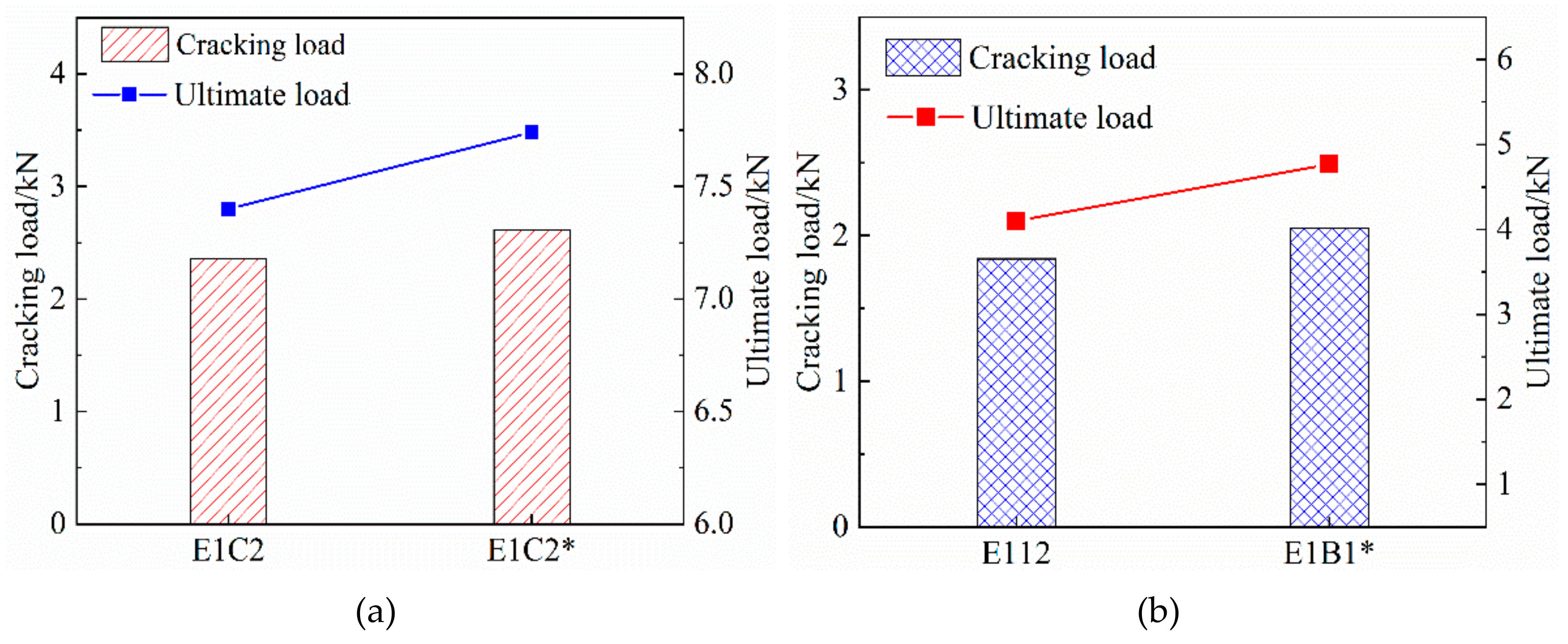
3.3.4. Effect of the Tensile Properties of Specimens Treated with Gum-Impregnated Adhesive Sand on the Surface of the Grid
4. Stress–Strain Intrinsic Structure Relationship Model
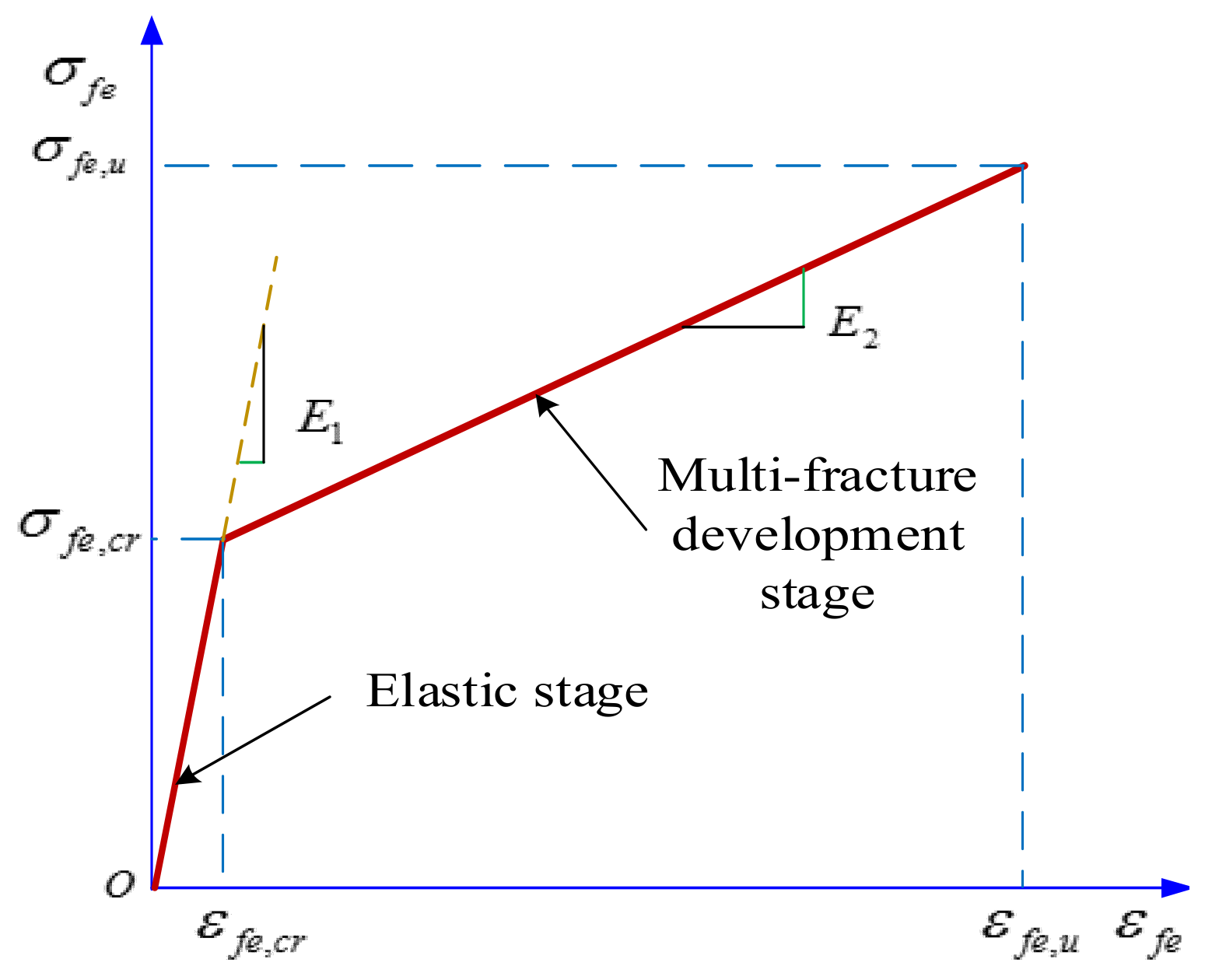
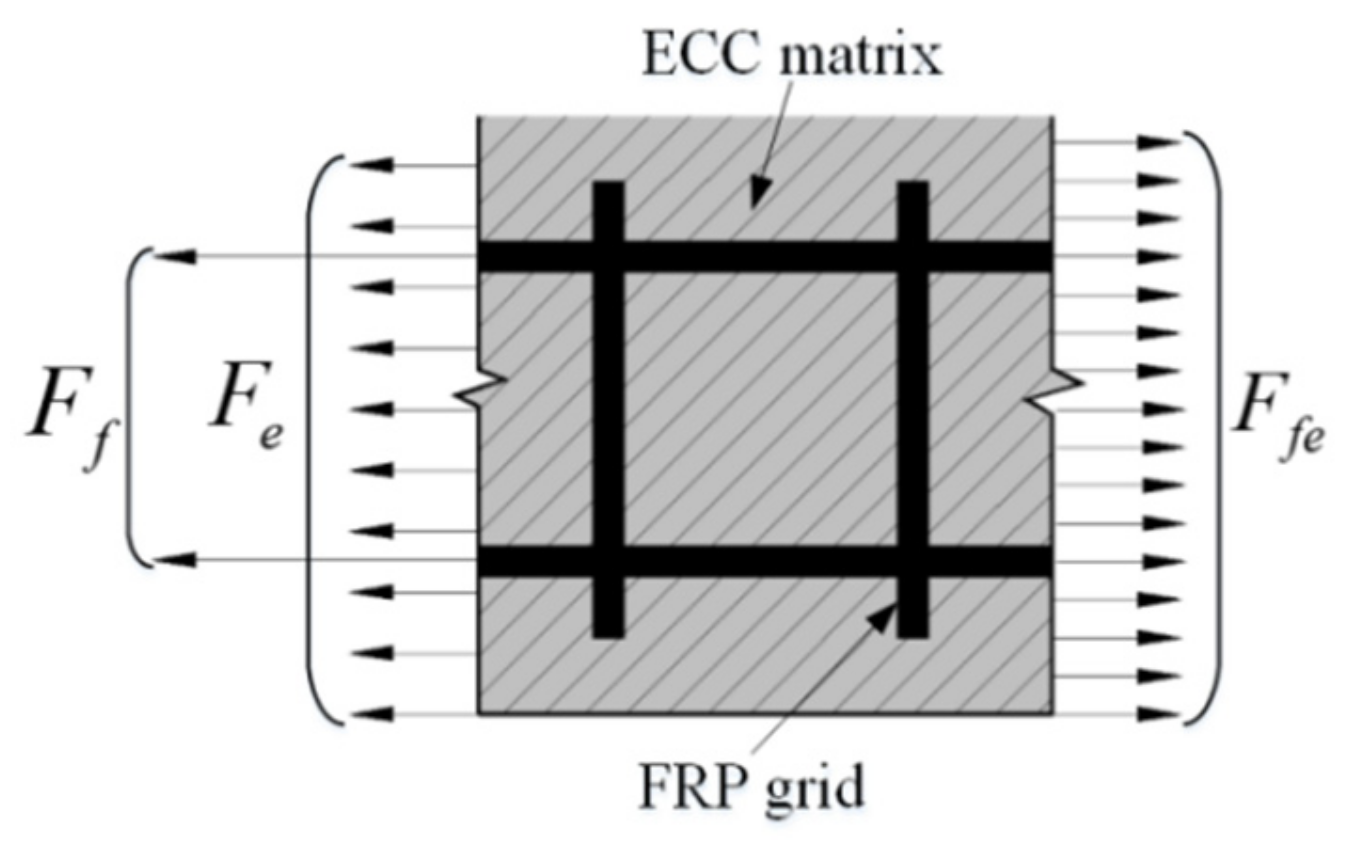
4.1. Model Construction
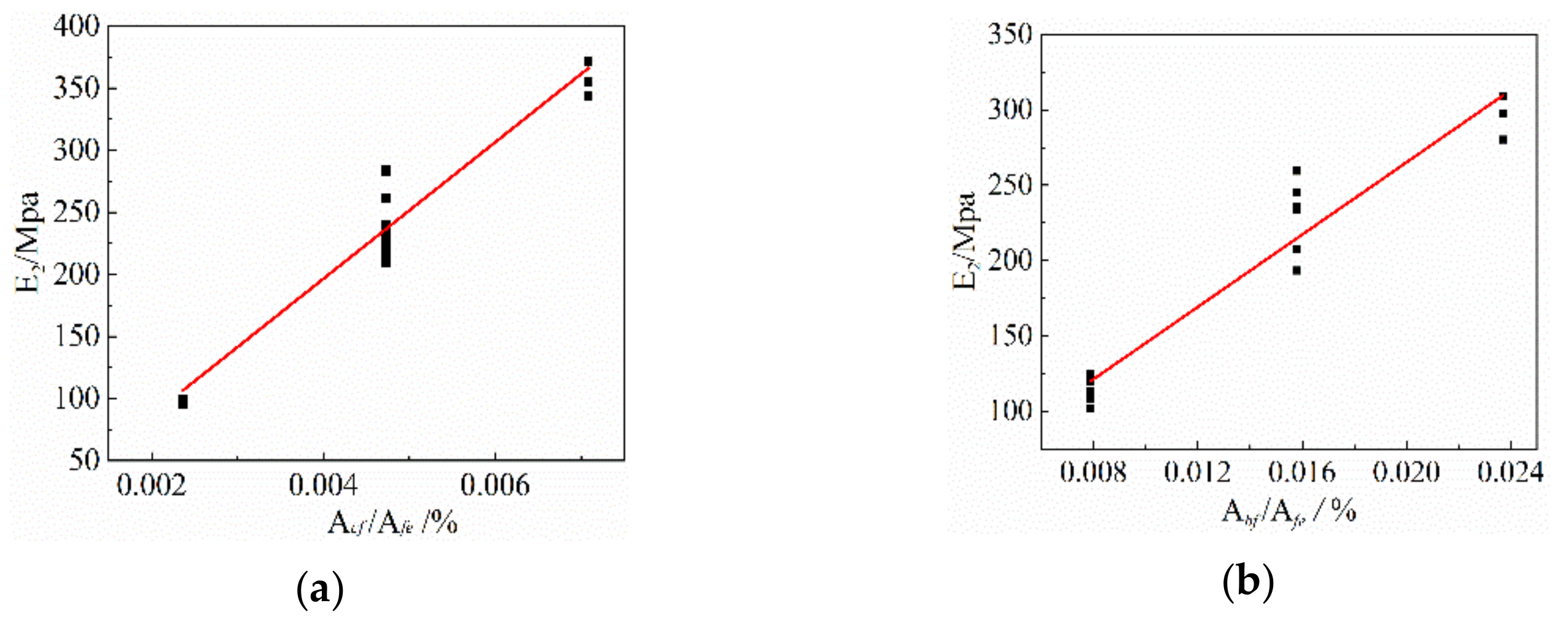
4.2. Analysis of Model Parameters
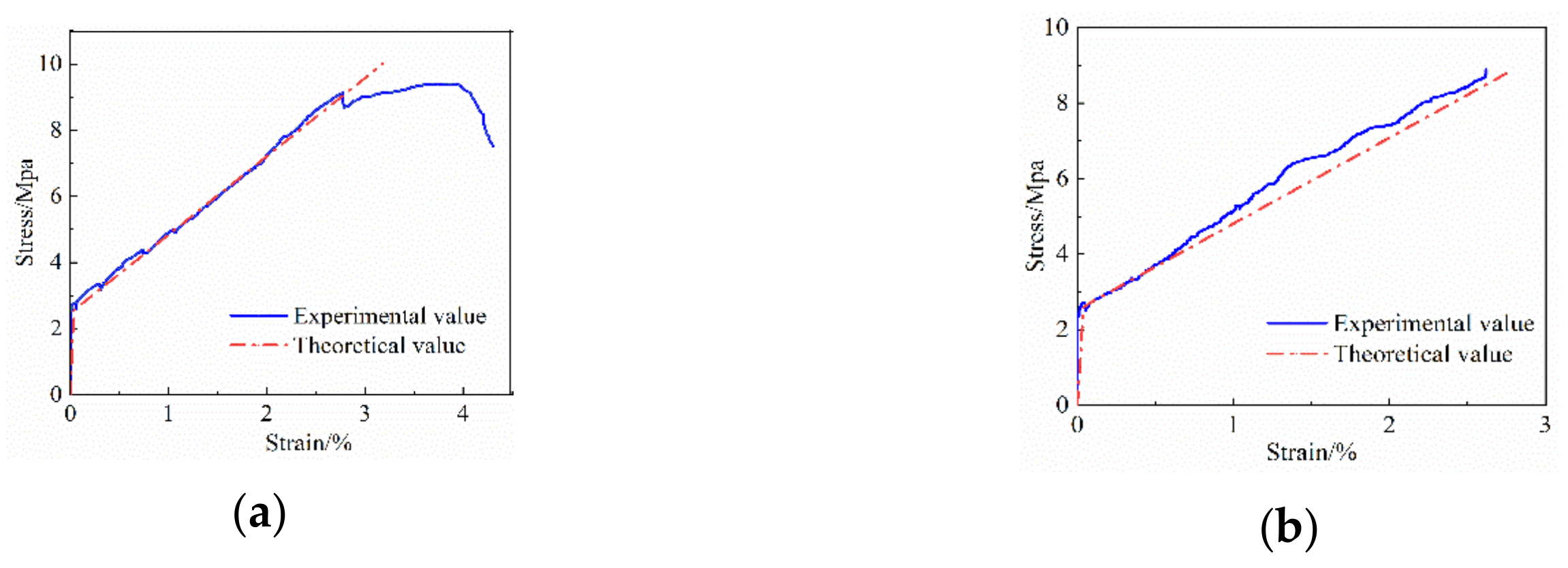
4.3. Model Validation
5. Conclusions
- (1)
- Before the specimen cracks, the FRP grid has little effect on enhancing the tensile properties of the specimen. After the specimen cracks, the FRP grid plays a strengthening role, which improves the strain strengthening performance of the ECC matrix, enhances the axial tensile stiffness and ultimate tensile capacity of the specimen, and effectively makes up for the lack of tensile strength of the ECC matrix.
- (2)
- Increasing the thickness of the ECC matrix can significantly improve the crack resistance of the FRP grid-reinforced ECC specimens, but the ultimate tensile strength is generally improved.
- (3)
- The ultimate tensile strength of FRP grid-reinforced ECC specimens can be significantly improved by increasing the number of grid reinforcement layers, but the improvement effect on crack resistance is general. In addition, the tensile properties of CFRP grid-reinforced ECC specimens are better than those of BFRP-reinforced ECC specimens under the same number of reinforcement layers.
- (4)
- The crack resistance and ultimate tensile strength of FRP grid-reinforced ECC composite specimens are slightly improved by dipping the FRP grid surface with adhesive sand.
- (5)
- Based on the experimental study, a constitutive model of axial tensile stress–strain of FRP grid-reinforced ECC composite specimens is proposed. The calculation results show that the theoretical values of the constitutive model are in good agreement with the experimental values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.Y. Research progress of concrete structures strengthened with fiber reinforced composites and steel. J. Build. Struct. 2018, 39, 138–146. [Google Scholar]
- Ai, S.X.; Yin, S.P.; Xu, S.L. Research progress and application of textile reinforced concrete. J. Civ. Eng. 2015, 48, 27–40. [Google Scholar]
- Triantafillou, T.C.; Papanicolaou, C.G.; Zissimopoulos, P.; Laourdekis, T. Concrete Confinement with Textile-Reinforced Mortar Jackets. ACI Struct. J. 2006, 103, 28–37. [Google Scholar]
- Dai, J.G.; Munir, S.; Ding, Z. Comparative Study of Different Cement-Based Inorganic Pastes towards the Development of FRIP Strengthening Technology. J. Compos. Constr. 2014, 18, A4013011. [Google Scholar] [CrossRef]
- Raoof, S.M.; Koutas, L.N.; Bournas, D.A. Bond between textile-reinforced mortar (TRM) and concrete substrates: Experimental investigation. Compos. Part B 2016, 98, 350–361. [Google Scholar] [CrossRef]
- Ding, Z.; Dai, J.G.; Muner, S. Study on an Improved Phosphate Cement Binder for the Development of Fiber-Reinforced Inorganic Polymer Composites. Polymers 2014, 6, 2819–2831. [Google Scholar] [CrossRef] [Green Version]
- Soranakom, C.; Mobasher, B. Geometrical and mechanical aspects of fabric bonding and pullout in cement composites. Mater. Struct. 2009, 42, 765–777. [Google Scholar] [CrossRef]
- Carozzi, F.G.; Poggi, C. Mechanical properties and debonding strength of Fabric Reinforced Cementitious Matrix (FRCM) systems for masonry strengthening. Compos. Part B Eng. 2015, 70, 215–230. [Google Scholar] [CrossRef]
- Li, V.C. Advances in ECC research. ACI Spec. Publ. Concr. Mater. Sci. Appl. 2002, 206, 373–400. [Google Scholar]
- Alyousif, A.; Lachemi, M.; Yildirim, G.; Aras, G.H.; Sahmaran, M. Influence of Cyclic Frost Deterioration on Water Sorptivity of Microcracked Cementitious Composites. J. Mater. Civ. Eng. 2016, 28, 04015159. [Google Scholar] [CrossRef]
- Hung, C.C.; Su, Y.F.; Su, Y.M. Mechanical properties and self-healing evaluation of strain-hardening cementitious composites with high volumes of hybrid pozzolan materials. Compos. Part B Eng. 2018, 133, 15–25. [Google Scholar] [CrossRef]
- Xu, S.L.; Li, Q.H.; Li, H.D. Experimental study on flexural properties of ultra-high toughness cement-based composites reinforced by carbon fiber woven mesh. J. Civ. Eng. 2007, 40, 69–76. [Google Scholar]
- Zhu, Z.F.; Wang, W.W. Mechanical properties test and constitutive relation model of basalt grid reinforced cement matrix composites under uniaxial tension. Acta Compos. Sin. 2017, 34, 2367–2374. [Google Scholar]
- Zheng, Y.H.; Wang, W.W.; Li, J.F.; Han, G. Tensile constitutive model of composite grid-high ductility fiber cement base. Ind. Archit. 2016, 46, 12–17. [Google Scholar]
- Li, B.; Xiong, H.; Jiang, J.; Dou, X. Tensile behavior of basalt textile grid reinforced Engineering Cementitious Composite. Compos. Part B Eng. 2018, 156, 185–200. [Google Scholar] [CrossRef]
- Li, C.H.; Yin, S.P.; Zhao, J.L. Tensile and Flexural Mechanical Properties of ECC Reinforced with Fiber Woven Mesh. J. Build. Mater. 2021, 1–11. Available online: http://kns.cnki.net/kcms/detail/31.1764.TU.27999.20707000007 (accessed on 17 May 2021).
- Lin, J.H.; Yu, J.T.; LIVictor, C. Mechanical properties of PVA fiber reinforced engineered cementitious composites after thermal treatment. Acta Mater. Compos. Sin. 2016, 33, 116–122. [Google Scholar]
- Yu, J.; Lin, J.; Zhang, Z.; Li, V.C. Experimental study on tensile properties of basalt fiber grid. Constr. Build. Mater. 2015, 99, 82–89. [Google Scholar] [CrossRef]
- Jiang, J.F.; Dou, X.X.; Sui, K. Experimental study on tensile properties of basalt fiber grid. Struct. Eng. 2018, 34, 76–83. [Google Scholar]
- Zhu, J.T.; Li, Z.Q.; Wang, X.L.; Li, K.; Liu, K.W. Constitutive relationship model of engineered cementitious composites under uniaxial tension. J. Basic Sci. Eng. 2021, 29, 471–482. [Google Scholar]



| Number | Specimen Number | Types of Grids | Number of Grid Layers | Thickness of Matrix/mm | Cross-Sectional Area/mm2 |
|---|---|---|---|---|---|
| 1 | E0 | / | / | 13 | 390 |
| 2 | E0C1 | CFRP | 1 | 13 | 390 |
| 3 | E1C1 | CFRP | 1 | 26 | 780 |
| 4 | E1C2 | CFRP | 2 | 26 | 780 |
| 5 | E1C3 | CFRP | 3 | 26 | 780 |
| 6 | E1C2 * | CFRP | 2 | 26 | 780 |
| 7 | E0B1 | BFRP | 1 | 13 | 390 |
| 8 | E1B1 | BFRP | 1 | 26 | 780 |
| 9 | E1B2 | BFRP | 2 | 26 | 780 |
| 10 | E1B3 | BFRP | 3 | 26 | 780 |
| 11 | E1B1 * | BFRP | 1 | 26 | 780 |
| Water | Cement | Fly Ash | Quartz Sand | Silica Fume | Water Reducer | PVA | Water Toglue Ratio | Sand to Glue Ratio |
|---|---|---|---|---|---|---|---|---|
| 1.42 | 1 | 2.33 | 0.67 | 0.1 | 0.019 | 0.002 | 0.5 | 0.2 |
| Material Name | Diameter/μm | Length/mm | Density/g/cm3 | Modulus of Elasticity/Gpa | Tensile Strength/Mpa | Elongation at Break/% |
|---|---|---|---|---|---|---|
| PVA | 39 | 12 | 1.3 | 40 | 1530 | 7 |
| Grid Type | |||||
|---|---|---|---|---|---|
| CFRP | 20 × 20 | 0.921 | 243.1 | 4255 | 1.75 |
| BFRP | 25 × 25 | 3.082 | 26.18 | 597.1 | 2.28 |
| Specimen Number | Multi-Crack Development Stage | |||||
|---|---|---|---|---|---|---|
| Cracking Load/kN | Cracking Stress/Mpa | Cracking Strain/10−4 | Ultimate Load/kN | Ultimate Stress/Mpa | Extreme Strain/10−2 | |
| E0–1 | 1.07 | 2.74 | 4.20 | 1.18 | 3.03 | 3.16 |
| E0–2 | 1.02 | 2.62 | 3.90 | 1.20 | 3.08 | 3.30 |
| E0–3 | 1.10 | 2.82 | 4.05 | 1.18 | 3.03 | 2.85 |
| Average | 1.06 | 2.73 | 4.05 | 1.19 | 3.04 | 3.10 |
| Coefficient of variation | 0.04 | 0.04 | 0.04 | 0.01 | 0.01 | 0.07 |
| E0C1–1 | 1.11 | 2.85 | 3.96 | 4.27 | 10.95 | 2.90 |
| E0C1-2 | 1.32 | 3.38 | 4.20 | 4.25 | 10.90 | 2.70 |
| E0C1-3 | 1.14 | 2.92 | 3.60 | 4.25 | 10.90 | 3.02 |
| Average | 1.19 | 3.05 | 3.92 | 4.26 | 10.91 | 2.87 |
| Coefficient of variation | 0.10 | 0.09 | 0.08 | 0.00 | 0.00 | 0.06 |
| E1C1-1 | 2.09 | 2.68 | 3.95 | 4.76 | 6.10 | 3.15 |
| E1C1-2 | 2.30 | 2.95 | 4.08 | 4.49 | 5.75 | 3.03 |
| E1C1-3 | 2.19 | 2.81 | 3.65 | 4.59 | 5.88 | 3.24 |
| Average | 2.19 | 2.81 | 3.89 | 4.61 | 5.91 | 3.14 |
| Coefficient of variation | 0.05 | 0.05 | 0.06 | 0.03 | 0.03 | 0.03 |
| E1C2-1 | 2.62 | 3.36 | 4.53 | 7.61 | 9.76 | 2.86 |
| E1C2-2 | 2.33 | 2.99 | 3.86 | 7.25 | 9.29 | 3.33 |
| E1C2-3 | 2.12 | 2.72 | 3.58 | 7.33 | 9.40 | 3.27 |
| Average | 2.36 | 3.02 | 3.99 | 7.40 | 9.48 | 3.15 |
| Coefficient of variation | 0.11 | 0.11 | 0.12 | 0.03 | 0.03 | 0.08 |
| E1C3-1 | 2.54 | 3.26 | 3.43 | 11.15 | 14.29 | 3.65 |
| E1C3-2 | 2.66 | 3.41 | 4.26 | 11.01 | 14.12 | 3.33 |
| E1C3-3 | 2.48 | 3.18 | 4.07 | 11.20 | 14.36 | 3.64 |
| Average | 2.56 | 3.28 | 3.92 | 11.12 | 14.26 | 3.54 |
| Coefficient of variation | 0.04 | 0.04 | 0.11 | 0.01 | 0.01 | 0.05 |
| E1C2*-1 | 2.52 | 3.23 | 3.85 | 7.89 | 10.12 | 3.11 |
| E1C2*-2 | 2.49 | 3.19 | 3.76 | 7.88 | 10.10 | 3.34 |
| E1C2*-3 | 2.83 | 3.63 | 4.00 | 7.44 | 9.54 | 3.07 |
| Average | 2.61 | 3.35 | 3.87 | 7.74 | 9.92 | 3.17 |
| Coefficient of variation | 0.07 | 0.07 | 0.03 | 0.03 | 0.3 | 0.06 |
| E0B1-1 | 1.25 | 3.21 | 4.02 | 3.81 | 9.77 | 2.57 |
| E0B1-2 | 0.96 | 2.46 | 3.72 | 3.72 | 9.54 | 2.91 |
| E0B1-3 | 1.28 | 3.28 | 4.10 | 3.54 | 9.08 | 2.50 |
| Average | 1.16 | 2.98 | 3.95 | 3.69 | 9.46 | 2.66 |
| Coefficient of variation | 0.15 | 0.15 | 0.05 | 0.04 | 0.04 | 0.08 |
| E1B1-1 | 1.93 | 2.47 | 3.70 | 4.18 | 5.36 | 2.60 |
| E1B1-2 | 1.73 | 2.22 | 3.39 | 4.18 | 5.36 | 2.90 |
| E1B1-3 | 1.85 | 2.37 | 3.62 | 3.93 | 5.04 | 2.20 |
| Average | 1.84 | 2.35 | 3.57 | 4.10 | 5.25 | 2.57 |
| Coefficient of variation | 0.10 | 0.13 | 0.16 | 0.14 | 0.18 | 0.35 |
| E1B2-1 | 2.50 | 3.21 | 3.59 | 6.20 | 7.95 | 2.57 |
| E1B2-2 | 1.94 | 2.49 | 3.75 | 6.93 | 8.88 | 2.73 |
| E1B2-3 | 2.21 | 2.83 | 3.50 | 5.80 | 7.44 | 2.76 |
| Average | 2.22 | 2.84 | 3.61 | 6.31 | 8.09 | 2.69 |
| Coefficient of variation | 0.13 | 0.13 | 0.04 | 0.09 | 0.09 | 0.04 |
| E1B3-1 | 2.32 | 2.97 | 3.99 | 8.95 | 11.47 | 2.99 |
| E1B3-2 | 2.54 | 3.26 | 3.92 | 8.66 | 11.10 | 2.83 |
| E1B3-3 | 2.28 | 2.92 | 4.20 | 8.61 | 11.04 | 2.80 |
| Average | 2.38 | 3.05 | 4.04 | 8.74 | 11.21 | 2.87 |
| Coefficient of variation | 0.06 | 0.06 | 0.04 | 0.02 | 0.02 | 0.04 |
| E1B1*-1 | 2.03 | 2.60 | 3.97 | 4.78 | 6.13 | 2.81 |
| E1B1*-2 | 1.95 | 2.50 | 3.78 | 4.90 | 6.28 | 3.00 |
| E1B1*-3 | 2.15 | 2.76 | 3.86 | 4.64 | 5.95 | 2.91 |
| Average | 2.05 | 2.62 | 3.80 | 4.77 | 6.12 | 2.91 |
| Coefficient of variation | 0.05 | 0.05 | 0.03 | 0.03 | 0.03 | 0.03 |
| Specimen Number | Cracking Load/kN | Ultimate Load/kN | ||||
|---|---|---|---|---|---|---|
| Experimental Value | Theoretical Value | Experimental Value | Theoretical Value | |||
| E0C1-1 | 1.11 | 1.17 | 0.95 | 4.27 | 4.07 | 1.05 |
| E0C1-2 | 1.32 | 1.24 | 1.06 | 4.25 | 4.14 | 1.03 |
| E0C1-3 | 1.14 | 1.06 | 1.07 | 4.25 | 3.97 | 1.07 |
| E1C1-1 | 2.09 | 2.24 | 0.93 | 4.76 | 4.86 | 0.98 |
| E1C1-2 | 2.30 | 2.32 | 0.99 | 4.49 | 4.93 | 0.91 |
| E1C1-3 | 2.19 | 2.08 | 1.06 | 4.59 | 4.69 | 0.98 |
| E1C2-1 | 2.62 | 2.68 | 0.98 | 7.61 | 8.47 | 0.90 |
| E1C2-2 | 2.33 | 2.28 | 1.02 | 7.25 | 8.08 | 0.90 |
| E1C2-3 | 2.12 | 2.12 | 1.00 | 7.33 | 7.92 | 0.92 |
| E1C3-1 | 2.54 | 2.18 | 1.16 | 11.15 | 11.17 | 1.00 |
| E1C3-2 | 2.66 | 2.70 | 0.98 | 11.01 | 11.68 | 0.94 |
| E1C3-3 | 2.48 | 2.58 | 0.96 | 11.20 | 11.56 | 0.97 |
| E1C2*-1 | 2.52 | 2.28 | 1.11 | 7.89 | 8.08 | 0.98 |
| E1C2*-2 | 2.49 | 2.22 | 1.12 | 7.88 | 8.03 | 0.98 |
| E1C2*-3 | 2.83 | 2.36 | 1.20 | 7.44 | 8.16 | 0.91 |
| Average | - | - | 1.03 | - | - | 0.97 |
| Variance | - | - | 0.007 | - | - | 0.002 |
| Coefficient of variation | - | - | 0.078 | - | - | 0.06 |
| E0B1-1 | 1.25 | 1.06 | 1.18 | 3.81 | 3.37 | 1.13 |
| E0B1-2 | 0.96 | 0.98 | 0.98 | 3.72 | 3.29 | 1.13 |
| E0B1-3 | 1.28 | 1.08 | 1.18 | 3.54 | 3.40 | 1.04 |
| E1B1-1 | 1.93 | 2.13 | 0.91 | 4.18 | 4.70 | 0.89 |
| E1B1-2 | 1.73 | 1.95 | 0.89 | 4.18 | 4.53 | 0.92 |
| E1B1-3 | 1.85 | 2.08 | 0.89 | 3.93 | 4.66 | 0.84 |
| E1B2-1 | 2.50 | 2.11 | 1.01 | 6.20 | 6.72 | 0.92 |
| E1B2-2 | 1.94 | 2.07 | 0.99 | 6.93 | 6.68 | 1.04 |
| E1B2-3 | 2.21 | 2.22 | 0.99 | 5.80 | 6.83 | 0.85 |
| E1B3-1 | 2.32 | 2.13 | 1.09 | 8.95 | 8.78 | 1.02 |
| E1B3-2 | 2.54 | 2.23 | 1.14 | 8.66 | 8.87 | 0.98 |
| E1B3-3 | 2.28 | 2.08 | 1.11 | 8.61 | 8.73 | 0.99 |
| E1B1*-1 | 2.03 | 1.94 | 1.04 | 4.78 | 4.52 | 1.06 |
| E1B1*-2 | 1.95 | 1.79 | 1.08 | 4.90 | 4.37 | 1.12 |
| E1B1*-3 | 2.15 | 1.86 | 1.15 | 4.64 | 4.44 | 1.05 |
| Average | - | - | 1.04 | - | - | 1.0 |
| Variance | - | - | 0.010 | - | - | 0.009 |
| Coefficient of variation | - | - | 0.097 | - | - | 0.097 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Lei, L.; Lai, S.; Liao, L.; Zhou, Z. Experimental Study on the Axial Tensile Properties of FRP Grid-Reinforced ECC Composites. Materials 2021, 14, 3936. https://doi.org/10.3390/ma14143936
Deng L, Lei L, Lai S, Liao L, Zhou Z. Experimental Study on the Axial Tensile Properties of FRP Grid-Reinforced ECC Composites. Materials. 2021; 14(14):3936. https://doi.org/10.3390/ma14143936
Chicago/Turabian StyleDeng, Langni, Lizhen Lei, Shijin Lai, Ling Liao, and Zheng Zhou. 2021. "Experimental Study on the Axial Tensile Properties of FRP Grid-Reinforced ECC Composites" Materials 14, no. 14: 3936. https://doi.org/10.3390/ma14143936
APA StyleDeng, L., Lei, L., Lai, S., Liao, L., & Zhou, Z. (2021). Experimental Study on the Axial Tensile Properties of FRP Grid-Reinforced ECC Composites. Materials, 14(14), 3936. https://doi.org/10.3390/ma14143936





