Theoretical Prediction Method for Erosion Damage of Horizontal Pipe by Suspended Particles in Liquid–Solid Flows
Abstract
:1. Introduction
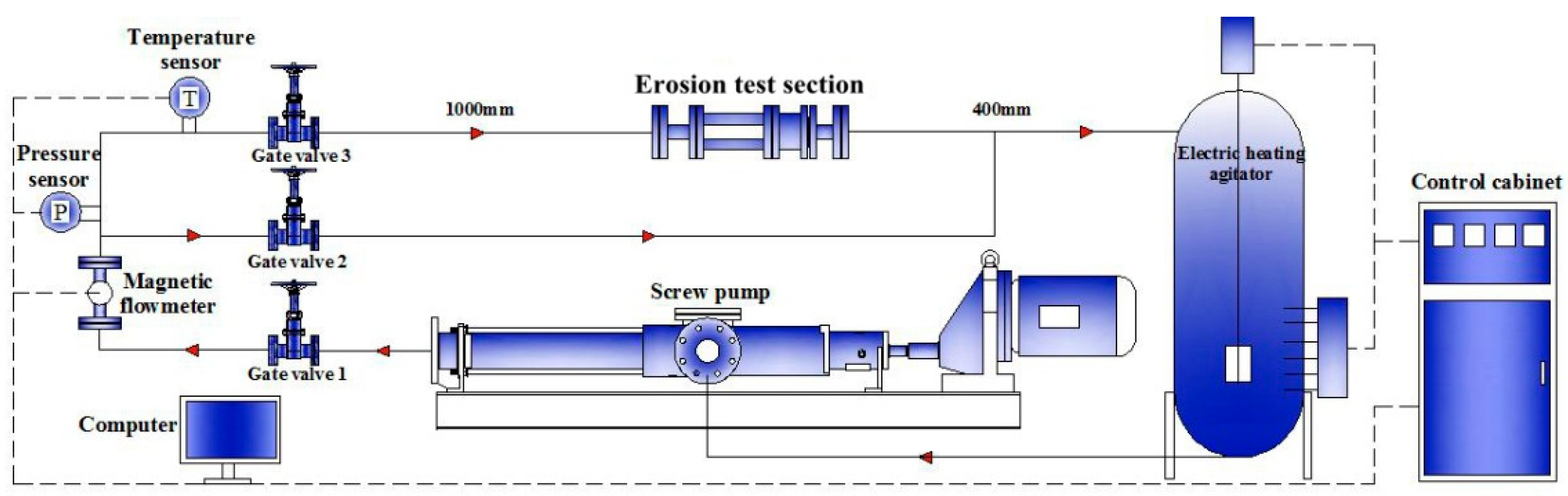
2. Calculation Methods
2.1. Calculation of Laminar and Turbulent Velocities of Liquid
2.2. Calculation of Axial and Radial Impact Velocities of Particles onto the Wall
2.3. Calculation of the Pipe Wall Erosion under Continuous Particle Impact
3. Results
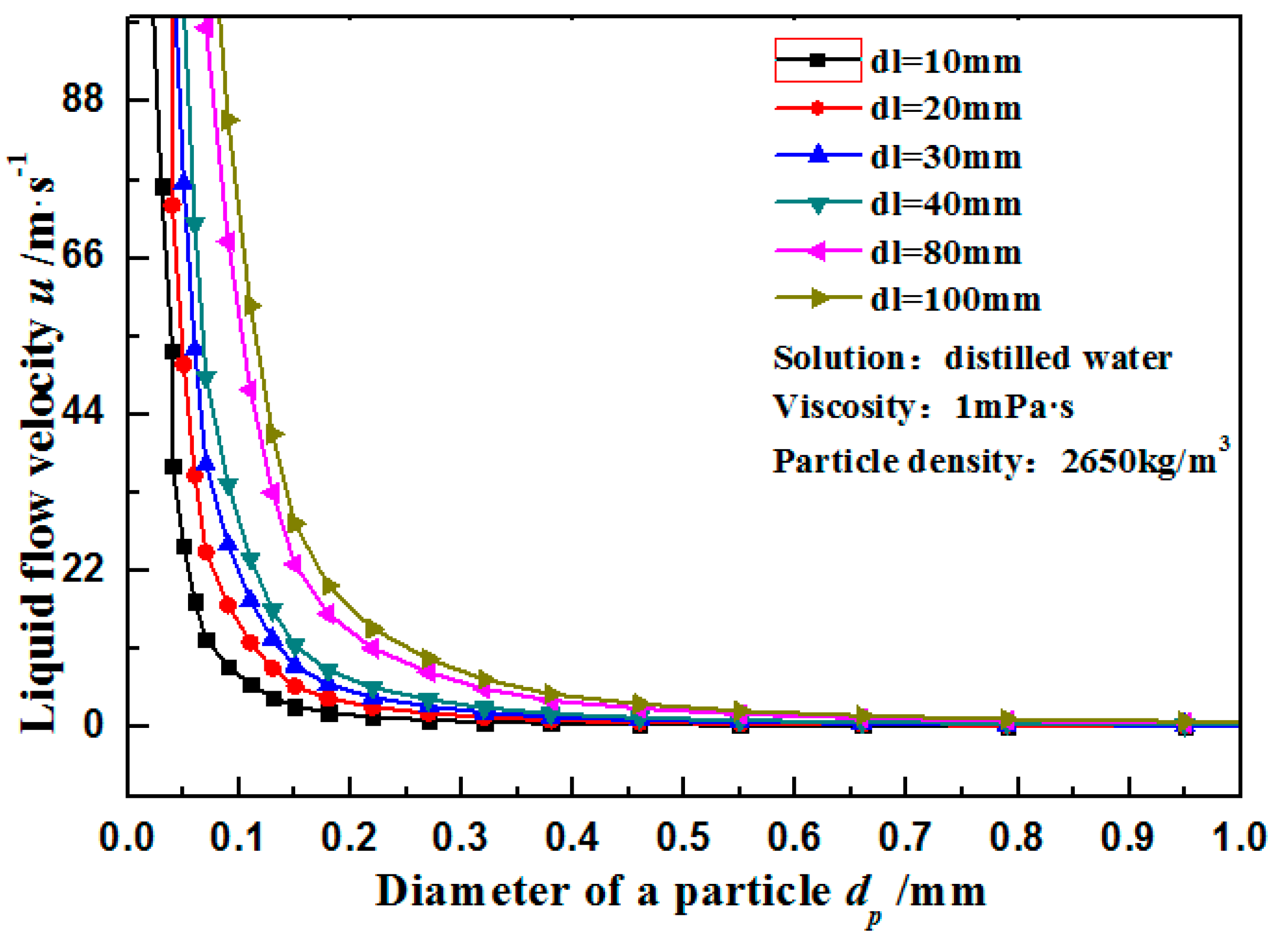
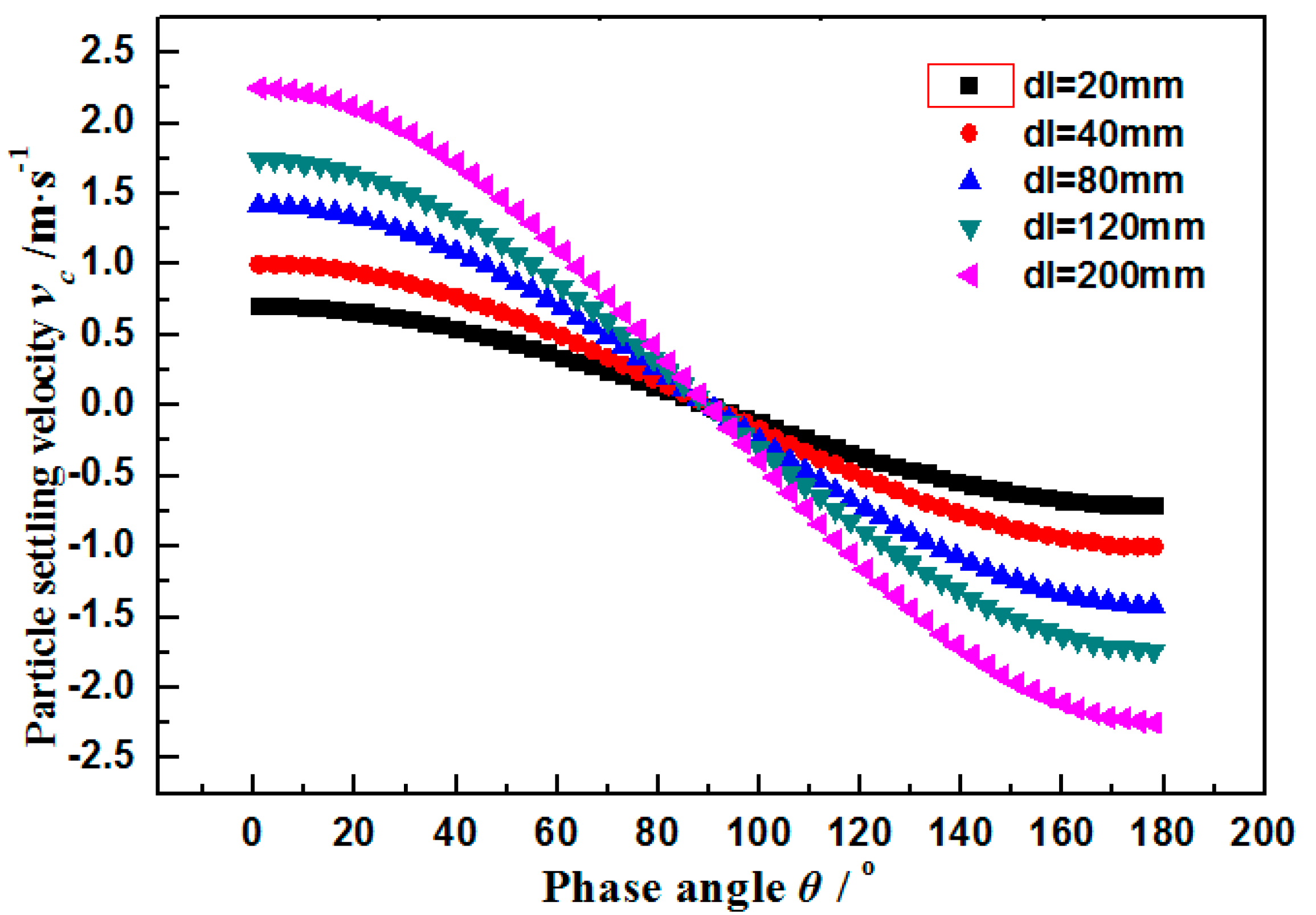
3.1. Calculated Results of Impact Parameters
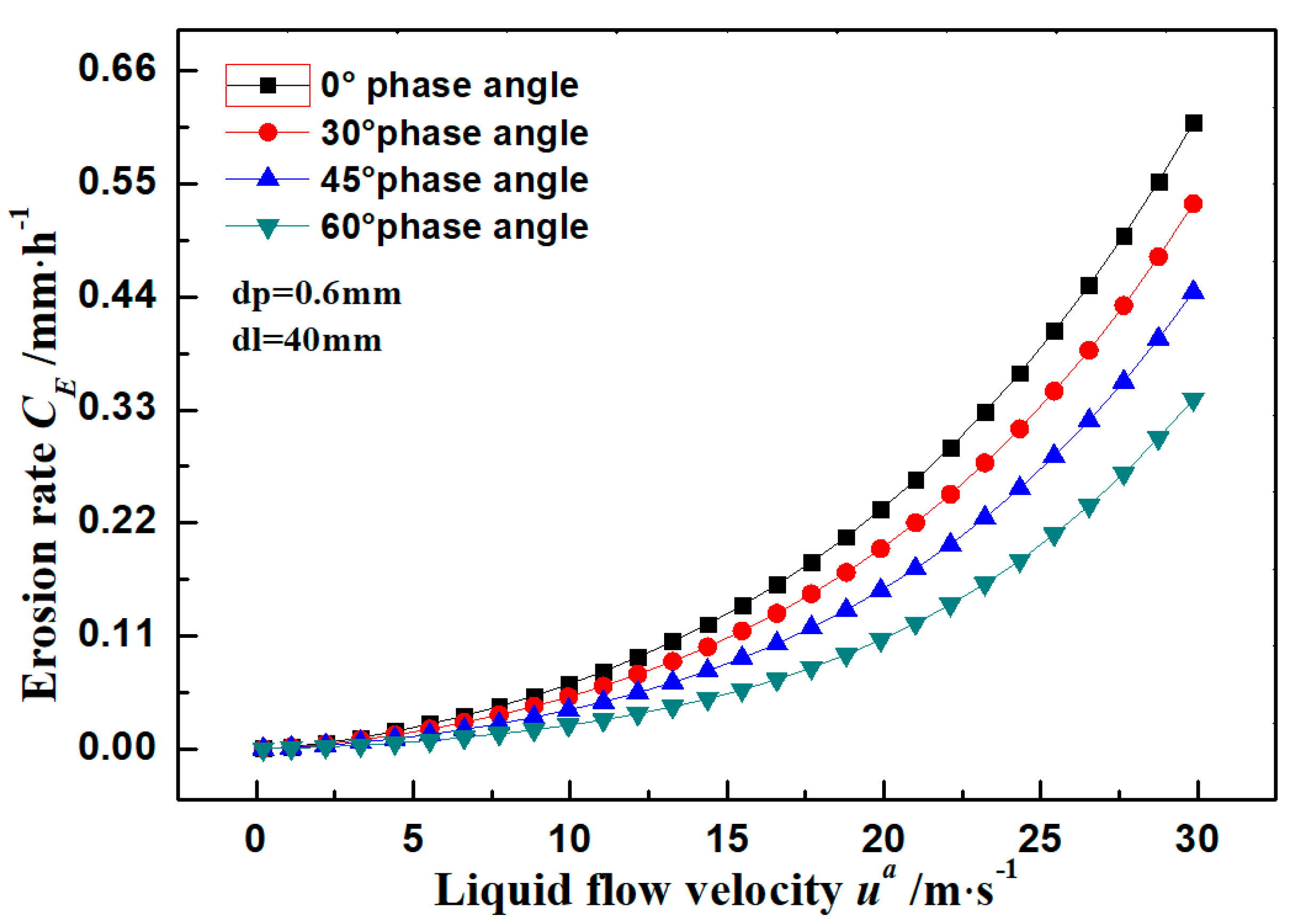
3.2. Pipe Erosion Rate
4. Discussion
5. Conclusions
- (1)
- When the settling velocity of the particles is greater than the fluctuating velocity of the particles, there is a significant difference in the erosion rate along the circumferential direction of the pipe wall; if not, there are no significant differences.
- (2)
- The experimental results showed that the existing model has a large error in predicting the erosion of the top and bottom walls of the pipe. If you can add material-related empirical coefficients to the model, or evenly suspend the particles, this error can be reduced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CE | Erosion rate, mm·s−1 |
| E* | equivalent elastic modulus, Pa |
| Fx | tangential contact force, N |
| Fy | normal contact force, N |
| h | total indentation depth, m |
| ks | intensity factor, Pa |
| L | scratch length, m |
| mp | particle mass, kg |
| N | critical particle impact time corresponding to material loss |
| Nc | actual particle impact time in a unit area |
| rp | particle radius, m |
| r | pipe radius, m |
| ua | average flow velocity of liquid in the pipe, m·s−1 |
| fluctuating velocity of the liquid, m·s−1 | |
| vx | tangential velocity of the particle, m·s−1 |
| vy | normal velocity of the particle, m·s−1 |
| vc | settling velocity of a particle, m·s−1 |
| σ | stress, Pa |
| σy | vertical material yield limit, Pa |
| α | particle impact angle, deg |
| β | pipe inclination angle, deg |
| θ | phase angle, deg |
| ∆ε | plastic strain scope |
| μ | coefficient of friction, dimensionless |
Appendix A. Calculation Formula of Pipe Erosion by Suspended Particles
| Solution | Flow Pattern | Erosion Rate | Parameter Expression | Judging Condition | Particle Impact Velocity Calculation | ||
| Liquid | Laminar flow | Re < 2000 | |||||
| Turbulent flow | α < α1 α > α1 | Re > 4000 | |||||
References
- Bitter, J.G.A. Study of erosion phenomenon-I. Wear 1963, 6, 169–176. [Google Scholar] [CrossRef]
- Tilly, G.P. Two Stage Mechanism of ductile erosion. Wear 1973, 23, 87–96. [Google Scholar] [CrossRef]
- Hutchings, I.M. Particle erosion of ductile metals: A mechanism of material removal. Wear 1974, 27, 121–128. [Google Scholar] [CrossRef]
- Neilson, J.H.; Gilchrist, A. Erosion by a stream of solid particles. Wear 1968, 11, 111–122. [Google Scholar] [CrossRef]
- Sheldon, G.L. Similarities and differences in the erosion behavior of materials. J. Basic Eng. 1970, 92, 619–626. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Tilly, G.P. Erosion caused by airborne particles. Wear 1969, 14, 63–79. [Google Scholar] [CrossRef]
- Guo, Y.J.; Wang, Y.Y.; Pang, Y.X. Research on erosion fatigue of carbon steel surface. J. Vib. Shock. 2005, 24, 44–49. [Google Scholar]
- Hutchings, I.M. A model for the erosion of metals by spherical particles at normal incidence. Wear 1981, 70, 269–281. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.K.; Chiovelli, S. A comprehensive phenomenological model for erosion of materials in jet flow. Powder Technol. 2008, 187, 237–279. [Google Scholar] [CrossRef]
- Nsoesie, S.; Liu, R.; Chen, K.Y.; Yao, M.X. Analytical modeling of solid-particle erosion of Stellite alloys in combination with experimental investigation. Wear 2014, 309, 226–232. [Google Scholar] [CrossRef]
- Cárach, J.; Hloch, S.; Petrů, J.; Nag, A.; Gombár, M.; Hromasová, M. Hydroabrasive disintegration of rotating Monel K-500 workpiece. Int. J. Adv. Manuf. Technol. 2018, 96, 981–1001. [Google Scholar] [CrossRef]
- Nunthavarawong, P. Slurry Erosion Model for Wear Performance Prediction of Tool Steel. Adv. Mater. Res. 2013, 717, 194–199. [Google Scholar] [CrossRef]
- Helland, E.; Occelli, R.; Tadrist, L. Numerical study of cluster formation in a gas-particle circulating fluidized bed. Powder Technol. 2000, 110, 210–221. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, N.; Wei, L.; Mi, H.; Dou, Y. A new phenomenological model for single particle erosion of plastic materials. Materials 2019, 12, 135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Dou, Y.; Li, H.; Cheng, J.; Wei, W. Establishment of a multi-particle erosion model based on the low-cycle fatigue law—An experimental study of erosion characteristics. Mater. Tehnol. 2020, 54, 321–326. [Google Scholar] [CrossRef]


| Qc (m3·h−1) | ua (m·s−1) | vx (m·s−1) | y (m·s−1) | θ (°) | vc (m·s−1) |
|---|---|---|---|---|---|
| 1 | 0.22 | 0.15 | 3.15 × 10−5 | 1 | 1.00 |
| 5 | 1.11 | 0.81 | 7.84 × 10−4 | 4 | 1.00 |
| 10 | 2.21 | 1.66 | 3.13 × 10−3 | 7 | 1.00 |
| 15 | 3.32 | 2.53 | 7.05 × 10−3 | 10 | 0.99 |
| 20 | 4.42 | 3.41 | 0.01 | 13 | 0.98 |
| 25 | 5.53 | 4.30 | 0.02 | 16 | 0.97 |
| 30 | 6.63 | 5.20 | 0.03 | 19 | 0.95 |
| 35 | 7.74 | 6.09 | 0.04 | 22 | 0.93 |
| 40 | 8.85 | 6.99 | 0.05 | 25 | 0.91 |
| 45 | 9.95 | 7.90 | 0.06 | 28 | 0.89 |
| 50 | 11.06 | 8.81 | 0.08 | 31 | 0.86 |
| 55 | 12.16 | 9.72 | 0.09 | 34 | 0.83 |
| 60 | 13.27 | 10.63 | 0.11 | 37 | 0.80 |
| 65 | 14.38 | 11.54 | 0.13 | 40 | 0.77 |
| 70 | 15.48 | 12.46 | 0.15 | 43 | 0.73 |
| 75 | 16.59 | 13.38 | 0.18 | 46 | 0.70 |
| 80 | 17.69 | 14.30 | 0.20 | 49 | 0.66 |
| 85 | 18.80 | 15.22 | 0.23 | 52 | 0.62 |
| 90 | 19.90 | 16.14 | 0.25 | 55 | 0.58 |
| 95 | 21.01 | 17.06 | 0.28 | 58 | 0.53 |
| 100 | 22.12 | 17.99 | 0.31 | 61 | 0.49 |
| 105 | 23.22 | 18.91 | 0.35 | 64 | 0.44 |
| 110 | 24.33 | 19.84 | 0.38 | 67 | 0.39 |
| 115 | 25.43 | 20.77 | 0.41 | 70 | 0.34 |
| 120 | 26.54 | 21.70 | 0.45 | 73 | 0.29 |
| 125 | 27.65 | 22.63 | 0.49 | 76 | 0.24 |
| 130 | 28.75 | 23.56 | 0.53 | 79 | 0.19 |
| 135 | 29.86 | 24.49 | 0.57 | 82 | 0.14 |
| Phase Angles (θ/°) | Erosion Rates (CE/mm·h−1) | Particle Impact Angles (α/°) | |||||
|---|---|---|---|---|---|---|---|
| 0.02/m·s−1 | 0.2/m·s−1 | 2/m·s−1 | 20/m·s−1 | 0.2/m·s−1 | 2/m·s−1 | 20/m·s−1 | |
| 1 | 1.02 × 10−3 | 5.75 × 10−3 | 3.23 × 10−2 | 1.82 × 10−1 | 78.74 | 26.67 | 2.88 |
| 4 | 1.32 × 10−3 | 7.42 × 10−3 | 4.17 × 10−2 | 2.34 × 10−1 | 78.72 | 26.62 | 2.87 |
| 7 | 1.06 × 10−3 | 5.94 × 10−3 | 3.34 × 10−2 | 1.88 × 10−1 | 78.66 | 26.50 | 2.85 |
| 10 | 9.08 × 10−4 | 5.11 × 10−3 | 2.87 × 10−2 | 1.61 × 10−1 | 78.57 | 26.32 | 2.83 |
| 13 | 8.04 × 10−4 | 4.52 × 10−3 | 2.54 × 10−2 | 1.43 × 10−1 | 78.45 | 26.08 | 2.80 |
| 16 | 7.22 × 10−4 | 4.06 × 10−3 | 2.28 × 10−2 | 1.28 × 10−1 | 78.30 | 25.78 | 2.76 |
| 19 | 6.54 × 10−4 | 3.68 × 10−3 | 2.07 × 10−2 | 1.16 × 10−1 | 78.11 | 25.41 | 2.72 |
| 22 | 5.96 × 10−4 | 3.35 × 10−3 | 1.89 × 10−2 | 1.06 × 10−1 | 77.88 | 24.98 | 2.67 |
| 25 | 5.45 × 10−4 | 3.06 × 10−3 | 1.72 × 10−2 | 9.69 × 10−2 | 77.61 | 24.48 | 2.61 |
| 28 | 4.99 × 10−4 | 2.81 × 10−3 | 1.58 × 10−2 | 8.87 × 10−2 | 77.30 | 23.92 | 2.54 |
| 31 | 4.57 × 10−4 | 2.57 × 10−3 | 1.45 × 10−2 | 8.13 × 10−2 | 76.93 | 23.30 | 2.47 |
| 34 | 4.19 × 10−4 | 2.36 × 10−3 | 1.33 × 10−2 | 7.46 × 10−2 | 76.50 | 22.61 | 2.39 |
| 37 | 3.85 × 10−4 | 2.16 × 10−3 | 1.22 × 10−2 | 6.84 × 10−2 | 76.01 | 21.86 | 2.30 |
| 40 | 3.53 × 10−4 | 1.98 × 10−3 | 1.12 × 10−2 | 6.27 × 10−2 | 75.43 | 21.05 | 2.20 |
| 43 | 3.23 × 10−4 | 1.82 × 10−3 | 1.02 × 10−2 | 5.74 × 10−2 | 74.77 | 20.17 | 2.10 |
| 46 | 2.95 × 10−4 | 1.66 × 10−3 | 9.33 × 10−3 | 5.25 × 10−2 | 74.01 | 19.24 | 2.00 |
| 49 | 2.69 × 10−4 | 1.51 × 10−3 | 8.51 × 10−3 | 4.79 × 10−2 | 73.12 | 18.24 | 1.89 |
| 52 | 2.45 × 10−4 | 1.38 × 10−3 | 7.74 × 10−3 | 4.35 × 10−2 | 72.08 | 17.19 | 1.77 |
| 55 | 2.22 × 10−4 | 1.25 × 10−3 | 7.01 × 10−3 | 3.94 × 10−2 | 70.86 | 16.07 | 1.65 |
| 58 | 2.00 × 10−4 | 1.12 × 10−3 | 6.32 × 10−3 | 3.55 × 10−2 | 69.41 | 14.91 | 1.53 |
| 61 | 1.79 × 10−4 | 1.00 × 10−3 | 5.65 × 10−3 | 3.18 × 10−2 | 67.68 | 13.69 | 1.40 |
| 64 | 1.58 × 10−4 | 8.90 × 10−4 | 5.01 × 10−3 | 2.82 × 10−2 | 65.58 | 12.42 | 1.26 |
| 67 | 1.38 × 10−4 | 7.79 × 10−4 | 4.38 × 10−3 | 2.46 × 10−2 | 63.00 | 11.11 | 1.12 |
| 70 | 1.19 × 10−4 | 6.68 × 10−4 | 3.76 × 10−3 | 2.11 × 10−2 | 59.80 | 9.75 | 0.98 |
| 73 | 9.91 × 10−5 | 5.58 × 10−4 | 3.14 × 10−3 | 1.76 × 10−2 | 55.75 | 8.36 | 0.84 |
| 76 | 7.90 × 10−5 | 4.44 × 10−4 | 2.50 × 10−3 | 1.41 × 10−2 | 50.55 | 6.93 | 0.70 |
| 79 | 5.78 × 10−5 | 3.25 × 10−4 | 1.83 × 10−3 | 1.03 × 10−2 | 43.79 | 5.48 | 0.55 |
| 82 | 3.42 × 10−5 | 1.92 × 10−4 | 1.08 × 10−3 | 6.08 × 10−3 | 34.96 | 4.00 | 0.40 |
| Materials | C | Si | Mn | P | S | Cr | Mo | Ni | Cu |
|---|---|---|---|---|---|---|---|---|---|
| 13Cr | 0.029 | 0.22 | 0.45 | 0.015 | 0.001 | 13.3 | 1.92 | 4.85 | 1.59 |
| Materials | Tensile Strength (MPa) | Yield Strength (MPa) | Elongation (%) | Hardness (HV) |
|---|---|---|---|---|
| 13Cr | 970 | 855 | 20 | 323.4 |
| Phase Angle (θ/deg) | Experimental Value (CE/mm·h−1) | Calculated Value (CE/mm·h−1) | Relative Error (%) |
|---|---|---|---|
| 0 | 1.20 × 10−2 | 1.49 × 10−2 | 24.17 |
| 45 | 8.30 × 10−3 | 9.62 × 10−3 | 15.90 |
| 90 | 5.70 × 10−3 | 6.54 × 10−3 | 14.74 |
| 135 | 2.10 × 10−3 | 1.84 × 10−3 | −12.38 |
| 180 | 1.40 × 10−3 | 8.01 × 10−4 | −42.79 |
| Flow Velocity (m·s−1) | Experimental Value (CE/mm·h−1) | Calculated Value (CE/mm·h−1) | Relative Error (%) |
|---|---|---|---|
| 0.6 | 1.20 × 10−2 | 1.49 × 10−2 | 24.17 |
| 1.2 | 1.70 × 10−2 | 1.95 × 10−2 | 21.76 |
| 1.8 | 2.30 × 10−2 | 2.63 × 10−2 | 14.35 |
| 2.4 | 3.16 × 10−2 | 3.51 × 10−2 | 11.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zhang, W.; Zhang, L.; Cheng, J. Theoretical Prediction Method for Erosion Damage of Horizontal Pipe by Suspended Particles in Liquid–Solid Flows. Materials 2021, 14, 4099. https://doi.org/10.3390/ma14154099
Liu G, Zhang W, Zhang L, Cheng J. Theoretical Prediction Method for Erosion Damage of Horizontal Pipe by Suspended Particles in Liquid–Solid Flows. Materials. 2021; 14(15):4099. https://doi.org/10.3390/ma14154099
Chicago/Turabian StyleLiu, Guoqiang, Wenzhe Zhang, Liang Zhang, and Jiarui Cheng. 2021. "Theoretical Prediction Method for Erosion Damage of Horizontal Pipe by Suspended Particles in Liquid–Solid Flows" Materials 14, no. 15: 4099. https://doi.org/10.3390/ma14154099






