Energy Structure and Luminescence of CeF3 Crystals
Abstract
1. Introduction
2. Materials and Methods
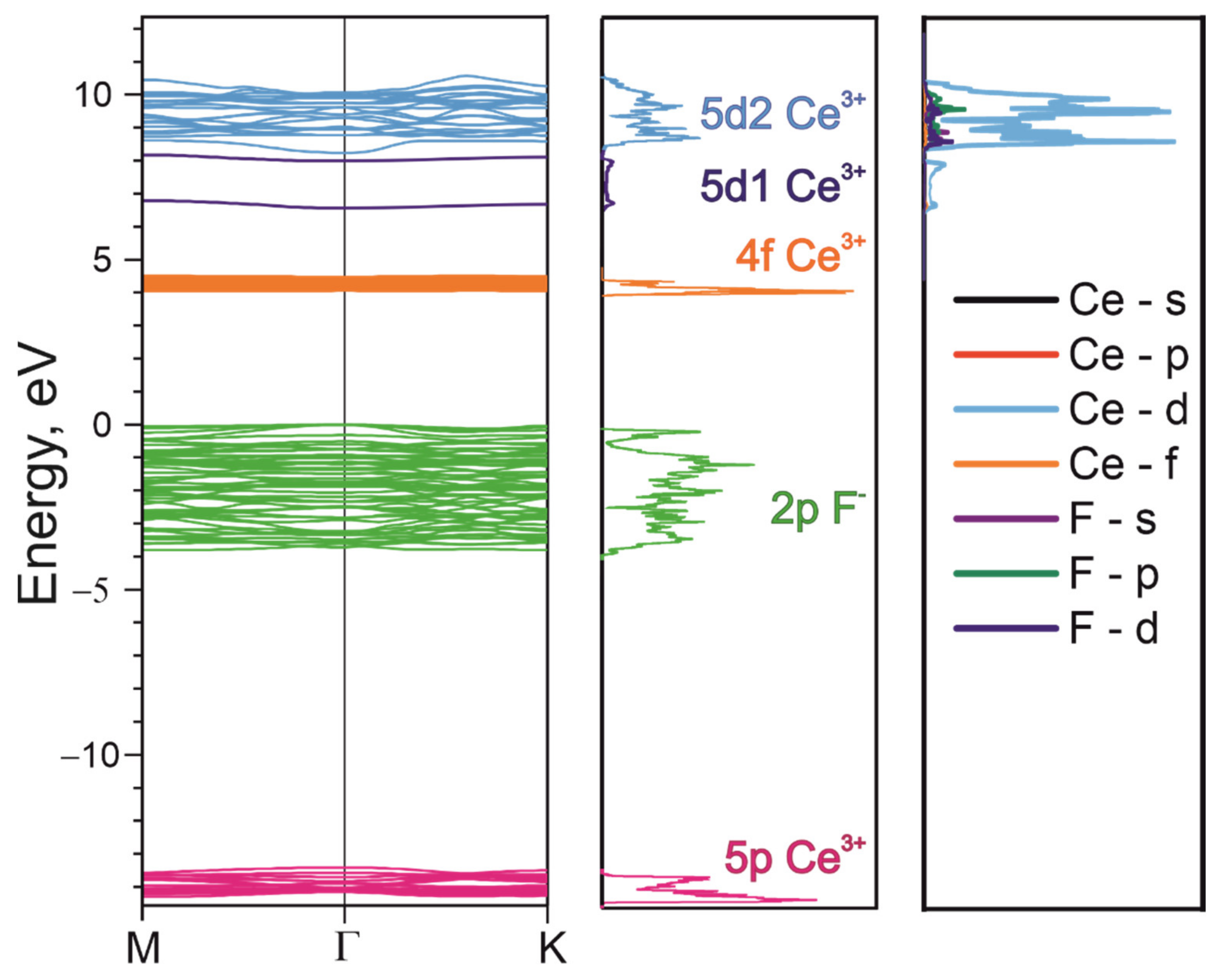
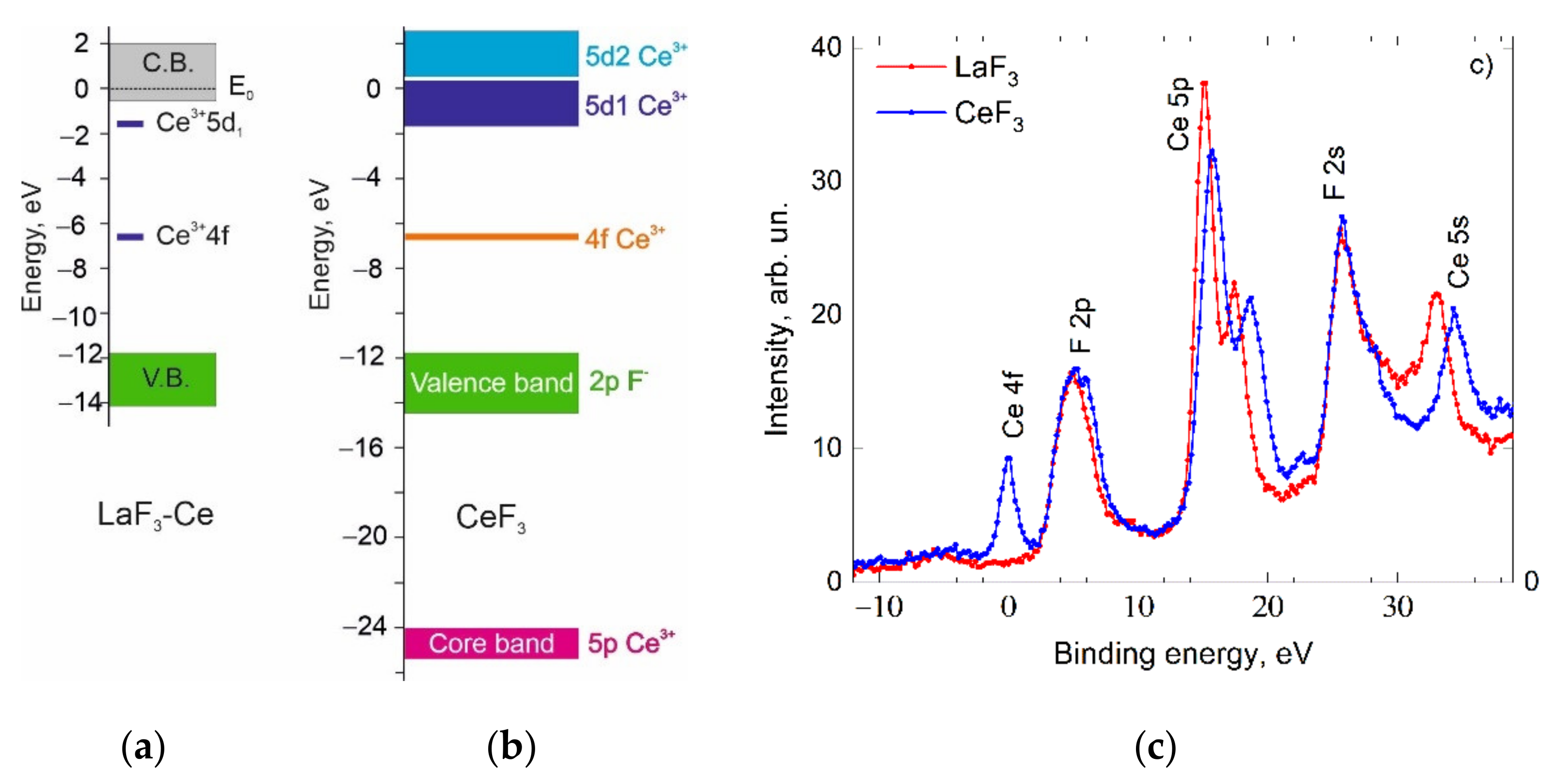
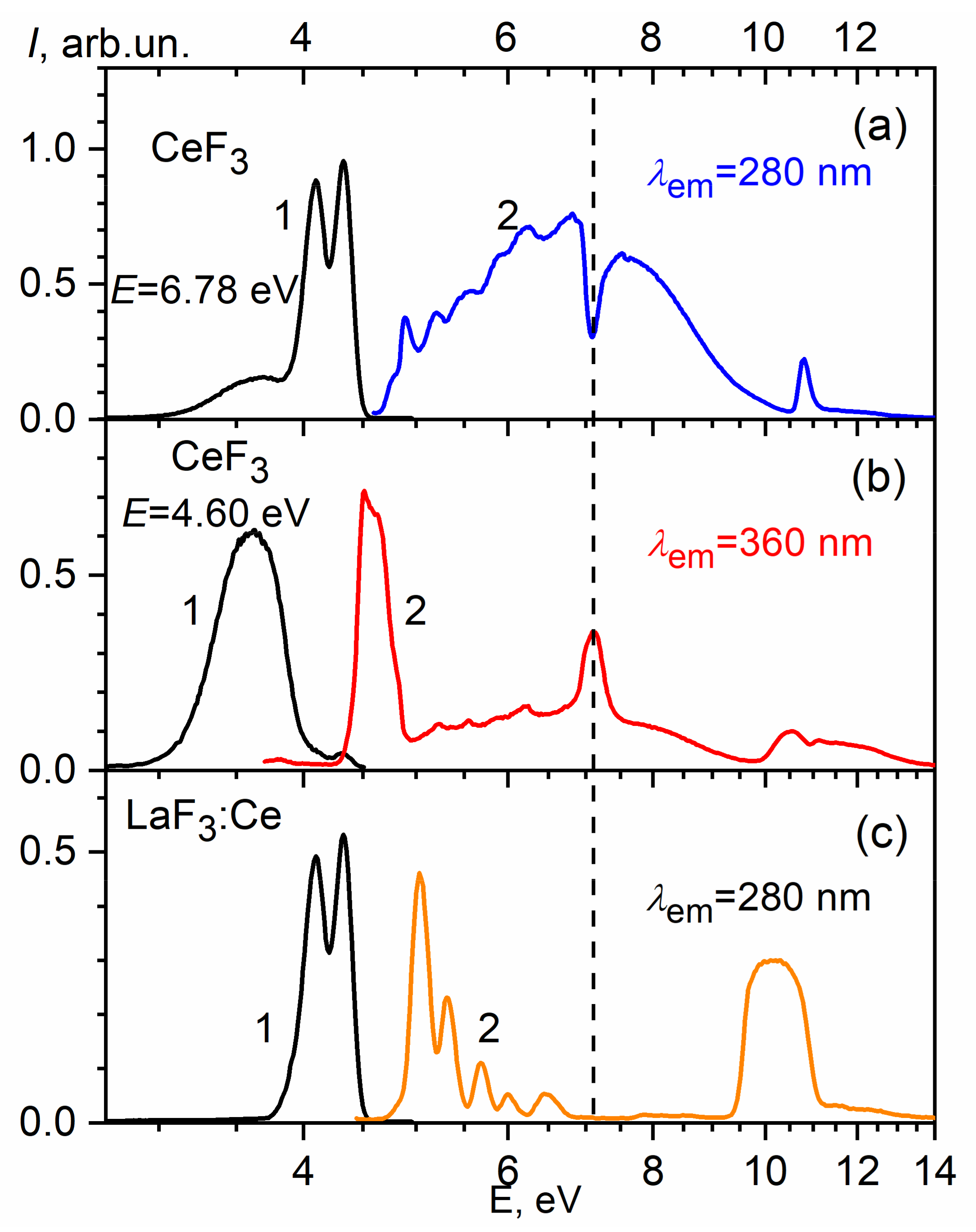
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Michałowska, J.; Józwik, J. Prediction of the parameters of magnetic field of CNC machine tools. Prz. Elektrotechniczny 2019, 95, 134–136. [Google Scholar] [CrossRef]
- Kapłonek, W.; Nadolny, K.; Krolczyk, G. The Use of Focus-Variation Microscopy for the Assessment of Active Surfaces of a New Generation of Coated Abrasive Tools. Meas. Sci. Rev. 2016, 16, 42–53. [Google Scholar] [CrossRef]
- Glowacz, A. Ventilation Diagnosis of Angle Grinder Using Thermal Imaging. Sensors 2021, 21, 2853. [Google Scholar] [CrossRef]
- Gelen, A.; Onur, S.B. Electrofilter Design for Flues and Energy Harvesting. J. Innov. Sci. Eng. 2021, 5, 41–49. [Google Scholar] [CrossRef]
- Wang, J.; Kochan, O.; Przystupa, K.; Su, J. Information-measuring System to Study the Thermocouple with Controlled Temperature Field. Meas. Sci. Rev. 2019, 19, 161–169. [Google Scholar] [CrossRef]
- Drga, R.; Janáčová, D.; Palenčár, R.; Ďuriš, S. Positioner and the Procedure for Measuring Spatial Characteristics. Meas. Sci. Rev. 2019, 19, 9–13. [Google Scholar] [CrossRef]
- Michałowska, J.; Pytka, J.; Tofil, A.; Krupski, P.; Puzio, Ł. Assessment of Training Aircraft Crew Exposure to Electromagnetic Fields Caused by Radio Navigation Devices. Energies 2021, 14, 254. [Google Scholar] [CrossRef]
- Arpin-Pont, J.; Gagnon, M.; Tahan, A.S.; Coutu, A.; Thibault, D. Methodology for estimating strain gauge measurement biases and uncertainties on isotropic materials. J. Strain Anal. Eng. Des. 2014, 50, 40–50. [Google Scholar] [CrossRef]
- Shu, C.; Kochan, O. Method of thermocouples self verification on operation place. Sens. Transducers 2013, 160, 55. [Google Scholar]
- Bennett, A. The calibration of thermistors over the temperature range 0–30 °C. Deep. Sea Res. Oceanogr. Abstr. 1972, 19, 157–163. [Google Scholar] [CrossRef]
- Zeng, F.; Sun, J.; Hu, X.; Fu, C. Thermal Finite Element Simulation of Dry Block Calibrator Based on Multi-fixed-Point Cells. Int. J. Thermophys. 2021, 42, 1–15. [Google Scholar] [CrossRef]
- Zhengbing, H.; Jotsov, V.; Jun, S.; Kochan, O.; Hu, Z.; Kochan, R.; Sasiuk, T. Data science applications to improve accuracy of thermocouples. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 4–6 September 2016; pp. 180–188. [Google Scholar]
- Glowacz, A. Fault diagnosis of electric impact drills using thermal imaging. Measurement 2021, 171, 108815. [Google Scholar] [CrossRef]
- Kozieł, P. Using the FTA method to analyze the quality of an uninterruptible power supply unitreparation UPS. Prz. Elektrotechniczny 2019, 95, 37–40. [Google Scholar] [CrossRef]
- Jun, S.; Kochan, O. The Mechanism of the Occurrence of Acquired Thermoelectric Inhomogeneity of Thermocouples and its Effect on the Result of Temperature Measurement. Meas. Tech. 2015, 57, 1160–1166. [Google Scholar] [CrossRef]
- Kim, Y.-G.; Song, C.H.; Gam, K.S.; Yang, I. Change in inhomogeneity with temperature between 180 °C and 950 °C in base-metal thermocouples. Meas. Sci. Technol. 2009, 20, 075102. [Google Scholar] [CrossRef]
- Nada, M.; Muramoto, Y.; Yokoyama, H.; Ishibashi, T.; Matsuzaki, H. Triple-mesa Avalanche Photodiode With Inverted P-Down Structure for Reliability and Stability. J. Light. Technol. 2014, 32, 1543–1548. [Google Scholar] [CrossRef]
- Trisna, B.A.; Suherlan; Wiriadinata, H.; Fajria, M.A.; Rifa’I, I.A.; Tistomo, A.S.; Zaid, G. Effect of Electrical Annealing to the Inhomogeneity Improvement of Type-S Thermocouples. J. Phys. Conf. Ser. 2018, 1065, 122001. [Google Scholar] [CrossRef]
- Jasiulewicz-Kaczmarek, M.; Antosz, K.; Żywica, P.; Mazurkiewicz, D.; Sun, B.; Ren, Y. Framework of machine criticality assessment with criteria interactions. Ekspolatacja i Niezawodn. Maint. Reliab. 2021, 23, 207–220. [Google Scholar] [CrossRef]
- Klym, H.; Ingram, A.; Shpotyuk, O.; Hadzaman, I.; Solntsev, V.; Hotra, O.; Popov, A.I. Positron annihilation characterization of free volume in micro- and macro-modified Cu0.4Co0.4Ni0.4Mn1.8O4 ceramics. Low Temp. Phys. 2016, 42, 601–605. [Google Scholar] [CrossRef][Green Version]
- Shpotyuk, O.; Calvez, L.; Petracovschi, E.; Klym, H.; Ingram, A.; Demchenko, P. Thermally-induced crystallization behaviour of 80GeSe2–20Ga2Se3 glass as probed by combined X-ray diffraction and PAL spectroscopy. J. Alloy. Compd. 2014, 582, 323–327. [Google Scholar] [CrossRef]
- Greengard, S. The Internet of Things; MIT Press: Cambridge, MA, USA, 2015; ISBN 9780262527736. [Google Scholar]
- Song, W.; Beshley, M.; Przystupa, K.; Beshley, H.; Kochan, O.; Pryslupskyi, A.; Pieniak, D.; Su, J. A Software Deep Packet Inspection System for Network Traffic Analysis and Anomaly Detection. Sensors 2020, 20, 1637. [Google Scholar] [CrossRef] [PubMed]
- Grochalski, K.; Jabłoński, P.; Talar, R.; Twardowski, P.; Wieczorowski, M.; Jakubek, B.; Rukat, W. Temperature Measurement of Modern Cutting Tools During Turning. Adv. Sci. Technol. Res. J. 2020, 14, 37–48. [Google Scholar] [CrossRef]
- Wang, T.P.; Bediones, D.P.; Henrikson, H.J.; Janhunen, E.J.; Bachalo, K.; Swirla, P. Stabilized metal sheathed type K and E thermocouples improve turbine efficiency. Adv. Instrum. Control 1997, 1, 439–448. [Google Scholar]
- Krolczyk, G.; Gajek, M.; Legutko, S. Predicting the tool life in the dry machining of duplex stainless steel. Eksploatacja i Niezawodność 2013, 15, 62–65. [Google Scholar]
- Ishchenko, V.; Pohrebennyk, V.; Borowik, B.; Falat, P.; Shaikhanova, A. Toxic substances in hazardous household waste. In Proceedings of the International Multidisciplinary Scientific GeoConference SGEM, Albena, Bulgaria, 2–8 July 2018; Volume 18, pp. 223–230. [Google Scholar]
- Jan, R.; Branislav, H.; Stanislav, Ď.; Peter, P.; Miroslav, C.; Alena, F.; Pavol, V. Factors Affecting Measurements of IOP Using Non-Contact Eye Tonometer. J. Mech. Eng. 2020, 70, 133–140. [Google Scholar] [CrossRef]
- Domagała, I.; Przystupa, K.; Firlej, M.; Pieniak, D.; Gil, L.; Borucka, A.; Naworol, I.; Biedziak, B.; Levkiv, M. Analysis of the Statistical Comparability of the Hardness and Wear of Polymeric Materials for Orthodontic Applications. Materials 2021, 14, 2925. [Google Scholar] [CrossRef] [PubMed]
- Bojkovski, J.; Fischer, J.; Machin, G.; Pavese, F.; Peruzzi, A.; Renaot, E.; Tegeler, E. A Roadmap for Thermal Metrology. Int. J. Thermophys. 2008, 30, 1–8. [Google Scholar] [CrossRef]
- Machin, G.; Bojkovski, J.; Del Campo, D.; Dogan, A.K.; Fischer, J.; Hermier, Y.; Merlone, A.; Nielsen, J.; Peruzzi, A.; Ranostaj, J.; et al. A European Roadmap for Thermometry. Int. J. Thermophys. 2014, 35, 385–394. [Google Scholar] [CrossRef]
- Vikhor, L.M.; Anatychuk, L.; Gorskyi, P.V. Electrical resistance of metal contact to Bi2Te3 based thermoelectric legs. J. Appl. Phys. 2019, 126, 164503. [Google Scholar] [CrossRef]
- Moses, W.; Derenzo, S. Cerium fluoride, a new fast, heavy scintillator. IEEE Trans. Nucl. Sci. 1989, 36, 173–176. [Google Scholar] [CrossRef][Green Version]
- Anderson, D. Cerium fluoride: A scintillator for high-rate applications. Nucl. Instrum. Methods Phys. Res. Sect. A 1990, 287, 606–612. [Google Scholar] [CrossRef]
- Kamenskikh, I.; Tishchenko, E.; Kirm, M.; Omelkov, S.; Belsky, A.; Vasil’Ev, A. Decay Kinetics of CeF3 under VUV and X-ray Synchrotron Radiation. Symmetry 2020, 12, 914. [Google Scholar] [CrossRef]
- Moses, W.; Derenzo, S.; Weber, M.; Ray-Chaudhuri, A.; Cerrina, F. Scintillation mechanisms in cerium fluoride. J. Lumin. 1994, 59, 89–100. [Google Scholar] [CrossRef]
- Wojtowicz, A.; Balcerzyk, M.; Berman, E.; Lempicki, A. Optical spectroscopy and scintillation mechanisms of CexLa1−xF3. Phys. Rev. B 1994, 49, 14880–14895. [Google Scholar] [CrossRef]
- Wojtowicz, A.; Berman, E.; Lempicki, A. Stoichiometric cerium compounds as scintillators, II. CeP/sub 5/O/sub 14/. IEEE Trans. Nucl. Sci. 1992, 39, 1542–1548. [Google Scholar] [CrossRef][Green Version]
- Williams, R.T.; Thoma, E.D.; Bunton, P.H. Energy Localization and Decay in Highly Ionic Crystals. MRS Proc. 1994, 348, 331. [Google Scholar] [CrossRef]
- Belsky, A.; Glukhov, R.; Martin, P.; Mikhailin, V.; Pedrini, C.; Vasil’Ev, A. VUV excitation of intrinsic luminescence of ionic crystals with complicated band structure. Simulation. J. Lumin. 1997, 72–74, 96–97. [Google Scholar] [CrossRef]
- Belsky, A.N.; Kamenskikh, I.; Mikhailin, V.V.; Pedrini, C.; Vasil’Ev, A.N.; Vasil’Ev, A. Energy transfer in inorganic scintillators. Radiat. Eff. Defects Solids 1999, 150, 1–10. [Google Scholar] [CrossRef]
- Li, P.; Gridin, S.; Ucer, K.B.; Williams, R.T.; Menge, P.R. Picosecond absorption spectroscopy of self-trapped excitons and Ce excited states in CeBr3 and La1−xCexBr3. Phys. Rev. B 2019, 99, 104301. [Google Scholar] [CrossRef]
- Klier, K.; Novak, P.; Miller, A.; Spirko, J.; Hatalis, M. Electronic structure of CeF3 and TbF3 by valence-band XPS and theory. J. Phys. Chem. Solids 2009, 70, 1302–1311. [Google Scholar] [CrossRef]
- Guss, P.; Foster, M.E.; Wong, B.; Doty, F.P.; Shah, K.; Squillante, M.R.; Shirwadkar, U.; Hawrami, R.; Tower, J.; Yuan, D. Results for aliovalent doping of CeBr3 with Ca2+. J. Appl. Phys. 2014, 115, 034908. [Google Scholar] [CrossRef]
- Narayan, R.; Miranda, R.; Rez, P. Simulating gamma-ray energy resolution in scintillators due to electron–hole pair statistics. Nucl. Instrum. Methods Phys. Res. Sect. B 2011, 269, 2667–2675. [Google Scholar] [CrossRef]
- Nishida, I.; Tatsumi, K.; Muto, S. Local Electronic and Atomic Structure of Ce3+-Containing Fluoride/Oxide Determined by TEM-EELS and First-Principles Calculations. Mater. Trans. 2009, 50, 952–958. [Google Scholar] [CrossRef]
- Saini, S.M.; Samant, S. First principle study of electronic and optical properties of CeF3 compound. In Proceedings of the Proceeding of International Conference on Recent Trends in Applied Physics and Material Science: RAM 2013, Bikaner, India, 1–2 February 2013; pp. 431–432. [Google Scholar]
- Chornodolskyy, Y.; Karnaushenko, V.; Vistovskyy, V.; Syrotyuk, S.; Gektin, A.; Voloshinovskii, A. Energy band structure peculiarities and luminescent parameters of CeX3 (X = Cl, Br, I) crystals. J. Lumin. 2021, 237, 118147. [Google Scholar] [CrossRef]
- Glukhov, R.; Belsky, A.; Pedrini, C.; Vasil’Ev, A. Simulation of energy conversion and transfer in CeF3 after VUV photon absorption. J. Alloy. Compd. 1998, 275-277, 488–492. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, G.; Wei, Y.; Han, Z.; Shi, J.; Hu, G.; Kirm, M.; Zimmerer, G. The dynamics properties on luminescence of CeF3 crystals. Surf. Rev. Lett. 2002, 9, 371–374. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Floris, A.; de Gironcoli, S.; Cococcioni, M. Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems. Int. J. Quantum Chem. 2014, 114, 14–49. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Zimmerer, G. SUPERLUMI: A unique setup for luminescence spectroscopy with synchrotron radiation. Radiat. Meas. 2007, 42, 859–864. [Google Scholar] [CrossRef]
- Dorenbos, P. Lanthanide 4f-electron binding energies and the nephelauxetic effect in wide band gap compounds. J. Lumin. 2013, 136, 122–129. [Google Scholar] [CrossRef]
- Pedrini, C.; Moine, B.; Gacon, J.C.; Jacquier, B. One- and two-photon spectroscopy of Ce3+ ions in LaF3-CeF3 mixed crystals. J. Phys. Condens. Matter 1992, 4, 5461–5470. [Google Scholar] [CrossRef]
- Auffray, E.; Buganov, O.V.; A Fedorov, A.; Korjik, M.; Mechinsky, V.; Tikhomirov, A.V.; Vasil’Ev, A.; Lecoq, P. Picosecond transient absorption rise time for ultrafast tagging of the interaction of ionizing radiation with scintillating crystals in high energy physics experiments. J. Instrum. 2014, 9, P07017. [Google Scholar] [CrossRef]
- Radzhabov, E.; Nepomnyashikh, A.I. F and Vk Centres in LaF3, CeF3 Crystals. 2015. Available online: http://arxiv.org/abs/1510.07781 (accessed on 30 June 2021).
- Gektin, A.; Shiran, N.; Nesterkina, V.; Boyarintseva, Y.; Baumer, V.; Stryganyuk, G.; Shimamura, K.; Villora, E. Luminescence of heavily Ce-doped alkaline-earth fluorides. J. Lumin. 2009, 129, 1538–1541. [Google Scholar] [CrossRef]
- Nikl, M.; Mares, J.A.; Mihóková, E.; Beitlerová, A.; Blazek, K.; Jindra, J. Energy transfer processes in CeF3 single crystals. Solid State Commun. 1993, 87, 185–188. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kochan, O.; Chornodolskyy, Y.; Selech, J.; Karnaushenko, V.; Przystupa, К.; Kotlov, A.; Demkiv, T.; Vistovskyy, V.; Stryhanyuk, H.; Rodnyi, P.; et al. Energy Structure and Luminescence of CeF3 Crystals. Materials 2021, 14, 4243. https://doi.org/10.3390/ma14154243
Kochan O, Chornodolskyy Y, Selech J, Karnaushenko V, Przystupa К, Kotlov A, Demkiv T, Vistovskyy V, Stryhanyuk H, Rodnyi P, et al. Energy Structure and Luminescence of CeF3 Crystals. Materials. 2021; 14(15):4243. https://doi.org/10.3390/ma14154243
Chicago/Turabian StyleKochan, Orest, Yaroslav Chornodolskyy, Jarosław Selech, Vladyslav Karnaushenko, Кrzysztof Przystupa, Aleksei Kotlov, Taras Demkiv, Vitaliy Vistovskyy, Hryhoriy Stryhanyuk, Piotr Rodnyi, and et al. 2021. "Energy Structure and Luminescence of CeF3 Crystals" Materials 14, no. 15: 4243. https://doi.org/10.3390/ma14154243
APA StyleKochan, O., Chornodolskyy, Y., Selech, J., Karnaushenko, V., Przystupa, К., Kotlov, A., Demkiv, T., Vistovskyy, V., Stryhanyuk, H., Rodnyi, P., Gektin, A., & Voloshinovskii, A. (2021). Energy Structure and Luminescence of CeF3 Crystals. Materials, 14(15), 4243. https://doi.org/10.3390/ma14154243






