Classifying Charge Carrier Interaction in Highly Compressed Elements and Silane
Abstract
:1. Introduction
2. Model Description
3. Results
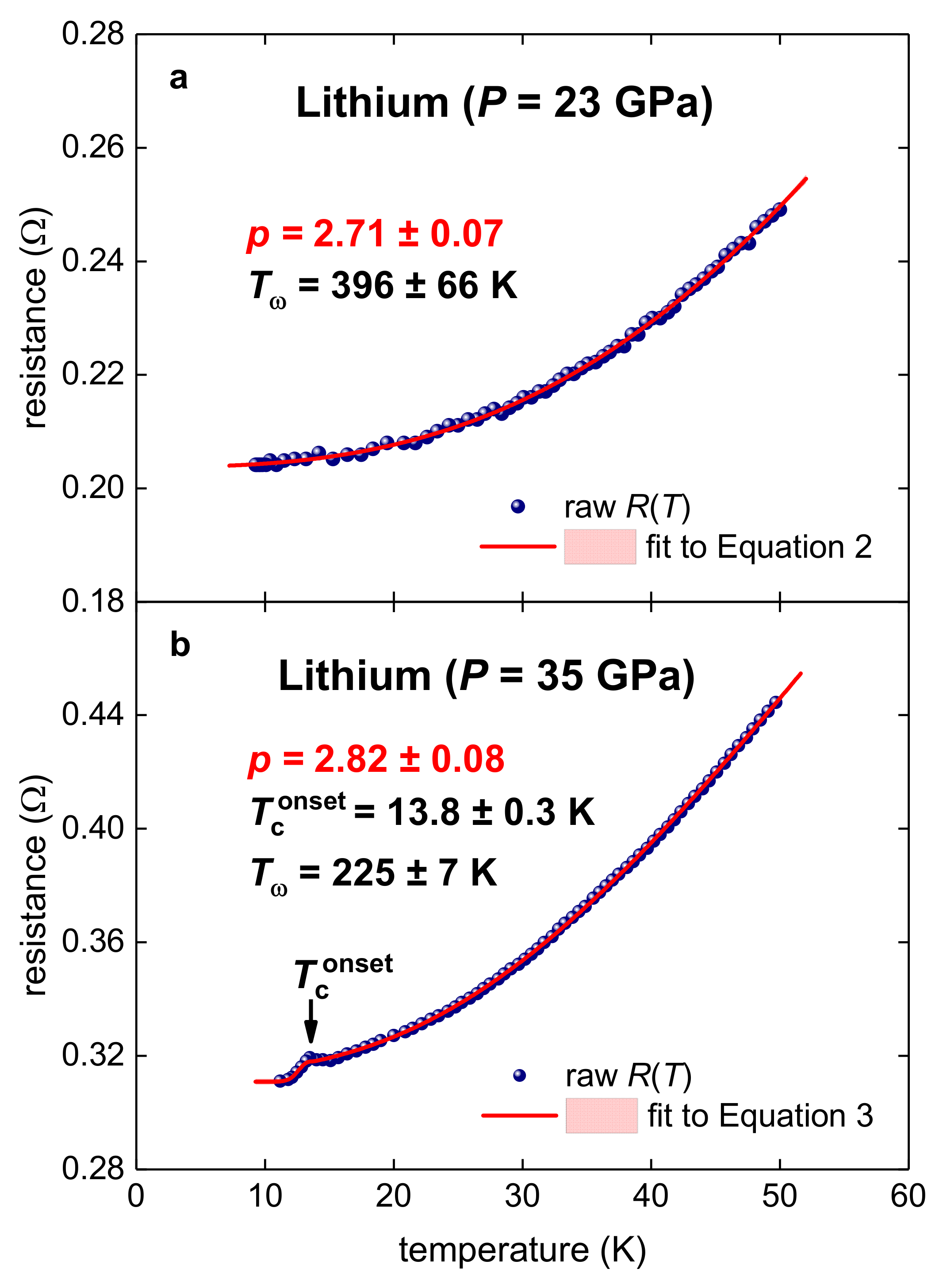
3.1. Highly Compressed Lithium
3.2. Highly Compressed Black Phosphorous
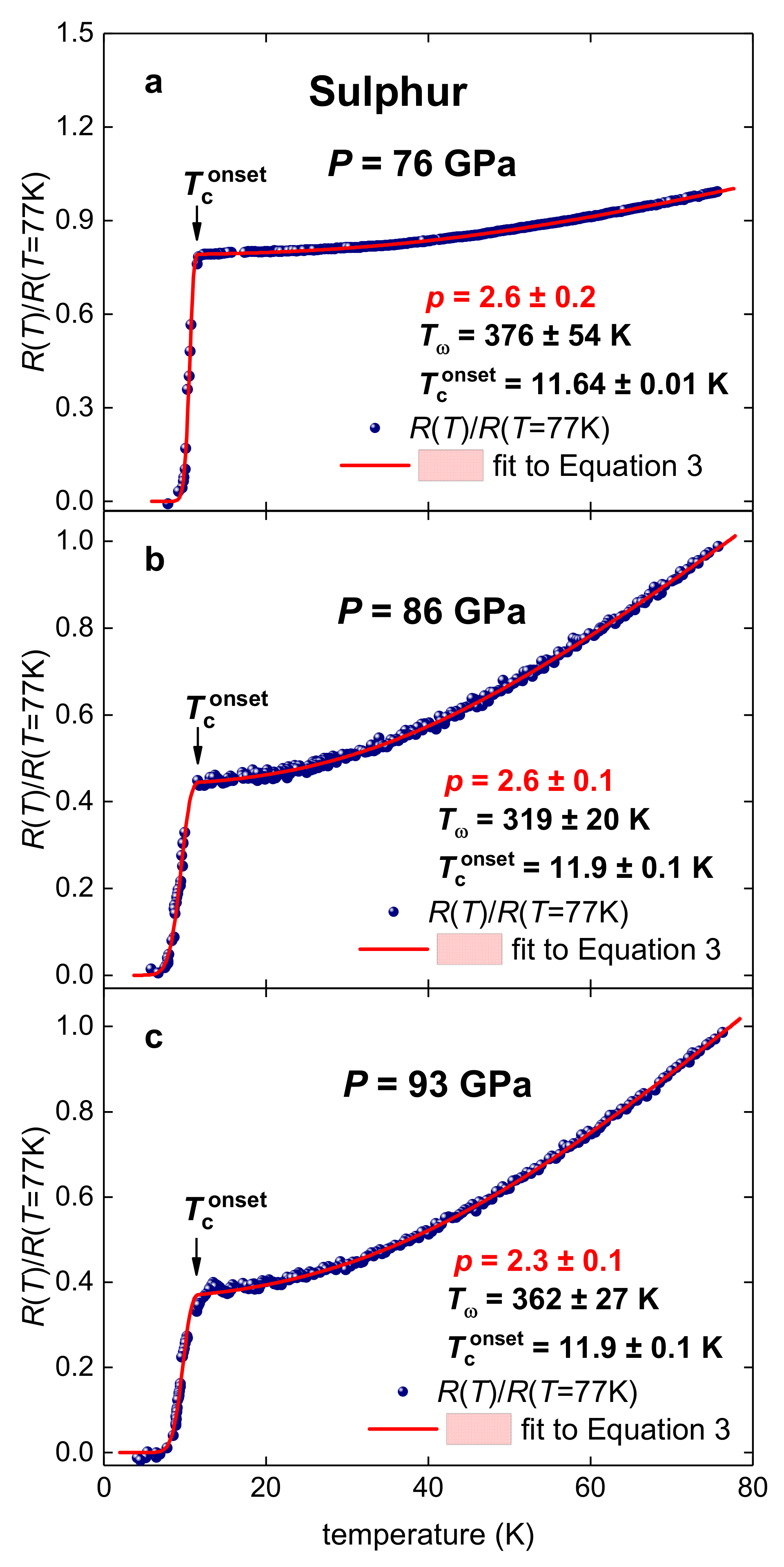
3.3. Highly Compressed Sulphur
3.4. Highly Compressed Silane
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Satterthwaite, C.B.; Toepke, I.L. Superconductivity of hydrides and deuterides of thorium. Phys. Rev. Lett. 1970, 25, 741–743. [Google Scholar] [CrossRef]
- Ashcroft, N.W. Metallic hydrogen: A high-temperature superconductor? Phys. Rev. Lett. 1968, 21, 1748–1749. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef] [Green Version]
- Semenok, D.V.; Kvashnin, A.G.; Ivanova, A.G.; Svitlyk, V.; Fominski, V.Y.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Troyan, I.A.; Oganov, A.R. Superconductivity at 161 K in thorium hydride ThH10: Synthesis and properties. Mater. Today 2020, 33, 36–44. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Semenok, D.V.; Kvashnin, A.G.; Huang, X.; Kruglov, I.A.; Galasso, M.; Song, H.; Duan, D.; Goncharov, A.F.; Prakapenka, V.B.; et al. Synthesis of molecular metallic barium superhydride: Pseudocubic BaH12. Nat. Commun. 2021, 12, 273. [Google Scholar] [CrossRef]
- Wang, N.; Shan, P.F.; Chen, K.Y.; Sun, J.P.; Yang, P.T.; Ma, X.L.; Wang, B.S.; Yu, X.H.; Zhang, S.; Chen, G.F.; et al. A low-Tc superconducting modification of Th4H15 synthesized under high pressure. Supercond. Sci. Technol. 2021, 34, 034006. [Google Scholar] [CrossRef]
- Pickard, C.J.; Errea, I.; Eremets, M.I. Superconducting hydrides under pressure. Annu. Rev. Condens. Matter Phys. 2020, 11, 57–76. [Google Scholar] [CrossRef] [Green Version]
- Flores-Livas, J.A.; Boeri, L.; Sanna, A.; Profeta, G.; Arita, R.; Eremets, M. A perspective on conventional high-temperature superconductors at high pressure: Methods and materials. Phys. Rep. 2020, 856, 1–78. [Google Scholar] [CrossRef]
- Feng, J.; Grochala, W.; Jaroń, T.; Hoffmann, R.; Bergara, A.; Ashcroft, N.W. Structures and potential superconductivity in SiH4 at high pressure: En route to “metallic hydrogen”. Phys. Rev. Lett. 2006, 96, 017006. [Google Scholar] [CrossRef]
- Eremets, M.I.; Trojan, I.A.; Medvedev, S.A.; Tse, J.S.; Yao, Y. Superconductivity in hydrogen dominant materials: Silane. Science 2008, 319, 1506–1509. [Google Scholar] [CrossRef]
- Talantsev, E.F. Advanced McMillan’s equation and its application for the analysis of highly-compressed superconductors. Supercond. Sci. Technol. 2020, 33, 094009. [Google Scholar] [CrossRef]
- Bloch, F. Zum elektrischen Widerstandsgesetz bei tiefen Temperaturen. Z. Phys. 1930, 59, 208–214. [Google Scholar] [CrossRef]
- Grüneisen, E. Die abhängigkeit des elektrischen widerstandes reiner metalle von der temperatur. Ann. Phys. 1933, 408, 530–540. [Google Scholar] [CrossRef]
- Mozaffari, S.; Sun, D.; Minkov, V.S.; Drozdov, A.P.; Knyazev, D.; Betts, J.B.; Einaga, M.; Shimizu, K.; Eremets, M.I.; Balicas, L. Superconducting phase-diagram of H3S under high magnetic fields. Nat. Commun. 2019, 10, 2522. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Tse, J.S.; Ma, Y.; Tanaka, K. Superconductivity in high-pressure SiH4. EPL 2007, 78, 37003. [Google Scholar] [CrossRef]
- Christensen, N.E.; Novikov, D.L. Predicted superconductive properties of lithium under pressure. Phys. Rev. Lett. 2001, 86, 1861–1864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, T.H.; Dunn, K.J. High-pressure and low-temperature study of electrical resistance of lithium. Phys. Rev. B 1986, 33, 807–811. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; Ishikawa, H.; Takao, D.; Yagi, T.; Amaya, K. Superconductivity in compressed lithium at 20 K. Nature 2002, 419, 597–599. [Google Scholar] [CrossRef] [PubMed]
- Struzhkin, V.V.; Eremets, M.I.; Gan, W.; Mao, H.-K.; Hemley, R.J. Superconductivity in dense lithium. Science 2002, 298, 1213–1215. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; Amaya, K.; Suzuki, N. Pressure-induced superconductivity in elemental materials. J. Phys. Soc. Jpn. 2005, 74, 1345–1357. [Google Scholar] [CrossRef] [Green Version]
- Deemyad, S.; Schilling, J.S. Superconducting phase diagram of Li metal in nearly hydrostatic pressures up to 67 GPa. Phys. Rev. Lett. 2003, 91, 167001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsuoka, T.; Shimizu, K. Direct observation of a pressure-induced metal-to-semiconductor transition in lithium. Nature 2009, 458, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, A.M.; Temple, S.R.; Bishop, J.K.; Deemyad, S. High-pressure superconducting phase diagram of 6Li: Isotope effects in dense lithium. Proc. Natl. Acad. Sci. USA 2015, 112, 60–64. [Google Scholar] [CrossRef] [Green Version]
- Profeta, G.; Franchini, C.; Lathiotakis, N.N.; Floris, A.; Sanna, A.; Marques, M.A.L.; Lueders, M.; Massidda, S.; Gross, E.K.U.; Continenza, A.A. Superconductivity in lithium, potassium, and aluminum under extreme pressure: A first-principles study. Phys. Rev. Lett. 2006, 96, 047003. [Google Scholar] [CrossRef]
- Buzea, C.; Robbie, K. Assembling the puzzle of superconducting elements: A review. Supercond. Sci. Technol. 2005, 18, R1–R8. [Google Scholar] [CrossRef]
- Yakovlev, E.N.; Stepanov, G.N.; Timofeev, Y.A.; Vinogradov, B.V. Superconductivity of sulphur at high pressure. JETP Lett. 1978, 28, 340–342. [Google Scholar]
- Zakharov, O.; Cohen, M.L. Theory of structural, electronic, vibrational, and superconducting properties of high-pressure phases of sulfur. Phys. Rev. B 1995, 52, 12572–12578. [Google Scholar] [CrossRef] [PubMed]
- Struzhkin, V.V.; Hemley, R.J.; Mao, H.-K.; Timofeev, Y.A. Superconductivity at 10–17 K in compressed sulphur. Nature 1997, 390, 382–384. [Google Scholar] [CrossRef]
- Kometani, S.; Eremets, M.I.; Shimizu, K.; Kobayashi, M.; Amaya, K. Observation of pressure induced superconductivity in sulphur. J. Phys. Soc. Jpn. 1997, 66, 2564–2565. [Google Scholar] [CrossRef]
- Rudin, S.P.; Liu, A.Y. Predicted simple-cubic phase and superconducting properties for compressed sulfur. Phys. Rev. Lett. 1999, 83, 3049–3052. [Google Scholar] [CrossRef]
- Whaley-Baldwin, J.; Hutcheon, M.; Pickard, C.J. Superconducting incommensurate host-guest phases in compressed elemental sulfur. Phys. Rev. B 2021, 103, 214111. [Google Scholar] [CrossRef]
- Wittig, J.; Matthias, B.T. Superconducting phosphorus. Science 1968, 160, 994–995. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; von Rohr, F.; Yi, W.; Zhou, Y.; Wang, Z.; Cai, S.; Zhang, S.; Li, X.; Li, Y.; et al. Electron-hole balance and the anomalous pressure-dependent superconductivity in black phosphorus. Phys. Rev. B 2017, 96, 224513. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Sun, J.; Shahib, P.; Gaoe, M.; MacDonald, A.H.; Uwatoko, Y.; Tao Xiang, T.; Goodenough, J.B.; Cheng, J.; Zhou, J. Pressure-induced phase transitions and superconductivity in a black phosphorus single crystal. Proc. Natl. Acad. Sci. USA 2018, 115, 9935–9940. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodin, A.S.; Carvalho, A.; Castro Neto, A.H. Strain-induced gap modification in black phosphorus. Phys. Rev. Lett. 2014, 112, 176801. [Google Scholar] [CrossRef] [Green Version]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef] [Green Version]
- Eliashberg, G.M. Interactions between electrons and lattice vibrations in a superconductor. Soviet Phys. JETP 1960, 11, 696–702. [Google Scholar]
- Matthias, B.T. Anticorrelations in superconductivity. Physica 1971, 55, 69–72. [Google Scholar] [CrossRef]
- Harshman, D.R.; Fiory, A.T. Compressed H3S: Inter-sublattice Coulomb coupling in a high-Tc superconductor. J. Phys. Condens. Matter 2017, 29, 445702. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.-T. Room-temperature-superconducting Tc driven by electron correlation. Sci. Rep. 2021, 11, 10329. [Google Scholar] [CrossRef]
- Monthoux, P.; Pines, D.; Lonzarich, G.G. Superconductivity without phonons. Nature 2007, 450, 1177–1183. [Google Scholar] [CrossRef]
- Talantsev, E.F. The dominance of non-electron-phonon charge carrier interaction in highly-compressed superhydrides. Supercond. Sci. Technol. 2021, 34. accepted. [Google Scholar]
- Jiang, H.; Bao, J.-K.; Zhai, H.-F.; Tang, Z.-T.; Sun, Y.-L.; Liu, Y.; Wang, Z.-C.; Bai, H.; Xu, Z.-A.; Cao, G.-H. Physical properties and electronic structure of Sr2Cr3As2O2 containing CrO2 and Cr2As2 square-planar lattices. Phys. Rev. B 2015, 92, 205107. [Google Scholar] [CrossRef] [Green Version]
- Talantsev, E.F. Quantifying the charge carrier interaction in metallic twisted graphene superlattices. Nanomaterials 2021, 11, 1306. [Google Scholar] [CrossRef]
- White, G.K.; Woods, S.B. Electrical and thermal resistivity of the transition elements at low temperatures. Philos. Trans. R. Soc. Lond. A 1959, 251, 273–302. [Google Scholar]
- Poker, D.B.; Klabunde, C.E. Temperature dependence of electrical resistivity of vanadium, platinum, and copper. Phys. Rev. B 1982, 26, 7012–7014. [Google Scholar] [CrossRef]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef] [Green Version]
- Talantsev, E.F.; Stolze, K. 2020 Resistive transition in hydrogen-rich superconductors. Supercond. Sci. Technol. 2021, 34, 064001. [Google Scholar] [CrossRef]
- Shirotani, I.; Mikami, J.; Adachi, T.; Katayama, Y.; Tsuji, K.; Kawamura, H.; Shimomura, O.; Nakajima, T. Phase transitions and superconductivity of black phosphorus and phosphorus-arsenic alloys at low temperatures and high pressures. Phys. Rev. B 1994, 50, 16274–16278. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, R.; Song, P.; Adachi, S.; Saito, Y.; Hara, H.; Yamashita, A.; Nakamura, K.; Yamamoto, S.; Tanaka, H.; Irifune, T. Pressure-induced superconductivity in tin sulfide. Phys. Rev. B 2019, 99, 184502. [Google Scholar] [CrossRef] [Green Version]


| p | Charge Carrier Interaction Mechanism | Integral Term in Equation (2) |
|---|---|---|
| 2 | the electron–electron interaction | |
| 3 | the electron–magnon interaction | |
| 5 | the electron–phonon interaction |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talantsev, E.F. Classifying Charge Carrier Interaction in Highly Compressed Elements and Silane. Materials 2021, 14, 4322. https://doi.org/10.3390/ma14154322
Talantsev EF. Classifying Charge Carrier Interaction in Highly Compressed Elements and Silane. Materials. 2021; 14(15):4322. https://doi.org/10.3390/ma14154322
Chicago/Turabian StyleTalantsev, Evgueni F. 2021. "Classifying Charge Carrier Interaction in Highly Compressed Elements and Silane" Materials 14, no. 15: 4322. https://doi.org/10.3390/ma14154322
APA StyleTalantsev, E. F. (2021). Classifying Charge Carrier Interaction in Highly Compressed Elements and Silane. Materials, 14(15), 4322. https://doi.org/10.3390/ma14154322






