Mesoscale Mechanisms in Viscoplastic Deformation of Metals and Their Applications to Constitutive Models
Abstract
:1. Introduction
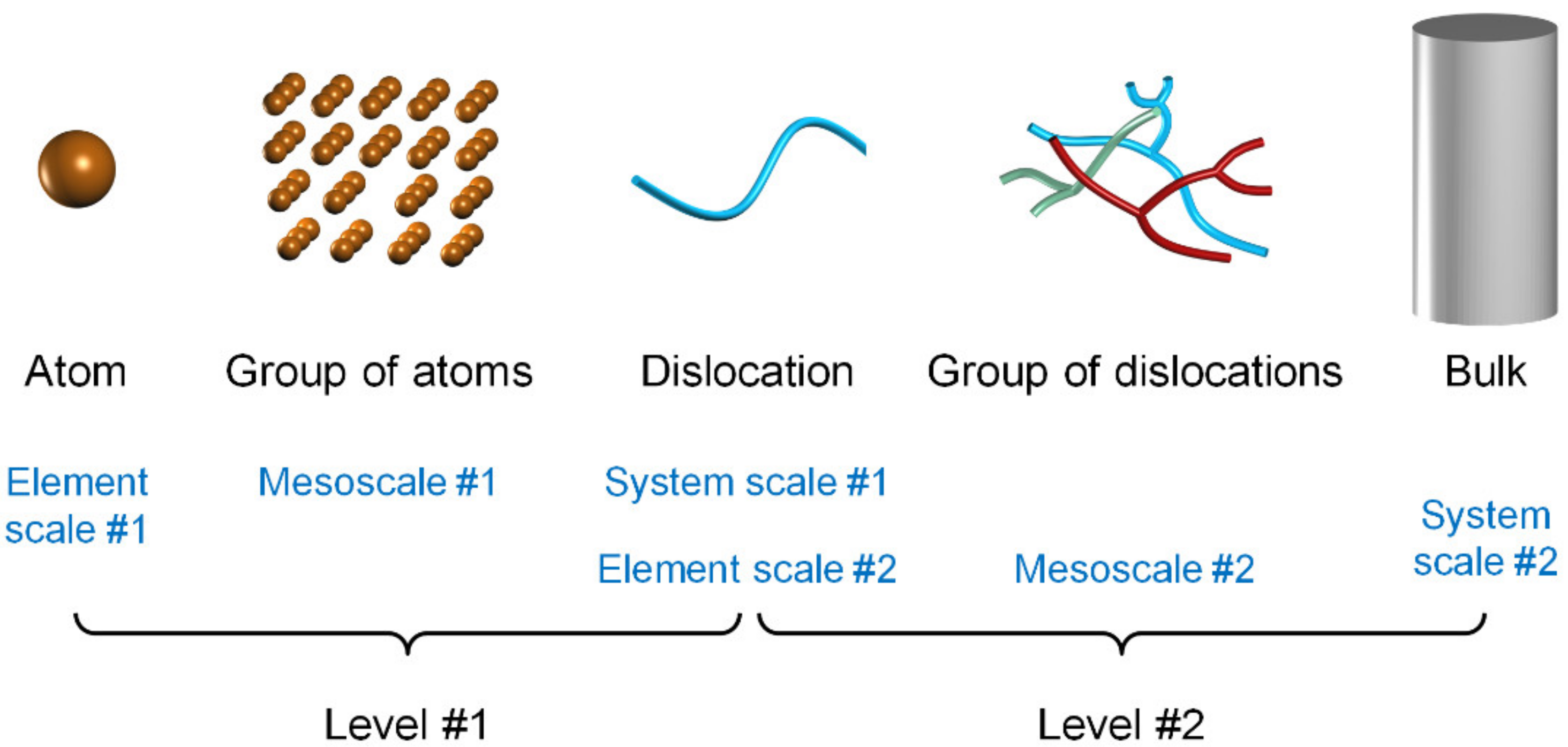
2. Two Levels of Mesoscales
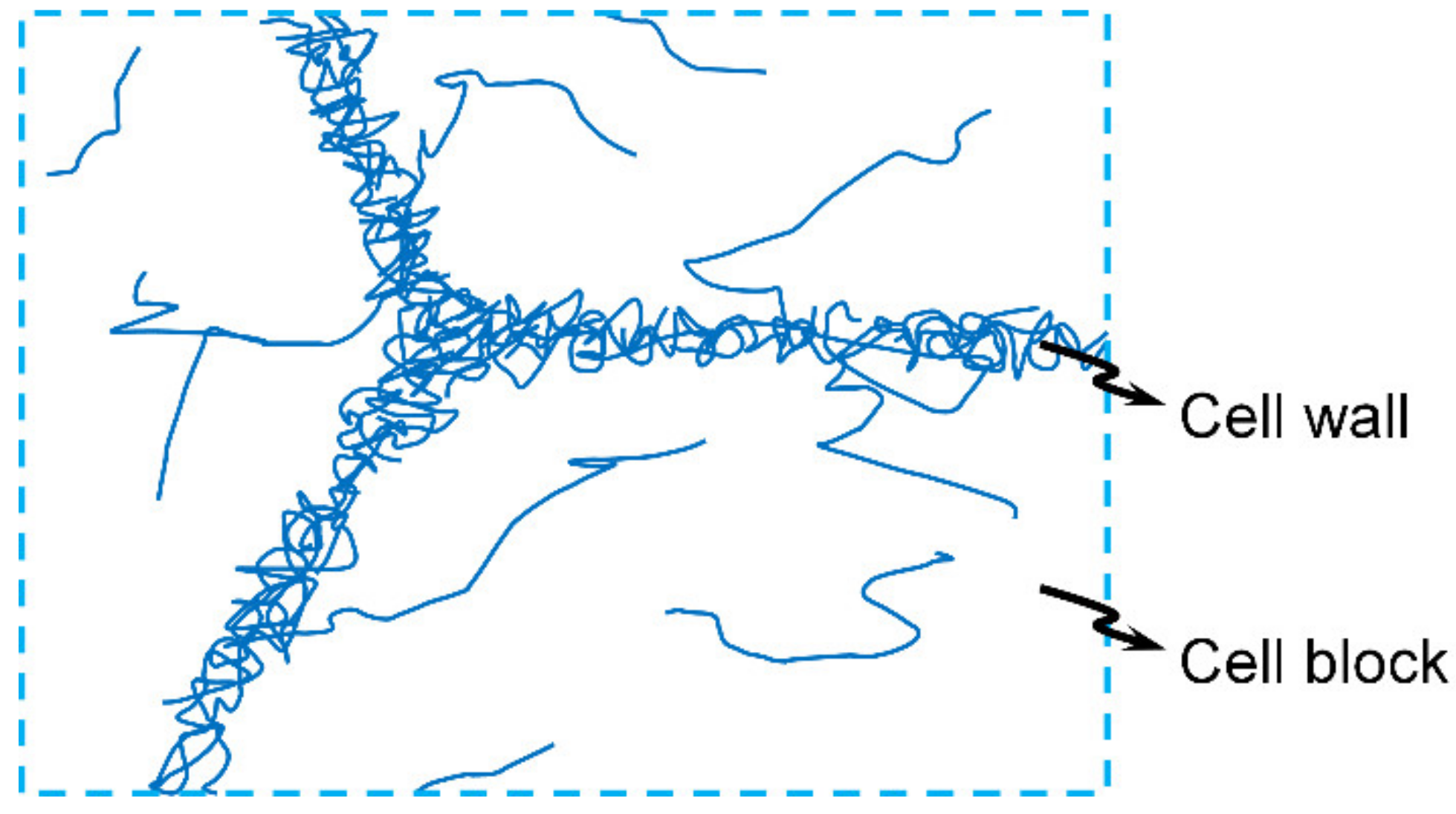
3. Mesoscale Structures and Relevant Processes
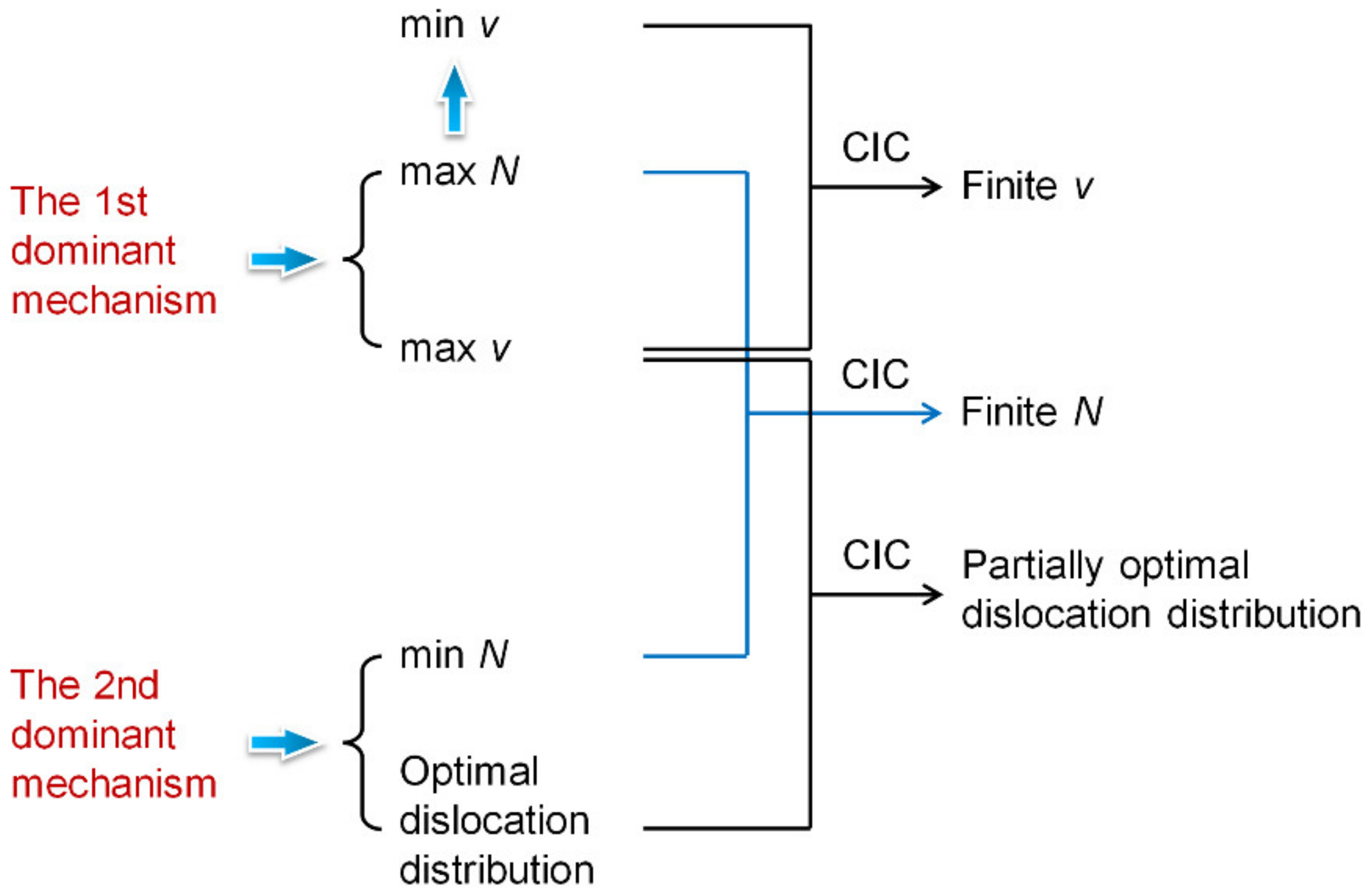
4. Dominant Mechanisms and Their Compromise in Competition
5. Applications to Constitutive Models
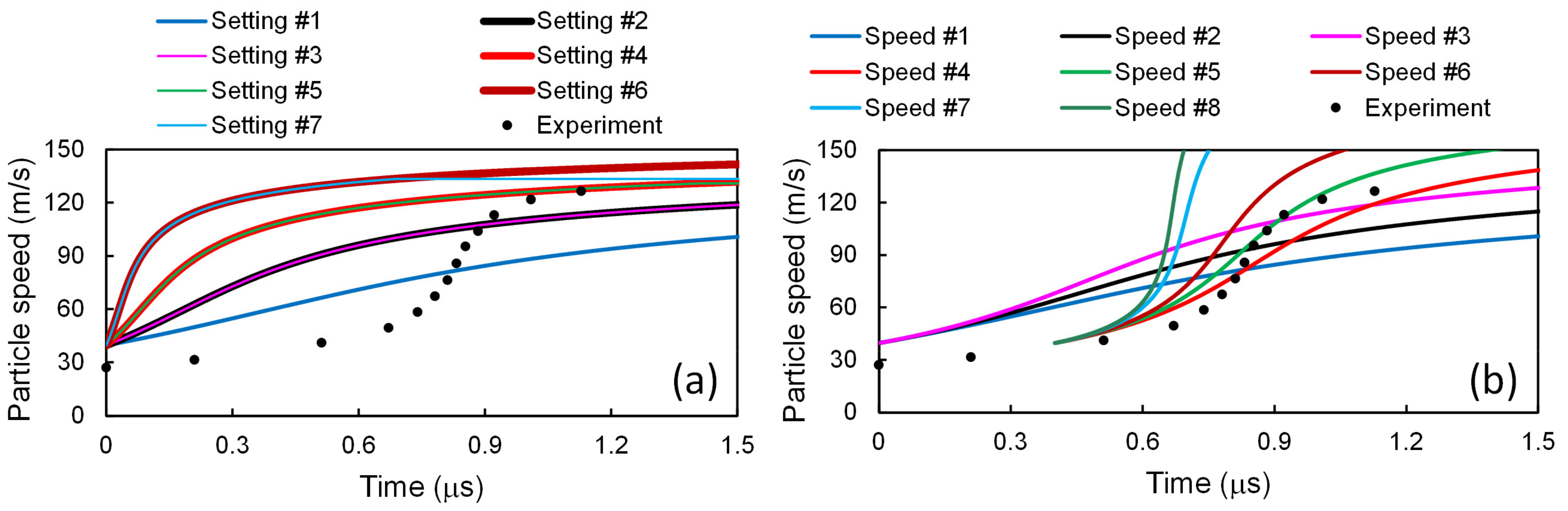
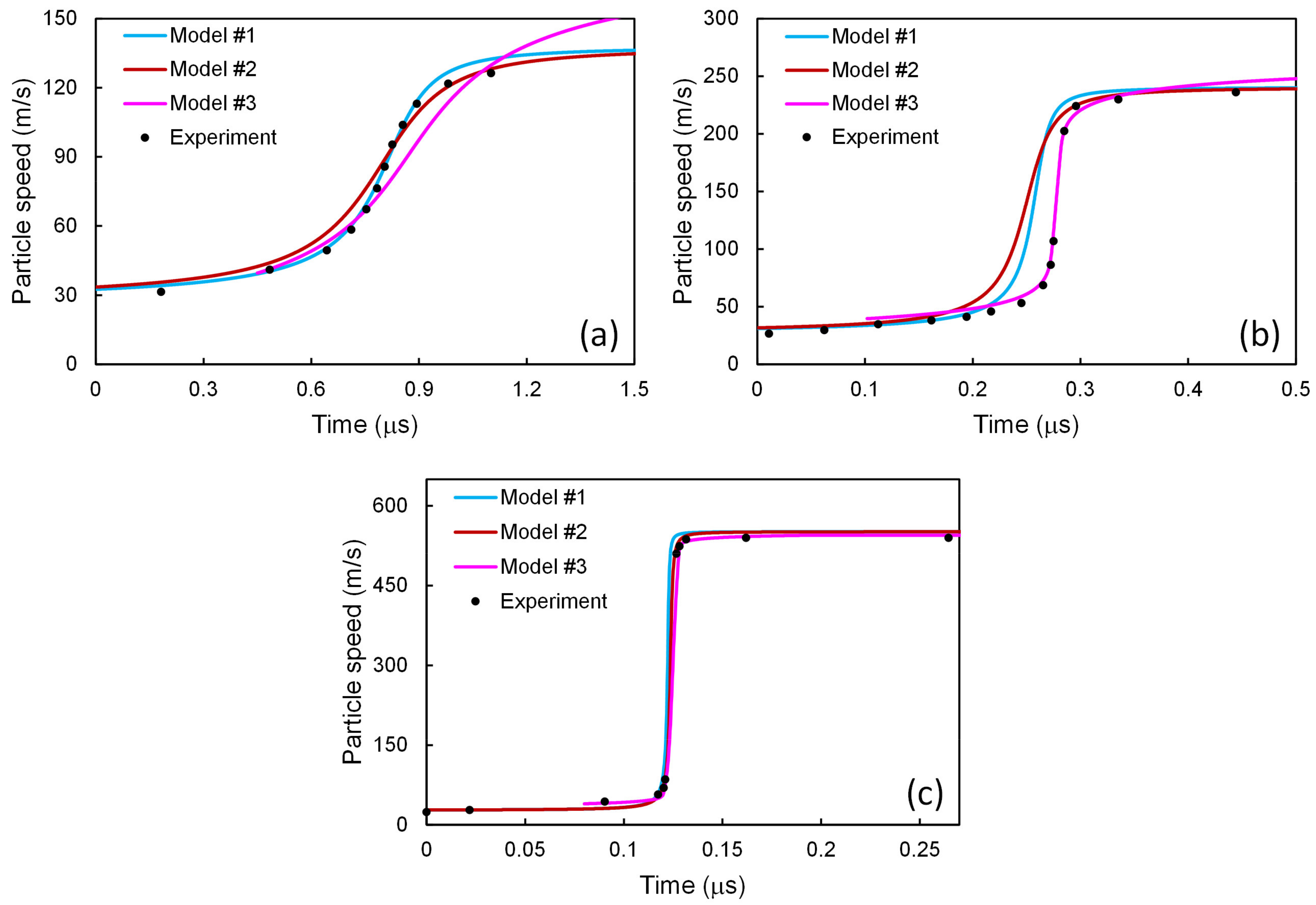
5.1. Application to Model #1
5.2. Application to Model #2
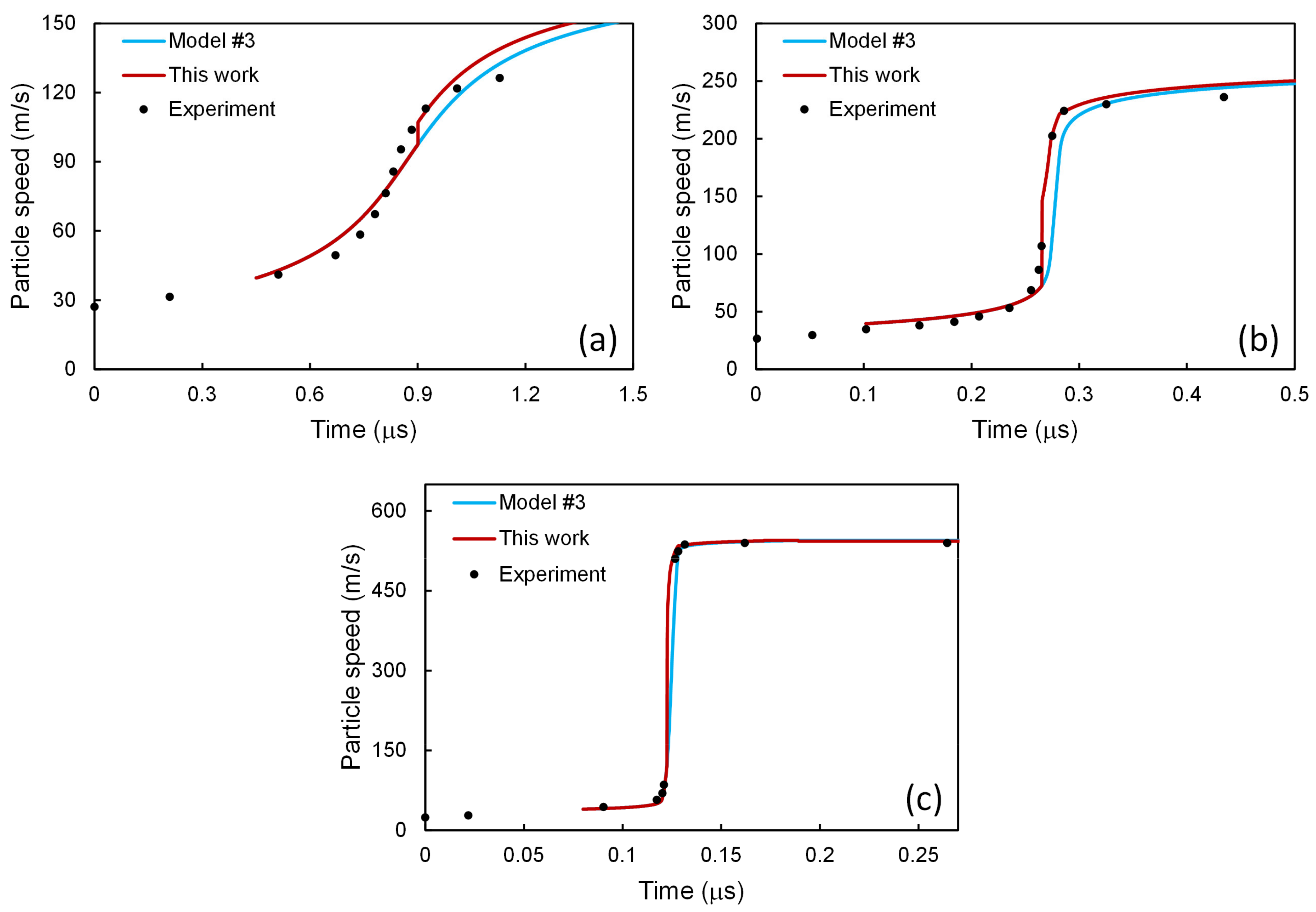
5.3. Application to Model #3
5.4. Summary
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vogler, T.J. On measuring the strength of metals at ultrahigh strain rates. J. Appl. Phys. 2009, 106, 053530. [Google Scholar] [CrossRef]
- Austin, R.A.; McDowell, D.L. A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates. Int. J. Plast. 2011, 27, 1–24. [Google Scholar] [CrossRef]
- Brown, J.L.; Alexander, C.S.; Asay, J.R.; Vogler, T.J.; Dolan, D.H.; Belof, J.L. Flow strength of tantalum under ramp compression to 250 GPa. J. Appl. Phys. 2014, 115, 043530. [Google Scholar] [CrossRef]
- Austin, R.A.; McDowell, D.L. Parameterization of a rate-dependent model of shock-induced plasticity for copper, nickel, and aluminum. Int. J. Plast. 2012, 32–33, 134–154. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strain, high strain rates and high temperatures. In: Proceedings of the 7th international symposium on ballistics. Hague 1983, 19–21, 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Steinberg, D.J.; Guinan, M.W. Constitutive Relations for the KOSPALL Code; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1973. [Google Scholar]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef] [Green Version]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef] [Green Version]
- Zerilli, F.J.; Armstrong, R.W. Description of tantalum deformation behavior by dislocation mechanics based constitutive relations. J. Appl. Phys. 1990, 68, 1580–1591. [Google Scholar] [CrossRef]
- Klepaczko, J. Thermally activated flow and strain rate history effects for some polycrystalline f.c.c. metals. Mater. Sci. Eng. 1975, 18, 121–135. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Kocks, U.F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Preston, D.L.; Tonks, D.L.; Wallace, D.C. Model of plastic deformation for extreme loading condtions. J. Appl. Phys. 2003, 93, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Barton, N.R.; Bernier, J.V.; Becker, R.; Arsenlis, A.; Cavallo, R.; Marian, J.; Rhee, M.; Park, H.-S.; Remington, B.A.; Olson, R.T. A multiscale strength model for extreme loading conditions. J. Appl. Phys. 2011, 109, 073501. [Google Scholar] [CrossRef]
- Sandfeld, S.; Hochrainer, T.; Zaiser, M.; Gumbsch, P. Continuum modeling of dislocation plasticity: Theory, numerical implementation, and validation by discrete dislocation simulations. J. Mater. Res. 2011, 26, 623–632. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ge, W.; Wang, W.; Yang, N.; Liu, X.; Wang, L.; He, X.; Wang, X.; Wang, J.; Kwauk, M. From Multiscale Modeling to Meso-Science: A Chemical Engineering Perspective; Springer: Berlin, Germany, 2013. [Google Scholar]
- Li, J.; Huang, W. Towards Mesoscience: The Principle of Compromise in Competition; Springer: Berlin, Germany, 2014. [Google Scholar]
- Li, J. Exploring the logic and landscape of the knowledge system: Multilevel structures, each multiscaled with complexity at the mesoscale. Engineering 2016, 2, 276–285. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Li, J.; Edwards, P.P. Mesoscience: Exploring the common principle at mesoscales. Natl. Sci. Rev. 2018, 5, 321–326. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Huang, W. From multiscale to mesoscience: Addressing mesoscales in mesoregimes of different levels. Annu. Rev. Chem. Biomol. Eng. 2018, 9, 41–60. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.L.; Li, J.; Chen, X. 110th Anniversary: Mesoscale complexity—To dodge or to confront? Ind. Eng. Chem. Res. 2019, 58, 12478–12484. [Google Scholar] [CrossRef]
- Molinari, A.; Ravichandran, G. Fundamental structure of steady plastic shock waves in metals. J. Appl. Phys. 2004, 95, 1718–1732. [Google Scholar] [CrossRef] [Green Version]
- Bader, S. Emergent physics at the mesoscale: Report from the special Kavli session at the 2012 APS March meeting. APSNews, 15 May 2012; p. 8. [Google Scholar]
- BESAC Subcommittee on Mesoscale Science. From Quanta to the Continuum: Opportunities for Mesoscale Science. A Report from the Basic Energy Sciences Advisory Committee; BESAC Subcommittee on Mesoscale Science: Washington, DC, USA, 2012. [Google Scholar]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bulatov, V.V. Probing the limits of metal plasticity with molecular dynamics simulations. Nature 2017, 550, 492–495. [Google Scholar] [CrossRef] [Green Version]
- Llorca, F. Modeling of post shock mechanical behaviour of copper in hydrocode calculations. J. Phys. IV 2006, 134, 29–35. [Google Scholar] [CrossRef]
- Bourne, N.K.; Gray, G.T., III; Millett, J.C.F. On the shock response of cubic metals. J. Appl. Phys. 2009, 106, 091301. [Google Scholar] [CrossRef]
- Bourne, N.K.; Millett, J.C.F.; Gray, G.T., III. On the shock compression of polycrystalline metals. J. Mater. Sci. 2009, 44, 3319–3343. [Google Scholar] [CrossRef]
- Roters, F.; Raabe, D.; Gottstein, G. Work hardening in heterogeneous alloys—A microstructural approach based on three internal state variables. Acta Mater. 2000, 48, 4181–4189. [Google Scholar] [CrossRef]
- Bay, B.; Hansen, N.; Hughes, D.A.; Kuhlmann-Wilsdorf, D. Evolution of FCC deformation structures in polyslip. Acta Metall. Mater. 1992, 40, 205–219. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F. A constitutive model for fcc single crystals based on dislocation densities and its application to uniaxial compression of aluminium single crystals. Acta Mater. 2004, 52, 3603–3612. [Google Scholar] [CrossRef]
- Ziegler, H. An Introduction to Thermomechanics, 1st ed.; North-Holland: New York, NY, USA, 1983. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Li, J.; Huang, W.; Chen, J.; Ge, W.; Hou, C. Mesoscience based on the EMMS principle of compromise in competition. Chem. Eng. J. 2018, 333, 327–335. [Google Scholar] [CrossRef]
- Grady, D.E. Strain-rate dependence of the effective viscosity under steady-wave shock compression. Appl. Phys. Lett. 1981, 38, 825–826. [Google Scholar] [CrossRef]
- Grady, D.E. Structured shock waves and the fourth-power law. J. Appl. Phys. 2010, 107, 013506. [Google Scholar] [CrossRef]
- Crowhurst, J.C.; Armstrong, M.R.; Knight, K.B.; Zaug, J.M.; Behymer, E.M. Invariance of the dissipative action at ultrahigh strain rates above the strong shock threshold. Phys. Rev. Lett. 2011, 107, 144302. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.C. Hidden Unity in Nature’s Law; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Kröner, E. Benefits and shortcomings of the continuous theory of dislocations. Int. J. Solids Struct. 2001, 38, 1115–1134. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Puzrin, A.M. Principles of Hyperplasticity: An Approach to Plasticity Theory Based on Thermodynamic Principles; Springer: London, UK, 2006. [Google Scholar]
- Swegle, J.W.; Grady, D.E. Shock viscosity and the prediction of shock wave rise times. J. Appl. Phys. 1985, 58, 692–701. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, J.; Huang, W.; Li, J. A direct solution to multi-objective optimization: Validation in solving the EMMS model for gas-solid fluidization. Chem. Eng. Sci. 2018, 192, 499–506. [Google Scholar] [CrossRef]
- Johnson, J.N.; Barker, L.M. Dislocation dynamics and steady plastic wave profiles in 6061-T6 aluminum. J. Appl. Phys. 1969, 40, 4321–4334. [Google Scholar] [CrossRef]


| Quantity | Definition |
|---|---|
| λ1,p | longitudinal plastic stretch |
| ξ | coordinate moving with C |
| Nm | mobile dislocation density |
| γp | plastic shear strain |
| τa | yield shear stress |
| T1 | longitudinal Piola-Kirchhoff stress |
| T2 | transverse Piola-Kirchhoff stress |
| F1 | function for elastic deformation |
| F2 | function for elastic deformation |
| ε1,e | longitudinal elastic strain |
| ε2,e | transverse elastic strain |
| A1, A2, B1, B2, D | intermediate parameters |
| A1n, A2n, B1n, B2n, Dn | intermediate parameters |
| B, G | intermediate parameters |
| up | particle speed |
| Parameter | Value | Unit | Definition |
|---|---|---|---|
| ρ0 | 2703 | kg/m3 | initial density |
| b | 2.86 × 10−10 | m | Burgers’ vector magnitude |
| a1 | 0 | m2/s2 | elastic constant |
| a1n | 0 | m2/s2 | elastic constant |
| a2 | 2.028 × 107 | m2/s2 | elastic constant |
| a3 | −2.044 × 107 | m2/s2 | elastic constant |
| a4 | −6.64 × 107 | m2/s2 | elastic constant |
| a5 | 1.575 × 108 | m2/s2 | elastic constant |
| a6 | −1.428 × 108 | m2/s2 | elastic constant |
| c1 | 0.168 | m/s | fitting parameter |
| 1.6 | MPa | fitting parameter | |
| M | 1.78 | inverse of the strain rate sensitivity | |
| τa0 | 120 | MPa | initial back stress |
| γ0 | 0.52 | reference strain | |
| n | 1.55 | hardening parameter | |
| Nm,HEL,w | 8.18 × 1012 | 1/m2 | initial mobile dislocation density in the cell wall |
| Nm,HEL,b | 8.00 × 1012 | 1/m2 | initial mobile dislocation density in the cell block |
| αb | 3.5 × 105 | 1/m | breeding coefficient |
| αt | 0 | trapping coefficient | |
| NHEL,w | 8.18 × 1012 | 1/m2 | initial total dislocation density in the cell wall |
| NHEL,b | 8.00 × 1012 | 1/m2 | initial total dislocation density in the cell block |
| λ1,HEL | 0.995758 | HEL longitudinal stretch | |
| T1,HEL | −475 | MPa | HEL longitudinal Piola-Kirchhoff stress |
| C | 5457.3146 | m/s | shock wave speed at σ1,– = 2.1 GPa |
| 5600.2774 | shock wave speed at σ1,– = 3.7 GPa | ||
| 6018.3672 | shock wave speed at σ1,– = 9.0 GPa | ||
| up,HEL | 27.295879 | m/s | HEL particle speed |
| Parameter | Value | Unit | Definition |
|---|---|---|---|
| αhet | 7.4 × 1013 | 1/m2 | heterogeneous nucleation coefficient |
| αann | 0.5 | annihilation coefficient | |
| αdis | 0.015 | network trapping coefficient | |
| αp | 0.02 | precipitate trapping coefficient | |
| dp | 1.0 × 10−8 | m | precipitate size |
| λp | 7.0 × 10−8 | m | precipitate spacing |
| d | 4.0 × 10−5 | m | mean grain size |
| m | 1.0 | shape constant | |
| fHEL | 1.0 | initial fraction of mobile dislocations | |
| δ | 3.5 × 105 | 1/m | multiplication coefficient |
| τa | 106 | MPa | lower-bound shear stress for heterogeneous nucleation |
| τb | 920 | MPa | upper-bound shear stress for heterogeneous nucleation |
| Parameter | Value | Unit | Definition |
|---|---|---|---|
| k | 1.380649 × 10−23 | J/K | Boltzmann’s constant |
| χ | 0.05 | scaling parameter | |
| νD | 8.0 × 1012 | 1/s | Debye’s frequency |
| g0 | 0.65 | thermal activation parameter | |
| q | 0.5 | thermal activation parameter | |
| r | 2.0 | thermal activation parameter | |
| μ0 | 27.627 | GPa | initial shear modulus |
| 1/μ0 (∂μ/∂p) | 65 × 10−3 | 1/GPa | pressure coefficient of shear modulus |
| 1/μ0 (∂μ/∂θ) | −0.62 × 10−3 | 1/K | temperature coefficient of shear modulus |
| θ0 | 300.0 | K | initial temperature |
| p0 | 0.0 | Pa | initial pressure |
| z | 4.0 | number of atoms per unit cell | |
| α0 | 1.0 | dislocation interaction coefficient | |
| β0 | 0.0 | long-range interaction factor | |
| βp | 0.84 | Orowan looping factor | |
| C | 5457.3146 | m/s | shock wave speed at σ1,– = 2.1 GPa |
| 5606.2939 | shock wave speed at σ1,– = 3.7 GPa | ||
| 6011.1869 | shock wave speed at σ1,– = 9.0 GPa | ||
| c0 | 5350.0 | m/s | material constant |
| s1 | 1.34 | material constant | |
| N+,w | 2.0 × 1014 | 1/m2 | initial total dislocation density in the cell wall |
| N+,b | 1.9 × 1014 | 1/m2 | initial total dislocation density in the cell block |
| f+ | 0.006 | initial fraction of mobile dislocations | |
| λ1,+ | 0.993711 | initial longitudinal stretch | |
| T1,+ | −675 | MPa | HEL longitudinal Piola-Kirchhoff stress |
| λ1,p,+ | 0.9994002 | initial longitudinal plastic stretch | |
| up,+ | 39.629214 | m/s | initial particle speed |
| b1 | −593 | K | thermomechanical parameter |
| b2 | −130 | K | thermomechanical parameter |
| b3 | 1350 | K | thermomechanical parameter |
| β | 1.0 | Taylor-Quinney coefficient | |
| cη | 880.0 | J/(g K) | specific heat at constant configuration |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.L.; Zhang, L.; Chen, K.; Lu, G. Mesoscale Mechanisms in Viscoplastic Deformation of Metals and Their Applications to Constitutive Models. Materials 2021, 14, 4667. https://doi.org/10.3390/ma14164667
Huang WL, Zhang L, Chen K, Lu G. Mesoscale Mechanisms in Viscoplastic Deformation of Metals and Their Applications to Constitutive Models. Materials. 2021; 14(16):4667. https://doi.org/10.3390/ma14164667
Chicago/Turabian StyleHuang, Wen Lai, Lin Zhang, Kaiguo Chen, and Guo Lu. 2021. "Mesoscale Mechanisms in Viscoplastic Deformation of Metals and Their Applications to Constitutive Models" Materials 14, no. 16: 4667. https://doi.org/10.3390/ma14164667






