Practical Use of Composite Materials Used in Military Aircraft
Abstract
1. Introduction
2. Description of the Tensile Test Stand, in Accordance with ASTM Standard
2.1. Research Description
- A series—Dialead K63712 modular fabric;
- B series—Roving IMS65 (Intermediate Modulus carbon fiber);
- C series—IMS65 CTLX biaxial fabric;
- D series—symmetrical Interglas 02037 fabric;
- E series—modular fabric IMS65.
2.2. Microstructure of Composite Materials
2.2.1. Description of the Test Stand
2.2.2. Analysis of the Obtained Results
2.3. Composite Laminate Hardness Testing
2.3.1. Description of the Measuring Station
- indication range: 0–100 Sh;
- pressure range within 1.961–490.3 N;
- load accuracy ±1%;
- measuring range: 20–90 Sh;
- load time 5–99 s (every 1s);
- mounting of interchangeable heads;
- resolution equal to: 0.1 or 0.5 Sh;
- magnification equal to 100×, 200×;
- maximum object height 210 mm;
- central unit with software.
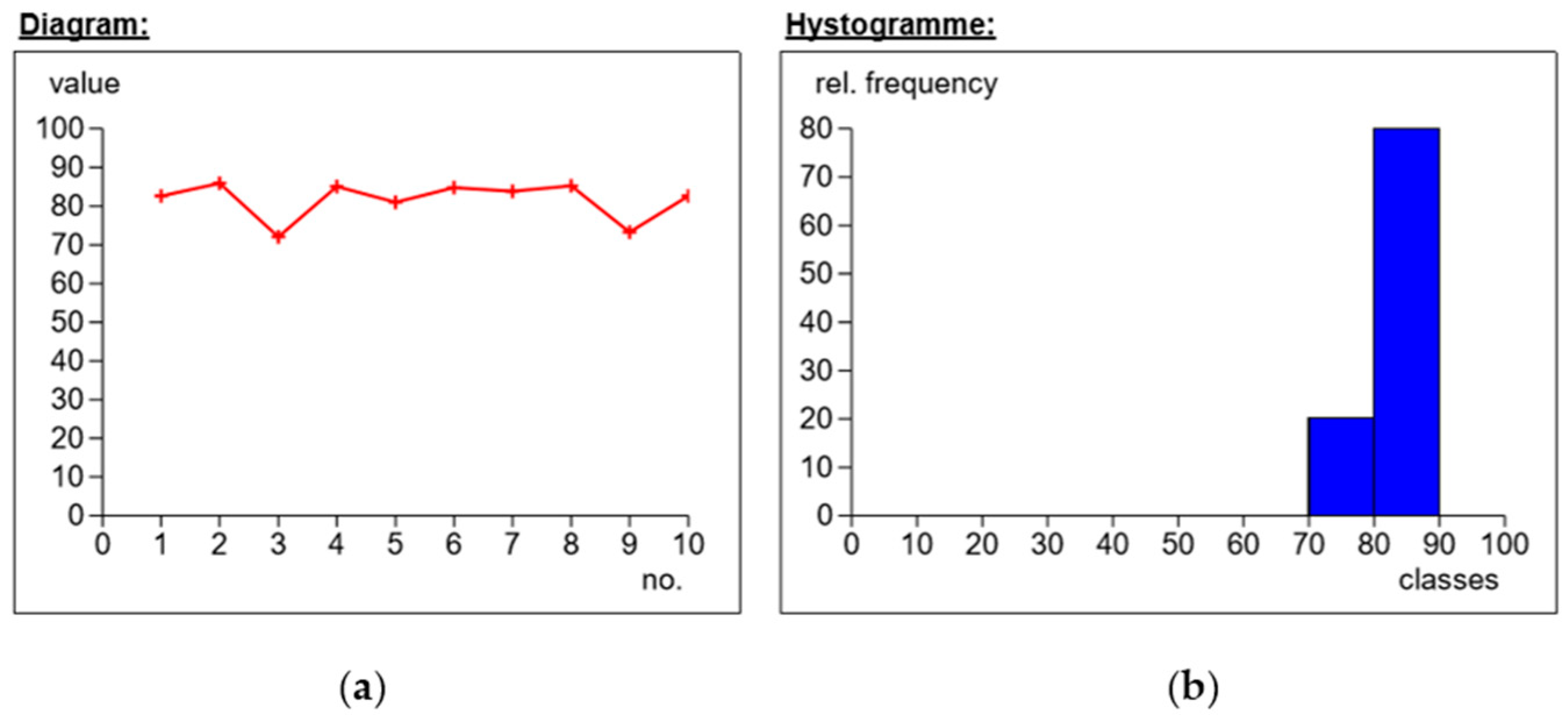
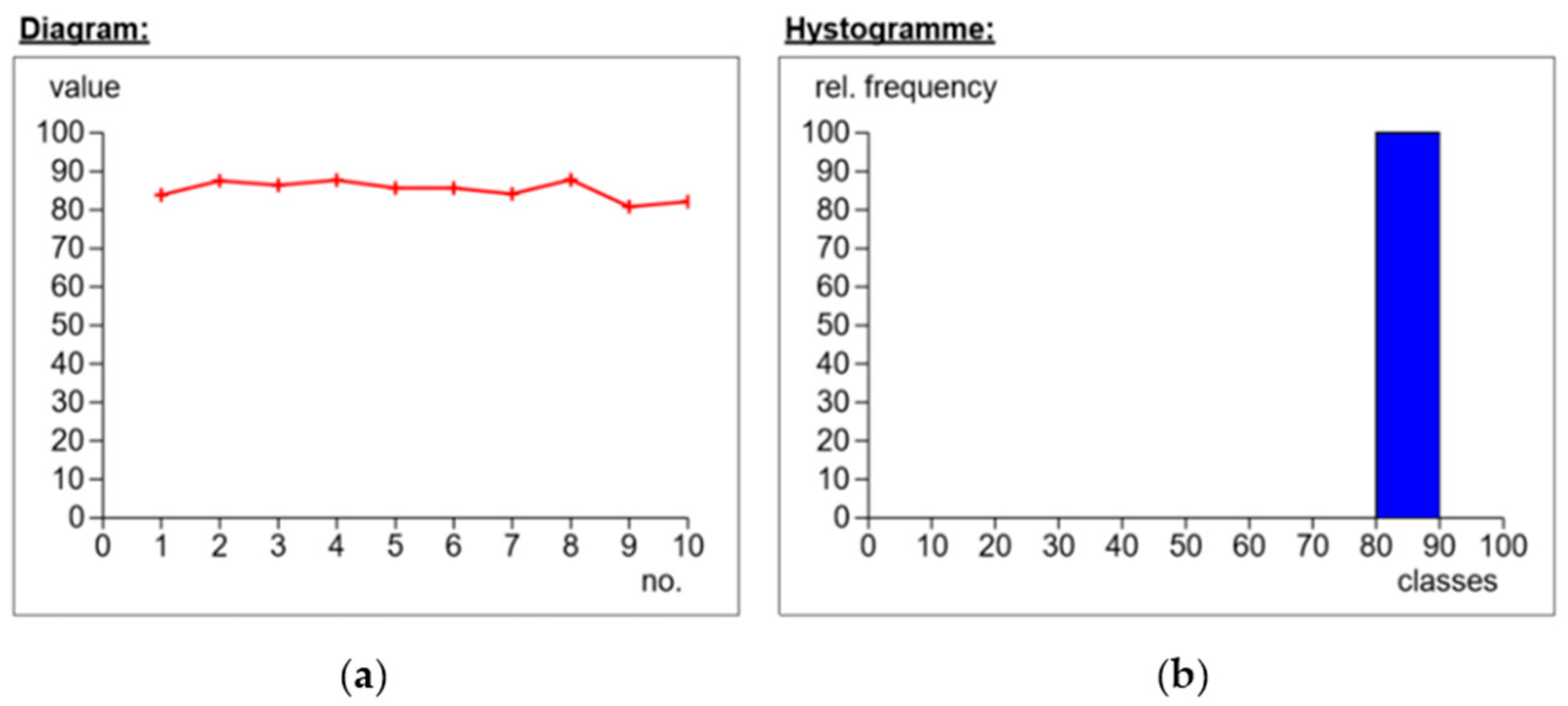
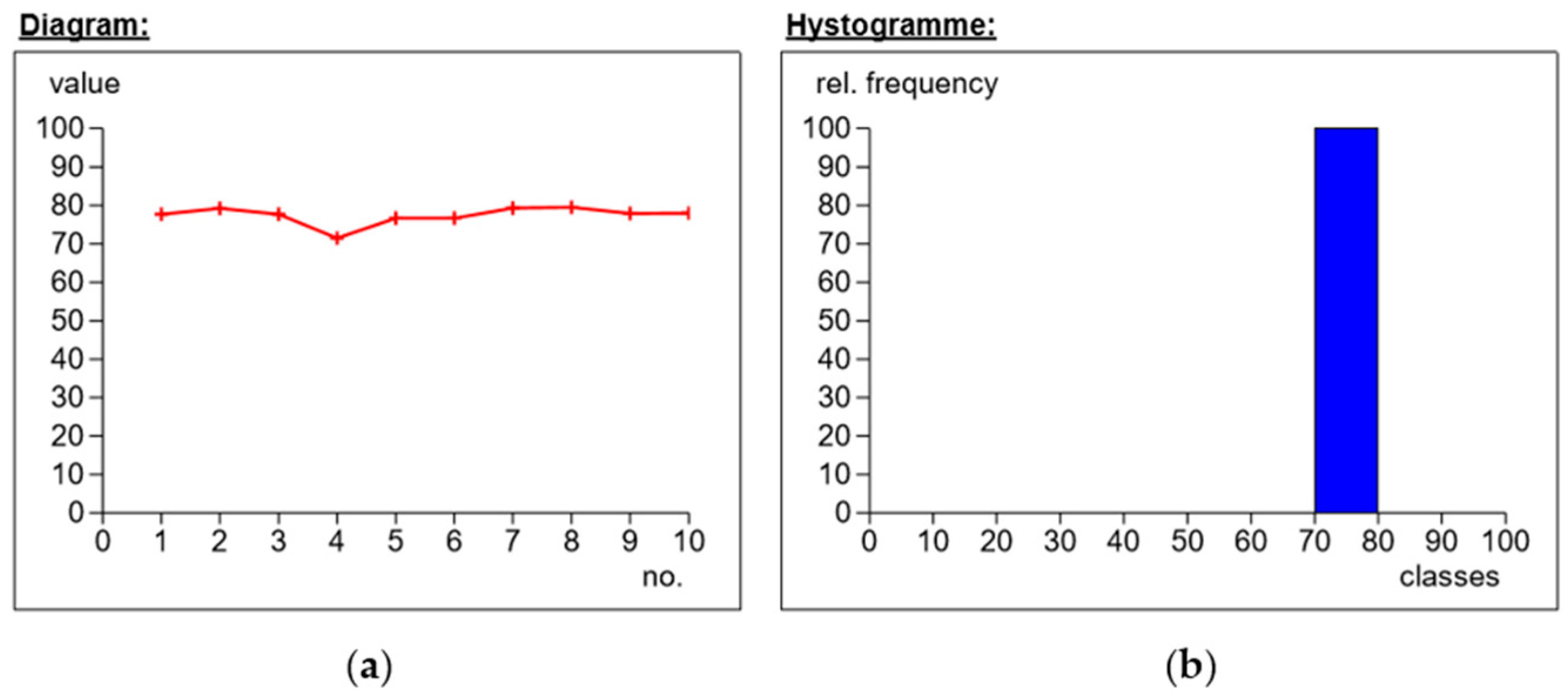
2.3.2. The Course of the Study and the Analysis of Measurements
2.4. Tensile Test Stand
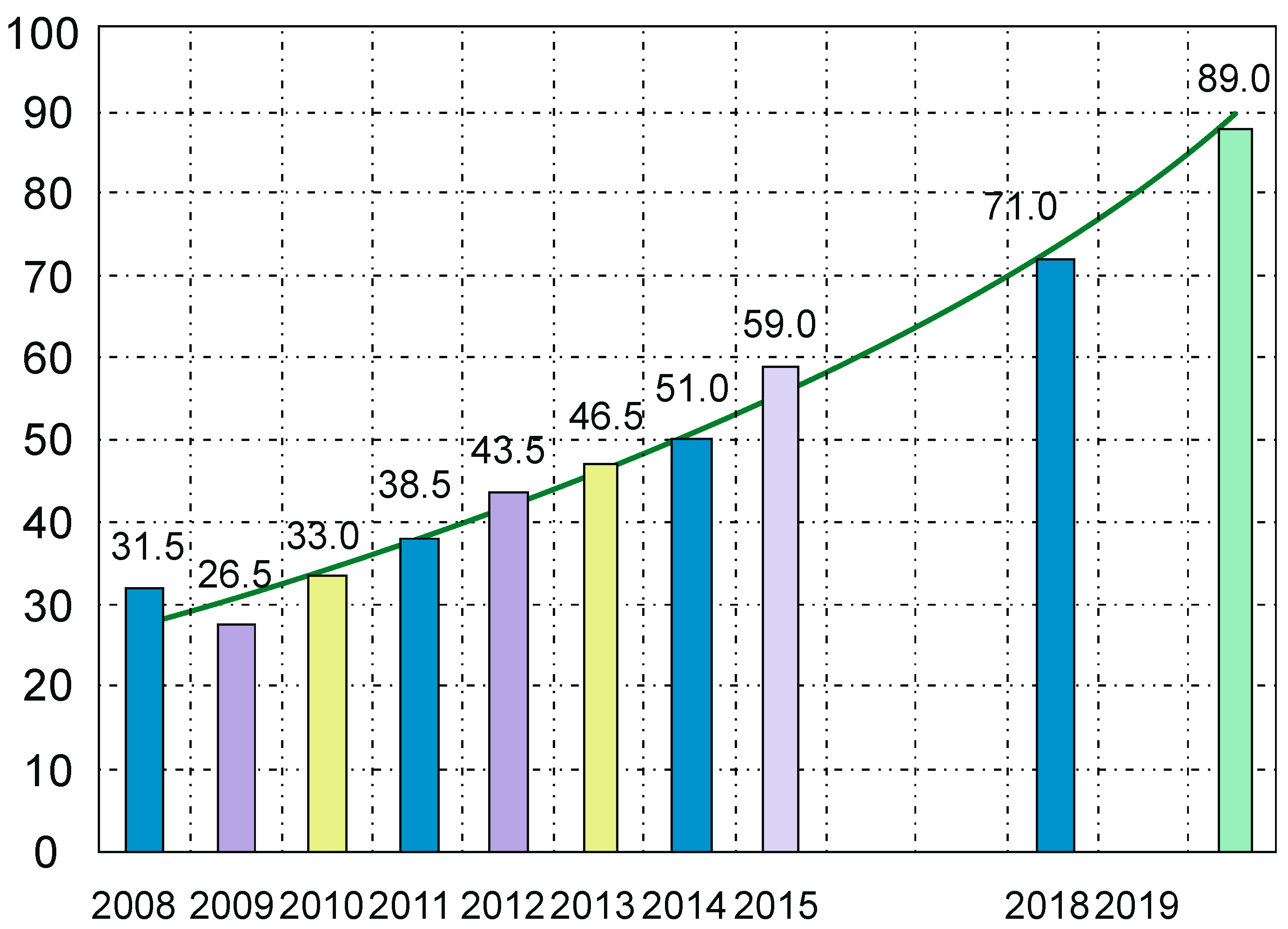
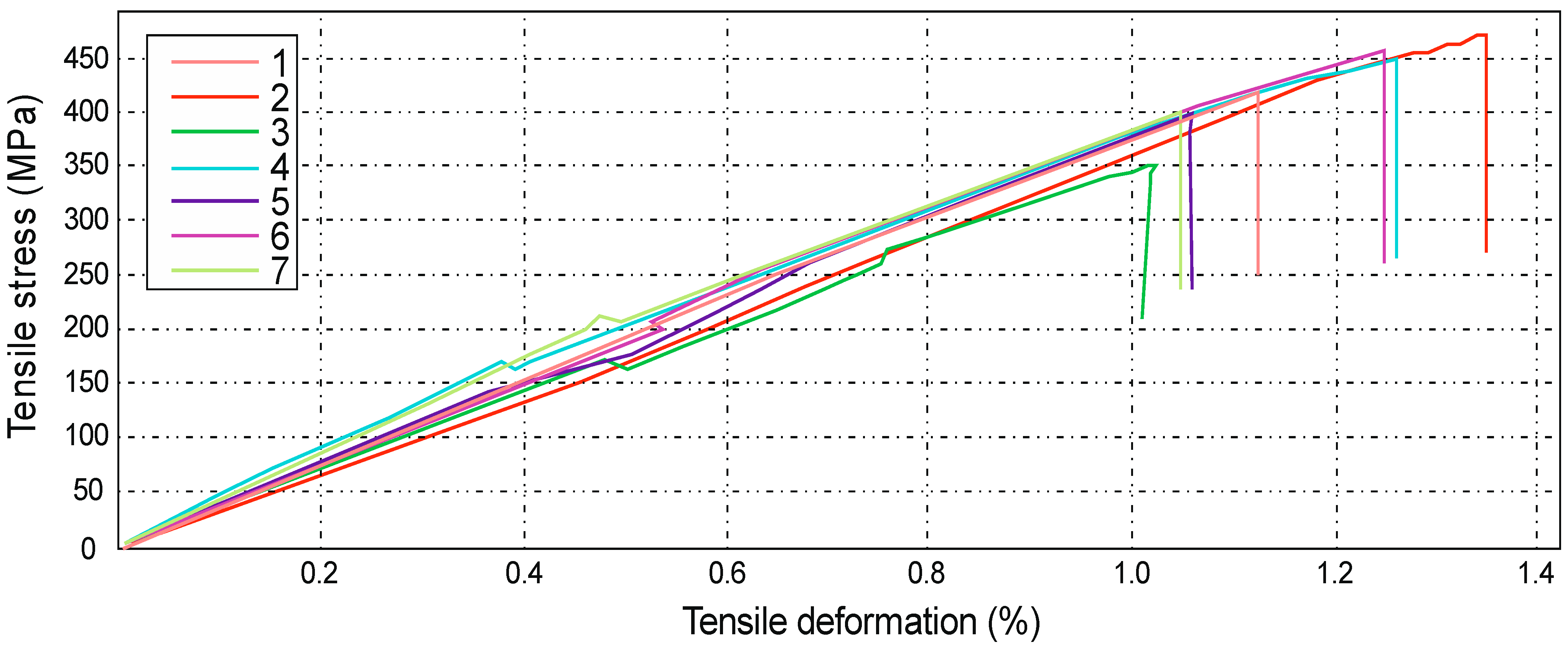
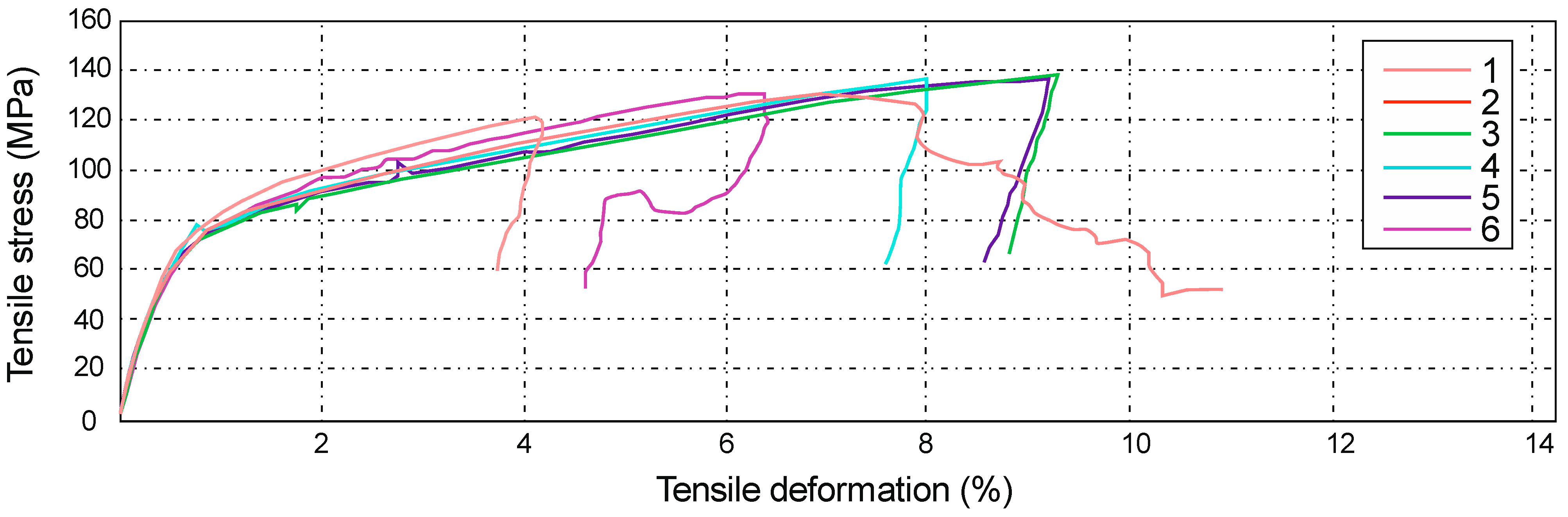
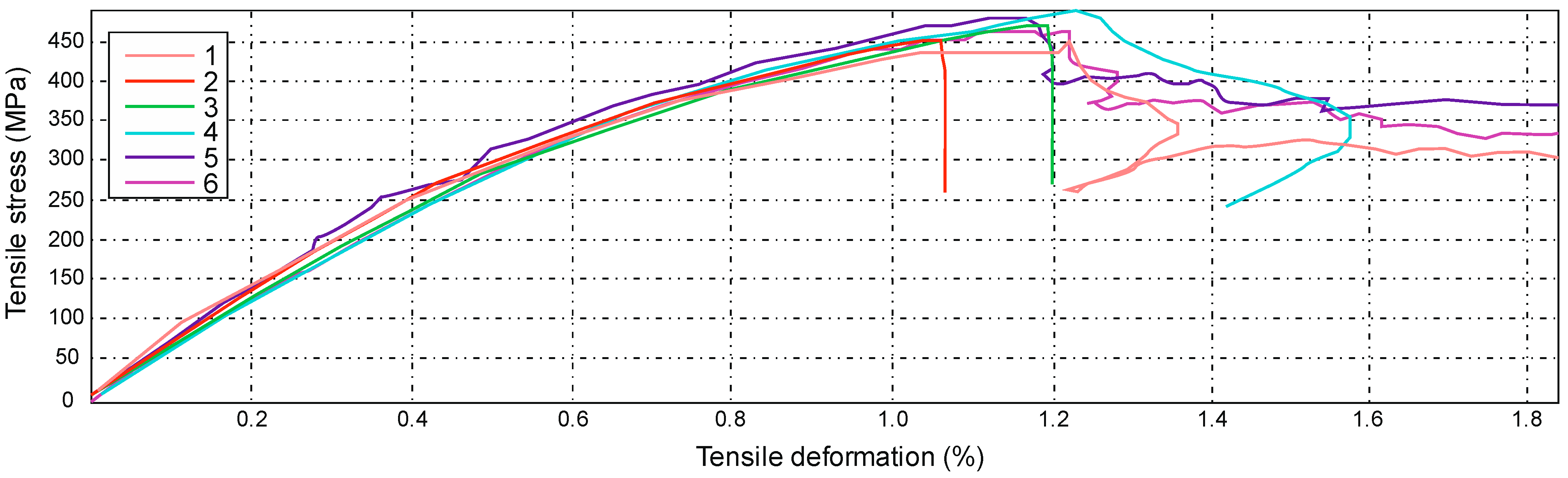
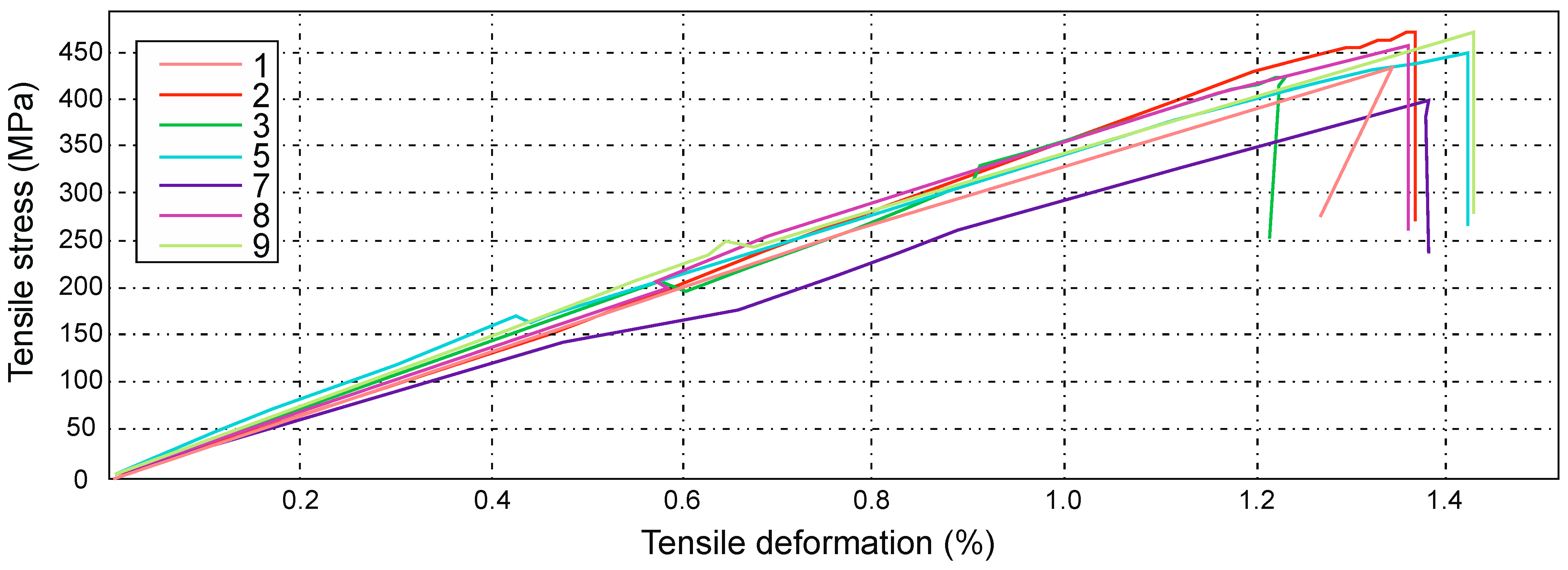
2.5. Research Results and Analysis of the Results
- The lowest value, in terms of tensile strength, was obtained for series B, which was Rm = 128 ± 11 MPa; the composite materials for this series were reinforced with a modular fabric of Dialead K63712 type with MGS L285/H285 warp, with 0/90° orientation.
- In the case of testing the strength of the E series composite material, which determined its highest averaged value, the obtained results significantly differed from the results from the other series. For example, with regard to the Roving IMS65 reinforced composite material, its value was Rm = 1450 ± 70 MPa.
- The tested sample No. 5 of series B (Table 3), which is a laminate of the Roving IMS65 reinforced composite material, with the 0/90° orientation, was characterized by the highest elongation (16.53 mm).
- The tested sample No. 2 of series E (Table 9), which was a laminate of a composite material reinforced with the IMS65 modular fabric, with the 0/90° orientation, was characterized by the lowest elongation, and its tensile strain was 0.798%.
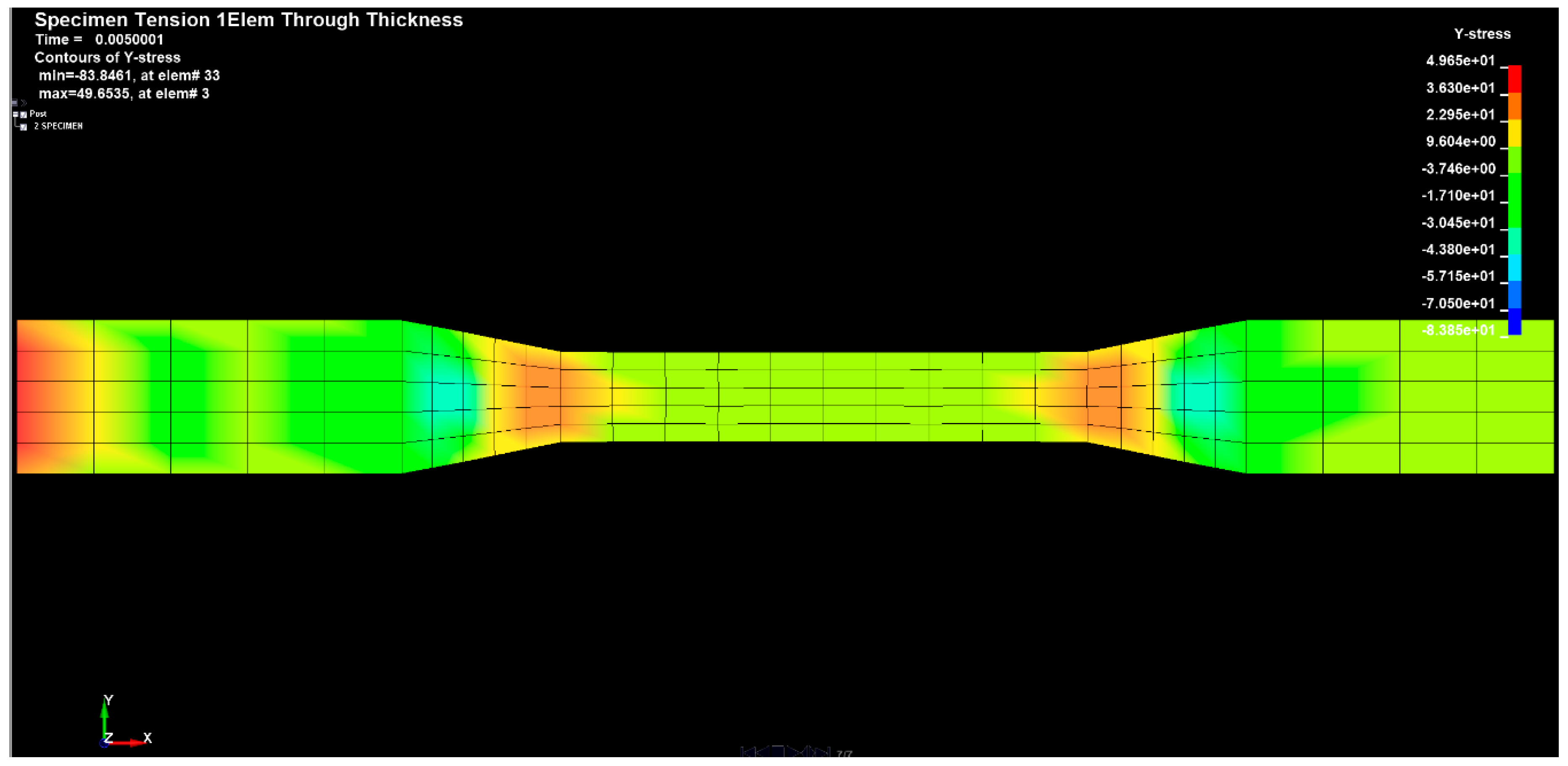
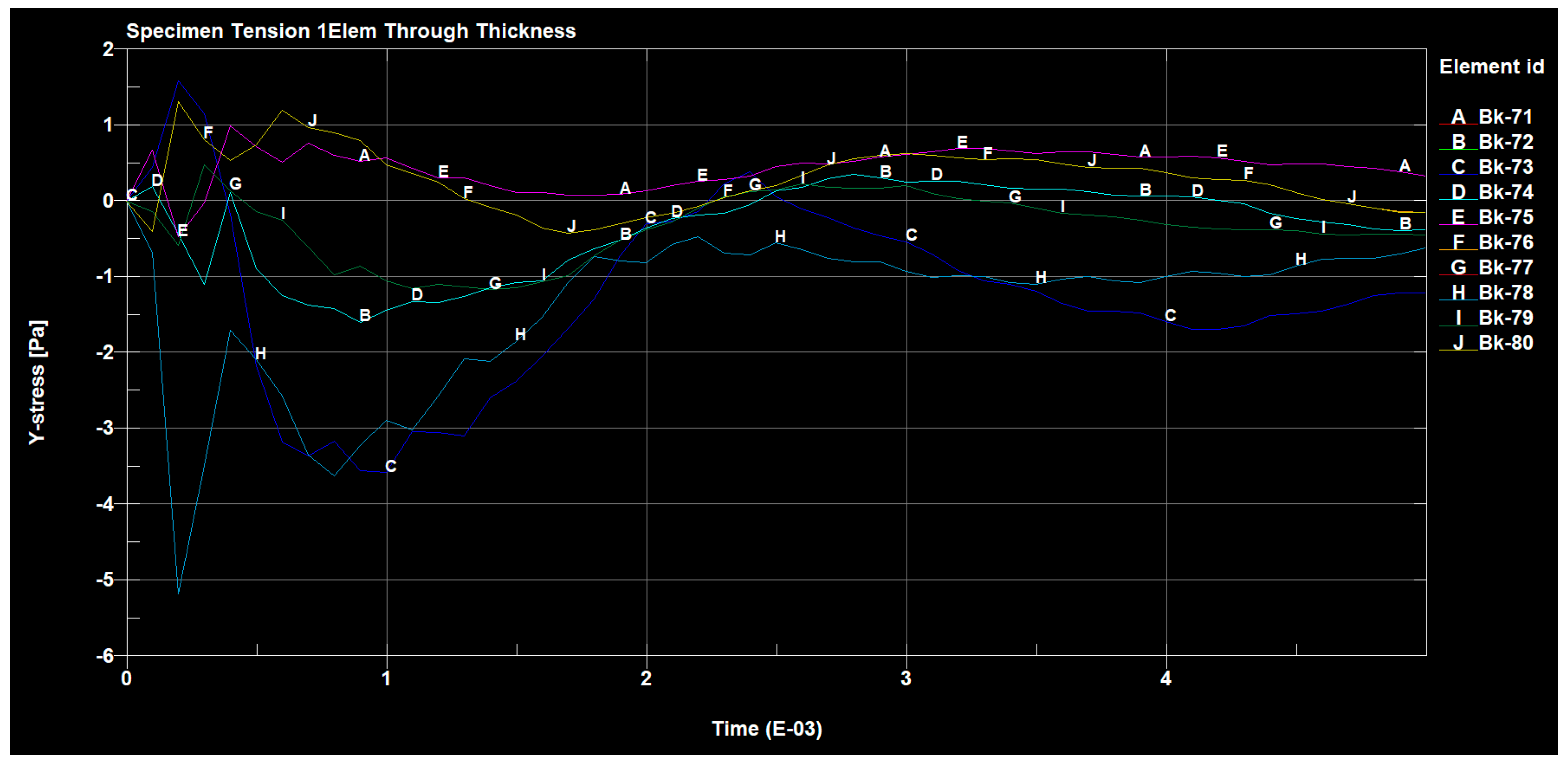
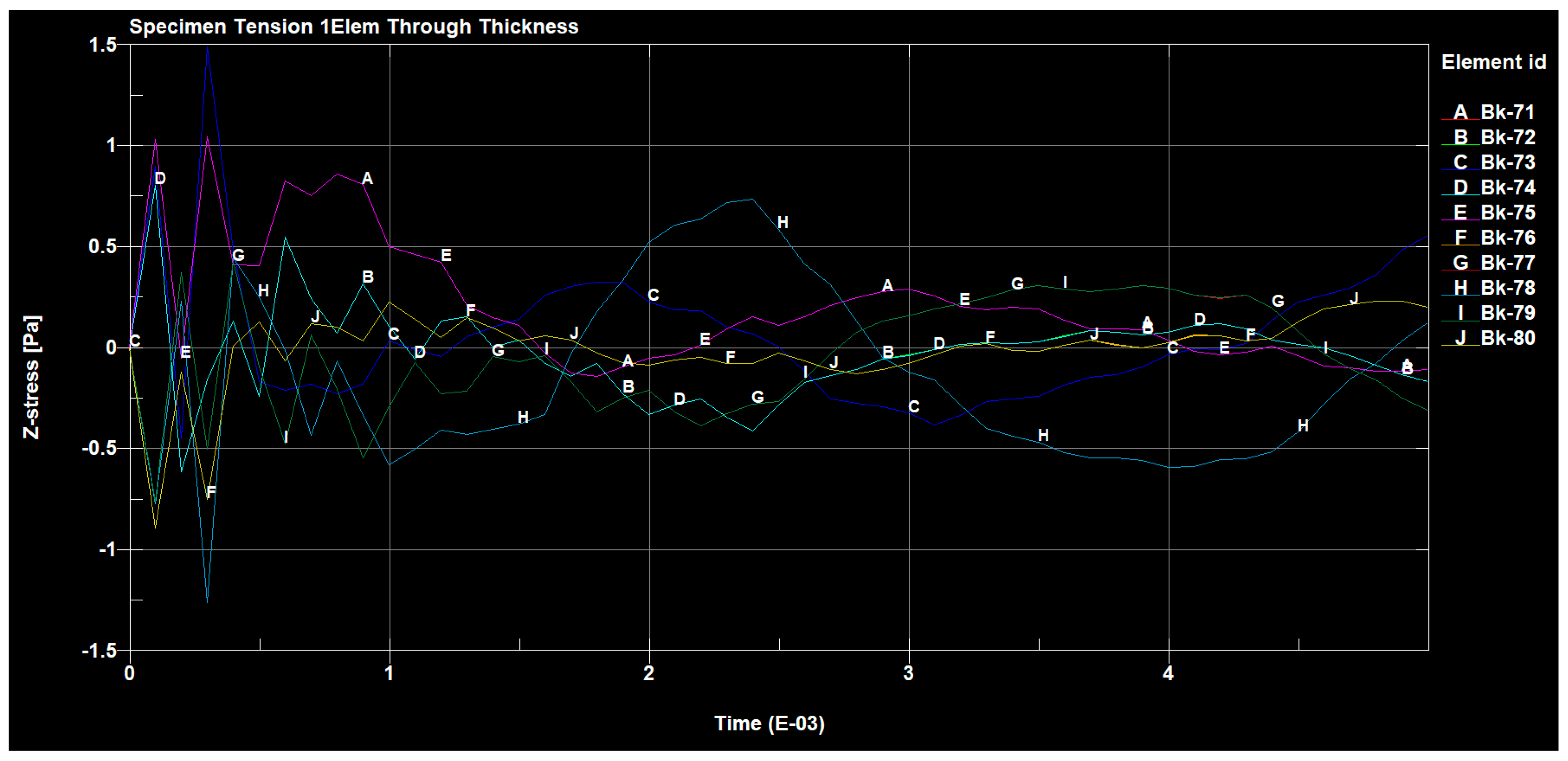
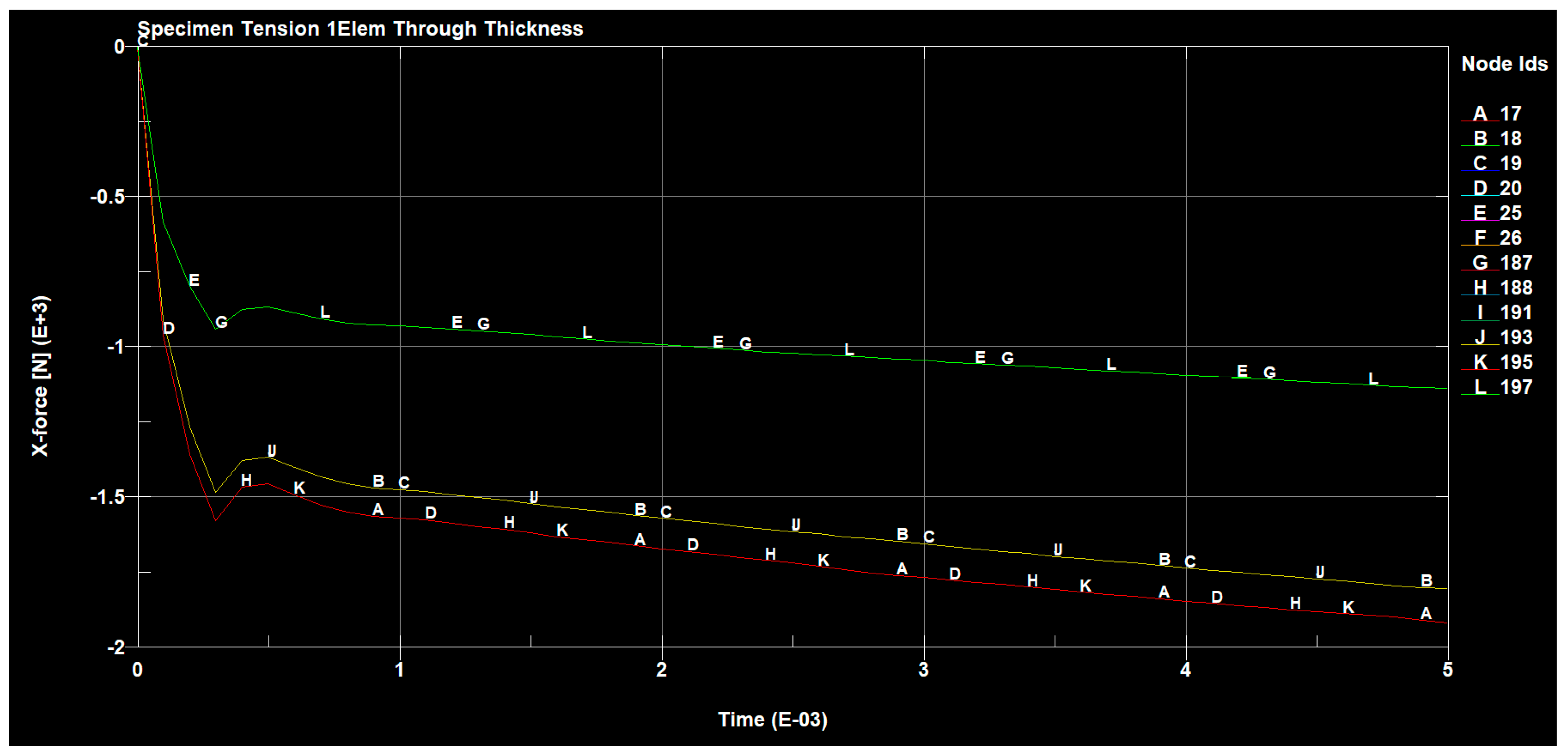
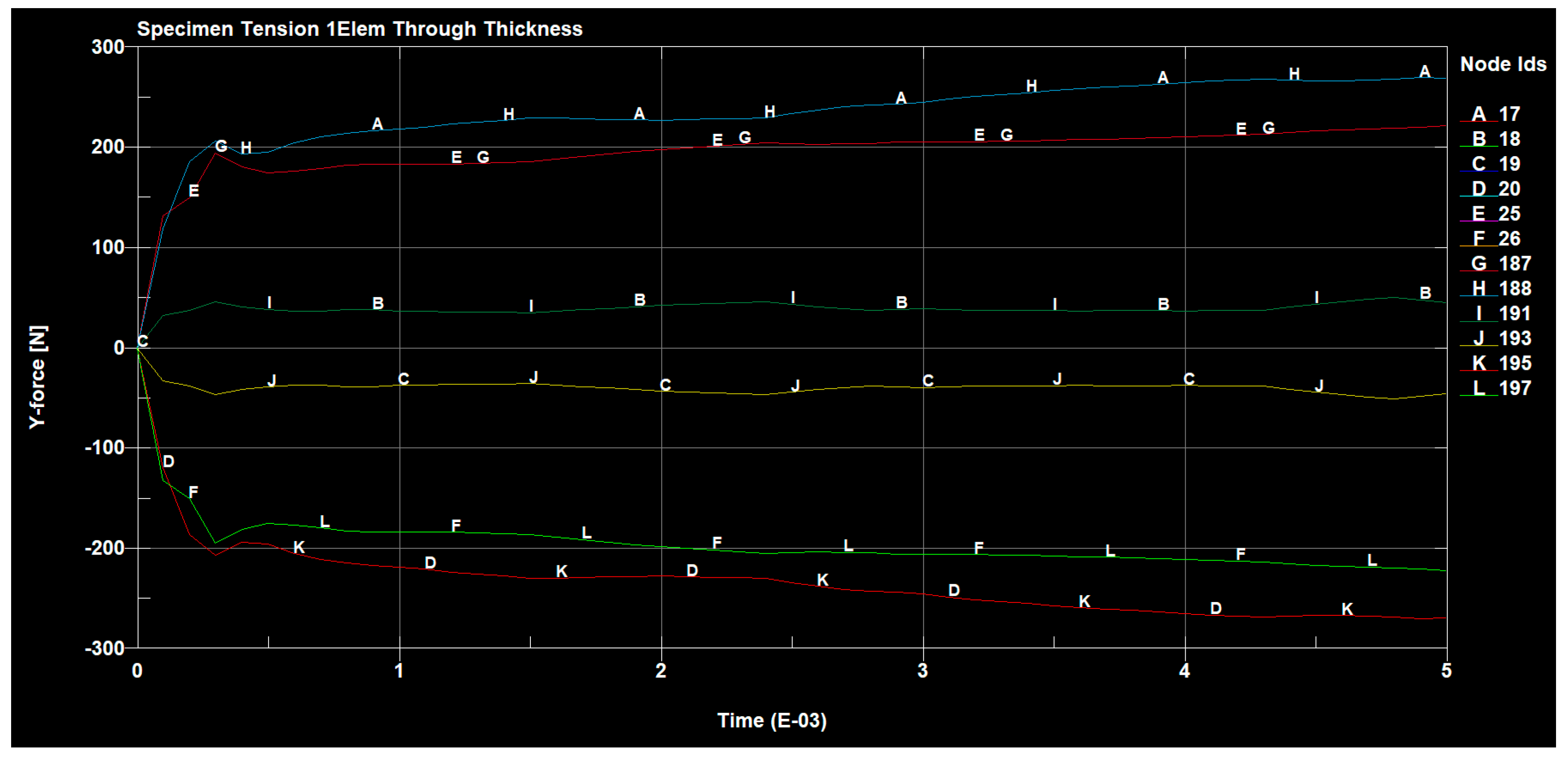
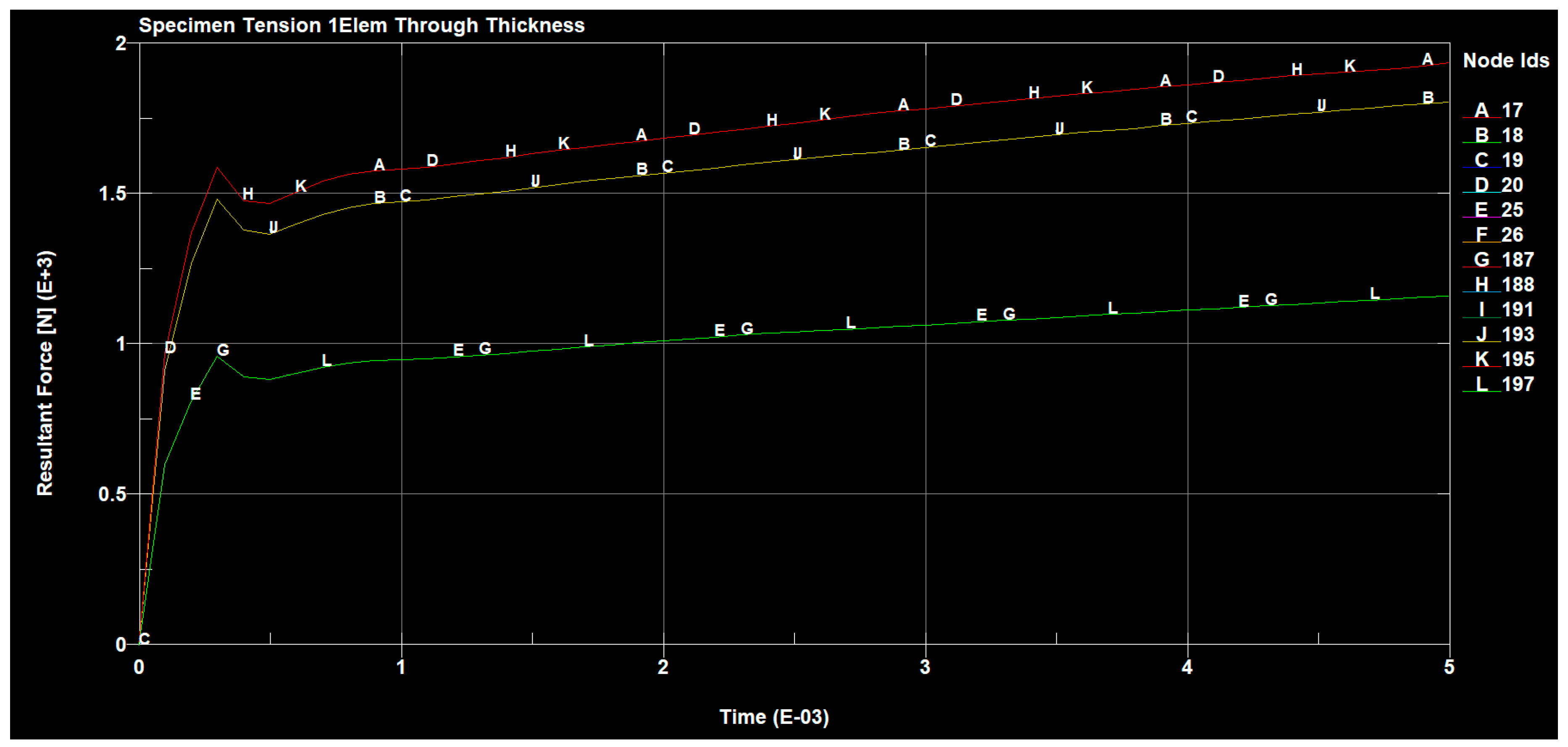
3. The Results of Research Carried out in an Environment of ANSYS and SolidWorks
3.1. Determination of the Interlayer Shear Strength of a Composite
3.2. Tensile Test of the Composite GLARE 3 Type
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bilyeu, B.; Brostow, W.; Menard, K.P. Epoxy thermosets and their applications. III. Kinetic equations and models. J. Mater. 2001, 23, 189–204. [Google Scholar]
- Rathod, V.T.; Kumar, J.S.; Jain, A. Polymer and ceramic nanocomposites for aerospace applications. Appl. Nanosci. 2017, 7, 519–548. [Google Scholar] [CrossRef]
- Kuczmaszewski, J.; Piesko, P.; Zawada-Michałowska, M. A Comparative Analysis of the Impact of CNC Miller Programming on Machining Effects. Multidiscip. Asp. Prod. Eng. 2018, 1, 161–167. [Google Scholar] [CrossRef]
- Kuczmaszewski, J.; Zaleski, K.; Matuszak, J.; Madry, J. Testing Geometric Precision and Surface Roughness of Titanium Alloy Thin-Walled Elements Processed with Milling. Lect. Notes Mech. Eng. 2019, 95–106. [Google Scholar] [CrossRef]
- Gontarz, A.; Dziubinska, A.; Winiarski, G.; Tofil, A. New Technologies for Producing Bicycle Hub Forging. In Proceedings of the MATEC Web of Conferences, the 2nd International Conference on Mechanical, System and Control Engineering (ICMSC 2018), Berlin, Germany, 17–20 August 2018; Volume 220, p. 02003. [Google Scholar] [CrossRef]
- Zagórski, I.; Korpysa, J. Surface quality assessment after milling AZ91D magnesium alloy using PCD tool. Materials 2020, 13, 617. [Google Scholar] [CrossRef]
- Setlak, L.; Kowalik, R. Examination of Multi-Pulse Rectifiers of PES Systems Used on Airplanes Compliant with the Concept of Electrified Aircraft. Appl. Sci. 2019, 9, 1520. [Google Scholar] [CrossRef]
- Youssef, A.A.; Budzynski, P.; Filiks, J.; Surowiec, Z. Improvement of tribological properties of aluminum by nitrogen implantation. Vacuum 2005, 78, 599–603. [Google Scholar] [CrossRef]
- Alsaadi, M.; Erklig, A.; Albu-khaleefah, K. Effect of Pistachio Shell Particle Content on the Mechanical Properties of Polymer Composite. Arab. J. Sci. Eng. 2018, 43, 4689–4696. [Google Scholar] [CrossRef]
- Ming-Sung, W.; Bo Cheng, J.; Xin, L.; Nutt, S. A recyclable epoxy for composite wind turbine blades. Adv. Manuf. Polym. Compos. Sci. 2019, 5, 114–127. [Google Scholar] [CrossRef]
- Rudawska, A.; Zaleski, K.; Miturska, I.; Skoczylas, A. Effect of the application of different surface treatment methods on the strength of titanium alloy sheet adhesive lap joints. Materials 2019, 12, 4173. [Google Scholar] [CrossRef]
- Sobaszek, L.; Gola, A.; Swic, A. Creating robust schedules based on previous production processes. Actual Probl. Econ. 2014, 158, 488–495. [Google Scholar]
- Patalas-Maliszewska, J.; Sliwa, M. The Role of Knowledge Acquisition in a Company-Research Results from German and Polish Manufacturing Companies. Found. Manag. 2017, 9, 87–98. [Google Scholar] [CrossRef]
- Kosicka, E.; Gola, A.; Pawlak, J. Application-based support of machine maintenance. IFAC-Pap. OnLine 2019, 52, 131–135. [Google Scholar] [CrossRef]
- Dalbehera, S.; Acharya, S.K. Impact of stacking sequence on tribological wear performance of woven jute-glass hybrid epoxy composites. Tribol. Mater. Surf. Interfaces 2015, 9, 196–201. [Google Scholar] [CrossRef]
- Bałdowska-Witos, P.; Kruszelnicka, W.; Kasner, R.; Tomporowski, A.; Flizikowski, J.; Kłos, Z.; Piotrowska, K.; Markowska, K. Application of LCA Method for Assessment of Environmental Impacts of a Polylactide (PLA) Bottle Shaping. Polymers 2020, 12, 388. [Google Scholar] [CrossRef] [PubMed]
- Debski, H.; Samborski, S. On stability and load-bearing capacity of thinwalled composite profiles subjected to eccentric compression. In Proceedings of the Advances in Engineering Materials, Structures and Systems: Innovations, Mechanics and Applications-7th International Conference on Structural Engineering, Mechanics and Computation, Cape Town, South Africa, 2–4 September 2019; pp. 831–836. [Google Scholar]
- Wolszczak, P.; Sadowski, T.; Samborski, S. On quantitative expression in fibrous composites based on an exemplary distribution of roving glass-fibers. Compos. Part B Eng. 2017, 129, 66–76. [Google Scholar] [CrossRef]
- Stănescu, M.M.; Bolcu, D. A Study of Some Mechanical Properties of a Category of Composites with a Hybrid Matrix and Natural Reinforcements. Polymers 2019, 11, 478. [Google Scholar] [CrossRef]
- Husnain, A.; Asra, T.; Amir, S.; Muhammad, F.; Muhammad, S.; Iqra, A.R.; Ayesha, A.; Adnan, M.; Muhammad, R.; Hafiz, H.; et al. Methods and composite materials—A review. Polym. Compos. 2019, 40, 1–16. [Google Scholar] [CrossRef]
- Gutowski, V.; Yang, W.; Li, S.; Dean, K.; Zhang, X. Lightweight Nanocomposite Materials. In Lightweight and Sustainable Materials for Automotive Applications; Taylor & Francis Group: Abingdon, UK, 2017; Volume 9, pp. 277–302. [Google Scholar] [CrossRef]
- Policandriotes, T.; Filip, P. Effects of selected nanoadditives on the friction and wear performance of carbon–carbon aircraft brake composites. Wear 2011, 271, 2280–2289. [Google Scholar] [CrossRef]
- Song, J.; Yu, Y.; Zhao, G.; Qiu, J.; Ding, Q. Improved Tribological Properties of Polyimide Composites by Micro–Nano Reinforcement. J. Appl. Polym. Sci. 2019, 136, 47900. [Google Scholar] [CrossRef]
- Sławski, S.; Szymiczek, M.; Domin, J. Influence of the reinforcement on the destruction image of the composites panels after applying impact load. In AIP Conference Proceedings, Proceedings of the 10th International Conference on Applied Mechanics, Bydgoszcz, Poland, 23 November 2018; Piatkowski, T., Ed.; AIP Publishing LLC: New York, NY, USA, 2019; Volume 2077, p. 2077. [Google Scholar] [CrossRef]
- Chabera, P.; Boczkowska, A.; Witek, A.; Oziebło, A. Fabrication and characterization of composite materials based on porous ceramic preform infiltrated by elastomer. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 193–199. [Google Scholar] [CrossRef]
- Sławski, S.; Szymiczek, M.; Kaczmarczyk, J.; Domin, J.; Duda, S. Experimental and numerical investigation of striker shape influence on the destruction image in multilayered composite after low velocity impact. Appl. Sci. 2020, 10, 288. [Google Scholar] [CrossRef]
- Hussain, O.; Saleem, S.; Ahmad, B. Implant materials for knee and hip joint replacement: A review from the tribological perspective. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 561, p. 012007. [Google Scholar] [CrossRef]
- Gadow, R.; Jiménez, M. Carbon fiber-reinforced carbon composites for aircraft brakes. Am. Ceram. Soc. Bull. 2019, 98, 28–34. [Google Scholar]
- Katiyar, J.K.; Sinha, S.K.; Kumar, A. Friction and Wear Durability Study of Epoxy-Based Polymer (SU-8) Composite Coatings with Talc and Graphite as Fillers. Wear 2016, 362–363, 199–208. [Google Scholar] [CrossRef]
- Jang, D.S.; Zhang, W.L.; Choi, H.J. Polypyrrole-wrapped halloysite nanocomposite and its rheological response under electric fields. J. Mater. Sci. 2014, 49, 7309–7316. [Google Scholar] [CrossRef]
- Korzec, I.; Lusiak, T.; Bugaj, M. Application concept for the new composite material for the rotorcraft. In Zvyšovanie Bezpečnosti a Kvality v Civilnom Letectve; Žilinská Univerzita v Žiline: Žiline, Slovakia, 2020; pp. 86–89. [Google Scholar] [CrossRef]
- Lusiak, T.; Korzec, I.; Czarnigowski, J.; Rękas, D.; Marciniak, M.; Komajda, K. Modern laminate composite designed for aircraft construction. J. Technol. Exploit. Mech. Eng. 2019, 5, 1–8. [Google Scholar] [CrossRef]
- Almataev, T.; Almataev, N.; Moidinov, D. Research of the Tribological Properties of Composite Polymer Materials during the Breaking-in Period. Bull. Sci. Pract. 2019, 5, 242–248. [Google Scholar] [CrossRef]
- Nagiev, A.G.; Sadykhov, V.V.; Gashimova, U.M. Identification of Properties of Composite Polymer Materials in the Space of Their Rotational–Viscous Characteristics. Tech. Phys. 2020, 65, 232–237. [Google Scholar] [CrossRef]
- Moskalyuk, O.A.; Samsonov, A.M.; Semenova, I.; Smirnova, V.E.; Yudin, V.E. Mechanical properties of polymeric composites with carbon dioxide particles. Tech. Phys. 2017, 62, 294–298. [Google Scholar] [CrossRef]
- Liu, N.; Jeffers, A.E. Isogeometric analysis of laminated composite and functionally graded sandwich plates based on a layerwise displacement theory. Compos. Struct. 2017, 176, 143–153. [Google Scholar] [CrossRef]
- Liu, N.; Ren, X.; Lua, J. An isogeometric continuum shell element for modeling the nonlinear response of functionally graded material structures. Compos. Struct. 2020, 237, 111893. [Google Scholar] [CrossRef]


















| Parameter | Dialead K63712 Modular Fabric | Roving MS65 | IMS65 CTLX Biaxial Fabric | Symmetrical Fabric Interglas 02037 | IMS65 Modular Fabric |
|---|---|---|---|---|---|
| Fabric sheet density (g/m2) | 41.9 | 32.3 | 66.8 | 47.5 | 27.2 |
| Thickness (mm) | 0.20 | 0.20 | 0.19 | 0.21 | 0.2 |
| Tensile strength (MPa) | 419 | 128 | 513 | 443 | 1450 |
| The Numbers of the Samples | Width (mm) | Thickness (mm) | Area (mm2) | Length (mm) |
|---|---|---|---|---|
| 1. | 25.2 | 2.18 | 55.0 | 150 |
| 2. | 25.2 | 2.36 | 59.4 | 150 |
| 3. | 25.2 | 2.38 | 59.9 | 150 |
| 4. | 25.6 | 2.34 | 60.0 | 150 |
| 5. | 25.2 | 2.39 | 60.1 | 150 |
| 6. | 25.1 | 2.31 | 58.0 | 150 |
| Average | 25.2 | 2.33 | 58.7 | 150 |
| The Numbers of the Samples | Tensile Stress (MPa) | Maximum Force (kN) | The greatest Tensile Deformation (%) | Maximum Displacement (mm) | Module (MPa) |
|---|---|---|---|---|---|
| 1. | 117 | 6.41 | 4.21 | 8.99 | 13,200 |
| 2. | 127 | 7.56 | 7.14 | 12.77 | 12,300 |
| 3. | 133 | 7.98 | 9.11 | 16.18 | 12,500 |
| 4. | 131 | 7.85 | 7.98 | 15.27 | 12,400 |
| 5. | 133 | 7.98 | 9.22 | 16.53 | 12,200 |
| 6. | 127 | 7.35 | 6.26 | 12.00 | 12,000 |
| Average | 128 | 7.52 | 7.32 | 13.62 | 12,400 |
| The Numbers of the Samples | Width (mm) | Thickness (mm) | Area (mm2) | Length (mm) |
|---|---|---|---|---|
| 1. | 25.1 | 2.30 | 57.8 | 150 |
| 2. | 25.2 | 2.49 | 62.7 | 150 |
| 3. | 25.2 | 2.49 | 62.7 | 150 |
| 4. | 25.1 | 2.32 | 58.3 | 150 |
| 5. | 25.2 | 2.42 | 61.0 | 150 |
| 6. | 25.2 | 2.42 | 60.9 | 150 |
| Average | 25.2 | 2.41 | 60.5 | 150 |
| The Numbers of the Samples | Tensile Stress (MPa) | Maximum Force (kN) | The Greatest Tensile Deformation (%) | Maximum Displacement (mm) | Module (MPa) |
|---|---|---|---|---|---|
| 1. | 512 | 29.54 | 1.17 | 6.24 | 58,300 |
| 2. | 484 | 30.35 | 1.31 | 4.18 | 62,000 |
| 3. | 514 | 32.19 | 1.25 | 4.63 | 56,900 |
| 4. | 533 | 31.05 | 1.32 | 7.20 | 53,500 |
| 5. | 526 | 32.12 | 1.24 | 5.02 | 63,400 |
| 6. | 510 | 31.06 | 1.26 | 4.66 | 54,900 |
| Average | 513 | 31.05 | 1.26 | 5.32 | 58,200 |
| The Numbers of the Samples | Width (mm) | Thickness (mm) | Area (mm2) | Length (mm) |
|---|---|---|---|---|
| 1. | 25.4 | 2.84 | 72.3 | 150 |
| 2. | 25.3 | 2.94 | 74.4 | 150 |
| 3. | 25.3 | 2.99 | 75.6 | 150 |
| 5. | 25.5 | 3.01 | 76.6 | 150 |
| 7. | 25.5 | 3.00 | 76.4 | 150 |
| 8. | 25.3 | 2.87 | 72.6 | 150 |
| 9. | 25.4 | 2.84 | 72.0 | 150 |
| Average | 25.4 | 2.93 | 74.3 | 150 |
| The Numbers of the Samples | Tensile Stress (MPa) | Maximum Force (kN) | The greatest Tensile Deformation (%) | Maximum Displacement (mm) | Module (MPa) |
|---|---|---|---|---|---|
| 1. | 467 | 33.78 | 1.39 | 5.36 | 37,300 |
| 2. | 447 | 33.28 | 1.37 | 4.65 | 36,000 |
| 3. | 426 | 32.21 | 1.23 | 5.19 | 36,300 |
| 5. | 419 | 32.14 | 1.43 | 5.27 | 32,700 |
| 7. | 414 | 31.63 | 1.37 | 4.93 | 37,900 |
| 8. | 456 | 33.14 | 1.37 | 5.47 | 37,500 |
| 9. | 472 | 34.02 | 1.41 | 7.09 | 37,700 |
| Average | 443 | 32.89 | 1.37 | 5.43 | 36,500 |
| The Numbers of the Samples | Width (mm) | Thickness (mm) | Area (mm2) | Length (mm) |
|---|---|---|---|---|
| 1. | 25.2 | 2.38 | 60.0 | 150 |
| 2. | 25.2 | 2.48 | 62.5 | 150 |
| 3. | 25.2 | 2.47 | 62.4 | 150 |
| 4. | 25.3 | 2.44 | 61.6 | 150 |
| 5. | 25.3 | 2.46 | 62.1 | 150 |
| 6. | 25.3 | 2.425 | 61.9 | 150 |
| Average | 25.2 | 2.45 | 61.8 | 150 |
| The Numbers of the Samples | Tensile Stress (MPa) | Maximum Force (kN) | The Greatest Tensile Deformation (%) | Maximum Displacement (mm) | Module (MPa) |
|---|---|---|---|---|---|
| 1. | 1490 | 89.65 | 1.03 | 10.63 | 161,000 |
| 2. | 1380 | 86.42 | 0.798 | 11.94 | 202,000 |
| 3. | 1450 | 90.15 | 1.02 | 11.89 | 176,000 |
| 4. | 1400 | 86.35 | 0.823 | 10.20 | 202,000 |
| 5. | 1480 | 91.71 | 1.000 | 11.33 | 191,000 |
| 6. | 1480 | 91.32 | 1.08 | 11.72 | 131,000 |
| Average | 1450 | 89.27 | 0.959 | 11.29 | 177,000 |
| Designation of the Series | Tensile Strength Rm (MPa) | |
|---|---|---|
| A | 419 | ±18 |
| B | 128 | ±11 |
| C | 513 | ±29 |
| D | 443 | ±29 |
| E | 1450 | ±70 |
| Series | Name | Weave | Sh°D |
|---|---|---|---|
| A | Modular fabric Dialead K63712 | 0/+90° | 81.6 |
| B | Roving IMS65 | 0/+90° | 80.2 |
| C | IMS65 CTLX biaxial fabric | +/−45° | 85.0 |
| D | Symmetrical fabric Interglas 02037 | 0/+90° | 77.3 |
| E | IMS65 modular fabric | 0/+90° | 83.5 |
| Aluminium Alloy | 2024 | |
|---|---|---|
| Composition | Cu | 4.6 |
| Mg | 1.4 | |
| Mn | 0.54 | |
| Fe | 0.18 | |
| Zn | 0.1 | |
| Si | 0.09 | |
| Ti | 0.02 | |
| Cr | 0.01 | |
| rest | 0.05 | |
| Material Type | Properties | ||
|---|---|---|---|
| Density (g/cm3) | E (GPa) | Rm (MPa) | |
| 2024 | 2.79 | 73 | 458 |
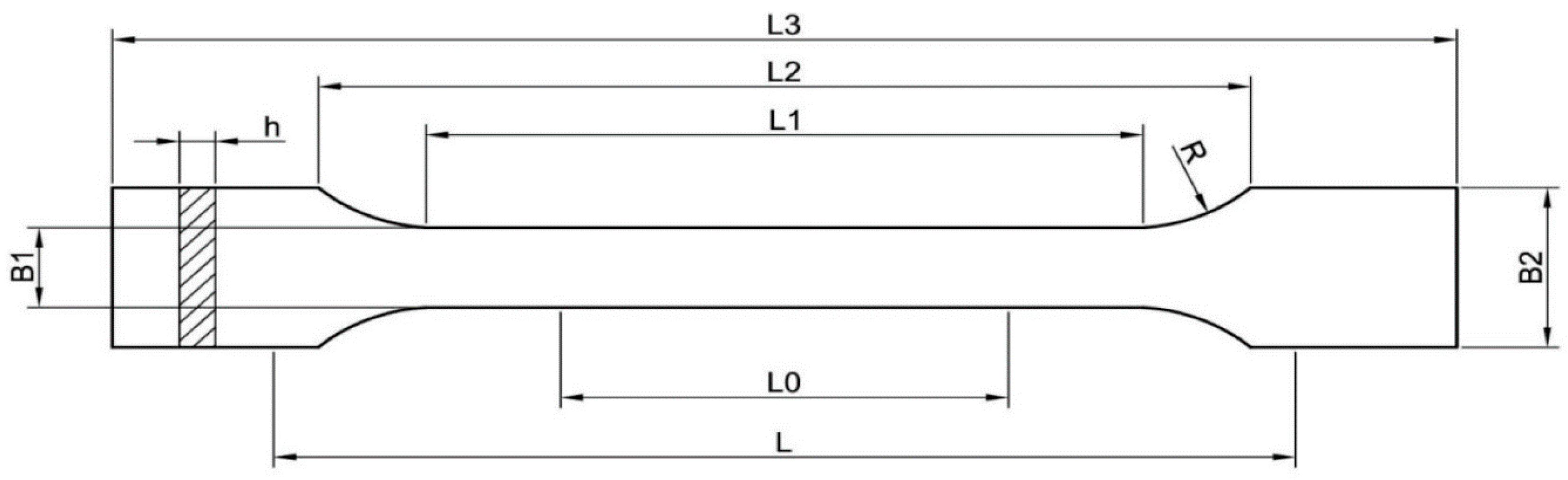
| Moulder Dimensions | Type B1 (mm) |
|---|---|
| L3—total length | 150 |
| L1—the length of the part delimited by lines | 40 |
| R—radius | 60 |
| L2—length between wide parallel parts | 106 |
| B2—width at the ends | 20 |
| B1—width of the narrow part | 10 |
| H—recommended thickness | 4 |
| L0—measuring length | 50 |
| L—initial distance between the handles | 115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setlak, L.; Kowalik, R.; Lusiak, T. Practical Use of Composite Materials Used in Military Aircraft. Materials 2021, 14, 4812. https://doi.org/10.3390/ma14174812
Setlak L, Kowalik R, Lusiak T. Practical Use of Composite Materials Used in Military Aircraft. Materials. 2021; 14(17):4812. https://doi.org/10.3390/ma14174812
Chicago/Turabian StyleSetlak, Lucjan, Rafał Kowalik, and Tomasz Lusiak. 2021. "Practical Use of Composite Materials Used in Military Aircraft" Materials 14, no. 17: 4812. https://doi.org/10.3390/ma14174812
APA StyleSetlak, L., Kowalik, R., & Lusiak, T. (2021). Practical Use of Composite Materials Used in Military Aircraft. Materials, 14(17), 4812. https://doi.org/10.3390/ma14174812







