A 3D Analysis of Dendritic Solidification and Mosaicity in Ni-Based Single Crystal Superalloys
Abstract
:1. Introduction
2. Materials and Methods
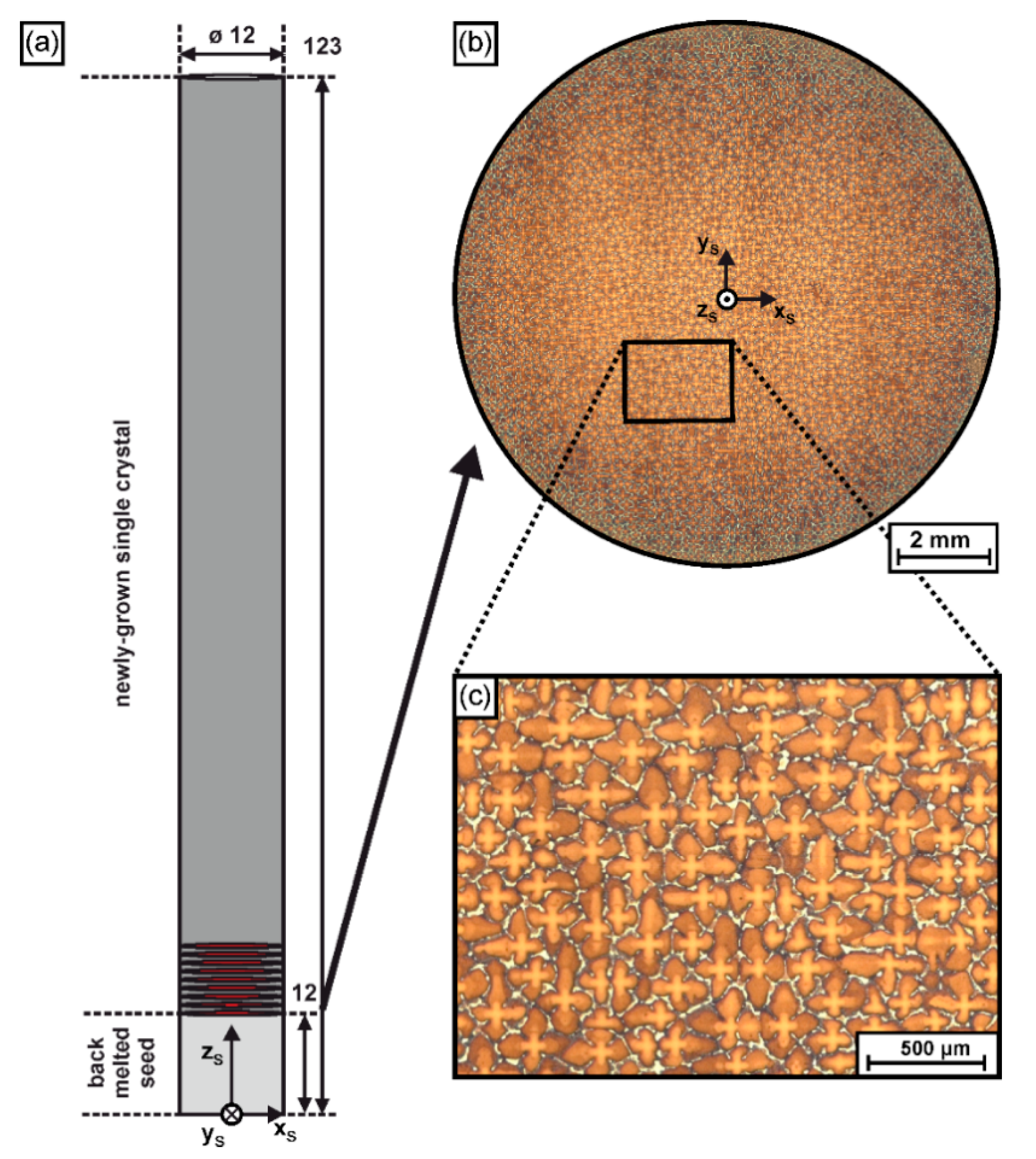
2.1. Crystal Growth/Solidification Experiments
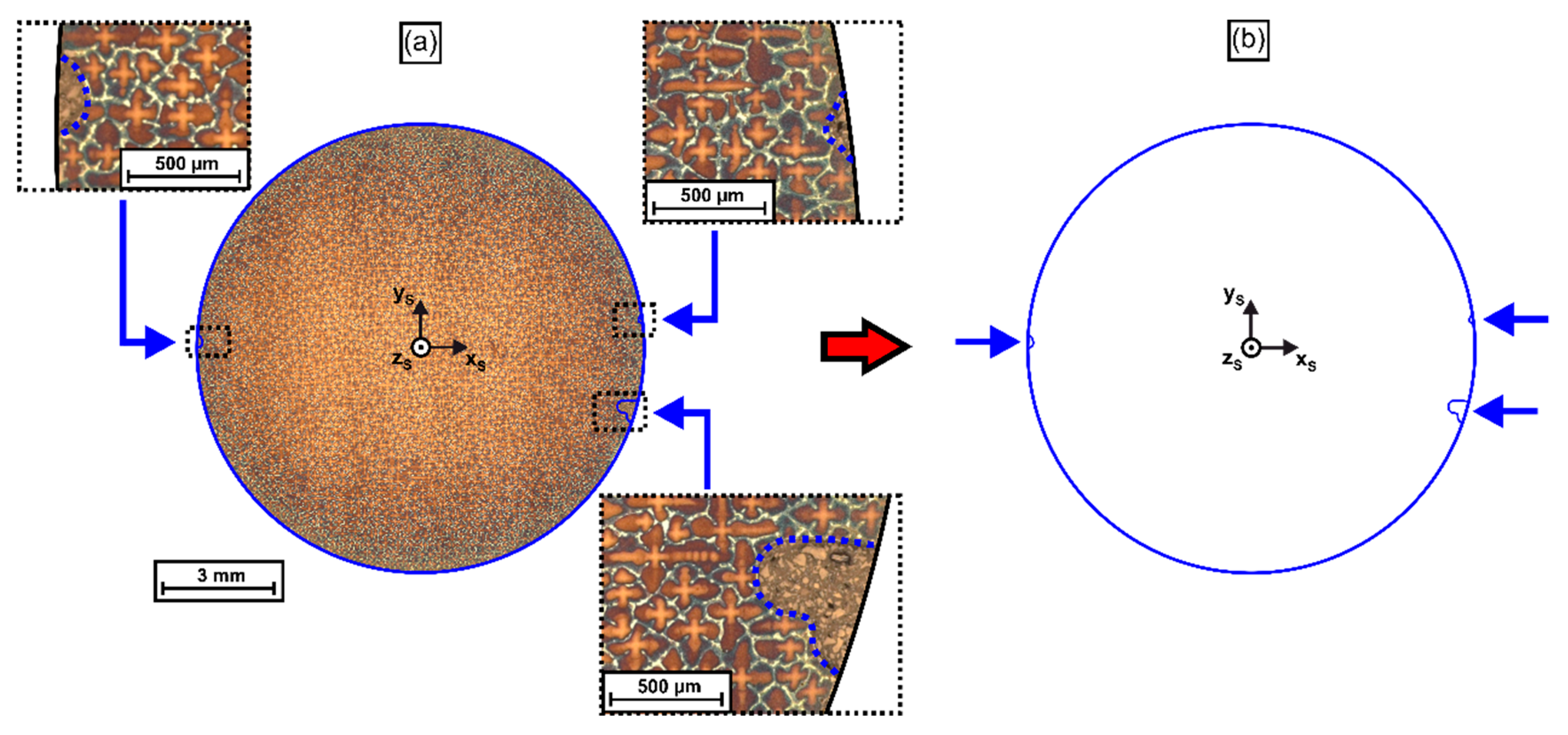
2.2. Tomographic Characterization, Metallographic Preparation and Crystallographic Analysis
3. Results
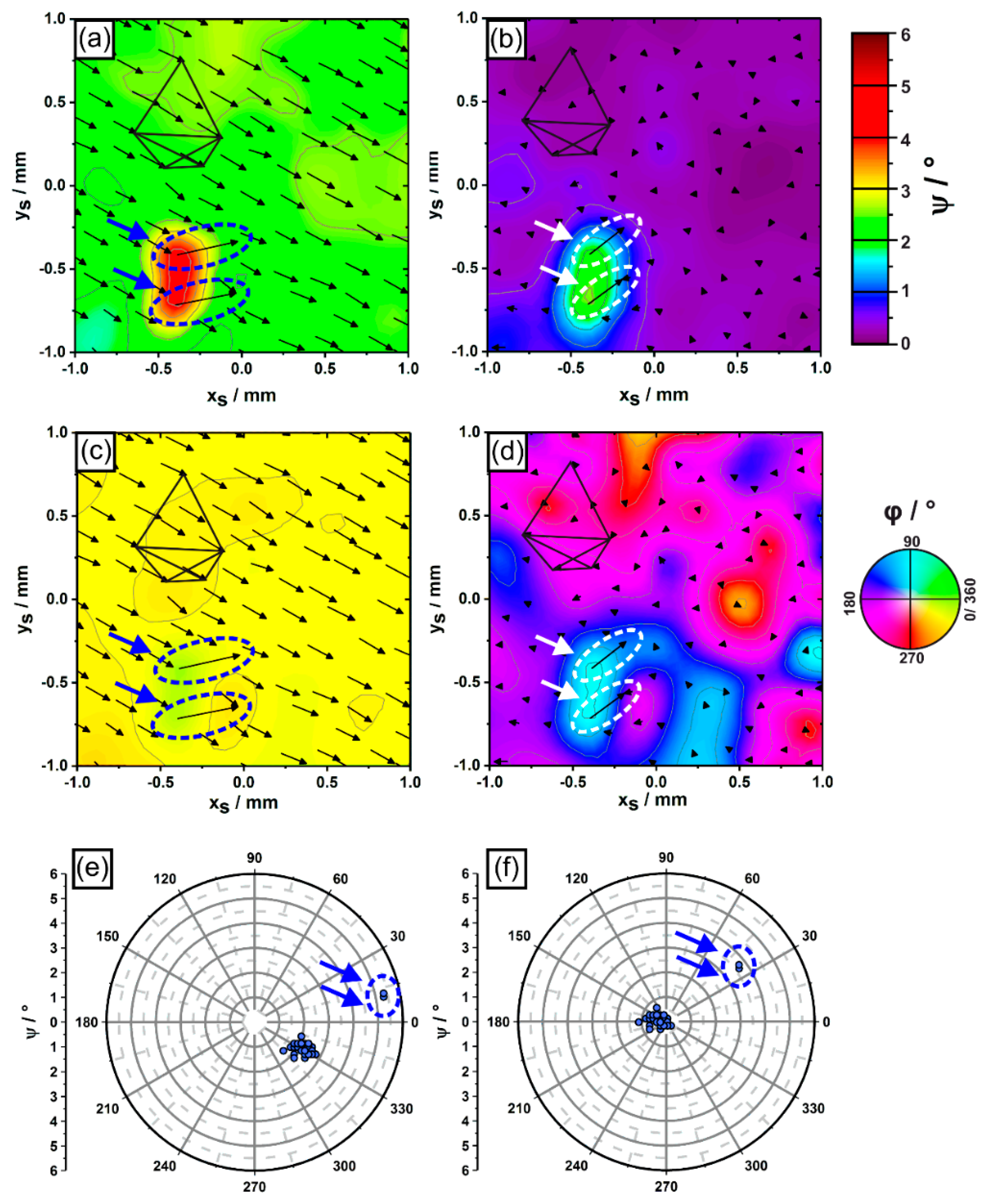
3.1. Dendrite Growth Directions
3.2. Crystal Orientations
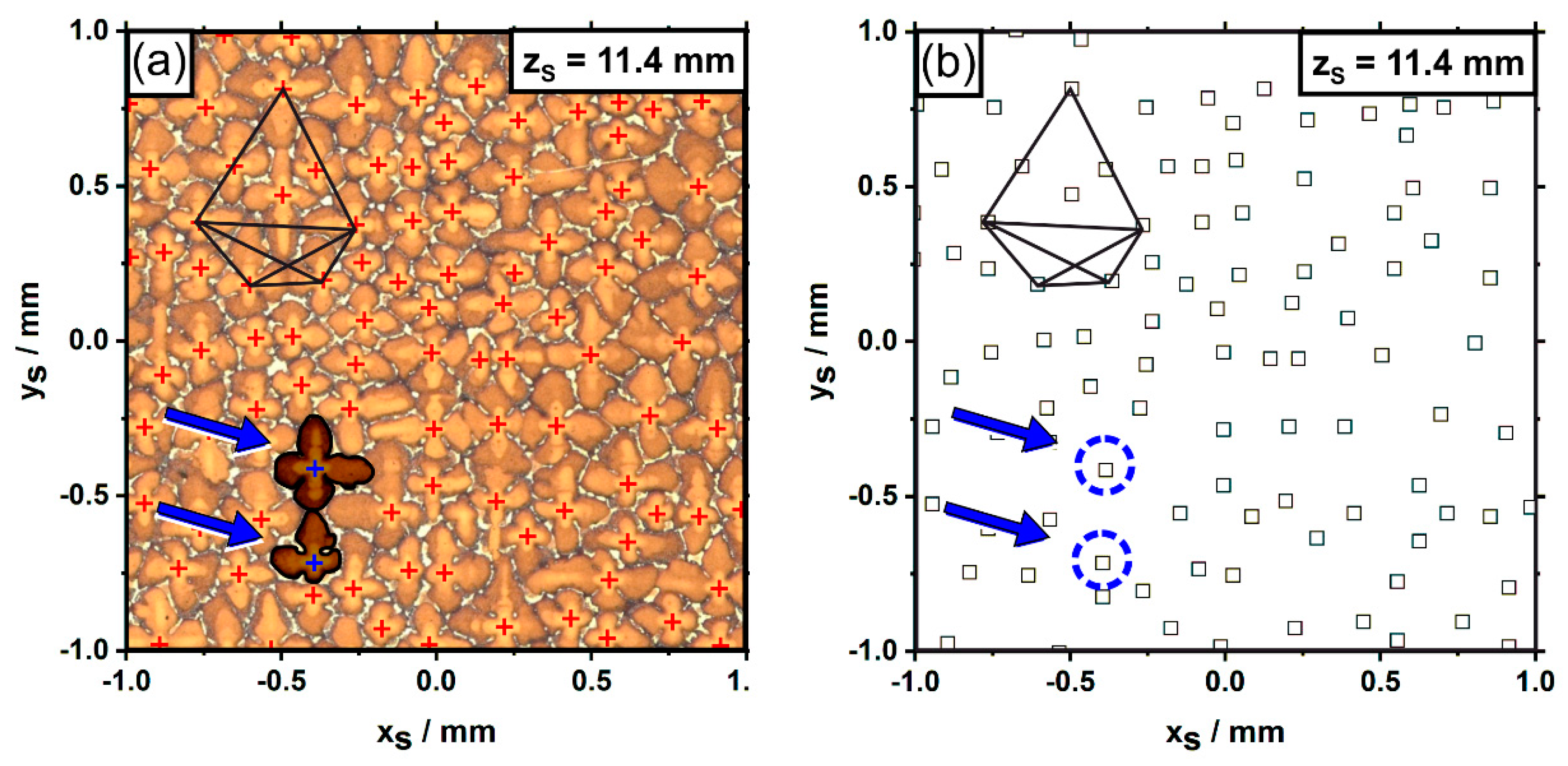
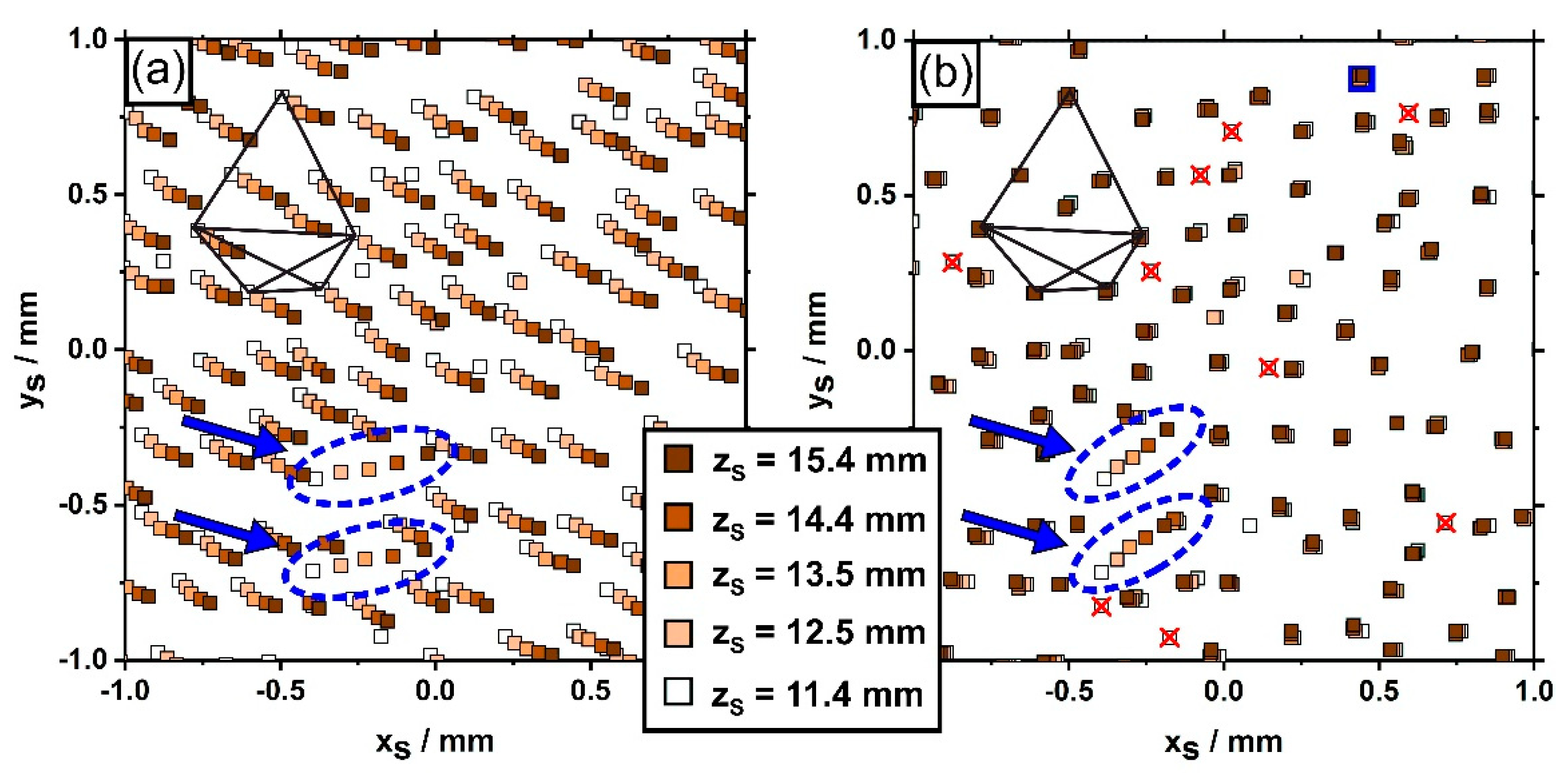
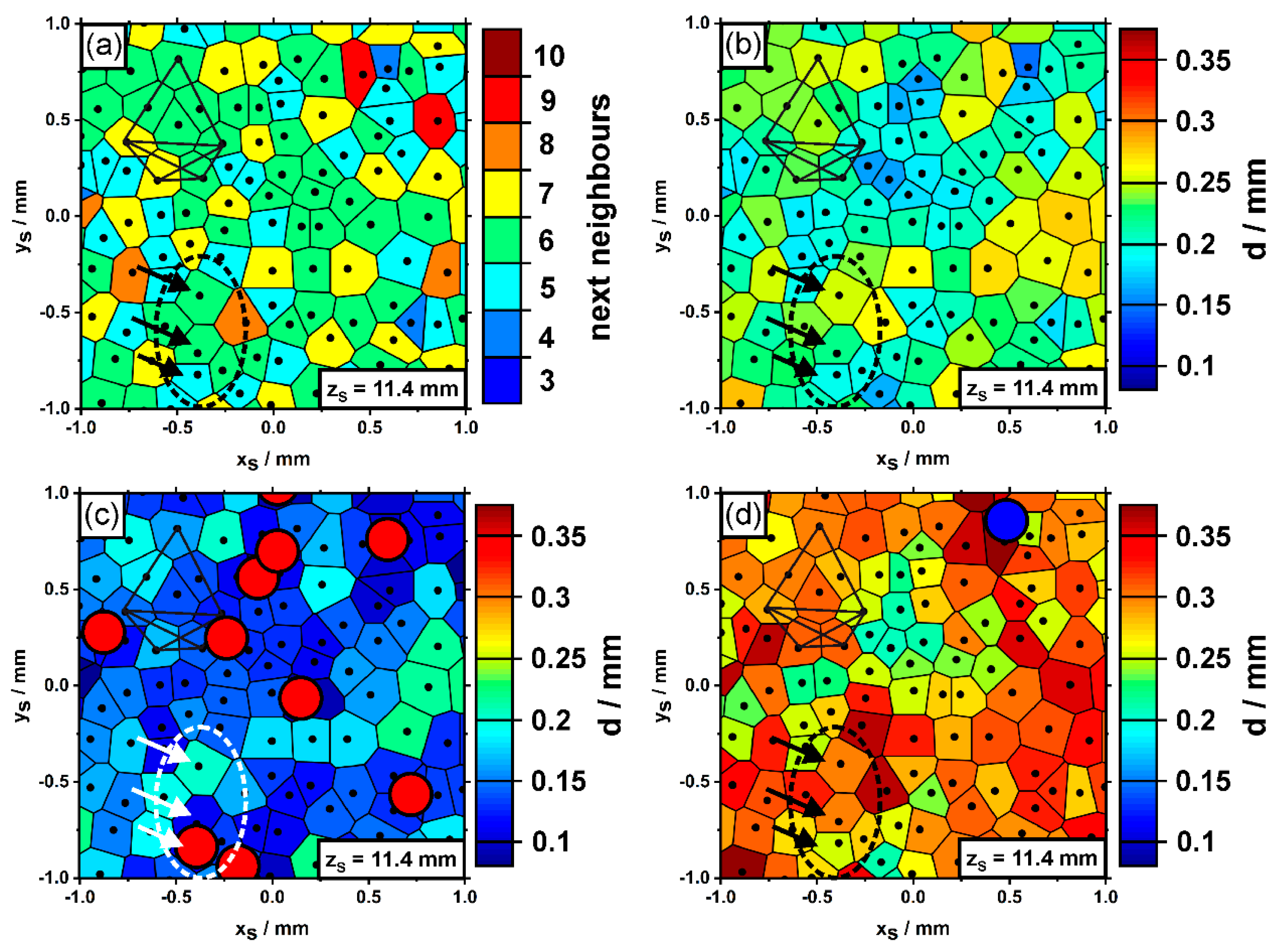
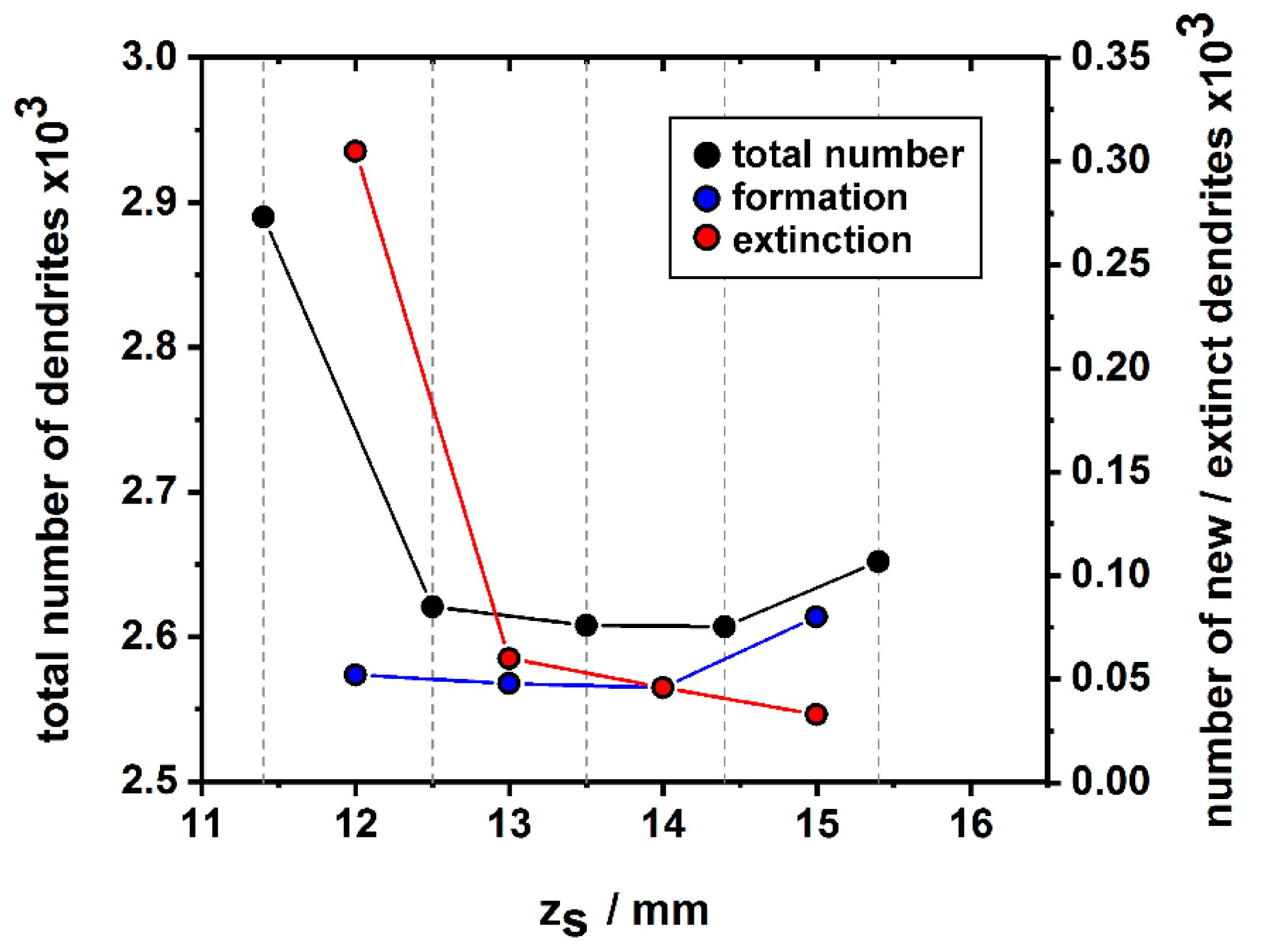
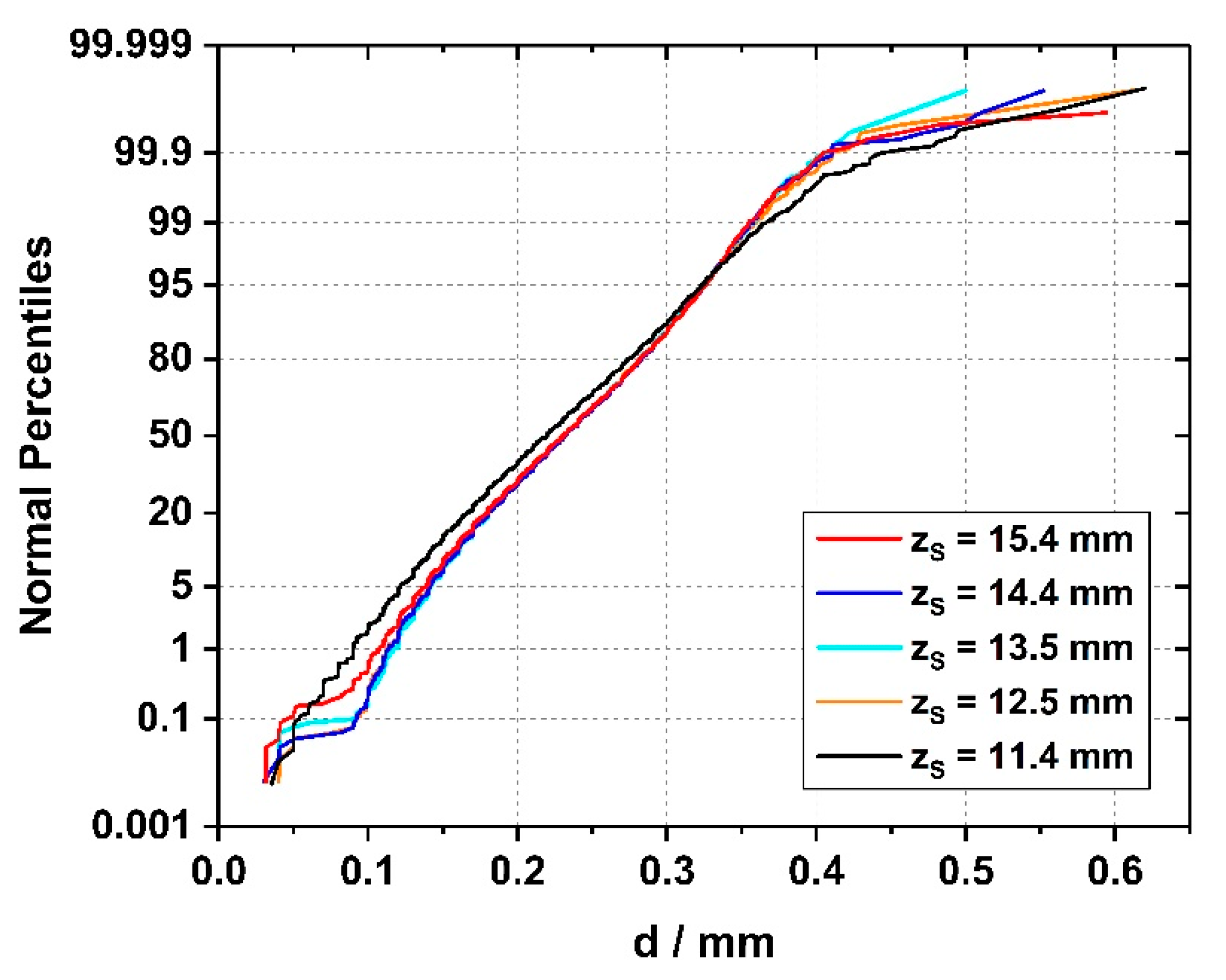
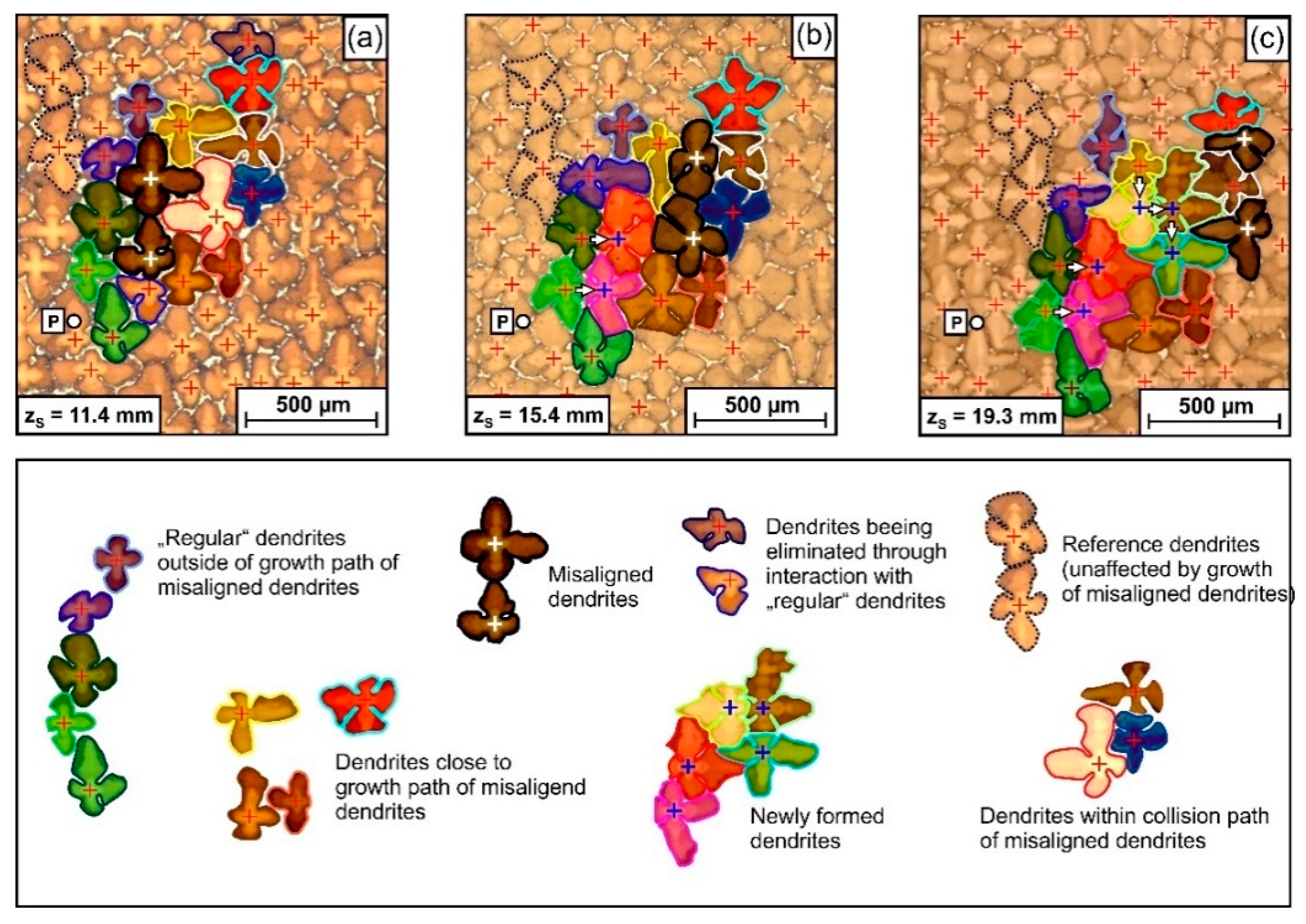
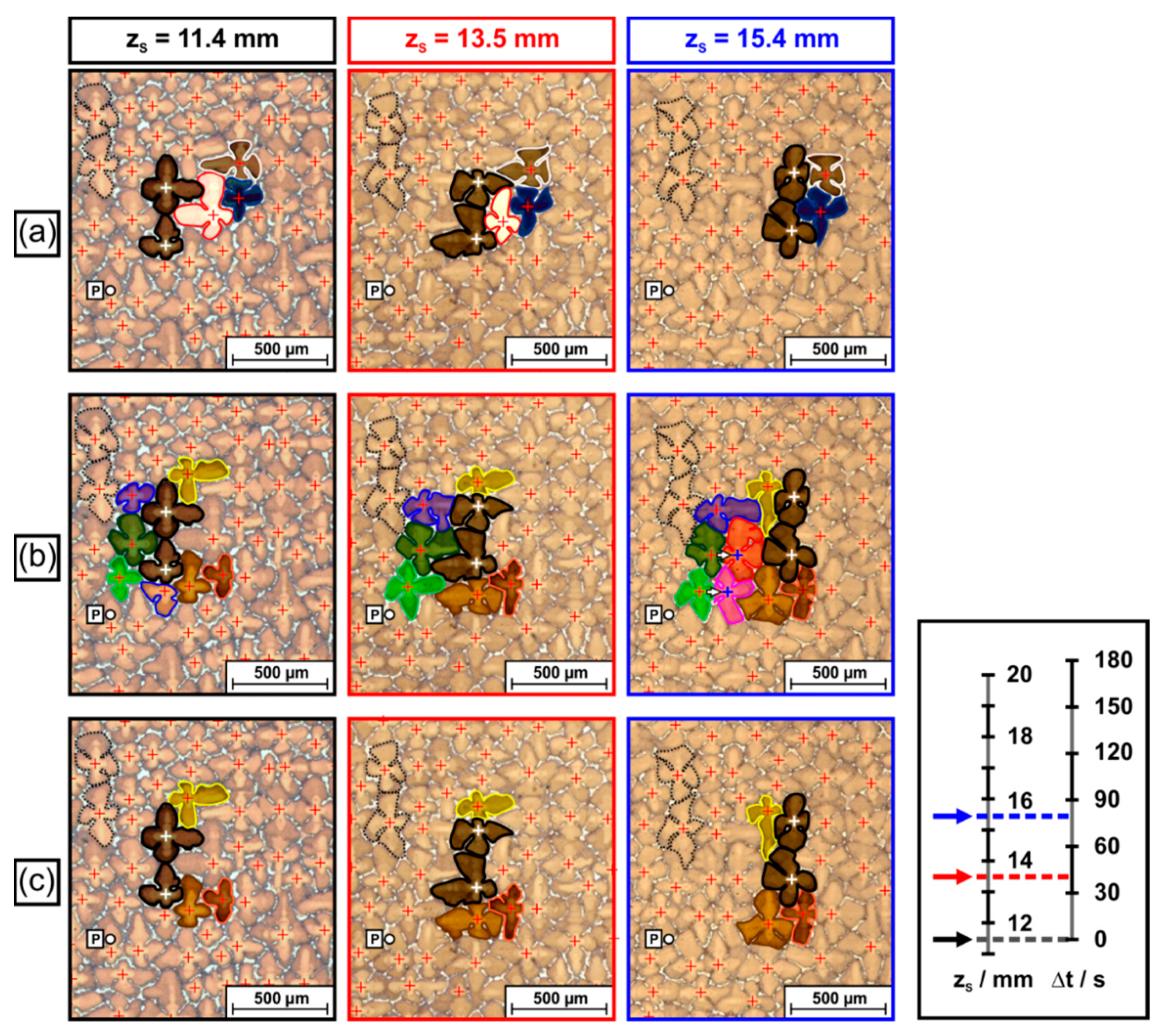
3.3. Evolution of Dendrite Patterns
3.4. Competitive Growth between Misoriented and Surrounding Dendrites
4. Discussion
5. Summary and Conclusions
- (1)
- The novel tomographic procedure described in the present work allows to evaluate the growth behavior of a large number of dendrites accounting for different individual growth directions. The 3D results can be visualized using color-coded orientation distribution maps where dendrite growth directions are represented by polar and azimuth angles.
- (2)
- The specimen cross sections consist of regions that frequently feature interdendrite misorientation angles less than 2°. However, a small number of isolated dendrites (0.24%) showed larger deviations in growth directions.
- (3)
- Individual dendrites grow in crystallographic <001> directions, which was shown using the recently developed rotation vector base-line electron back scatter diffraction method (RVB-EBSD method). This confirms that crystal mosaicity is directly related to dendrite misorientations.
- (4)
- Statistical distributions of primary dendrite arm spacings were evaluated. It was found that in the early stages of seeded Bridgman solidification, many dendrites form. Their number subsequently decreases, however, due to competitive dendrite growth as constant solidification conditions are established. The later solidification stages are characterized by a balance between the formation of new and the extinction of pre-existing dendrites.
- (5)
- A local scenario was documented, where two slightly misoriented dendrites strongly affect the growth kinetic of their environment. These two dendrites followed their deviating growth direction and overgrew other dendrites in their growth path. The space behind these two dendrites was subsequently filled with new tertiary dendrites, branching out from secondary dendrite arms of regularly oriented surrounding dendrites from different sides. The technique presented in this work not only provides sound statistic information on the average growth behavior but also allows to study such unusual local events.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Versnyder, F.L.; Shank, M.E. The development of columnar grain and single crystal high temperature materials through directional solidification. Mater. Sci. Eng. 1970, 6, 213–247. [Google Scholar] [CrossRef]
- Meetham, G.W. The Development of Gas Turbine Materials; Applied Science Publishers: London, UK, 1981. [Google Scholar]
- McLean, M. Directionally Solidified Materials for High Temperature Service; The Metals Society: London, UK, 1983. [Google Scholar]
- Durand-Charree, M. The Microstructure of Superalloys; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Bürgel, R.; Maier, H.J.; Niendorf, T. Hochtemperaturlegierungen. In Handbuch Hochtemperatur-Werkstofftechnik; Bürgel, R., Maier, H.J., Niendorf, T., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2011; pp. 340–484. [Google Scholar]
- Reed, R.C. The Superalloys—Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Evans, R.W.; Wilshire, B. Creep of Metals and Alloys; Institute of Metals: London, UK, 1985. [Google Scholar]
- Cadek, J. Creep in Metallic Materials; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Quested, P.N.; McLean, M. Solidification morphologies in directionally solidified superalloys. Mater. Sci. Eng. 1984, 65, 171–180. [Google Scholar] [CrossRef]
- Parsa, A.B.; Wollgramm, P.; Buck, H.; Somsen, C.; Kostka, A.; Povstugar, I.; Choi, P.P.; Raabe, D.; Dlouhy, A.; Müller, J.; et al. Advanced scale bridging microstructure analysis of single crystal Ni-base superalloys. Adv. Eng. Mater. 2015, 17, 216–230. [Google Scholar] [CrossRef]
- Nörtershäuser, P.; Frenzel, J.; Ludwig, A.; Neuking, K.; Eggeler, G. The effect of cast microstructure and crystallography on rafting, dislocation plasticity and creep anisotropy of single crystal Ni-base superalloys. Mater. Sci. Eng. A 2015, 626, 305–312. [Google Scholar] [CrossRef]
- Pollock, T.M.; Murphy, W.H. The breakdown of single-crystal solidification in high refractory nickel-base alloys. Metall. Mater. Trans. A 1996, 27, 1081–1094. [Google Scholar] [CrossRef]
- Hobbs, R.A.; Tin, S.; Rae, C.M.F. A castability model based on elemental solid-liquid partitioning in advanced nickel-base single-crystal superalloys. Metall. Mater. Trans. A 2005, 36, 2761–2773. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Volek, A.; Singer, R.F. Influence of solidification conditions on the castability of nickel-base superalloy IN792. Metall. Mater. Trans. A 2005, 36, 651–656. [Google Scholar] [CrossRef]
- Rappaz, M.; Rettenmayr, M. Simulation of solidification. Curr. Opin. Solid State Mater. Sci. 1998, 3, 275–282. [Google Scholar] [CrossRef]
- Gilman, J.J. The Art and Science of Growing Crystals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1963. [Google Scholar]
- Hong, J.P.; Ma, D.X.; Wang, J.; Wang, F.; Dong, A.P.; Sun, B.D.; Bührig-Polaczek, A. Geometrical effect of freckle formation on directionally solidified superalloy CM247 LC components. J. Alloys Compd. 2015, 648, 1076–1082. [Google Scholar] [CrossRef]
- Ma, D.X.; Zhou, B.; Buhrig-Polaczek, A. Investigation of freckle formation under various solidification conditions. In Euro Superalloys 2010; Heilmaier, M., Ed.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2011; Volume 278, pp. 428–433. [Google Scholar]
- Auburtin, P.; Wang, T.; Cockcroft, S.L.; Mitchell, A. Freckle formation and freckle criterion in superalloy castings. Metall. Mater. Trans. B 2000, 31, 801–811. [Google Scholar] [CrossRef]
- Aveson, J.W.; Tennant, P.A.; Foss, B.J.; Shollock, B.A.; Stone, H.J.; D’Souza, N. On the origin of sliver defects in single crystal investment castings. Acta Mater. 2013, 61, 5162–5171. [Google Scholar] [CrossRef]
- Carney, C.A.; Beech, J. The origin of sliver defects in single crystal turbine blades. In Decennial International Conference on Solidification Processing; Beech, J., Ed.; Department of Engineering Materials, University of Sheffield: Sheffield, UK, 1997. [Google Scholar]
- Yang, C.; Liu, L.; Zhao, X.; Zhang, J.; Sun, D.; Fu, H. Formation of stray grains during directional solidification of a superalloy AM3. Appl. Phys. A 2013, 114, 979–983. [Google Scholar] [CrossRef]
- Zhou, Y.Z. Formation of stray grains during directional solidification of a nickel-based superalloy. Scr. Mater. 2011, 65, 281–284. [Google Scholar] [CrossRef]
- Darwin, C.G. XCII. The reflexion of X-rays from imperfect crystals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 800–829. [Google Scholar] [CrossRef] [Green Version]
- Bellet, D. Etude Des Textures des Superalliages Monocristallins Par Diffraction et Diffusion Des Rayonnements: X, γ et Neutrons. Ph.D. Thesis, Université Joseph Fourier (Grenoble), Grenoble, France, 1990. [Google Scholar]
- Brückner, U.; Epishin, A.; Link, T. Local X-ray diffraction analysis of the structure of dendrites in single-crystal nickel-base superalloys. Acta Mater. 1997, 45, 5223–5231. [Google Scholar] [CrossRef]
- Klam, H.; Blank, E. The growth of modern superalloy single crystals. In Proceedings of the First Conference on Advanced Materials and Processes (EUROMAT’89), Aachen, Germany, 22–24 November 1989; pp. 407–412. [Google Scholar]
- Doherty, R.D. Comments on “Mechanical deformation of dendrites by fluid flow during the solidification of undercooled melts”. Scr. Mater. 2003, 49, 1219–1222. [Google Scholar] [CrossRef]
- Hallensleben, P.; Scholz, F.; Thome, P.; Schaar, H.; Steinbach, I.; Eggeler, G.; Frenzel, J. On crystal mosaicity in single crystal Ni-based superalloys. Crystals 2019, 9, 149. [Google Scholar] [CrossRef] [Green Version]
- Sass, V.; Glatzel, U.; Feller-Kniepmeier, M. Anisotropic creep properties of the Nickel-base superalloy CMSX-4. Acta Mater. 1996, 44, 1967–1977. [Google Scholar] [CrossRef]
- Pollock, T.M.; Argon, A.S. Creep resistance of CMSX-3 Nickel base superalloy single crystals. Acta Metall. Mater. 1991, 40, 1–30. [Google Scholar]
- Rae, C.M.F.; Reed, R.C. Primary creep in single crystal superalloys. Acta Mater. 2007, 55, 1067–1081. [Google Scholar] [CrossRef]
- Ram, F.; Li, Z.; Zaefferer, S.; Haghighat, S.M.H.; Zhu, Z.; Raabe, D.; Reed, R.C. On the origin of creep dislocations in a Ni-base, single-crystal superalloy: An ECCI, EBSD, and dislocation dynamics-based study. Acta Mater. 2016, 109, 151–161. [Google Scholar]
- Harris, K.; Erickson, G.L.; Brentnall, W.D.; Aurrecoechea, J.M.; Sikkenga, S.L.; Kubarych, K.G. Development of the rhenium containing superalloys CMSX-4 & CM 186 LC for single crystal blade and directionally solidified vane applications in advanced turbine engines. In Superalloys 1992; Antolovich, S.D., Ed.; TMS: Champion, PA, USA; pp. 297–306.
- He, J.; Scholz, F.; Horst, O.M.; Thome, P.; Frenzel, J.; Eggeler, G.; Gault, B. On the rhenium segregation at the low angle grain boundary in a single crystal Ni-base superalloy. Scr. Mat. 2020, 185, 88–93. [Google Scholar]
- D’Souza, N.; Newell, M.; Devendra, K.; Jennings, P.A.; Ardakani, M.G.; Shollock, B.A. Formation of low angle boundaries in Ni-based superalloys. Mater. Sci. Eng. A 2005, 413, 567–570. [Google Scholar] [CrossRef]
- Newell, M.; D’Souza, N.; Green, N.R. Formation of low angle boundaries in Ni-based superalloys. Int. J. Cast Met. Res. 2009, 22, 66–69. [Google Scholar] [CrossRef]
- Newell, M.; Devendra, K.; Jennings, P.A.; D’Souza, N. Role of dendrite branching and growth kinetics in the formation of low angle boundaries in Ni–base superalloys. Mater. Sci. Eng. A 2005, 412, 307–315. [Google Scholar] [CrossRef]
- Schaefer, R.; Black, D.; Vaudin, M.; Mueller, B.; Giamei, A. Geometry and mechanisms of dendrite misalignments in superalloy single crystals. In Proceedings of the 4th Decennial International Conference on Solidification Processing, Sheffield, UK, 7–10 July 1997; pp. 37–40. [Google Scholar]
- Aveson, J.W.; Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Tandjaoui, A.; Billia, B.; Goodwin, K.; Lafford, T.A.; Baruchel, J.; Stone, H.J.; et al. Dendrite bending during directional solidification. In Superalloys 2012; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 615–624. [Google Scholar]
- Aveson, J.W.; Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noel, N.; D’Souza, N.; Stone, H.J. Origins of misorientation defects in single crystal castings: A time resolved in situ synchrotron X-ray radiography study. In Eurosuperalloys 2014—2nd European Symposium on Superalloys and Their Applications; Guedou, J.Y., Chone, J., Eds.; EDP Sciences: Les Ulis, France, 2014; Volume 14. [Google Scholar]
- Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Baruchel, J.; Billia, B. In Situ Investigation of Dendrite Deformation During Upward Solidification of Al-7wt.%Si. JOM-US 2014, 66, 1408–1414. [Google Scholar] [CrossRef]
- Lee, D.N.; Kim, K.; Lee, Y.; Choi, C.-H. Factors determining crystal orientation of dendritic growth during solidification. Mater. Chem. Phys. 1997, 47, 154–158. [Google Scholar] [CrossRef]
- Mullis, A.M. Growth induced dendritic bending and rosette formation during solidification in a shearing flow. Acta Mater. 1999, 47, 1783–1789. [Google Scholar] [CrossRef]
- Uehara, T.; Tsujino, T. Phase field simulation of stress evolution during solidification. J. Cryst. Growth 2005, 275, e219–e224. [Google Scholar] [CrossRef]
- Uehara, T.; Fukui, M.; Ohno, N. Phase field simulations of stress distributions in solidification structures. J. Cryst. Growth 2008, 310, 1331–1336. [Google Scholar] [CrossRef]
- Wagner, A.; Shollock, B.A.; McLean, M. Grain structure development in directional solidification of nickel-base superalloys. Mater. Sci. Eng. A 2004, 374, 270–279. [Google Scholar] [CrossRef]
- Dragnevski, K.; Mullis, A.M.; Walker, D.J.; Cochrane, R.F. Mechanical deformation of dendrites by fluid flow during the solidification of undercooled melts. Acta Mater. 2002, 50, 3743–3755. [Google Scholar] [CrossRef]
- Mullis, A.M.; Walker, D.J.; Battersby, S.E.; Cochrane, R.F. Deformation of dendrites by fluid flow during rapid solidification. Mater. Sci. Eng. A 2001, 304–306, 245–249. [Google Scholar] [CrossRef]
- Pilling, J.; Hellawell, A. Mechanical deformation of dendrites by fluid flow. Metall. Mater. Trans. A 1996, 27, 229–232. [Google Scholar] [CrossRef]
- Thome, P.; Medghalchi, S.; Frenzel, J.; Schreuer, J.; Eggeler, G. Ni-base superalloy single crystal (SX) mosaicity characterized by the Rotation Vector Base Line Electron Back Scatter Diffraction (RVB-EBSD) method. Ultramicroscopy 2019, 206, 112817. [Google Scholar] [CrossRef]
- Siredey, N.; Boufoussi, M.B.; Denis, S.; Lacaze, J. Dendritic growth and crystalline quality of nickel-base single grains. J. Cryst. Growth 1993, 130, 132–146. [Google Scholar] [CrossRef]
- Weiland, H.; Rouns, T.N.; Liu, J. The role of particle stimulated nucleation during recrystallization of an aluminium-manganese alloy. Z. Metallkd. 1994, 85, 592–597. [Google Scholar]
- Li, M.; Ghosh, S.; Rouns, T.N.; Weiland, H.; Richmond, O.; Hunt, W. Serial sectioning method in the construction of 3-D microstructures for particle-reinforced MMCs. Mat. Char. 1998, 41, 81–95. [Google Scholar] [CrossRef]
- Sidhu, R.S.; Chawla, N. Three-dimensional microstructure characterization of Ag3Sn intermetallics in Sn-rich solder by serial sectioning. Mat. Char. 2004, 52, 225–230. [Google Scholar] [CrossRef]
- Spowart, J.E. Automated serial sectioning for 3-d analysis of microstructures. Scr. Mater. 2006, 55, 5–10. [Google Scholar] [CrossRef]
- Yokomizo, T.; Enomoto, M.; Umezawa, O.; Spanos, G.; Rosenberg, R.O. Three-dimensional distribution, morphology, and nucleation site of intragranular ferrite in association with inclusions. Mater. Sci. Eng. A 2003, 344, 261–267. [Google Scholar] [CrossRef]
- Meng, X.B.; Lu, Q.; Zhang, X.L.; Li, J.G.; Chen, Z.Q.; Wang, Y.H.; Zhou, Y.Z.; Jin, T.; Sun, X.F.; Hu, Z.Q. Mechanism of competitive growth during directional solidification of a nickel-base superalloy in a three-dimensional reference frame. Acta Mat. 2012, 60, 3965–3975. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, M.; Yu, D.; Zhou, X.; Gu, Y.; Fu, H. Dependence of competitive grain growth on secondary dendrite orientation during directional solidification of a Ni-based superalloy. Metall. Mater. Trans. A 2013, 44A, 5113–5121. [Google Scholar] [CrossRef]
- Hu, S.; Liu, L.; Yang, W.; Zhang, J.; Huang, T.; Wang, Y.; Zhou, X. Competitive converging dendrites growth depended on dendrite spacing distribution of Ni-based bi-crystal superalloys. J. Alloys Compd. 2018, 735, 1878–1884. [Google Scholar] [CrossRef]
- Hallensleben, P.; Schaar, H.; Thome, P.; Jöns, N.; Jafarizadeh, J.; Steinbach, I.; Eggeler, G.; Frenzel, J. On the evolution of cast microstructures during processing of single crystal Ni-base superalloys using a Bridgman seed technique. Mat. Des. 2017, 128, 98–111. [Google Scholar] [CrossRef]
- Imagic-IMS. Available online: https://imagic.ch/en/imagic-ims (accessed on 11 July 2021).
- CorelDRAW Graphics Suite. Available online: https://www.coreldraw.com/en/ (accessed on 11 July 2021).
- ImageJ. Available online: https://imagej.de.softonic.com/ (accessed on 11 July 2021).
- Scholz, F.; Cevik, M.; Hallensleben, P.; Thome, P.; Eggeler, G.; Frenzel, J. Image and dendrite position raw-data generated in the present work. Zenodo 2021. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Miller, J.D.; Oppedal, A.L.; Solanki, K.N. Characterizing the local primary dendrite arm spacing in directionally solidified dendritic microstructures. Metall. Mater. Trans. A 2013, 45, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Aurenahmmer, F.; Klein, R. Voronoi Diagrams. In Handbook of Computational Geometry, 1st ed.; Sack, J.-R., Urrutia, J., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2000; pp. 201–290. [Google Scholar]
- Hielscher, R.; Schaeben, H. A novel pole figure inversion method: Specification of the MTEX algorithm. J. Appl. Cryst. 2008, 41, 1024–1037. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture analysis with MTEX—Free and open source software toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef] [Green Version]
- MATLAB. Available online: https://de.mathworks.com/products/matlab.html (accessed on 11 July 2021).
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Shimokawabe, T.; Aoki, T. Primary arm array during directional solidification of single-crystal binary alloy: Large scale phase-field study. Acta Mater. 2016, 118, 230–243. [Google Scholar] [CrossRef] [Green Version]
- Randle, V.; Engler, O. Introduction to Texture Analysis: Macrotexture, Microtexture and Orientation Mapping; CRC Press LLC.: Boca Raton, FL, USA, 2000. [Google Scholar]
- Zhou, Y.Z.; Volek, A.; Green, N.R. Mechanism of competitive grain growth in directional solidification of a nickel-base superalloy. Acta Mater. 2008, 56, 2631–2637. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kautz, E.; Yener, B.; Lewis, D. Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 2016, 123, 176–187. [Google Scholar]
- Nenchev, B.; Strickland, J.; Tassenberg, K.; Perry, S.; Gill, S.; Dong, H. Automatic recognition of dendritic solidification structures DenMap. J. Imaging 2020, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Stan, T.; Thompson, Z.T.; Voorhees, P.W. Optimizing convolution neural networks to perform semantic segmentation on large materials imaging datasets: X-ray tomography and serial sectioning. Mater. Charact. 2020, 160, 110119. [Google Scholar] [CrossRef]
- Scholz, F. Metallkundliche Untersuchung zur Mosaizität in einkristallinen Nickel-Basis-Superlegierungen. Ph.D. Thesis, Ruhr University Bochum, Bochum, Germany, 2021. [Google Scholar]
- Wang, Z.; Li, J.; Wang, J.; Zhou, Y. Phase field modeling the selection mechanism of primary dendritic spacing in directional solidification. Acta Mater. 2012, 60, 1957–1964. [Google Scholar] [CrossRef]
- Steinbach, I. Effect of interface anisotropy on spacing selection in constrained dendrite growth. Acta Mater. 2008, 56, 4965–4971. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 3rd ed.; Trans Tech Publications Ltd.: Aedermannsdorf Switzerland, 1992. [Google Scholar]
- Dantzig, J.A.; Rappaz, M. Solidification., 1st ed.; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Wang, F.; Wu, Z.; Ma, D.; Bührig-Polaczek, A. Effect of directional solidification variables on the microstructures of single-crystal turbine blades of Nickel-based superalloy. Adv. Eng. Mater. 2017, 19, 1700297. [Google Scholar] [CrossRef]
- D’Souza, N.; Ardakani, M.G.; Wagner, A.; Shollock, B.A.; McLean, M. Morphological aspects of competitive grain growth during directional solidification of a nickel-base superalloy, CMSX4. J. Mater. Sci. 2002, 37, 481–487. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wang, Y.; Wang, J. Phase-field study of competitive dendritic growth of converging grains during directional solidification. Acta Mater. 2012, 60, 1478–1493. [Google Scholar] [CrossRef]
- Takaki, T.; Shimokawabe, T.; Ohno, M.; Yamanaka, A.; Aoki, T. Unexpected selection of growing dendrites by very-large-scale phase-field simulation. J. Cryst. Growth 2013, 382, 21–25. [Google Scholar] [CrossRef]
- Hu, M.; Sun, C.; Fang, H.; Zhu, M. Competitive dendrite growth during directional solidification of a transparent alloy: Modeling and experiment. Eur. Phys. J. E 2020, 43, 16. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scholz, F.; Cevik, M.; Hallensleben, P.; Thome, P.; Eggeler, G.; Frenzel, J. A 3D Analysis of Dendritic Solidification and Mosaicity in Ni-Based Single Crystal Superalloys. Materials 2021, 14, 4904. https://doi.org/10.3390/ma14174904
Scholz F, Cevik M, Hallensleben P, Thome P, Eggeler G, Frenzel J. A 3D Analysis of Dendritic Solidification and Mosaicity in Ni-Based Single Crystal Superalloys. Materials. 2021; 14(17):4904. https://doi.org/10.3390/ma14174904
Chicago/Turabian StyleScholz, Felicitas, Mustafa Cevik, Philipp Hallensleben, Pascal Thome, Gunther Eggeler, and Jan Frenzel. 2021. "A 3D Analysis of Dendritic Solidification and Mosaicity in Ni-Based Single Crystal Superalloys" Materials 14, no. 17: 4904. https://doi.org/10.3390/ma14174904
APA StyleScholz, F., Cevik, M., Hallensleben, P., Thome, P., Eggeler, G., & Frenzel, J. (2021). A 3D Analysis of Dendritic Solidification and Mosaicity in Ni-Based Single Crystal Superalloys. Materials, 14(17), 4904. https://doi.org/10.3390/ma14174904






