Valley Vortex Assisted and Topological Protected Microparticles Manipulation with Complicated 2D Patterns in a Star-like Sonic Crystal
Abstract
:1. Introduction
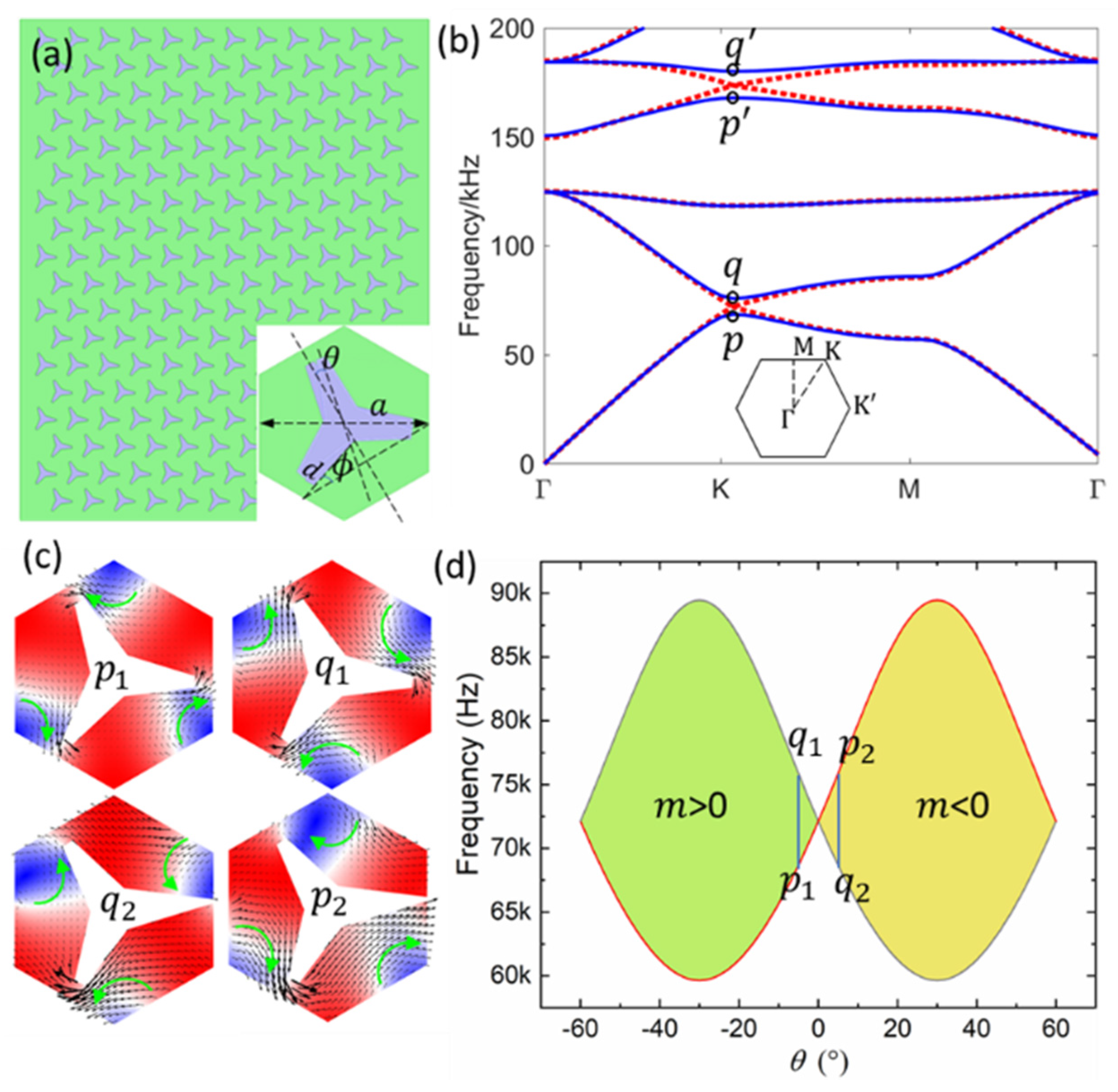
2. Structure and Design Methods
3. Results
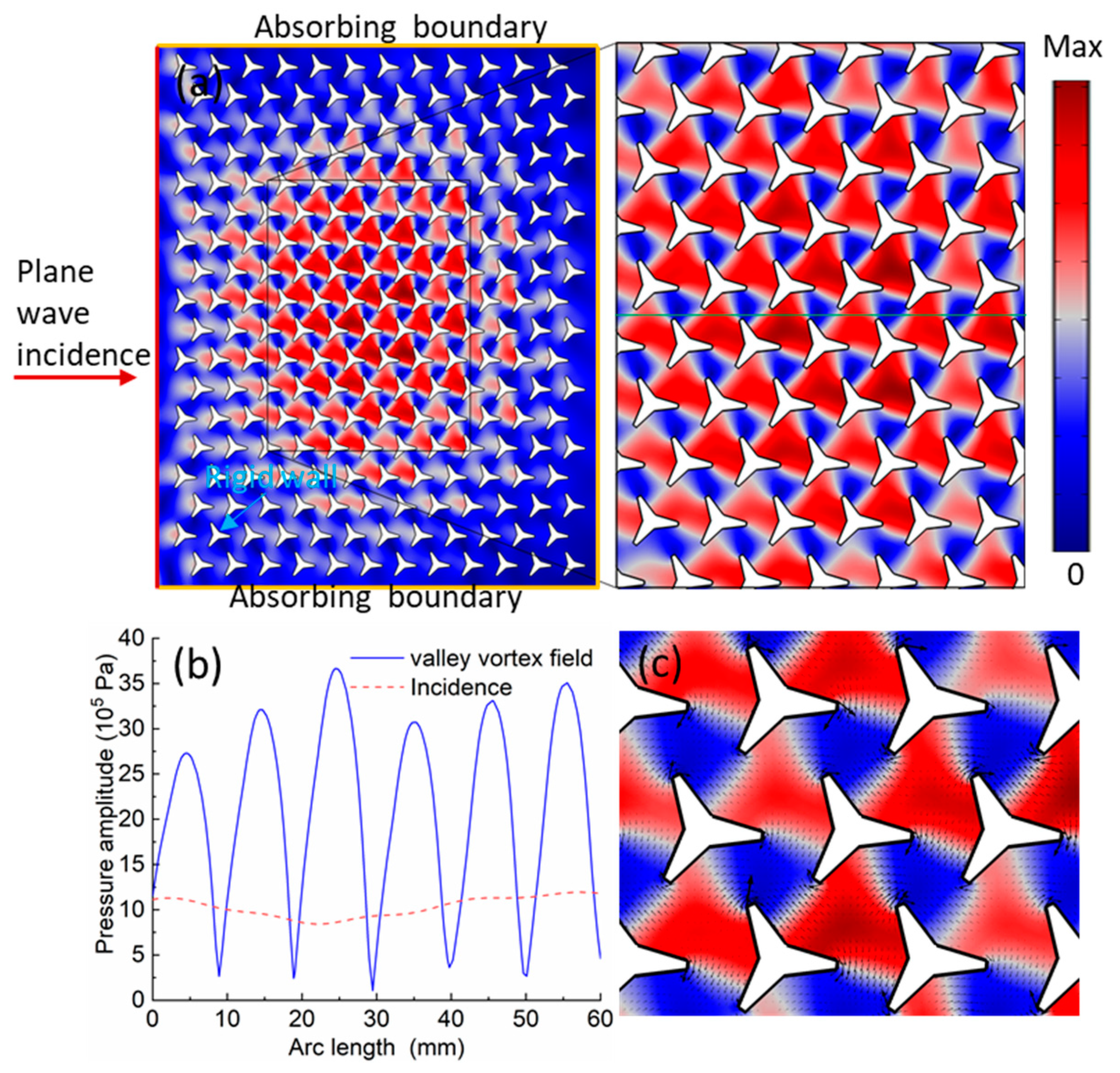
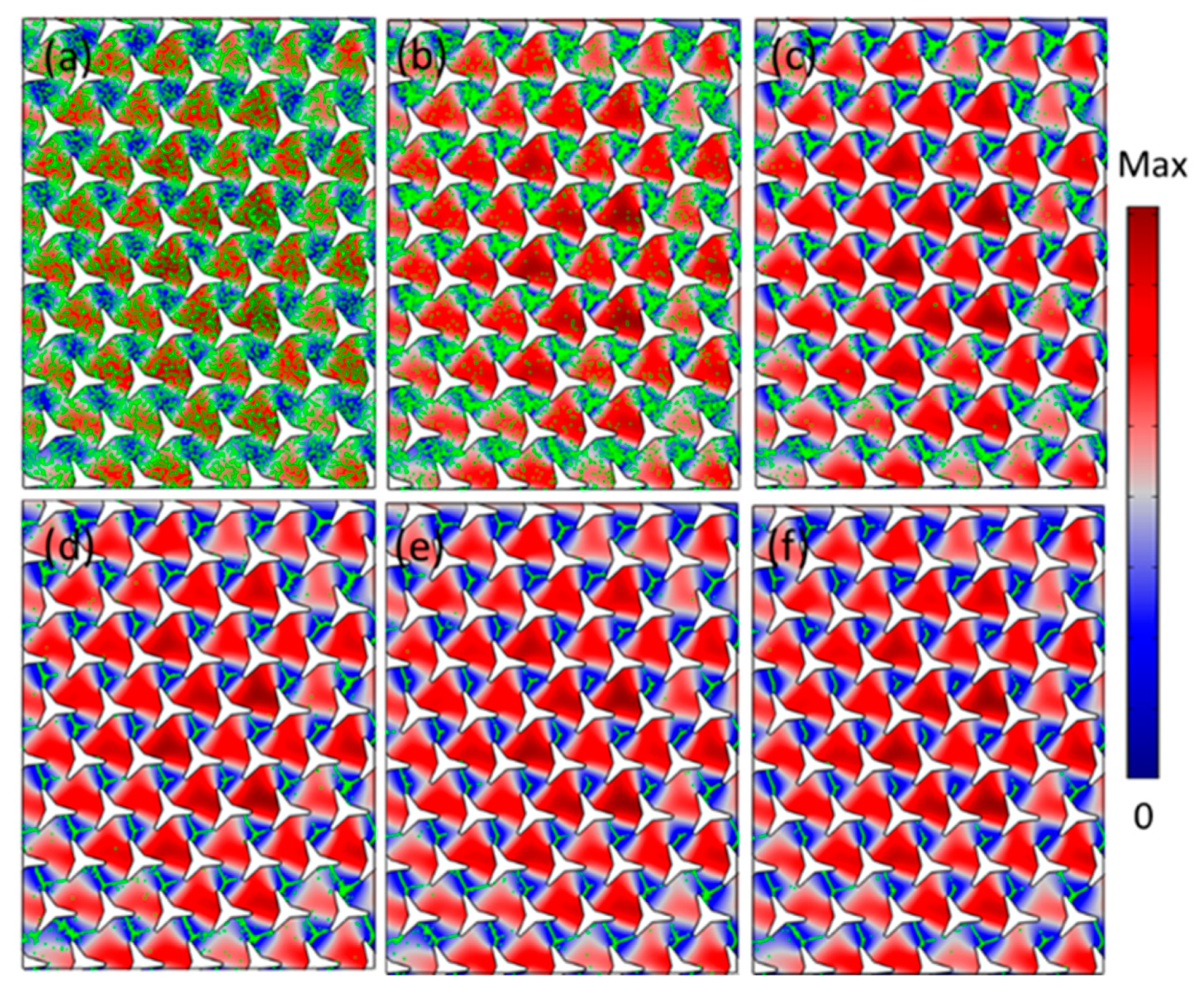
3.1. 2D Patterns and Particles Aggregation in the Sonic Crystals at the Different States
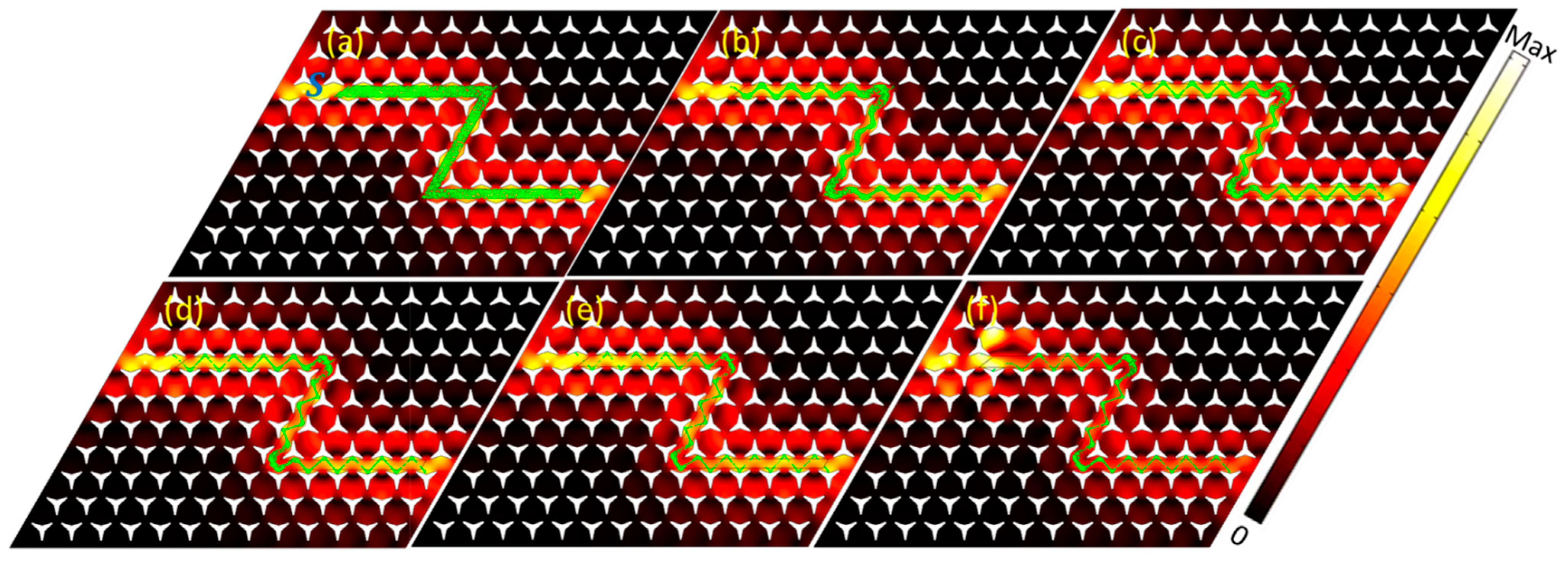
3.2. Topologically Protected Edge State and Its Microparticles Control along the Sharp Corner
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Timonen, J.V.I.; Latikka, M.; Leibler, L.; Ras, R.H.A.; Ikkala, O. Switchable static and dynamic self-assembly of magnetic droplets on superhydrophobic surfaces. Science 2013, 341, 253–257. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Torab, P.; Mach, K.E.; Surrette, C.; England, M.R.; Craft, D.W.; Thomas, N.J.; Liao, J.C.; Puleo, C.; Wong, P.K. Adaptable microfluidic system for single-cell pathogen classification and antimicrobial susceptibility testing. Proc. Natl. Acad. Sci. USA 2019, 116, 10270–10279. [Google Scholar] [CrossRef] [Green Version]
- Khandurina, J.; Guttman, A. Bioanalysis in microfluidic devices. J. Chromatogr. A 2002, 943, 159–183. [Google Scholar] [CrossRef]
- Armstrong, J.P.K.; Armstrong, J.P.; Puetzer, J.L.; Serio, A.; Guex, A.G.; Kapnisi, M.; Breant, A.; Stevens, M.M. Generating multifunctional acoustic tweezers in Petri dishes for contactless, precise manipulation of bioparticles. Adv. Mater. 2018, 30, e1802649. [Google Scholar] [CrossRef] [Green Version]
- Cacace, T.; Memmolo, P.; Villone, M.M.; de Corato, M.; Mugnano, M.; Paturzo, M.; Maffettone, P.L. Assembling and rotating erythrocyte aggregates by acoustofluidic pressure enabling full phase-contrast tomography. Lab Chip 2019, 19, 3123–3132. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, A.; Rufo, J.; Guo, F.; Gu, Y.; Li, P.; Lata, J.; Huang, T.J. Acoustic tweezers for the life sciences. Nat. Methods 2018, 15, 1021–1028. [Google Scholar] [CrossRef] [Green Version]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef] [PubMed]
- Hejazian, M.; Li, W.; Nguyen, N.T. Lab on a chip for continuous-flow magnetic cell separation. Lab Chip 2015, 15, 959–970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Probst, R.; Shapiro, B. Three-dimensional electrokinetic tweezing: Device design, modeling, and control algorithms. J. Micromech. Microeng. 2011, 21, 027004. [Google Scholar] [CrossRef] [Green Version]
- Drinkwater, B.W. Dynamic-field devices for the ultrasonic manipulation of microparticles. Lab Chip 2016, 16, 2360–2375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, X.; Li, P.; Lin, S.S.; Stratton, Z.S.; Nama, N.; Guo, F.; Slotcavage, D.; Mao, X.; Shi, J.; Costanzo, F.; et al. Surface acoustic wave microfluidics. Lab Chip 2013, 13, 3626–3649. [Google Scholar] [CrossRef] [PubMed]
- Devendran, C.; Albrecht, T.; Brenker, J.; Alan, T.; Neild, A. The importance of travelling wave components in standing surface acoustic wave (SSAW) systems. Lab Chip 2016, 16, 3756–3766. [Google Scholar] [CrossRef] [PubMed]
- Arrabito, G.; Galati, C.; Castellano, S.; Pignataro, B. Luminometric sub-nanoliter droplet-to-droplet array (LUMDA) and its application to drug screening by phase I metabolism enzymes. Lab Chip 2013, 13, 68–72. [Google Scholar] [CrossRef]
- Tian, L.; Martin, N.; Bassindale, P.G.; Patil, A.J.; Li, M.; Barnes, A.; Mann, S. Spontaneous assembly of chemically encoded two-dimensional coacervate droplet arrays by acoustic wave patterning. Nat. Commun. 2016, 7, 1–10. [Google Scholar]
- Collins, D.J.; O’Rorke, R.; Neild, A.; Han, J.; Ai, Y. Acoustic fields and microfluidic patterning around embedded micro-structures subject to surface acoustic waves. Soft Matter 2019, 15, 86918705. [Google Scholar] [CrossRef]
- Chen, W.; Holm, S. Modified Szabo’s wave equation models for lossy media obeying frequency power law. J. Acoust. Soc. Am. 2003, 114, 2570–2574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Ma, Z.; Ai, Y. Submicron particle concentration and patterning with ultralow frequency acoustic vibration. Anal. Chem. 2020, 92, 12795–12800. [Google Scholar] [CrossRef]
- Melde, K.; Mark, A.G.; Qiu, T.; Fischer, P. Holograms for acoustics. Nature 2016, 537, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Cheng, F.; Liu, G.; Li, K.; Guo, Z. Dexterous formation of unconventional Chladni patterns using standing bulk acoustic waves. Appl. Phys. Lett. 2020, 117, 184101. [Google Scholar] [CrossRef]
- Dai, H.; Xia, B.; Yu, D. Acoustic patterning and manipulating microparticles using phononic crystal. J. Phys. D Appl. Phys. 2019, 52, 425302. [Google Scholar] [CrossRef]
- Fard, S.M.; Peters, H.; Kessissoglou, N.; Marburg, S. Three-dimensional analysis of a noise barrier using a quasi-periodic boundary element method. J. Acoust. Soc. Am. 2015, 137, 3107–3114. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Liu, P.; Guo, X.; Zhou, S.; Dong, Y. 2D acoustofluidic patterns in an ultrasonic chamber modulated by phononic crystal structures. Microfluid. Nanofluid. 2020, 24, 1–22. [Google Scholar] [CrossRef]
- Dai, H.; Chen, T.; Jiao, J.; Xia, B.; Yu, D. Topological valley vortex manipulation of microparticles in phononic crystals. J. Appl. Phys. 2019, 126, 145101. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Ke, M.; Liu, Z. Valley vortex states in sonic crystals. Phys. Rev. Lett. 2016, 116, 093901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, G.; Xiao, M.; Chan, C.T. Topological phases in acoustic and mechanical systems. Nat. Rev. Phys. 2019, 1, 281–294. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Deng, W.; Huang, X.; Li, F.; Zhang, F.; Chen, S.; Liu, Z. Valley topological phases in bilayer sonic crystals. Phys. Rev. Lett. 2018, 120, 116802. [Google Scholar] [PubMed] [Green Version]
- Zhang, Z.; Tian, Y.; Cheng, Y.; Wei, Q.; Liu, X.; Christensen, J. Topological acoustic delay line. Phys. Rev. Appl. 2018, 9, 034032. [Google Scholar] [CrossRef] [Green Version]
- Geng, Z.G.; Peng, Y.G.; Shen, Y.X.; Zhao, D.G.; Zhu, X.F. Acoustic delay-line filters based on largely distorted topological insulators. Appl. Phys. Lett. 2018, 113, 033503. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2017, 13, 369–374. [Google Scholar]
- Chen, C.; Chen, T.; Wang, Y.; Wu, J.; Zhu, J. Observation of topological locally resonate and Bragg edge modes in a two-dimensional slit-typed sonic crystal. Appl. Phys. Express 2019, 12, 097001. [Google Scholar] [CrossRef]
- Geng, Z.G.; Peng, Y.G.; Li, P.Q.; Shen, Y.X.; Zhao, D.G.; Zhu, X.F. Mirror-symmetry induced topological valley transport along programmable boundaries in a hexagonal sonic crystal. J. Phys. Condens. Matter 2019, 31, 245403. [Google Scholar] [CrossRef]
- Xia, J.P.; Jia, D.; Sun, H.X.; Yuan, S.Q.; Ge, Y.; Si, Q.R.; Liu, X.J. Programmable coding acoustic topological insulator. Adv. Mater. 2018, 30, 1805002. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Chen, T.; Song, A.; Song, X.; Zhu, J. Switchable asymmetric acoustic transmission based on topological insulator and metasurfaces. J. Phys. D Appl. Phys. 2020, 53, 44LT01. [Google Scholar] [CrossRef]
- Dai, H.; Liu, L.; Xia, B.; Yu, D. Experimental realization of topological on-chip acoustic tweezers. Phys. Rev. Appl. 2021, 15, 064032. [Google Scholar] [CrossRef]
- Sharma, G.S.; Faverjon, B.; Dureisseix, D.; Skvortsov, A.; MacGillivray, I.; Audoly, C.; Kessissoglou, N. Acoustic performance of a periodically voided viscoelastic medium with uncertainty in design parameters. J. Vib. Acous. 2020, 142, 061002. [Google Scholar] [CrossRef]
- Gor'kov, L.P. On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys. Dokl. 1962, 6, 773–775. [Google Scholar]
- Bruus, H. Acoustofluidics 7: The acoustic radiation force on small particles. Lab Chip 2012, 12, 1014–1021. [Google Scholar] [CrossRef] [PubMed]
- Riaud, A.; Wang, W.; Thai, A.L.; Taly, V. Mechanical characterization of cells and microspheres sorted by acoustophoresis with in-line resistive pulse sensing. Phys. Rev. Appl. 2020, 13, 034058. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Sala, R.; Sancho, J.; Sanchez, J.V.; Gomez, V.; Llinares, J.; Meseguer, F. Sound attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Sanchez-Dehesa, J.; Garcia-Chocano, V.M.; Torrent, D.; Cervera, F.; Cabrera, S. Noise control by sonic crystal barriers made of recycled materials. J. Acoust. Soc. Am. 2011, 129, 1173–1183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elmadih, W.; Chronopoulos, D.; Zhu, J. Metamaterials for simultaneous acoustic and elastic bandgaps. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. On superscattering of sound waves by a lattice of disk-shaped cavities in a soft material. Appl. Phys. Lett. 2020, 116, 041602. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound scattering by a bubble metasurface. Phys. Rev. B 2020, 102, 214308. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Chen, T.; Chen, C.; Ding, W. Valley Vortex Assisted and Topological Protected Microparticles Manipulation with Complicated 2D Patterns in a Star-like Sonic Crystal. Materials 2021, 14, 4939. https://doi.org/10.3390/ma14174939
Zhu J, Chen T, Chen C, Ding W. Valley Vortex Assisted and Topological Protected Microparticles Manipulation with Complicated 2D Patterns in a Star-like Sonic Crystal. Materials. 2021; 14(17):4939. https://doi.org/10.3390/ma14174939
Chicago/Turabian StyleZhu, Jian, Tianning Chen, Chen Chen, and Wei Ding. 2021. "Valley Vortex Assisted and Topological Protected Microparticles Manipulation with Complicated 2D Patterns in a Star-like Sonic Crystal" Materials 14, no. 17: 4939. https://doi.org/10.3390/ma14174939
APA StyleZhu, J., Chen, T., Chen, C., & Ding, W. (2021). Valley Vortex Assisted and Topological Protected Microparticles Manipulation with Complicated 2D Patterns in a Star-like Sonic Crystal. Materials, 14(17), 4939. https://doi.org/10.3390/ma14174939




