Independent Lung Ventilation-Experimental Studies on a 3D Printed Respiratory Tract Model
Abstract
1. Introduction
2. Materials and Methods
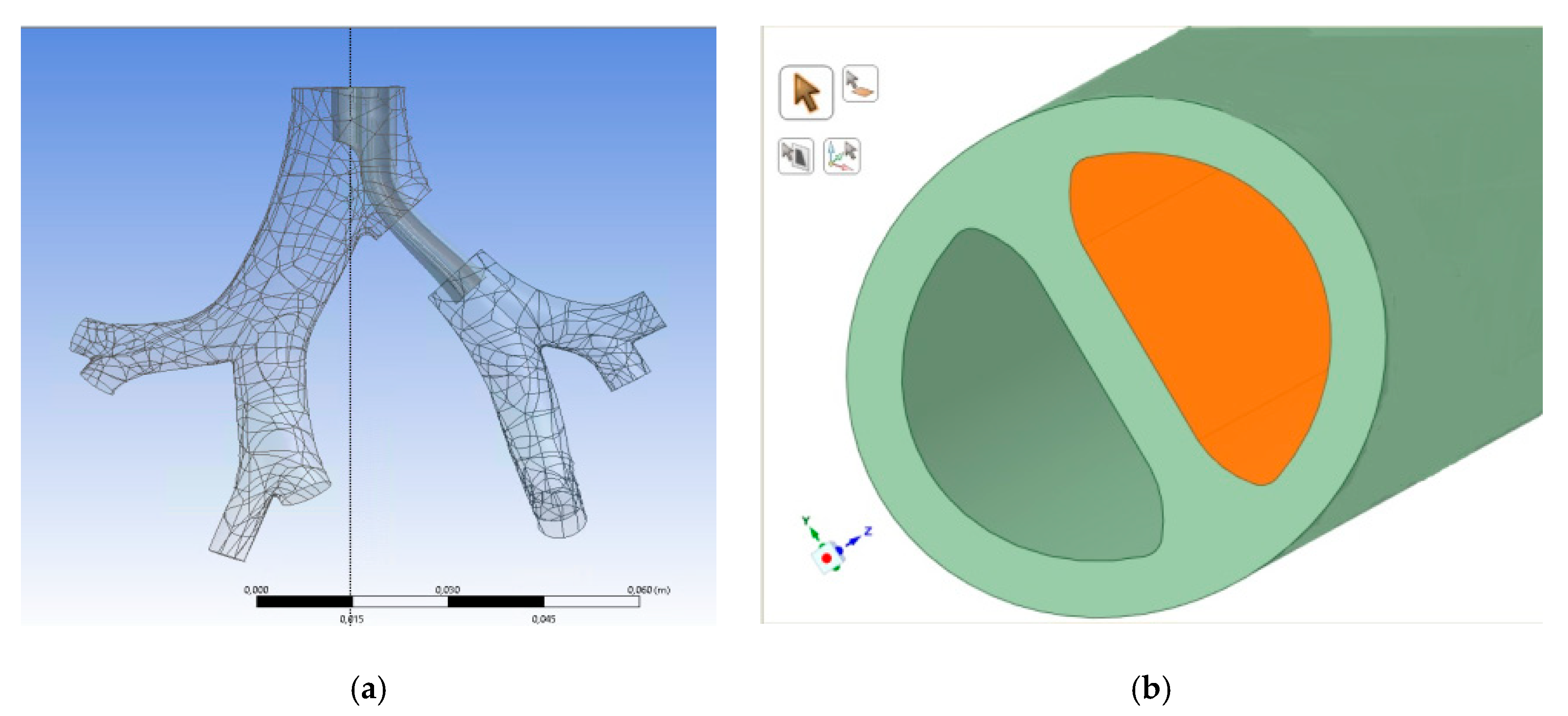
2.1. Model Preparation and 3D Printing
2.2. Experimental Setup
2.3. Numerical Simulations
3. Results and Discussion
3.1. Impact of Double-Lumen ETT
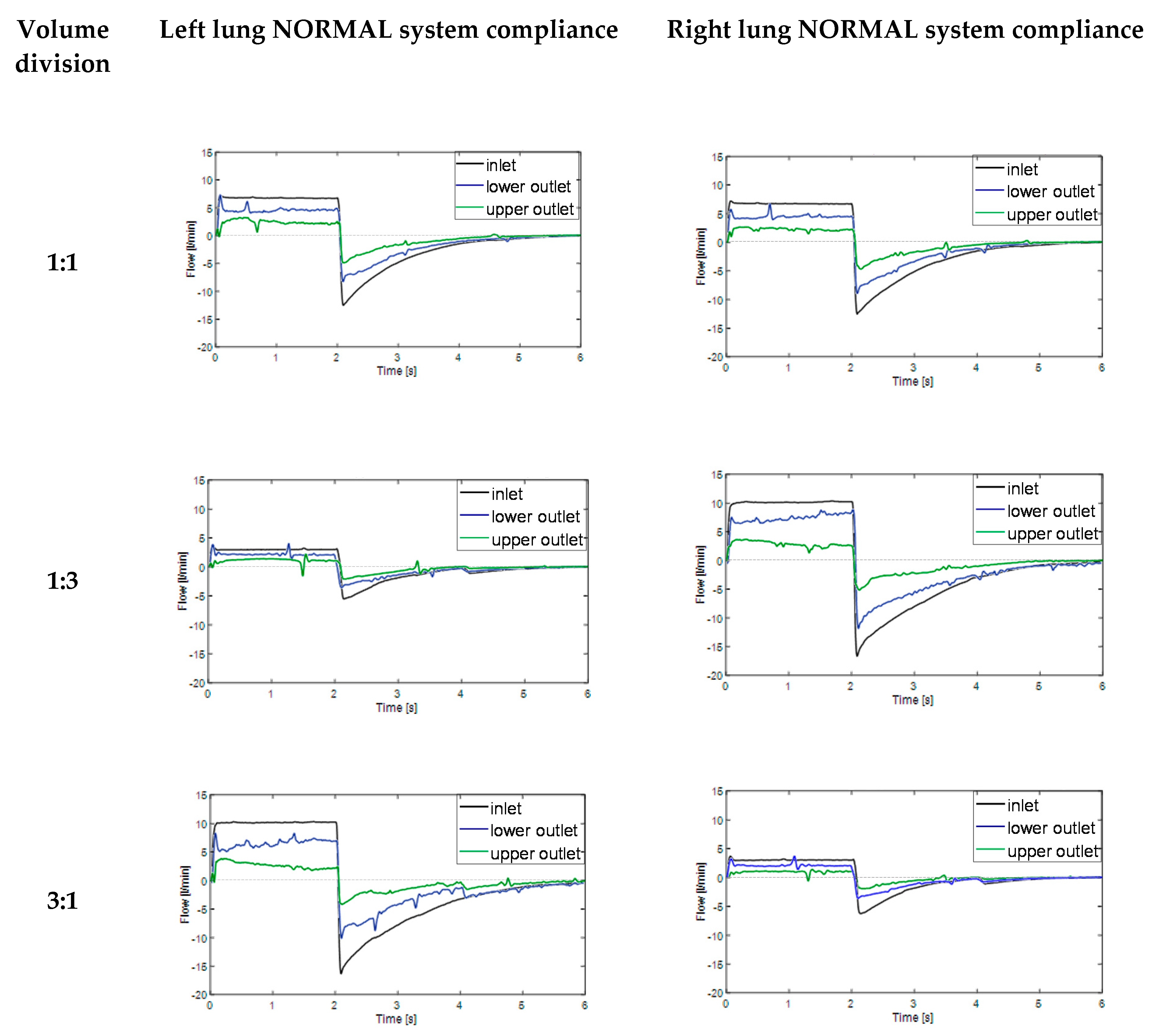
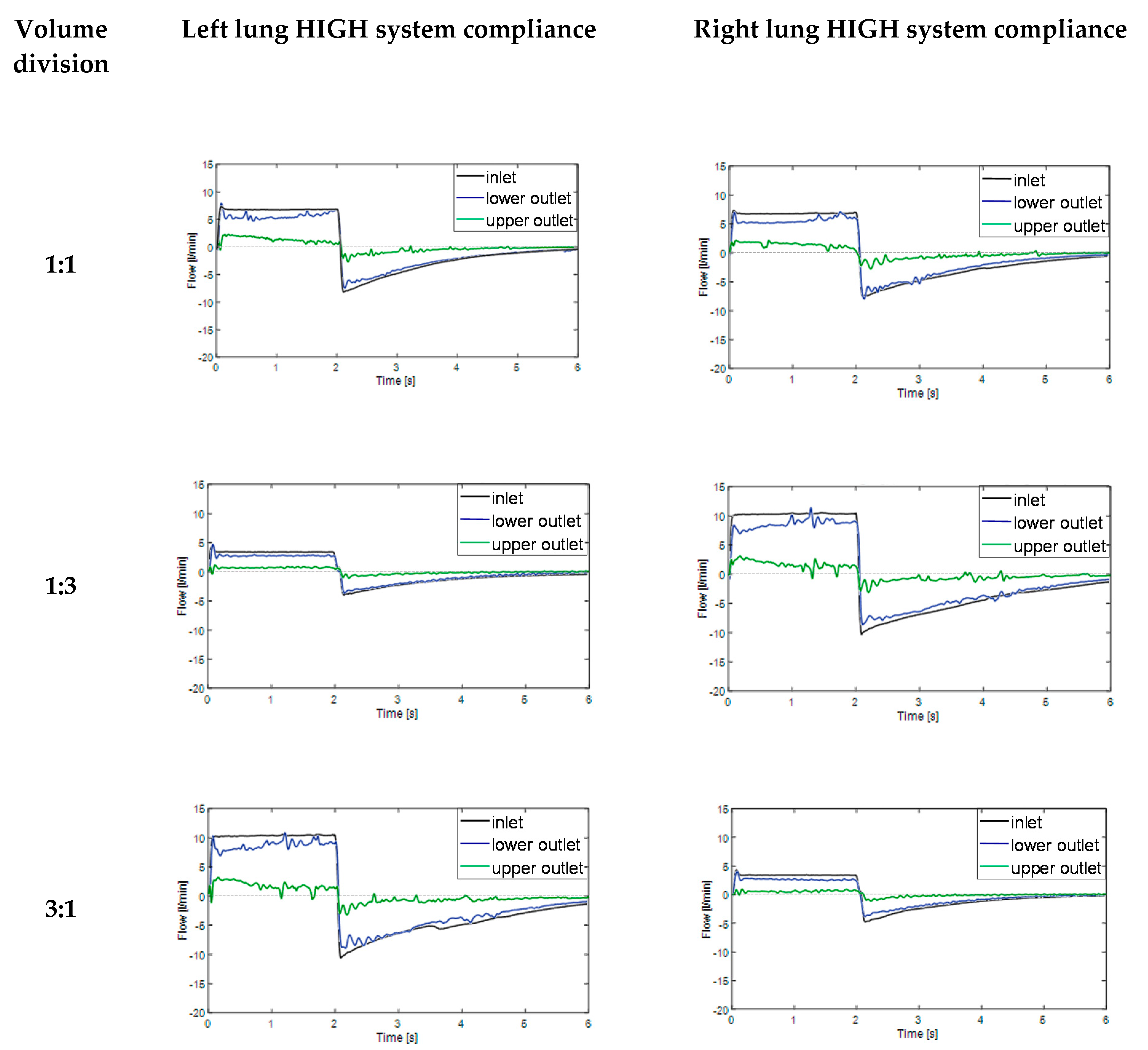
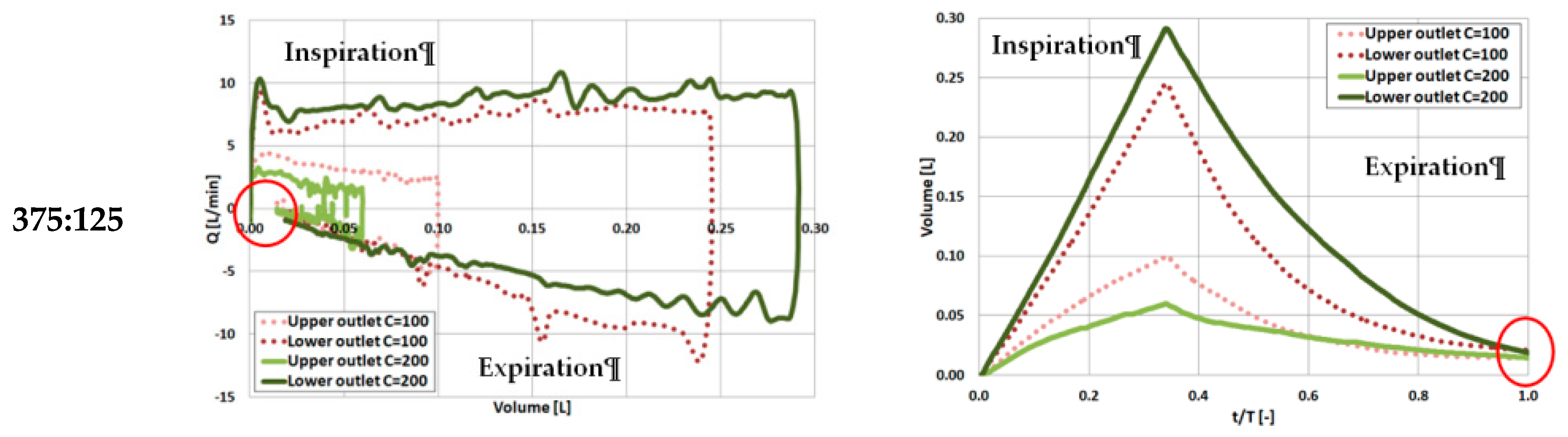
3.2. Impact of System Compliance
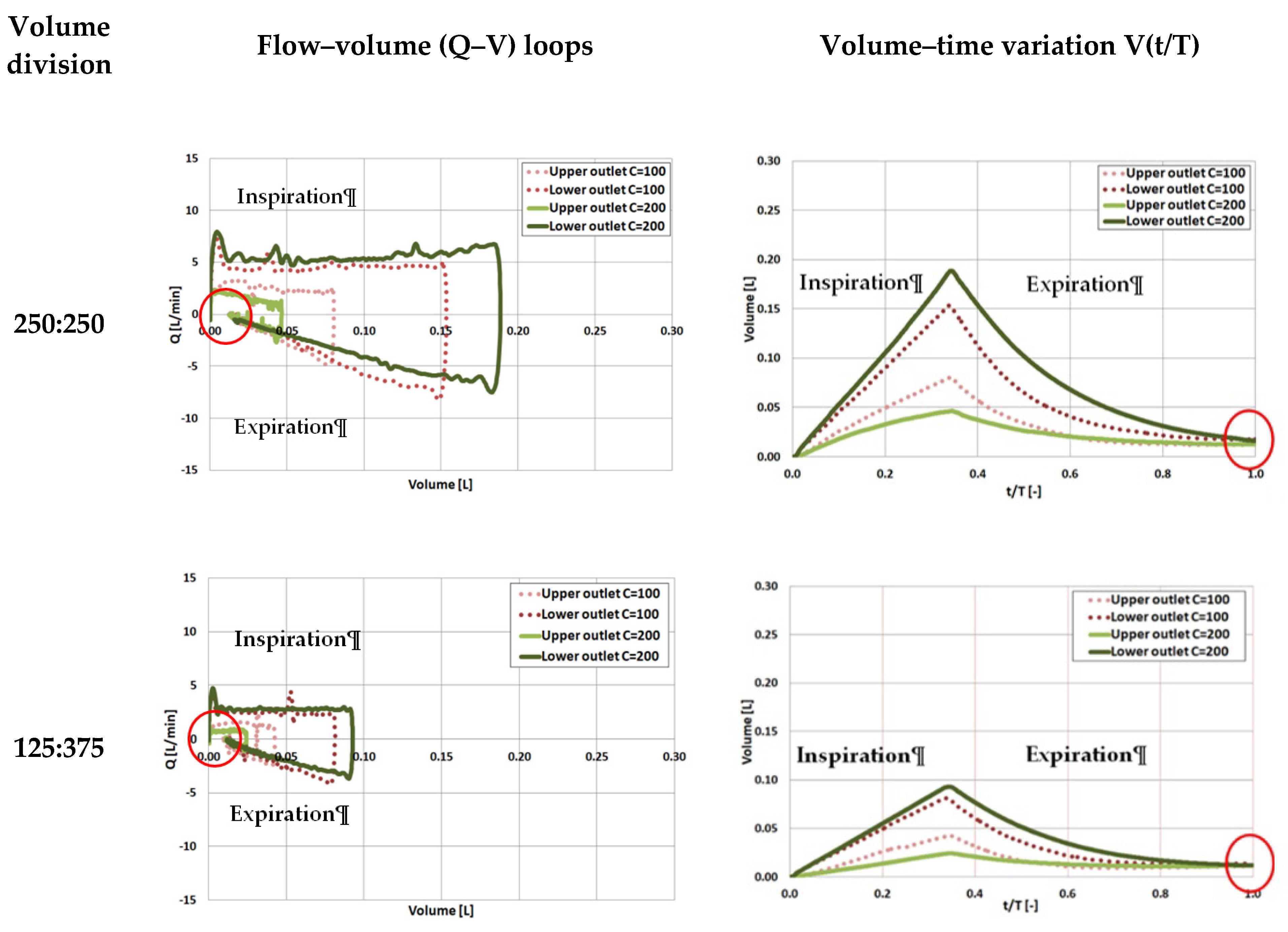
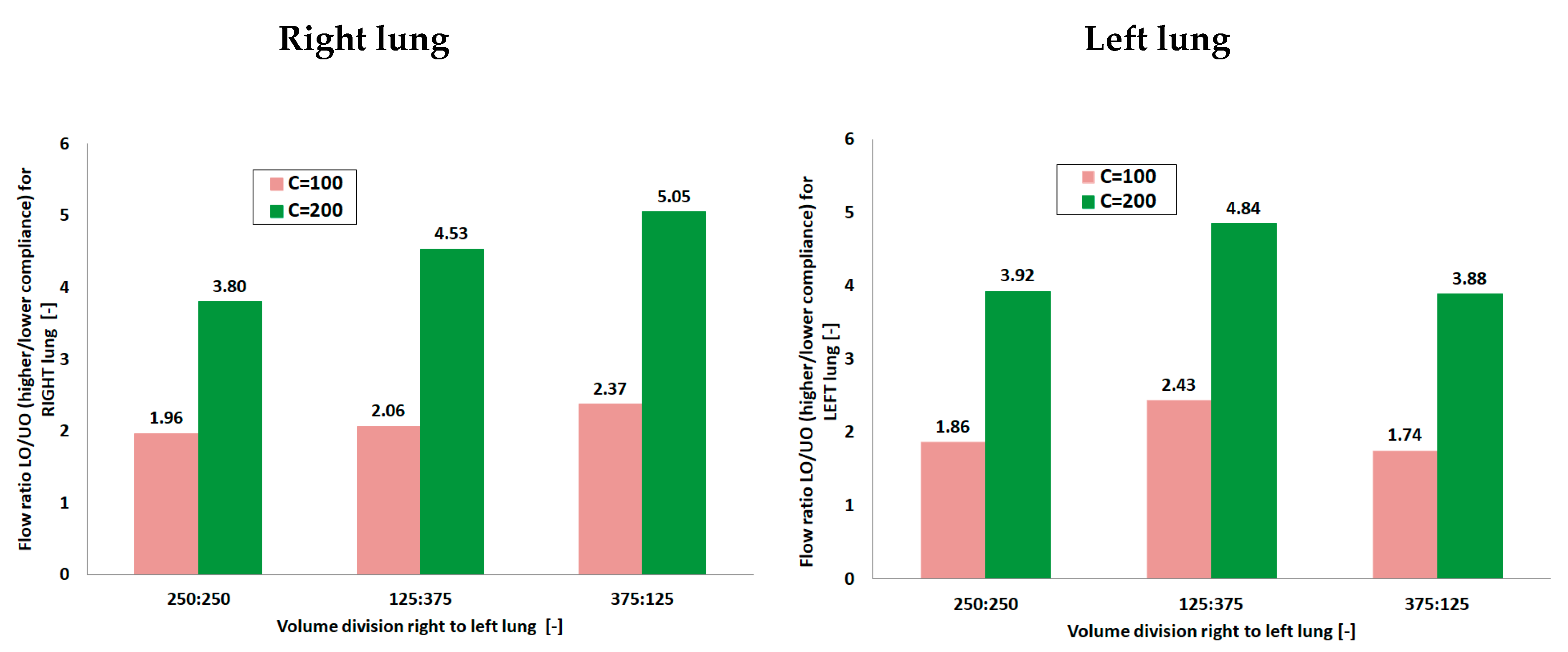
3.3. Flow Distribution Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sawulski, S.; Nestorowicz, A.; Wośko, J.; Dąbrowski, W.; Kowalczyk, M.; Fijałkowska, A. Independent lung ventilation for treatment of post-traumatic ARDS. Anaesth. Intens. Ther. 2012, 44, 85–88. [Google Scholar]
- Berg, S.; Bittner, E.A.; Berra, L.; Kacmarek, R.M.; Sonny, A. Independent lung ventilation: Implementation strategies and review of literature. World J. Crit. Care Med. 2019, 8, 49–58. [Google Scholar] [CrossRef]
- Ranney, M.L.; Griffeth, V.; Jha, A.K. Critical Supply Shortages—The Need for Ventilators and Personal Protective Equipment during the COVID-19 Pandemic. N. Engl. J. Med. 2020, 382, e41. [Google Scholar] [CrossRef]
- Buczkowski, P.W.; Fombon, F.N.; Russell, W.C.; Thompson, J.P. Effects of helium on high frequency jet ventilation in model of airway stenosis. Br. J. Anaesth. 2005, 95, 701–705. [Google Scholar] [CrossRef][Green Version]
- Nagels, M.A.; Carter, J.E. Large Eddy simulation of high frequency oscillating flow in as asymmetric branching airway model. Med. Eng. Phys. 2009, 31, 1148–1153. [Google Scholar] [CrossRef]
- Tanaka, G.; Ogata, T.; Oka, K.; Tanishita, K. Spatial and temporal variation of secondary flow during oscillatory flow in model human central airways. J. Biomech. Eng. 1999, 121, 565–573. [Google Scholar] [CrossRef]
- Heraty, K.; Laffey, J.; Quinlan, N. Fluid dynamics of gas exchange in high-frequency oscillatory ventilation: In vitro investigations in idealized and anatomically realistic airway bifurcation models. Ann. Biomed. Eng. 2008, 36, 1856–1869. [Google Scholar] [CrossRef]
- Alzahranny, M.; Banerjee, A.; Salzman, G. The role of coupled resistance-compliance in upper tracheobronchial airways under high frequency oscillatory ventilation. Med. Eng. Phys. 2014, 36, 1593–1604. [Google Scholar] [CrossRef]
- Chang, H.K. Mechanisms of gas transport during ventilation by high-frequency oscillation. J. Appl. Physiol. 1984, 56, 553–563. [Google Scholar] [CrossRef]
- Henderson, W.R.; Sheel, A.W. Pulmonary mechanics during mechanical ventilation. Respir. Physiol. Neurobiol. 2012, 180, 162–172. [Google Scholar] [CrossRef]
- Alzahrany, M.; Banerjee, A.; Salzman, G. Flow transport and gas mixing during invasive high frequency oscillatory ventilation. Med. Eng. Phys. 2014, 36, 647–658. [Google Scholar] [CrossRef] [PubMed]
- Green, A.S. Modelling of peak-flow wall shear stress in major airways of the lung. J. Biomech. 2004, 37, 661–667. [Google Scholar] [CrossRef]
- Muller, W.J.; Gerjarusek, S.; Scherer, P.W. Studies of wall shear and mass transfer in a large scale model of neonatal high-frequency jet ventilation. Ann. Biomed. Eng. 1990, 18, 69–88. [Google Scholar] [CrossRef]
- Van Rhein, T.; Alzahrany, M.; Banerjee, A.; Salzman, G. Fluid flow and particle transport in mechanically ventilated airways. Part I. Fluid flow structures. Med. Biol. Comput. 2016, 54, 1085–1096. [Google Scholar] [CrossRef]
- Osswald, M.; Wegmann, A.; Greif, R.; Theiler, L.; Pedersen, T.H. Facilitation of bronchoscopy teaching with easily accessible low-cost 3D-printing. Trends Anaesth. Crit. Care 2017, 15, 37–41. [Google Scholar] [CrossRef]
- Akiba, T.; Inagaki, T.; Nakada, T. Three-dimensional printing model of anomalous bronchi before surgery. Ann. Thorac. Cardiovasc. Surg. 2014, 20, 659–662. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, K.; Yamasaki, N.; Tsuchiya, T.; Miyazaki, T.; Kamohara, R.; Hatachi, G. Three-dimensional (3D) bronchial tree model for bronchial resection with pulmonary segmentectomy. J. Thorac. Dis. 2018, 10, 179–182. [Google Scholar] [CrossRef] [PubMed]
- Les, A.S.; Ohye, R.G.; Filbrun, A.G.; Ghadimi Mahani, M.; Flanagan, C.L.; Daniels, R.C.; Kidwell, K.M.; Zopf, D.A.; Hollister, S.J.; Green, G.E. 3D-printed, externally-implanted, bioresorbable airway splints for severe tracheobronchomalacia. Laryngoscope 2019, 129, 1763–1771. [Google Scholar] [CrossRef]
- Morrison, R.J.; Hollister, S.J.; Niedner, M.F. Mitigation of tracheobronchomalacia with 3D-printed personalized medical devices in pediatric patients. Sci. Transl. Med. 2015, 7, 285ra64. [Google Scholar] [CrossRef]
- Su, W.-C.; Chen, Y.; Xi, J. Estimation of the deposition of ultrafine 3D printing particles in human tracheobronchial airways. J. Aerosol Sci. 2020, 149, 105605. [Google Scholar] [CrossRef]
- Tian, G.; Longest, P.W.; Su, G.; Hindle, M. Characterization of respiratory drug delivery with enhanced condensational growth (ECG) using an individual path model of the entire tracheobronchial airways. Ann. Biomed. Eng. 2011, 39, 1136–1153. [Google Scholar] [CrossRef] [PubMed]
- Tian, G.; Longest, P.W.; Su, G.; Walenga, R.L.; Hindle, M. Development of a stochastic individual path (SIP) model for predicting the tracheobronchial deposition of pharmaceutical aerosols: Effects of transient inhalation and sampling the airways. J. Aerosol Sci. 2011, 42, 781–799. [Google Scholar] [CrossRef]
- Krenke, R.; Guć, M.; Grabczak, E.M. Development of an electronic manometer for intrapleural pressure monitoring. Respiration 2011, 82, 377–385. [Google Scholar] [CrossRef] [PubMed]
- Zielinska-Krawczyk, M.; Grabczak, E.M.; Michnikowski, M. Patterns of pleural pressure amplitude and respiratory rate changes during therapeutic thoracentesis. BMC Pulm. Med. 2018, 18, 36. [Google Scholar] [CrossRef] [PubMed]
- Alzahrany, M.; Banerjee, A. A biomechanical model of pendelluft induced lung injury. J. Biomech. 2015, 48, 1804–1810. [Google Scholar] [CrossRef]
- Bauer, K.; Brucker, C. The role of ventilation frequency in airway reopening. J. Biomech. 2009, 42, 1108–1113. [Google Scholar] [CrossRef]
- Ionescu, C.M.; De Keyser, R.M.C. Respiratory mechanics assessed by pressure-volume loops with forced oscillations. Comput. Methods Biomech. Biomed. Eng 2005, 8 (Suppl. S1), S143–S144. [Google Scholar] [CrossRef][Green Version]
- Pierce, L.N. Management of the Mechanically Ventilated Patient, 2nd ed.; Elsevier: Philadelphia, PA, USA, 2007. [Google Scholar]
- Yoshida, T.; Torsani, V.; Gomes, S.; De Santis, R.R.; Beraldo, M.A.; Costa, E.L.V.; Amato, M.B.P. Spontaneous effort causes occult pendelluft during mechanical ventilation. Am. J. Respir. Crit. Care Med. 2013, 188, 1420–1427. [Google Scholar] [CrossRef]
- Alzahrany, M.; Banerjee, A. Effect of inhaled gas density on the pendelluft-induced lung injury. J. Biomech. 2016, 49, 4039–4047. [Google Scholar] [CrossRef]
- Alzahrany, M.; Van Rhein, T.; Banerjee, A.; Salzman, G. Fluid flow and particle transport in mechanically ventilated airways. Part II. Particle transport. Med. Biol. Comput. 2016, 54, 1097–1109. [Google Scholar] [CrossRef]
- Sosnowski, T.R.; Zaniewska, A.; Kramek-Romanowska, K. Experimental Studies on Particle Deposition in Obstructed Bronchial Bifurcations. In Respiratory Drug Delivery Europe 2011; Dalby, R.N., Byron, P.R., Peart, J., Suman, J.D., Young, P.M., Eds.; VCU/Davis Healthcare Publ.: Richmond, VA, USA, 2011; Volume 2, pp. 543–546. [Google Scholar]
- Johari, N.H.; Osman, K.; Helmi, N.H.N.; Abdul Kadir, M.A.R. Comparative analysis of realistic CT-scan and simplified human airway models in airflow simulation. Comput. Methods Biomech. Biomed. Eng. 2013, 18, 48–56. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Values |
|---|---|
| Model Material | PLA (3DGence) |
| Support Material | BVOH (Verbatim) |
| Printing temperature | 200 (°C) |
| Infill percent | 20 (%) |
| Infill pattern | Zig Zag |
| Side walls | 2 |
| Top walls | 6 |
| Bottom walls | 4 |
| Bed adhesion | Raft |
| Layer height | 0.15 (mm) |
| Printing time | 9 h 50 min |
| Parameter | Values | Unit |
|---|---|---|
| System static compliance, C |
| mL/cm H2O |
| Tidal volume, VT |
| mL |
| Inspiration-expiration ratio, I:E |
| - |
| Duration of the breath cycle, T |
| S |
| Breath frequency, f |
| 1/min |
| Tidal volume (VT) division (right to left lung) |
| - |
| VT Division | Resistance (cm H2O/L/s) | Pressure Ratio LO/UO Right Lung | Pressure Ratio LO/UO Left Lung | Flow Ratio LO/UO Right Lung | Flow Ratio LO/UO Left Lung |
|---|---|---|---|---|---|
| 1:1 with ETT | 15 | 1.01 | 1.02 | 1.96 | 1.86 |
| 1:1 no ETT | 2.5 | 1.02 | 1.00 | 1.85 | 1.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kramek-Romanowska, K.; Stecka, A.M.; Zieliński, K.; Dorosz, A.; Okrzeja, P.; Michnikowski, M.; Odziomek, M. Independent Lung Ventilation-Experimental Studies on a 3D Printed Respiratory Tract Model. Materials 2021, 14, 5189. https://doi.org/10.3390/ma14185189
Kramek-Romanowska K, Stecka AM, Zieliński K, Dorosz A, Okrzeja P, Michnikowski M, Odziomek M. Independent Lung Ventilation-Experimental Studies on a 3D Printed Respiratory Tract Model. Materials. 2021; 14(18):5189. https://doi.org/10.3390/ma14185189
Chicago/Turabian StyleKramek-Romanowska, Katarzyna, Anna M. Stecka, Krzysztof Zieliński, Agata Dorosz, Piotr Okrzeja, Marcin Michnikowski, and Marcin Odziomek. 2021. "Independent Lung Ventilation-Experimental Studies on a 3D Printed Respiratory Tract Model" Materials 14, no. 18: 5189. https://doi.org/10.3390/ma14185189
APA StyleKramek-Romanowska, K., Stecka, A. M., Zieliński, K., Dorosz, A., Okrzeja, P., Michnikowski, M., & Odziomek, M. (2021). Independent Lung Ventilation-Experimental Studies on a 3D Printed Respiratory Tract Model. Materials, 14(18), 5189. https://doi.org/10.3390/ma14185189






