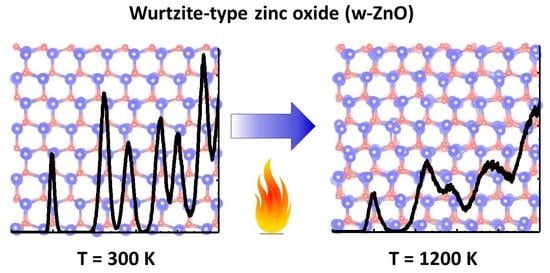
Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy

Bocharov, Dmitry; Pudza, Inga; Klementiev, Konstantin; Krack, Matthias; Kuzmin, Alexei

doi:10.3390/ma14185206

Submit to this Journal Review for this Journal Edit a Special Issue

Article Menu

...

Open AccessArticle

Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy

Dmitry Bocharov

^1,*

Inga Pudza

Konstantin Klementiev

Matthias Krack

and

Alexei Kuzmin

^1,*

Institute of Solid State Physics, University of Latvia, Kengaraga Street 8, LV-1063 Riga, Latvia

MAX IV Laboratory, Lund University, P.O. Box 118, SE-221 00 Lund, Sweden

Laboratory for Materials Simulations, Paul Scherrer Institut (PSI), CH-5232 Villigen, Switzerland

Authors to whom correspondence should be addressed.

Academic Editors: Ana Pimentel and Daniela Nunes

Materials 2021, 14(18), 5206; https://doi.org/10.3390/ma14185206

Received: 5 August 2021 / Revised: 3 September 2021 / Accepted: 8 September 2021 / Published: 10 September 2021

(This article belongs to the Special Issue ZnO Materials: Synthesis, Properties and Applications)

View Full-Text Download PDF

Browse Figures

Citation Export

Abstract

Wurtzite-type zinc oxide (w-ZnO) is a widely used material with a pronounced structural anisotropy along the c axis, which affects its lattice dynamics and represents a difficulty for its accurate description using classical models of interatomic interactions. In this study, ab initio molecular dynamics (AIMD) was employed to simulate a bulk w-ZnO phase in the NpT ensemble in the high-temperature range from 300 K to 1200 K. The results of the simulations were validated by comparison with the experimental Zn K-edge extended X-ray absorption fine structure (EXAFS) spectra and known diffraction data. AIMD NpT simulations reproduced well the thermal expansion of the lattice, and the pronounced anharmonicity of Zn–O bonding was observed above 600 K. The values of mean-square relative displacements and mean-square displacements for Zn–O and Zn–Zn atom pairs were obtained as a function of interatomic distance and temperature. They were used to calculate the characteristic Einstein temperatures. The temperature dependences of the O–Zn–O and Zn–O–Zn bond angle distributions were also determined. View Full-Text

Keywords: ZnO; zinc oxide; ab initio molecular dynamics; extended X-ray absorption fine structure

▼ Show Figures

Graphical abstract

This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Share and Cite

MDPI and ACS Style

Bocharov, D.; Pudza, I.; Klementiev, K.; Krack, M.; Kuzmin, A. Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy. Materials 2021, 14, 5206. https://doi.org/10.3390/ma14185206

AMA Style

Bocharov D, Pudza I, Klementiev K, Krack M, Kuzmin A. Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy. Materials. 2021; 14(18):5206. https://doi.org/10.3390/ma14185206

Chicago/Turabian Style

Bocharov, Dmitry, Inga Pudza, Konstantin Klementiev, Matthias Krack, and Alexei Kuzmin. 2021. "Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy" Materials 14, no. 18: 5206. https://doi.org/10.3390/ma14185206

Find Other Styles

Note that from the first issue of 2016, MDPI journals use article numbers instead of page numbers. See further details here.

Article Metrics

Abstract views Pdf views Html views

Article Menu

Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy

Abstract

Share and Cite

Article Metrics

Article Access Statistics

Article Access Map by Country/Region

Further Information

Guidelines

MDPI Initiatives

Follow MDPI