An Upper Bound Solution for the Compression of an Orthotropic Cylinder
Abstract
:1. Introduction
2. Statement of the Problem
3. Kinematically Admissible Velocity Field
4. Upper Bound Solution
5. Numerical Examples
6. Conclusions
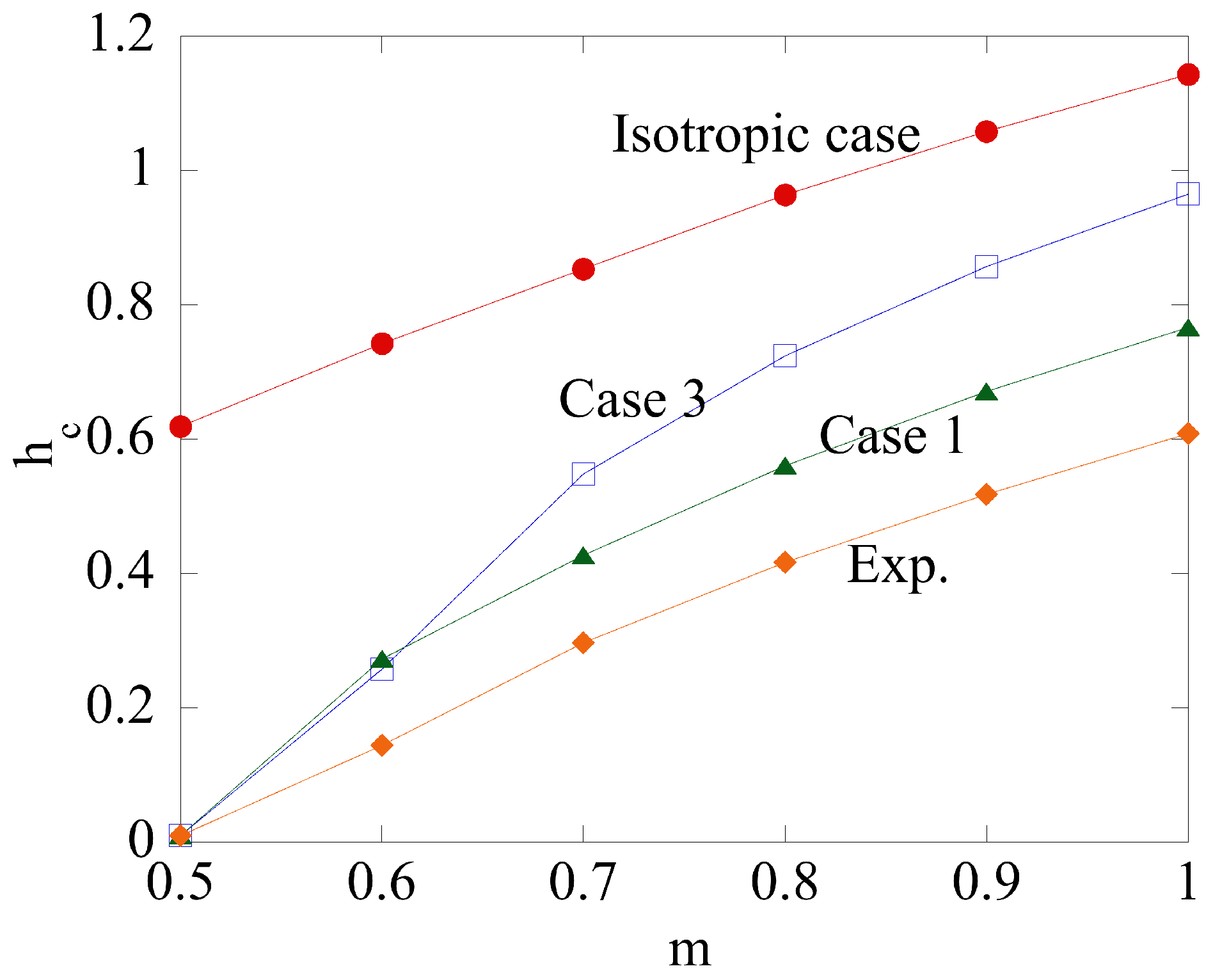
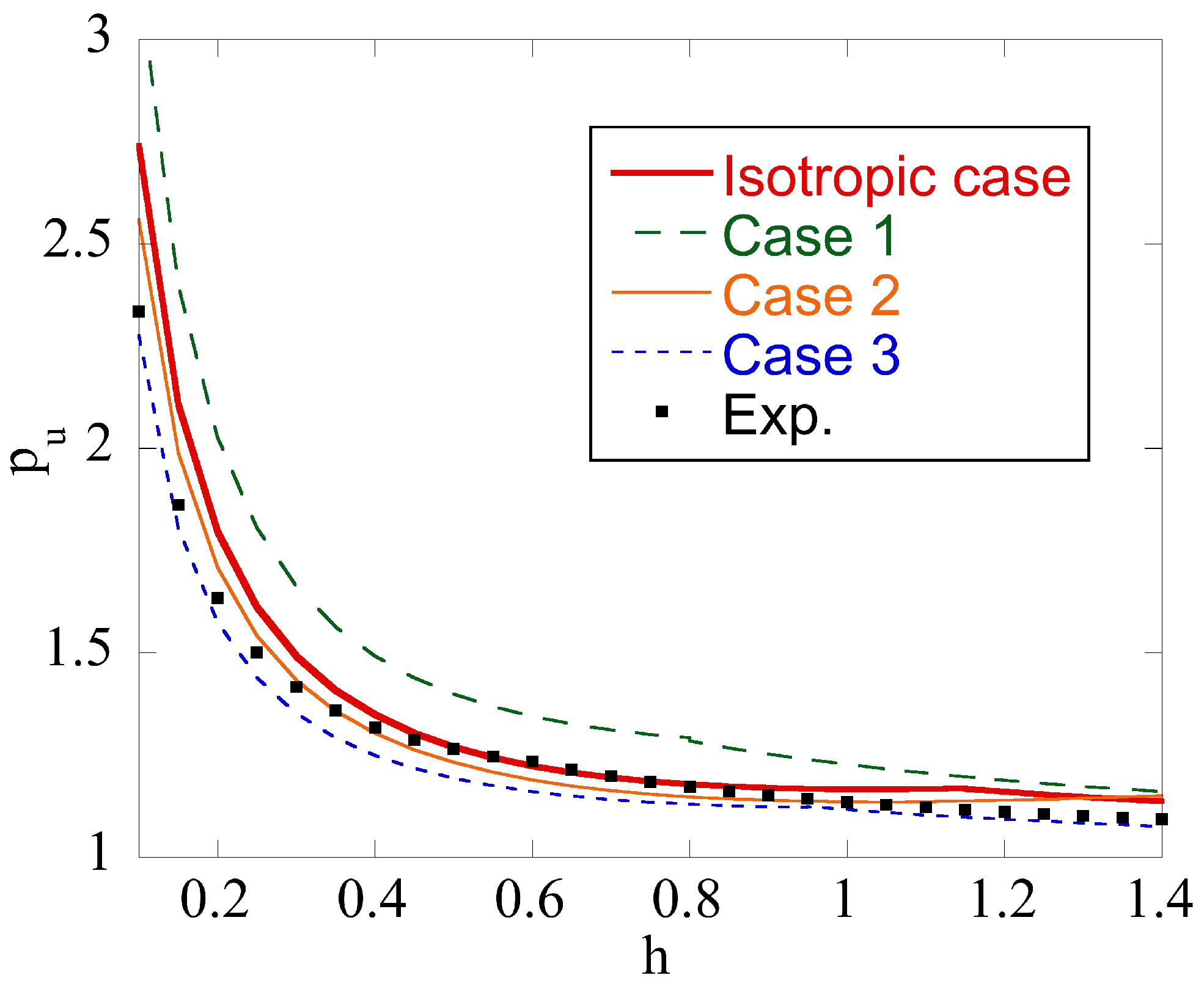
- Plastic anisotropy affects the limit load required to deform the specimen. It may increase or decrease the limit load as compared to the isotropic case (Figure 5).
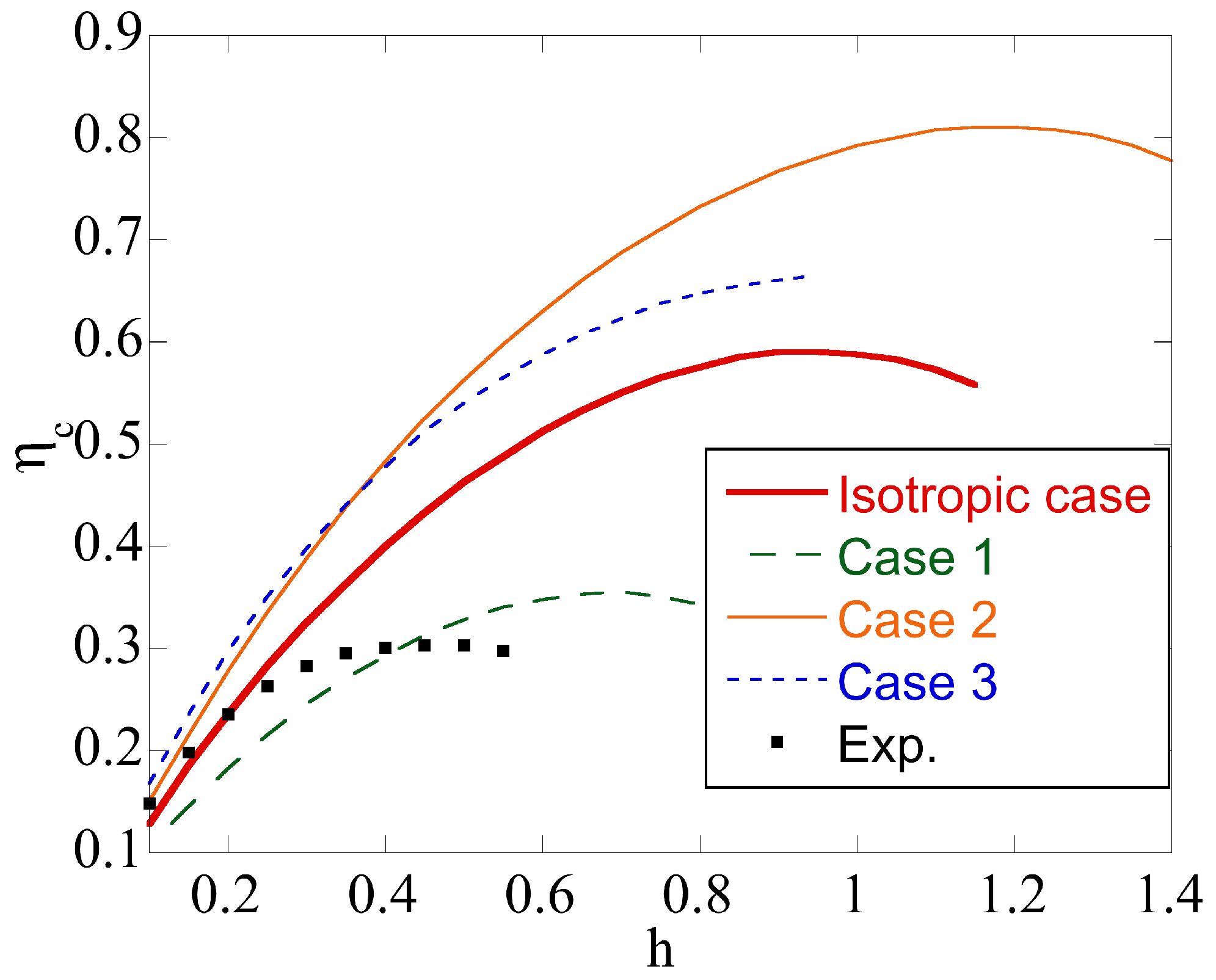
- The upsetting of a cylinder is often used as a friction test. Plastic anisotropy significantly affects the region of sticking friction (Figure 6). Since Equation (8) is not valid in this region, this effect of plastic anisotropy should be taken into account in the interpretation of the friction test results.
- Five dimensionless parameters classify the boundary value problem. Therefore, its systematic parametric analysis is invisible. An advantage of the proposed solution is that it quickly estimates the upper bound limit load for a given set of parameters.
- The real velocity field is singular near the friction surface if in Equation (8). The solution proposed accounts for this singularity, which is impossible when using ordinary finite element solutions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| and | unit base vectors |
| m | friction factor |
| unit vector normal to the velocity discontinuity line | |
| dimensionless upper bound limit load | |
| cylindrical coordinate system | |
| and | radial and axial velocities |
| F, G, H and M | material parameters introduced in Equation (2) |
| half-height of the cylinder | |
| P | force |
| radius of the cylinder | |
| S | shear yield stress in the -plane |
| U | velocity of the plate |
| plastic work rate at the velocity discontinuity line | |
| plastic work rate at the friction surface | |
| plastic work rate in the plastic region | |
| , and Z | tensile yield stresses in the radial, circumferential, and axial directions |
| equivalent strain rate | |
| , , and | strain rate components referred to the cylindrical coordinate system |
| , , and | dimensionless strain rate components introduced in Equation (11) |
| , and h | dimensionless quantities introduced after Equation (9) |
| , , and | stress components referred to the cylindrical coordinate system |
| friction stress | |
| orientation of the tangent to the velocity discontinuity line | |
| plastic work rate per unit volume |
References
- Soavi, F.; Tomesani, L.; Zurla, O. Incipient upsetting of solid cylinders between rigid and elastic tools. Int. J. Mech. Sci. 1994, 36, 601–614. [Google Scholar] [CrossRef]
- Bugini, A.; Maccarini, G.; Giardini, C. The evaluation of flow stress and friction in upsetting of rings and cylinders. Ann. CIRP 1993, 42, 335–338. [Google Scholar] [CrossRef]
- Hsu, T.C.; Young, A.J. Plastic deformation in the compression test of pure copper. J. Strain Anal. 1967, 2, 159–170. [Google Scholar] [CrossRef]
- Petruska, J.; Janicek, L. On the evaluation of strain inhomogeneity by hardness measurement of formed products. J. Mater. Process. Technol. 2003, 143–144, 300–305. [Google Scholar] [CrossRef]
- Petty, D.; Watts, G.; Ingham, P.; Bettess, P.; Grant, C. Experimental and numerical prediction of the upsetting of a hot steel cylinder. J. Mater. Process. Technol. 1991, 28, 407–426. [Google Scholar] [CrossRef]
- Bricout, J.P.; Oudin, J.; Liebaert, P.; Ravalard, Y. Hot-upsetting tests on steel cylinders after solidification. J. Mater. Process. Technol. 1992, 30, 315–328. [Google Scholar] [CrossRef]
- Ganser, H.-P.; Atkins, A.G.; Kolednik, O.; Fischer, F.D.; Richard, O. Upsetting of cylinders: A comparison of two different damage indicators. Trans. ASME J. Eng. Mater. Technol. 2001, 123, 94–99. [Google Scholar] [CrossRef]
- Narayanasamy, R.; Pandey, K.S. Phenomenon of barrelling in aluminium solid cylinders during cold-upset forming. J. Mater. Process. Technol. 1997, 70, 17–21. [Google Scholar] [CrossRef]
- Lin, F.C.; Lin, S.Y. Effect of frictional constraints on the barreling formations in cylinder upsetting with a hollow die. Mater. Manuf. Process. 2002, 17, 199–212. [Google Scholar] [CrossRef]
- Malayappan, S.; Narayanasamy, R. Observations of barrelling in aluminium solid cylinders during cold upsetting using different lubricants. Mater. Sci. Technol. 2003, 19, 1705–1708. [Google Scholar] [CrossRef]
- Malayappan, S.; Narayanasamy, R. Barrelling of aluminium solid cylinders during cold upsetting. Mater. Technol. 2005, 20, 6–11. [Google Scholar] [CrossRef]
- Malayappan, S.; Esakkimuthu, G. Barrelling of aluminium solid cylinders during cold upsetting, with different frictional conditions at the faces. Int. J. Adv. Mater. Technol. 2006, 29, 41–48. [Google Scholar]
- Solhjoo, S. A note on “Barrel Compression Test”: A method for evaluation of friction. Comput. Mater. Sci. 2010, 49, 435–438. [Google Scholar] [CrossRef]
- Ghassemali, E.; Tan, M.-J.; Jarfors, A.E.W.; Lim, S.C.V. Optimization of axisymmetric open-die micro-forging/extrusion processes: An upper bound approach. Int. J. Mech. Sci. 2013, 71, 58–67. [Google Scholar] [CrossRef]
- Zhou, W.; Lin, J.; Dean, T.A.; Wang, L. Analysis and modeling of a novel process for extruding curved metal alloy profiles. Int. J. Mech. Sci. 2018, 138–139, 524–536. [Google Scholar] [CrossRef]
- Alexandrov, S.; Richmond, O. Singular plastic flow fields near surfaces of maximum friction stress. Int. J. Non-Linear Mech. 2001, 36, 1–11. [Google Scholar] [CrossRef]
- Alexandrov, S.; Jeng, Y.-R. Singular rigid/plastic solutions in anisotropic plasticity under plane strain conditions. Cont. Mech. Therm. 2013, 25, 685–689. [Google Scholar] [CrossRef]
- Chen, J.-S.; Pan, C.; Rogue, C.M.O.L.; Wang, H.-P. A Lagrangian reproducing kernel particle method for metal forming analysis. Comp. Mech. 1998, 22, 289–307. [Google Scholar] [CrossRef]
- Facchinetti, M.; Miszuris, W. Analysis of the maximum friction condition for green body forming in an ANSYS environment. J. Eur. Ceram. Soc. 2016, 36, 2295–2302. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, S.; Mishuris, G.; Mishuris, W.; Sliwa, R.E. On the dead zone formation and limit analysis in axially symmetric extrusion. Int. J. Mech. Sci. 2001, 43, 367–379. [Google Scholar] [CrossRef]
- Alexandrov, S.; Lyamina, E.; Jeng, J.-R. A general kinematically admissible velocity field for axisymmetric forging and its application to hollow disk forging. Int. J. Adv. Manuf. Technol. 2017, 88, 3113–3122. [Google Scholar] [CrossRef]
- Bina, E.P.; Heshmatollah, H. Limit analysis of plane strain compression of cylindrical billets between flat dies. Int. J. Adv. Manuf. Technol. 2021. [Google Scholar] [CrossRef]
- Liu, J.Y. Upper-bound solutions of some axisymmetric cold forming problems. Trans. ASME J. Eng. Ind. 1971, 93, 1134–1144. [Google Scholar] [CrossRef]
- Avitzur, B.; Sauerwine, F. Limit analysis of hollow disk forging. Part 1: Upper bound. Trans. ASME J. Eng. Ind. 1978, 100, 340–344. [Google Scholar] [CrossRef]
- Avitzur, B.; Van Tyne, C.J. Ring formation: An upper bound approach. Part 1: Flow pattern and calculation of power. Trans. ASME J. Eng. Ind. 1982, 104, 231–237. [Google Scholar] [CrossRef]
- Ma, X.; Barnett, M.R.; Kim, Y.H. Experimental and theoretical investigation of compression of a cylinder using a rotating platen. Int. J. Mech. Sci. 2003, 45, 1717–1737. [Google Scholar] [CrossRef]
- Alexandrov, S.; Tzou, G.-Y.; Hsia, S.-Y. A new upper bound solution for a hollow cylinder subject to compression and twist. Proc. IMechE Part C J. Mech. Eng. Sci. 2004, 218, 369–375. [Google Scholar] [CrossRef]
- Hill, R. The plastic torsion of anisotropic bars. J. Mech. Phys. Solids 1954, 2, 87–91. [Google Scholar] [CrossRef]
- Durban, D.; Birman, V. Elasto-plastic analysis of an anisotropic rotating disc. Acta Mech. 1983, 49, 1–10. [Google Scholar] [CrossRef]
- Callioglu, H.; Topcu, M.; Tarakcilar, A.R. Elastic-plastic analysis of an orthotropic rotating disc. Int. J. Mech. Sci. 2006, 48, 985–990. [Google Scholar] [CrossRef]
- Alexandrova, N.; Vila Real, P.M.M. Effect of plastic anisotropy on stress-strain field in thin rotating disks. Thin-Walled Struct. 2006, 44, 897–903. [Google Scholar] [CrossRef]
- Leu, S.-Y. Static and kinematic limit analysis of orthotropic strain-hardening pressure vessels involving large deformation. Int. J. Mech. Sci. 2009, 51, 508–514. [Google Scholar] [CrossRef]
- Thakur, P.; Kumar, N.; Sethi, M. Elastic-plastic stresses in a rotating disc of transversely isotropic material fitted with a shaft and subjected to thermal gradient. Meccanica 2021, 56, 1165–1175. [Google Scholar] [CrossRef]
- Lyamina, E.; Tzou, G.-Y.; Hsia, S.-Y. An upper bound solution for upsetting of anisotropic hollow cylinders. Mater. Sci. Forum 2009, 623, 71–78. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Clarendon Press: Oxford, UK, 1950; pp. 154–196. [Google Scholar]
- Alexandrov, S.; Lyamina, E.; Manach, P.-Y. Solution behavior near very rough walls under axial symmetry: An exact solution for anisotropic rigid/plastic material. Symmetry 2021, 13, 184. [Google Scholar] [CrossRef]
- Christodoulou, N.; Turner, P.A.; Ho, E.T.C.; Chow, C.K.; Resta Levi, M. Anisotropy of Yielding in a Zr-2.5Nb Pressure Tube Material. Metall. Mater. Trans. A 2000, 31, 409–420. [Google Scholar] [CrossRef]



| FZ2 | HZ2 | GZ2 | MZ2 | |
|---|---|---|---|---|
| Exp. Value | 0.378 | 0.1 | 0.623 | 2.558 |
| Y/Z | Θ/Z | S/Z | |
|---|---|---|---|
| Isotropic Case | 1 | 1 | |
| Case 1 | 1.2 | 1.5 | |
| Case 2 | 0.8 | 0.7 | |
| Case 3 | 0.8 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, L.; Alexandrov, S.; Wang, Y.-C. An Upper Bound Solution for the Compression of an Orthotropic Cylinder. Materials 2021, 14, 5253. https://doi.org/10.3390/ma14185253
Lang L, Alexandrov S, Wang Y-C. An Upper Bound Solution for the Compression of an Orthotropic Cylinder. Materials. 2021; 14(18):5253. https://doi.org/10.3390/ma14185253
Chicago/Turabian StyleLang, Lihui, Sergei Alexandrov, and Yun-Che Wang. 2021. "An Upper Bound Solution for the Compression of an Orthotropic Cylinder" Materials 14, no. 18: 5253. https://doi.org/10.3390/ma14185253
APA StyleLang, L., Alexandrov, S., & Wang, Y.-C. (2021). An Upper Bound Solution for the Compression of an Orthotropic Cylinder. Materials, 14(18), 5253. https://doi.org/10.3390/ma14185253








