Full-Field Temperature Measurement of Stainless Steel Specimens Subjected to Uniaxial Tensile Loading at Various Strain Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
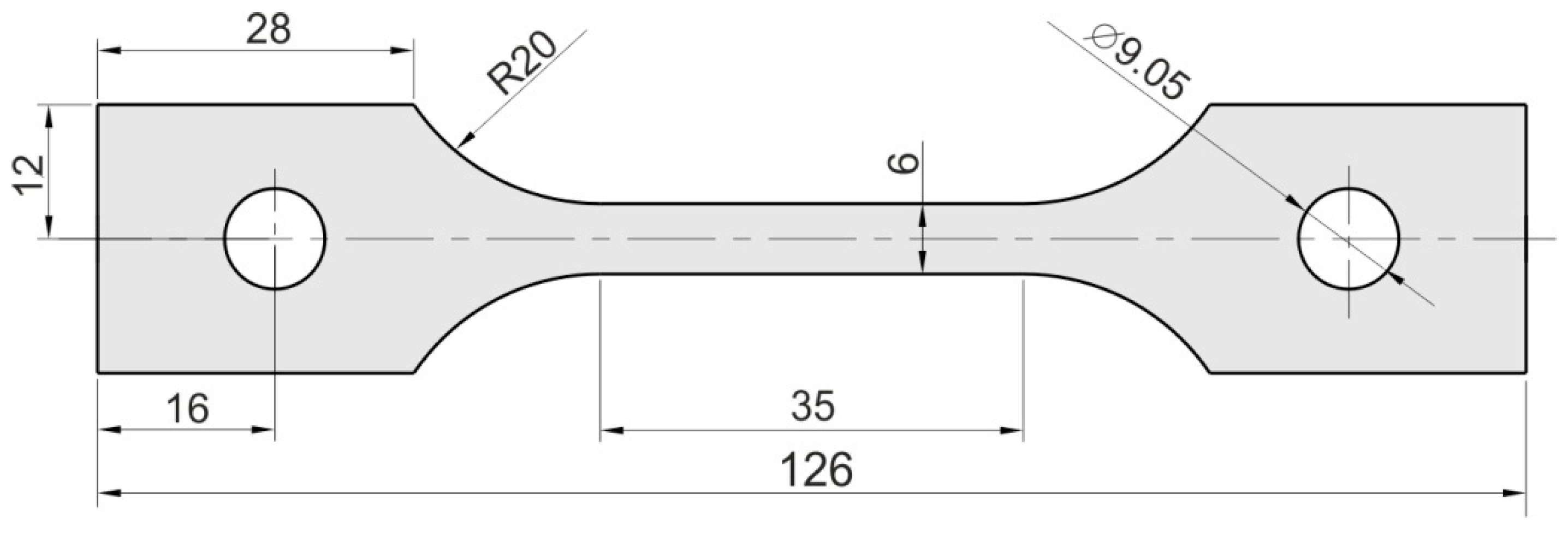
2.2. Uniaxial Tensile Test
2.3. Digital Image Correlation Technique
- a stable solution for full-field analyses of test objects of just a few millimeters up to structural components of several metres in size,
- it is a material-independent and non-contact measuring system,
- it performs high-precision measurements with a 3D measurement resolution in the sub-micrometer range,
- it is a high-resolution for point-based and full-field measurements.
2.4. Infrared (IR) Thermal Mapping
2.5. Analysis of Variance
3. Results and Discussion
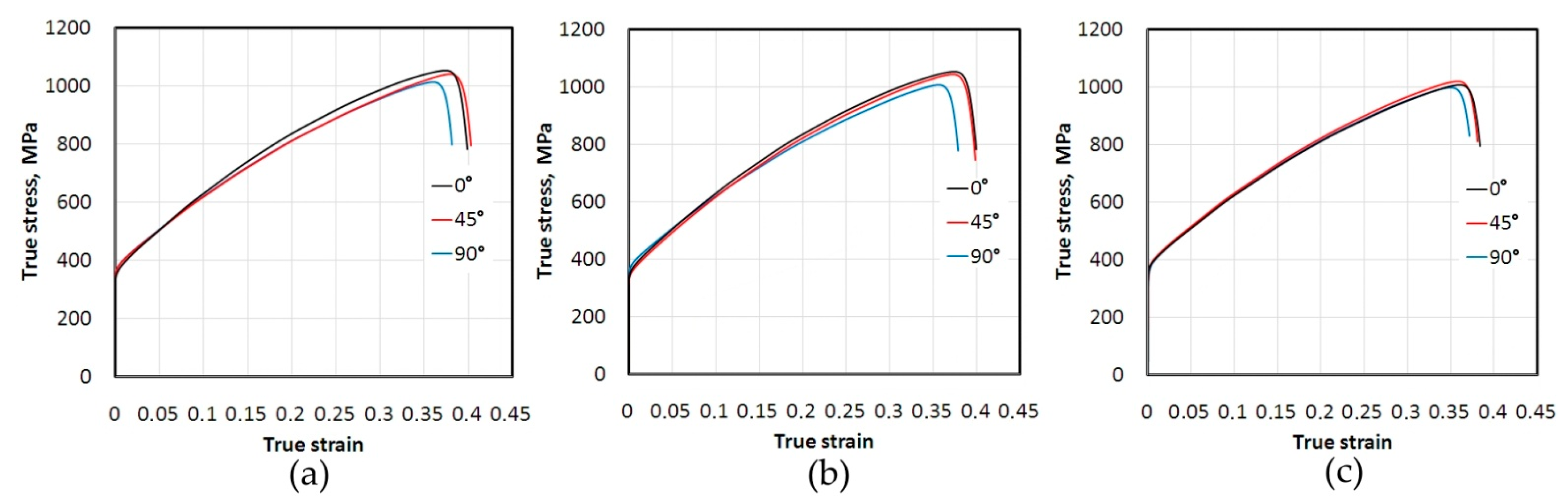
3.1. Experimental Investigations
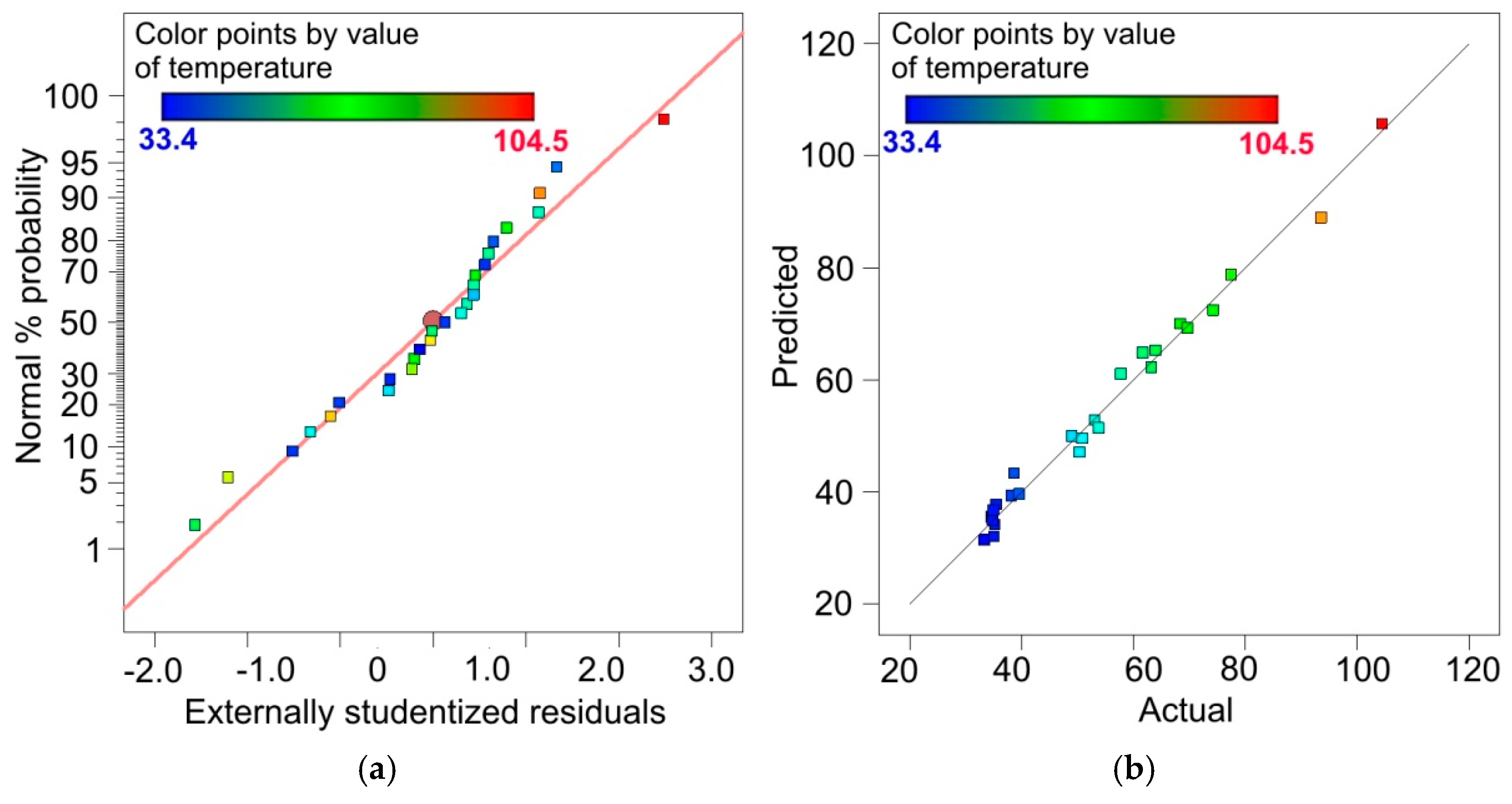
3.2. Analysis of Variance (ANOVA) for 321 Steel Samples
4. Conclusions
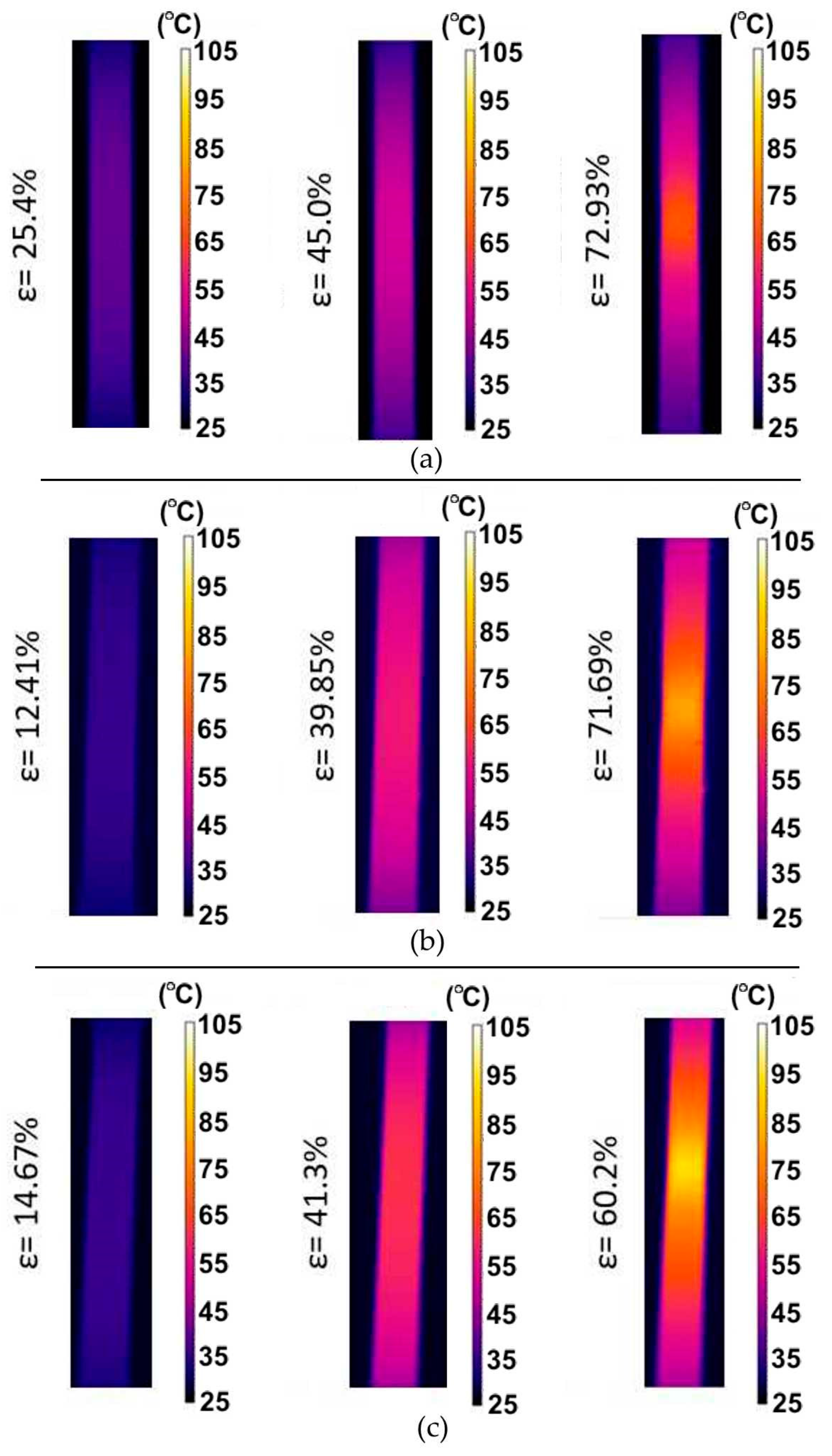
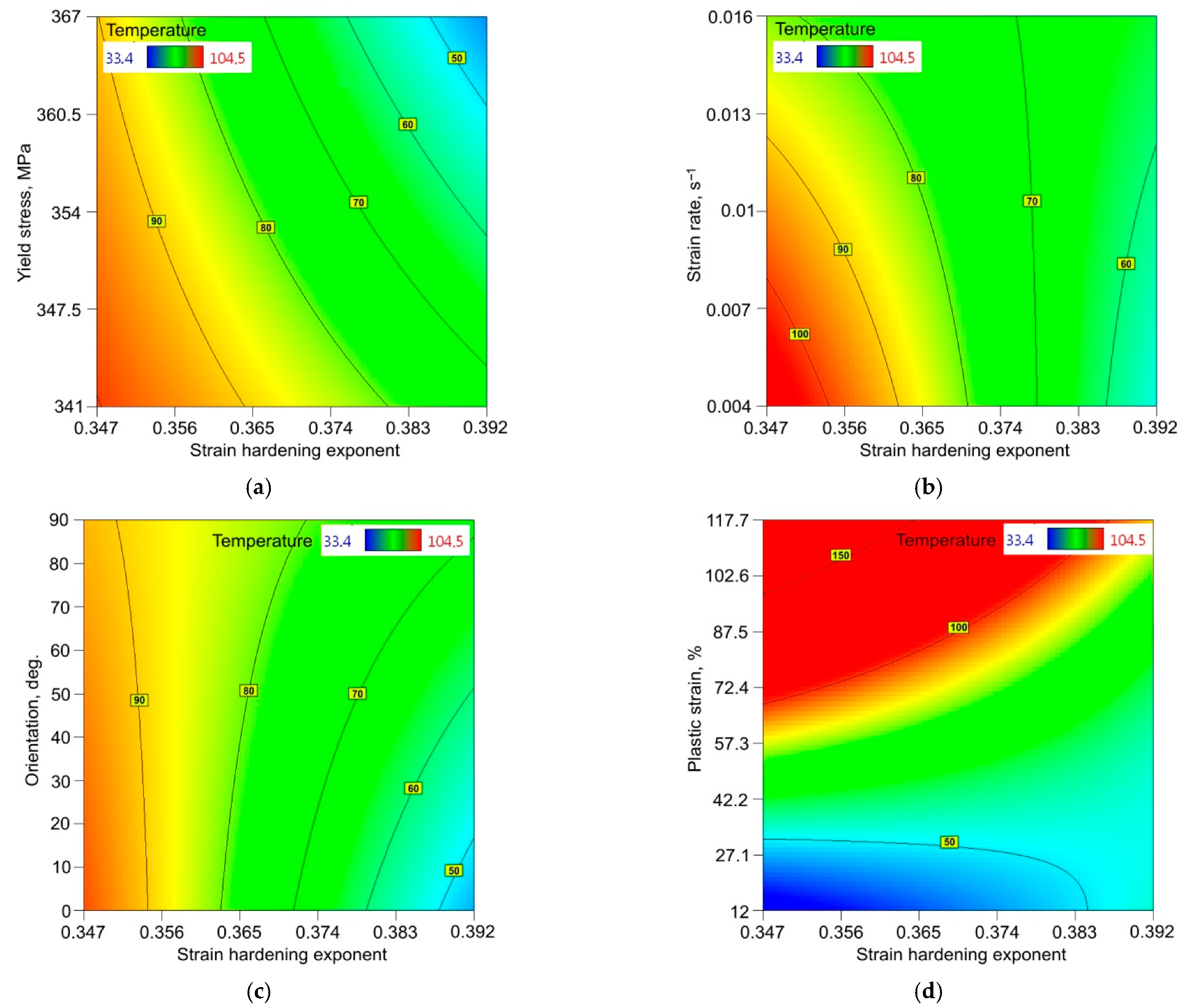
- The heat during stretching of the samples was not generated proportionally over the entire length of the samples. In the range of proportional deformation (before necking formation), the zone with the highest temperature was located approximately centrally along the distance between the grippers of the testing machine.
- At the moment of formation of a necking at the highest strain rate, the maximum sample temperature increased more than four times compared to the initial temperature. This phenomenon was observed for all sample orientations analysed.
- The character of the effect of plastic strain on the maximum temperature generated in the specimens was close to a linear trend in the range of strain rates analysed.
- A synergistic effect of the SHE and YS revealed that heat was generated more rapidly towards small values of SHE and YS.
- For small values of SHE, the sample orientation in interaction with the SHE did not significantly affect the temperature value.
- For all the orientations analysed, the temperature increased in a similar way with increasing PS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pater, Z.; Samołyk, G. Podstawy Technologii Obróbki Plastycznej Metali; Politechnika Lubelska: Lublin, Poland, 2013. [Google Scholar]
- Di Gioacchino, F.; Edwards, T.E.J.; Wells, G.N.; Clegg, W.J. A new mechanism of strain transfer in polycrystals. Sci. Rep. 2020, 10, 10082. [Google Scholar] [CrossRef]
- Physics on Nondestructive Evaluation. Iowa State University. Available online: https://www.nde-ed.org/Physics/Materials/Structure/anisotropy.xhtml (accessed on 19 August 2021).
- Yang, G.; Park, S.J. Deformation of single crystals, polycrystalline materials, and thin films: A review. Materials 2019, 12, 2003. [Google Scholar] [CrossRef]
- Venkataraman, A.; Sangid, M.D. Deformation Mechanisms at Grain Boundaries in Polycrystals; Final Report to U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award#DE-SC001428; Purdue University: West Lafayette, IN, USA, 2019. [Google Scholar]
- Luo, H.; Sheng, H.; Zhang, H.; Wang, F.; Fan, J.; Du, J.; Liu, J.P.; Szlufarska, I. Plasticity without dislocations in a polycrystalline intermetallic. Nat. Commun. 2019, 10, 3587. [Google Scholar] [CrossRef] [PubMed]
- Bahrami, A.; Taheri, P. A study on the failure of AISI 304 stainless steel tubes in a gas heater unit. Metals 2019, 9, 969. [Google Scholar] [CrossRef]
- Bansod, A.V.; Patil, A.P.; Moon, A.P.; Khobragade, N.N. Intergranular corrosion behavior of low-nickel and 304 austenitic stainless steels. J. Mater. Eng. Perform. 2016, 25, 3615–3626. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Roa, J.J.; Wheeler, J.M.; Trifonov, T.; Fargas, G.; Mateo, A.; Michler, J.; Jiménez-Piqué, E. Deformation of polycrystalline TRIP stainless steel micropillars. Mater. Sci. Eng. A 2015, 647, 51–57. [Google Scholar] [CrossRef]
- Di Gioacchino, F.; da Fonseca, J.Q. An experimental study of the polycrystalline plasticity of austenitic stainless steel. Int. J. Plast. 2015, 74, 92–109. [Google Scholar] [CrossRef]
- Cheong, K.S.; Busso, E.P. Discrete dislocation density modelling of single phase FCC polycrystal aggregates. Acta Mater. 2004, 52, 5665–5675. [Google Scholar] [CrossRef]
- Ichiyanagi, K.; Takagi, S.; Kawai, N.; Fukaya, R.; Nozawa, S.; Nakamura, K.G.; Liss, K.D.; Kimura, M.; Adachi, S.I. Microstructural deformation process of shock-compressed polycrystalline aluminum. Sci. Rep. 2019, 9, 7604. [Google Scholar] [CrossRef]
- Korsunsky, A.M. Crystal plasticity and hardening: A dislocation dynamics study. Procedia Eng. 2009, 1, 241–244. [Google Scholar]
- Farren, W.S.; Taylor, G.I. The heat developped during plastic extension of metal. Proc. R. Soc. A 1925, 107, 422–451. [Google Scholar]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. A 1933, 143, 307–326. [Google Scholar]
- Bodelot, L.; Sabatier, L.; Charkaluk, E.; Dufrenoy, P. Optical and infrared coupled full-field measurements at a mesoscopic scale. In Proceedings of the 9th International Conference on Quantitative InfraRed Thermography, Kraków, Poland, 2–5 July 2008. [Google Scholar]
- Boulanger, T.; Chrysochoos, A.; Mabru, C.; Galtier, A. Calorimetric analysis of dissipative and thermoelastic effects associated with the fatigue behavior of steels. Int. J. Fatigue 2004, 26, 221–229. [Google Scholar] [CrossRef]
- Ait-Amokhtar, H.; Fressengeas, C.; Boudrahem, S. The dynamics of Portevin-Le Chatelier bands in an Al-Mg alloy from infrared thermography. Mater. Sci. Eng. A 2008, 488, 540–546. [Google Scholar] [CrossRef]
- Völkl, R.; Fischer, B. Mechanical testing of ultra-high temperature alloys. Exp. Mech. 2004, 44, 121–127. [Google Scholar] [CrossRef]
- Anwander, M.; Zagar, B.G.; Weiss, B.; Weiss, H. Noncontacting strain measurements at high temperatures by the digital laser speckle technique. Exp. Mech. 2000, 40, 98–105. [Google Scholar] [CrossRef]
- Pan, B.; Wu, D.; Gao, J. High-temperature strain measurement using active imaging digital image correlation and infrared radiation heating. J. Strain. Anal. Eng. Des. 2013, 49, 224–232. [Google Scholar] [CrossRef]
- Pan, B.; Wu, D.; Wang, Z.; Xia, Y. High-temperature digital image correlation method for full-field deformation measurement at 1200 °C. Meas. Sci. Technol. 2011, 22, 015701. [Google Scholar] [CrossRef]
- Sharpe, W.N. A high-frequency high-temperature optical strain/displacement gage. Exp. Mech. 2009, 50, 227–237. [Google Scholar] [CrossRef]
- Orteu, J.J.; Rotrou, Y.; Sentenac, T.; Robert, L. An innovative method for 3-D shape, strain and temperature full-field measurement using a single type of camera: Principle and preliminary results. Exp. Mech. 2007, 48, 163–179. [Google Scholar] [CrossRef][Green Version]
- Tung, S.H.; Sui, C.H. Application of digital-image-correlation techniques in analysing cracked cylindrical pipes. Sadhana 2010, 35, 557–567. [Google Scholar] [CrossRef]
- Hild, F.; Bouterf, A.; Forquin, P.; Roux, S. On the use of digital image correlation for the analysis of the dynamic behavior of materials. In The Micro-World Observed by Ultra High-Speed Cameras; Tsuji, K., Ed.; Springer: Cham, Switzerland, 2018; pp. 185–206. [Google Scholar]
- Wattrisse, B.; Chrysochoos, A.; Muracciole, J.-M.; Nemoz-Gaillard, M. Kinematic manifestations of localisation phenomena in steels by digital image correlation. Eur. J. Mech. A Solids 2001, 20, 189–211. [Google Scholar] [CrossRef]
- Hung, P.C.; Voloshin, A.S. In-plane strain measurement by Digital Image Correlation. J. Braz. Soc. Mech. Sci. Eng. 2003, 25, 215–221. [Google Scholar] [CrossRef]
- Feng, X.; Xue, F. Characterization of 3D printed bolts based on digital image correlation and infrared thermography. Mater. Des. 2020, 191, 108641. [Google Scholar] [CrossRef]
- Cholewa, N.; Summers, P.T.; Feih, S.; Mouritz, A.P.; Lattimer, B.Y.; Case, S.W. A technique for coupled thermomechanical response measurement using infrared Thermography and Digital Image Correlation (TDIC). Exp. Mech. 2016, 56, 145–164. [Google Scholar] [CrossRef]
- Żaba, K.; Trzepieciński, T.; Puchlerska, S.; Noga, P.; Balcerzak, M. Coupled thermomechanical response measurement of deformation of nickel-based superalloys using full-field digital image correlation and infrared thermography. Materials 2021, 14, 2163. [Google Scholar] [CrossRef] [PubMed]
- Chrysochoos, A.; Huon, V.; Jourdan, F.; Muracciole, J.M.; Peyrux, R.; Wattrisse, B. Use of full-field digital image correlation and infrared thermography measurements for the thermomechanical analysis of material behaviour. Strain 2010, 46, 117–130. [Google Scholar] [CrossRef]
- Maynadier, A.; Poncelet, M.; Lavernhe-Taillard, K.; Roux, S. One-shot measurement of thermal and kinematic fields: Infrared image correlation (IRIC). Exp. Mech. 2011, 52, 241–255. [Google Scholar] [CrossRef]
- Curà, F.; Curti, G.; Sesana, R. A new iteration method for the thermographic determination of fatigue limit in steels. Int. J. Fatigue 2005, 27, 453–459. [Google Scholar] [CrossRef]
- Doudard, C.; Calloch, S.; Cugy, P.; Galtier, A.; Hild, F. A probabilistic two-scale model for high-cycle fatigue life predictions. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 279–288. [Google Scholar] [CrossRef]
- ASTM International. ASTM International. ASTM E8/E8M-11. Standard test methods for tension testing of metallic materials. In ASTM Book of Standards; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- SAE International. AMS 5604-Steel, Corrosion and Heat Resistant, Sheet, Strip, and Plate 18Cr-10.5Ni-0.40Ti (SAE 30321) Solution Heat Treated; SAE International: Warrendale, PA, USA, 1991. [Google Scholar]
- Zielecki, W.; Kubit, A.; Święch, Ł. Analiza Doświadczalna Odkształcenia Elementów Klejonych w Próbie Statycznego Oddzierania. Pomiary Autom. Robot. 2013, 2, 71–78. [Google Scholar]
- Trzepieciński, T.; Szpunar, M.; Kaščák, Ľ. Modeling of friction phenomena of TI-6AL-4V sheets based on backward elimination regression and multi-layer artificial neural networks. Materials 2021, 14, 2570. [Google Scholar] [CrossRef] [PubMed]
- Brennhaugen, D.D.E.; Georgarakis, K.; Yokoyama, Y.; Nakayama, K.S.; Arnberg, L.; Aune, R.E. Probing heat generation during tensile plastic deformation of a bulk metallic glass at cryogenic temperature. Sci. Rep. 2018, 8, 16317. [Google Scholar] [CrossRef]
- Kostina, A.; Iziumowa, A.; Plekhov, O. energy dissipation and storage in iron under plastic deformation (experimental study and numerical simulation). Frat. Ed. Integrità Strutt. 2014, 27, 28–37. [Google Scholar] [CrossRef]
- Rusinek, A.; Klepaczko, J.R. Experiments on heat generated during plastic deformation and stored energy for TRIP steels. Mater. Des. 2009, 30, 35–48. [Google Scholar] [CrossRef]
- Klitschke, S.; Trondl, A.; Huberth, F.; Liewald, M. Adiabatic heating under various loading situations and strain rates for advanced high-strength steels. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012123. [Google Scholar] [CrossRef]
- Sada, N.B. The plastic depth of heat treatment steel alloy (AISI 01) due to torsion test. J. Appl. Sci. 2005, 5, 1196–1199. [Google Scholar] [CrossRef][Green Version]
- Shen, Y.F.; Li, X.X.; Sun, X.; Wang, Y.D.; Zuo, L. Twinning and martensite in a 304 austenitic stainless steel. Mater. Sci. Eng. A 2012, 552, 514–522. [Google Scholar]
- Song, G.S.; Ji, K.S.; Song, H.W.; Zhang, S.H. Microstructure transformation and twinning mechanism of 304 stainless steel tube during hydraulic bulging. Mater. Res. Express 2019, 6, 1265h9. [Google Scholar] [CrossRef]
- Rubtsov, V.E.; Kolubaev, A.V. Effect of heat generation due to plastic deformation on behavior of surface-layer material during sliding. J. Frict. Wear 2009, 30, 324. [Google Scholar] [CrossRef]
- Maj, M. Wpływ Kierunku Wstępnego Odkształcenia na Proces Magazynowania Energii w Polikryształach. Ph.D. Thesis, Instytut Podstawowych Problemów Techniki Polskiej Akademii Nauk, Warsaw, Poland, 2007. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sen, A.; Srivastava, M. Regression Analysis Theory, Methods, and Applications; Springer: New York, NY, USA, 1990. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Alexopoulos, E.C. Introduction to multivariate regression analysis. Hippokratia 2010, 14, 23–28. [Google Scholar] [PubMed]
- Chauhan, S.R.; Dass, K. Dry sliding wear behaviour of titanium (grade 5) alloy by using response surface methodology. Adv. Tribol. 2013, 2013, 272106. [Google Scholar] [CrossRef]
- Khalatbari, H. Investigation of Formability of Material in Incremental Sheet Metal Forming Process. Master’s Thesis, Eastern Mediterranean University, Farmagusta, Cyprus, 2012. [Google Scholar]
- Venugopal, V.; Kumar, K.J.; Muralidharan, S.; Parasuraman, S.; Raj, P.V.; Kumar, K.V. Optimization and in-vivo evaluation of isradipine nanoparticles using Box-Behnken design surface response methodology. OpenNano 2016, 1, 1–15. [Google Scholar] [CrossRef]




| C (Max.) | Si | Mo | Mn (Max.) | P + S (Max.) | Cr | Ni | Ti (Max.) | N (Max.) | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 0.08 | 0.25–1.00 | 0.75 | 2.0 | 0.04 P 0.03 S | 17.0–19.0 | 9.0–12.0 | 0.7 | 0.1 | balance |
| Parameter | Unit | Value |
|---|---|---|
| Resolution | pixel | 2048 × 1536 |
| Measuring range | °C | −40 ÷ +2000 |
| Refresh rate | Hz | 30 |
| Thermal sensitivity | mK | 30 |
| Parameter | Name | Unit | Type | Minimum | Maximum |
|---|---|---|---|---|---|
| A | Strain hardening exponent | - | Numeric | 0.35 | 0.392 |
| B | Yield stress | MPa | Numeric | 341 | 367 |
| C | Strain rate | s−1 | Numeric | 4 × 10−3 | 16 × 10−3 |
| D | Sample orientation | deg. | Numeric | 0 | 90 |
| E | Percentage strain | % | Numeric | 12 | 117.7 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value | Meaning |
|---|---|---|---|---|---|---|
| Model | 8991.31 | 14 | 642.24 | 53.30 | <0.0001 | significant |
| A—strain hardening exponent | 26.04 | 1 | 26.04 | 2.16 | 0.1723 | - |
| B—yield stress | 39.77 | 1 | 39.77 | 3.30 | 0.0993 | - |
| C—strain rate | 0.5708 | 1 | 0.5708 | 0.0474 | 0.8321 | - |
| D—sample orientation | 13.38 | 1 | 13.38 | 1.11 | 0.3167 | - |
| E—plastic strain | 989.76 | 1 | 989.76 | 82.14 | <0.0001 | - |
| AB | 1.11 | 1 | 1.11 | 0.0920 | 0.7679 | - |
| AC | 9.23 | 1 | 9.23 | 0.7664 | 0.4019 | - |
| AD | 22.41 | 1 | 22.41 | 1.86 | 0.2025 | - |
| AE | 171.00 | 1 | 171.00 | 14.19 | 0.0037 | - |
| BC | 4.45 | 1 | 4.45 | 0.3696 | 0.5568 | - |
| BE | 36.85 | 1 | 36.85 | 3.06 | 0.1109 | - |
| CE | 758.38 | 1 | 758.38 | 62.94 | <0.0001 | - |
| DE | 2.40 | 1 | 2.40 | 0.1992 | 0.6649 | - |
| E2 | 66.37 | 1 | 66.37 | 5.51 | 0.0409 | - |
| Residual | 120.49 | 10 | 12.05 | - | - | - |
| Cor Total | 9111.80 | 24 | - | - | - | - |
| Standard Deviation | 3.47 | R2 | 0.9868 |
|---|---|---|---|
| Mean | 54.09 | Adjusted R2 | 0.9683 |
| Coefficient of variation, % | 6.42 | Predicted R2 | 0.8982 |
| - | - | Adequacy precision | 27.6342 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żaba, K.; Trzepieciński, T.; Rusz, S.; Puchlerska, S.; Balcerzak, M. Full-Field Temperature Measurement of Stainless Steel Specimens Subjected to Uniaxial Tensile Loading at Various Strain Rates. Materials 2021, 14, 5259. https://doi.org/10.3390/ma14185259
Żaba K, Trzepieciński T, Rusz S, Puchlerska S, Balcerzak M. Full-Field Temperature Measurement of Stainless Steel Specimens Subjected to Uniaxial Tensile Loading at Various Strain Rates. Materials. 2021; 14(18):5259. https://doi.org/10.3390/ma14185259
Chicago/Turabian StyleŻaba, Krzysztof, Tomasz Trzepieciński, Stanislav Rusz, Sandra Puchlerska, and Maciej Balcerzak. 2021. "Full-Field Temperature Measurement of Stainless Steel Specimens Subjected to Uniaxial Tensile Loading at Various Strain Rates" Materials 14, no. 18: 5259. https://doi.org/10.3390/ma14185259
APA StyleŻaba, K., Trzepieciński, T., Rusz, S., Puchlerska, S., & Balcerzak, M. (2021). Full-Field Temperature Measurement of Stainless Steel Specimens Subjected to Uniaxial Tensile Loading at Various Strain Rates. Materials, 14(18), 5259. https://doi.org/10.3390/ma14185259








