Modeling and Characterization of Complex Concentrated Alloys with Reduced Content of Critical Raw Materials
Abstract
:1. Introduction
2. Materials and Methods
- Using Boltzmann’s equations, the mixing entropy was determined:where R is the gas’s constant (8.314 J/molK); ci is the molar fraction of the element i.
- The enthalpy of mixing (ΔHmix) was calculated using the Miedema macroscopic model [24]:where ΔHij is the binary enthalpy of the alloy; i and j are the elements introduced to the mix.
- The atomic size difference (δ) was calculated using Equation (3) [15]where ri is the atomic radius of element i; is the average atomic radius.
- The derived parameter Ω, which is influenced by the mixing entropy and the mixing enthalpy [25], was calculated using the following equation:where Tm is the melting temperature calculated with , where Tmi is the melting temperature of element i.
- The Allen electronegativity difference (Δχ) was calculated using Equation (5) [26]:where is the electronegativity after Pauling for element i; is the electronegativity average.
- The valence electron concentration (VEC) was calculated (Equation (6)) to determine the type of solid solution that is found in the alloy [27]:where VECi is the valence electron concentration of element i.
- The geometrical parameter (Λ) depends on the mixing entropy (ΔSmix) and the atomic size difference (δ) of the mixture [28], expressed as follows:
3. Results
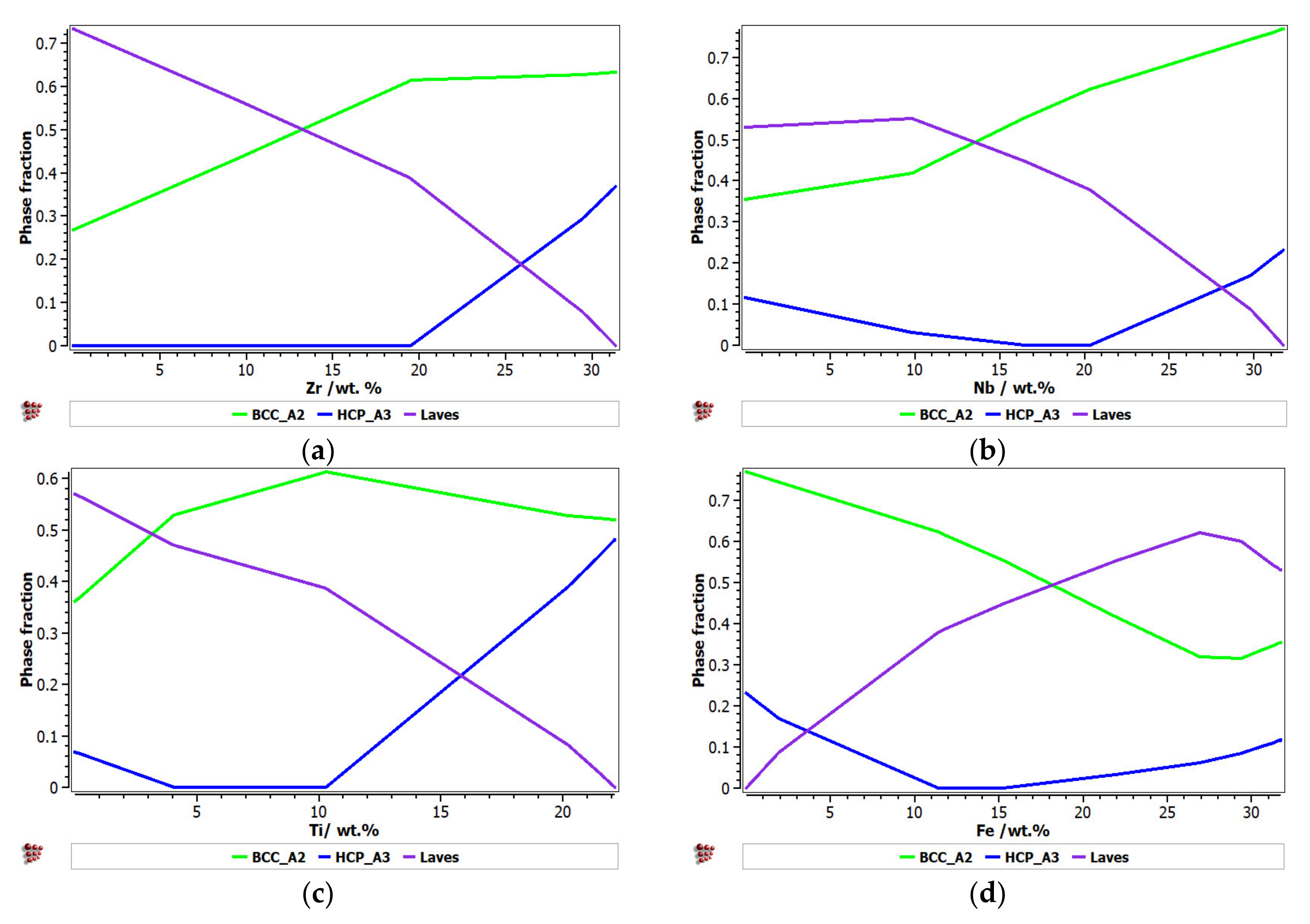
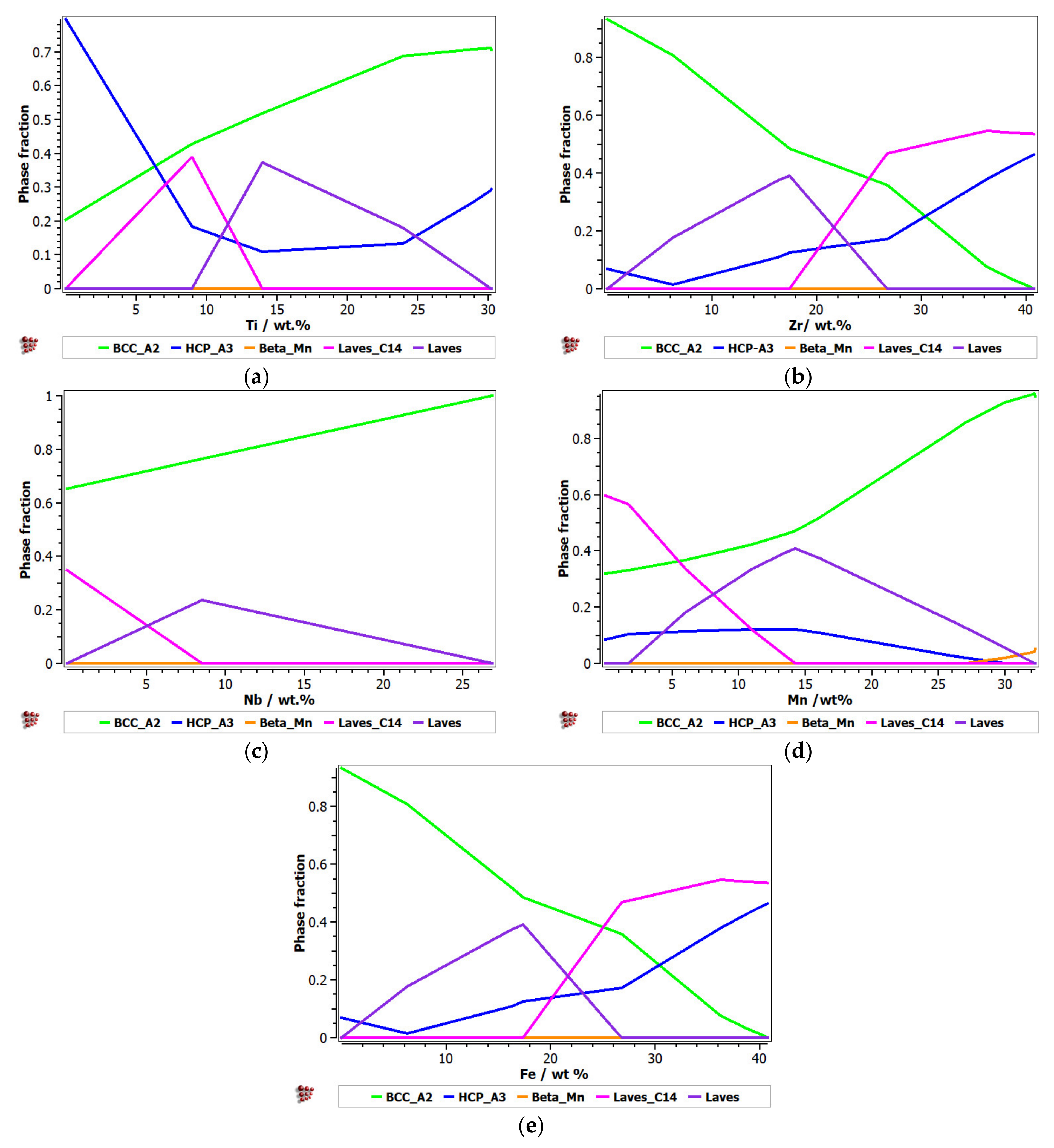
3.1. CCAs Structure Design Depending on Concentration
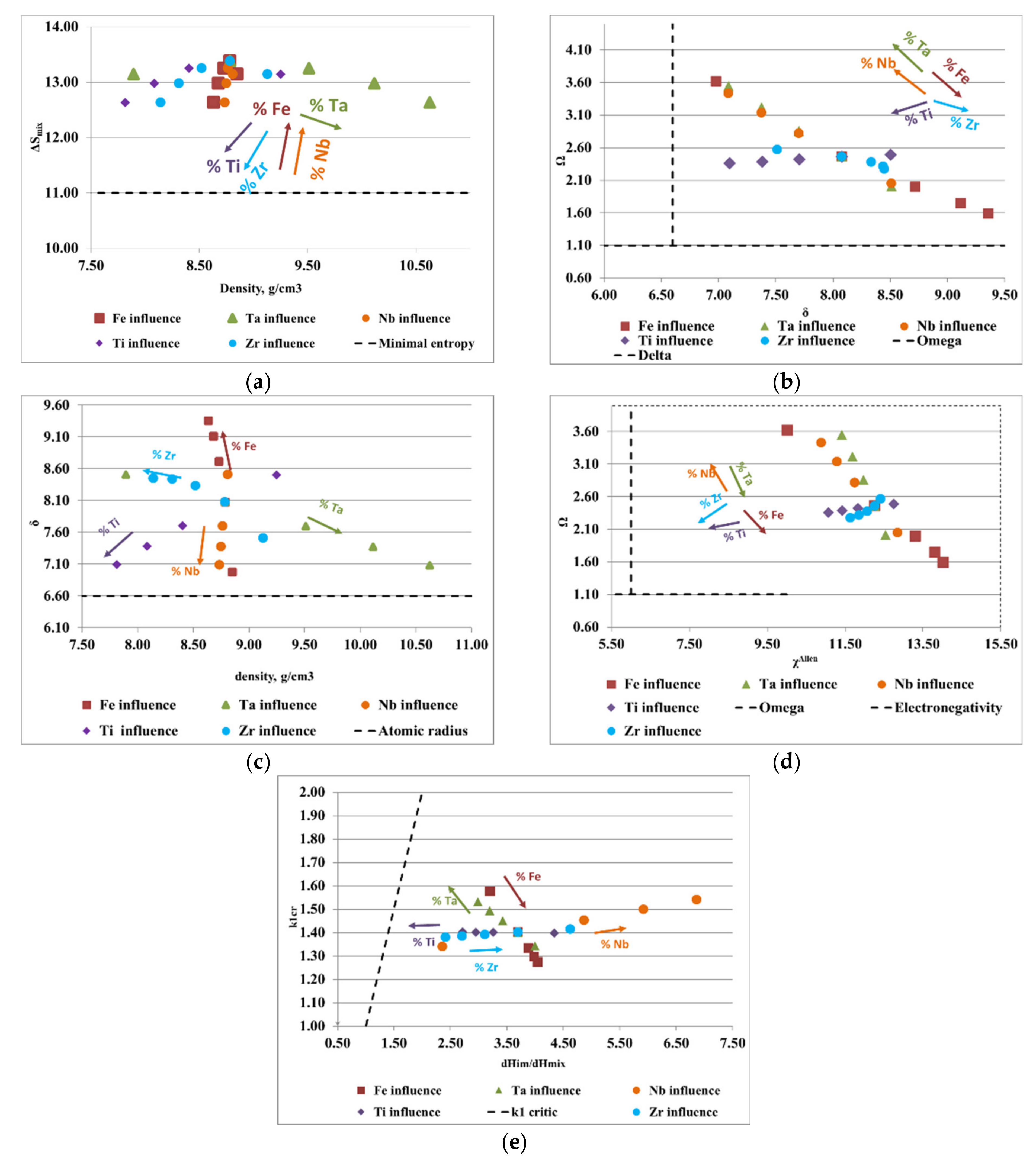
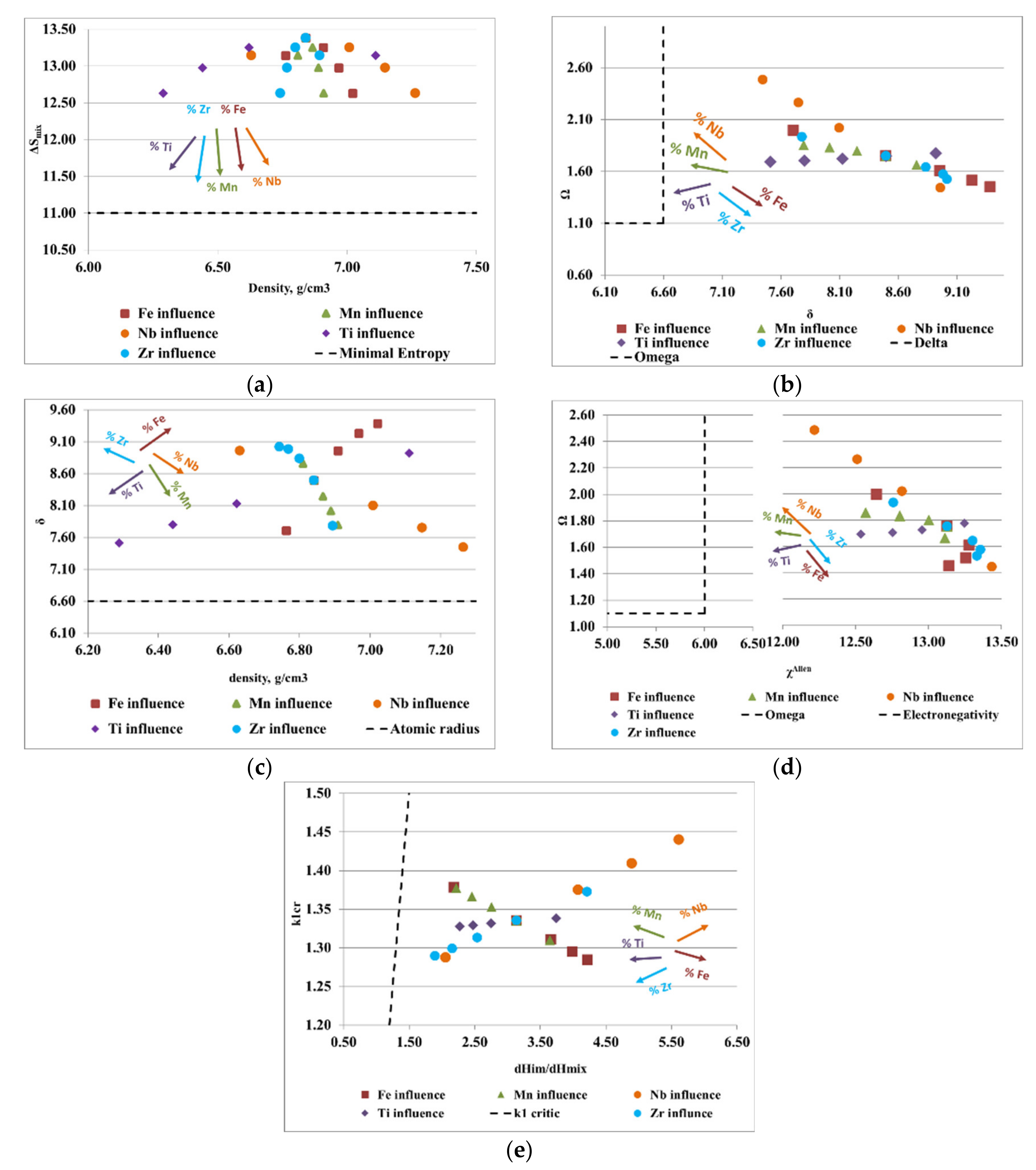
3.2. Kinetic and Thermodynamic Criteria Calculation
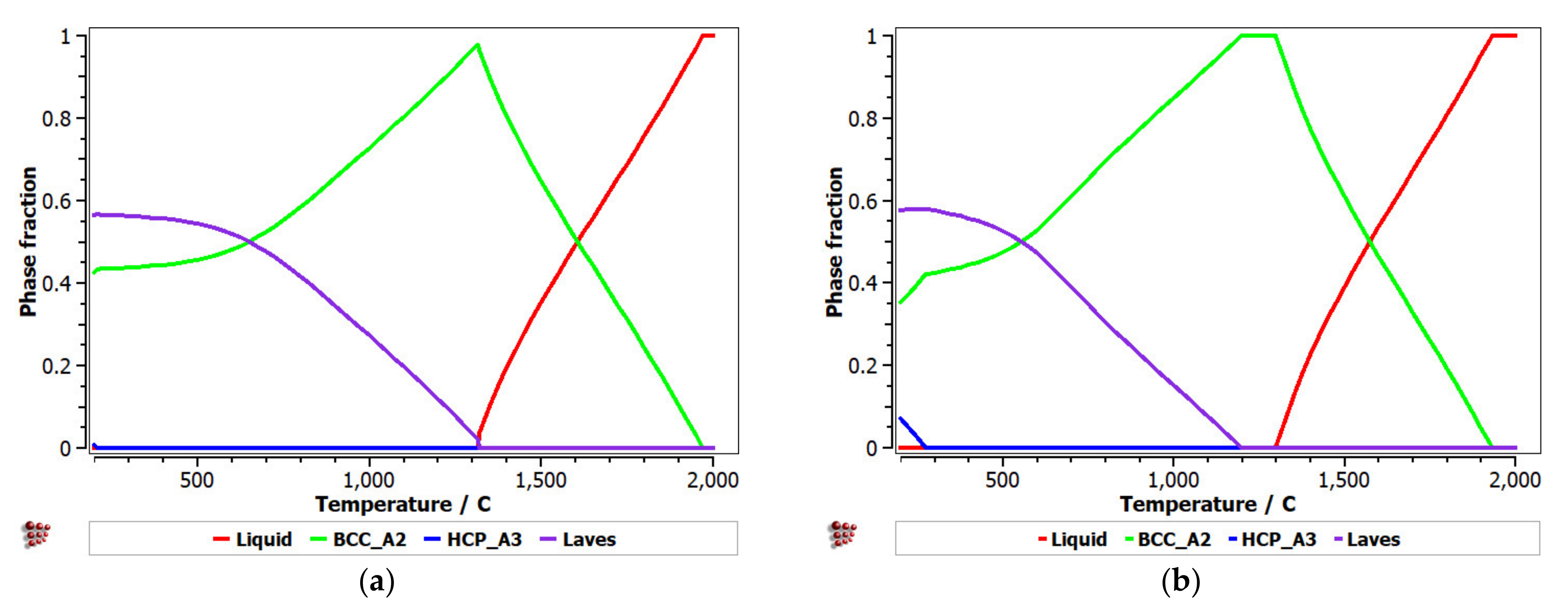
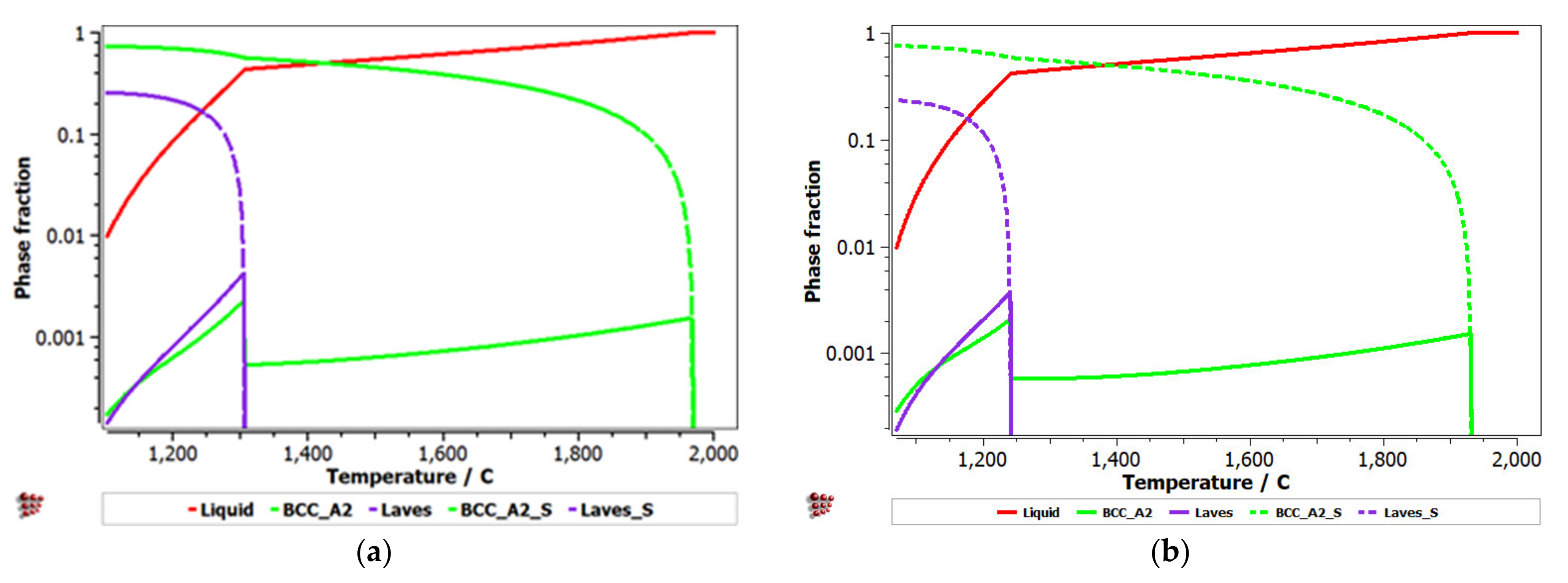
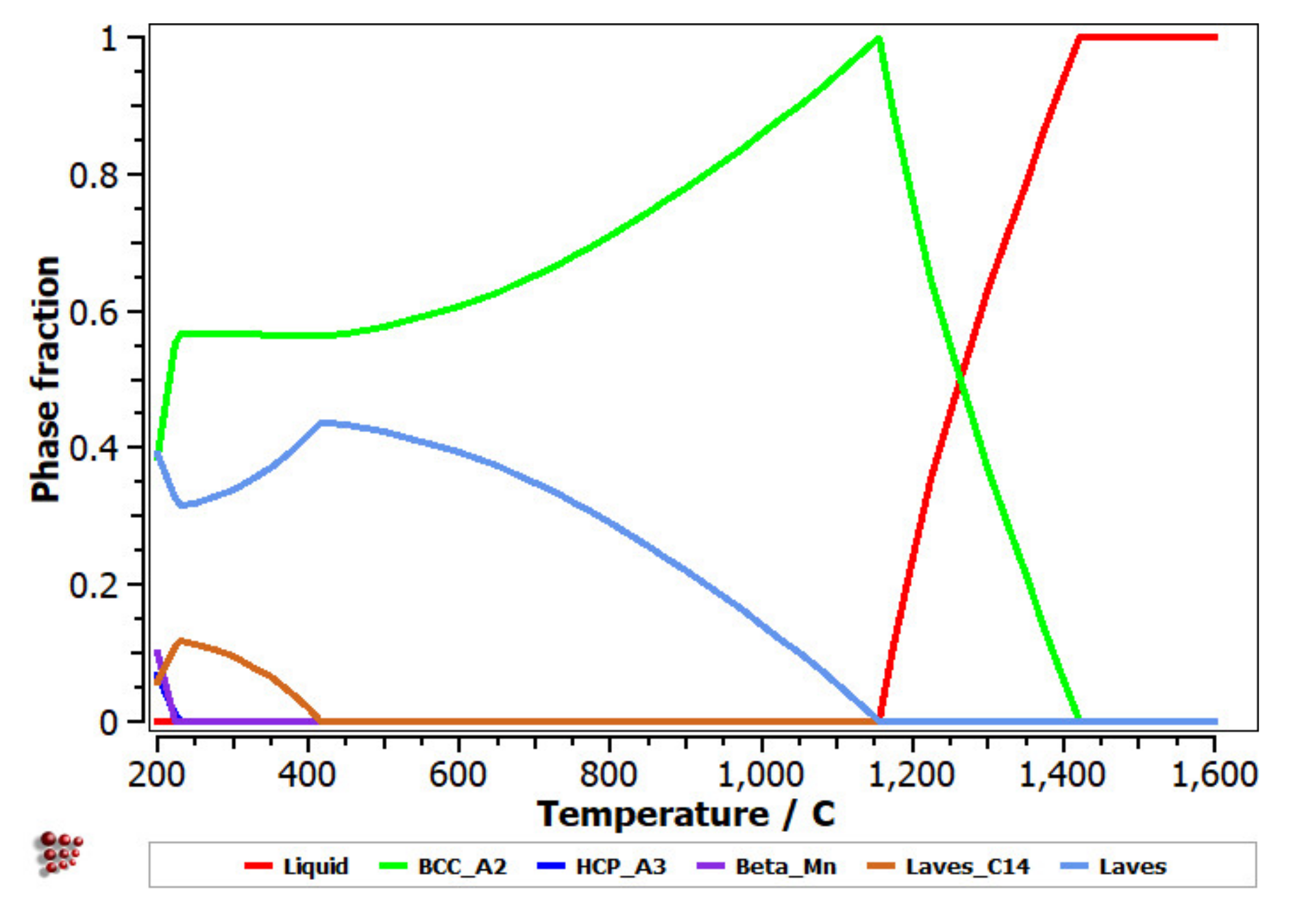
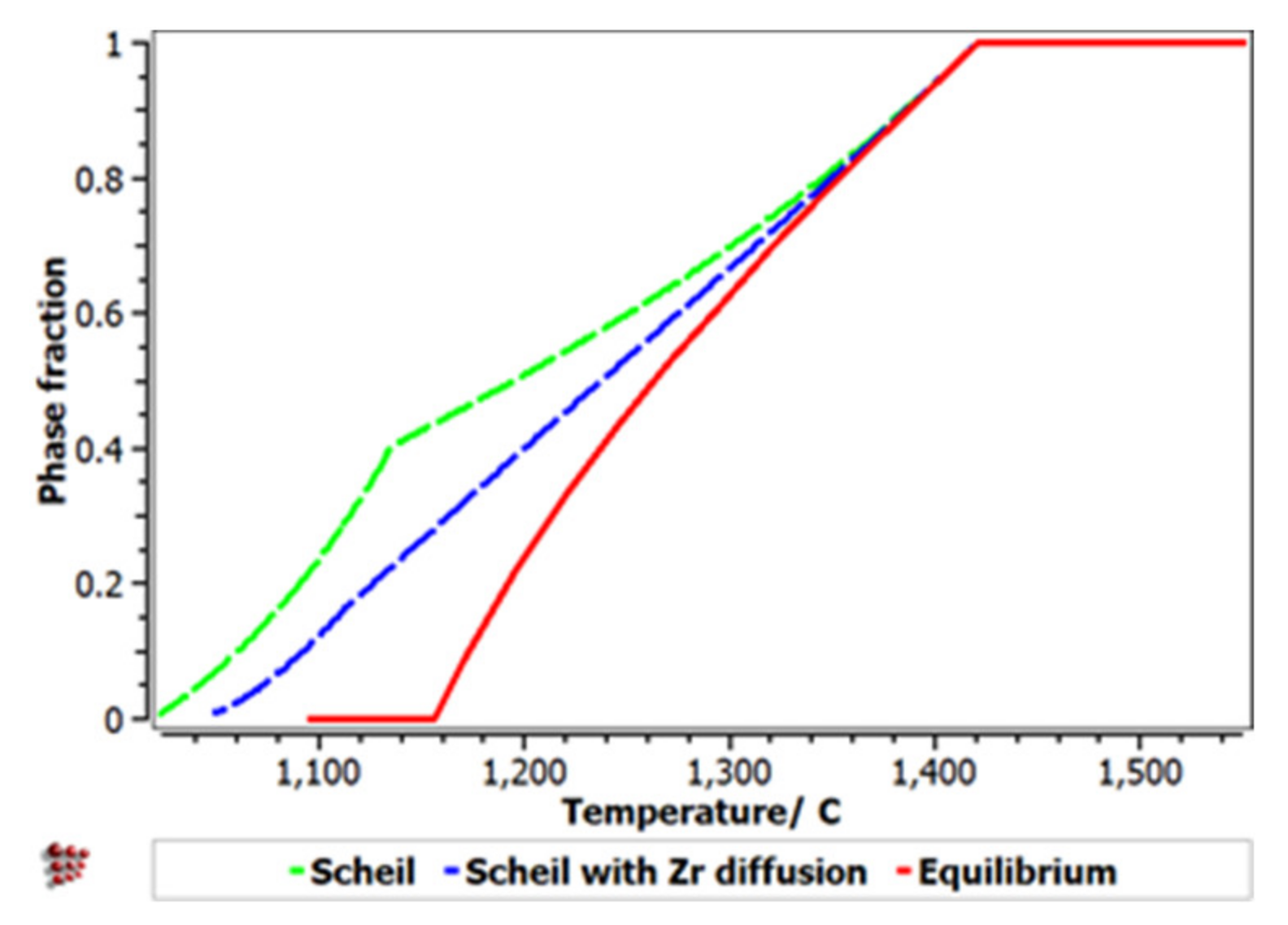
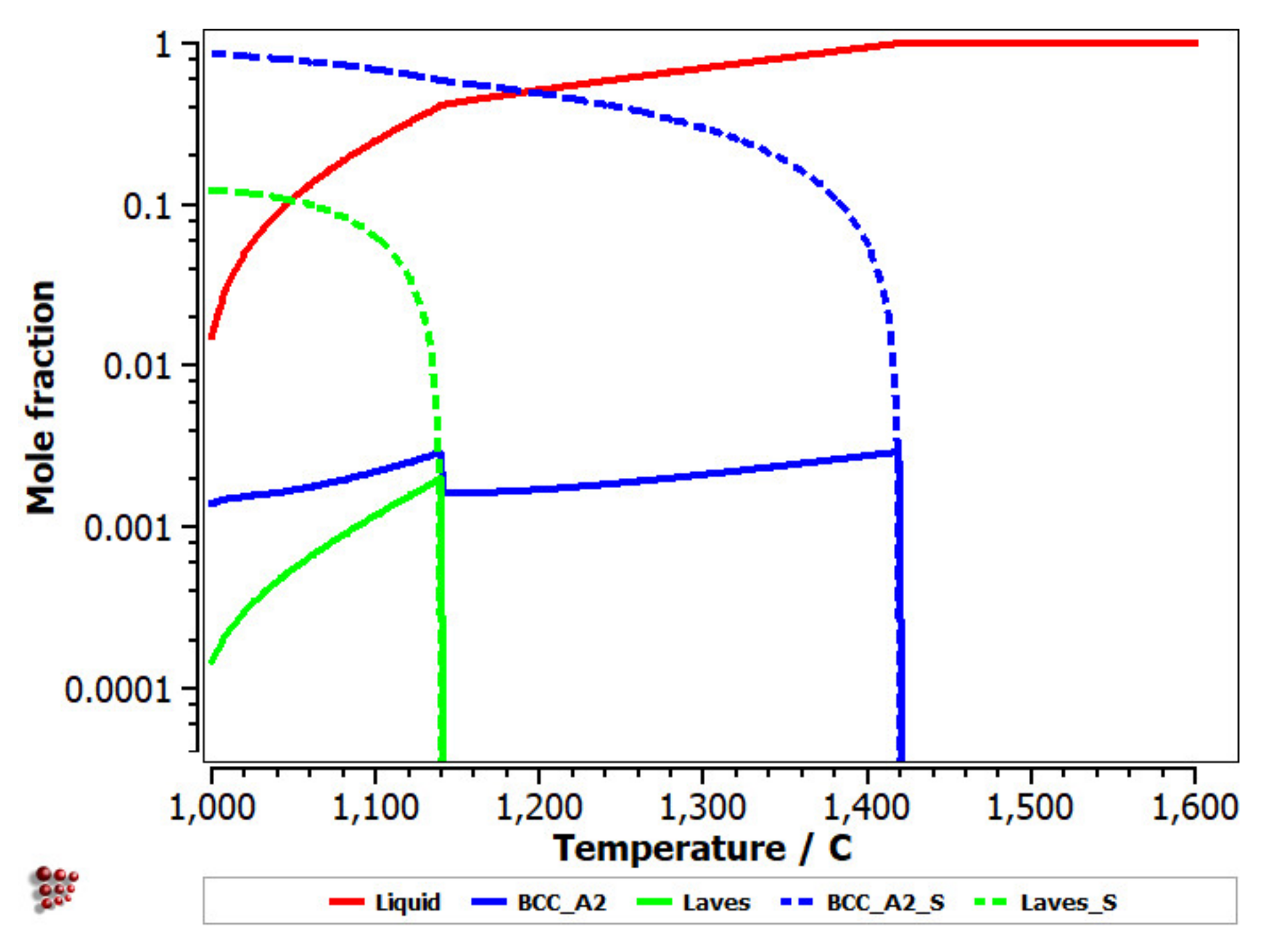
3.3. CCA Selection Using the CALPHAD Method and Kinetic and Thermodynamic Criteria
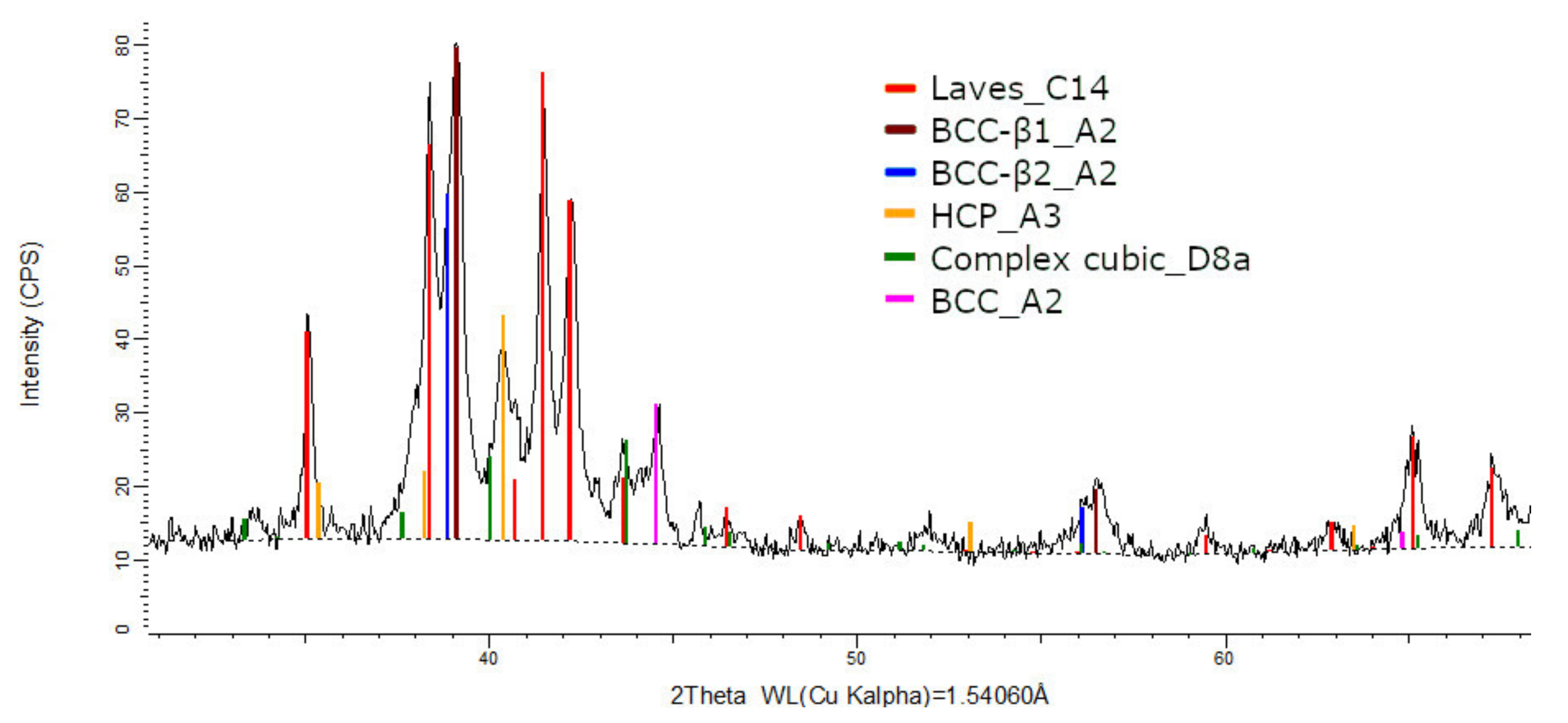
3.4. Empirical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Constantinescu, D.; Cârlan, B.A. A short history of the iron and steel industry in Central Europe during the Roman Iron Age. In Proceedings of the 25th International Conference on Metallurgy and Materials Metal 2016, Brno, Czech Republic, 25–27 May 2016; Available online: http://metal2016.tanger.cz/en/ (accessed on 30 January 2017).
- Tylecote, R.F. A History of Metallurgy, 2nd ed.; The Institute of Materials: London, UK, 1992; ISBN 1-902653-79-3. [Google Scholar]
- Santos, G.A. The importance of metallic materials as biomaterials. J. Tissue Eng. Regen. Med. 2017, 3, 300–302. [Google Scholar] [CrossRef] [Green Version]
- Wintermantel, E.; Mayer, J.; Ruffieux, K.; Bruinink, A.; Eckert, K.L. Biomaterials, human tolerance and integration. Chirurg 1999, 70, 847–857. [Google Scholar] [CrossRef]
- Chen, Q.; Thouas, G.A. Metallic implant biomaterials. Mater. Sci. Eng. R Rep. 2015, 87, 1–57. [Google Scholar] [CrossRef]
- Silver, F.H.; Christiansen, D.L. Biomaterials Science and Biocompatibility; Springer: Berlin, Germany, 1999. [Google Scholar]
- Love, B. Metallic Biomaterials; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar] [CrossRef]
- Gunnarsdóttir, I.; Davidsdottir, B.; Worrell, E.; Sigurgeirsdóttir, S. Sustainable energy development: History of the concept and emerging themes. Renew. Sustain. Energy Rev. 2021, 141, 110770. [Google Scholar] [CrossRef]
- European Commission Report. Critical Raw Materials Resilience: Charting a Path towards Greater Security and Sustainability. Communication from the Commission to the European Parliament COM (2020) 474 Final, Brussels. Available online: https://www.europeansources.info/record/critical-raw-materials-resilience-charting-a-path-towards-greater-security-and-sustainability/ (accessed on 3 September 2021).
- Hofmann, M.; Hofmann, H.; Hagelüken, C.; Hool, A. Critical raw materials: A perspective from the materials science community. Sustain. Mater. Technol. 2018, 17, e00074. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Gorsse, S.; Couzinié, J.P.; Miracle, D.B. From high-entropy alloys to complex concentrated alloys. Comptes Rendus Phys. 2018, 19, 721–736. [Google Scholar] [CrossRef]
- Gorsse, S.; Miracle, D.B.; Senkov, O.N. Mapping the world of complex concentrated alloys. Acta Mater. 2017, 135, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, S. Complex concentrated alloys (CCAs)—Current understanding and future opportunities. Metals 2020, 10, 1253. [Google Scholar] [CrossRef]
- Zhang, Y. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Manzoni, A.M.; Glatzel, U. New multiphase compositionally complex alloys driven by the high entropy alloy approach. Mater. Charact. 2019, 147, 512–532. [Google Scholar] [CrossRef]
- Syrovatka, M. On sustainability interpretations of the ecological footprint. Ecol. Econom. 2020, 169, 106543. [Google Scholar] [CrossRef]
- Agren, J. CALPHAD—An approach to predict microstructural stability. Mater. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F.; Chen, S.; Cao, W. Computational Thermodynamics Aided High-Entropy Alloy Design. JOM 2012, 64, 839–845. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miller, J.D.; Miracle, D.B.; Woodward, C. Accelerated exploration of multi-principal element alloys with solid solution phases. Nat. Commun. 2015, 6, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Mao, H.; Chen, Q. Database development and Calphad calculations for high entropy alloys: Challenges, strategies, and tips. Mater. Chem. Phys. 2018, 210, 279–290. [Google Scholar] [CrossRef]
- Lederer, Y.; Toher, C.; Vecchio, K.S.; Curtarolo, S. The search for high entropy alloys: A high–throughput ab–initio approach. Acta Mater. 2018, 159, 364–383. [Google Scholar] [CrossRef] [Green Version]
- Troparevsky, M.C.; Morris, J.R.; Kent, P.R.; Lupini, A.R.; Stocks, G.M. Criteria for predicting the formation of single-phase high-entropy alloys. Phys. Rev. 2018, 5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, A.; Inoue, A. Calculations of Mixing Enthalpy and Mismatch Entropy for Ternary Amorphous Alloys. Mater. Trans. JIM 2000, 41, 1372–1378. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Poletti, M.G.; Battezzati, L. Electronic and thermodynamic criteria for the occurrence of high entropy alloys in metallic systems. Acta Mater. 2014, 75, 297–306. [Google Scholar] [CrossRef]
- Guo, S. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.K.; Kumar, N.; Dwivedi, A.; Subramaniam, A. A geometrical parameter for the formation of disordered solid solutions in multi-component alloys. Intermetallics 2014, 53, 112–119. [Google Scholar] [CrossRef]
- Cardonne, S.M.; Kumar, P.; Michaluk, C.A.; Schwartz, H.D. Tantalum and its Alloys. Int. J. Refract. Hard Met. 1995, 13, 187–194. [Google Scholar] [CrossRef]
- Ferro, P.; Bonollo, F. Materials selection in a critical raw materials perspective. Mater. Des. 2019, 177, 107848. [Google Scholar] [CrossRef]
- Cârlan Șerban, B.A. Theoretical and Experimental Researches Regarding the Obtaining of New High Entropy Alloy with Biocompatible Properties. Ph.D. Thesis, Politehnica University of Bucharest, Bucharest, Romania, October 2020. [Google Scholar]











| Critical Raw Materials in 2020 | ||||
|---|---|---|---|---|
| Antimony | Fluorspar | Magnesium | Scandium | Titanium |
| Baryte | Gallium | Natural graphite | Silicon | Strontium |
| Beryllium | Germanium | Natural rubber | Tantalum | |
| Bismuth | Hafnium | Niobium | Tungsten | |
| Borate | Heavy rare earth elements | Platinum group metals | Vanadium | |
| Cobalt | Light rare earth elements | Phosphate rock | Bauxite | |
| Coking Coal | Indium | Phosphorus | Lithium | |
| Alloy | ∆Smix, J/mol•K | ∆Hmix, kJ/mol | δ, % | VEC, % | ∆χAllen, % | Tm | Ω | ∆Him | k1cr | ρ, g/cm3 |
|---|---|---|---|---|---|---|---|---|---|---|
| FeTa0.5Nb0.5Ti1.5Zr0.5 | 12.42 | −15.56 | 8.02 | 5.25 | 12.78 | 2201.78 | 1.76 | −15.56 | 1.31 | 7.61 |
| FeTa0.5Nb0.5TiZr0.5 | 12.89 | −16.41 | 8.52 | 5.43 | 13.28 | 2239.01 | 1.76 | −16.41 | 1.31 | 8.06 |
| FeMnNb0.5TiZr0.5 | 12.97 | −15.38 | 8.23 | 5.88 | 12.92 | 1927.40 | 1.63 | −15.38 | 1.33 | 6.65 |
| Alloy | Composition Tip | wt.% | Density g/cm3 | |||||
|---|---|---|---|---|---|---|---|---|
| Ti | Fe | Mn | Nb | Ta | Zr | |||
| FeTa0.5Nb0.5Ti1.5Zr0.5 | Analyses | 24.17 | 19.15 | 15.55 | 27.56 | 13.57 | 7.61 | |
| Nominal | 23.14 | 18.02 | - | 14.97 | 29.17 | 14.7 | ||
| FeMnNb0.5TiZr0.5 | Analyses | 17.89 | 21.73 | 22.36 | 22.04 | 15.97 | 6.65 | |
| Nominal | 19.09 | 22.28 | 21.92 | 18.53 | - | 18.18 | ||
| FeTa0.5Nb0.5TiZr0.5 | Analyses | 18.83 | 21.21 | 15.27 | 29.74 | 14.95 | 8.06 | |
| Nominal | 16.73 | 19.51 | - | 16.22 | 31.62 | 15.92 | ||
| FeTa0.5Nb0.5Ti1.5Zr0.5 remelted | Analyses | 19.2 | 18.42 | - | 15.8 | 25 | 12.4 | 7.61 |
| Nominal | 22.16 | 20.28 | 16.39 | 27.52 | 13.65 | 7.61 | ||
| Phase | Composition, wt.% | ||||
|---|---|---|---|---|---|
| Zr | Nb | Ti | Ta | Fe | |
| DR | 4.17 | 30.30 | 43.39 | 14.38 | 7.76 |
| ID1 | 14.16 | 4.01 | 45.47 | 2.35 | 34.01 |
| ID2 | 6.88 | 15.23 | 51.36 | 5.53 | 20.99 |
| ID3 | 11.98 | 7.18 | 45.62 | 3.74 | 31.48 |
| ID4 | 9.76 | 14.75 | 41.87 | 9.03 | 24.59 |
| ID5 | 11.59 | 9.03 | 41.48 | 5.66 | 32.24 |
| Phase | Composition, wt.% | ||||
|---|---|---|---|---|---|
| Zr | Nb | Ti | Ta | Fe | |
| DR | 0.00 | 32.84 | 31.57 | 29.00 | 6.58 |
| ID1 | 14.70 | 0.00 | 46.94 | 2.36 | 36.00 |
| ID2 | 13.64 | 6.06 | 37.13 | 5.11 | 38.06 |
| ID3 | 13.52 | 6.00 | 37.83 | 5.16 | 37.49 |
| ID4 | 11.70 | 8.03 | 36.61 | 8.06 | 35.61 |
| ID5 | 4.38 | 24.93 | 45.90 | 16.78 | 8.01 |
| Phase | Composition, wt.% | ||||
|---|---|---|---|---|---|
| Zr | Nb | Ti | Ta | Fe | |
| DR | - | 28.95 | 21.93 | 41.02 | 8.11 |
| ID1 | 17.26 | 4.05 | 40.96 | 6.31 | 31.42 |
| ID2 | 10.35 | 7.18 | 27.13 | 14.73 | 40.61 |
| ID3 | 4.84 | 13.16 | 60.68 | 8.83 | 12.49 |
| Phase | Composition, wt.% | ||||
|---|---|---|---|---|---|
| Zr | Nb | Ti | Ta | Fe | |
| DR | 7.33 | 16.20 | 30.65 | 32.41 | 13.41 |
| ID1 | 6.82 | 12.70 | 38.86 | 25.72 | 12.70 |
| ID2 | 7.00 | 13.26 | 39.33 | 20.78 | 17.21 |
| Alloy | Vickers Microhardness, HV |
|---|---|
| FeTa0.5Nb0.5Ti1.5Zr0.5 | 802.8 |
| re-melted FeTa0.5Nb0.5Ti1.5Zr0.5 | 699.0 |
| FeTa0.5Nb0.5TiZr0.5 | 898.2 |
| FeMnNb0.5TiZr0.5 | 802.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Șerban, B.-A.; Badea, I.-C.; Constantin, N.; Mitrică, D.; Olaru, M.T.; Burada, M.; Anasiei, I.; Bejan, S.-E.; Ghiță, A.-N.; Popescu, A.M.-J. Modeling and Characterization of Complex Concentrated Alloys with Reduced Content of Critical Raw Materials. Materials 2021, 14, 5263. https://doi.org/10.3390/ma14185263
Șerban B-A, Badea I-C, Constantin N, Mitrică D, Olaru MT, Burada M, Anasiei I, Bejan S-E, Ghiță A-N, Popescu AM-J. Modeling and Characterization of Complex Concentrated Alloys with Reduced Content of Critical Raw Materials. Materials. 2021; 14(18):5263. https://doi.org/10.3390/ma14185263
Chicago/Turabian StyleȘerban, Beatrice-Adriana, Ioana-Cristina Badea, Nicolae Constantin, Dumitru Mitrică, Mihai Tudor Olaru, Marian Burada, Ioana Anasiei, Simona-Elena Bejan, Andreea-Nicoleta Ghiță, and Ana Maria-Julieta Popescu. 2021. "Modeling and Characterization of Complex Concentrated Alloys with Reduced Content of Critical Raw Materials" Materials 14, no. 18: 5263. https://doi.org/10.3390/ma14185263
APA StyleȘerban, B.-A., Badea, I.-C., Constantin, N., Mitrică, D., Olaru, M. T., Burada, M., Anasiei, I., Bejan, S.-E., Ghiță, A.-N., & Popescu, A. M.-J. (2021). Modeling and Characterization of Complex Concentrated Alloys with Reduced Content of Critical Raw Materials. Materials, 14(18), 5263. https://doi.org/10.3390/ma14185263









