Evolutionary Optimization of Machining Parameters Based on Surface Roughness in End Milling of Hot Rolled Steel
Abstract
:1. Introduction
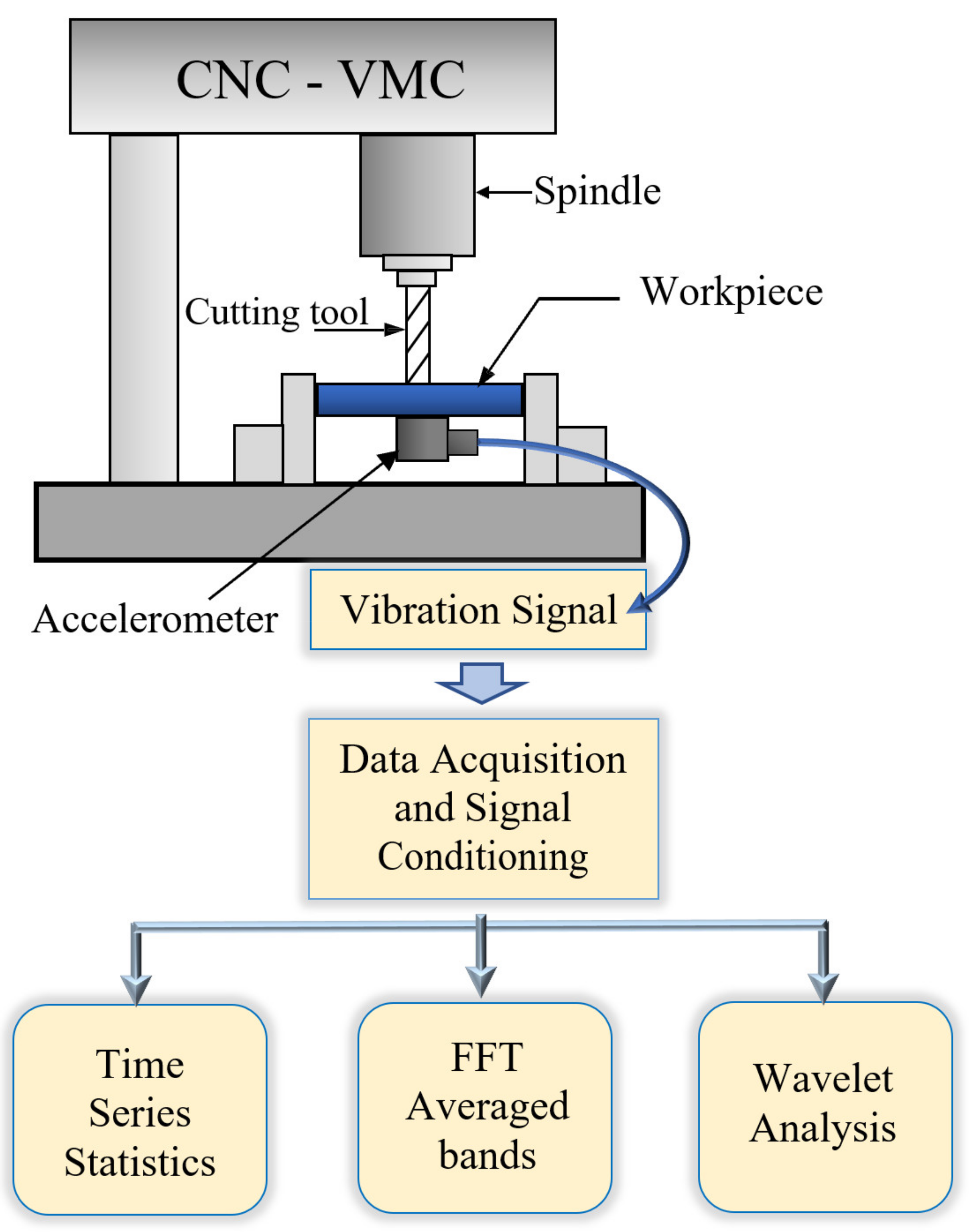
2. Experiment Setup and Feature Extraction
3. Methods
3.1. Genotype and Candidate Fitness
3.2. Evolutionary Algorithms
3.2.1. Genetic Algorithm (GA)
- (1)
- A random population of P individuals is initialized; each individual is a binary string of size corresponding to the size of the reduced feature set. Parameters such as the number of generations, G; and probabilities of mutation and crossover, pm and pc, respectively, are predetermined. Generation counter is initialized to 0. Values of these parameters can be found in Table 3.
- (2)
- A mating pool is created using a tournament selector operator of size 2; two individuals are picked at random from the parent population and the one with the higher fitness (lower surface roughness value) is inserted into the mating pool. The size of the pool is the same as the population size.
- (3)
- A pair of individuals is then picked sequentially from the mating pool and two offspring individuals created using a single point recombination operator with bit-wise mutation with probabilities pc and pm.
- (4)
- The offspring population is merged with the parent population and the combined population is ranked according to individual fitness. The top half of the population is retained as the next generation.
- (5)
- Generation counter is incremented, and steps 2–5 are repeated until generation counter = G.
3.2.2. Particle Swarm Optimization (PSO)
3.2.3. Differential Evolution (DE)
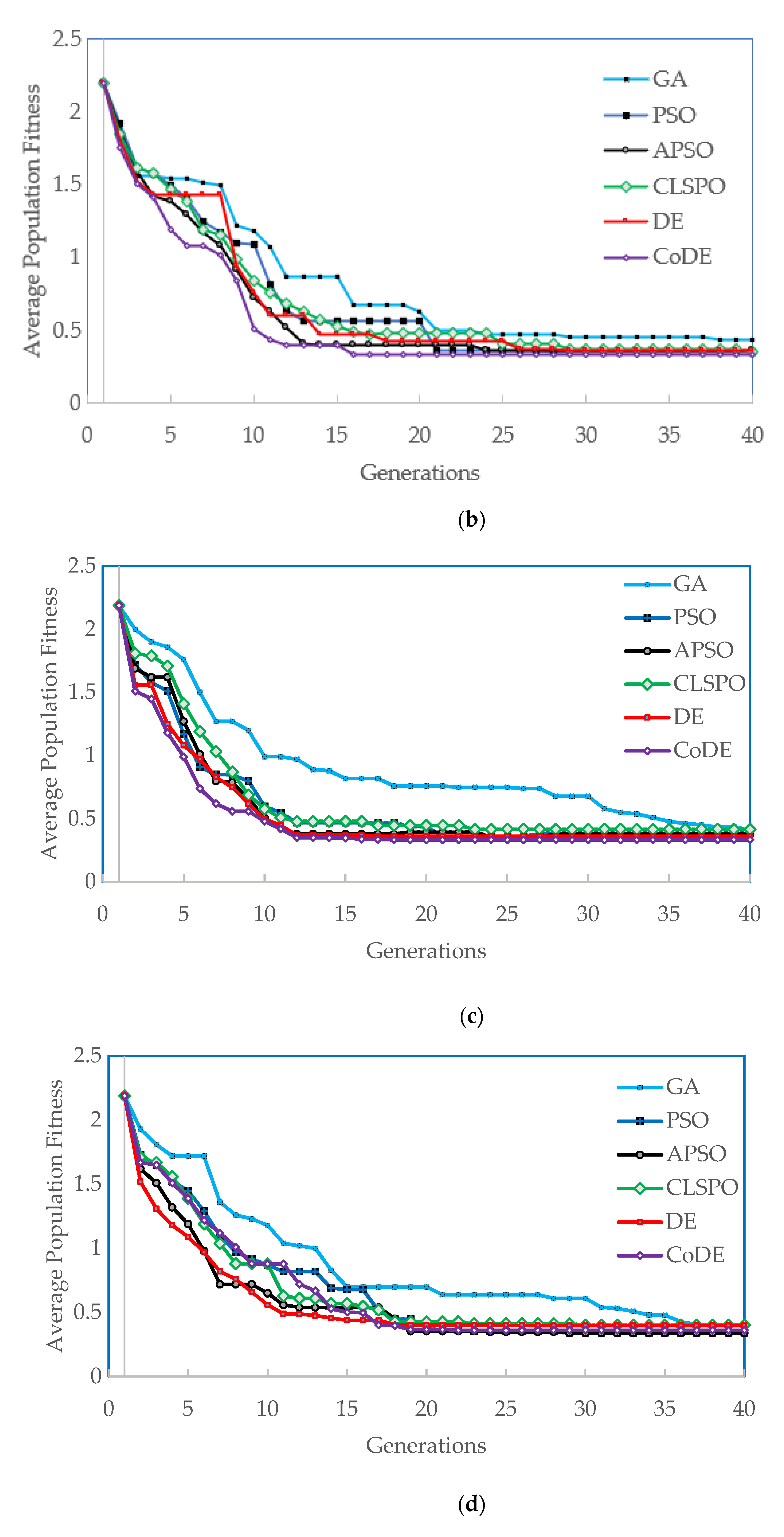
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Element | Weight % |
|---|---|
| Carbon (C) | 0.26 |
| Copper (Cu) | 0.2 |
| Manganese (Mn) | 0.75 |
| Phosphorous (P) | 0.04 max |
| Sulphur (S) | 0.05 max |
| Iron (Fe) | Balance |
| Property | Value |
|---|---|
| Tensile Strength (annealed) | 400–545 MPa |
| Ductility | 22% |
| Hardness | 140 BHN |
| Property | Value |
|---|---|
| Density, g/cm3 | 7.87 |
| Melting point | 1421–1465 °C |
| Thermal conductivity (W/m·K) | 89.0 (20 °C) |
| Coefficient of thermal expansion, (10−6/K) | 12.4 (20–100 °C) |
References
- Lou, S.-J.; Chen, J.C. In-Process Surface Roughness Recognition (ISRR) System in End-Milling Operations. Int. J. Adv. Manuf. Technol. 1999, 15, 200–209. [Google Scholar] [CrossRef]
- Chakguy, P.; Siwaporn, K.; Pisal, Y. Optimal cutting condition determination for desired surface roughness in end milling. Int. J. Adv. Manuf. Technol. 2009, 41, 440–451. [Google Scholar]
- Öktem, H. An integrated study of surface roughness for modelling and optimization of cutting parameters during end milling operation. Int. J. Adv. Manuf. Technol. 2009, 43, 852–861. [Google Scholar] [CrossRef]
- Ding, T.; Zhang, S.; Wang, Y.; Zhu, X. Empirical models and optimal cutting parameters for cutting forces and surface roughness in hard milling of AISI H13 steel. Int. J. Adv. Manuf. Technol. 2010, 51, 45–55. [Google Scholar] [CrossRef]
- Al-Zubaidi, S.; Ghani, J.A.; Haron, C.H.C. Application of ANN inMilling Process: A Review. Model. Simul. Eng. 2011, 2011, 696275. [Google Scholar] [CrossRef]
- Zaidan, A.; Shammari, M.; Amwead, K.A.; Hadi, A.S. Effect of Cutting Parameters on Surface Roughness When Milling Hardened AISI D2 Steel (56 HRC) Using Taguchi Techniques. In Proceedings of the ASME 2012 International Mechanical Engineering Congress & Exposition IMECE2012, Houston, TX, USA, 9–15 November 2012. [Google Scholar]
- Chen, C.C.; Liu, N.M.; Chiang, K.T.; Chen, H.L. Experimental investigation of tool vibration and surface roughness in the precision end-milling process using the singular spectrum analysis. Int. J. Adv. Manuf. Technol. 2012, 63, 797–815. [Google Scholar] [CrossRef]
- Saric, T.; Simunovic, G.; Simunovic, K. Use of Neural Networks in Prediction and Simulation of Steel Surface Roughness. Int. J. Simul. Model. 2013, 12, 225–236. [Google Scholar] [CrossRef]
- Alrashdan, A.; Bataineh, O.; Shbool, M. Multi-criteria end milling parameters optimization of AISI D2 steel using genetic algorithm. Int. J. Adv. Manuf. Technol. 2014, 73, 1201–1212. [Google Scholar] [CrossRef]
- Bhogal, S.S.; Sindhu, C.; Dhami, S.S.; Pabla, B.S. Minimization of Surface Roughness and Tool Vibration in CNC Milling Operation. J. Optim. 2015, 2015, 192030. [Google Scholar] [CrossRef]
- Angelos, P.; Markopoulos, S.G.; Dimitrios, E.M. On the use of back propagation and radial basis function neural networks in surface roughness prediction. J. Ind. Eng. Int. 2016, 12, 389–400. [Google Scholar]
- PoTsang, B.H. An intelligent neural-fuzzy model for an in-process surface roughness monitoring system in end milling operations. J. Intell. Manuf. 2016, 27, 689–700. [Google Scholar]
- PoTsang, B.H.; Zang, H.J.; Lin, Y.C. Development of a Grey online modeling surface roughness monitoring system in end milling operations. J. Intell. Manuf. 2019, 30, 1923–1936. [Google Scholar]
- Lin, W.J.; Lo, S.H.; Young, H.T.; Hung, C.L. Evaluation of Deep Learning Neural Networks for Surface Roughness Prediction Using Vibration Signal Analysis. Appl. Sci. 2019, 9, 1462. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.C.; Wu, K.D.; Shih, W.C.; Hsu, P.K.; Hung, J.P. Prediction of Surface Roughness Based on Cutting Parameters and Machining Vibration in End Milling Using Regression Method and Artificial Neural Network. Appl. Sci. 2020, 10, 3941. [Google Scholar] [CrossRef]
- Eser, A.; Ayyildiz, E.A.; Ayyildiz, M.; Kara, F. Artificial Intelligence-Based Surface Roughness Estimation Modelling for Milling of AA6061 Alloy. Adv. Mater. Sci. Eng. 2021, 2021, 5576600. [Google Scholar] [CrossRef]
- Adamczak, S.; P Zmarzły, P. Research of the influence of the 2D and 3D surface roughness parameters of bearing raceways on the vibration level. IOP Conf. Ser. J. Phys. Conf. Ser. 2019, 1183, 012001. [Google Scholar] [CrossRef]
- Abu-Mahfouz, I.; El Ariss, O.; Rahman, A.H.M.E.; Banerjee, A. Surface roughness prediction as a classification problem using support vector machine. Int. J. Adv. Manuf. Technol. 2017, 92, 803–815. [Google Scholar] [CrossRef]
- Abu-Mahfouz, I.; Banerjee, A.; Rahman, E. Evaluation of Clustering Techniques to Predict Surface Roughness during Turning of Stainless-Steel Using Vibration Signals. Materials 2021, 14, 5050. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Kononenko, I.; Simec, E.; Robnik-Sikonja, M. Overcoming the myopia of indictive algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Roffo, G. Feature Selection Library, MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/68210-feature-selection-library (accessed on 4 July 2021).
- Hopfensitz, M.; Mussel, C.; Wawra, C.; Maucher, M.; Kuhl, M.; Neumann, H.; Kestler, H.A. Multiscale binarization of gene expression data for reconstructing Boolean networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume IV, pp. 1942–1948. [Google Scholar]
- Zambrano-Bigiarini, M.; Clerc, M.; Rojas, R. Standard particle swarm optimization 2011 at CEC-2013: A baseline for future PSO improvements. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2337–2344. [Google Scholar]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S.H. Adaptive particle swarm optimization. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 1362–1381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Opt. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, A.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]


| Axial depth of cut (ap) = 0.381 mm | |||||||||
| Speed | N = 1500 rpm | N = 2000 rpm | N = 3000 rpm | ||||||
| Vc = 59.847 m/min | Vc = 79.796 m/min | Vc = 119.695 m/min | |||||||
| f (mm/tooth) Vf (mm/min) | 0.0127 76.2 | 0.0169 101.6 | 0.0212 127.0 | 0.0095 76.2 | 0.0127 101.6 | 0.0159 127.0 | 0.0085 101.6 | 0.0106 127.0 | 0.0127 152.4 |
| Ra (µm) | 0.416 | 0.302 | 0.326 | 0.328 | 0.304 | 0.454 | 0.364 | 0.314 | 0.414 |
| Speed | N = 4000 rpm | N = 5000 rpm | - | ||||||
| Vc = 159.593 m/min | Vc = 199.491 m/min | - | |||||||
| f (mm/tooth) Vf (mm/min) | 0.0079 127.0 | 0.0095 152.4 | 0.0111 177.8 | 0.0076 152.4 | 0.0089 177.8 | 0.0102 203.2 | - | - | - |
| Ra (µm) | 0.392 | 0.282 | 0.328 | 0.302 | 0.424 | 0.448 | - | - | - |
| Axial depth of cut (ap) = 0.762 mm | |||||||||
| Speed | N = 1500 rpm | N = 2000 rpm | N = 3000 rpm | ||||||
| Vc = 59.847 m/min | Vc = 79.796 m/min | Vc = 119.695 m/min | |||||||
| f (mm/tooth) Vf (mm/min) | 0.0127 76.2 | 0.0169 101.6 | 0.0212 127.0 | 0.0095 76.2 | 0.0127 101.6 | 0.0159 127.0 | 0.0085 101.6 | 0.0106 127.0 | 0.0127 152.4 |
| Ra (µm) | 0.93 | 0.852 | 0.558 | 0.64 | 0.896 | 0.902 | 0.494 | 0.418 | 0.482 |
| Speed | N = 4000 rpm | N = 5000 rpm | - | ||||||
| Vc = 159.593 m/min | Vc = 199.491 m/min | - | |||||||
| f (mm/tooth) Vf (mm/min) | 0.0079 127.0 | 0.0095 152.4 | 0.0111 177.8 | 0.0076 152.4 | 0.0089 177.8 | 0.0102 203.2 | - | - | - |
| Ra (µm) | 0.834 | 0.678 | 0.384 | 0.864 | 1.048 | 1.638 | - | - | - |
| Axial depth of cut (ap) = 1.524 mm | |||||||||
| Speed | N = 1500 rpm | N = 2000 rpm | N = 3000 rpm | ||||||
| Vc = 59.847 m/min | Vc = 79.796 m/min | Vc = 119.695 m/min | |||||||
| f (mm/tooth) Vf (mm/min) | 0.0127 76.2 | 0.0169 101.6 | 0.0212 127.0 | 0.0095 76.2 | 0.0127 101.6 | 0.0159 127.0 | 0.0085 101.6 | 0.0106 127.0 | 0.0127 152.4 |
| Ra (µm) | 1.186 | 0.814 | 0.726 | 0.596 | 0.838 | 0.868 | 1.34 | 1.108 | 1.01 |
| Speed | N = 4000 rpm | N = 5000 rpm | - | ||||||
| Vc = 159.593 m/min | Vc = 199.491 m/min | - | |||||||
| f (mm/tooth) Vf (mm/min) | 0.0079 127.0 | 0.0095 152.4 | 0.0111 177.8 | 0.0076 152.4 | 0.0089 177.8 | 0.0102 203.2 | - | - | - |
| Ra (µm) | 0.82 | 1.612 | 1.49 | 2.084 | 1.98 | 1.79 | - | - | - |
| Feature Name | Original Size | ReliefF | RFE | SFAD |
|---|---|---|---|---|
| Fast Fourier Transform Averages | 32 | 4 | 2 | 0 |
| Mean of raw time series | 1 | 1 | 1 | 0 |
| Skewness of raw time series | 1 | 1 | 0 | 0 |
| Standard deviation of raw time series | 1 | 0 | 1 | 0 |
| Kurtosis of raw time series | 1 | 0 | 0 | 0 |
| Variance of raw time series | 1 | 0 | 0 | 0 |
| Mexican Hat coefficients | 64 | 8 | 5 | 0 |
| Coiflet wavelet coefficients | 64 | 6 | 2 | 0 |
| Kurtoses of wavelet approximations | 10 | 1 | 1 | 2 |
| Skewness of wavelet approximations | 10 | 1 | 0 | 2 |
| Kurtoses of wavelet details | 10 | 1 | 0 | 2 |
| Skewness of wavelet details | 10 | 0 | 1 | 2 |
| RMS of wavelet approximations | 10 | 1 | 0 | 2 |
| RMS of wavelet details | 10 | 1 | 1 | 2 |
| Crest factors of wavelet approximations | 10 | 1 | 1 | 2 |
| Crest factors of wavelet details | 10 | 0 | 0 | 2 |
| Total | 245 | 26 | 15 | 16 |
| GA | PSO | APSO | CLPSO | DE | CoDE | |
|---|---|---|---|---|---|---|
| Population size P | 25 | 25 | 25 | 25 | 25 | 25 |
| Max generations G | 40 | 40 | 40 | 40 | 40 | 40 |
| Crossover probability pm | 0.9 | - | - | - | 0.9 | 0.9 |
| Mutation probability pc | 0.05 | - | - | - | - | - |
| Inertial weight ω (start, end) | - | 0.9, 0.4 | 0.9, *1 | 0.9, 0.4 | - | - |
| Acceleration weight 1, c1 (start, end) | - | 0.5, 2.5 | 2.0, *2 | - | - | - |
| Acceleration weight 2, c2 (start, end) | - | 2.5, 0.5 | 2.0, *2 | - | - | - |
| Acceleration coefficient, c | - | - | 1.5 | - | - | |
| Scale factor F | - | - | - | 0.9 | 0.9 |
| Evolutionary Algorithms | |||||||
|---|---|---|---|---|---|---|---|
| Feature Sets | Binarization | GA | PSO | APSO | CLPSO | DE | CoDE |
| ReliefF | BKMC | 0.375 | 0.326 | 0.302 | 0.318 | 0.298 | 0.292 |
| ReliefF | BASC | 0.392 | 0.338 | 0.322 | 0.329 | 0.309 | 0.301 |
| RFE | BKMC | 0.357 | 0.302 | 0.302 | 0.302 | 0.311 | 0.302 |
| RFE | BASC | 0.382 | 0.329 | 0.329 | 0.329 | 0.329 | 0.314 |
| SFAD | BKMC | 0.428 | 0.389 | 0.372 | 0.370 | 0.358 | 0.328 |
| SFAD | BASC | 0.440 | 0.402 | 0.398 | 0.382 | 0.369 | 0.364 |
| Evolutionary Algorithms | |||||||
|---|---|---|---|---|---|---|---|
| Feature Sets | Binarization | GA | PSO | APSO | CLPSO | DE | CoDE |
| ReliefF | BKMC | 0.395 | 0.366 | 0.359 | 0.371 | 0.371 | 0.321 |
| ReliefF | BASC | 0.409 | 0.387 | 0.381 | 0.418 | 0.362 | 0.334 |
| RFE | BKMC | 0.432 | 0.353 | 0.357 | 0.352 | 0.361 | 0.331 |
| RFE | BASC | 0.408 | 0.344 | 0.340 | 0.402 | 0.398 | 0.362 |
| SFAD | BKMC | 0.488 | 0.431 | 0.421 | 0.479 | 0.388 | 0.377 |
| SFAD | BASC | 0.540 | 0.501 | 0.476 | 0.424 | 0.404 | 0.374 |
| Evolutionary Algorithms | |||||||
|---|---|---|---|---|---|---|---|
| Feature Sets | Binarization | GA | PSO | APSO | CLPSO | DE | CoDE |
| ReliefF | BKMC | 40 * | 32 | 28 | 27 | 22 | 20 |
| ReliefF | BASC | 40 * | 29 | 25 | 20 | 18 | 17 |
| RFE | BKMC | 38 | 26 | 22 | 24 | 23 | 22 |
| RFE | BASC | 37 | 28 | 29 | 28 | 26 | 23 |
| SFAD | BKMC | 40 * | 31 | 30 | 29 | 27 | 27 |
| SFAD | BASC | 40 * | 35 | 32 | 27 | 29 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Mahfouz, I.; Banerjee, A.; Rahman, E. Evolutionary Optimization of Machining Parameters Based on Surface Roughness in End Milling of Hot Rolled Steel. Materials 2021, 14, 5494. https://doi.org/10.3390/ma14195494
Abu-Mahfouz I, Banerjee A, Rahman E. Evolutionary Optimization of Machining Parameters Based on Surface Roughness in End Milling of Hot Rolled Steel. Materials. 2021; 14(19):5494. https://doi.org/10.3390/ma14195494
Chicago/Turabian StyleAbu-Mahfouz, Issam, Amit Banerjee, and Esfakur Rahman. 2021. "Evolutionary Optimization of Machining Parameters Based on Surface Roughness in End Milling of Hot Rolled Steel" Materials 14, no. 19: 5494. https://doi.org/10.3390/ma14195494
APA StyleAbu-Mahfouz, I., Banerjee, A., & Rahman, E. (2021). Evolutionary Optimization of Machining Parameters Based on Surface Roughness in End Milling of Hot Rolled Steel. Materials, 14(19), 5494. https://doi.org/10.3390/ma14195494





