Anisotropic Mechanical Response and Strain Localization of a Metallic Glassy-Fiber-Reinforced Polyethylene Terephthalate Fabric
Abstract
:1. Introduction
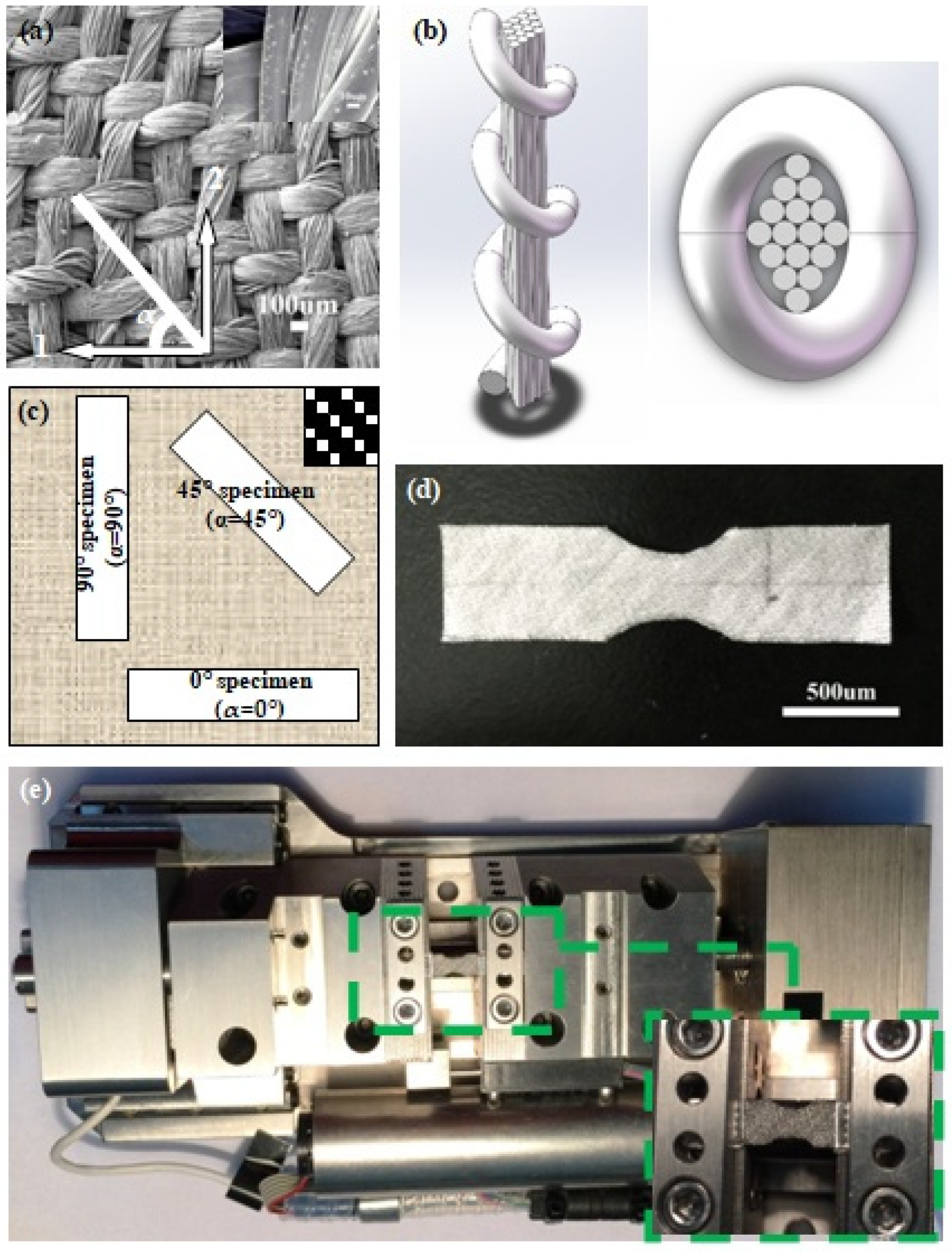
2. Materials and Experimental Methods
3. Results and Discussion
4. Conclusions
- (1)
- The MGF is attributed to the enhanced mechanical properties of the fabric. The deformation processes of the MGF and polymer fiber are similar and can be divided into the elastic stage and the plastic stage. Although they had almost the same elastic strain limit, the MGF exhibited a much higher yield stress in the elastic strain modulus compared with the polymer fiber. According to the mixing rule, the MGF is beneficial to the mechanical enhancement of fabric.
- (2)
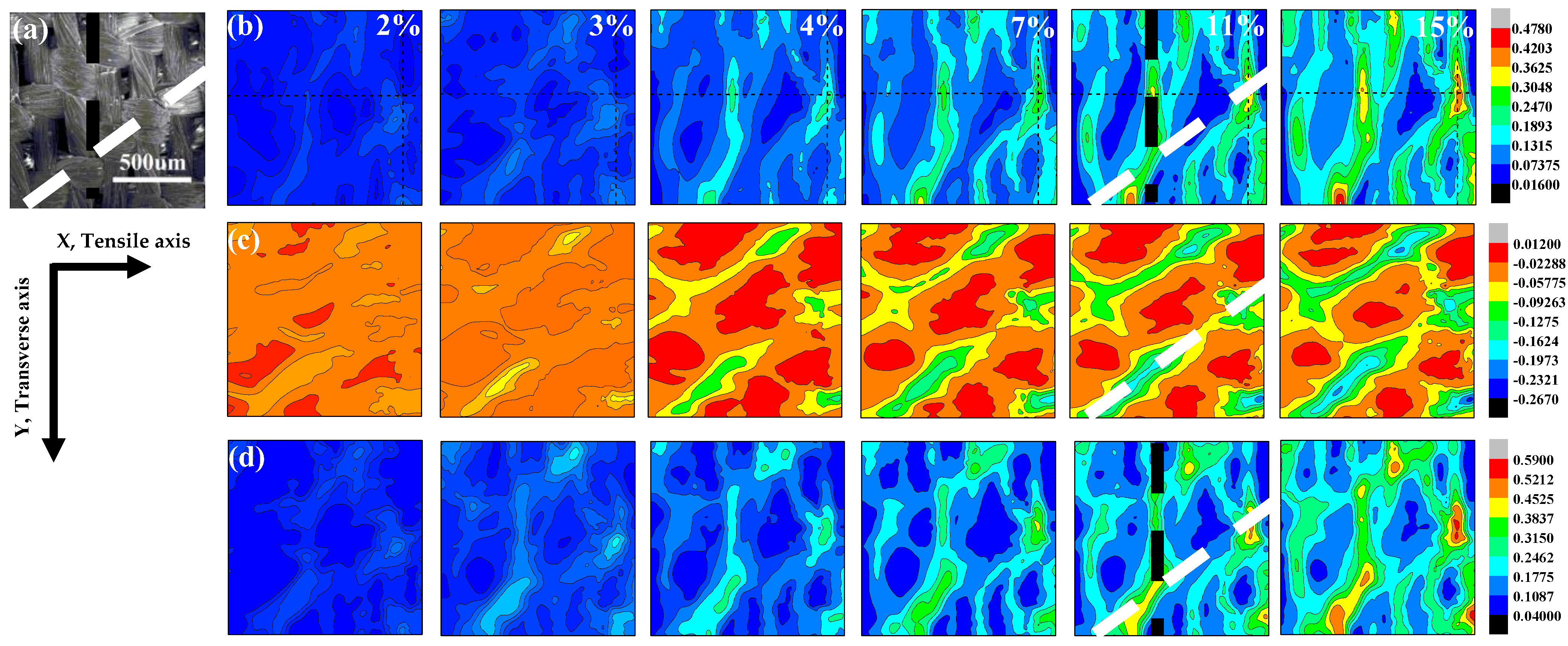
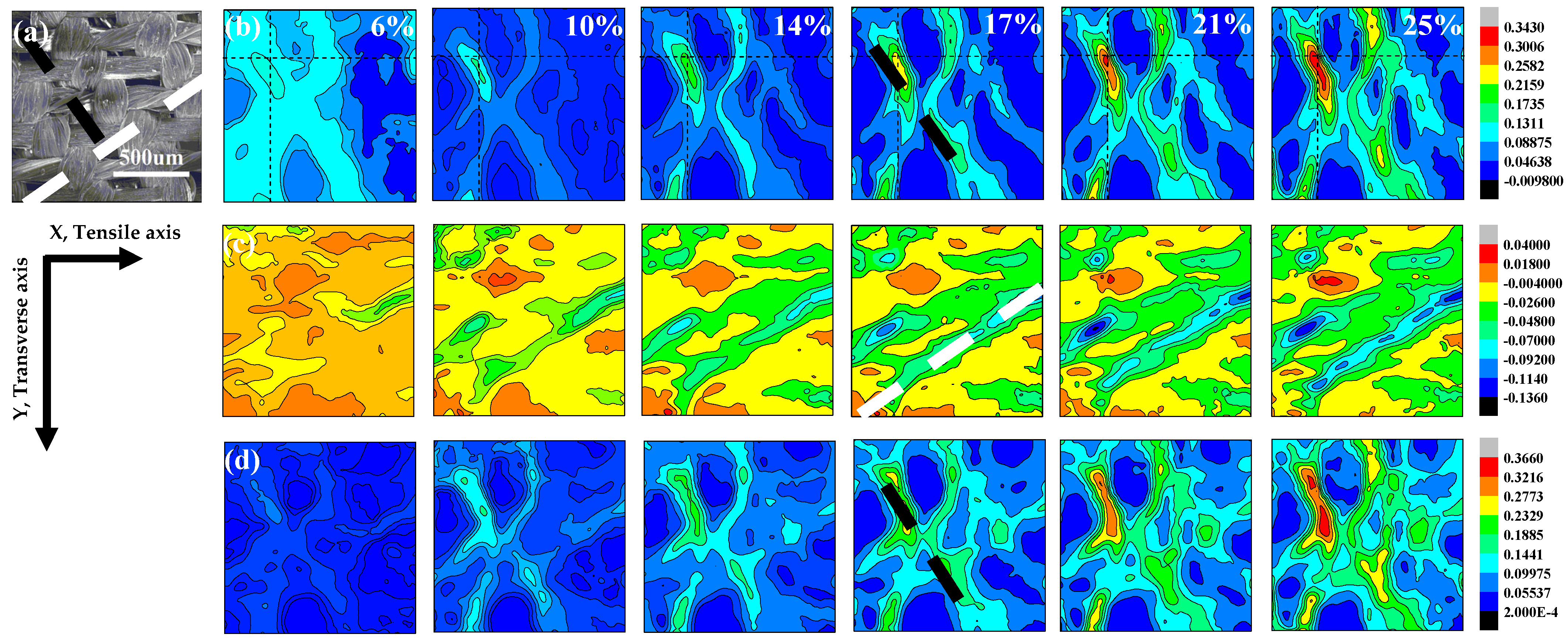
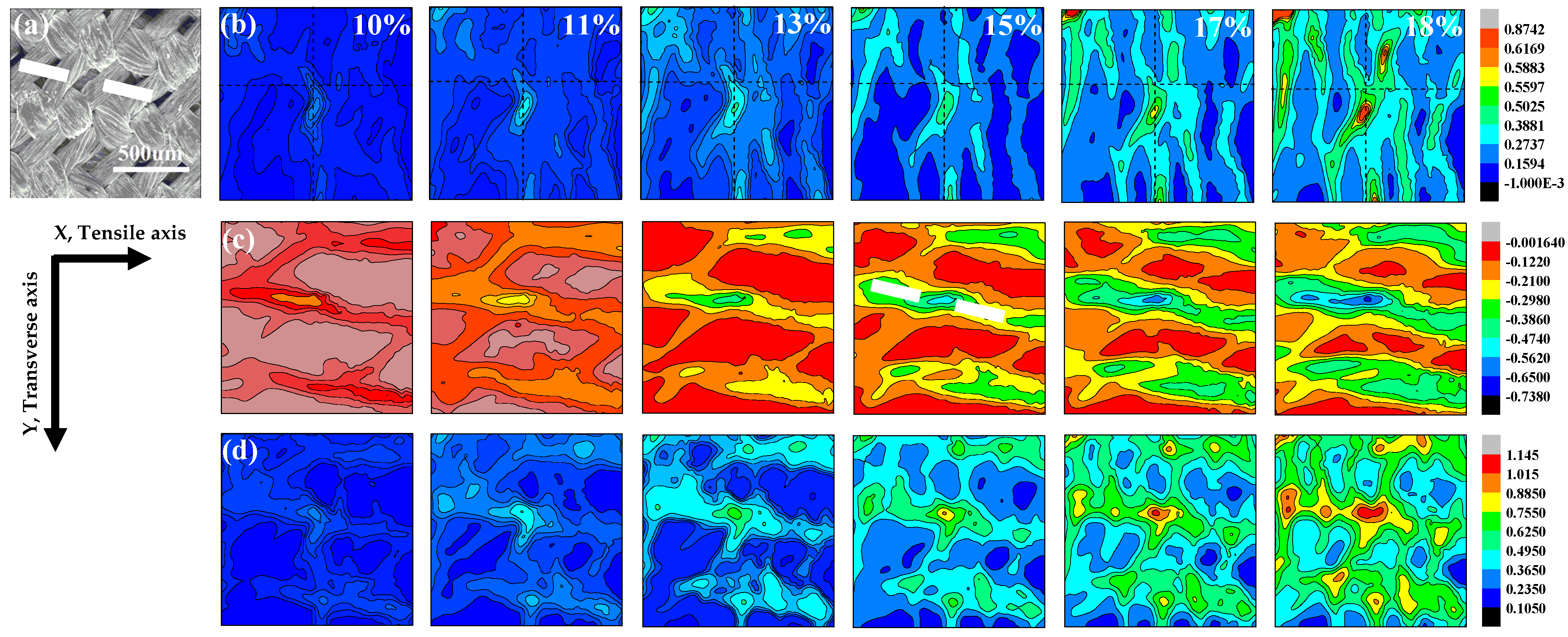
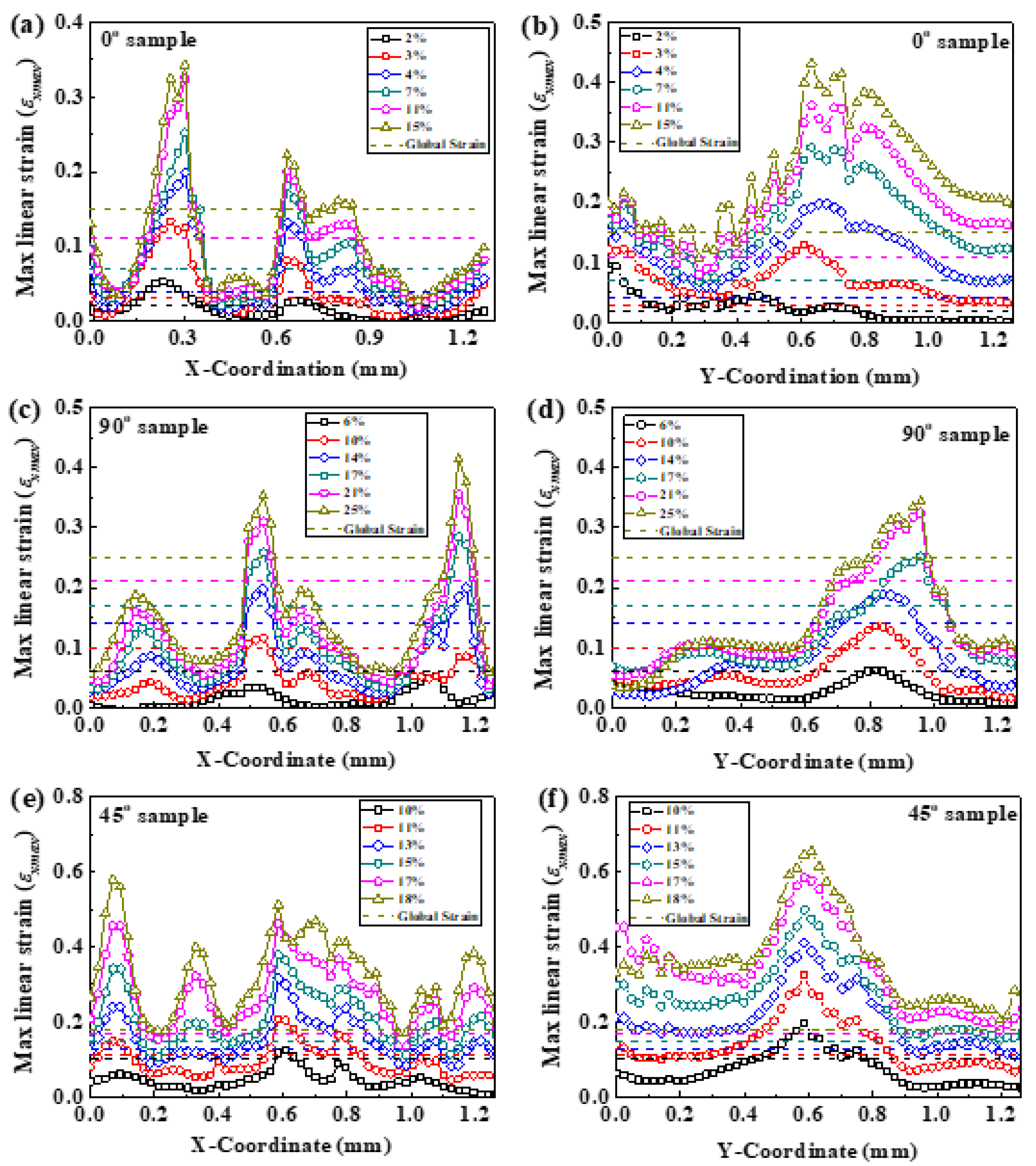
- The restraint of warp yarn on weft in the process of deformation is verified to be beneficial to the strain localization, which is the main cause of the fracture for fabric. With the local strain accumulation, the strain-concentration regions emerge. For the 0° and 90° specimens, the fiber bundles are parallel or perpendicular to the tensile axis. With the global strain increasing, the cross-section of the specimen decreases, resulting in the restraint of warp yarn on weft, and leading to strain localization behaviors. Moreover, the strain-concentration striations appear at the warp and weft intersections or along the boundaries of the warp bundles. For the 45° specimen, fiber bundles rotate towards the direction parallel to the load as the load increases gradually, which bring about the restraint effect and strain localization, and some small, isolated regions locate in the center of the 45° specimen.
- (3)
- The orientation of the fiber bundles strongly affects the fracture mechanism of the fabric because of different local fracture mechanisms. For the 0° and 90° specimens, the strain-concentration striations expose the fiber pull-out mechanism with straight fracture edges, and the 45° specimen is confirmed to fracture by shearing with a rough conical fracture surface due to the small, separated strain-concentration regions and the fiber trellising effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, T.; Wang, Y.L.; Wang, G. Review of the mechanical properties of a 3D woven composite and its applications. Polymer 2018, 57, 740–756. [Google Scholar] [CrossRef]
- Alexander, J.; Augustine, B.S.M.; Prudhuvi, S.; Paudel, A. Hygrothermal effect on natural frequency and damping characteristics of basalt/epoxy composites. Mater. Today 2016, 3, 1666–1671. [Google Scholar] [CrossRef]
- Zhou, G.W.; Sun, Q.P.; Li, D.Y.; Meng, Z.X.; Peng, Y.H.; Zeng, D.; Su, X.M. Effects of fabric architectures on mechanical and damage behaviors in carbon/expoxy woven composites under multiaxial stress states. Polym. Test. 2020, 90, 106657. [Google Scholar] [CrossRef]
- Wang, Y.J. Mechanical properties of stitched multiaxial fabric reinforced composites from manual layup process. Appl. Compos. Mater. 2002, 9, 81–97. [Google Scholar] [CrossRef]
- Tableau, N.; Aboura, Z.; Khellil, K.; Laurin, F. Multiaxial loading on a 3D woven carbon fiber reinforced plastic composite using tensile-torsion test: Identification of the first damage envelope and associated damage mechanisms. Compos. Struct. 2019, 227, 111305. [Google Scholar] [CrossRef]
- Cai, D.A.; Zhou, G.M.; Wang, X.P.; Li, C.; Deng, J. Experimental investigation on mechanical properties of unidirectional and woven fabric glass/ epoxy composites under off-axis tensile loading. Polym. Test. 2017, 58, 142–152. [Google Scholar] [CrossRef]
- Cai, D.A.; Tang, J.; Zhou, G.M.; Wang, X.P.; Li, C.; Silberschmidt, V.V. Failure analysis of plain woven glass/epoxy laminates: Comparison of off-axis and biaxial tension loadings. Polym. Test. 2017, 60, 307–320. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.W.; Sun, Q.P.; Meng, Z.X.; Li, D.Y.; Peng, Y.H.; Zeng, D.; Su, X.M. Experimental investigation on the effects of fabric architectures on mechanical and damage behaviors of carbon/epoxy woven composites. Compos. Struct. 2021, 257, 113366. [Google Scholar] [CrossRef]
- Guo, Q.W.; Zhang, Y.F.; Guo, R.Q.; Sun, X.L.; Chen, L. Experimental and numerical study of in-plane shear properties and failure process of multiaxial 3D angle-interlock woven composites. Compos. Struct. 2021, 261, 113296. [Google Scholar] [CrossRef]
- Koohbor, B.; Ravindran, S.; Kidane, A. A multiscale experimental approach for correlating global and local deformation response in woven composites. Compos. Struct. 2018, 194, 328–334. [Google Scholar] [CrossRef]
- Zhai, Z.Y.; Jiang, B.Y.; Drummer, D. Strain rate-dependent mechanical behavior of quasi-unidirectional E-glass fabric reinforced polypropylene composites under off-axis tensile loading. Polym. Test. 2018, 69, 276–285. [Google Scholar] [CrossRef]
- Lu, Z.X.; Zhou, Y.; Yang, Z.Y.; Liu, Q. Multi-scale finite element analysis of 2.5D woven fabric composites under on-axis and off-axis tension. Comput. Mater. Sci. 2013, 79, 485–494. [Google Scholar] [CrossRef]
- Inoue, A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Acta Mater. 2000, 48, 279–306. [Google Scholar] [CrossRef]
- Johnson, W.L. Bulk glass-forming metallic alloys: Science and technology. MRS Bull. 1999, 24, 42–56. [Google Scholar] [CrossRef]
- Wang, W.H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar] [CrossRef]
- Jang, D.C.; Greer, J.R. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nat. Mater. 2010, 9, 215–219. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.N.; Shao, Y.; Liu, C.T.; Yao, K.F. How does the structural inhomogeneity influence the shear band behaviours of metallic glasses. Philos. Mag. 2020, 100, 1663–1681. [Google Scholar] [CrossRef]
- Kumar, G.; Desai, A.; Schroers, J. Bulk metallic glass: The smaller the better. Adv. Mater. 2011, 23, 461–476. [Google Scholar] [CrossRef]
- Jang, D.C.; Gross, C.T.; Greer, J.R. Effects of size on the strength and deformation mechanism in Zr-based metallic glasses. Int. J. Plast. 2011, 27, 858–867. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.D.; Zhang, Y.H.; Xie, J.X. Microwave absorbing properties of composites filled with glass-coated Fe69Co10Si8B13 amorphous microwire. Mater. Sci. Eng. B 2010, 175, 233–237. [Google Scholar] [CrossRef]
- Qin, F.X.; Peng, H.X.; Prunier, C.; Brosseau, C. Mechanical-elactromagnetic coupling of microwire polymer composites at microwave frequencies. Appl. Phys. Lett. 2010, 97, 153502. [Google Scholar] [CrossRef] [Green Version]
- Marin, P.; Cortina, D.; Hernando, A. High-frequency behavior of amorphous microwires and its applications. J. Magn. Magn. Mater. 2005, 290, 1597–1600. [Google Scholar] [CrossRef]
- Phan, M.H.; Peng, H.X. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2007, 53, 323–420. [Google Scholar] [CrossRef]
- Qin, F.X.; Peng, H.X. Ferromagnetic microwires enabled multifunctional composite materials. Prog. Mater. Sci. 2013, 58, 183–259. [Google Scholar] [CrossRef]
- Moron, C.; Carracedo, M.T. Magneto-impedance effect in amorphous wires. J. Mater. Process. Technol. 2003, 143, 126–129. [Google Scholar] [CrossRef]
- Li, D.R.; Lu, Z.C.; Zhou, S.X. Giant stress-impedance effect in amorphous and thermally annealed Fe73.5Cu1Nb3Si13.5B9 ribbons. Sens. Actuators A 2003, 109, 68–71. [Google Scholar] [CrossRef]
- Churyukanova, M.; Kaloshkin, S.; Shuvaeva, E.; Stepashkin, A.; Zhdanova, M.; Aronin, A.; Aksenov, O.; Arakelov, P.; Zhukova, V.; Zhukov, A. Non-contact method for stress monitoring based on stress dependence of magnetic properties of Fe-based microwires. J. Alloys Compd. 2018, 748, 199–205. [Google Scholar] [CrossRef]
- Allue, A.; Corte-Leon, P.; Gondra, K.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Smart composites with embedded magnetic microwire inclusions allowing non-contact stresses and temperature monitoring. Compos. Part A 2019, 120, 12–20. [Google Scholar] [CrossRef]
- Dong, B.; Tian, L.; Pan, B. Tensile testing of carbon fiber multifilament using an advanced video extensometer assisted by dual reflector imaging. Measurement 2019, 138, 325–331. [Google Scholar] [CrossRef]
- Denis, Y.; Guzman-Maldonado, E.; Morestin, F.; Hamila, N. Ultraviolet digital image correlation for molten thermoplastic composites under finite strain. Exp. Mech. 2019, 59, 439–451. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, robust and accurate digital image correlation calculation without redundant computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Yang, J.S.; Yang, X.G.; Zhu, H.X.; Shi, D.Q.; Chen, X.D.; Qi, H.Y. The effect of off-axis angles on the mesoscale deformation response and failure behavior of an rthotropic textile carbon-epoxy composite. Compos. Struct. 2018, 206, 952–959. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.P.; Pan, B. Experimental study of tensile properties and deformation evolutions of 2D and 2.5D woven SiO2f/SiO2 composites using single-camera stereo-digital image correlation. Compos. Struct. 2018, 200, 589–598. [Google Scholar] [CrossRef]
- Koohbor, B.; Ravindran, S.; Kidane, A. Meso-scale strain localization and failure response of an orthotropic woven glass-fiber reinforced composite. Compos. Part B 2015, 78, 308–318. [Google Scholar] [CrossRef]
- Pankowa, M.; Justusson, B.; Riosbaas, M.; Waas, A.M.; Yen, C.F. Effect of fiber architecture on tensile fracture of 3D woven textile composites. Compos. Struct. 2019, 225, 111139. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, W.Z.; Zhang, Y.N.; Ding, Z.J. Cluster analysis of acoustic emission signals and deformation measurement for delaminated glass fiber epoxy composites. Compos. Struct. 2018, 195, 349–358. [Google Scholar] [CrossRef]
- Borstnar, G.; Gillard, F.; Mavrogordato, M.N.; Sinclair, I.; Spearing, S.M. Three-dimensional deformation mapping of Mode I interlaminar crack extension in particle-toughened interlayers. Acta Mater. 2015, 103, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Szebenyi, G.; Hliva, V. Detection of delamination in polymer composites by digital image correlation-experimental test. Polymers 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Bie, B.X.; Huang, J.Y.; Su, B.; Lu, L.; Fan, D.; E, J.C.; Sun, T.; Fezzaa, K.; Qi, M.L.; Luo, S.N. Dynamic tensile deformation and damage of B4C-reinforced Al composites: Time-resolved imaging with synchrotron x-rays. Mater. Sci. Eng. A 2016, 664, 86–93. [Google Scholar] [CrossRef] [Green Version]
- Nayak, S.; Das, S. Spatial damage sensing ability of metallic particulate-reinforced cementitious composites: Insights from electrical resistance tomography. Mater. Des. 2019, 175, 107817. [Google Scholar] [CrossRef]
- Chiriac, H.; Ovari, T.A. Amorphous glass-covered magnetic wires: Prepatation, properties, applications. Prog. Mater. Sci. 1996, 40, 333–407. [Google Scholar] [CrossRef]
- Hussain, I.; Tong, X.; Wang, G.; Wang, J.G.; Yi, J.; Zhang, D.S.; Zhai, Q.J. Cooling rate-dependent yield behavior of metallic glass wires. Mater. Sci. Eng. A 2017, 683, 236–243. [Google Scholar] [CrossRef]
- Hussain, I.; Jiang, Y.Y.; Jia, Y.D.; Wang, G.; Zhai, Q.J.; Chan, K.C.; Yi, J. Tensile behavior of Cu-coated Pd40Cu30Ni10P20 metallic glassy wire. Sci. Rep. 2018, 8, 5659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lichtenecker, K. Dielektrizitatskonstante naturlicher und kunstlicher Mischkorper. Phys. Z. 1926, 27, 115–158. [Google Scholar]
- Cho, J.; Fenner, J.; Werner, B.; Daniel, I.M. A constitutive model for fiber-reinforced polymer composites. J. Compos. Mater. 2010, 44, 3133–3150. [Google Scholar] [CrossRef]
- Atkin, R.J.; Fox, N. An Introduction to the Theory of Elasticity; Longman: London, UK, 1980. [Google Scholar]
- Koohbor, B.; Ravindran, S.; Kidane, A. Meso-scale study of non-linear tensile response and fiber trellising mechanisms in woven composites. J. Reinf. Plast. Comp. 2016, 35, 986–995. [Google Scholar] [CrossRef]
- Godara, A.; Raabe, D. Influence of fiber orientation on global mechanical behaviour and mesoscale strain localization in a short glass-fiber-reinforced epoxy polymer composite during tensile deformation investigated using digital image correlation. Compos. Sci. Technol. 2007, 67, 2417–2427. [Google Scholar] [CrossRef]
- Xue, P.; Cao, J.; Chen, J.L. Integrated micro/macro-mechanical model of woven fabric composites under large deformation. Compos. Struct. 2005, 70, 69–80. [Google Scholar] [CrossRef]
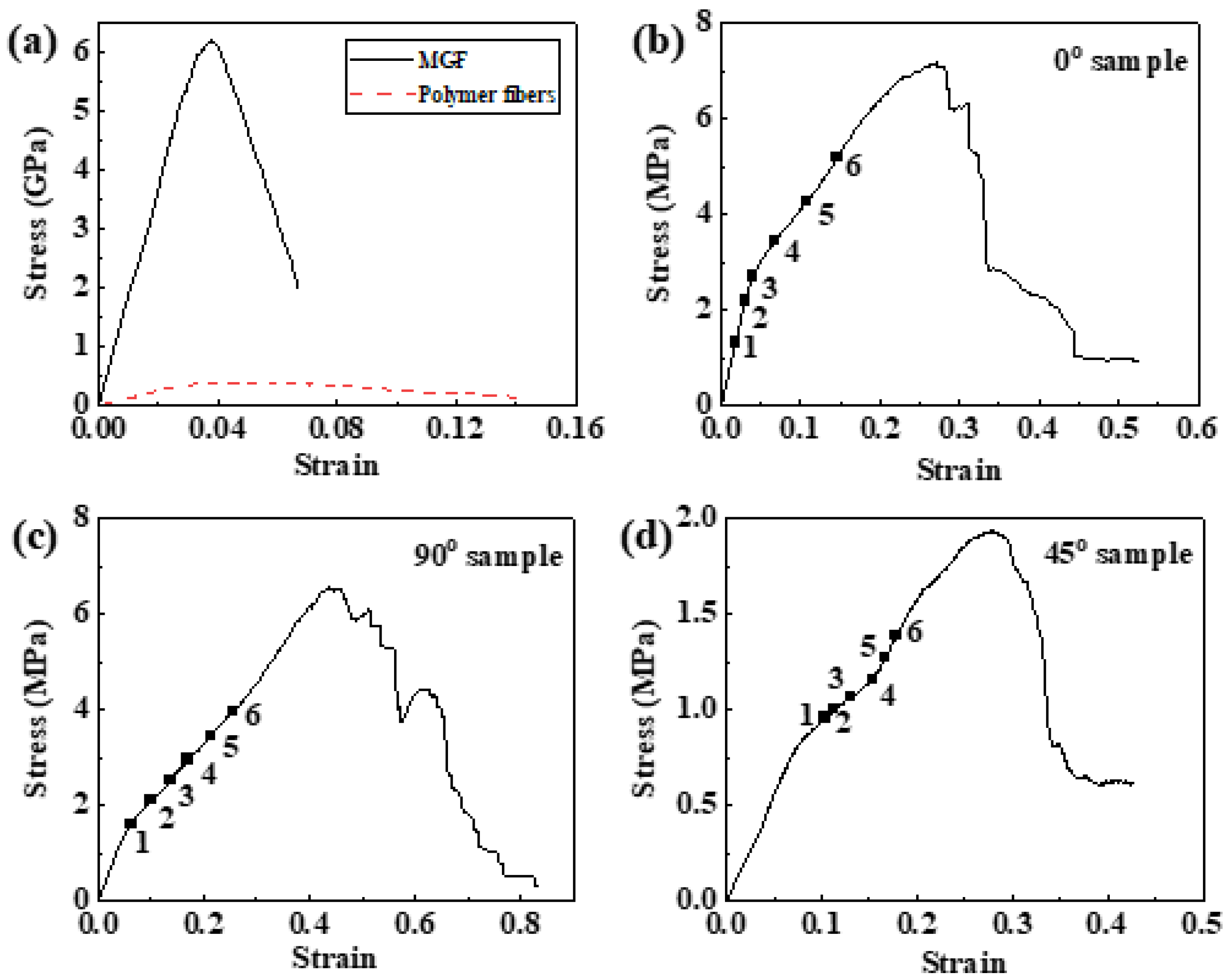

| Sample | E (GPa) | εe | σy (MPa) | σt (MPa) | εp |
|---|---|---|---|---|---|
| MGF | 186.5 | 0.03 | 5.2 | 6.2 | 0.04 |
| Polymer fiber | 12.3 | 0.03 | 0.3 | 0.4 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Huang, B.; Shen, J.; Yi, J.; Jia, Y.; Xue, R.; Wang, G. Anisotropic Mechanical Response and Strain Localization of a Metallic Glassy-Fiber-Reinforced Polyethylene Terephthalate Fabric. Materials 2021, 14, 5619. https://doi.org/10.3390/ma14195619
Li J, Huang B, Shen J, Yi J, Jia Y, Xue R, Wang G. Anisotropic Mechanical Response and Strain Localization of a Metallic Glassy-Fiber-Reinforced Polyethylene Terephthalate Fabric. Materials. 2021; 14(19):5619. https://doi.org/10.3390/ma14195619
Chicago/Turabian StyleLi, Jie, Bo Huang, Jun Shen, Jun Yi, Yandong Jia, Rongjie Xue, and Gang Wang. 2021. "Anisotropic Mechanical Response and Strain Localization of a Metallic Glassy-Fiber-Reinforced Polyethylene Terephthalate Fabric" Materials 14, no. 19: 5619. https://doi.org/10.3390/ma14195619






