Effect of Volume Tie Ratio in the Engineered Cementitious Composites Plastic Hinges on the Seismic Performance of RC Composite Bridge Columns
Abstract
:1. Introduction
2. Target Experimental Program and Results
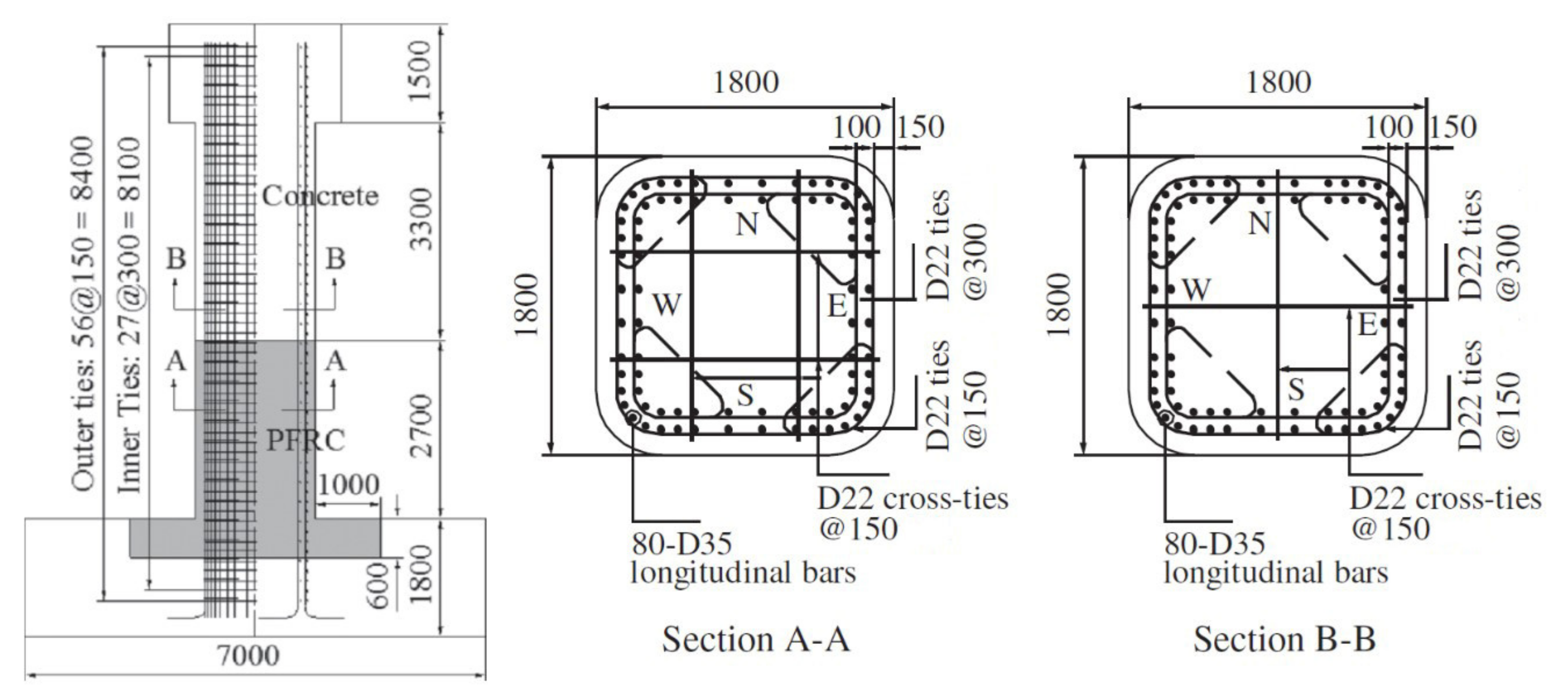
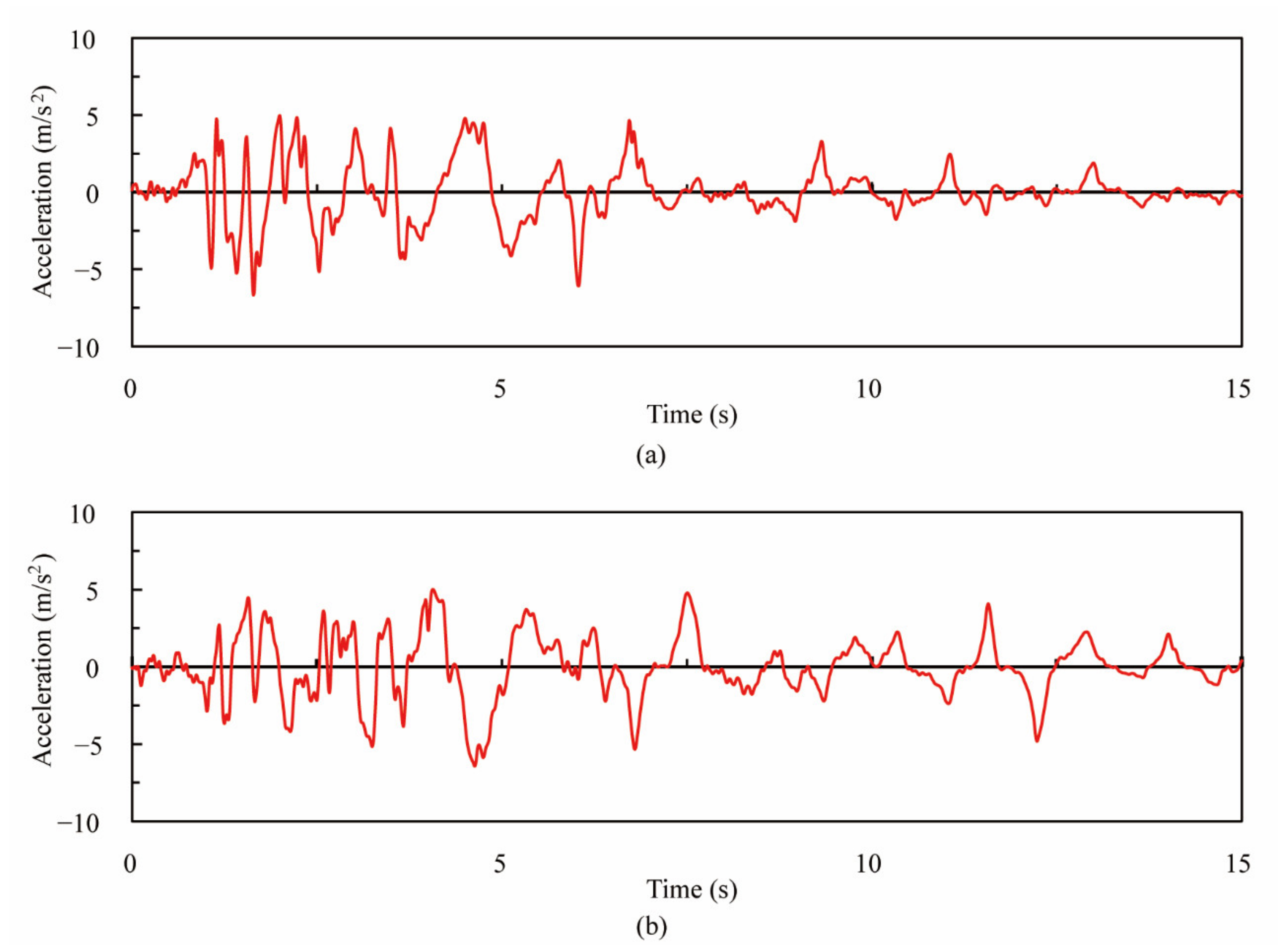
2.1. Target Experimental Program
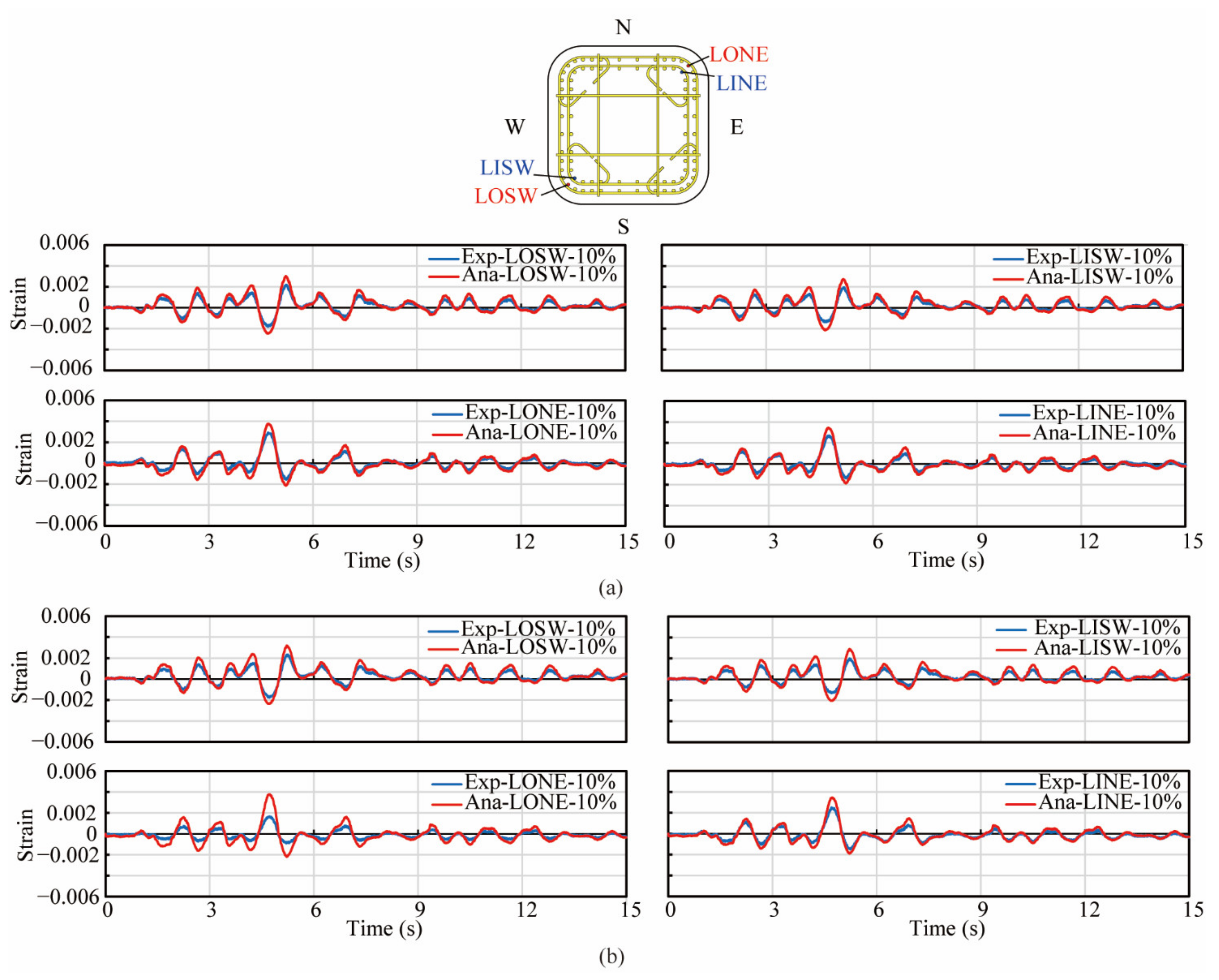
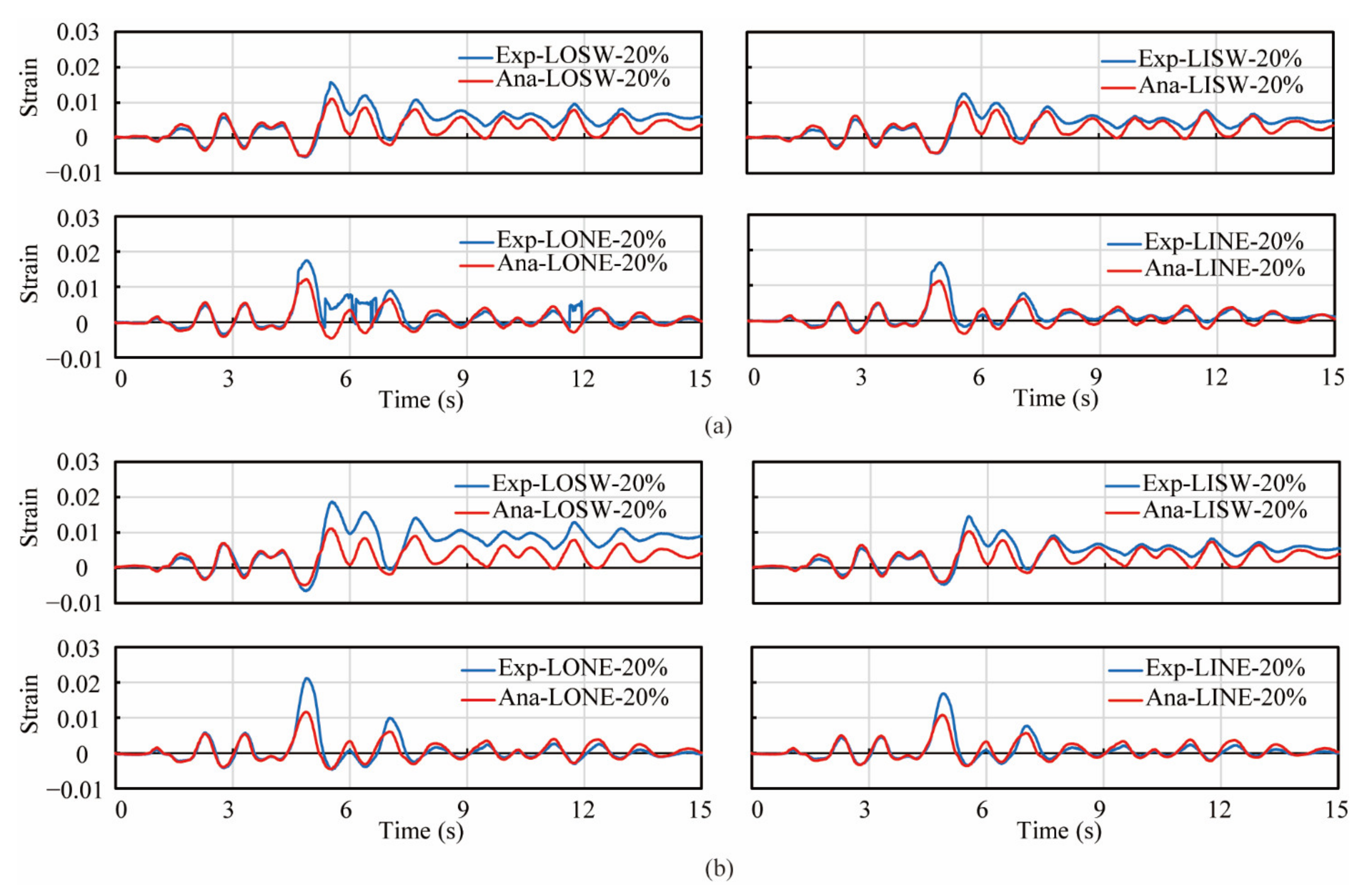
2.2. Target Experimental Results
3. Fiber Element-Based Analysis
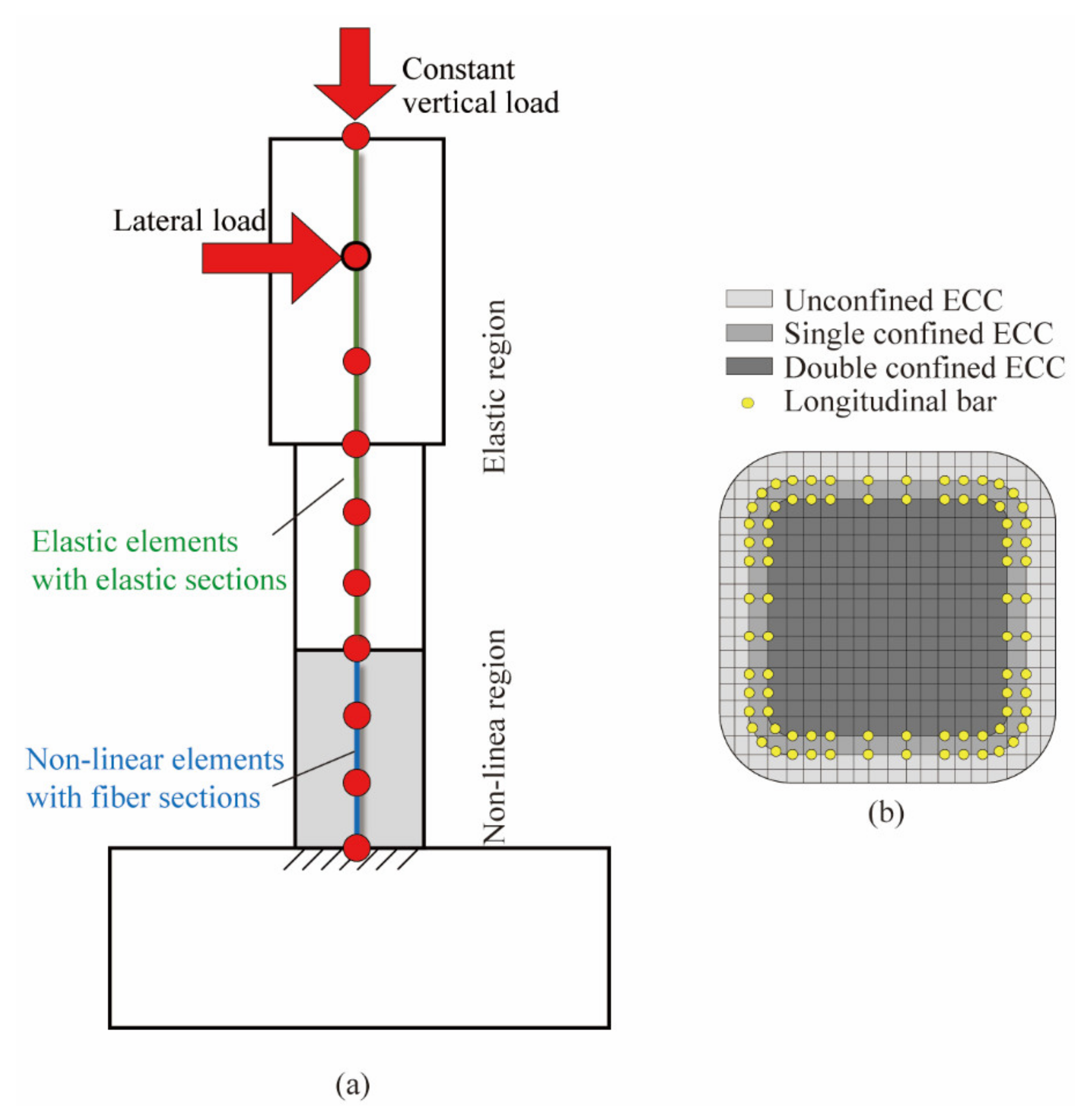
3.1. Analytical Model
3.2. Effect of Lateral Confinement
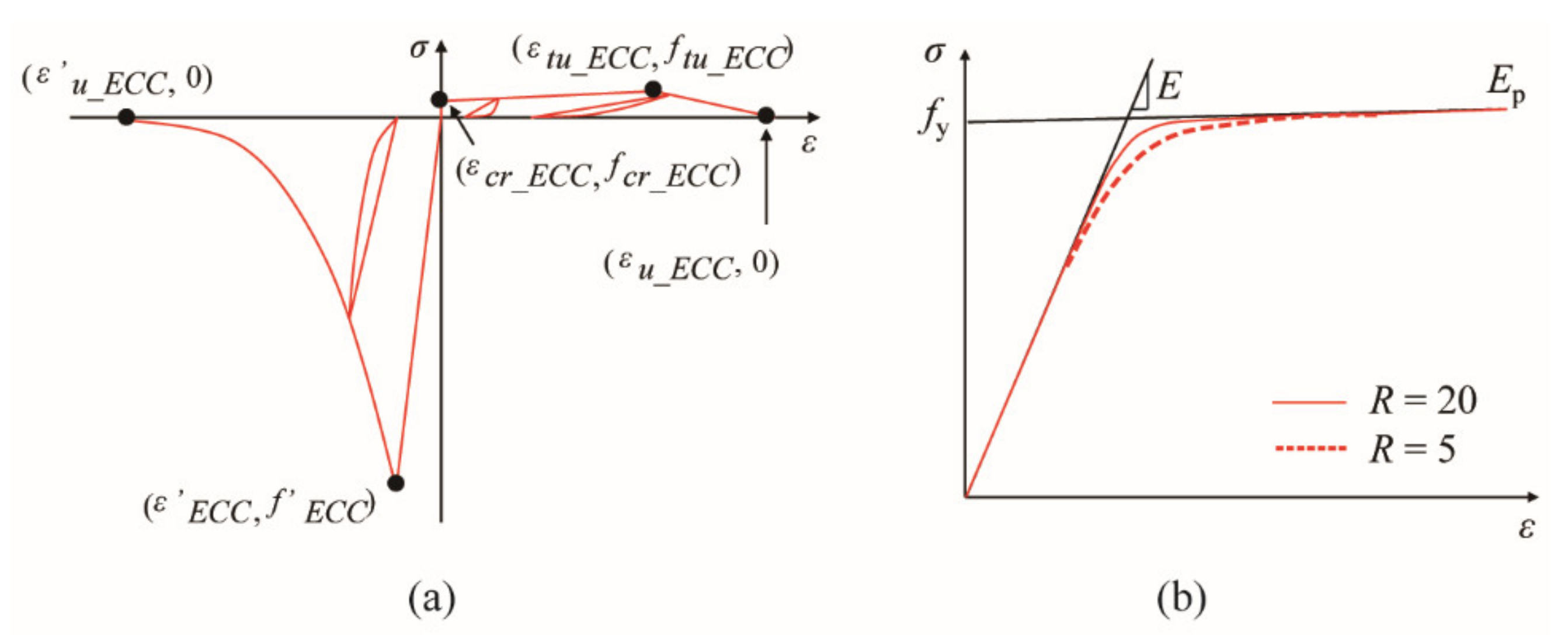
3.3. Material Models
3.4. Analytical Correlation Results
4. Effect of Volume Tie Ratio
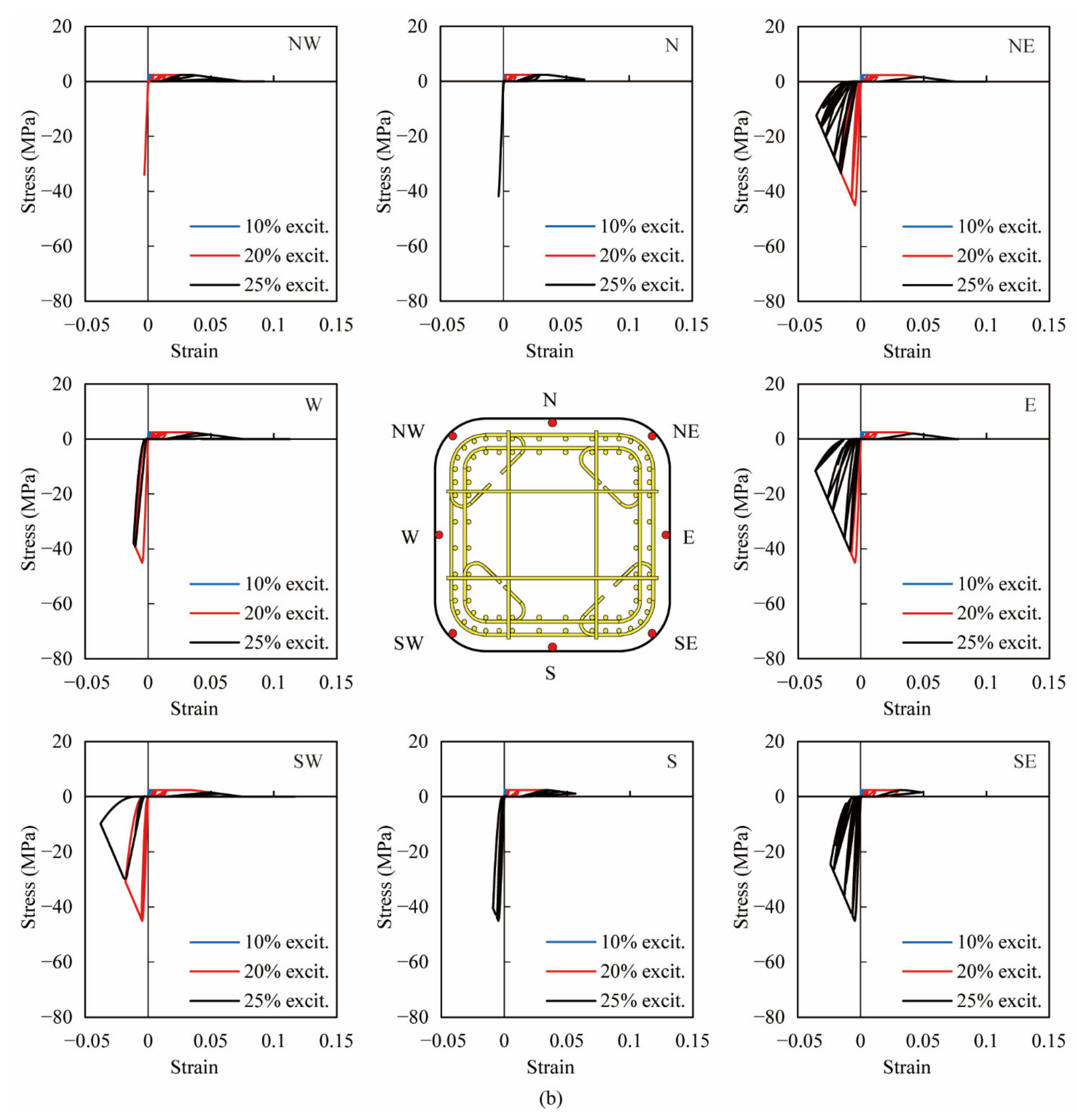
4.1. Hysteresis of Stress-Strain in Extreme Fibers of Cover and Core Concrete
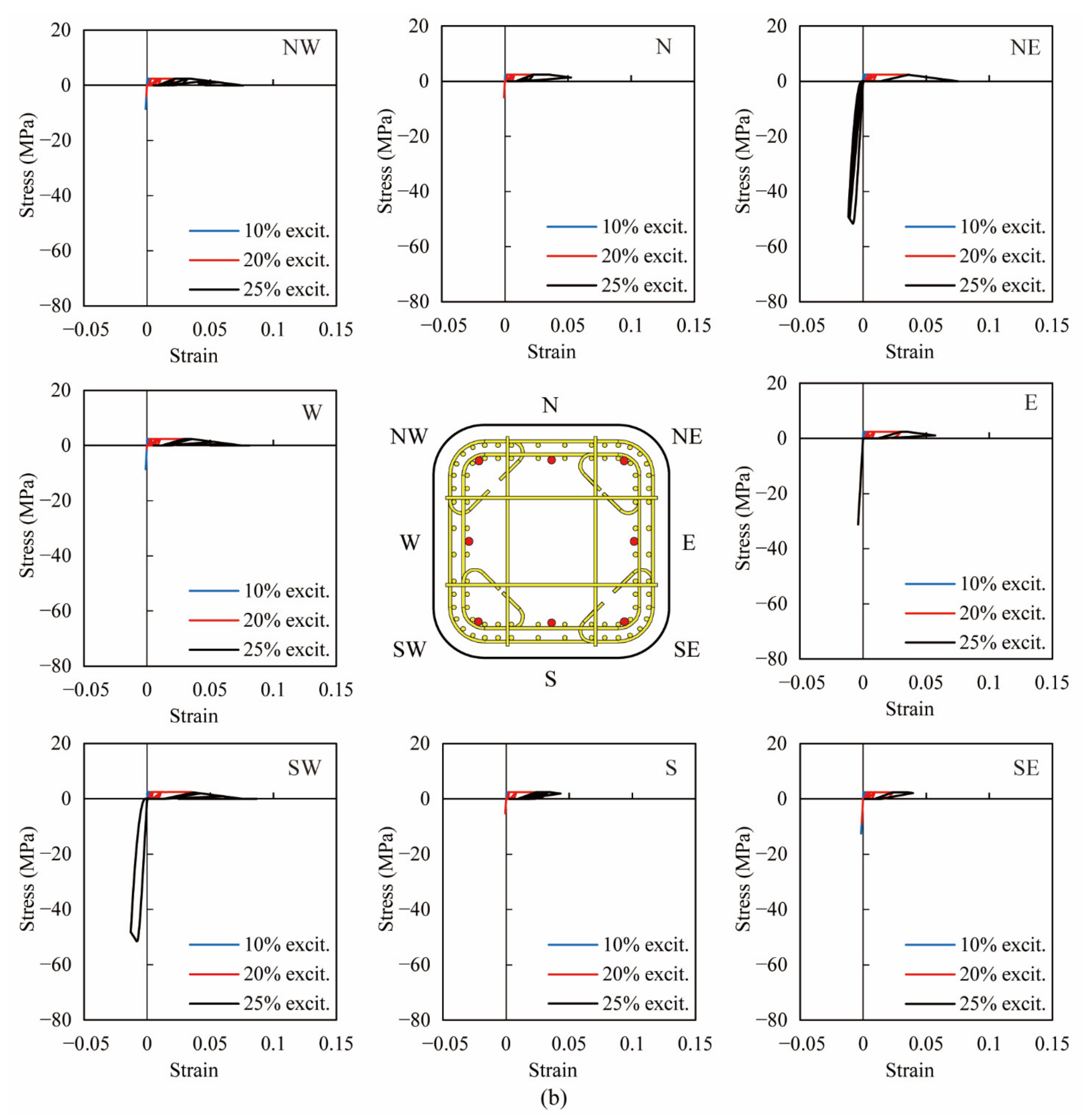
4.2. Hysteresis of Stress-Strain in Longitudinal Bars
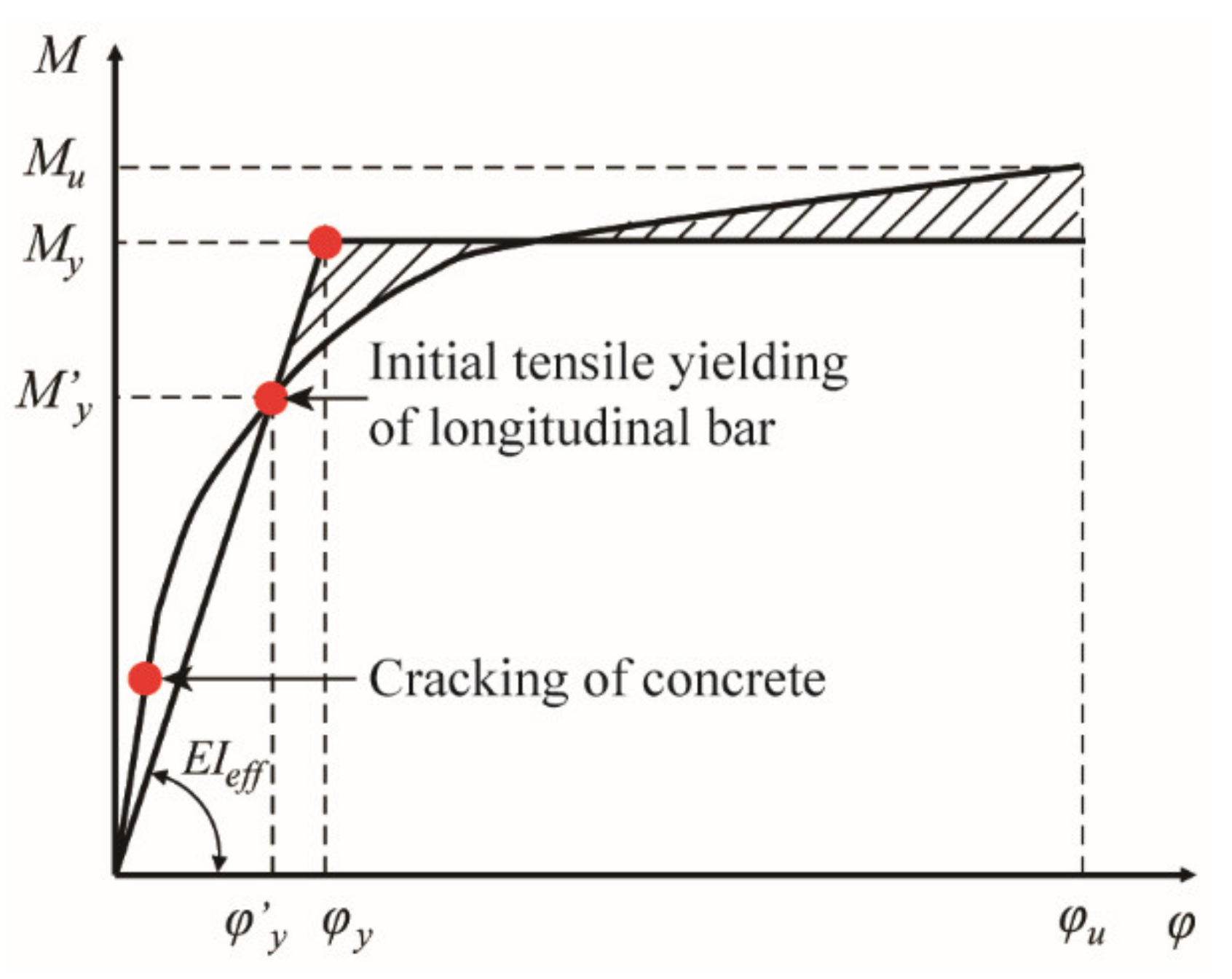
4.3. Maximum Allowable Displacement for Design
5. Conclusions
- (1)
- The proposed calculation for the lateral confining stress of the ECC cover was verified to be valid due to the analytical results being in good agreement with the experiments based on the fiber-element-based analysis. It also indicates that the reduction in the volume tie ratio has little effect on the hysteresis of lateral force displacement because the ECC cover has already provided substantial lateral confinement.
- (2)
- The reduction in the volume tie ratio has little effect on the stress-strain hysteresis of the ECC cover, but it has an effect on the stress-strain hysteresis of core ECC due to different compressive strengths in core ECC resulting from a different extent of lateral confinement. With the reduction in the volume tie ratio, the ECC cover can reduce the local buckling in longitudinal bars only if the column undergoes small or moderate nonlinear deformation. Once the deformation was large, more ties were still essential to provide necessary lateral confinement to mitigate local buckling of the longitudinal bars.
- (3)
- Based on the theory of equivalent yielding curvature, the volume tie ratio in ECC plastic hinges has a limited effect on the maximum allowable displacement for design. The maximum allowable displacement of the composite column with a volume tie ratio of 1.51% is larger than that with a volume tie ratio of 0.76% by 3.4 mm. It indicates that the increase in the volume tie ratio in the plastic hinge region of the ECC column is no longer significantly effective in enhancing the ductility of the column. It is possible to reduce the quantity of ties in the plastic hinge region and therefore to reduce the difficulty in placing concrete during the construction phase and prevent potential placing defects and future durability problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, T.-H.; Lee, K.-M.; Yoon, C.; Shin, H.M. Inelastic Behavior and Ductility Capacity of Reinforced Concrete Bridge Piers under Earthquake. I: Theory and Formulation. J. Struct. Eng. 2003, 129, 1199–1207. [Google Scholar] [CrossRef]
- Chang, G.A.; Mander, J.B. Seismic Energy Based Fatigue Damage Analysis of Bridge Columns: Part 1—Evaluation of Seismic Capacity; University at Buffalo: Buffalo, NY, USA, 1994. [Google Scholar]
- Gomes, A.; Appleton, J. Nonlinear Cyclic Stress-Strain Relationship of Reinforcing Bars Including Buckling. Eng. Struct. 1997, 19, 822–826. [Google Scholar] [CrossRef]
- Han, Q.; Du, X.; Liu, J.; Li, Z.; Li, L.; Zhao, J. Seismic Damage of Highway Bridges during the 2008 Wenchuan Earthquake. Earthq. Eng. Eng. Vib. 2009, 8, 263–273. [Google Scholar] [CrossRef]
- JSCE. Recommendations for Design and Construction of High Performance Fiber Reinforced Cement Composites with Multiple Fine Cracks (HPFRCC); Maruzen Press: Tokyo, Japan, 2008. [Google Scholar]
- Li, V.C. Engineered Cementitious Composites (ECC)—Tailored Composites through Micromechanical Modeling; CRC Press: London, UK, 1998; p. 38. [Google Scholar]
- Fischer, G.; Li, V.C. Effect of Matrix Ductility on Deformation Behavior of Steel-Reinforced ECC Flexural Members under Reversed Cyclic Loading Conditions. ACI Struct. J. 2002, 99, 781–790. [Google Scholar]
- Saiidi, M.S.; Wang, H. Exploratory Study of Seismic Response of Concrete Columns with Shape Memory Alloys Reinforcement. ACI Struct. J. 2006, 103, 436–443. [Google Scholar]
- Kawashima, K.; Zafra, R.; Sasaki, T.; Kajiwara, K.; Nakayama, M. Effect of Polypropylene Fiber Reinforced Cement Composite and Steel Fiber Reinforced Concrete for Enhancing the Seismic Performance of Bridge Columns. J. Earthq. Eng. 2011, 15, 1194–1211. [Google Scholar] [CrossRef]
- Kawashima, K.; Zafra, R.G.; Sasaki, T.; Kajiwara, K.; Nakayama, M.; Unjoh, S.; Sakai, J.; Kosa, K.; Takahashi, Y.; Yabe, M. Seismic Performance of a Full-Size Polypropylene Fiber-Reinforced Cement Composite Bridge Column Based on E-Defense Shake Table Experiments. J. Earthq. Eng. 2012, 16, 463–495. [Google Scholar] [CrossRef]
- Zhang, W.; Matsuzaki, H.; Kawashima, K. Effect of Tie Bar Volume on the Seismic Performance of Polypropylene Fiber Reinforced Columns Based on Hybrid Loading Experiments. J. JSCE 2013, 69, I_807–I_820. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Feng, Z.; Deng, K.; Yu, Y.; Hu, Z.; Jin, H. Axial Behavior of Reinforced PP-ECC Column and Hybrid NSC-ECC Column under Compression. Eng. Struct. 2019, 195, 223–230. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Tan, J.; Vandevyvere, B. Nonlinear Finite-Element Analysis for Hysteretic Behavior of ECC-Encased CFST Columns. Structures 2020, 25, 670–682. [Google Scholar] [CrossRef]
- Japan Road Association. Design Specifications of Highway Bridges, Part V Seismic Design; Maruzen: Tokyo, Japan, 2002. [Google Scholar]
- Zafra, R.; Kawashima, K.; Sasaki, T.; Kajiwara, K.; Nakayama, M. Cyclic Stress-Strain Response of Polypropylene Fiber Reinforced Cement Composites. J. JSCE 2010, 66, 162–171. [Google Scholar] [CrossRef]
- Zhang, R. Research on the Effect of Tie Bars on the Seismic Performance of High-Performance Columns Based on Hybrid Loading Experiments. Master Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2012. [Google Scholar]
- Kent, D.C.; Park, R. Flexural Members with Confined Concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Sakai, J.; Kawashima, K. Unloading and Reloading Stress–Strain Model for Confined Concrete. J. Struct. Eng. 2006, 132, 112–122. [Google Scholar] [CrossRef]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-Strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates. ACI J. Proc. 1982, 79, 13–27. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Richart, F.E.; Anton, B.; Rex, L.B. A Study of the Failure of Concrete under Combined Compressive Stresses; Engineering Experiment Station, University of Illinois at Urbana Champaign, College of Engineering Unrana Champaign: Urbana, IL, USA, 1928. [Google Scholar]
- Han, T.S.; Feenstra, P.H.; Billington, S.L. Simulation of Highly Ductile Fiber-Reinforced Cement-Based Composite Components Under Cyclic Loading. ACI Struct. J. 2003, 100, 749–757. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Administration of Transportation People’s Republic of China. Guidelines for Seismic Design of Highway Bridges; China Communications Press: Beijing, China, 2008.







| W/B 1 (%) | FA/B 2 (%) | Unit Weight (kg/m3) | ||
|---|---|---|---|---|
| W | B | PP 3 | ||
| 27 | 33 | 371 | 1400 | 27 |
| Physical Quantity | Similitude Relation | Similitude Parameter |
|---|---|---|
| 6/35 | ||
| 6/35 | ||
| 1 | ||
| 1 | ||
| 36/1225 |
| Parameters | Unconfined ECC | Double-Confined ECC | Triple-Confined ECC | ||
|---|---|---|---|---|---|
| PFRC-1 | PFRC-2 | PFRC-1 | PFRC-2 | ||
| (MPa) | 45.05 | 51.03 | 47.69 | 61.05 | 51.66 |
| 0.0047 | 0.0078 | 0.0061 | 0.013 | 0.0081 | |
| 0.047 | |||||
| (MPa) | 2.4 | ||||
| 0.000293 | |||||
| (MPa) | 2.4 | ||||
| 0.035 | |||||
| Properties | PFRC-1 | PFRC-2 |
|---|---|---|
| (MPa) | 507 | |
| (MPa) | 182,000 | |
| Ratio between post-yield tangent and initial elastic tangent | 0.01 | |
| Parameter to control the transition from elastic to plastic branches | 18 | |
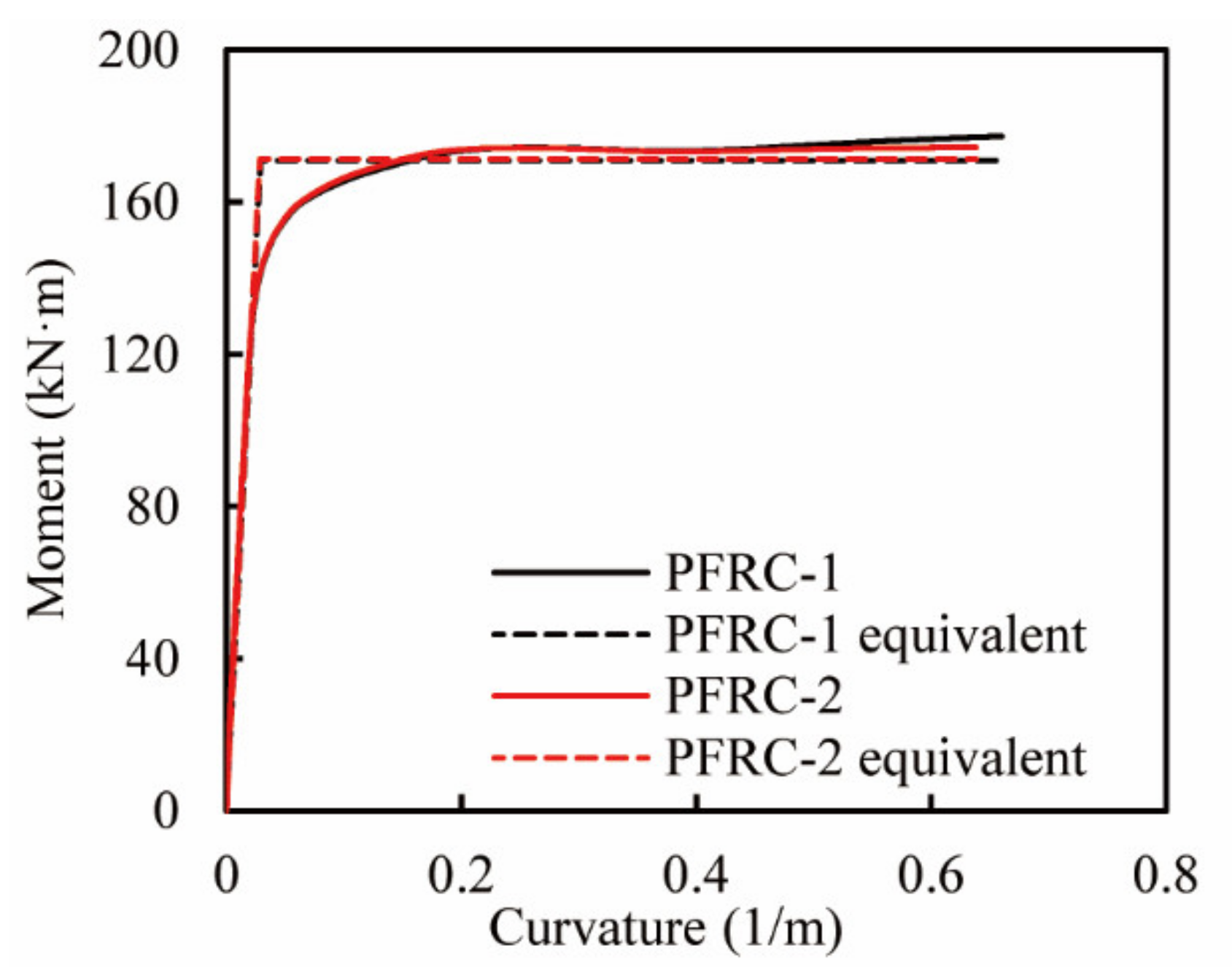
| Column | (kN·m) | (kN·m) | (1/m) | (kN·m) | (1/m) | (1/m) | (m) | (mm) | |
|---|---|---|---|---|---|---|---|---|---|
| PFRC-1 | 127.84 | 170.98 | 0.0289 | 177.29 | 0.6637 | 0.6348 | 0.06348 | 0.2 | 98.7 |
| PFRC-2 | 127.87 | 171.39 | 0.0284 | 174.31 | 0.6387 | 0.6103 | 0.06103 | 0.2 | 95.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Chen, K.; Zhang, R.; Li, X.; Zhang, W. Effect of Volume Tie Ratio in the Engineered Cementitious Composites Plastic Hinges on the Seismic Performance of RC Composite Bridge Columns. Materials 2021, 14, 5739. https://doi.org/10.3390/ma14195739
Li Q, Chen K, Zhang R, Li X, Zhang W. Effect of Volume Tie Ratio in the Engineered Cementitious Composites Plastic Hinges on the Seismic Performance of RC Composite Bridge Columns. Materials. 2021; 14(19):5739. https://doi.org/10.3390/ma14195739
Chicago/Turabian StyleLi, Qian, Kedao Chen, Rui Zhang, Xi Li, and Wenjin Zhang. 2021. "Effect of Volume Tie Ratio in the Engineered Cementitious Composites Plastic Hinges on the Seismic Performance of RC Composite Bridge Columns" Materials 14, no. 19: 5739. https://doi.org/10.3390/ma14195739
APA StyleLi, Q., Chen, K., Zhang, R., Li, X., & Zhang, W. (2021). Effect of Volume Tie Ratio in the Engineered Cementitious Composites Plastic Hinges on the Seismic Performance of RC Composite Bridge Columns. Materials, 14(19), 5739. https://doi.org/10.3390/ma14195739






