Bone Stress Evaluation with and without Cortical Bone Using Several Dental Restorative Materials Subjected to Impact Load: A Fully 3D Transient Finite-Element Study
Abstract
:1. Introduction
2. Materials and Methods
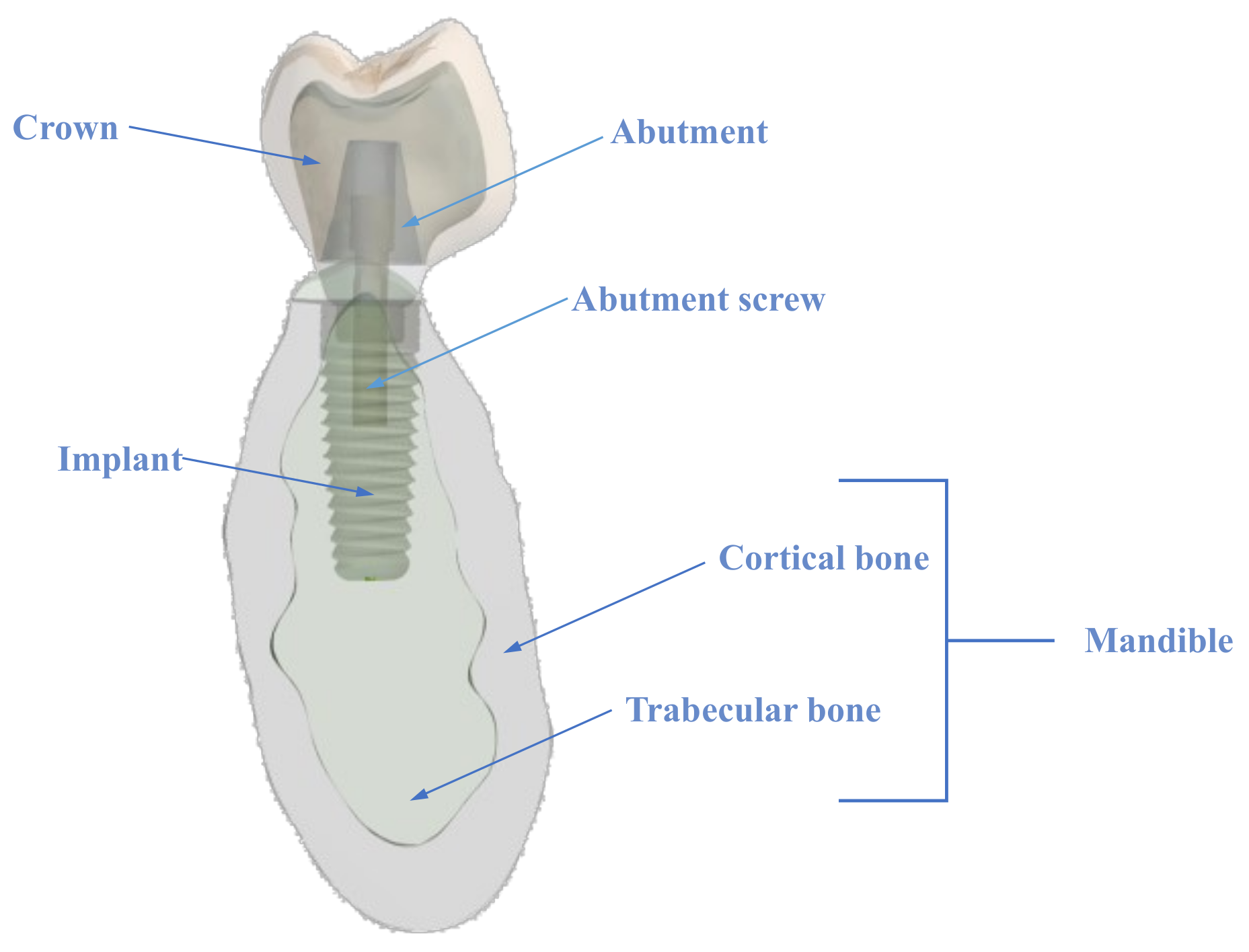
2.1. The Model
2.1.1. The Crown
2.1.2. The Abutment and Screw
2.1.3. The Implant
2.1.4. The Mandible
2.1.5. The Loading Plate
2.2. Geometry of the Assembled Model
2.3. Materials of the Model
2.4. Numerical Simulation
2.4.1. Simulation Setup
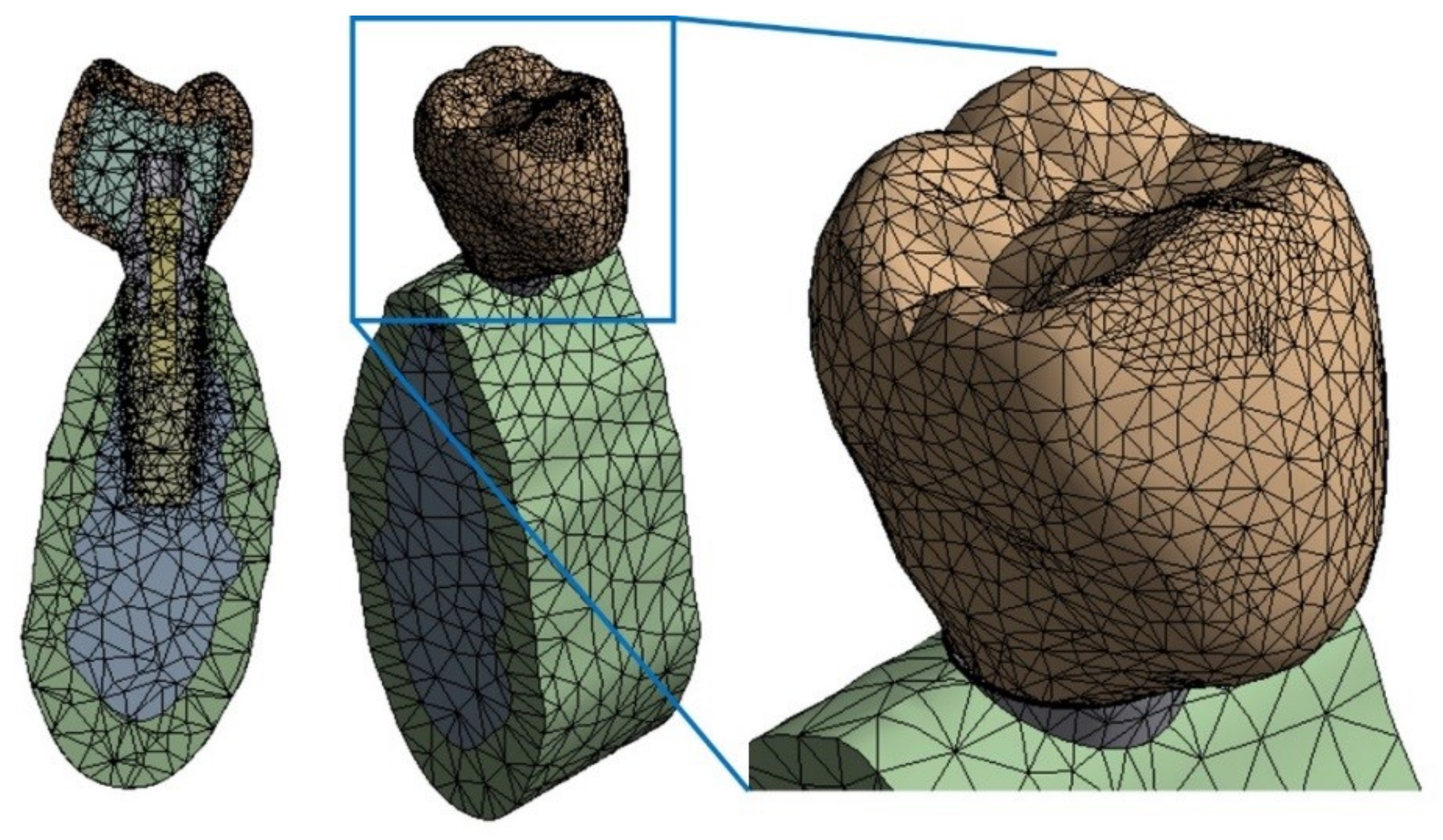
2.4.2. Finite Element Mesh
2.4.3. Initial and Boundary Conditions
2.4.4. Simulation Time
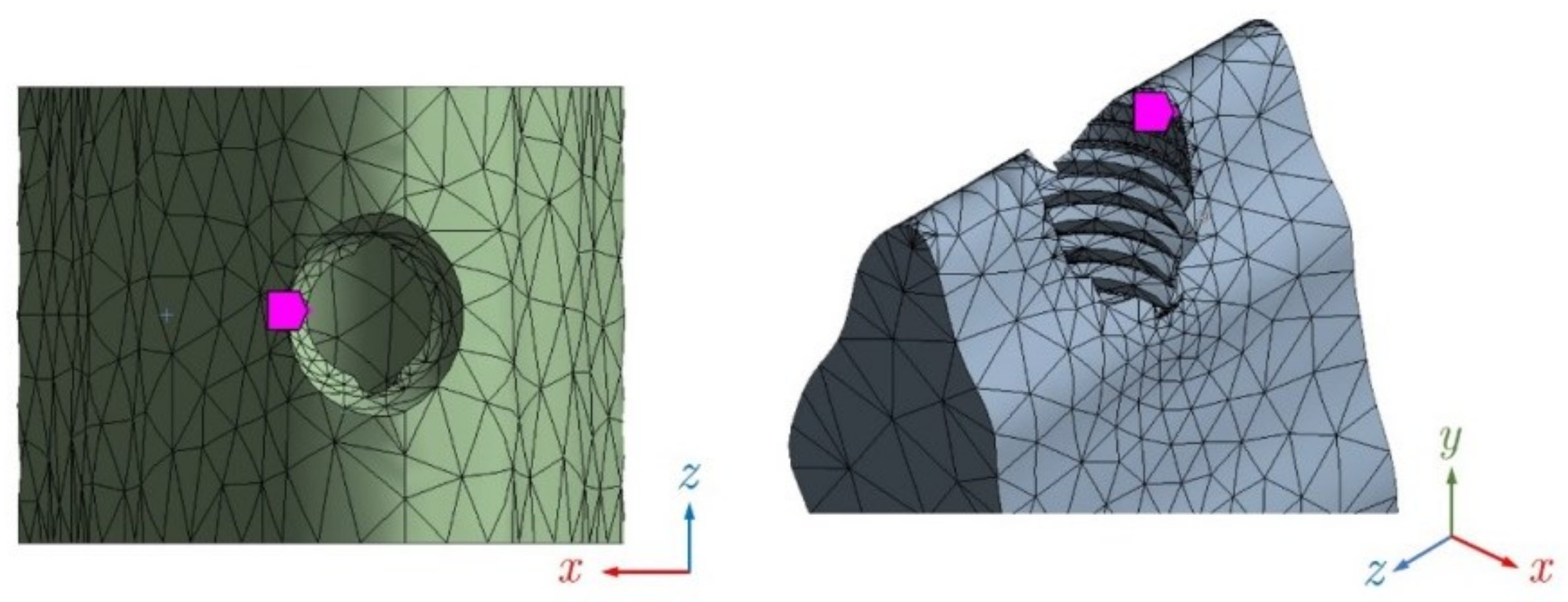
2.4.5. Node Selection
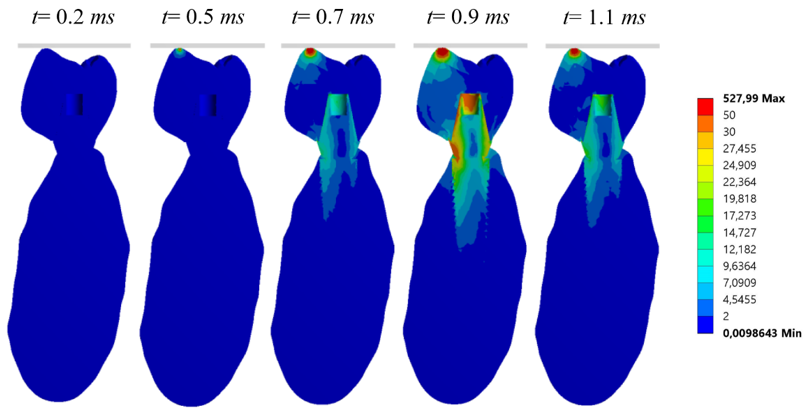
3. Results
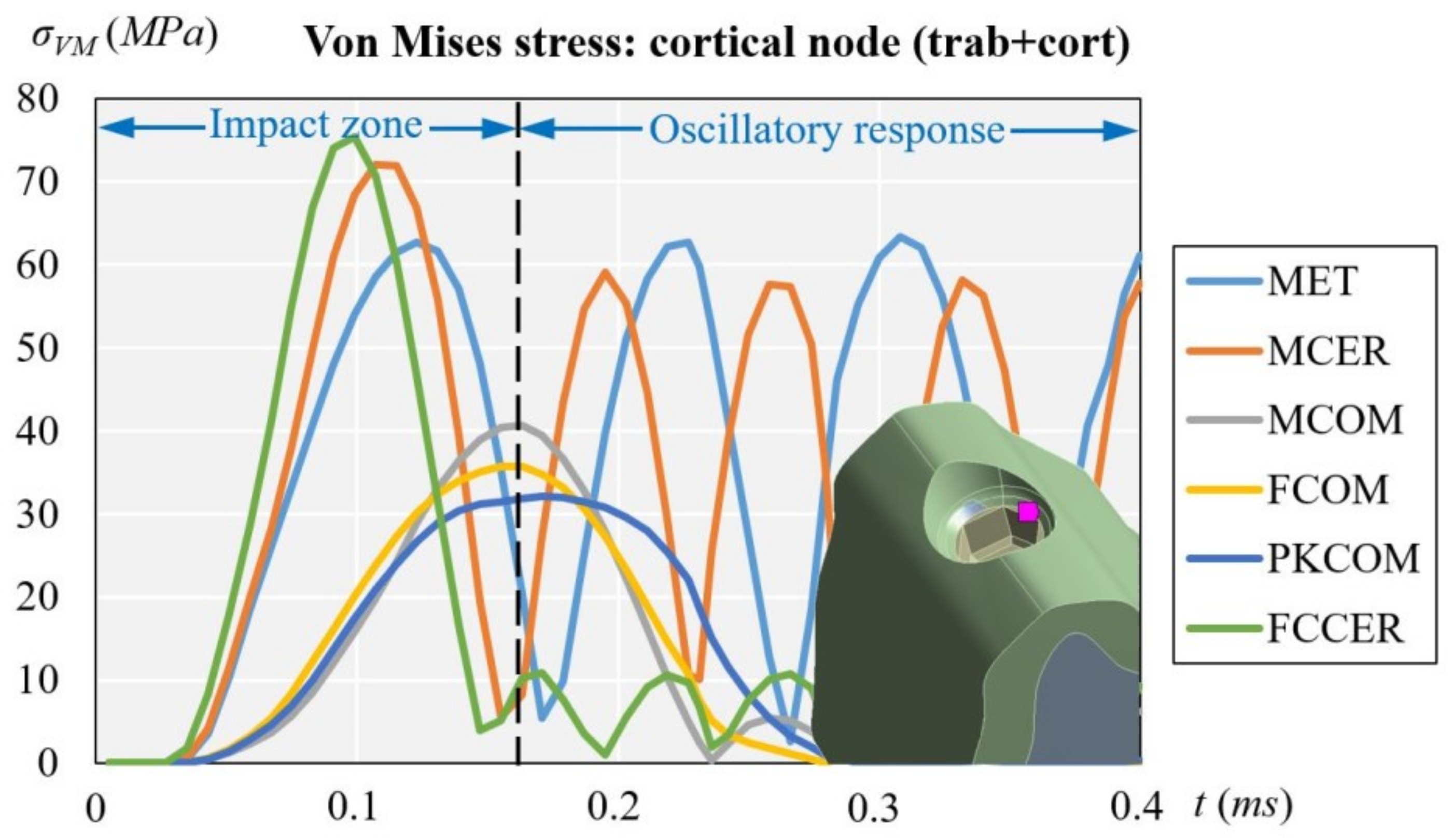
3.1. Cortical Node (with Cortical and Trabecular Bone)
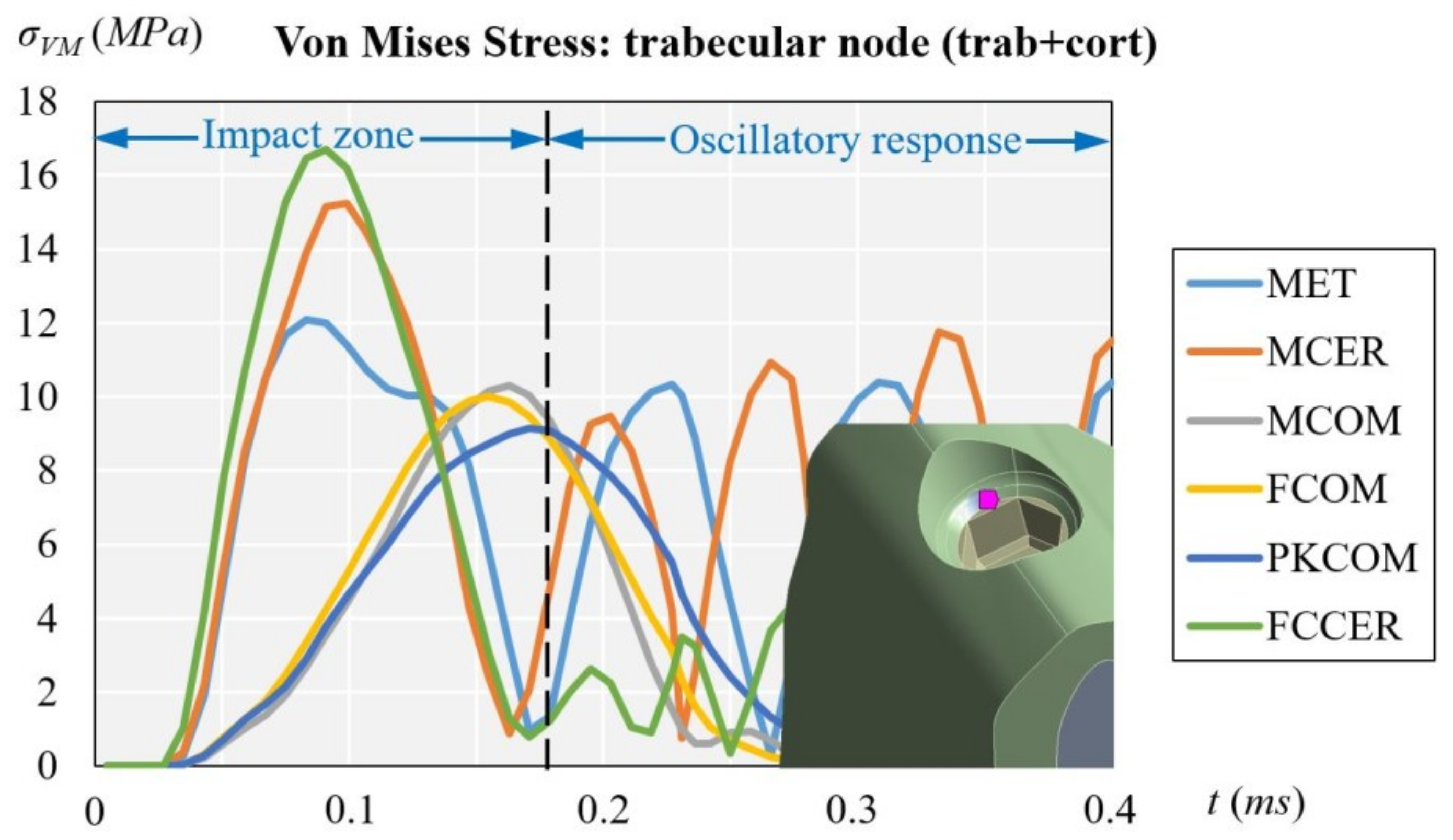
3.2. Trabecular Node (with Cortical and Trabecular Bone)
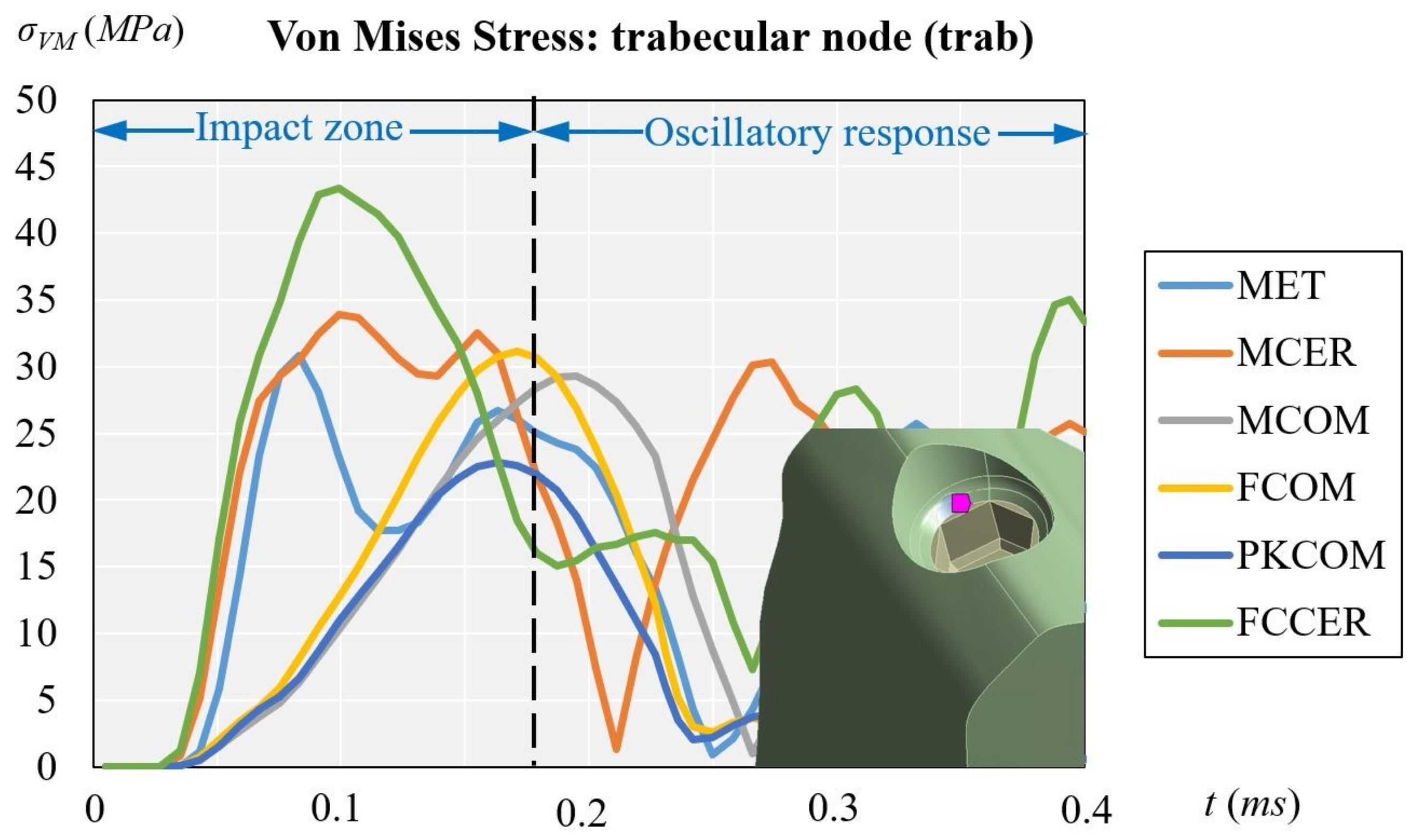
3.3. Trabecular Node (with Trabecular Bone Only)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MET | Metal crown |
| MCER | Metal-Ceramic crown |
| MCOM | Metal-Composite crown |
| FCOM | Carbon fiber-Composite crown |
| PKCOM | Peek-Composite crown |
| FCCER | Carbon Fiber-Ceramic crown |
| FEA | Finite Element Analysis |
| DIC | Digital Image Correlation |
| CAD | Computer-Aided Design |
| CT Scan | Computer Tomography Scanner |
References
- Esposito, M.; Hirsch, J.M.; Lekholm, U.; Thomsen, P. Biological factors contributing to failures of osseointegrated oral implants. (I): Success criteria and epidemiology. Eur. J. Oral Sci. 1998, 106, 527–551. [Google Scholar] [CrossRef]
- Maglione, M.; Vaccari, L.; Mancini, L.; Ciancio, R.; Bedolla, D.; Bevilacqua, L.; Tonellato, P. Micro-ATR FTIR, SEM-EDS, and X-ray Micro-CT: An Innovative Multitechnique Approach to Investigate Bone Affected by Peri-implantitis. Int. J. Oral Maxillofac. Implants 2019, 34, 631–641. [Google Scholar] [CrossRef]
- Earthman, J.C.; Li, Y.; Van Schoiack, L.R.; Sheets, C.G.; Wu, J.C. Reconstructive Materials and Bone Tissue Engineering in Implant Dentistry. Dent. Clin. N. Am. 2006, 50, 229. [Google Scholar] [CrossRef]
- Tribst, J.; Piva, A.D.; Borges, A. Biomechanical tools to study dental implants: A literature review. Braz. Dent Sci. 2016, 19, 5. [Google Scholar] [CrossRef]
- Tang, Q.; Du, C.; Hu, J.; Wang, X.; Yu, T. Surface rust detection using ultrasonic waves in a cylindrical geometry by finite element simulation. Infrastructures 2018, 3, 29. [Google Scholar] [CrossRef] [Green Version]
- Jerban, S.; Ma, Y.; Nazaran, A.; Dorthe, E.; Cory, E.; Carl, M.; D’Lima, D.; Sah, R.; Chang, E.; Du, J. Detecting stress injury (fatigue fracture) in fibular cortical bone using quantitative ultrashort echo time-magnetization transfer (UTE-MT): An ex vivo study. NMR Biomed. 2018, 31, e3994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hériveaux, E.; Audoin, B.; Biateau, C.; Nguyen, V.H.; Haïat, G. Ultrasonic Propagation in a Dental Implant. Ultrasound Med. Biol. 2020, 46, 1464–1473. [Google Scholar] [CrossRef] [PubMed]
- Pesqueira, A.; Goiato, M.; Filho, H.; Monteiro, D.; Dos Santos, D.; Haddad, M. Use of stress analysis methods to evaluate the biomechanics of oral rehabilitation with implants. J. Oral Implantol. 2014, 40, 217–228. [Google Scholar] [CrossRef]
- McCormick, N.; Lord, J. Digital image correlation. Materials Today 2010, 13, 52–54. [Google Scholar] [CrossRef]
- Magne, P.; Silva, M.; Oderich, E.; Boff, L.; Enciso, R. Damping behavior of implant-supported restorations. Clin. Oral Implants Res. 2013, 24, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Duyck, J.; Rønold, H.J.; Van Oosterwyck, H.; Naert, I.; Vander Sloten, J.; Ellingsen, J.E. The influence of static and dynamic loading on marginal bone reactions around osseointegrated implants: An animal experimental study. Clin. Oral Implants Res. 2001, 12, 207–218. [Google Scholar] [CrossRef]
- Galindo-Moreno, P.; Fernández-Jiménez, A.; Avila-Ortiz, G.; Silvestre, F.J.; Hernández-Cortés, P.; Wang, H.L. Marginal bone loss around implants placed in maxillary native bone or grafted sinuses: A retrospective cohort study. Clin. Oral Implants Res. 2014, 25, 378–384. [Google Scholar] [CrossRef] [Green Version]
- Lin, D.; Li, Q.; Li, W.; Swain, M. Dental implant induced bone remodeling and associated algorithms. J. Mech. Behav. Biomed. Mater. 2009, 2, 410–432. [Google Scholar] [CrossRef] [PubMed]
- Cicciu, M.; Cervino, G.; Milone, D.; Risitano, G. FEM Investigation of the Stress Distribution over Mandibular Bone Due to Screwed Overdenture Positioned on Dental Implants. Materials 2018, 11, 1512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Jansen, J.; Walboomers, F.; van den Beucken, J. Mechanical aspects of dental implants and osseointegration: A narrative review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103574. [Google Scholar] [CrossRef]
- Kitagawa, T.; Tanimoto, Y.; Nemoto, K.; Aida, M. Influence of cortical bone quality on stress distribution in bone around dental implant. Dent. Materials J. 2005, 24, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Wachter, N.J.; Krischak, G.D.; Mentzel, M.; Sarkar, M.R.; Ebinger, T.; Kinzl, L.; Claes, L.; Augat, P. Correlation of bone mineral density with strength and microstructural parameters of cortical bone in vitro. Bone 2002, 31, 90–95. [Google Scholar] [CrossRef]
- Kayabasi, O.; Yuzbasıoglu, E.; Erzincanli, F. Static, dynamic and fatigue behaviors of dental implant using finite element method. J. Adv. Eng. Softw. 2006, 37, 649–658. [Google Scholar] [CrossRef]
- Benazzi, S.; Nguyen, H.N.; Kullmer, O.; Kupczik, K. Dynamic Modelling of Tooth Deformation Using Occlusal Kinematics and Finite Element Analysis. PLoS ONE 2016, 11, e0152663. [Google Scholar] [CrossRef]
- Razaghi, R.; Mallakzadeh, M.; Haghpanahi, M. Dynamic simulation and finite Element analysis of the maxillary bone injury around dental implant during chewing different food. Biomed. Eng. Appl. BasisCommun. 2016, 28, 1650014. [Google Scholar] [CrossRef]
- Chang, Y.; Tambe, A.; Maeda, Y.; Wada, M.; Gonda, T. Finite element analysis of dental implants with validation: To what extent can we expect the model to predict biological phenomena? A literature review and proposal for classification of a validation process. Implant Dent. 2018, 4, 7–12. [Google Scholar] [CrossRef]
- Geramizadeh, M.; Katoozian, H.; Amid, R.; Kadkhodazadeh, M. Finite Element Analysis of Dental Implants with and without Microthreads under Static and Dynamic Loading. J. Long-Term Eff. Med. Implants 2017, 27, 25–35. [Google Scholar] [CrossRef]
- Canto-Naves, O.; Marimon, X.; Ferrer, M.; Cabratosa-Termes, J. Comparison between experimental digital image processing and numerical methods for stress analysis in dental implants with different restorative materials. J. Mech. Behav. Biomed. Mater. 2021, 113, 104092. [Google Scholar] [CrossRef]
- Solidworks Dassault Systemes. 2020. Available online: www.solidworks.com (accessed on 3 August 2021).
- MIS Implants Tech. Ltd. 2021. Available online: https://www.mis-implants.com (accessed on 3 August 2021).
- NewTom. 2021. Available online: https://www.newtom.it (accessed on 3 August 2021).
- Lakatos, É.; Magyar, L.; Bojtár, I. Material Properties of the Mandibular Trabecular Bone. J. Med. Eng. 2014, 2014, 470539. [Google Scholar] [CrossRef]
- Geng, J.P.; Tan, K.B.; Liu, G.R. Application of finite element analysis in implant dentistry: A review of the literature. J. Prosthet. Dent. 2001, 85, 585–598. [Google Scholar] [CrossRef] [Green Version]
- Micro Medica Srl. 2021. Available online: http://micromedicasrl.it (accessed on 3 August 2021).
- Renishaw. 2021. Available online: https://www.renishaw.com (accessed on 3 August 2021).
- VITA Zahnfabrik, H. Rauter GmbH & Co. 2021. Available online: www.vita-zahnfabrik.com (accessed on 3 August 2021).
- Heraeus Kulzer GmbH. 2021. Available online: https://www.kulzer.de (accessed on 3 August 2021).
- Ivoclar Vivadent. 2021. Available online: https://www.ivoclarvivadent.es (accessed on 3 August 2021).
- Invibio. 2021. Available online: https://invibio.com (accessed on 3 August 2021).
- Van Eijden, T.M. Biomechanics of the Mandible. Crit. Rev. Oral Biol. Med. 2000, 11, 123–136. [Google Scholar] [CrossRef]
- Peck, C.C. Biomechanics of occlusion—Implications for oral rehabilitation. J. Oral Rehabil. 2016, 43, 205–214. [Google Scholar] [CrossRef] [PubMed]
- Ansys® Academic Research Mechanical, Release 18.1. 2020. Available online: www.ansys.com (accessed on 3 August 2021).
- Minami, I.; Oogai, K.; Nemoto, T.; Nakamura, T.; Igarashi, Y.; Wakabayashi, N. Measurement of jerk-cost using a triaxial piezoelectric accelerometer for the evaluation of jaw movement smoothness. J. Oral Rehabil. 2010, 37, 590–595. [Google Scholar] [CrossRef] [PubMed]
- Dattakumar, S.S.; Ganeshan, V. Converting Dynamic Impact Events to Equivalent Static Loads in Vehicle Chassis. Master Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2017. [Google Scholar]
- Conserva, E.; Menini, M.; Tealdo, T.; Bevilacqua, M.; Pera, F.; Ravera, G.; Pera, P. Robotic chewing simulator for dental materials testing on a sensor-equipped implant setup. Int. J. Prosthodont. 2008, 21, 501–508. [Google Scholar] [PubMed]
- Menini, M.; Conserva, E.; Tealdo, T.; Bevilacqua, M.; Pera, F.; Ravera, G.; Pera, P. The use of a masticatory robot to analyze the shock absorption capacity of different restorative materials for implant prosthesis. J. Biol. Res. 2011, 84, 118–119. [Google Scholar] [CrossRef]
- Menini, M.; Conserva, E.; Tealdo, T.; Bevilacqua, M.; Pera, F.; Signori, A. Shock Absorption Capacity of Restorative Materials for Dental Implant Prostheses: An In Vitro Study. Int. J. Prosthodont. 2013, 26, 549–556. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vigolo, P.; Gracis, S.; Carboncini, F.; Mutinelli, S. Internal- vs External-Connection Single Implants: A Retrospective Study in an Italian Population Treated by Certified Prosthodontists. Int. J. Oral Maxillofac. Implants 2016, 31, 1385–1396. [Google Scholar] [CrossRef] [PubMed] [Green Version]







| Material Name | Manufacturer | Young Modulus [MPa] | Poisson Ratio | Density [g/cm3] | |
|---|---|---|---|---|---|
| Crown | FCOM Carbon fiber-composite BioCarbon Bridge fibers Composite BioXfill | Micro Medica Micro Medica | 300,000 22,000 | 0.3 0.3 | 1.40 8.30 |
| MCER Metal-ceramic Co-Cr alloy Ceramic VMK 95 | Renishaw Vita | 208,000 69,000 | 0.31 0.28 | 8.90 2.50 | |
| MCOM Metal-composite Co-Cr alloy Composite BioXfill | Renishaw Micro-Medica | 208,000 22,000 | 0.31 0.3 | 8.90 8.30 | |
| MET Full metal Co-Cr Alloy, Mo, W | Heraeus Kulzer | 208,000 | 0.31 | 8.90 | |
| FCCER Carbon fiber-ceramic Carbon Fiber Bridge Ceramic IPS e.max | Micro-Medica Ivoclar Vivadent | 66,000 95,000 | 0.3 0.2 | 1.4 2.5 | |
| PKCOM PEEK-composite PEEK Optima Composite BioXfill | Invibio Micro-Medica | 4,100 22,000 | 0.36 0.3 | 1.3 8.30 | |
| Implant | Ti-6-Al-4V ELI | MIS | 113,800 | 0.34 | 4.43 |
| Bone | Cortical bone | [27,28] | 15,000 | 0.3 | 1.79 |
| Trabecular bone | [28] | 500 | 0.3 | 0.45 |
| Model | Initial Mass (g) | Added Mass (g) |
|---|---|---|
| ET | 8.62 | 0 |
| MCER | 6.73 | 1.89 |
| MCOM | 6.63 | 1.99 |
| FCOM | 5.23 | 3.39 |
| PKCOM | 7.20 | 1.42 |
| FCCER | 5.07 | 3.55 |
| Model | Added Mass with Cortical (g) | Added Mass without Cortical (g) |
|---|---|---|
| MET | 0 | 2.27 |
| MCER | 1.89 | 4.16 |
| MCOM | 1.99 | 4.26 |
| FCOM | 3.39 | 5.66 |
| PKCOM | 1.42 | 3.69 |
| FCCER | 3.55 | 5.82 |
| Node | Cortical Bone Trabecular Bone | ||
|---|---|---|---|
| Simulation 1 | Trabecular | X | X |
| Cortical | X | X | |
| Simulation 2 | Trabecular | X | |
| Maximum Von Mises Stress (MPa) | |||||||
|---|---|---|---|---|---|---|---|
| Node | Bone | MET | MCER | MCOM | FCOM | PKCOM | FCCER |
| Cortical | trab + cort | 63.35 | 72.06 | 40.71 | 35.70 | 32.05 | 75.46 |
| Trabecular | trab + cort | 12.09 | 15.23 | 10.30 | 10.01 | 9.15 | 16.69 |
| Trabecular | Trab | 30.80 | 33.87 | 29.30 | 31.14 | 22.80 | 43.33 |
| trab vs. trab + cort ∆σvM (%) | 60.75% | 55.03% | 64.85% | 67.85% | 59.87% | 61.48% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina-Galvez, R.; Cantó-Navés, O.; Marimon, X.; Cerrolaza, M.; Ferrer, M.; Cabratosa-Termes, J. Bone Stress Evaluation with and without Cortical Bone Using Several Dental Restorative Materials Subjected to Impact Load: A Fully 3D Transient Finite-Element Study. Materials 2021, 14, 5801. https://doi.org/10.3390/ma14195801
Medina-Galvez R, Cantó-Navés O, Marimon X, Cerrolaza M, Ferrer M, Cabratosa-Termes J. Bone Stress Evaluation with and without Cortical Bone Using Several Dental Restorative Materials Subjected to Impact Load: A Fully 3D Transient Finite-Element Study. Materials. 2021; 14(19):5801. https://doi.org/10.3390/ma14195801
Chicago/Turabian StyleMedina-Galvez, Raul, Oriol Cantó-Navés, Xavier Marimon, Miguel Cerrolaza, Miquel Ferrer, and Josep Cabratosa-Termes. 2021. "Bone Stress Evaluation with and without Cortical Bone Using Several Dental Restorative Materials Subjected to Impact Load: A Fully 3D Transient Finite-Element Study" Materials 14, no. 19: 5801. https://doi.org/10.3390/ma14195801
APA StyleMedina-Galvez, R., Cantó-Navés, O., Marimon, X., Cerrolaza, M., Ferrer, M., & Cabratosa-Termes, J. (2021). Bone Stress Evaluation with and without Cortical Bone Using Several Dental Restorative Materials Subjected to Impact Load: A Fully 3D Transient Finite-Element Study. Materials, 14(19), 5801. https://doi.org/10.3390/ma14195801










