Phosphorus Substitution Preference in Ye’elimite: Experiments and Density Functional Theory Simulations
Abstract
:1. Introduction
2. Experiments and DFT Simulations
2.1. Experiments
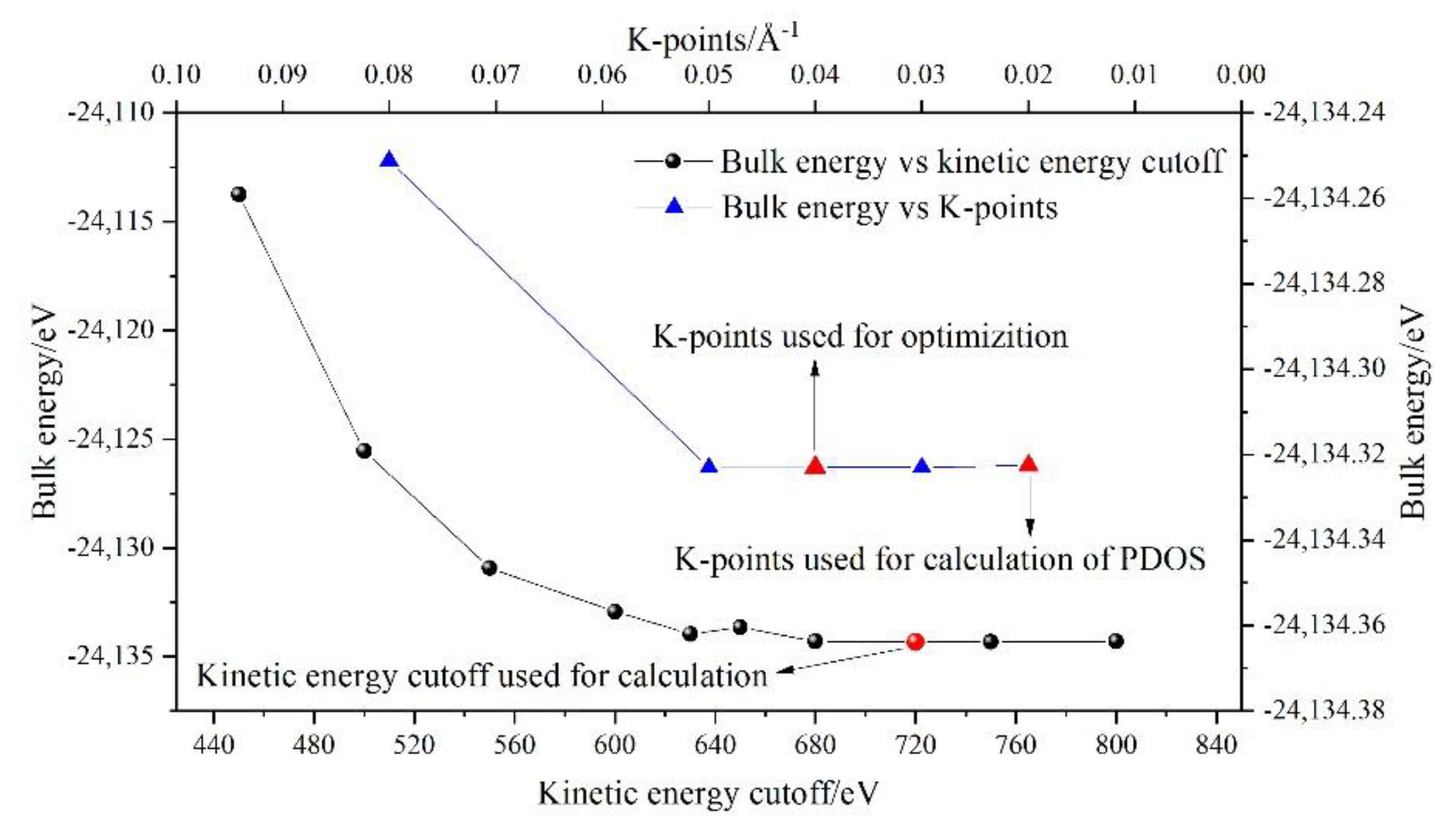
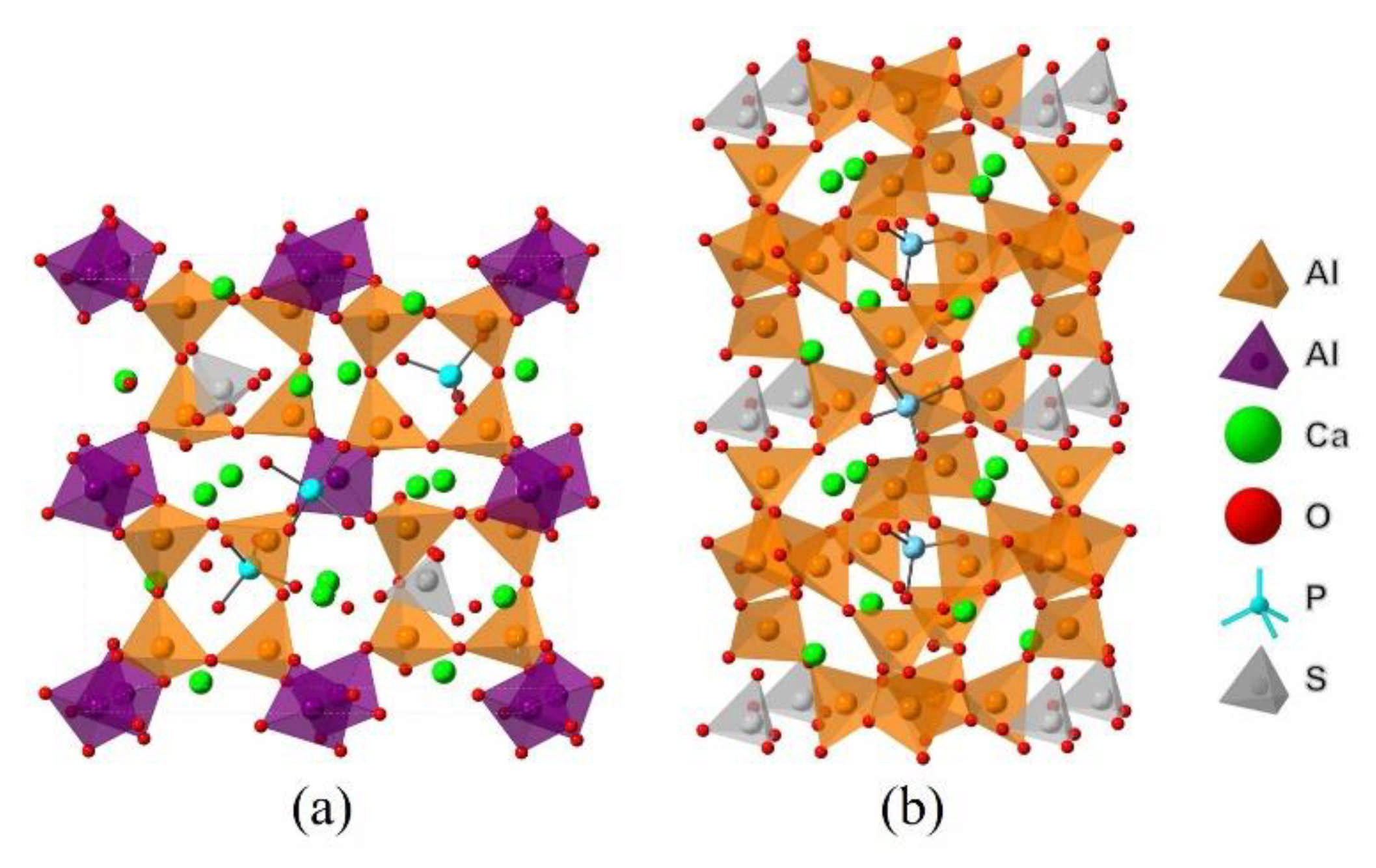
2.2. DFT Simulations
3. Results
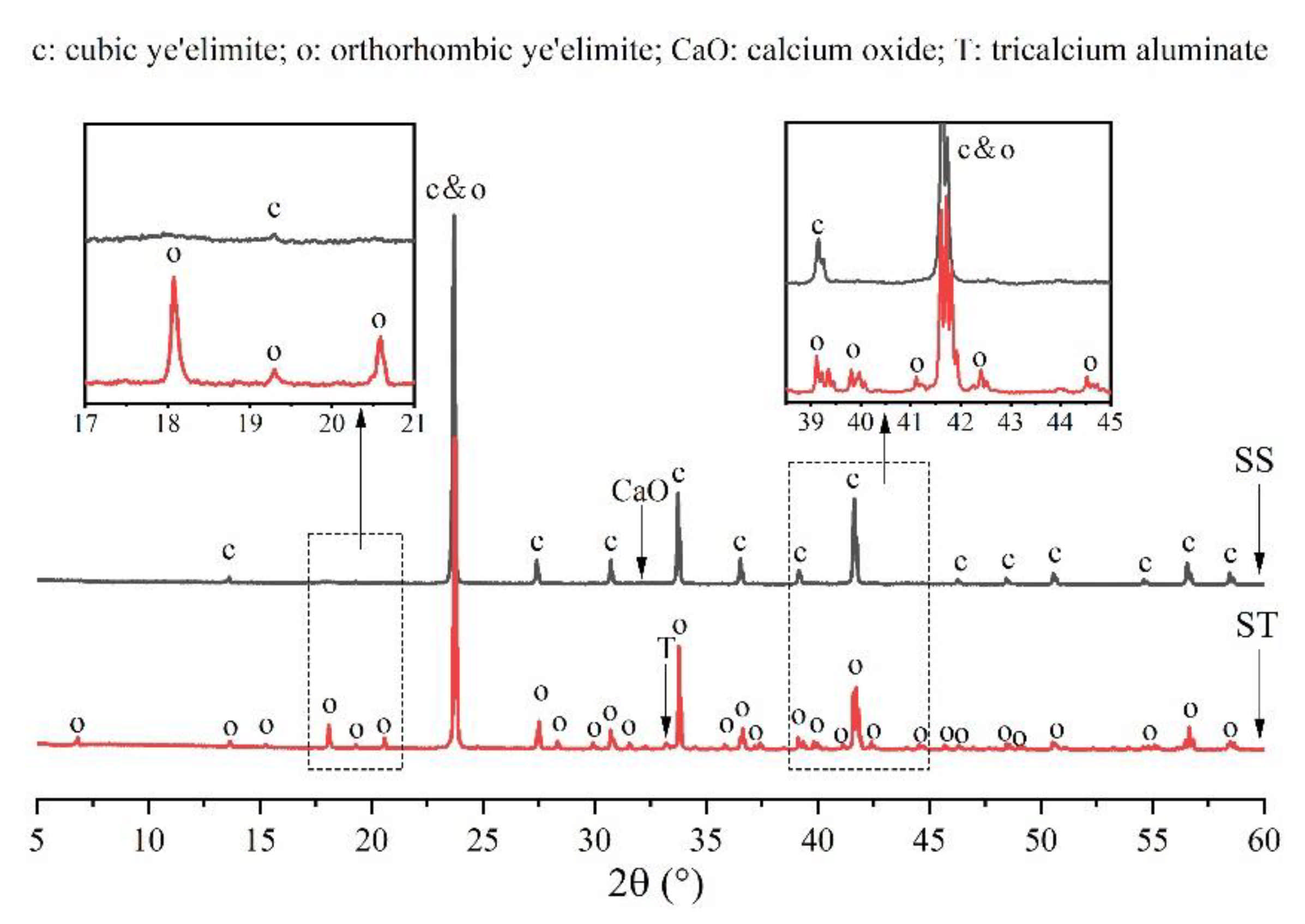
3.1. Elemental Distribution in P-Doped Ye’elimite
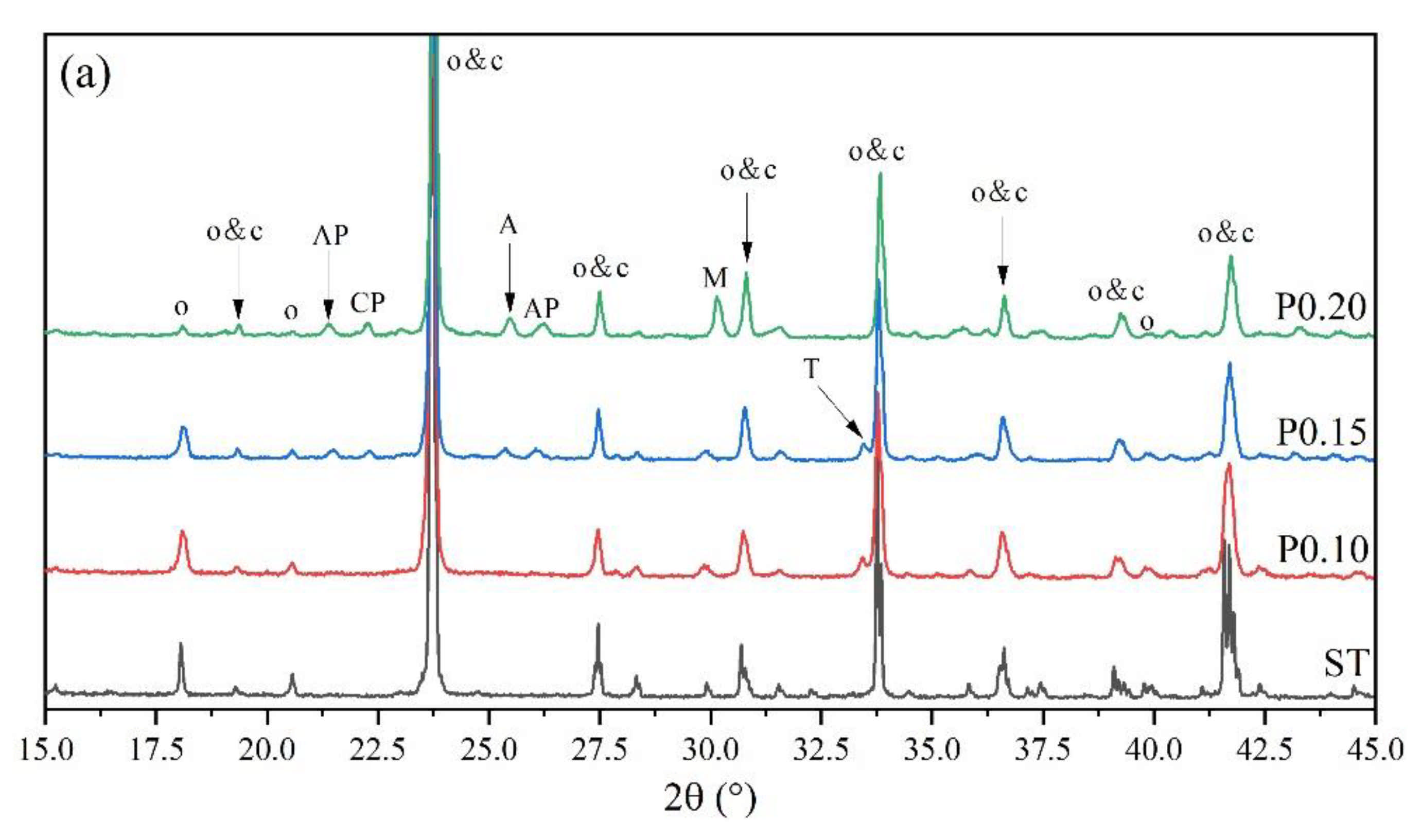
3.2. Rietveld Quantitative Phases Analysis of Synthesized Clinkers
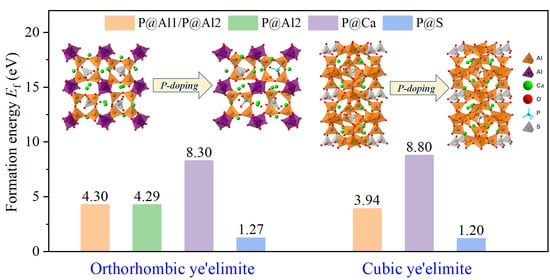
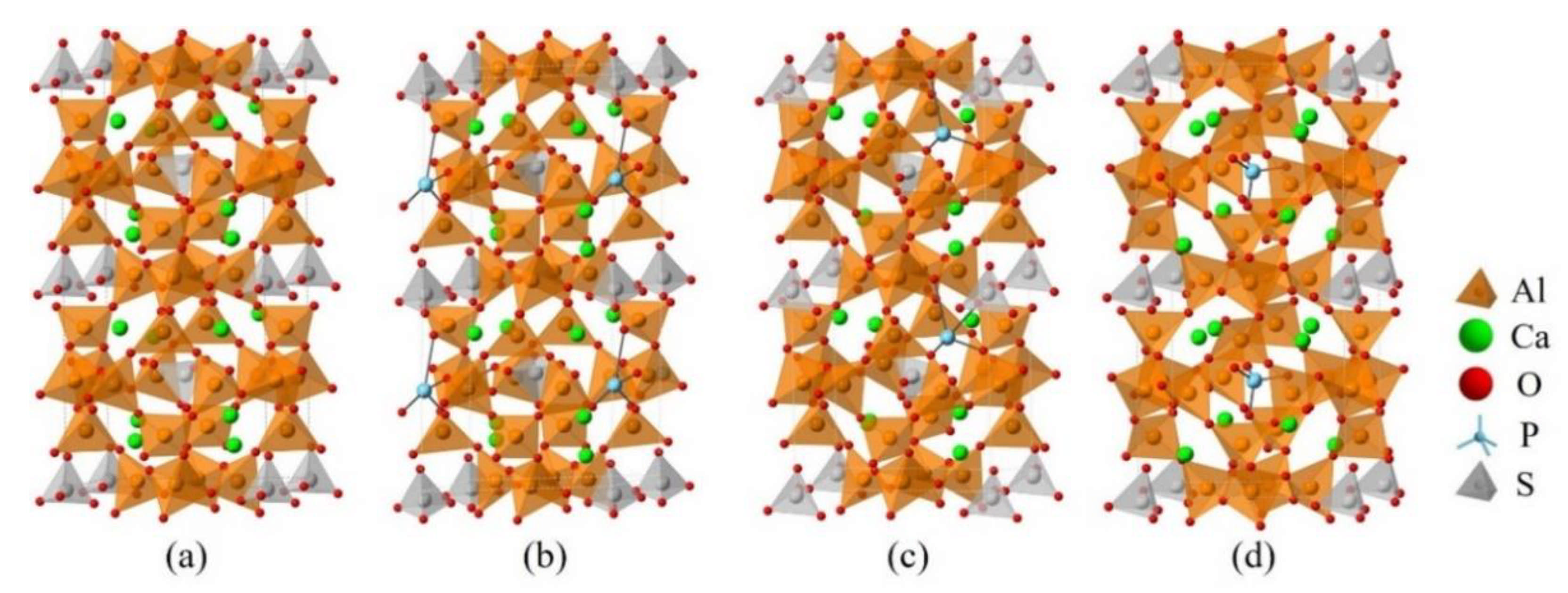
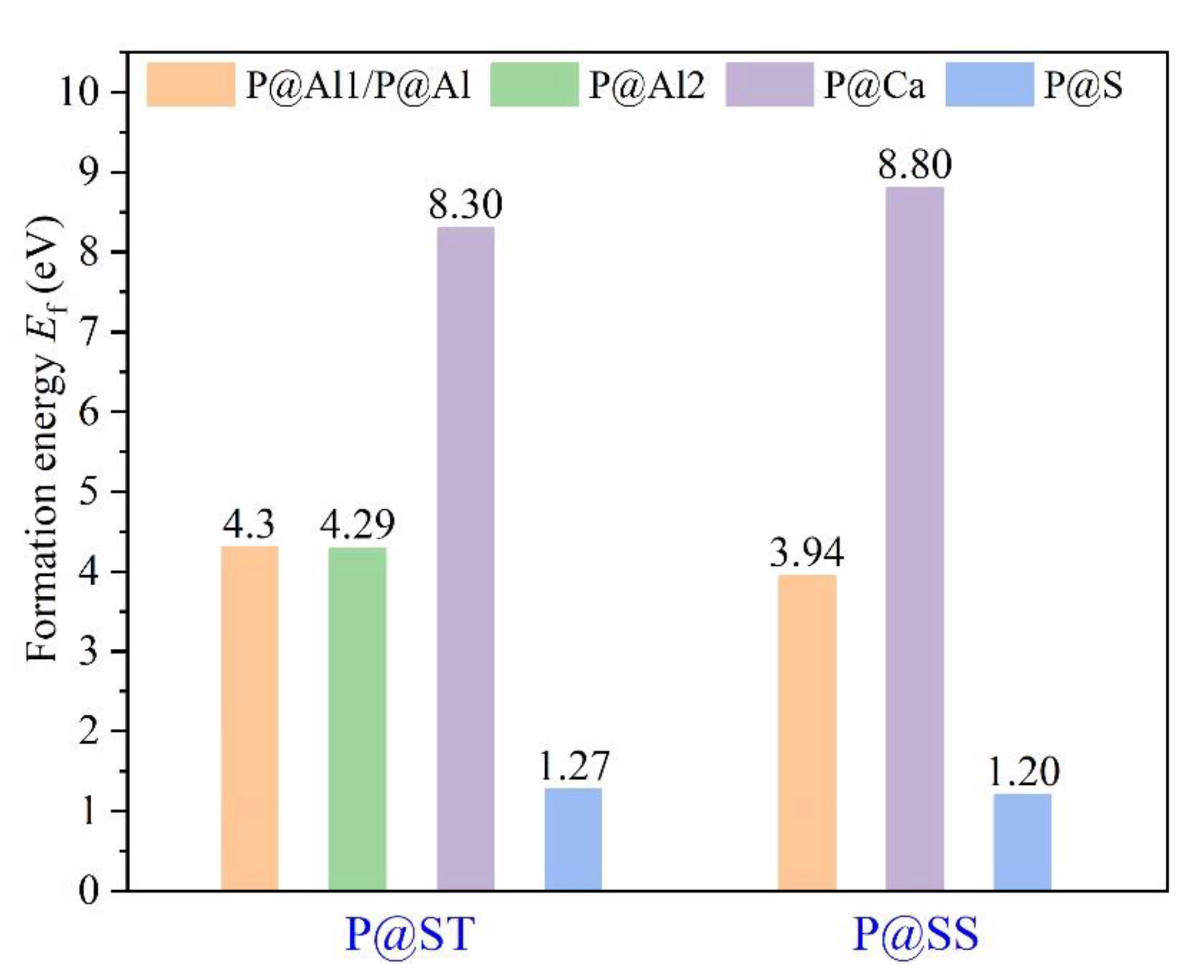
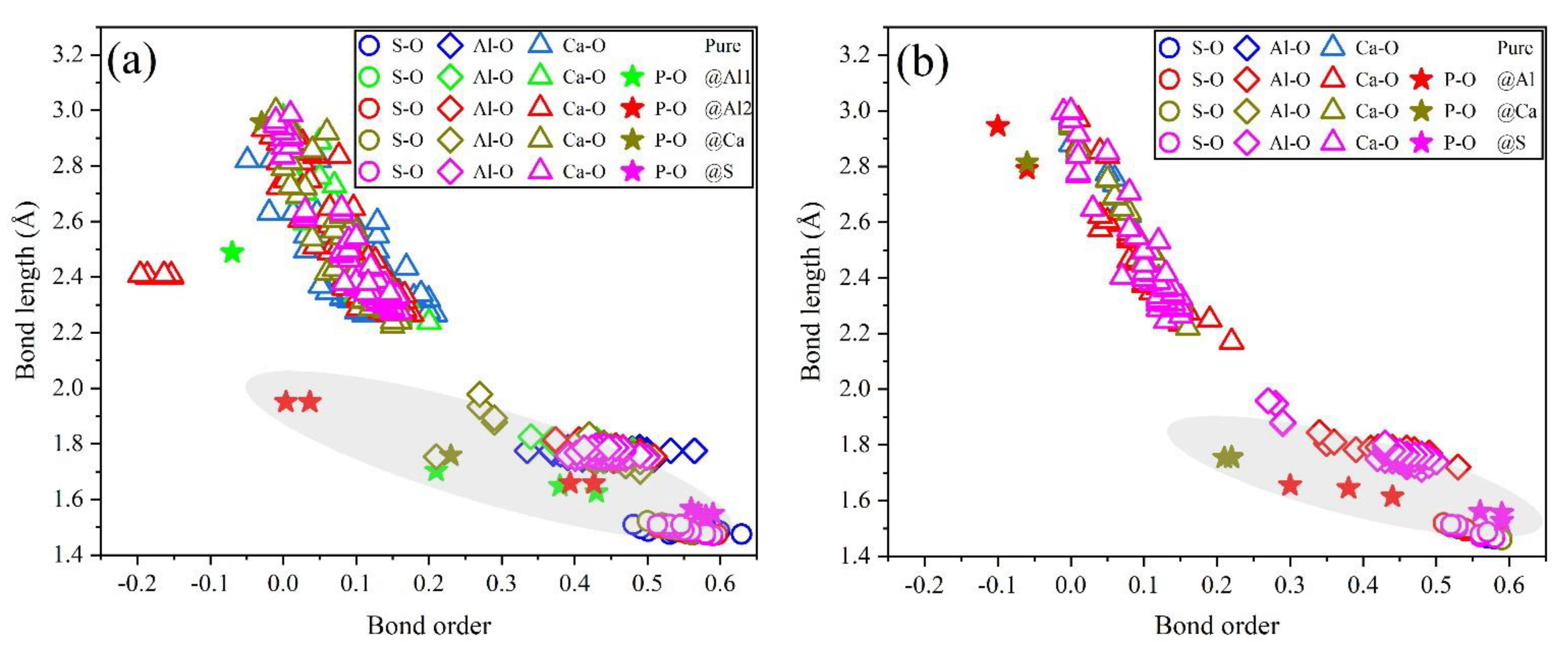
3.3. Defect Formation Energies of P-Doped Ye’elimite
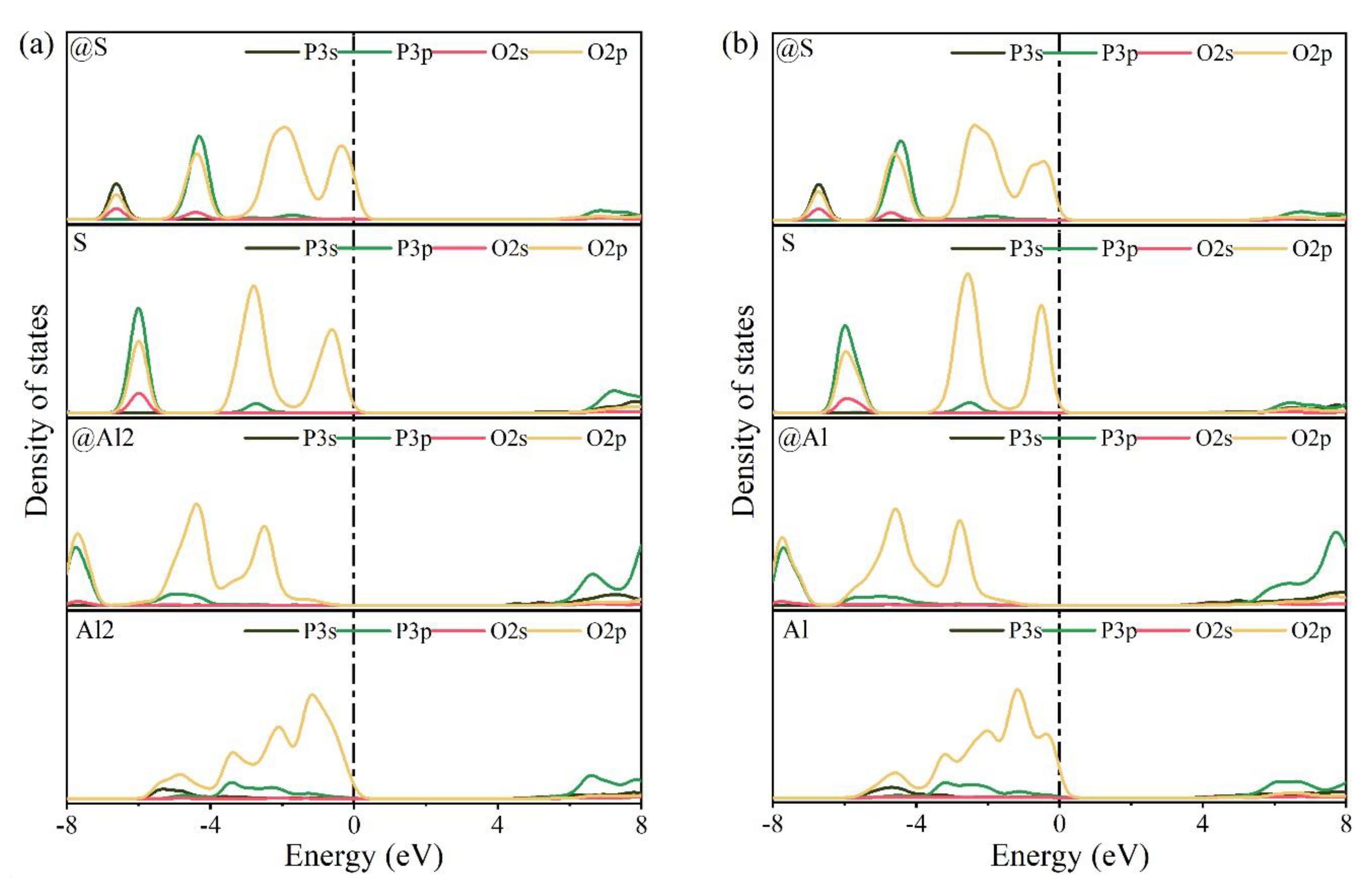
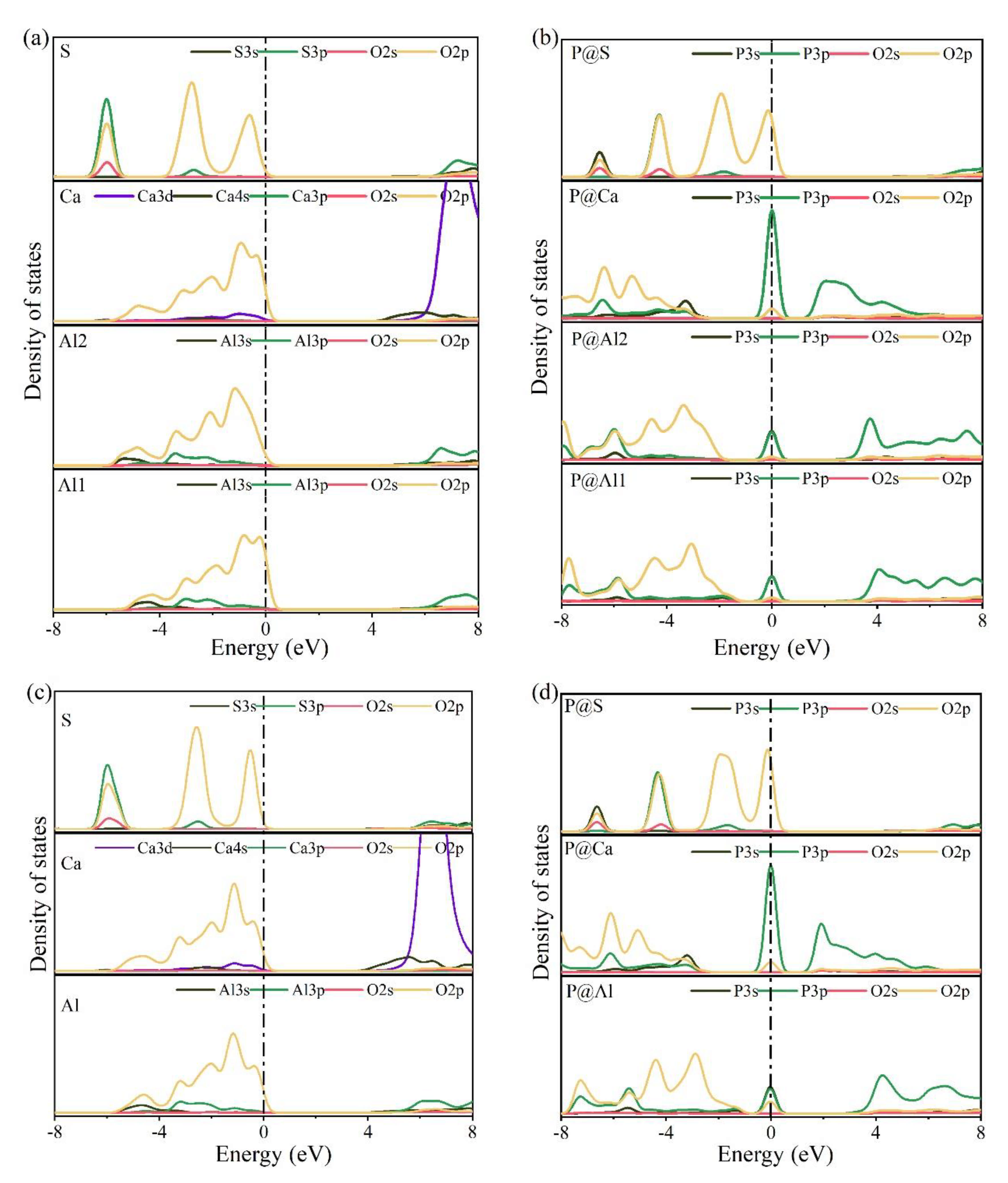
3.4. Electronic Structural Matching
4. Discussion
5. Conclusions
- Experiments and Rietveld analysis confirmed that doped P entered ye’elimite to form P-doped solid solutions, resulting in increased impurity contents in clinkers, a crystal system transformation from the orthorhombic to the cubic system, and a decrease in the ye’elimite interplanar spacing.
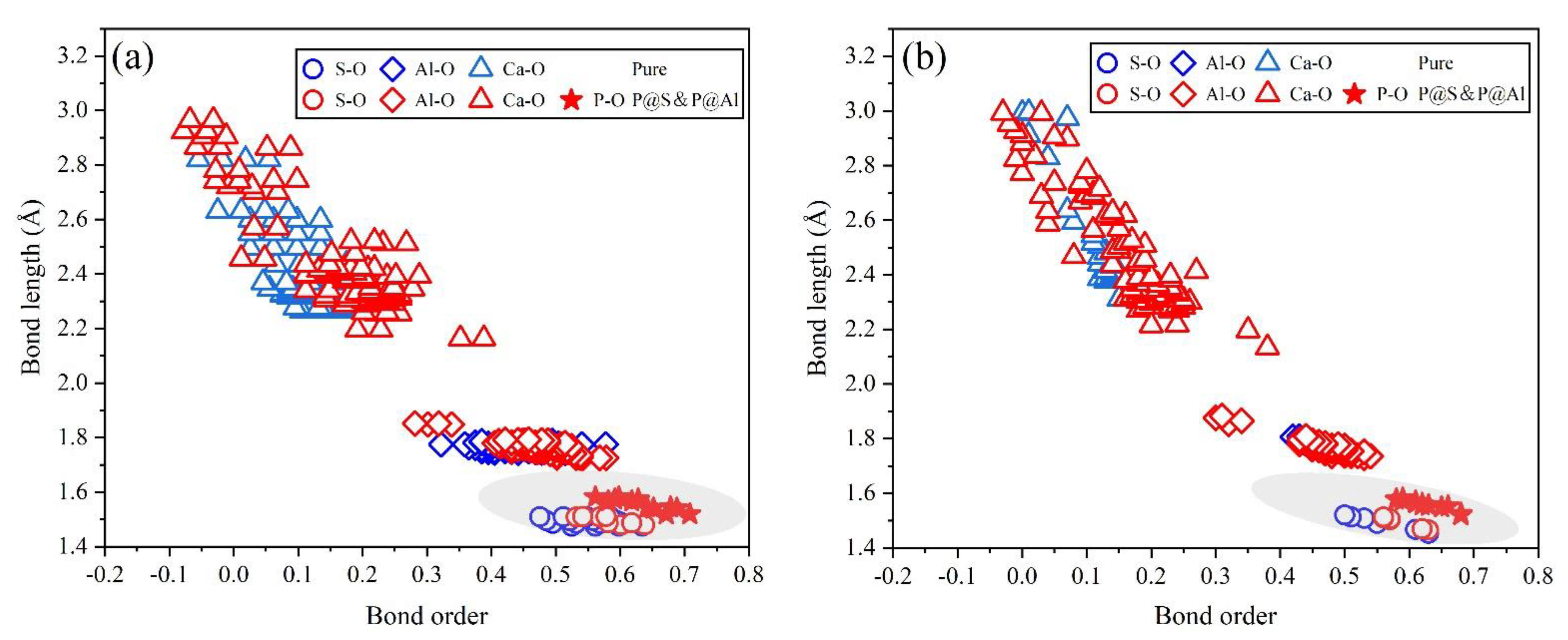
- Based on calculation results of Ef, additional energies were required for P atoms to substitute Ca/Al atoms compared with those for substituting S atoms for both orthorhombic and cubic structures of ye’elimite. By combining the BL–BO and PDOS calculation results, the doped P atoms preferably substituted S atoms; the second possible substituted atoms were Al atoms, while there was only a slight possibility for substitution of Ca atoms.
- The substitution of P atoms for S atoms can be verified using the elemental distribution in P-doped ye’elimite and the increasing residual CaSO4 contents. The crystal system transformation and a decrease in the ye’elimite interplanar spacing can also imply that the substitution of P atoms for Al atoms occurred substantially.
- Based on analysis of phosphorus substitution preference in ye’elimite, the co-substituting P-doped ye’elimite were proposed to be the most probably models. Through values of Ef, comparison of XRD patterns and electronic structural matching, the rationality of the model for co-substituting P-doped ye’elimite can be verified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Phases | Supercells | Relax | PDOS |
|---|---|---|---|
| Orthorhombic ye’elimite | 1 × 1 × 1 | 2 × 2 × 3 | 4 × 4 × 5 |
| Cubic ye’elimite | 2 × 1 × 1 | 1 × 3 × 3 | 3 × 5 × 5 |
| Oxides | P2O5 | Al2O3 | CaO | SO3 | O2 |
|---|---|---|---|---|---|
| Identification of Materials Project | mp-2452 | mp-1143 | mp-2605 | mp-561397 | mp-1009490 |
| Space group | FDD2 | R-3C | Fm-3m | P21/c | C2/M |
| Cells | 1 × 1 × 1 | 1 × 1 × 1 | 1 × 1 × 1 | 1 × 1 × 1 | 1 × 1 × 1 |
| Number of atoms | 2 | 2 | 1 | 4 | 1 |
| a/Å | 16.59 | 4.81 | 4.84 | 13.43 | 4.72 |
| b/Å | 8.17 | 4.81 | 4.84 | 4.18 | 4.73 |
| c/Å | 5.55 | 13.12 | 4.84 | 9.75 | 4.96 |
| α/° | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 |
| β/° | 90.00 | 90.00 | 90.00 | 153.05 | 123.11 |
| γ/° | 90.00 | 120.00 | 90.00 | 90.00 | 90.00 |
| V/Å3 | 751.81 | 262.26 | 113.33 | 247.98 | 93.14 |
| GBulk (eV) | −98.40 | −74.83 | −12.81 | −92.84 | −9.08 |
| G (eV) | −49.20 | −37.42 | −12.81 | −23.21 | −9.08 |
| Configurations | Lattice Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| a/Å | b/Å | c/Å | α/° | β/° | γ/° | volume/Å3 | ||
| P@ST (1 × 1 × 1) | Ref. [12] | 13.04 | 13.04 | 9.17 | 90.00 | 90.00 | 90.00 | 1557.78 |
| Pure 1 | 13.09 | 13.26 | 9.25 | 90.00 | 90.00 | 90.00 | 1606.36 | |
| @Al1 | 12.97 | 13.04 | 9.52 | 90.00 | 90.00 | 90.06 | 1609.79 | |
| @Al2 | 13.17 | 13.33 | 9.02 | 90.04 | 90.00 | 90.00 | 1584.44 | |
| @Ca | 13.04 | 13.22 | 9.33 | 89.55 | 89.40 | 89.50 | 1606.85 | |
| @S | 13.04 | 13.22 | 9.32 | 89.59 | 89.45 | 89.57 | 1607.25 | |
| P@SS (2 × 1 × 1) | Ref [16] | 18.42 | 9.21 | 9.21 | 90.00 | 90.00 | 90.00 | 779.96 |
| Pure 1 | 18.55 | 9.27 | 9.23 | 90.02 | 89.98 | 89.37 | 1586.91 | |
| @Al | 19.04 | 9.30 | 9.04 | 91.34 | 92.01 | 86.71 | 1595.49 | |
| @Ca | 18.75 | 9.30 | 9.14 | 89.34 | 90.35 | 89.34 | 1593.46 | |
| @S | 18.53 | 9.26 | 9.23 | 89.87 | 90.13 | 89.49 | 1584.47 | |
| Sample | Configurations | Et/eV | Eb 1/eV | Ef/eV |
|---|---|---|---|---|
| P@ST | Pure | −48,268.83 | −770.23 | - |
| @Al1 | −48,477.11 | −764.33 | 4.30 | |
| @Al2 | −48,477.13 | −764.35 | 4.29 | |
| @Ca | −46,685.89 | −763.60 | 8.30 | |
| @S | −48,103.16 | −775.02 | 1.27 | |
| P@SS | Pure | −48,268.60 | −770.00 | - |
| @Al | −48,477.61 | −764.83 | 3.94 | |
| @Ca | −46,684.65 | −762.36 | 8.80 | |
| @S | −48,103.06 | −774.92 | 1.20 |
References
- Bizzozero, J.; Gosselin, C.; Scrivener, K.L. Expansion Mechanisms in Calcium Aluminate and Sulfoaluminate Systems with Calcium Sulfate. Cem. Concr. Res. 2014, 56, 190–202. [Google Scholar] [CrossRef]
- Glasser, F.P.; Zhang, L. High-Performance Cement Matrices Based on Calcium Sulfoaluminate-Belite Compositions. Cem. Concr. Res. 2001, 31, 1881–1886. [Google Scholar] [CrossRef]
- Quillin, K. Performance of Belite-Sulfoaluminate Cements. Cem. Concr. Res. 2001, 31, 1341–1349. [Google Scholar] [CrossRef]
- Cui, C.; Meng, K.; Xu, C.; Liang, Z.; Li, H.; Pei, H. Analytical Solution for Longitudinal Vibration of a Floating Pile in Saturated Porous Media Based on a Fictitious Saturated Soil Pile Model. Comput. Geotech. 2021, 131, 2411–2502. [Google Scholar] [CrossRef]
- Khalil, N.; Aouad, G.; El Cheikh, K.; Remond, S. Use of Calcium Sulfoaluminate Cements for Setting Control of 3D-Printing Mortars. Constr. Build. Mater. 2017, 157, 382–391. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, J.; Wang, Y.; Yi, N.; Cui, C. Strength Performance and Microstructure of Calcium Sulfoaluminate Cement-Stabilized Soft Soil. Sustainability 2021, 13, 2295. [Google Scholar] [CrossRef]
- Juenger, M.C.G.; Winnefeld, F.; Provis, J.L.; Ideker, J.H. Advances in Alternative Cementitious Binders. Cem. Concr. Res. 2011, 41, 1232–1243. [Google Scholar] [CrossRef]
- Shi, C.; Jiménez, A.F.; Palomo, A. New Cements for the 21St Century: The Pursuit of an Alternative to Portland Cement. Cem. Concr. Res. 2011, 41, 750–763. [Google Scholar] [CrossRef]
- Shi, C.; Qu, B.; Provis, J.L. Recent Progress in Low-Carbon Binders. Cem. Concr. Res. 2019, 122, 227–250. [Google Scholar] [CrossRef]
- Bullerjahn, F.; Boehm-Courjault, E.; Zajac, M.; Ben Haha, M.; Scrivener, K. Hydration Reactions and Stages of Clinker Composed Mainly of Stoichiometric Ye’elimite. Cem. Concr. Res. 2019, 116, 120–133. [Google Scholar] [CrossRef]
- El Khessaimi, Y.; El Hafiane, Y.; Smith, A. Examination of Ye’elimite Formation Mechanisms. J. Eur. Ceram. Soc. 2019, 39, 5086–5095. [Google Scholar] [CrossRef]
- Cuesta, A.; de la Torre, A.G.; Losilla, E.R.; Peterson, V.K.; Rejmak, P.; Ayuela, A.; Frontera, C.; Aranda, M.A.G. Structure, Atomistic Simulations, and Phase Transition of Stoichiometric Yeelimite. Chem. Mater. 2013, 25, 1680–1687. [Google Scholar] [CrossRef] [Green Version]
- Bullerjahn, F.; Scholten, T.; Scrivener, K.L.; Ben Haha, M.; Wolter, A. Formation, Composition and Stability of Ye’elimite and Iron-Bearing Solid Solutions. Cem. Concr. Res. 2020, 131, 106009. [Google Scholar] [CrossRef]
- Zhao, P.; Bao, X.; Chen, H.; Wang, S.; Lu, L.; De La Torre, A.G.; Cheng, X. Hydration Mechanisms of Ba-Doped Ye’elimite: Effect of Ba/Ca Ratio on Hydration Behavior. Constr. Build. Mater. 2020, 264, 120258. [Google Scholar] [CrossRef]
- Zea-Garcia, J.D.; Santacruz, I.; Aranda, M.A.G.; De la Torre, A.G. Alite-Belite-Ye’elimite Cements: Effect of Dopants on the Clinker Phase Composition and Properties. Cem. Concr. Res. 2019, 115, 192–202. [Google Scholar] [CrossRef]
- Cuesta, A.; De la Torre, Á.G.; Losilla, E.R.; Santacruz, I.; Aranda, M.A.G. Pseudocubic Crystal Structure and Phase Transition in Doped Ye’elimite. Cryst. Growth Des. 2014, 14, 5158–5163. [Google Scholar] [CrossRef] [Green Version]
- Cuesta, A.; Álvarez-Pinazo, G.; Sanfélix, S.G.; Peral, I.; Aranda, M.A.G.; De, L.T.A.G. Hydration Mechanisms of Two Polymorphs of Synthetic Ye’elimite. Cem. Concr. Res. 2014, 63, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.; Zhao, J.; Shang, X.; Yu, X.; Zhang, Y.; Zhang, T. Rietveld Refinement for Sr(Ba)-Bearing Ye’elimite. Adv. Cem. Res. 2016, 28, 583–593. [Google Scholar] [CrossRef]
- Zhao, J.; Chang, J. Crystallographic Analysis of Sr-Bearing Ye’elimite. J. Inorg. Organometall. Polym. Mater. 2017, 27, 1694–1702. [Google Scholar] [CrossRef]
- Zhao, J.; Chang, J. Kinetic Analysis for Formation Process of Sr-Bearing Ye’elimite. J. Inorg. Organometall. Polym. Mater. 2017, 27, 1861–1869. [Google Scholar] [CrossRef]
- Tao, Y.; Li, N.; Zhang, W.; Wang, F.; Hu, S. Understanding the Zinc Incorporation into Silicate Clinker During Waste Co-Disposal of Cement Kiln: A Density Functional Theory Study. J. Clean. Prod. 2019, 232, 329–336. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, L.; Fan, G.; Chen, Y.; Huang, G.; Zhang, H.; Zhu, J.; Guan, X. Probing the Exact Form and Doping Preference of Magnesium in Ordinary Portland Cement Clinker Phases: A Study from Experiments and DFT Simulations. Cem. Concr. Res. 2021, 144, 106420. [Google Scholar] [CrossRef]
- Laanaiya, M.; Bouibes, A.; Zaoui, A. Structural Stability of Belite Sulfoaluminate Clinkering Polymorphs. Solid State Ion. 2021, 365, 115641. [Google Scholar] [CrossRef]
- Wang, Q.; Gu, X.; Zhou, H.; Chen, X.; Shen, X. Cation Substitution Induced Reactivity Variation on the Tricalcium Silicate Polymorphs Determined from First-Principles Calculations. Constr. Build. Mater. 2019, 216, 239–248. [Google Scholar] [CrossRef]
- Tao, Y.; Zhang, W.; Li, N.; Shang, D.; Xia, Z.; Wang, F. Fundamental Principles that Govern the Copper Doping Behavior in Complex Clinker System. J. Am. Ceram. Soc. 2018, 101, 2527–2536. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, Y.; Zhang, L.; Guo, B.; Fan, G.; Guan, X.; Zhao, R. Revealing the Doping Mechanism of Barium in Sulfoaluminate Cement Clinker Phases. J. Clean. Prod. 2021, 295, 126405. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, Y.; Zhang, L.; Yang, K.; Guan, X.; Zhao, R. Insights on Substitution Preference of Pb Ions in Sulfoaluminate Cement Clinker Phases. Materials 2021, 14, 44. [Google Scholar] [CrossRef] [PubMed]
- Cai, Q.; Jiang, J.; Ma, B.; Shao, Z.; Hu, Y.; Qian, B.; Wang, L. Efficient Removal of Phosphate Impurities in Waste Phosphogypsum for the Production of Cement. Sci. Total Environ. 2021, 780, 146600. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Yao, X.; Ren, C.; Yao, Y.; Wang, W. Recycling Phosphogypsum as a Sole Calcium Oxide Source in Calcium Sulfoaluminate Cement and its Environmental Effects. J. Environ. Manag. 2020, 271, 110986. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Qian, J. Utilisation of Phosphogypsum for Sulfate-Rich Belite Sulfoaluminate Cement Production. Adv. Cem. Res. 2015, 27, 515–525. [Google Scholar] [CrossRef]
- Huang, Y.; Qian, J.; Kang, X.; Yu, J.; Fan, Y.; Dang, Y.; Zhang, W.; Wang, S. Belite-Calcium Sulfoaluminate Cement Prepared with Phosphogypsum: Influence of P2O5 and F on the Clinker Formation and Cement Performances. Constr. Build. Mater. 2019, 203, 432–442. [Google Scholar] [CrossRef]
- Shen, Y.; Qian, J.; Huang, Y.; Yang, D. Synthesis of Belite Sulfoaluminate-Ternesite Cements with Phosphogypsum. Cem. Concr. Compos. 2015, 63, 67–75. [Google Scholar] [CrossRef]
- Huang, Y.; Qian, J.; Lu, L.; Zhang, W.; Wang, S.; Wang, W.; Cheng, X. Phosphogypsum as a Component of Calcium Sulfoaluminate Cement: Hazardous Elements Immobilization, Radioactivity and Performances. J. Clean Prod. 2020, 248, 119287. [Google Scholar] [CrossRef]
- Lazic, B.; Krüger, H.; Kahlenberg, V.; Konzett, J.; Kaindl, R. Incommensurate Structure of Ca2Al2O5 at High Temperatures--Structure Investigation and Raman Spectroscopy. Acta Crystallogr. 2010, 64, 417–425. [Google Scholar] [CrossRef]
- Cheng, G.C.H.; Zussman, J. The Crystal Structure of Anhydrite (CaSO4). Acta Crystallogr. 1963, 16, 767–769. [Google Scholar] [CrossRef] [Green Version]
- Boysen, H.; Lerch, M.; Stys, A.; Senyshyn, A. Structure and Oxygen Mobility in Mayenite (Ca12Al14O33): A High-Temperature Neutron Powder Diffraction Study. Acta Crystallogr. 2007, 63, 675–682. [Google Scholar] [CrossRef]
- Mondal, P.; Jeffery, J.W. The Crystal Structure of Tricalcium Aluminate, Ca3Al2O6. Acta Crystallogr. 2010, 31, 689–697. [Google Scholar] [CrossRef]
- Yashima, M.; Sakai, A.; Kamiyama, T.; Hoshikawa, A. Crystal Structure Analysis of Beta-Tricalcium Phosphate Ca3(PO4)2 by Neutron Powder Diffraction. J. Solid State Chem. 2003, 175, 272–277. [Google Scholar] [CrossRef]
- Verbraeken, M.C.; Suard, E.; Irvine, J.T.S. Structural and Electrical Properties of Calcium and Strontium Hydrides. J. Mater. Chem. 2009, 19, 2766–2770. [Google Scholar] [CrossRef]
- Muraoka, Y.; Kihara, K. The Temperature Dependence of the Crystal Structure of Berlinite, a Quartz-Type Form of Alpo 4. Phys. Chem. Miner. 1997, 24, 243–253. [Google Scholar] [CrossRef]
- Clark, S.J.; Segallii, M.D.; Pickardii, C.J.; Hasnipiii, P.J.; Probertiv, M. First Principles Methods Using Castep. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Yue, W. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Chl, P. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Calos, N.J.; Kennard, C.; Whittaker, A.K.; Davis, R.L. Structure of Calcium Aluminate Sulfate Ca4Al6O16S. J. Solid State Chem. 1995, 119, 1–7. [Google Scholar] [CrossRef]
- Tao, Y.; Zhang, W.; Shang, D.; Xia, Z.; Li, N.; Ching, W.; Wang, F.; Hu, S. Comprehending the Occupying Preference of Manganese Substitution in Crystalline Cement Clinker Phases: A Theoretical Study. Cem. Concr. Res. 2018, 109, 19–29. [Google Scholar] [CrossRef]
- Zhou, H.; Gu, X.; Sun, J.; Yu, Z.; Huang, H.; Wang, Q.; Shen, X. Research on the Formation of M1-Type Alite Doped with Mgo and so3—a Route to Improve the Quality of Cement Clinker with a High Content of Mgo. Constr. Build. Mater. 2018, 182, 156–166. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, K.; Chen, Y.; Fan, G.; Zhang, L.; Guo, B.; Guan, X.; Zhao, R. Revealing the Substitution Preference of Zinc in Ordinary Portland Cement Clinker Phases: A Study from Experiments and Dft Calculations. J. Hazard. Mater. 2020, 409, 124504. [Google Scholar] [CrossRef] [PubMed]
- Kohan, A.F.; Ceder, G.; Morgan, D.; Van de Walle, C.G. First-Principles Study of Native Point Defects in Zno. Phys. Rev. B 2000, 61. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wei, S.; Li, S.; Xia, J. Design of Shallow Acceptors in Zno: First-Principles Band-Structure Calculations. Cem. Concr. Res. 2006, 74. [Google Scholar] [CrossRef]
- West, D.; Sun, Y.Y.; Zhang, S.B. Importance of the Correct Fermi Energy on the Calculation of Defect Formation Energies in Semiconductors. Appl. Phys. Lett. 2012, 101, 082105. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Walle, C. First-Principles Calculations for Point Defects in Solids. Rev. Mod. Phys. 2014, 86, 253. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Shen, X.; Wang, Q.; Pan, Z. Kinetics of Calcium Sulfoaluminate Formation from Tricalcium Aluminate, Calcium Sulfate and Calcium Oxide. Cem. Concr. Res. 2014, 55, 79–87. [Google Scholar] [CrossRef]
- Puertas, F.; Varela, M.T.B.; Molina, S.G. Kinetics of the Thermal Decomposition of C4A3S in Air. Cem. Concr. Res. 1995, 25, 572–580. [Google Scholar] [CrossRef]
- Guerra, C.F.; Handgraaf, J.W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi Deformation Density (Vdd) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and Vdd Methods for Charge Analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]







| Nomenclature | Molar Ratios of Raw Materials | Sintering Conditions |
|---|---|---|
| ST | CaCO3: Al2O3: CaSO4 = 3:3:1 | 1300 °C for 4 h |
| SS | CaCO3: Na2CO3: Al2O3: Fe2O3: SiO2: CaSO4 = 2.8:0.1:2.8:0.1:0.2:1 | 1250 °C for 4 h |
| Px 1 | CaCO3: Ca3(PO4)2: Al2O3:CaSO4 = (3–3x): x: 3:1 | 1300 °C for 4 h |
| Phases | Formula | COD Code | Reference |
|---|---|---|---|
| Ye’elimite (orthorhombic) | Ca4Al6SO16 | 4001772 | [12] |
| Ye’elimite (cubic) | Ca3.8Na0.2Al5.6Fe0.2Si0.2SO16 | 4511960 | [16] |
| Monocalcium aluminate | CaAl2O4 | 4308075 | [34] |
| Anhydrite | CaSO4 | 5000040 | [35] |
| Mayenite | Ca12Al14O33 | 2102955 | [36] |
| Tricalcium aluminate | Ca3Al2O6 | 9015966 | [37] |
| Calcium phosphate | Ca3(PO4)2 | 1517238 | [38] |
| Calcium oxide | CaO | 7200686 | [39] |
| Aluminum phosphate | AlPO4 | 9006404 | [40] |
| Phases | Samples | |||
|---|---|---|---|---|
| ST | P0.10 | P0.15 | P0.20 | |
| Orthorhombic ye’elimite | 96.4 | 75.8 | 61.5 | 44.7 |
| Cubic ye’elimite | - | 18.5 | 30.2 | 39.8 |
| Calcium aluminate phases 1 | 2.8 | 5.7 | 6.4 | 11.6 |
| Anhydrite | - | - | 0.6 | 1.2 |
| Calcium oxide | 0.8 | - | - | - |
| Calcium/aluminum phosphate 2 | - | - | 1.3 | 2.7 |
| Ratio of cubic ye’elimite to orthorhombic ye’elimite | 0 | 0.24 | 0.49 | 0.89 |
| Total contents of ye’elimite | 96.4 | 94.3 | 91.7 | 84.6 |
| Ions | Coordination Numbers | Radius (pm) |
|---|---|---|
| P5+ | 4 | 17 |
| 5 | 29 | |
| 6 | 38 | |
| Ca2+ | 6 | 100 |
| 7 | 106 | |
| 8 | 112 | |
| S6+ | 4 | 12 |
| Al3+ | 4 | 39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Huang, J.; Yu, C.; Cui, C.; Chang, J. Phosphorus Substitution Preference in Ye’elimite: Experiments and Density Functional Theory Simulations. Materials 2021, 14, 5874. https://doi.org/10.3390/ma14195874
Zhao J, Huang J, Yu C, Cui C, Chang J. Phosphorus Substitution Preference in Ye’elimite: Experiments and Density Functional Theory Simulations. Materials. 2021; 14(19):5874. https://doi.org/10.3390/ma14195874
Chicago/Turabian StyleZhao, Jiuye, Jiazhi Huang, Chunyang Yu, Chunyi Cui, and Jun Chang. 2021. "Phosphorus Substitution Preference in Ye’elimite: Experiments and Density Functional Theory Simulations" Materials 14, no. 19: 5874. https://doi.org/10.3390/ma14195874
APA StyleZhao, J., Huang, J., Yu, C., Cui, C., & Chang, J. (2021). Phosphorus Substitution Preference in Ye’elimite: Experiments and Density Functional Theory Simulations. Materials, 14(19), 5874. https://doi.org/10.3390/ma14195874