A Numerical Analysis of Resin Flow in Woven Fabrics: Effect of Local Tow Curvature on Dual-Scale Permeability
Abstract
1. Introduction
1.1. Background
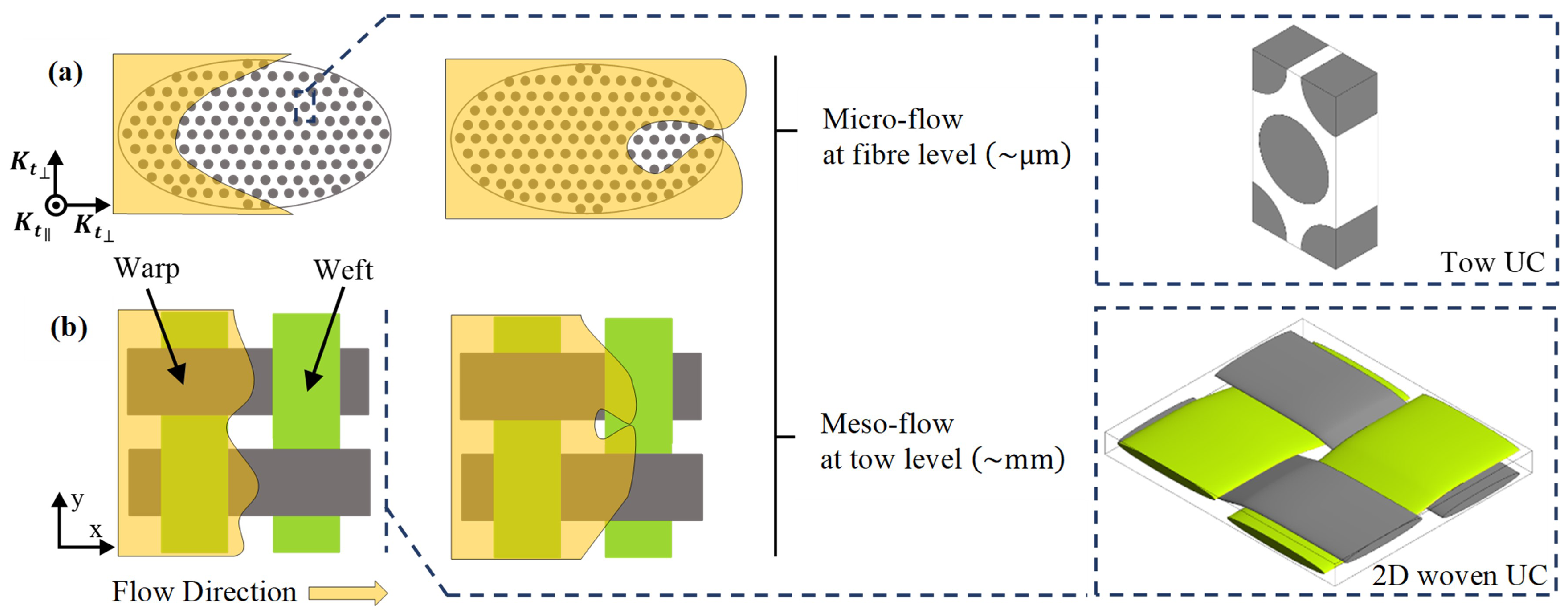
1.2. Dual-Scale Porous Media Modelling
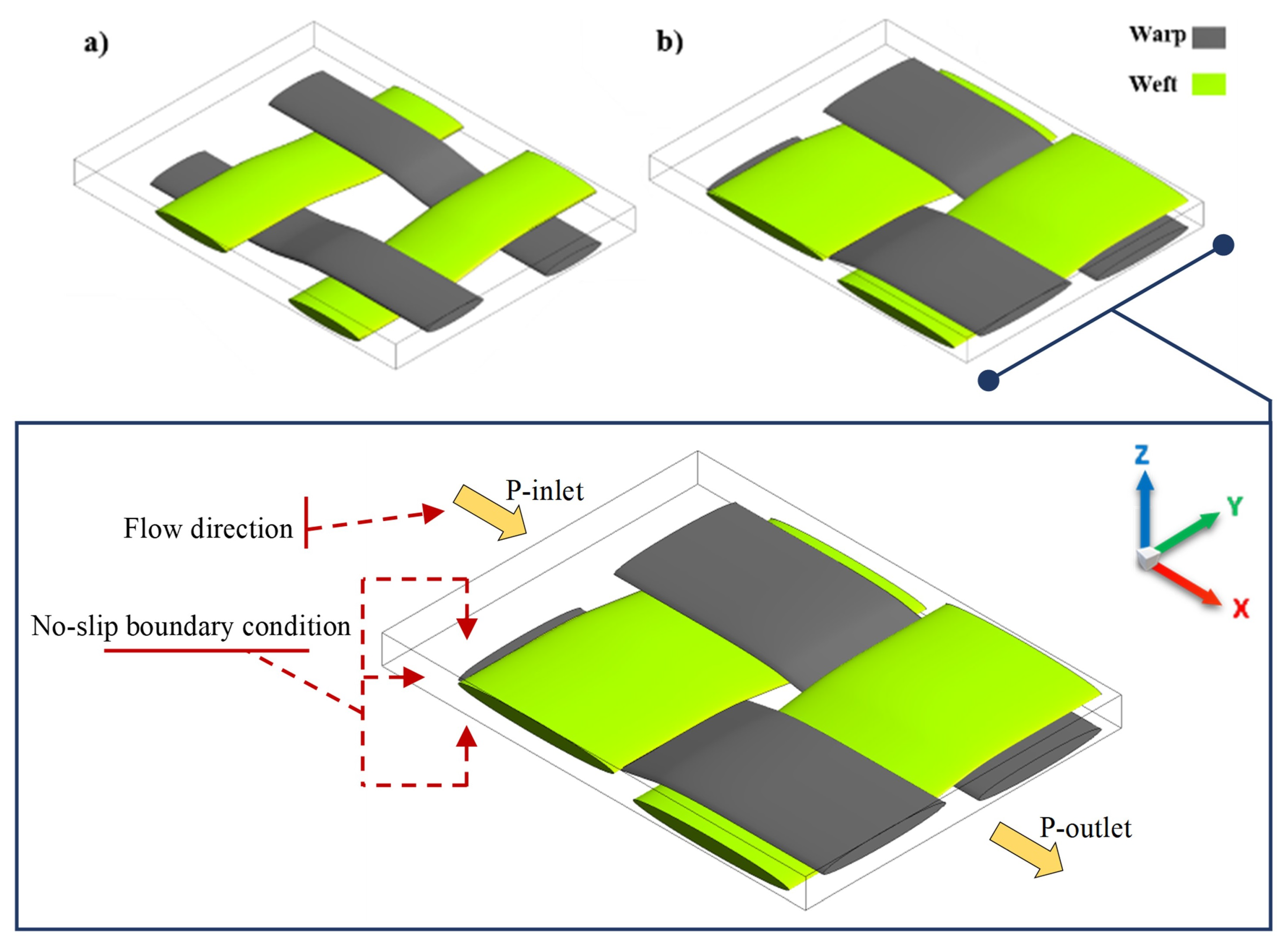
2. Methodology
2.1. Continuity and Momentum Equations
2.2. Permeable and Impermeable Tows
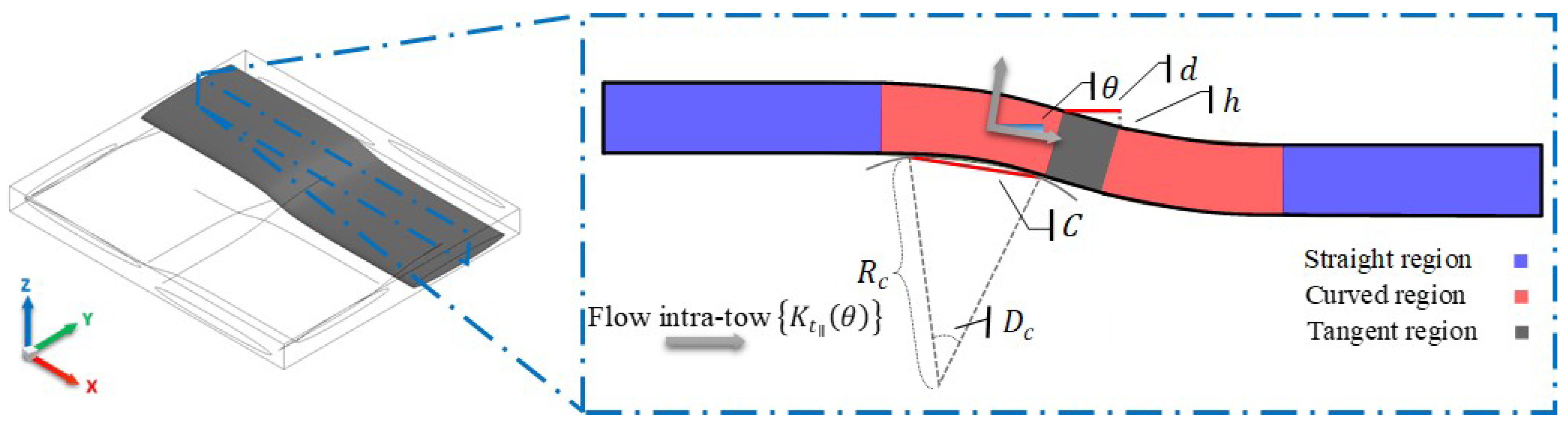
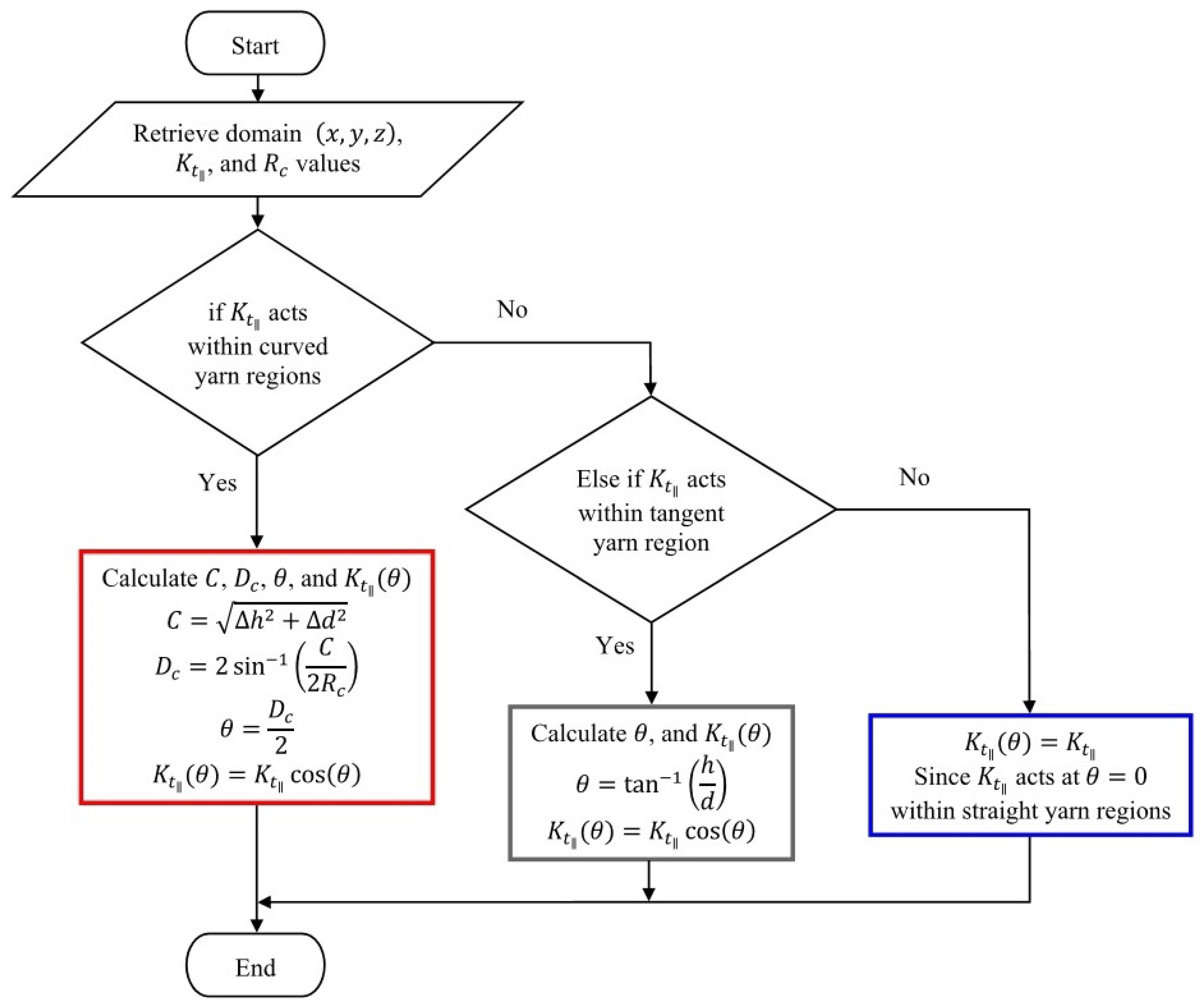
2.3. Local Curvature
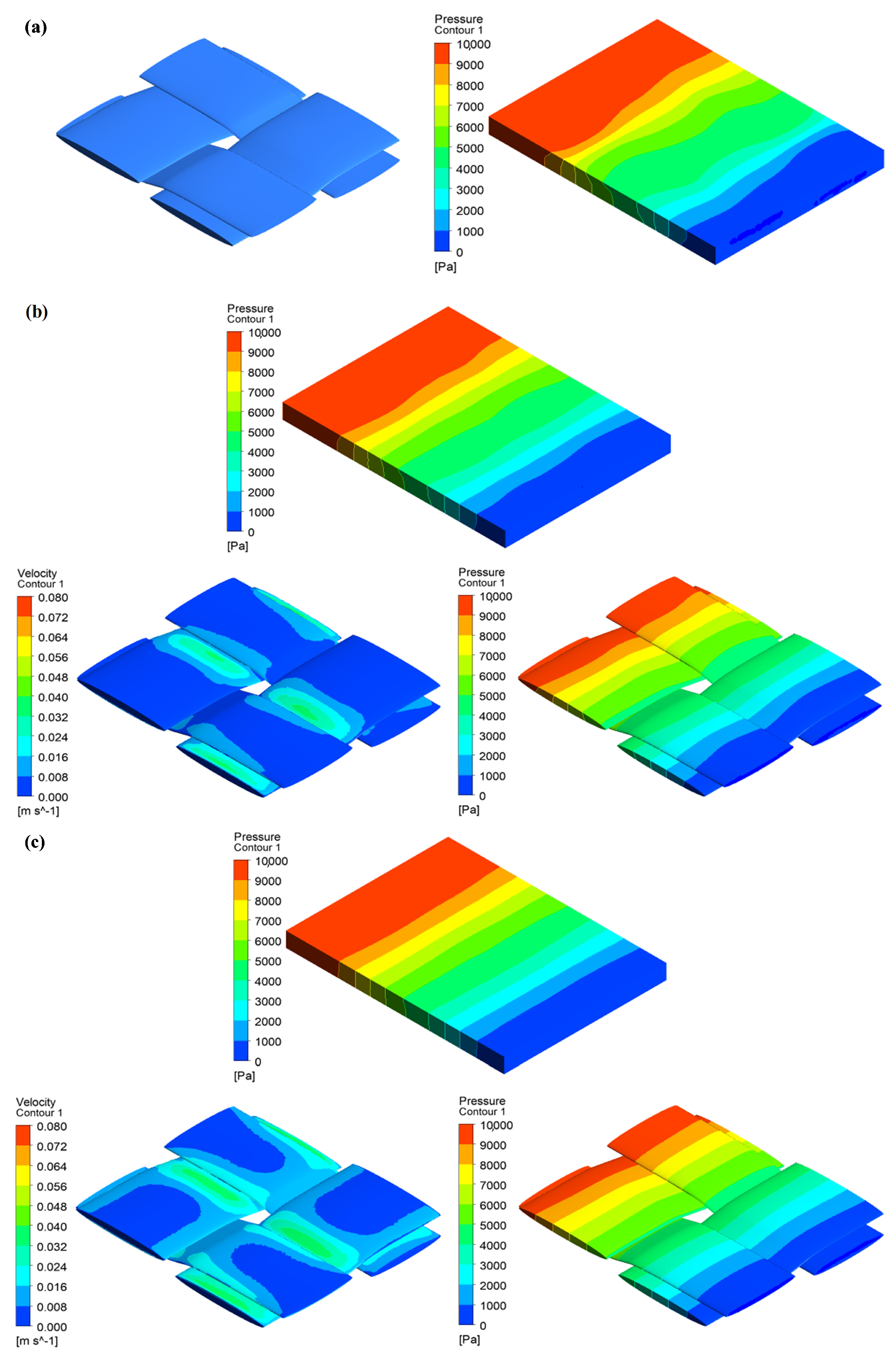
3. Results and Discussion
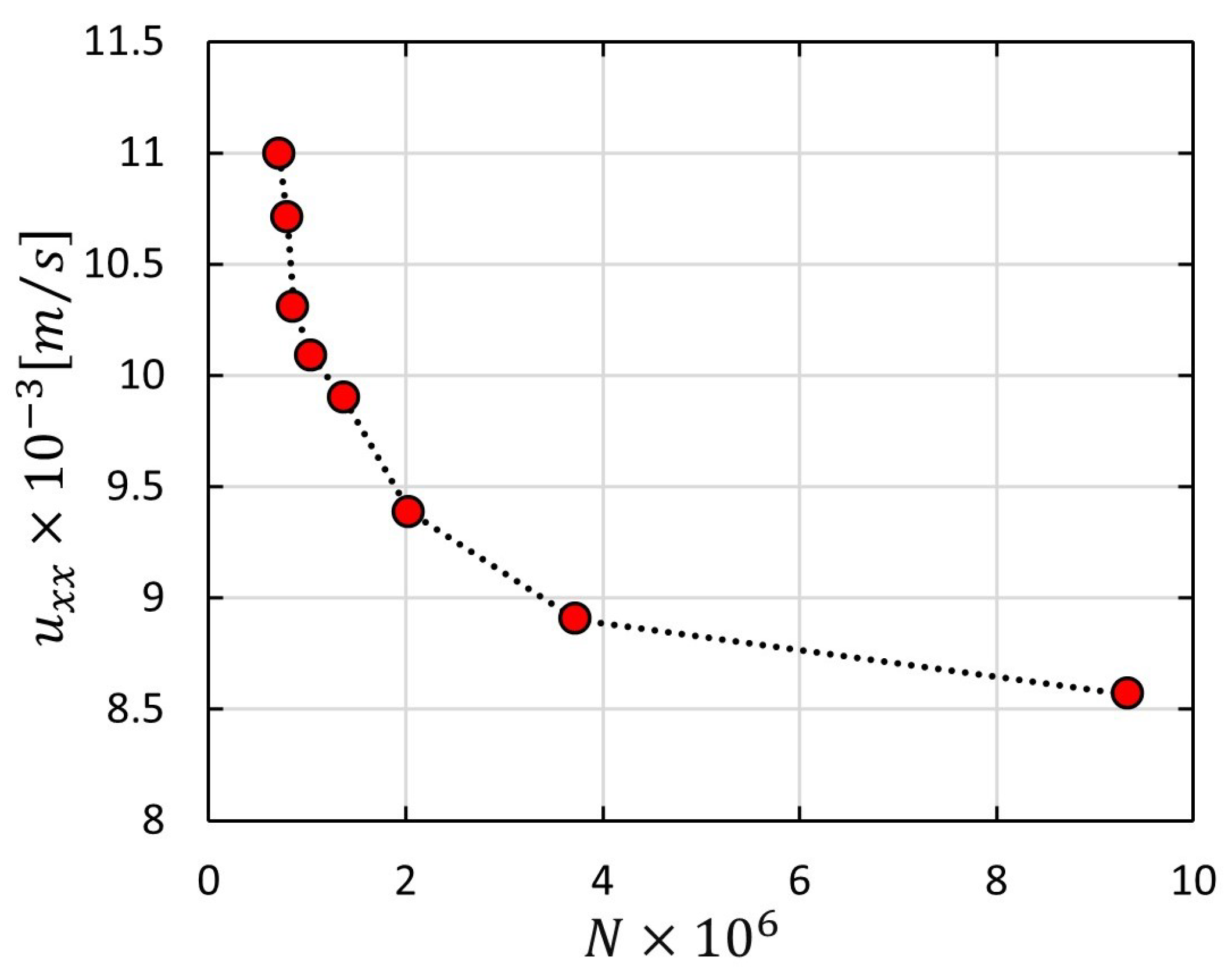
3.1. Mesh Dependency Study
3.2. A Woven Fabric of Elliptic Permeable and Impermeable Tows
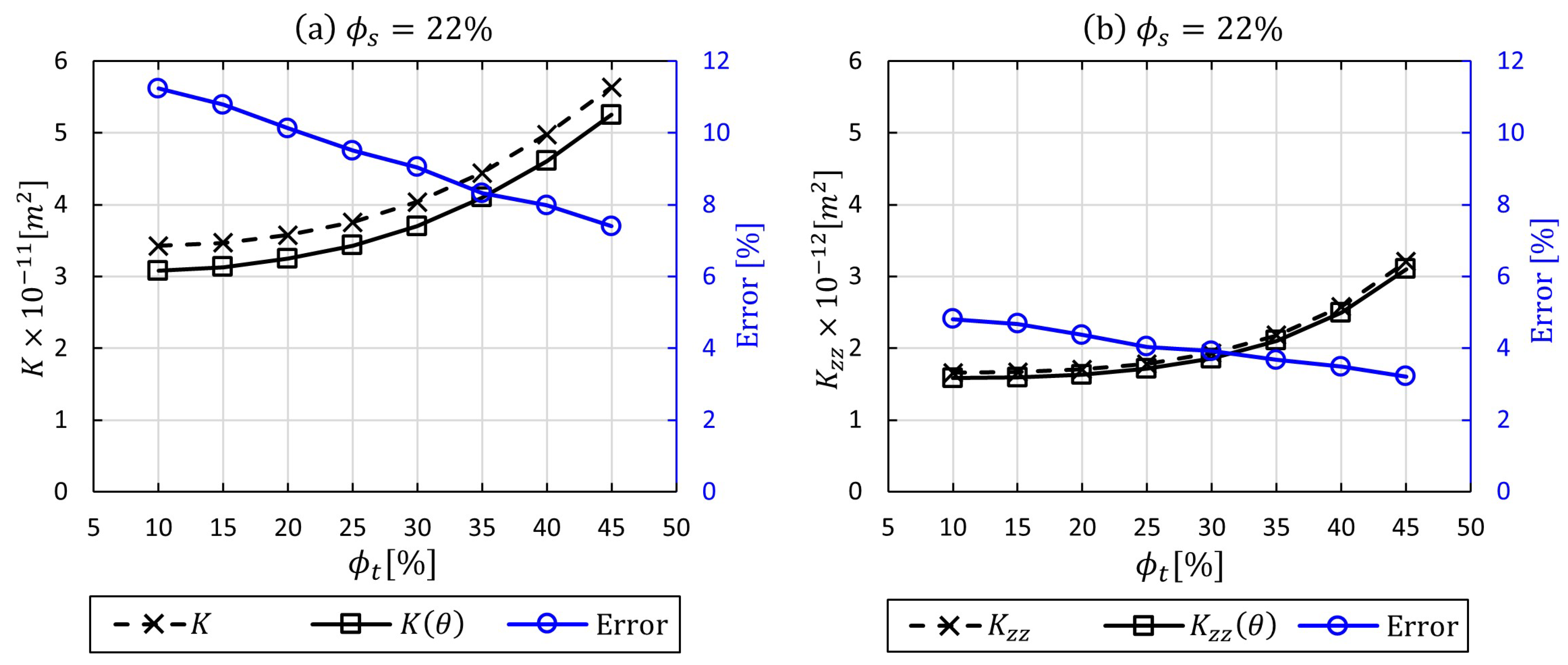
3.3. Degree of Local Curvature in Woven Tows
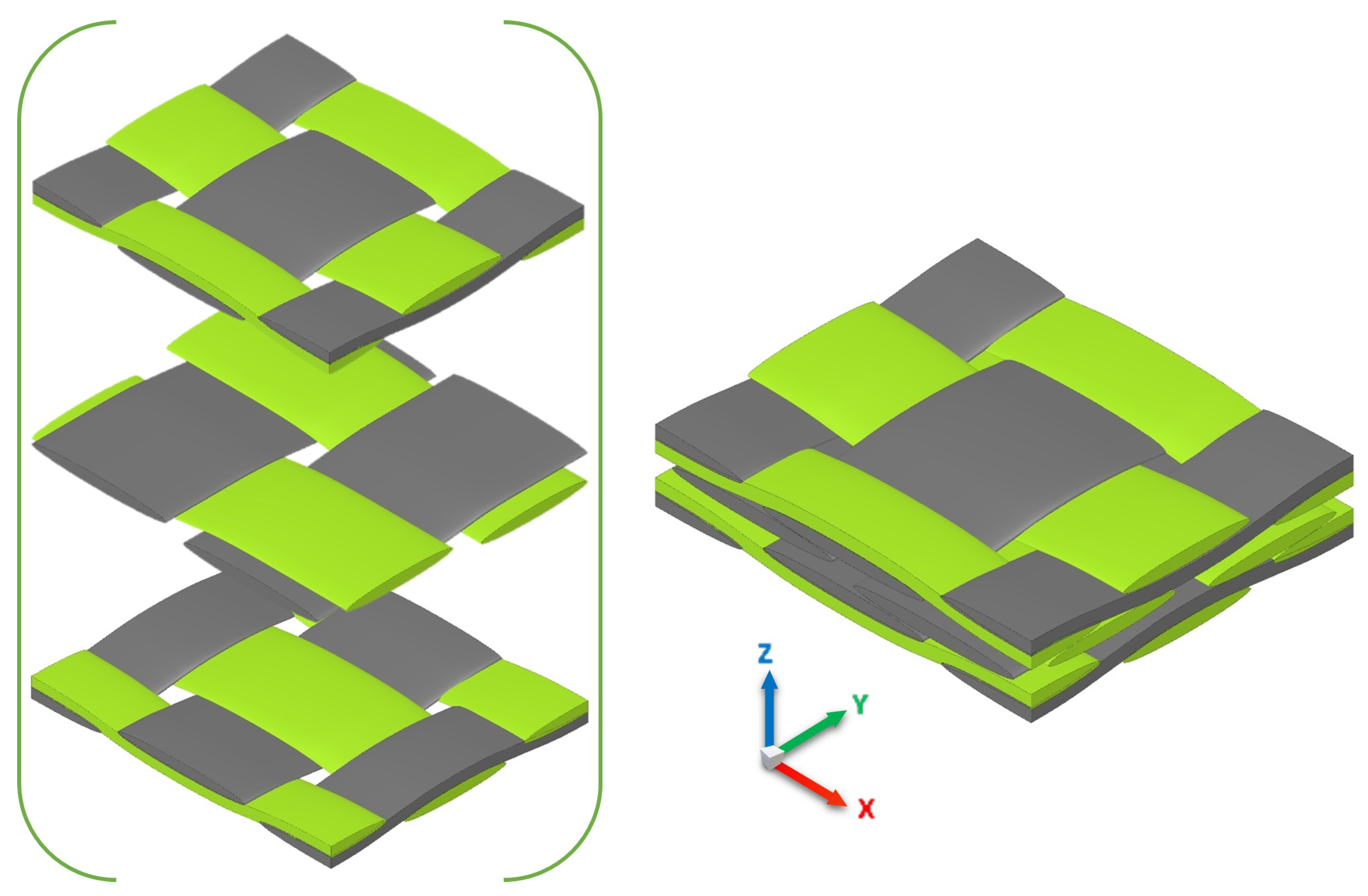
3.4. Degree of Local Curvature in Multi-Layer Structure with Nesting
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Latin letters: | |
| C | Chord length, m |
| Degree of curvature | |
| d | Distance, m |
| Gravitational acceleration, m/s | |
| h | Height of curvature, m |
| Permeability tensor, m | |
| p | Pressure, Pa |
| R | Radius, m |
| S | Source term |
| t | Time, s |
| Volume averaged velocity vector, m/s | |
| Volume fraction | |
| Global coordinate system | |
| Latin letters: | |
| Rotation angle between global and principal coordinate system | |
| Dynamic viscosity, Pa·s | |
| Density, kg/m | |
| Stress tensor vector, Pa | |
| Porosity | |
| subscripts: | |
| c | Curvature |
| f | Fibre/filament |
| o | Overall/global |
| t | Intra-tow/microscopic/local/tow |
| s | Inter-tow/single scale |
| Global coordinate system | |
| ‖ | Longitudinal/parallel |
| ⊥ | Transverse/perpendicular |
| Abbreviation: | |
| CFD | Computational fluid dynamics |
| LBM | Lattice Boltzmann method |
| LCM | Liquid composite moulding |
| N-S | Naiver-Stokes |
| RTM | Resin transfer moulding |
| RVE | Representative volume element |
| UC | Unit cell |
| UDF | User-defined function |
References
- Gascón, L.; García, J.; LeBel, F.; Ruiz, E.; Trochu, F. Numerical prediction of saturation in dual scale fibrous reinforcements during Liquid Composite Molding. Compos. Part A Appl. Sci. Manuf. 2015, 77, 275–284. [Google Scholar] [CrossRef]
- Kuentzer, N.; Simacek, P.; Advani, S.G.; Walsh, S. Permeability characterization of dual scale fibrous porous media. Compos. Part A Appl. Sci. Manuf. 2006, 37, 2057–2068. [Google Scholar] [CrossRef]
- Tan, H.; Pillai, K.M. Multiscale modeling of unsaturated flow in dual-scale fiber preforms of liquid composite molding I: Isothermal flows. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1–13. [Google Scholar] [CrossRef]
- Bodaghi, M.; Lomov, S.; Simacek, P.; Correia, N.; Advani, S. On the variability of permeability induced by reinforcement distortions and dual scale flow in liquid composite moulding: A review. Compos. Part A Appl. Sci. Manuf. 2019, 120, 188–210. [Google Scholar] [CrossRef]
- Liu, B.; Bickerton, S.; Advani, S.G. Modelling and simulation of resin transfer moulding (RTM)—gate control, venting and dry spot prediction. Compos. Part A Appl. Sci. Manuf. 1996, 27, 135–141. [Google Scholar] [CrossRef]
- Li, S.; Gauvin, R. Numerical analysis of the resin flow in resin transfer molding. J. Reinf. Plast. Compos. 1991, 10, 314–327. [Google Scholar]
- Bruschke, M.; Advani, S. A numerical approach to model non-isothermal viscous flow through fibrous media with free surfaces. Int. J. Numer. Methods Fluids 1994, 19, 575–603. [Google Scholar] [CrossRef]
- Phelan, F.R., Jr. Simulation of the injection process in resin transfer molding. Polym. Compos. 1997, 18, 460–476. [Google Scholar] [CrossRef]
- Soukane, S.; Trochu, F. Application of the level set method to the simulation of resin transfer molding. Compos. Sci. Technol. 2006, 66, 1067–1080. [Google Scholar] [CrossRef]
- Parnas, R.S.; Phelan, F. The effect of heterogeneous porous media on mold filling in resin transfer molding. Sampe Quart 1991, 22, 53–60. [Google Scholar]
- Binetruy, C.; Hilaire, B.; Pabiot, J. The interactions between flows occurring inside and outside fabric tows during RTM. Compos. Sci. Technol. 1997, 57, 587–596. [Google Scholar] [CrossRef]
- Lekakou, C.; Bader, M. Mathematical modelling of macro-and micro-infiltration in resin transfer moulding (RTM). Compos. Part A Appl. Sci. Manuf. 1998, 29, 29–37. [Google Scholar] [CrossRef]
- De Parseval, Y.; Pillai, K.; Advani, S.G. A simple model for the variation of permeability due to partial saturation in dual scale porous media. Transport Porous Med. 1997, 27, 243–264. [Google Scholar] [CrossRef]
- Pillai, K.; Advani, S. A model for unsaturated flow in woven fiber preforms during mold filling in resin transfer molding. J. Compos. Mater. 1998, 32, 1753–1783. [Google Scholar] [CrossRef]
- Wang, Y.; Grove, S. Modelling microscopic flow in woven fabric reinforcements and its application in dual-scale resin infusion modelling. Compos. Part A Appl. Sci. Manuf. 2008, 39, 843–855. [Google Scholar] [CrossRef]
- Gascón, L.; García, J.; LeBel, F.; Ruiz, E.; Trochu, F. A two-phase flow model to simulate mold filling and saturation in Resin Transfer Molding. Int. J. Mater. Form. 2016, 9, 229–239. [Google Scholar] [CrossRef]
- Parnas, R.S.; Howard, J.G.; Luce, T.L.; Advani, S.G. Permeability characterization. Part 1: A proposed standard reference fabric for permeability. Polym. Compos. 1995, 16, 429–445. [Google Scholar] [CrossRef]
- Zhong, W.; Xing, M.; Chen, S. A statistic model of mold filling through fibrous structures. J. Compos. Mater. 2004, 38, 1545–1557. [Google Scholar] [CrossRef]
- Wu, C.H.; James Wang, T.; James Lee, L. Trans-plane fluid permeability measurement and its applications in liquid composite molding. Polym. Compos. 1994, 15, 289–298. [Google Scholar] [CrossRef]
- Spaid, M.A.; Phelan, F.R., Jr. Modeling void formation dynamics in fibrous porous media with the lattice Boltzmann method. Compos. Part A Appl. Sci. Manuf. 1998, 29, 749–755. [Google Scholar] [CrossRef]
- Verrey, J.; Michaud, V.; Månson, J.A. Dynamic capillary effects in liquid composite moulding with non-crimp fabrics. Compos. Part A Appl. Sci. Manuf. 2006, 37, 92–102. [Google Scholar] [CrossRef]
- Sadiq, T.; Advani, S.; Parnas, R. Experimental investigation of transverse flow through aligned cylinders. Int. J. Multiph. Flow 1995, 21, 755–774. [Google Scholar] [CrossRef]
- Belov, E.B.; Lomov, S.V.; Verpoest, I.; Peters, T.; Roose, D.; Parnas, R.; Hoes, K.; Sol, H. Modelling of permeability of textile reinforcements: Lattice Boltzmann method. Compos. Sci. Technol. 2004, 64, 1069–1080. [Google Scholar] [CrossRef]
- Tahir, M.W.; Hallström, S.; Åkermo, M. Effect of dual scale porosity on the overall permeability of fibrous structures. Compos. Sci. Technol. 2014, 103, 56–62. [Google Scholar] [CrossRef]
- Senoguz, M.; Dungan, F.; Sastry, A.; Klamo, J. Simulations and experiments on low-pressure permeation of fabrics: Part II—The variable gap model and prediction of permeability. J. Compos. Mater. 2001, 35, 1285–1322. [Google Scholar]
- Weitzenböck, J.; Shenoi, R.; Wilson, P. Radial flow permeability measurement. Part A: Theory. Compos. Part A Appl. Sci. Manuf. 1999, 30, 781–796. [Google Scholar] [CrossRef]
- Chan, A.W.; Hwang, S.T. Anisotropic in-plane permeability of fabric media. Polym. Eng. Sci. 1991, 31, 1233–1239. [Google Scholar] [CrossRef]
- Weitzenbock, J.R. Flow Characterization in Resin Transfer Moulding. Ph.D. Thesis, University of Southampton, Southampton, UK, November 1996. [Google Scholar]
- Parnas, R.S.; Salem, A.J.; Sadiq, T.A.; Wang, H.P.; Advani, S.G. The interaction between micro-and macro-scopic flow in RTM preforms. Compos. Struct. 1994, 27, 93–107. [Google Scholar] [CrossRef]
- Chan, A.W.; Larive, D.E.; Morgan, R.J. Anisotropic permeability of fiber preforms: Constant flow rate measurement. J. Compos. Mater. 1993, 27, 996–1008. [Google Scholar] [CrossRef]
- Lei, G.; Dong, P.; Mo, S.; Yang, S.; Wu, Z.; Gai, S. Calculation of full permeability tensor for fractured anisotropic media. J. Pet. Explor. Prod. Technol. 2015, 5, 167–176. [Google Scholar] [CrossRef]
- Ranganathan, S.; Phelan, F.R., Jr.; Advani, S.G. A generalized model for the transverse fluid permeability in unidirectional fibrous media. Polym. Compos. 1996, 17, 222–230. [Google Scholar] [CrossRef]
- Nedanov, P.B.; Advani, S.G. Numerical computation of the fiber preform permeability tensor by the homogenization method. Polym. Compos. 2002, 23, 758–770. [Google Scholar] [CrossRef]
- Syerko, E.; Binetruy, C.; Comas-Cardona, S.; Leygue, A. A numerical approach to design dual-scale porosity composite reinforcements with enhanced permeability. Mater. Des. 2017, 131, 307–322. [Google Scholar] [CrossRef]
- Gebart, B.R. Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 1992, 26, 1100–1133. [Google Scholar] [CrossRef]
- Skartsis, L.; Khomami, B.; Kardos, J. A semi-analytical one-dimensional model for viscoelastic impregnation of fibrous media. Adv. Mater. 1994, 25, 38–44. [Google Scholar]
- Westhuizen, J.; Plessis, J.P.D. Quantification of unidirectional fiber bed permeability. J. Compos. Mater. 1994, 28, 619–637. [Google Scholar] [CrossRef]
- Neuman, S.P. Theoretical derivation of Darcy’s law. Acta Mech. 1977, 25, 153–170. [Google Scholar] [CrossRef]
- Luminari, N. Modeling and Simulation of Flows over and through Fibrous Porous Media. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, March 2018. [Google Scholar]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Med. 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Zijl, W.; Stam, J. Modeling permeability in imperfectly layered porous media. I. Derivation of block-scale permeability tensor for thin grid-blocks. Math. Geol. 1992, 24, 865–883. [Google Scholar] [CrossRef]
- Hoes, K.; Dinescu, D.; Sol, H.; Vanheule, M.; Parnas, R.S.; Luo, Y.; Verpoest, I. New set-up for measurement of permeability properties of fibrous reinforcements for RTM. Compos. Part A Appl. Sci. Manuf. 2002, 33, 959–969. [Google Scholar] [CrossRef]
- Luo, Y.; Verpoest, I.; Hoes, K.; Vanheule, M.; Sol, H.; Cardon, A. Permeability measurement of textile reinforcements with several test fluids. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1497–1504. [Google Scholar] [CrossRef]
- Long, A.; Brown, L. Modelling the geometry of textile reinforcements for composites: TexGen. In Composite Reinforcements for Optimum Performance; Elsevier: Amsterdam, The Netherlands, 2011; pp. 239–264. [Google Scholar]
- Hwang, W.R.; Advani, S.G. Numerical simulations of Stokes–Brinkman equations for permeability prediction of dual scale fibrous porous media. Phys. Fluids 2010, 22, 113101. [Google Scholar] [CrossRef]
- Šimáček, P.; Advani, S.G. Permeability model for a woven fabric. Polym. Compos. 1996, 17, 887–899. [Google Scholar] [CrossRef]
- Chen, B.; Chou, T.W. Compaction of woven-fabric preforms: Nesting and multi-layer deformation. Compos. Sci. Technol. 2000, 60, 2223–2231. [Google Scholar] [CrossRef]
- Dungan, F.; Senoguz, M.; Sastry, A.; Faillaci, D. Simulations and experiments on low-pressure permeation of fabrics: Part I—3D modeling of unbalanced fabric. J. Compos. Mater. 2001, 35, 1250–1284. [Google Scholar]
- Saunders, R.; Lekakou, C.; Bader, M. Compression and microstructure of fibre plain woven cloths in the processing of polymer composites. Compos. Part A Appl. Sci. Manuf. 1998, 29, 443–454. [Google Scholar] [CrossRef]
- Lomov, S.V.; Verpoest, I.; Peeters, T.; Roose, D.; Zako, M. Nesting in textile laminates: Geometrical modelling of the laminate. Compos. Sci. Technol. 2003, 63, 993–1007. [Google Scholar] [CrossRef]
- Grujicic, M.; Chittajallu, K.; Walsh, S. Effect of shear, compaction and nesting on permeability of the orthogonal plain-weave fabric preforms. Mater. Chem. Phys. 2004, 86, 358–369. [Google Scholar] [CrossRef]



| Reference | [%] | [%] | Packing Arrangement | Dual-Scale Approach | |
|---|---|---|---|---|---|
| Sadiq et al. [22] | 1.0406 | 25 | 61.6 | Array of solid and porous | 1D Darcy’s equation |
| 1.198 | 31 | 70.9 | circular fibre bundles | ||
| Ranganathan et al. [32] | 1 | 30 | 45 | Hexagonal arraignments | Stoke flow equations |
| for open region and | |||||
| if | in elliptic tows | Brinkman equation for | |||
| porous region | |||||
| Nedanov and Advani [33] | 1.003 | 29 | 39 | Hexagonal packing of | CFD package FIDAP, |
| numerically solves | |||||
| fibres in woven fabric | stokes flow and | ||||
| Brinkman equation | |||||
| Belov et al. [23] | 1.25 | 42 | 66 | A plain-woven fabric | Lattice Boltzmann |
| method, WiseTex | |||||
| software | |||||
| Tahir et al. [24] | 1.03 | 25 | 62 | Hexagonal arrangements of | ANSYS-Fluent, Navier- |
| fibres in circular tows | stokes equations for | ||||
| within unit cell | dual scale | ||||
| Syerko et al. [34] | 4.6 | 36 | 62 | Quadradic Packing | Applied Brinkman |
| equations and mass | |||||
| conservation |
| Parameters | Value | Units |
|---|---|---|
| Width warp yarns | mm | |
| Gap warp yarns | mm | |
| Width fill yarns | mm | |
| Gap fill yarns | mm | |
| Areal density | 420 | g/m |
| Specific density | 2520 | kg/m |
| Yarn tex warp | 580 | g/km |
| Yarn tex weft | 600 | g/km |
| [%] | [m] | [m] | [m] | |
|---|---|---|---|---|
| Current Study | Belov et al. [23] | |||
| 44 | 1 | |||
| 66 | 1 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, H.; Jabbari, M.; Soutis, C. A Numerical Analysis of Resin Flow in Woven Fabrics: Effect of Local Tow Curvature on Dual-Scale Permeability. Materials 2021, 14, 405. https://doi.org/10.3390/ma14020405
Alotaibi H, Jabbari M, Soutis C. A Numerical Analysis of Resin Flow in Woven Fabrics: Effect of Local Tow Curvature on Dual-Scale Permeability. Materials. 2021; 14(2):405. https://doi.org/10.3390/ma14020405
Chicago/Turabian StyleAlotaibi, Hatim, Masoud Jabbari, and Constantinos Soutis. 2021. "A Numerical Analysis of Resin Flow in Woven Fabrics: Effect of Local Tow Curvature on Dual-Scale Permeability" Materials 14, no. 2: 405. https://doi.org/10.3390/ma14020405
APA StyleAlotaibi, H., Jabbari, M., & Soutis, C. (2021). A Numerical Analysis of Resin Flow in Woven Fabrics: Effect of Local Tow Curvature on Dual-Scale Permeability. Materials, 14(2), 405. https://doi.org/10.3390/ma14020405







