Prediction of Flow Stress of Annealed 7075 Al Alloy in Hot Deformation Using Strain-Compensated Arrhenius and Neural Network Models
Abstract
:1. Introduction
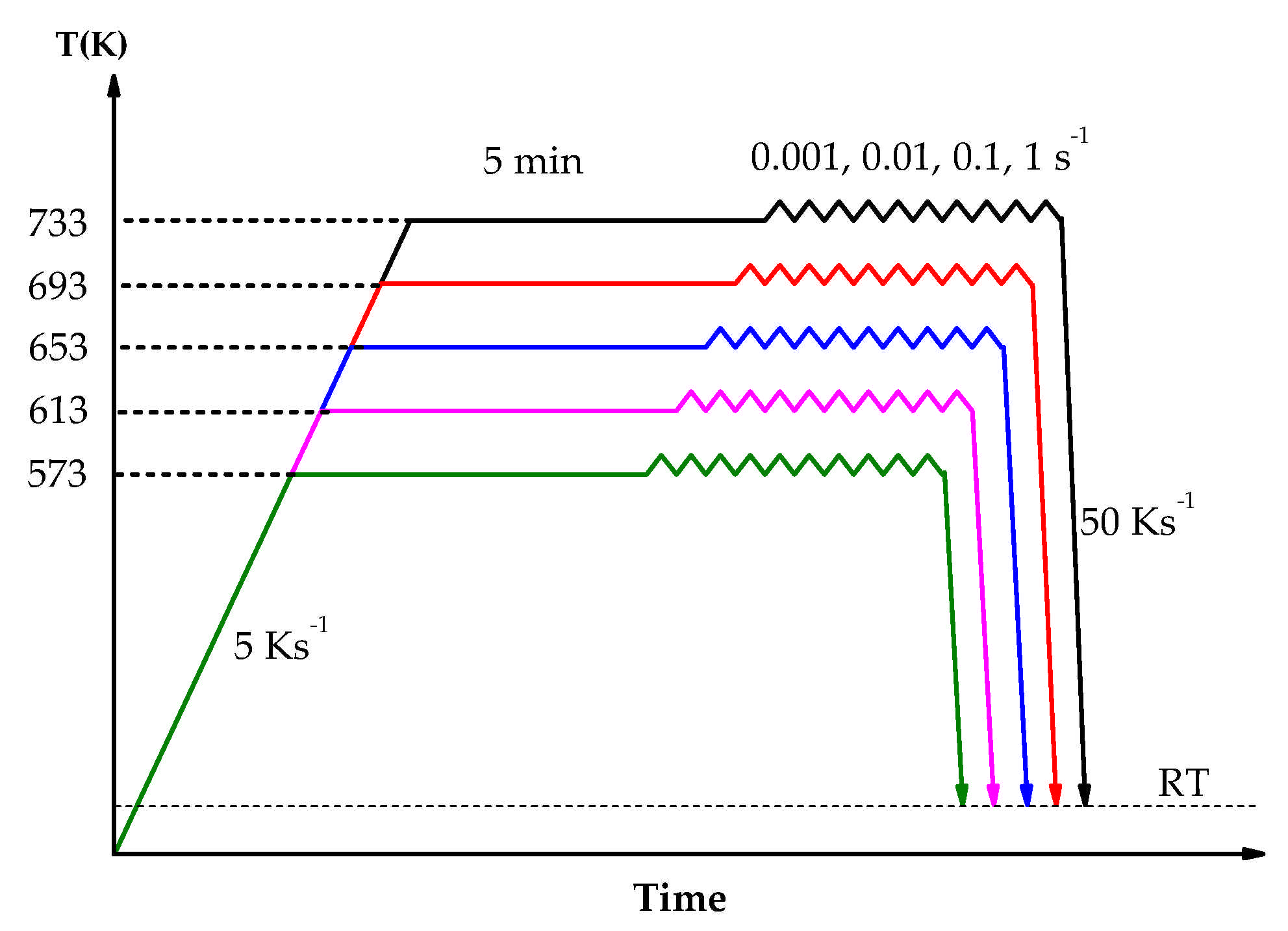
2. Materials and Experiments
3. Results and Discussion
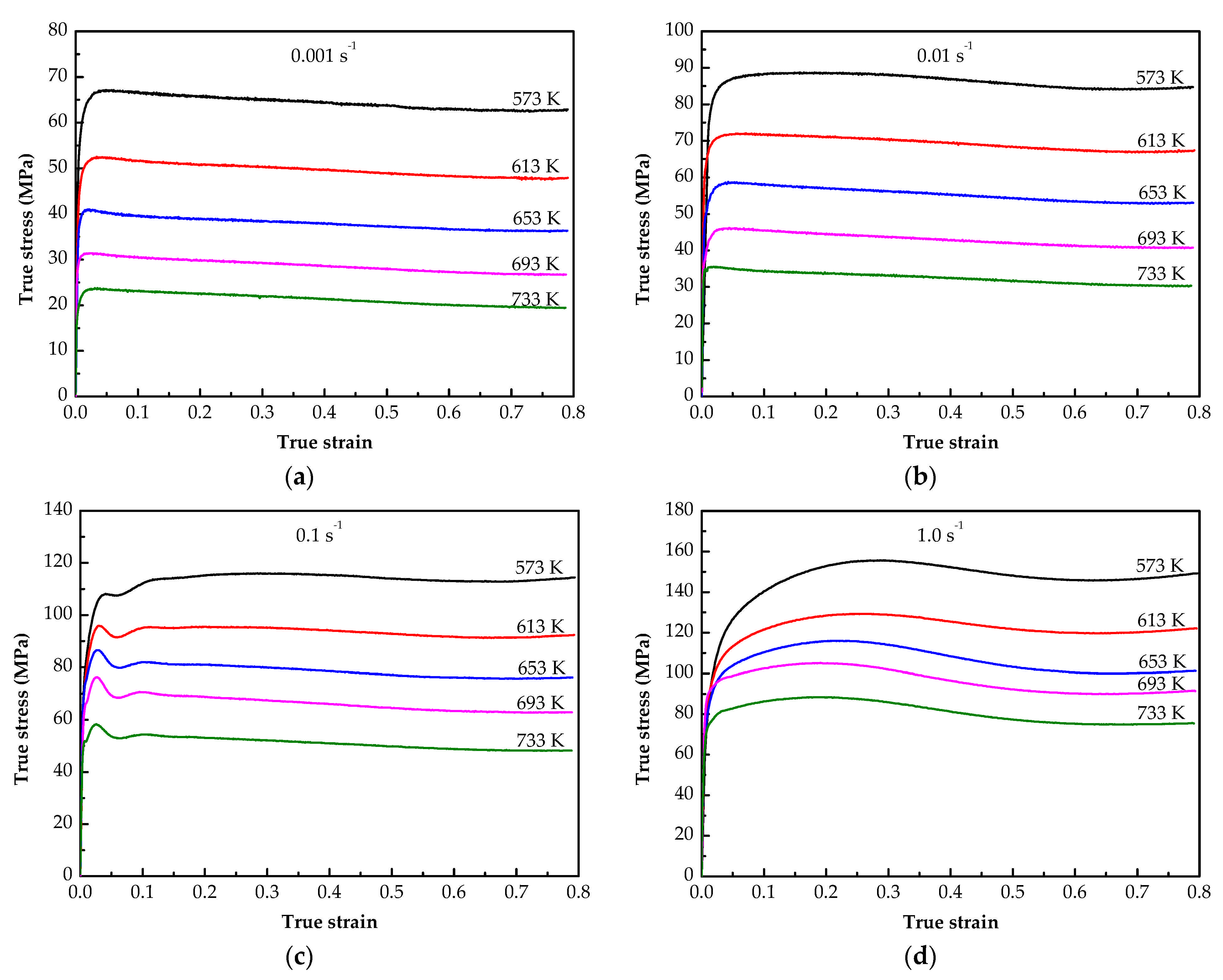
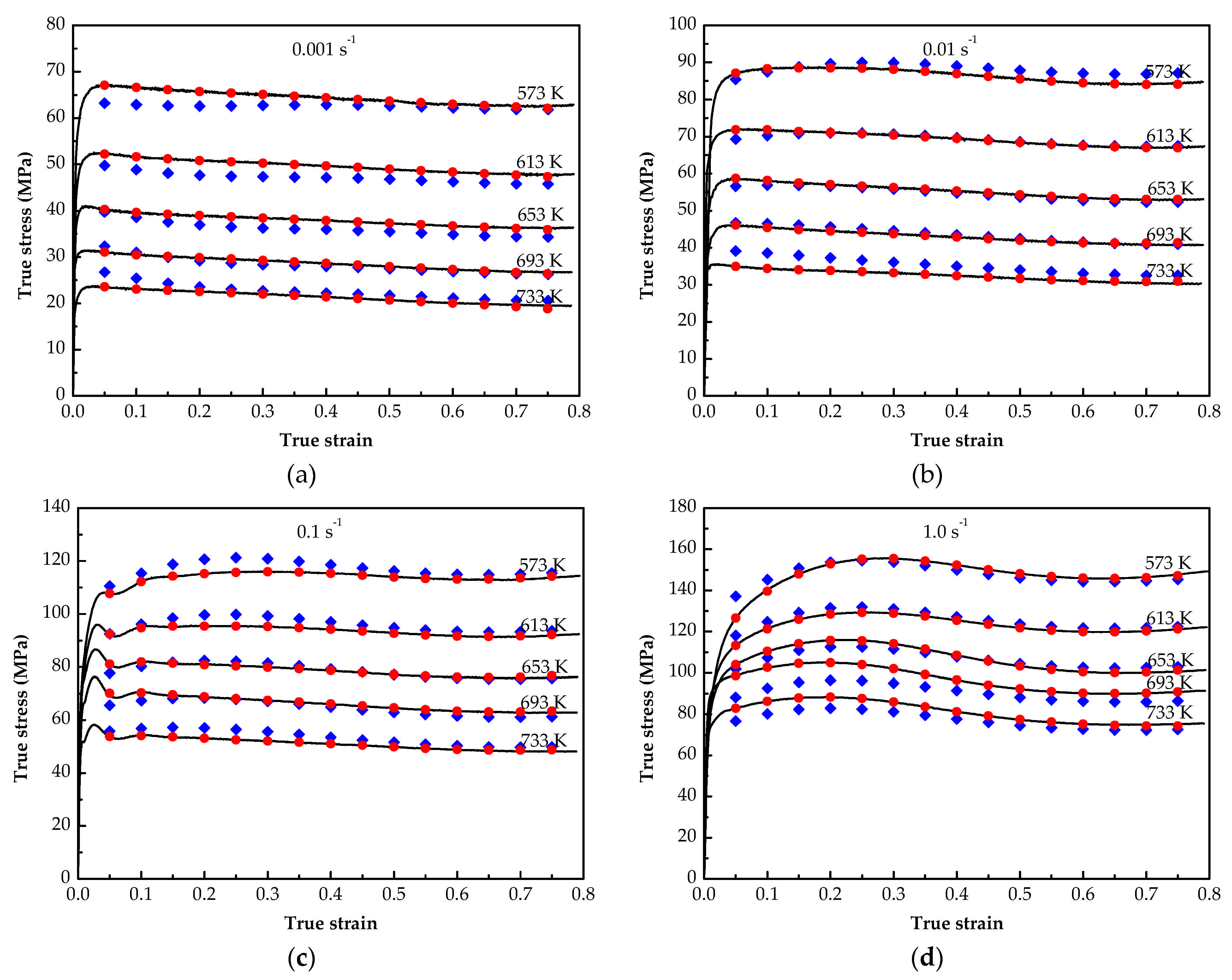
3.1. Flow Stress Characteristics
3.2. Construction of SCAM Model
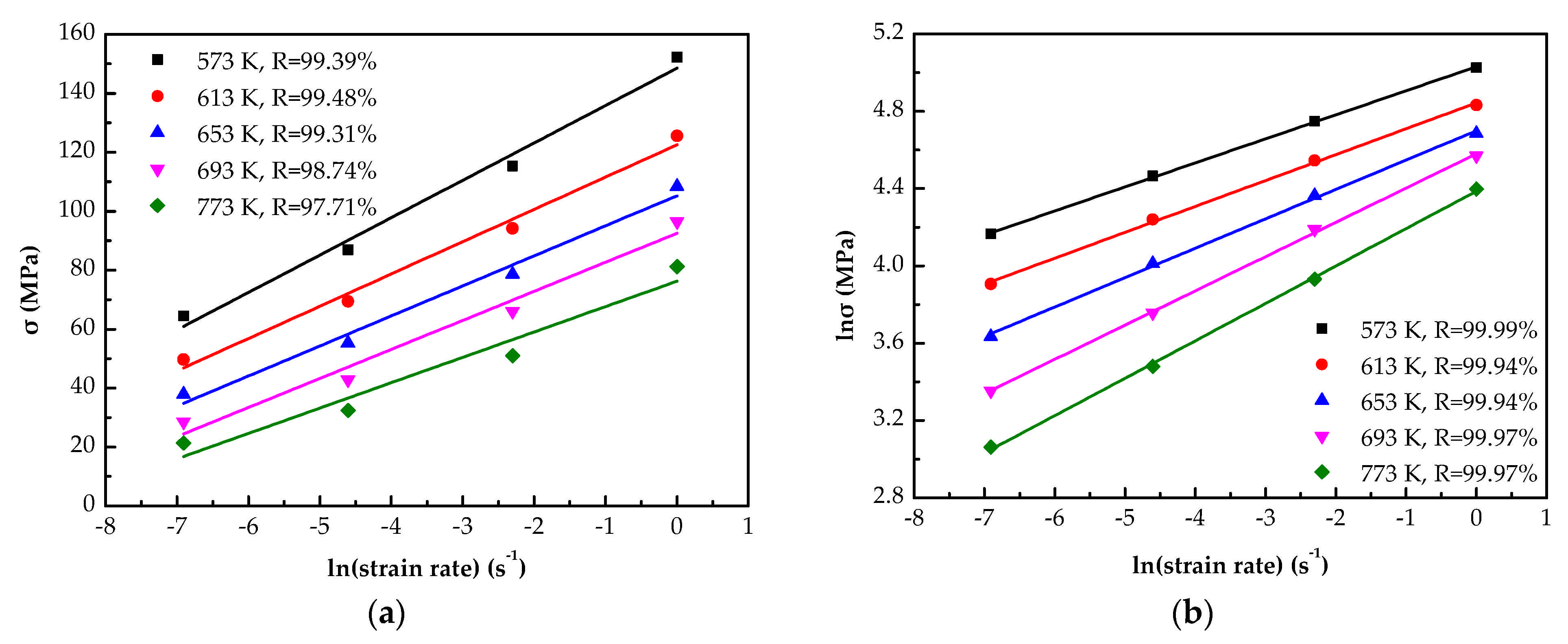
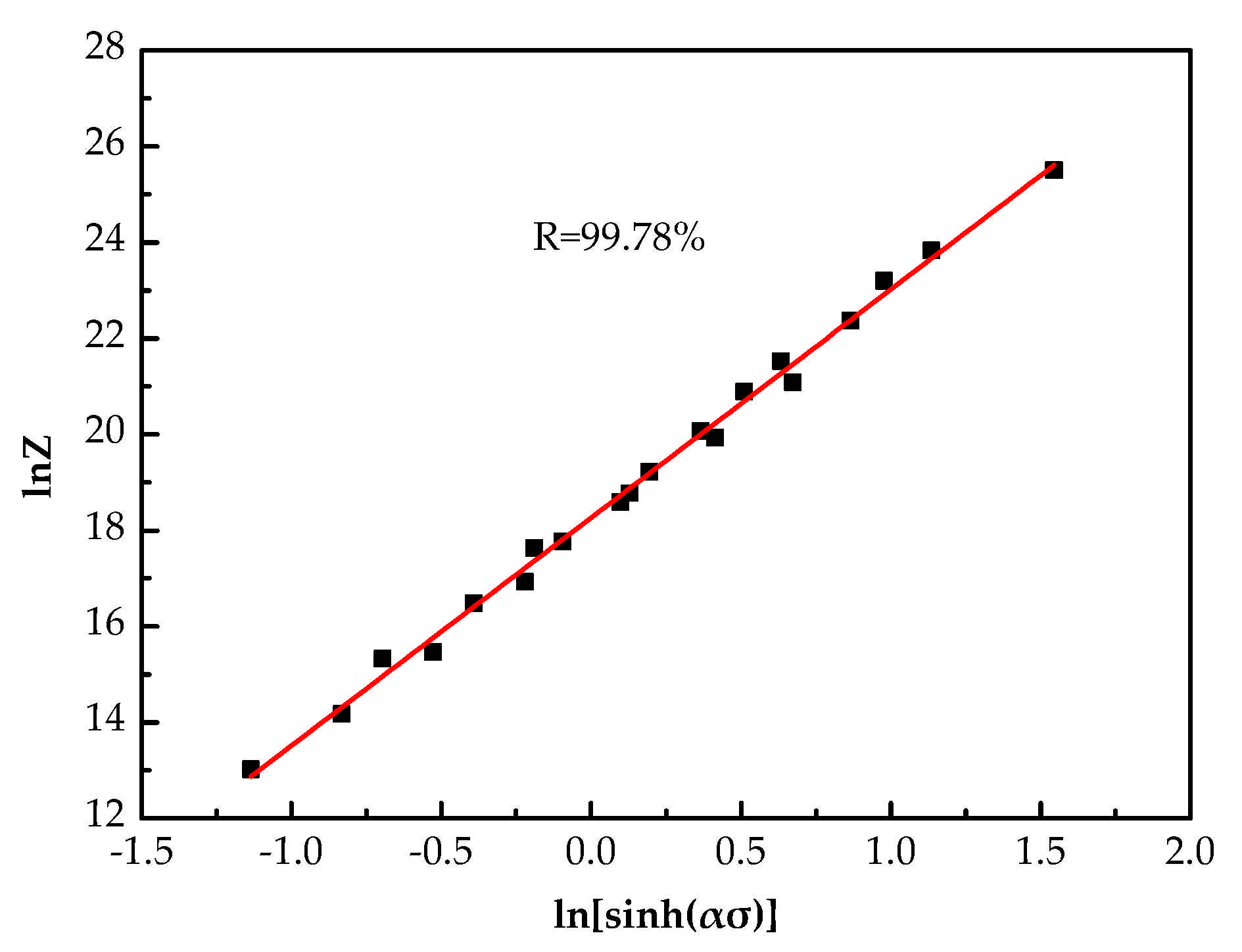
3.2.1. Determination of Material Constants
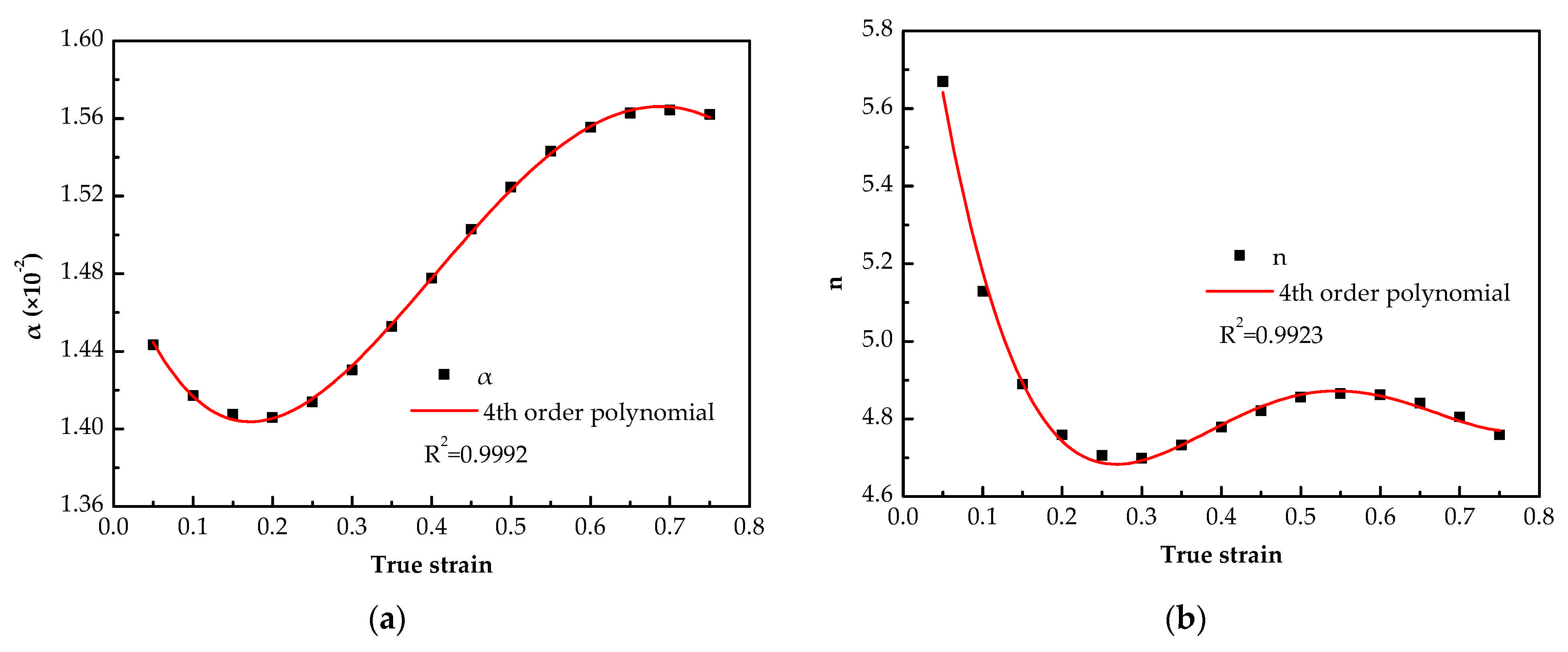
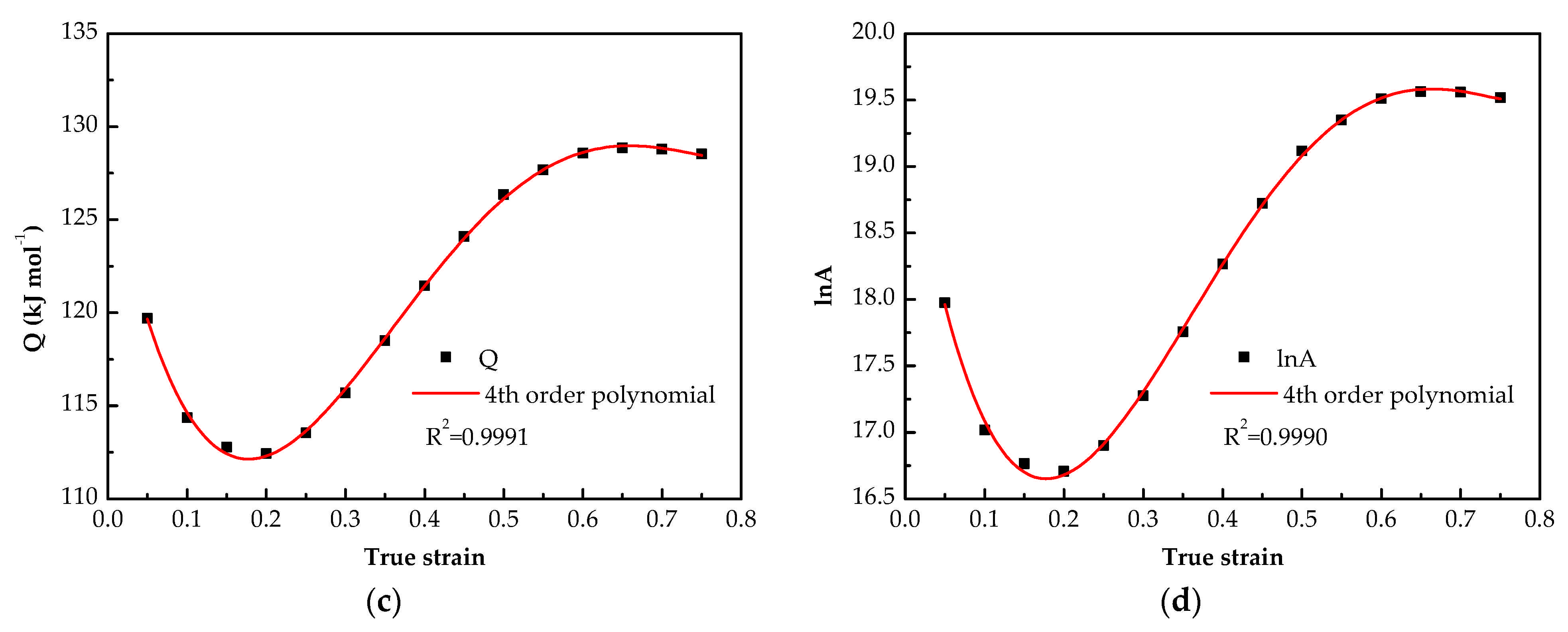
3.2.2. The Compensation of Strain for Material Constants
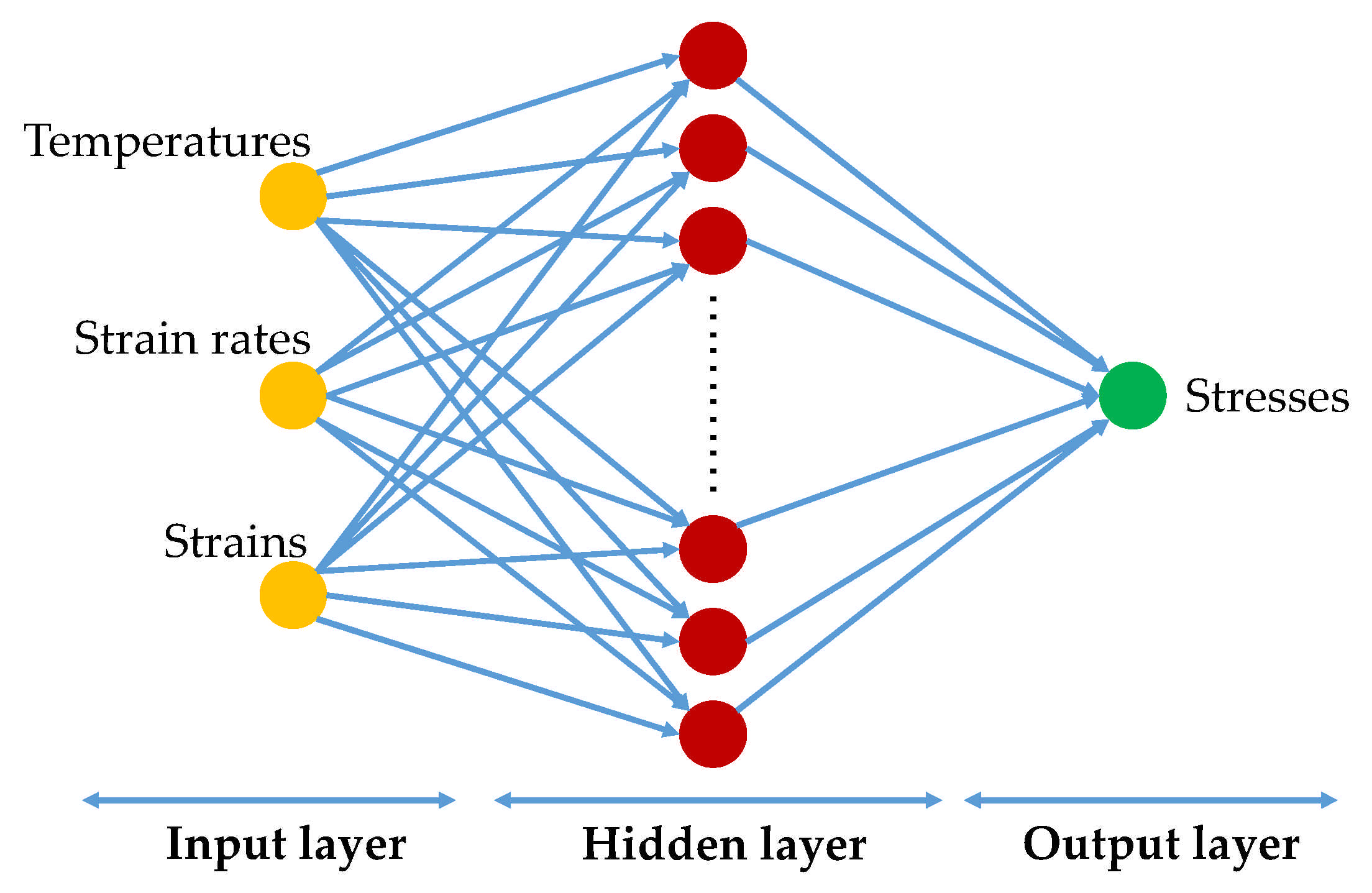
3.3. Construction of BP-ANN Model
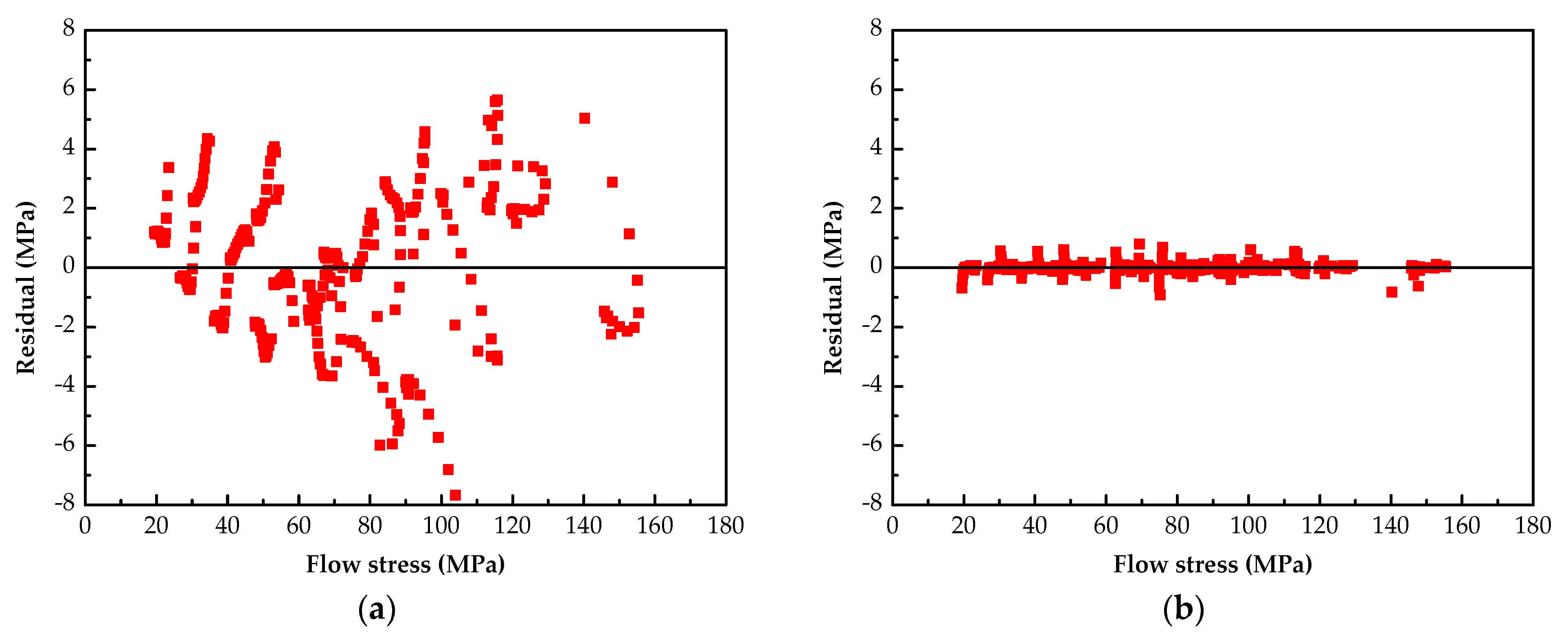
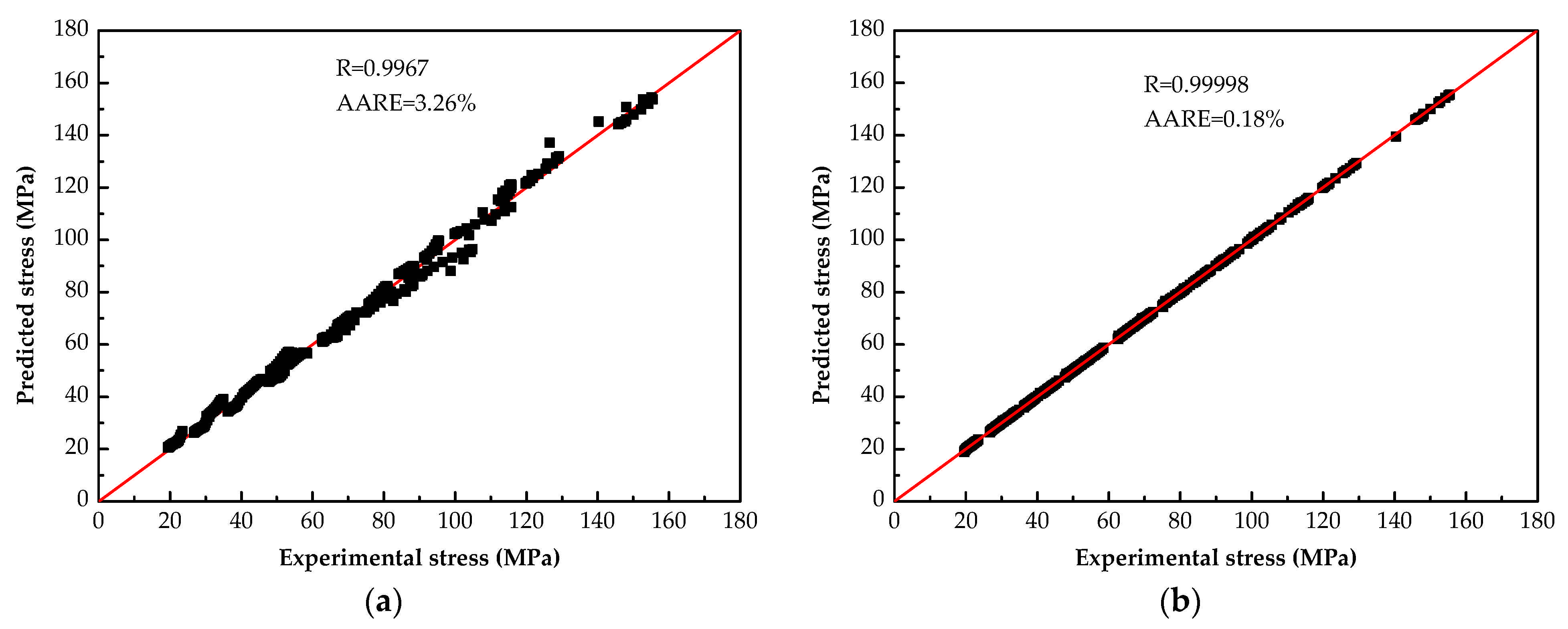
3.4. Evaluation of Prediction Effect of Two Constitutive Models
4. Conclusions
- The flow stress of the annealed 7075 Al alloy decreases as temperature increases and strain rate decreases.
- The material constant (i.e., α, n, Q and lnA) in the SCAM model has a fourth-order polynomial relationship with the strain, and the activation energy varies in the range of 112.4312 and 128.8533 kJ mol−1.
- The flow stress predicted by the BP-ANN model is more consistent with the experimental values than that predicted by the SCAM model. The residual for the BP-ANN model was controlled within 1 MPa, while it is about ±8 MPa for the SCAM model.
- The R and AARE were obtained from the SCAM model are 0.9967 and 3.26%, respectively, while the R and AARE were superior in the BP-ANN model at 0.99998 and 0.18%, respectively, which reveals that the predicted accuracy of BP-ANN model is higher than that SCAM model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.S.; Chen, Y.J.; Hu, J.L. Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 2018, 97, 22–34. [Google Scholar] [CrossRef]
- Shin, J.; Kim, T.; Kim, D.E.; Kim, D.; Kim, K. Castability and mechanical properties of new 7xxx aluminum alloys for automotive chassis/body applications. J. Alloys Compd. 2016, 698, 577–590. [Google Scholar] [CrossRef]
- Ibrahim, M.F.; Samuel, A.M.; Samuel, F.H. A preliminary study on optimizing the heat treatment of high strength Al-Cu-Mg-Zn alloys. Mater. Des. 2014, 57, 342–350. [Google Scholar] [CrossRef]
- Wang, H.R.; Wang, C.G.; Li, M.Y.; Ma, R.; Zhao, J. Constitutive equations for describing the hot compressed behavior of TC4-DT titanium alloy. Materials 2020, 13, 3424. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.C.; Zhang, S.Y.; Liu, X.L.; Feng, F. A flow stress model of 300M steel for isothermal tension. Materials 2021, 14, 252. [Google Scholar] [CrossRef]
- Guo, Y.H.; Xuanyuan, Y.D.; Ly, X.N.; Yang, S. Hot Deformation behaviors of the Mg-3Sn-2Al-1Zn alloy: Investigation on its constitutive equation, processing map, and microstructure. Materials 2020, 13, 312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, L.; Liu, Z.Y.; Bai, S.; Zhao, J.G.; Zeng, D.P.; Wang, J.; Cao, J.; Hu, Y.C. Hot deformation behavior considering strain effects and recrystallization mechanism of an Al-Zn-Mg-Cu Alloy. Materials 2020, 13, 1743. [Google Scholar] [CrossRef]
- Lin, Y.C.; Li, L.T.; Fu, Y.X.; Jiang, Y.Q. Hot compressive deformation behavior of 7075 Al alloy under elevated temperature. J. Mater. Sci. 2012, 47, 1306–1318. [Google Scholar] [CrossRef]
- Wu, B.; Li, M.Q.; Ma, D.W. The flow behavior and constitutive equations in isothermal compression of 7050 aluminum alloy. Mater. Sci. Eng. A 2012, 542, 79–87. [Google Scholar] [CrossRef]
- Xu, L.; Dai, G.Z.; Huang, X.M.; Zhao, J.W.; Han, J.; Gao, J.W. Foundation and application of Al-Zn-Mg-Cu alloy flow stress constitutive equation in friction screw press die forging. Mater. Des. 2013, 47, 465–472. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, S.H.; Li, L.; Lu, S.H.; Gong, H. Modified constitutive model and workability of 7055 aluminum alloy in hot plastic compression. J. Cent. South Univ. 2019, 26, 2930–2942. [Google Scholar] [CrossRef]
- Rezaei Ashtiani, H.R.; Shahsavari, P. A comparative study on the phenomenological and artificial neural network models to predict hot deformation behavior of AlCuMgPb alloy. J. Alloys Compd. 2016, 4, 300. [Google Scholar]
- Rezaei Ashtiani, H.R.; Shahsavari, P. Strain-dependent constitutive equations to predict high temperature flow behavior of AA2030 aluminum alloy. Mech. Mater. 2016, 100, 209–218. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, G.Q.; Yu, J.Q. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy. Mater. Des. 2015, 74, 25–35. [Google Scholar] [CrossRef]
- Peng, W.W.; Zeng, W.D.; Wang, Q.J.; Yu, H.Q. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models. Mater. Des. 2013, 51, 95–104. [Google Scholar] [CrossRef]
- Rezaei Ashtiani, H.R.; Parsa, M.H.; Bisadi, H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum. Mater. Sci. Eng. A 2012, 545, 61–67. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Abedi, H.R. The flow behavior modeling of cast A356 aluminum alloy at elevated temperatures considering the effect of strain. Mater. Sci. Eng. A 2012, 535, 252–257. [Google Scholar] [CrossRef]
- Li, J.; Li, F.G.; Cai, J.; Wang, R.T.; Yaun, Z.W.; Xue, F.M. Flow behavior modeling of the 7050 aluminum alloy at elevated temperatures considering the compensation of strain. Mater. Des. 2012, 42, 369–377. [Google Scholar] [CrossRef]
- Gan, C.L.; Zheng, K.H.; Qi, W.J.; Wang, M.J. Constitutive equations for high temperature flow stress prediction of 6063 Al alloy considering compensation of strain. Trans. Nonferrous Met. Soc. China 2014, 24, 3486–3491. [Google Scholar] [CrossRef]
- Dai, Q.S.; Deng, Y.L.; Tang, J.G.; Wang, Y. Deformation characteristics and strain-compensated constitutive equation for AA5083 aluminum alloy under hot compression. Trans. Nonferrous Met. Soc. China 2019, 29, 2252–2261. [Google Scholar] [CrossRef]
- Ji, G.L.; Li, F.G.; Li, Q.H.; Li, H.Q.; Li, Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A 2011, 528, 4774–4782. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Cao, Y.; Liu, C.J.; Luo, R.; Li, N.; Shu, G.; Huang, G.J.; Liu, Q. Dynamic behavior and modified artificial neural network model for predicting flow stress during hot deformation of Alloy 925. Mater. Today Commun. 2020, 101329. [Google Scholar] [CrossRef]
- Zhao, J.W.; Ding, H.; Zhao, W.J.; Huang, M.L.; Wei, D.B.; Jiang, Z.Y. Modelling of the hot deformation behaviour of a titanium alloy using constitutive equations and artificial neural network. Comp. Mater. Sci. 2014, 92, 47–56. [Google Scholar] [CrossRef]
- Sabokpa, O.; Zarei-Hanzaki, A.; Abedi, H.R.; Haghdadi, N. Artificial neural network modeling to predict the high temperature flow behavior of an AZ81 magnesium alloy. Mater. Des. 2012, 39, 390–396. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.D.; Han, Y.F.; Ma, X.; Zhao, Y.Q.; Guo, P.; Wang, G.; Dargusch, M.S. Determination of the influence of processing parameters on the mechanical properties of the Ti-6Al-4V alloy using an artificial neural network. Comp. Mater. Sci. 2012, 60, 239–244. [Google Scholar] [CrossRef]
- Shokry, A.; Gowid, S.; Kharmanda, G.; Mahdi, E. Constitutive models for the prediction of the hot deformation behavior of the 10%Cr steel alloy. Materials 2019, 12, 2873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, K.; Pan, Q.L.; Li, R.S.; Liu, S.H.; Huang, Z.Q.; He, X. Constitutive modeling of the hot deformation behavior in 6082 aluminum alloy. J. Mater. Eng. Perform. 2019, 28, 981–994. [Google Scholar] [CrossRef]
- Luo, R.; Cao, Y.; Qiu, Y.; Cui, S.G.; Zhou, H.T.; Zhou, Y.M.; Yuan, F.; Zhangxiao, P.P.; Cheng, X.N. Investigation of constitutive model of as-extruded spray-forming 7055 aluminum alloy based on BP artificial neural network. J. Aeronaut. Mater. 2021, 41, 35–44. [Google Scholar]
- Zhang, B.; Zhao, F.F.; Chen, H.F.; Yang, Y.; Ma, Y.H.; Qi, K. Hot compression deformation of cobalt-based superalloy GH5605. Chin. J. Nonferrous Met. 2021, 31, 879–889. [Google Scholar]
- Yang, Q.Y.; Deng, Z.H.; Zhang, Z.Q.; Liu, Q.; Jia, Z.H.; Huang, G.J. Effects of strain rate on flow stress behavior and dynamic recrystallization mechanism of Al-Zn-Mg-Cu aluminum alloy during hot deformation. Mater. Sci. Eng. A 2016, 662, 204–213. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Gupta, R.K.; Kumar, V.A.; Sarath Krishnan, A.; Niteshraj, J. Hot Deformation Behavior of Aluminum Alloys AA7010 and AA7075. J. Mater. Eng. Perform. 2019, 28, 5021–5036. [Google Scholar] [CrossRef]
- Hu, H.E.; Zhen, L.; Yang, L.; Shao, W.Z.; Zhang, B.Y. Deformation behavior and microstructure evolution of 7050 aluminum alloy during high temperature deformation. Mater. Sci. Eng. A 2008, 488, 64–71. [Google Scholar] [CrossRef]
- Jin, N.P.; Zhang, H.; Han, Y.; Wu, W.X.; Chen, J.H. Hot deformation behavior of 7150 aluminum alloy during compression at elevated temperature. Mater. Charact. 2009, 60, 530–536. [Google Scholar] [CrossRef]
- He, J.L.; Zhang, D.T.; Zhang, W.W.; Qiu, C.; Zhang, W. Constitutive equation and hot compression deformation behavior of homogenized Al–7.5Zn–1.5Mg–0.2Cu–0.2Zr alloy. Materials 2017, 10, 1193. [Google Scholar] [CrossRef]
- Cerri, E.; Evangelista, E.; Forcellese, A.; McQueen, H.J. Comparative hot workability of 7012 and 7075 alloys after different pretreatments. Mater. Sci. Eng. A 1995, 197, 181–198. [Google Scholar] [CrossRef]
- Huang, C.Q.; Jia, X.D.; Zhang, Z.W. A modified back propagation artificial neural network model based on genetic algorithm to predict the flow behavior of 5754 aluminum alloy. Materials 2018, 11, 855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, Y.; Qiao, G.J.; Sun, J.P.; Zou, D.N. A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models. Comp. Mater. Sci. 2013, 67, 93–103. [Google Scholar] [CrossRef]
- Liu, X.Y.; Yang, C.; Yang, X.R.; Qiang, M.; Zhang, Q.Q. A constitutive model of ultrafine grained pure titanium deformation at elevated temperature based on artificial neural network. Rare Met. Mater. Eng. 2018, 47, 3038–3044. [Google Scholar]


| Fe | Si | Cr | Mn | Ti | Cu | Mg | Zn | Al |
|---|---|---|---|---|---|---|---|---|
| 0.20 | 0.07 | 0.21 | 0.06 | 0.02 | 1.54 | 2.68 | 5.76 | Bal. |
| Parameter | α | n | Q (kJ mol−1) | A |
|---|---|---|---|---|
| Value | 1.48 × 102 | 4.78 | 121.45 | 8.5665 × 107 |
| Parameter | C0 | C1 | C2 | C3 | C4 |
|---|---|---|---|---|---|
| α | 1.49 | −1.15 | 4.56 | −5.02 | 1.54 |
| n | 6.33 | −16.45 | 56.51 | −77.30 | 36.67 |
| lnA | 19.46 | −37.33 | 156.03 | −214.29 | 96.95 |
| Q | 128.30 | −214.57 | 896.39 | −1228.97 | 554.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Bu, H.; Li, M.; Lu, X. Prediction of Flow Stress of Annealed 7075 Al Alloy in Hot Deformation Using Strain-Compensated Arrhenius and Neural Network Models. Materials 2021, 14, 5986. https://doi.org/10.3390/ma14205986
Yang H, Bu H, Li M, Lu X. Prediction of Flow Stress of Annealed 7075 Al Alloy in Hot Deformation Using Strain-Compensated Arrhenius and Neural Network Models. Materials. 2021; 14(20):5986. https://doi.org/10.3390/ma14205986
Chicago/Turabian StyleYang, Hongbin, Hengyong Bu, Mengnie Li, and Xin Lu. 2021. "Prediction of Flow Stress of Annealed 7075 Al Alloy in Hot Deformation Using Strain-Compensated Arrhenius and Neural Network Models" Materials 14, no. 20: 5986. https://doi.org/10.3390/ma14205986
APA StyleYang, H., Bu, H., Li, M., & Lu, X. (2021). Prediction of Flow Stress of Annealed 7075 Al Alloy in Hot Deformation Using Strain-Compensated Arrhenius and Neural Network Models. Materials, 14(20), 5986. https://doi.org/10.3390/ma14205986






