Large Deflection Analysis of Peripherally Fixed Circular Membranes Subjected to Liquid Weight Loading: A Refined Design Theory of Membrane Deflection-Based Rain Gauges
Abstract
:1. Introduction
2. Membrane Equation and Its Solution
3. Results and Discussions
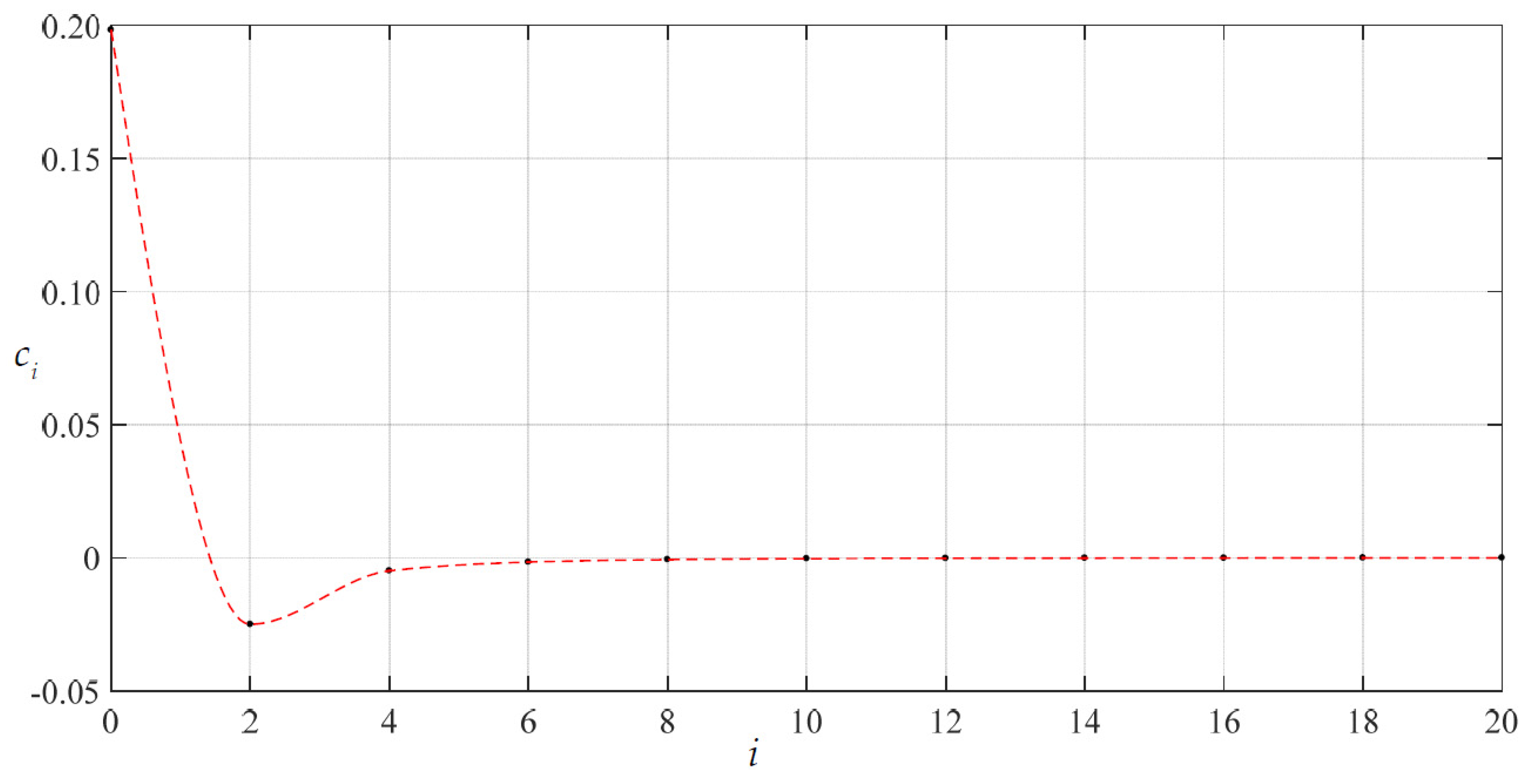
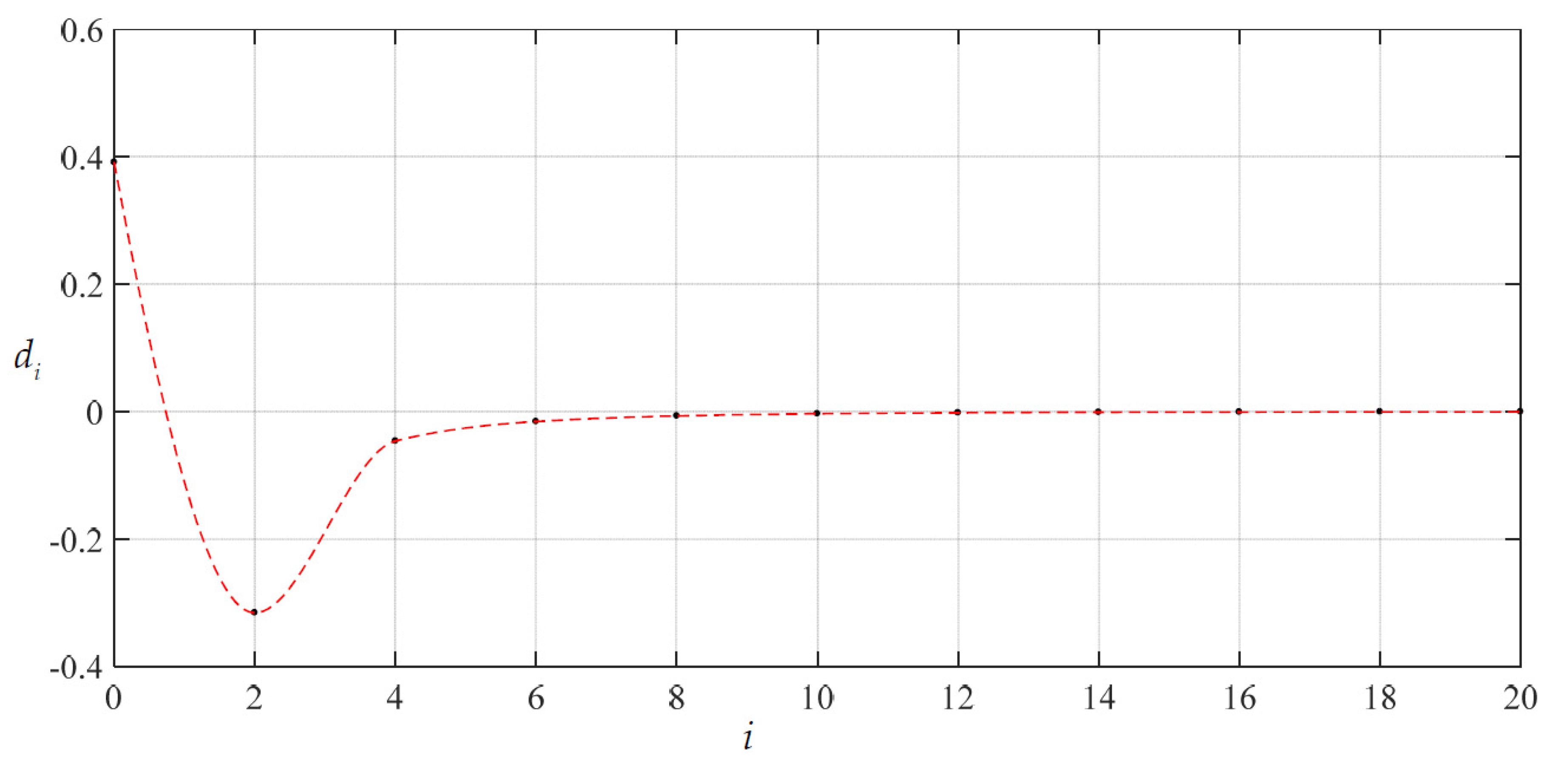
3.1. The Convergence of the Power Series Solutions Obtained
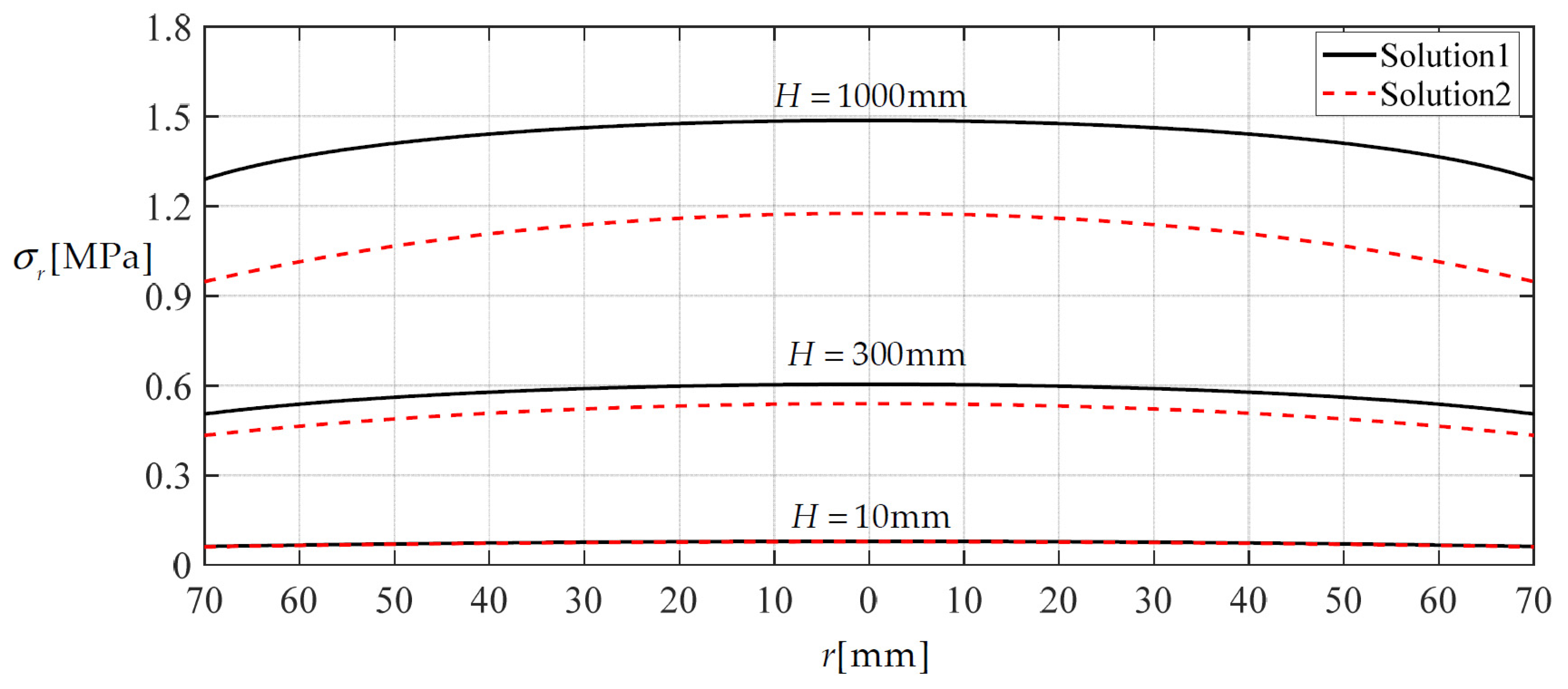
3.2. The Improved Effect of the Integro-Differential Out-of-Plane Equilibrium Equation
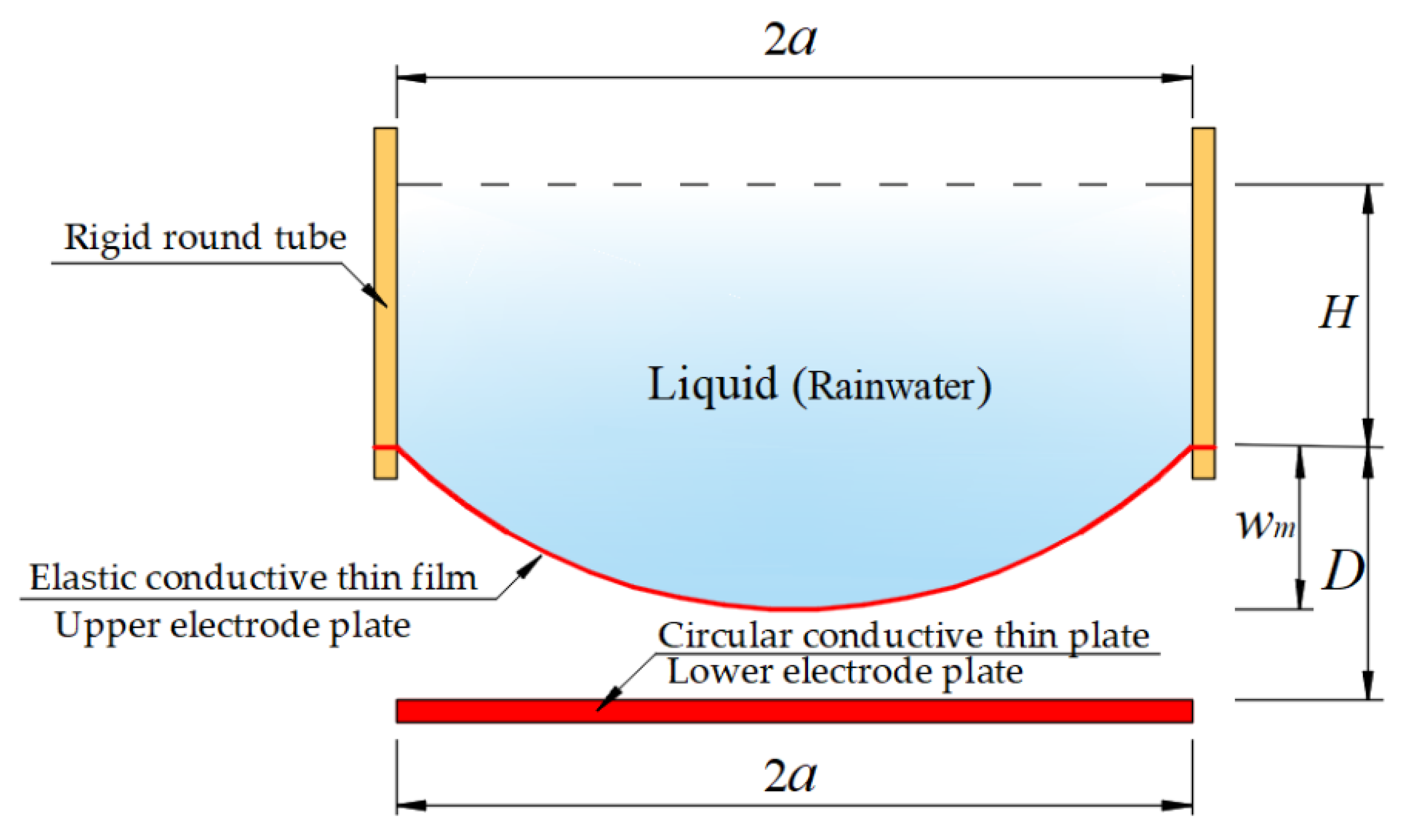
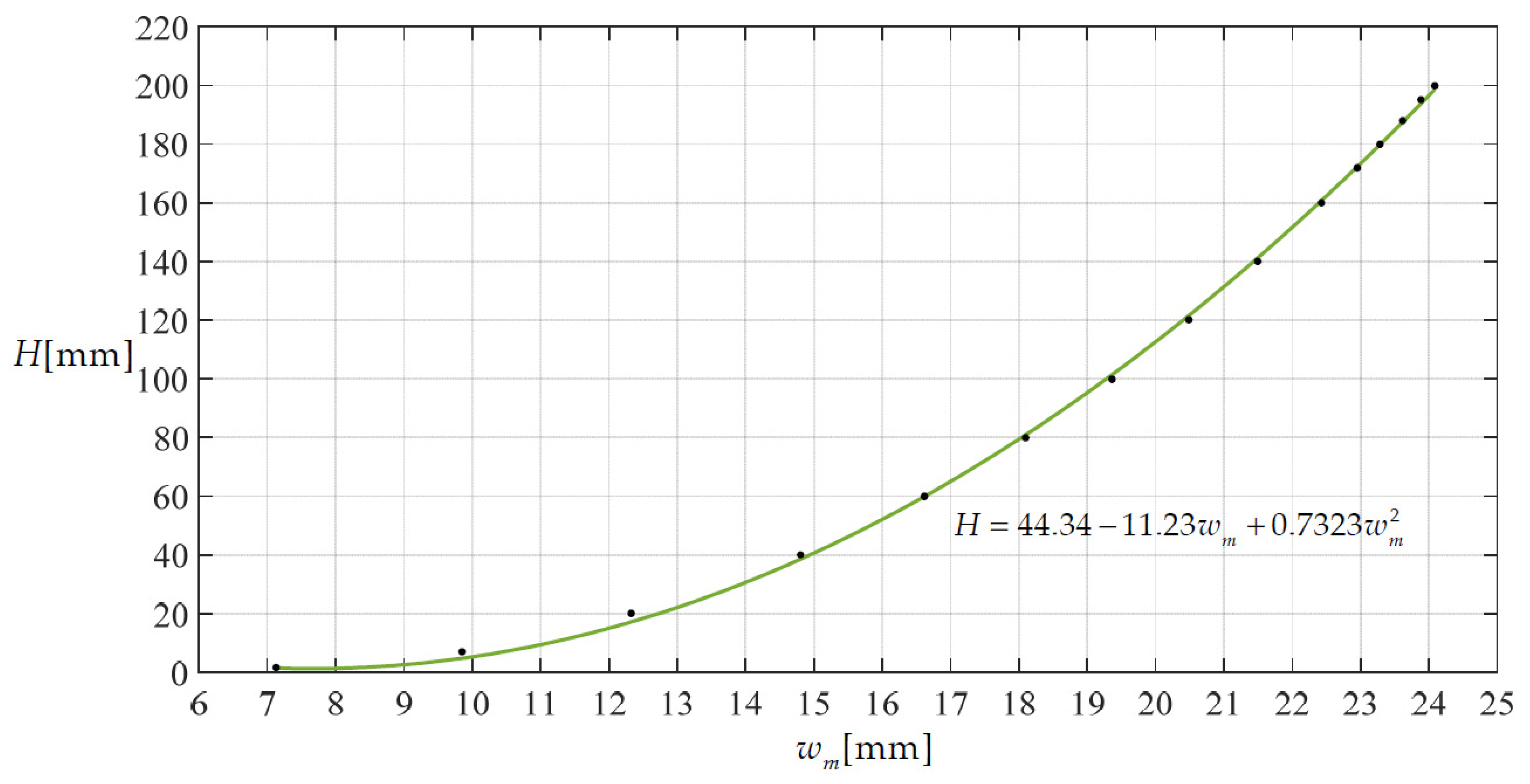
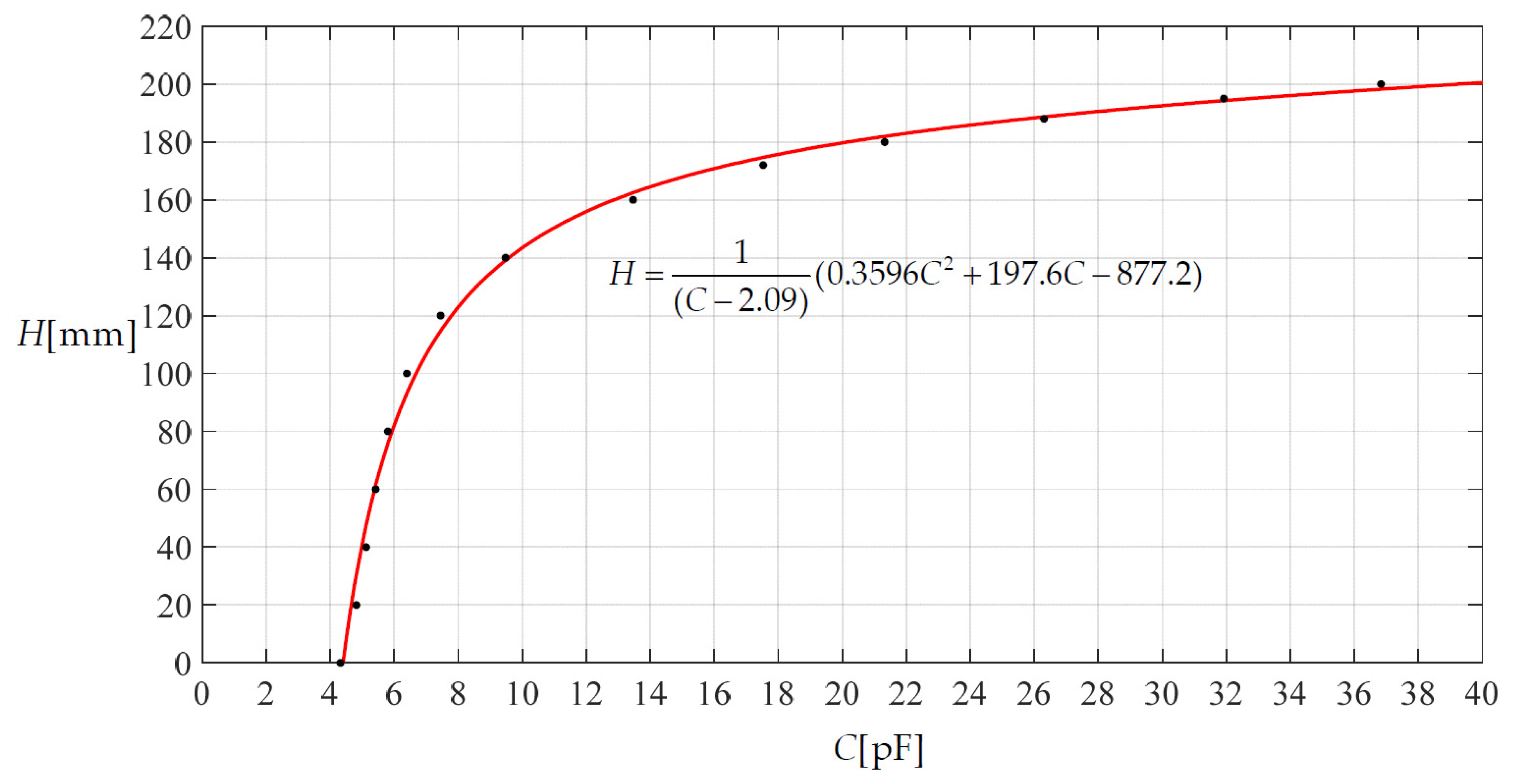
3.3. Two Typical Applications of the Closed-form Solution Given
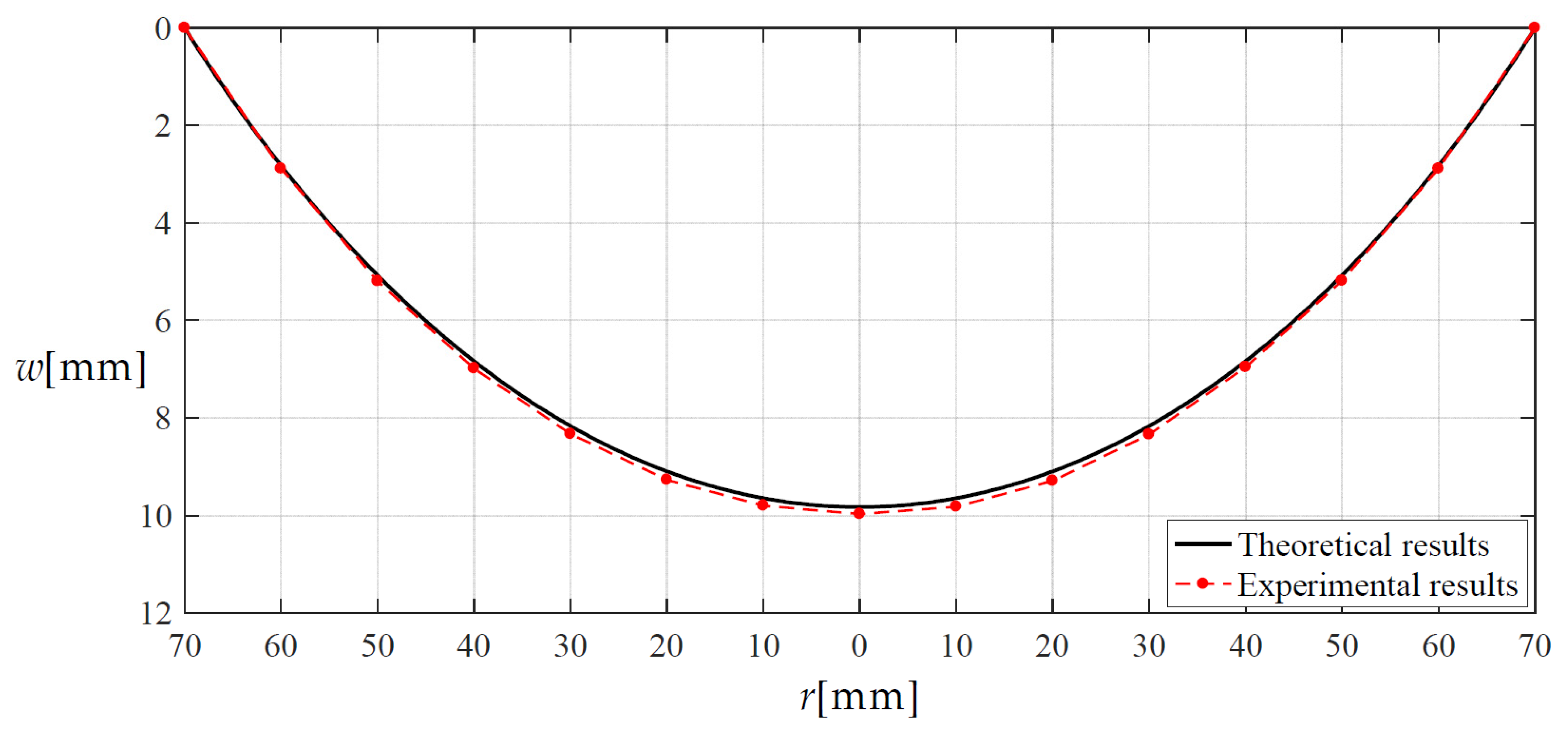
3.4. Confirmatory Experiment
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Radius of the circular membrane |
| h | Thickness of the circular membrane |
| E | Young’s modulus of elasticity |
| ν | Poisson’s ratio |
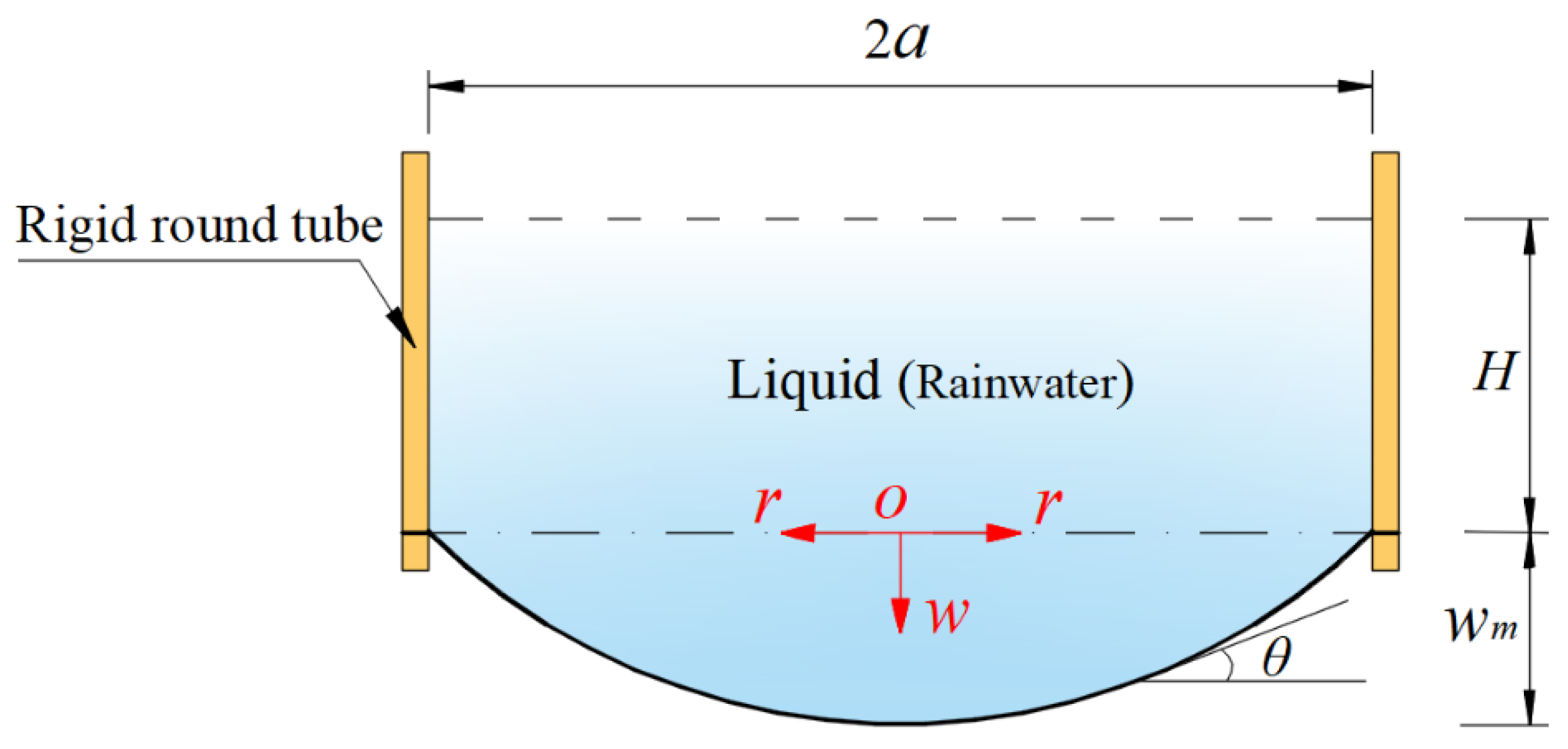
| H | Height of the liquid in the storage container |
| ρ | Density of the liquid in the storage container |
| g | Acceleration of gravity |
| r | Radial coordinate of the cylindrical coordinate system (r, φ, w) |
| φ | Circumferential angle coordinate of (r, φ, w) |
| w | Axial coordinate of (r, φ, w) as well as transverse displacement |
| u | Radial displacement of the deflected circular membrane |
| wm | Maximum deflection of the deflected circular membrane |
| q(r) | Transverse loads that varies continuously with the radial coordinate r |
| F(r) | External force produced by q(r) within radius r |
| σr | Radial stress |
| σt | Circumferential stress |
| er | Radial strain |
| et | Circumferential strain |
| θ | Rotation angle of the deflected circular membrane |
| π | Pi (ratio of circumference to diameter) |
| W | Dimensionless transverse displacement (w/a) |
| Sr | Dimensionless radial stress (σr/E) |
| St | Dimensionless circumferential stress (σt/E) |
| H0 | Dimensionless height H (H/a) |
| G | Dimensionless quantity (ρga2/Eh) |
| x | Dimensionless radial coordinate (r/a) |
| C | Capacitance of a non-parallel plate capacitor |
| D | Initial gap of the non-parallel plate capacitor |
| bi | Coefficients of the power series for capacitance C |
| ci | Coefficients of the power series for Sr |
| di | Coefficients of the power series for W |
Appendix A
Appendix B
Appendix C
References
- Bernardo, P.; Iulianelli, A.; Macedonio, F.; Drioli, E. Membrane technologies for space engineering. J. Membrane Sci. 2021, 626, 119177. [Google Scholar] [CrossRef]
- Suresh, K.; Katara, N. Design and development of circular ceramic membrane for wastewater treatment. Mater. Today Proc. 2021, 43, 2176–2181. [Google Scholar] [CrossRef]
- Tai, Y.; Zhou, K.; Chen, N. Dynamic Properties of Microresonators with the Bionic Structure of Tympanic Membrane. Sensors 2020, 20, 6958. [Google Scholar] [CrossRef]
- Dadgar-Rad, F.; Imani, A. Theory of gradient-elastic membranes and its application in the wrinkling analysis of stretched thin sheets. J. Mech. Phys. Solids 2019, 132, 103679. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.-Y.; Lu, X.-C.; Yang, Z.-X.; He, X.-T. Steady fluid–structure coupling interface of circular membrane under liquid weight loading: Closed-form solution for differential-integral equations. Mathematics 2021, 9, 1105. [Google Scholar] [CrossRef]
- Dai, Z.; Lu, N. Poking and bulging of suspended thin sheets: Slippage, instabilities, and metrology. J. Mech. Phys. Solids 2021, 149, 104320. [Google Scholar] [CrossRef]
- Liu, T.; Wang, X.H.; Qiu, X.M.; Zhang, X.H. Theoretical study on the parameter sensitivity over the mechanical states of inflatable membrane antenna. Aerosp. Sci. Technol. 2020, 102, 105843. [Google Scholar] [CrossRef]
- Williams, J.G. Energy release rates for the peeling of flexible membranes and the analysis of blister tests. Int. J. Fract. 1997, 87, 265–288. [Google Scholar] [CrossRef]
- Wang, J.; Lou, Y.; Wang, B.; Sun, Q.; Zhou, M.; Li, X. Highly sensitive, breathable, and flexible pressure sensor based on electrospun membrane with assistance of AgNW/TPU as composite dielectric layer. Sensors 2020, 20, 2459. [Google Scholar] [CrossRef]
- Lian, Y.-S.; Sun, J.-Y.; Zhao, Z.-H.; Li, S.-Z.; Zheng, Z.-L. A refined theory for characterizing adhesion of elastic coatings on rigid substrates based on pressurized blister test methods: Closed-form solution and energy release rate. Polymers 2020, 12, 1788. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.-Y.; Shi, B.-B.; Zhao, Z.-H.; He, X.-T. A theoretical study on an elastic polymer thin film-based capacitive wind-pressure sensor. Polymers 2020, 12, 2133. [Google Scholar] [CrossRef] [PubMed]
- Jindal, S.K.; Varma, M.A.; Thukral, D. Comprehensive assessment of MEMS double touch mode capacitive pressure sensor on utilization of SiC film as primary sensing element: Mathematical modelling and numerical simulation. Microelectron. J. 2018, 73, 30–36. [Google Scholar] [CrossRef]
- Lee, H.Y.; Choi, B. Theoretical and experimental investigation of the trapped air effect on air-sealed capacitive pressure sensor. Sens. Actuat. A-Phys. 2015, 221, 104–114. [Google Scholar] [CrossRef]
- Liao, M.; Liao, A.; Liu, J.; Cai, Z.; Liu, H.; Ma, T. A novel method and system for the fast calibration of tipping bucket rain gauges. J. Hydrol. 2021, 597, 125782. [Google Scholar] [CrossRef]
- Sypka, P. Dynamic real-time volumetric correction for tipping-bucket rain gauges. Agric. For. Meteorol. 2019, 271, 158–167. [Google Scholar] [CrossRef]
- Yang, Z.-X.; Sun, J.-Y.; Zhao, Z.-H.; Li, S.-Z.; He, X.-T. A closed-form solution of prestressed annular membrane internally-connected with rigid circular plate and transversely-loaded by central shaft. Mathematics 2020, 8, 521. [Google Scholar] [CrossRef] [Green Version]
- Khapin, A.V.; Abdeev, B.M.; Makhiyev, B.E. Optimal size of an axisymmetric perfectly flexible membrane with a rigid centre loaded with a concentrated static force. IOP Conf. Ser. Mater. Sci. Eng. 2020, 775, 012138. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.-X.; He, X.-T.; Wen, S.-R. Closed-form solution and experimental verification for the axisymmetric deformation problem of blistering circular thin polymer films under uniformly distributed gas pressure. Polymers 2020, 12, 1130. [Google Scholar] [CrossRef]
- Huang, P.F.; Song, Y.P.; Li, Q.; Liu, X.Q.; Feng, Y.Q. A theoretical study of circular orthotropic membrane under concentrated load: The relation of load and deflection. IEEE Access 2020, 8, 126127–126137. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Dong, J.; Zheng, Z.L.; Yang, Z.X. Closed-form solution of axisymmetric deformation of prestressed Föppl-Hencky membrane under constrained deflecting. Struct. Eng. Mech. 2019, 69, 693–698. [Google Scholar]
- Chen, S.L.; Zheng, Z.L. Large deformation of circular membrane under the concentrated force. Appl. Math. Mech. 2003, 24, 28–31. [Google Scholar]
- Hencky, H. On the stress state in circular plates with vanishing bending stiffness. Z. Angew. Math. Phys. 1915, 63, 311–317. (In German) [Google Scholar]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its portion. Appl. Math. Mech. 1981, 2, 653–668. [Google Scholar]
- Sun, J.Y.; Rong, Y.; He, X.T.; Gao, X.W.; Zheng, Z.L. Power series solution of circular membrane under uniformly distributed loads: Investigation into Hencky transformation. Stuct. Eng. Mech. 2013, 45, 631–641. [Google Scholar] [CrossRef]
- Sun, J.Y.; Lian, Y.S.; Li, Y.M.; He, X.T.; Zheng, Z.L. Closed-form solution of elastic circular membrane with initial stress under uniformly-distributed loads: Extended Hencky solution. Z. Angew. Math. Mech. 2015, 95, 1335–1341. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.R.; Chen, Y.L.; Long, D.; Guan, Y.C.; Liu, L.Q.; Zhang, Z. Extended Hencky solution for the blister test of nanomembrane. Extreme Mech. Lett. 2018, 22, 69–78. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.-Y.; Zhao, Z.-H.; He, X.-T. Large deflection analysis of axially symmetric deformation of prestressed circular membranes under uniform lateral loads. Symmetry 2020, 12, 1343. [Google Scholar] [CrossRef]
- Mei, D.; Sun, J.-Y.; Zhao, Z.-H.; He, X.-T. A closed-form solution for the boundary value problem of gas pressurized circular membranes in contact with frictionless rigid plates. Mathematics 2020, 8, 1017. [Google Scholar] [CrossRef]
- Shi, B.-B.; Sun, J.-Y.; Huang, T.-K.; He, X.-T. Closed-form solution for circular membranes under in-plane radial stretching or compressing and out-of-plane gas pressure loading. Mathematics 2021, 9, 1238. [Google Scholar] [CrossRef]
- Antonova, I.; Nebogatikova, N.; Zerrouki, N.; Kurkina, I.; Ivanov, A. Flexibility of Fluorinated Graphene-Based Materials. Materials 2020, 13, 1032. [Google Scholar] [CrossRef] [Green Version]
- Chulkin, P.; Łapkowski, M. An Insight into Ionic Conductivity of Polyaniline Thin Films. Materials 2020, 13, 2877. [Google Scholar] [CrossRef] [PubMed]
- Molla-Alipour, M.; Ganji, B.A. Analytical analysis of mems capacitive pressure sensor with circular diaphragm under dynamic load using differential transformation method (DTM). Acta Mech. Solida Sin. 2015, 28, 400–408. [Google Scholar] [CrossRef]
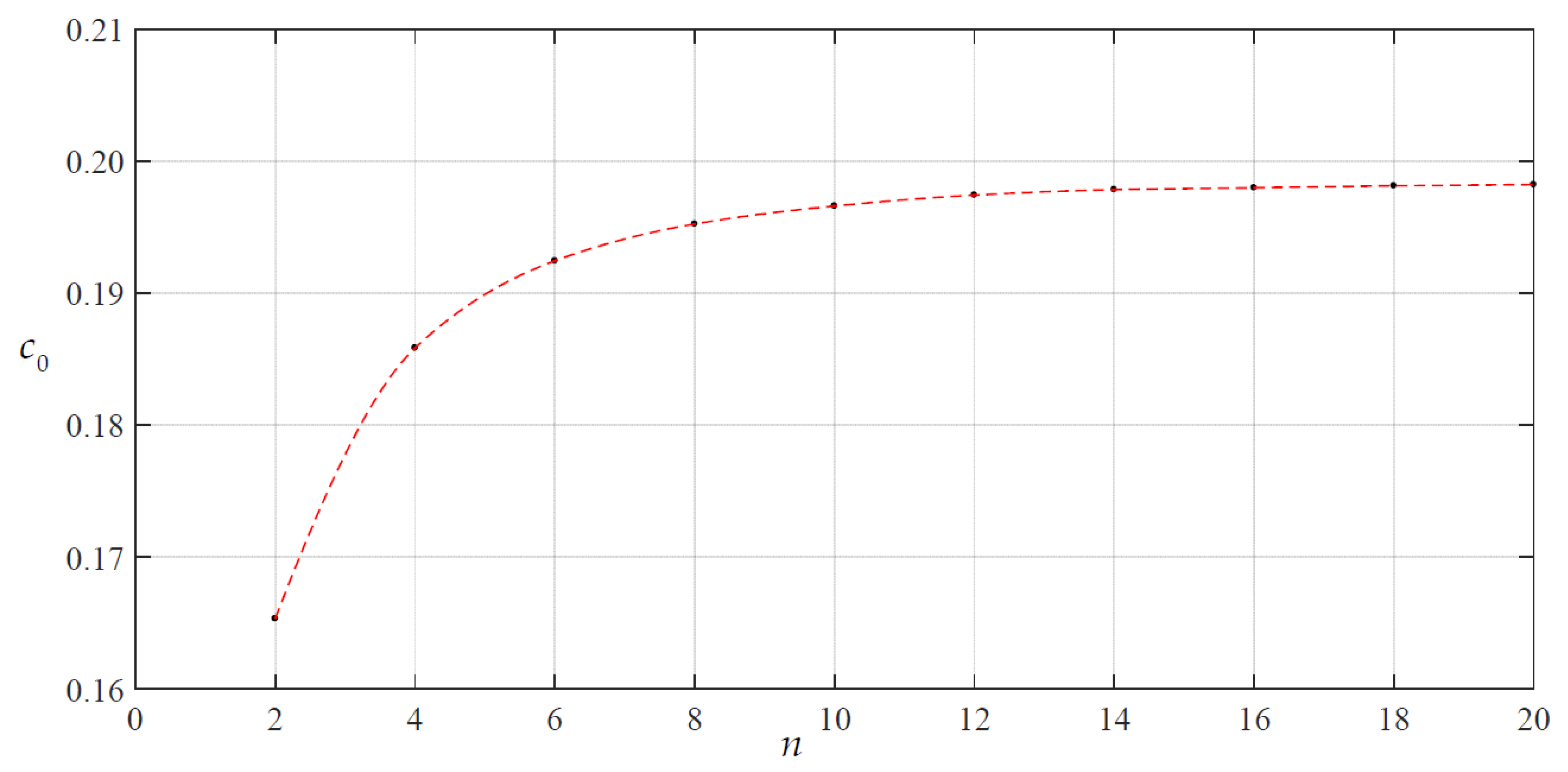



| n | c0 | d0 |
|---|---|---|
| 2 | 1.65316391 × 10−1 | 3.77658452 × 10−1 |
| 4 | 1.85832249 × 10−1 | 3.95315235 × 10−1 |
| 6 | 1.92438471 × 10−1 | 3.95548206 × 10−1 |
| 8 | 1.95231453 × 10−1 | 3.94159221 × 10−1 |
| 10 | 1.96595308 × 10−1 | 3.93001167 × 10−1 |
| 12 | 1.97422893 × 10−1 | 3.92241509 × 10−1 |
| 14 | 1.97834610 × 10−1 | 3.91803156 × 10−1 |
| 16 | 1.97977443 × 10−1 | 3.91614348 × 10−1 |
| 18 | 1.98125067 × 10−1 | 3.91540206 × 10−1 |
| 20 | 1.98216876 × 10−1 | 3.91482802 × 10−1 |
| i | ci | di |
|---|---|---|
| 0 | 1.98216876 × 10−1 | 3.91482802 × 10−1 |
| 2 | −2.49493987 × 10−2 | −3.15907573 × 10−1 |
| 4 | −4.85171579 × 10−3 | −4.60740692 × 10−2 |
| 6 | −1.58206170 × 10−3 | −1.55521234 × 10−2 |
| 8 | −6.42288769 × 10−4 | −6.76343212 × 10−3 |
| 10 | −2.94655565 × 10−4 | −3.32901660 × 10−3 |
| 12 | −1.46220841 × 10−4 | −1.76487967 × 10−3 |
| 14 | −7.66573427 × 10−5 | −9.83324535 × 10−4 |
| 16 | −4.18541507 × 10−5 | −5.67748867 × 10−4 |
| 18 | −2.35781462 × 10−5 | −3.36715864 × 10−4 |
| 20 | −1.36166630 × 10−5 | −2.03918152 × 10−4 |
| Test Points | Radius | Experimental Results | Calculated Results | Relative Errors |
|---|---|---|---|---|
| 1 | 60 | 2.89 | 2.8400 | 1.73% |
| 2 | 50 | 5.19 | 5.1016 | 1.70% |
| 3 | 40 | 6.99 | 6.8729 | 1.67% |
| 4 | 30 | 8.33 | 8.2082 | 1.46% |
| 5 | 20 | 9.27 | 9.1414 | 1.39% |
| 6 | 10 | 9.80 | 9.6937 | 1.08% |
| 7 | 0 | 9.97 | 9.8766 | 0.94% |
| 8 | 10 | 9.82 | 9.6937 | 1.29% |
| 9 | 20 | 9.29 | 9.1414 | 1.60% |
| 10 | 30 | 8.34 | 8.2082 | 1.58% |
| 11 | 40 | 6.96 | 6.8729 | 1.25% |
| 12 | 50 | 5.19 | 5.1016 | 1.70% |
| 13 | 60 | 2.89 | 2.8400 | 1.73% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.-Y.; Zhang, Q.; Wu, J.; Li, X.; He, X.-T. Large Deflection Analysis of Peripherally Fixed Circular Membranes Subjected to Liquid Weight Loading: A Refined Design Theory of Membrane Deflection-Based Rain Gauges. Materials 2021, 14, 5992. https://doi.org/10.3390/ma14205992
Sun J-Y, Zhang Q, Wu J, Li X, He X-T. Large Deflection Analysis of Peripherally Fixed Circular Membranes Subjected to Liquid Weight Loading: A Refined Design Theory of Membrane Deflection-Based Rain Gauges. Materials. 2021; 14(20):5992. https://doi.org/10.3390/ma14205992
Chicago/Turabian StyleSun, Jun-Yi, Qi Zhang, Ji Wu, Xue Li, and Xiao-Ting He. 2021. "Large Deflection Analysis of Peripherally Fixed Circular Membranes Subjected to Liquid Weight Loading: A Refined Design Theory of Membrane Deflection-Based Rain Gauges" Materials 14, no. 20: 5992. https://doi.org/10.3390/ma14205992
APA StyleSun, J.-Y., Zhang, Q., Wu, J., Li, X., & He, X.-T. (2021). Large Deflection Analysis of Peripherally Fixed Circular Membranes Subjected to Liquid Weight Loading: A Refined Design Theory of Membrane Deflection-Based Rain Gauges. Materials, 14(20), 5992. https://doi.org/10.3390/ma14205992







