Design of Composites by Infiltration Process: A Case Study of Liquid Ir-Si Alloy/SiC Systems
Abstract
:1. Introduction
2. Theory
2.1. Predictions of Thermodynamic Properties of Metallic Melts
2.2. Structural Information: and Microscopic Functions
2.3. Surface Properties
2.4. Transport Properties
2.5. Non-Reactive Infiltration: Metal/Metal and Metal/Ceramic Composites
3. Results and Discussion
3.1. Thermodynamics of Ir-Si Melts: Miedema’s Model and Free Volume Theory
3.2. Density/Molar Volume of Ir-Si Melts
3.3. Structural Information: Concentration Fluctuations in the Long-Wavelength Limit and Chemical Short-Range Order Parameter in Ir-Si Melts
3.4. Surface Segregation and Surface Tension of Liquid Ir-Si Alloys: QCA Modelling
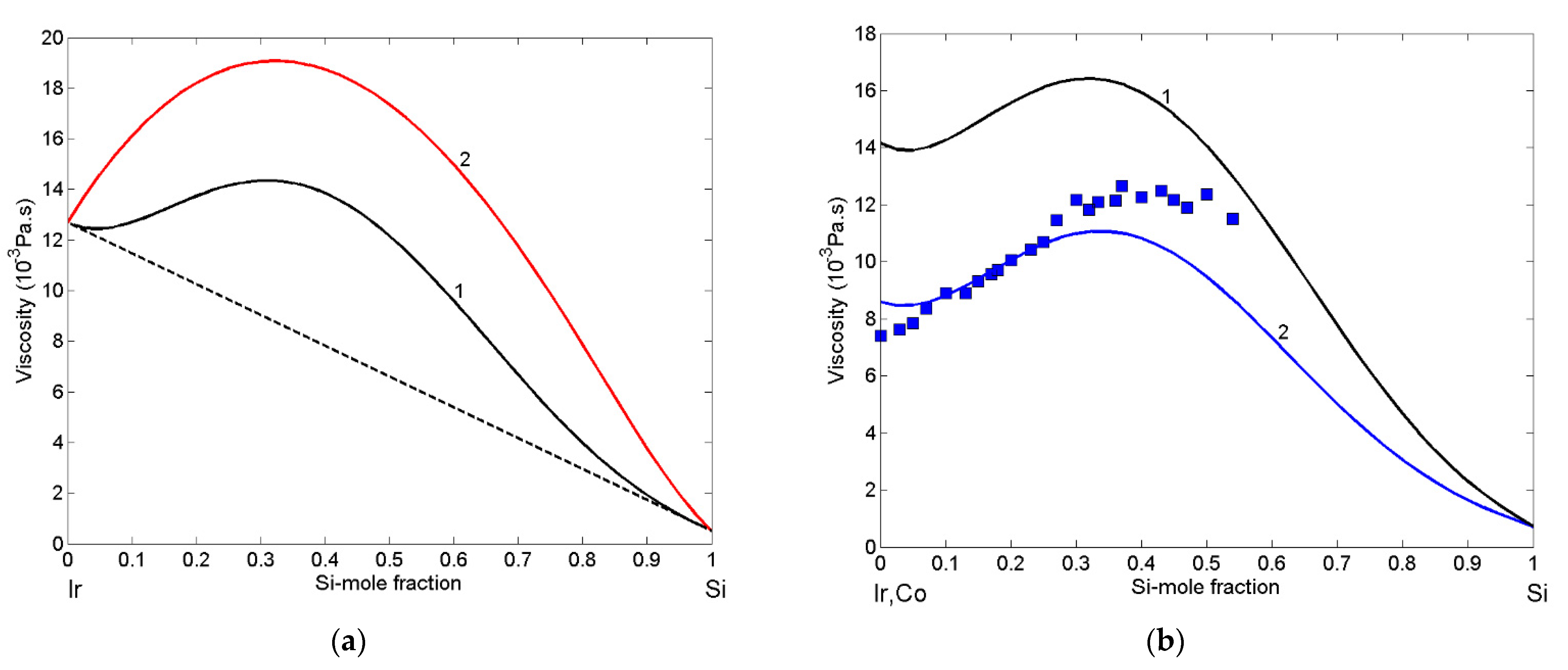
3.5. Viscosity
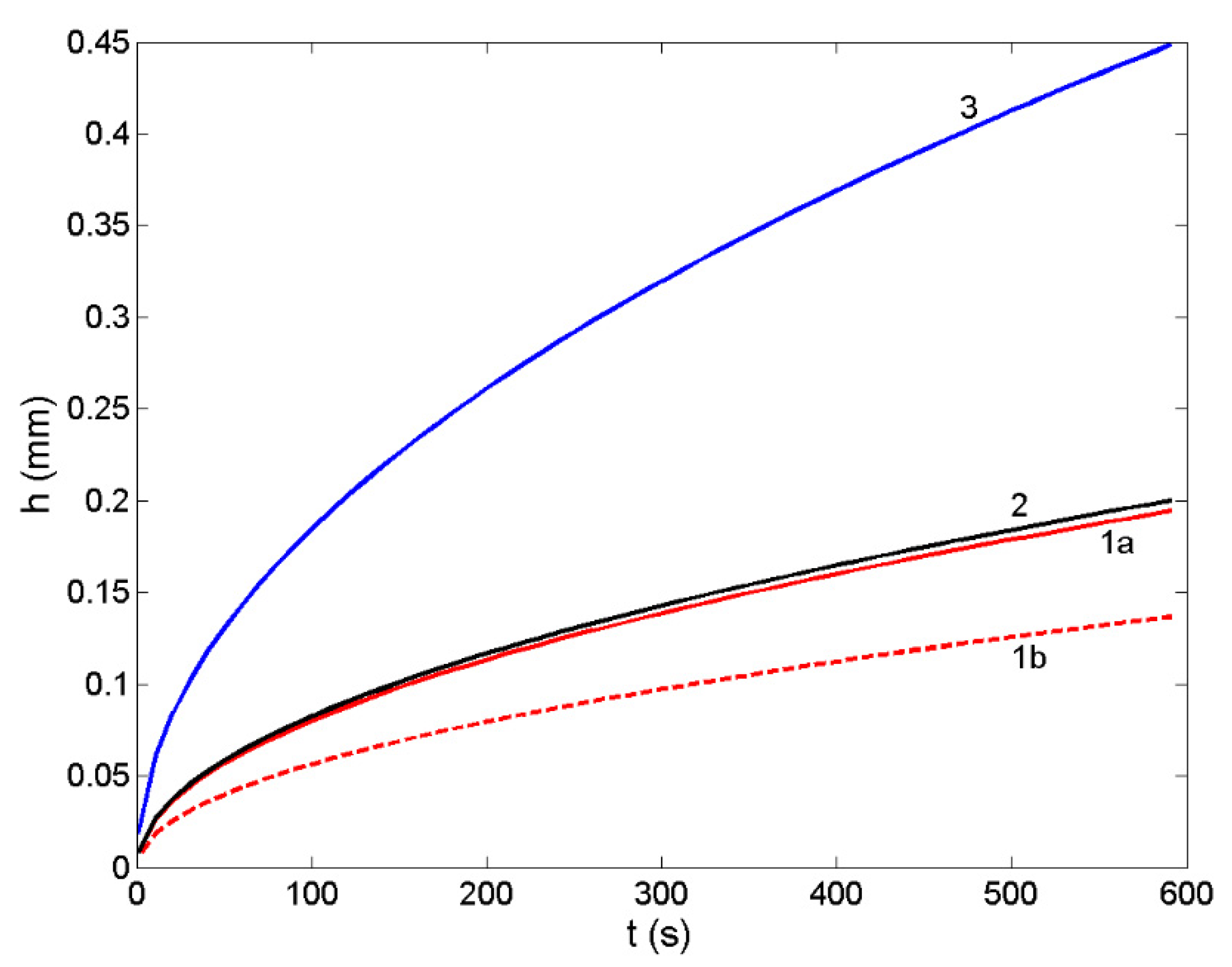
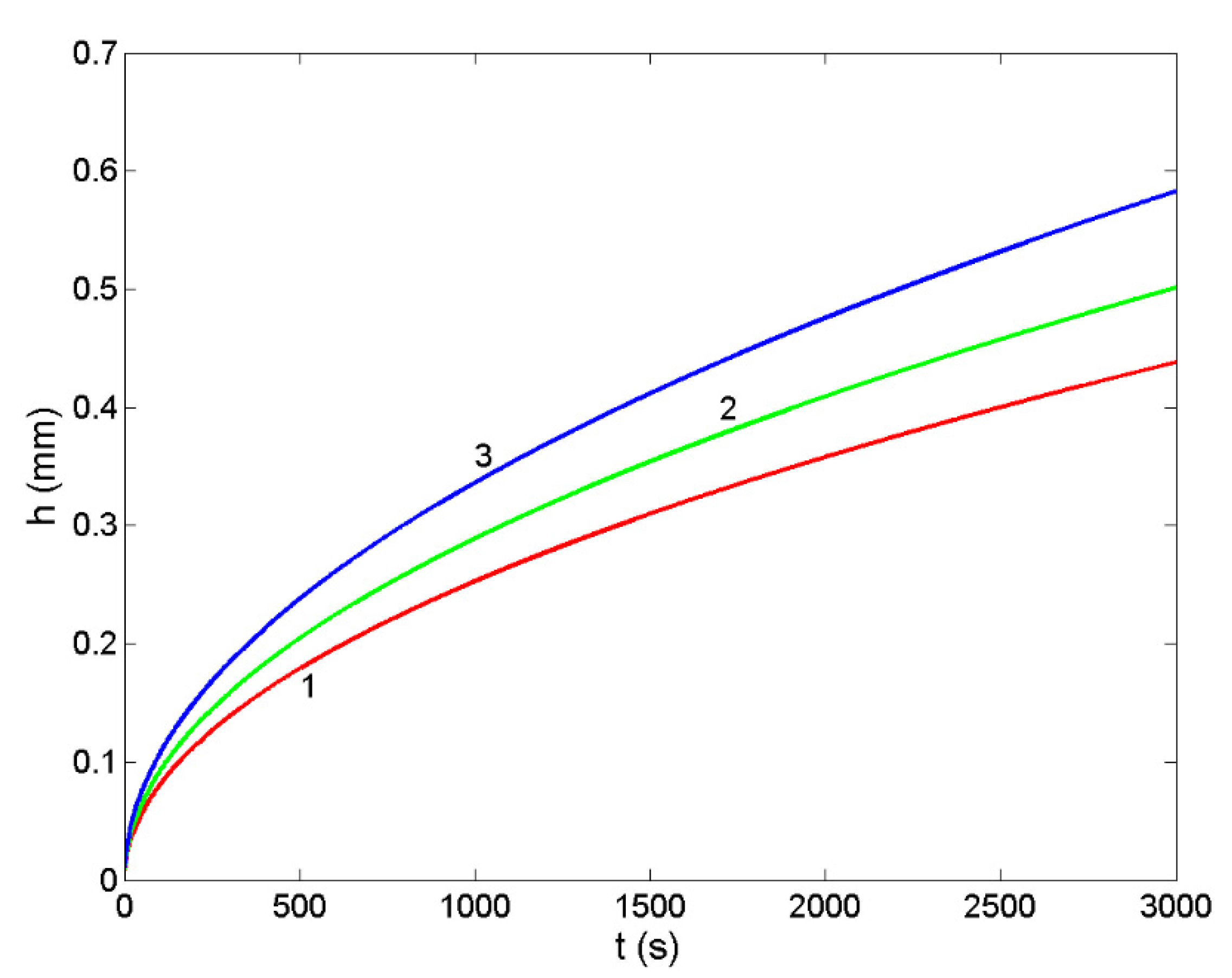
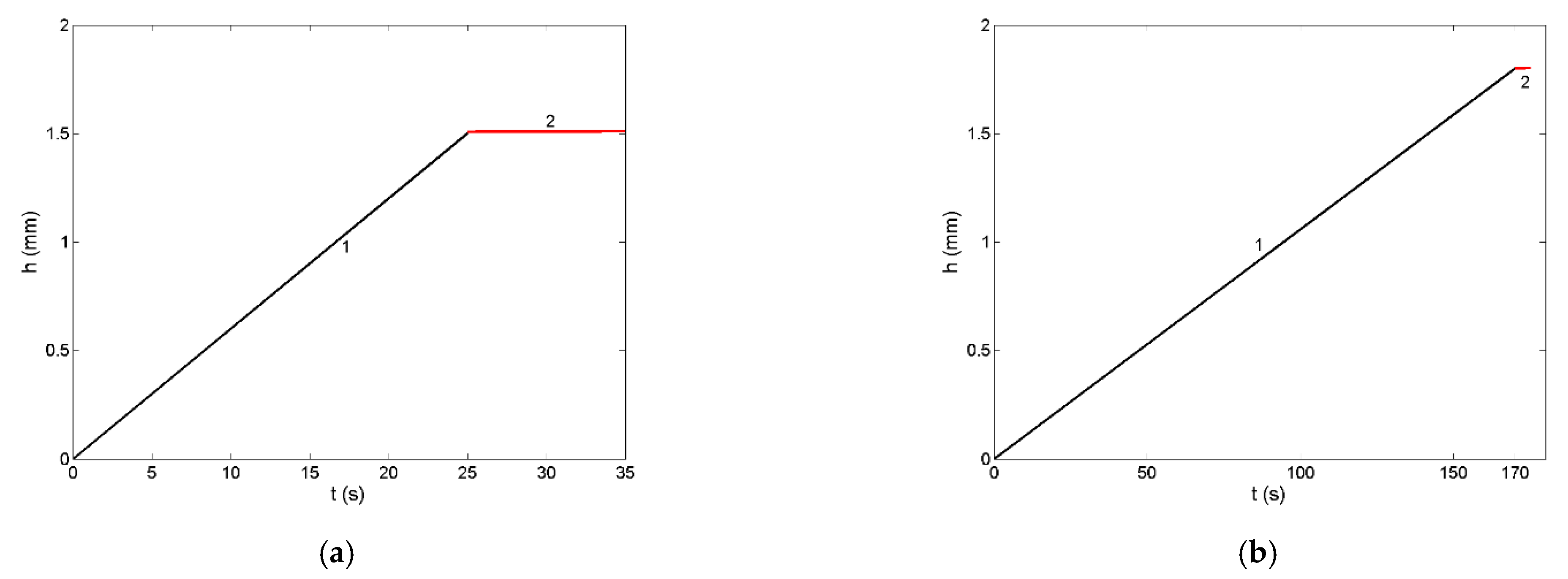
3.6. Non-Reactive Infiltration: Case Study of a Liquid Ir-Si Alloy/SiC System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| components of an alloy | |
| () | activity of component |
| () | composition of component |
| composition of and in an alloy | |
| surface composition of components and | |
| GM | Gibbs free energy of mixing |
| excess Gibbs free energy of mixing | |
| enthalpy of mixing | |
| distance which interatomic potential extends in a cell of atom i in pure liquid | |
| distance which interatomic potential extends in a cell of atom in a liquid A − B alloy | |
| approximately the mean of | |
| Boltzmann’s constant | |
| () | atomic mass of component i |
| Avogadro’s number | |
| parameter of nearly random configuration of atoms in an alloy | |
| interaction parameter at the equiatomic composition | |
| surface coordination fraction | |
| gas constant | |
| surface area of an alloy | |
| concentration fluctuations in the long wavelength limit | |
| Scc(0, id) | concentration fluctuations for the ideal mixing |
| excess entropy of mixing | |
| configurational excess entropy | |
| vibrational excess entropy | |
| T | absolute temperature |
| () | atomic volume of the component |
| excess volume | |
| Uii | depth of potential energy in a cell of atom in pure liquid |
| depth of potential energy in a cell of atom in a liquid alloy | |
| coordination number | |
| mean surface area of an alloy | |
| () | surface area of atomic species |
| α1 | short-range order parameter |
| auxiliary function for the bulk phase | |
| auxiliary function for the surface phase | |
| () | activity coefficient of component |
| , () | work function of component |
| viscosity of liquid alloys | |
| () | viscosity of component |
| additive viscosity (ideal mixture) | |
| excess viscosity | |
| stoichiometric coefficients | |
| exchange energy | |
| surface tension (liquid-gas) of liquid alloys | |
| surface tension of pure component | |
| surface tension of pure component | |
| (i = A, B) | hard sphere diameter of component i |
| θ | contact angle between liquid and solid phases |
| K | constant |
| reff = r | pore radius |
| infiltration depth | |
| infiltration time | |
References
- Allevato, C.E.; Vining, C.B. Phase diagram and electrical behavior of silicon-rich iridium silicide compounds. J. Alloys Compd. 1993, 200, 99–105. [Google Scholar] [CrossRef]
- Chung, C.K.; Hwang, J. Epitaxial iridium silicide formation during deposition of Ir on Si(100) at high temperature under ultrahigh vacuum. J. Appl. Phys. 1994, 76, 1937–1939. [Google Scholar] [CrossRef]
- Lange, D.A.; Gibson, G.A.; Falco, C.M. Growth and structure of IrSi3 on Si(111). J. Appt. Phys. 1994, 75, 2917–2920. [Google Scholar] [CrossRef]
- Kurt, R.W.; Pitschke, A.; Heinrich, J.; Schumann, W.K. Preparation of iridium silicide thin films by means of Electron Beam Evaporation. In Proceedings of the 16th International Conference on Thermoelectrics (ICT ‘97. XVI), Dresden, Germany, 26–29 August 1997; Cadoff, I.B., Miller, E., Eds.; IEEE Service Center: Piscataway, NY, USA, 1997; pp. 303–306. [Google Scholar]
- Almendra, A.; Rodríguez, A.; Rodríguez, T.; Martín, P.; Jiménez, J. Micro-Raman study of iridium silicides. J. Raman Spectrosc. 2002, 33, 80–83. [Google Scholar] [CrossRef]
- Ma, X. Infrared absorption characteristics of polycrystalline iridium-silicide thin films. Thin Solid Films 2005, 484, 257–260. [Google Scholar] [CrossRef]
- Allevato, C.E.; Vining, C.B. Thermoelectric properties of semiconducting iridium silicides. In Proceedings of the 28th Intersociety Energy Conversion Engineering Conference (IECEC-93), Atlanta, GA, USA, 8–13 August 1993; American Chemical Society: Washington, DC, USA, 1993; p. 1239. [Google Scholar]
- Chung, C.K.; Hwang, J.; Jaw, T.H.; Wuu, D.S. Electrical properties of Ir-silicide formation on p-Si(100) in ultra-high vacuum. Thin Solid Films 2000, 373, 68–72. [Google Scholar] [CrossRef]
- Novakovic, R.; Korthaus, B. Advanced ceramics for use in highly oxidizing and corrosive environments: Silicides. Key Eng. Mater. 2001, 201, 183–217. [Google Scholar] [CrossRef]
- Caccia, M.; Amore, S.; Giuranno, D.; Novakovic, R.; Ricci, E.; Narciso, J. Towards optimization of SiC/CoSi2 of composite material manufacture via reactive infiltration: Wetting study of SiCo alloys on carbon materials. J. Eur. Ceram. Soc. 2015, 35, 4099–4106. [Google Scholar] [CrossRef]
- Caccia, M.; Narciso, J. Key parameters in the manufacture of SiC-based composite materials by reactive melt infiltration. Materials 2019, 12, 2425. [Google Scholar] [CrossRef] [Green Version]
- Camarano, A.D.; Giuranno, D.; Narciso, J. New advanced SiC-based composite materials for use in highly oxidizing environments: Synthesis of SiC/IrSi3. J. Eur. Ceram. 2020, 40, 603–611. [Google Scholar] [CrossRef]
- Camarano, A.; Giuranno, D.; Narciso, J. SiC-IrSi3 for high oxidation resistance. Materials 2020, 13, 98. [Google Scholar] [CrossRef] [Green Version]
- Yamabe-Mitarai, Y.; Ro, Y.; Maruko, T.; Harada, H. Ir-Base Refractory Superalloys for Ultra-High Temperatures. Metall. Mater. Trans. A 1998, 29, 537–549. [Google Scholar] [CrossRef]
- Sha, J.B.; Yamabe-Mitarai, Y. Ir-Nb-Si ternary refractory superalloys with a three-phase fcc/L12/silicide structure for high-temperature applications. Intermetallics 2007, 15, 1638–1649. [Google Scholar] [CrossRef]
- Okamoto, H. Comment on Ir-Si (Iridium-Silicon). J. Phase Equilib. Diff. 1995, 16, 473–474. [Google Scholar] [CrossRef]
- Okamoto, H. Ir-Si (Iridium-Silicon). J. Phase Equilib. Diff. 2007, 28, 495. [Google Scholar] [CrossRef]
- Korst, W.L.; Finnie, L.N.; Searcy, A.W. The crystal structures of the monosilicides of Osmium, Iridium and Ruthenium. J. Phys. Chem. 1957, 61, 1541–1543. [Google Scholar] [CrossRef]
- Finnie, L.N. Structures and compositions of the silicides of ruthenium, osmium, rhodium and iridium. J. Less-Common Met. 1962, 4, 24–34. [Google Scholar] [CrossRef]
- Engström, I.; Zackrisson, F. X-Ray studies of silicon-rich iridium silicides. Acta Chem. Scand. 1970, 24, 2109–2116. [Google Scholar] [CrossRef]
- White, J.G.; Hockings, E.F. Crystal structure of iridium trisilicide, IrSi3. Inorg. Chem. 1971, 10, 1034–1035. [Google Scholar]
- Wittmer, M.; Oelhafen, P.; Tu, K.N. Electronic structure of iridium silicides. Phys. Rev. 1986, 33, 5391–5400. [Google Scholar] [CrossRef]
- Engström, I.; Lindsten, T.; Zdansky, E. The crystal structure of the iridium silicide Ir3Si5. Acta Chem. Scand. 1987, A41, 237–242. [Google Scholar] [CrossRef]
- Searcy, A.W.; Finnie, L.N. Stability of solid phases in the ternary systems of silicon and carbon with rhenium and the six platinum metals. J. Am. Ceram. 1962, 45, 268–273. [Google Scholar] [CrossRef]
- Sha, J.B.; Yamabe-Mitarai, Y. Phase and microstructural evolution of Ir-Si binary alloys with fcc/silicide structure. Intermetallics 2006, 14, 672–684. [Google Scholar] [CrossRef]
- Meschel, S.V.; Kleppa, O.J. Standard enthalpies of formation of some 5d transition metal silicides by high temperature direct synthesis calorimetry. J. Alloy. Compd. 1998, 280, 231–239. [Google Scholar] [CrossRef]
- Meschel, S.V.; Kleppa, O.J. Thermochemistry of alloys of transition metals and lanthanide metals with some IIIB and IVB elements in the periodic table. J. Alloy. Compd. 2001, 321, 183–200. [Google Scholar] [CrossRef]
- Kleppa, O.J.; Topor, L. Standard enthalpies of formation of RuSi, RhSi, and IrSi. Z. Met. 1988, 79, 623–628. [Google Scholar]
- Iida, T.; Guthrie, R.I.L. The Thermophysical Properties of Liquid Metals, Fundamentals, 1st ed.; University Press: Oxford, UK, 2015; Volume 1, pp. 1–353. [Google Scholar]
- Pauling, L. Nature of the Chemical Bonding, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960; pp. 1–664. [Google Scholar]
- Singh, R.N.; March, N.H. Principles. In Intermetallic Compounds. Principles and Practice, 1st ed.; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons: New York, NY, USA, 1995; Volume 1, pp. 661–686. [Google Scholar]
- Miedema, A.R.; de Boer, F.R.; Boom, R. Model predictions for the enthalpy of formation of transition metal alloys. CALPHAD 1977, 1, 341–359. [Google Scholar] [CrossRef]
- Niessen, A.K.; de Boer, F.R.; Boom, R.; de Châtel, P.F.; Mattens, W.C.M.; Miedema, A.R. Model predictions for the enthalpy of formation of transition metal alloys II. CALPHAD 1983, 7, 51–70. [Google Scholar] [CrossRef]
- Miedema, A.R.; Niessen, A.K. The enthalpy of solution for solid binary alloys of two 4d-transition metals. CALPHAD 1983, 7, 27–36. [Google Scholar] [CrossRef]
- de Boer, F.R.; Boom, R.; Mattens, W.C.M.; Miedema, A.R.; Niessen, A.K. Cohesion in Metals, Transition Metal Alloys, 1st ed.; North Holland: Amsterdam, The Netherlands, 1988; pp. 1–127. [Google Scholar]
- Tanaka, T.; Gokcen, N.A.; Morita, Z. Relationship between enthalpy of mixing and excess entropy in liquid binary alloys. Z. Metallkd. 1990, 81, 49–54. [Google Scholar]
- Tanaka, T.; Gokcen, N.A.; Morita, Z.-I.; Iida, T. Thermodynamic relationship between enthalpy of mixing and excess entropy in liquid binary alloys. Z. Metallkd. 1993, 84, 192–199. [Google Scholar]
- Tanaka, T.; Gokcen, N.A.; Kumar, K.C.H.; Hara, S.; Morita, Z.-I. Thermodynamic relationship between enthalpy of mixing and excess entropy in solid solutions of binary alloys. Z. Metallkd. 1996, 87, 779–783. [Google Scholar]
- Novakovic, R.; Tanaka, T.; Muolo, M.L.; Lee, J.; Passerone, A. Bulk and surface transport properties of liquid Ag-X (X = Ti, Hf) compound forming alloys. Surf. Sci. 2005, 591, 56–69. [Google Scholar] [CrossRef]
- Costa, C.; Delsante, S.; Borzone, G.; Zivkovic, D.; Novakovic, R. Thermodynamic and surface properties of liquid Co-Cr-Ni alloys. J. Chem. Thermodyn. 2014, 6, 73–84. [Google Scholar] [CrossRef]
- Novakovic, R.; Giuranno, D.; Caccia, M.; Amore, S.; Nowak, R.; Sobczak, N.; Narciso, J.; Ricci, E. Thermophysical properties of liquid Co-Si alloys. J. Molec. Liq. 2016, 221, 346–353. [Google Scholar] [CrossRef] [Green Version]
- Moelwyn-Hughes, E.A. Physical Chemistry, 2nd ed.; Pergamon Press: New York, NY, USA, 1961; pp. 786–788. [Google Scholar]
- Takeuchi, A.; Inoue, A. Mixing enthalpy of liquid phase calculated by Miedema’s scheme and approximated with sub-regular solution model for assessing forming ability of amorphous and glassy alloys. Intermetallics 2010, 18, 1779–1789. [Google Scholar] [CrossRef]
- Bhatia, A.B.; Thornton, D.E. Structural aspects of the electrical resistivity of binary alloys. Phys. Rev. B 1970, 2, 3004–3012. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction, 1st ed.; Addison-Wesley: Reading, MA, USA, 1969; pp. 1–381. [Google Scholar]
- Terzieff, P. The viscosity of liquid alloys. J. Alloys Compd. 2008, 453, 233–240. [Google Scholar] [CrossRef]
- Iida, T.; Ueda, M.; Morita, Z. On the excess viscosity of liquid alloys and the atomic interaction of their constituents. Tetsu Hagane 1976, 62, 1169–1178. [Google Scholar] [CrossRef] [Green Version]
- Terzieff, P. The viscosity of liquid alloys of polyvalent metals with Cu, Ag and Au: Theoretical treatments based on the enthalpy of mixing. Physica B 2009, 404, 2039–2044. [Google Scholar] [CrossRef]
- Eremenko, V.N.; Lesnik, N.D. The kinetics of the infiltration of porous materials with liquid metals. In The Role of Surface Phenomena in Metallurgy, 1st ed.; Eremenko, V.N., Ed.; Consultants Bureau: New York, NY, USA, 1963; pp. 102–116. [Google Scholar]
- Voytovych, R.; Bougiouri, V.; Calderon, N.R.; Narciso, J.; Eustathopoulos, N. Reactive infiltration of porous graphite by NiSi alloys. Acta Mater. 2008, 56, 2237–2246. [Google Scholar] [CrossRef]
- Israel, R.; Voytovych, R.; Protsenko, P.; Drevet, B.; Camel, D.; Eustathopoulos, N. Capillary interactions between molten silicon and porous graphite. J. Mater. Sci. 2010, 45, 2210–2217. [Google Scholar] [CrossRef]
- Eustathopoulos, N.; Israel, R.; Drevet, B.; Camel, D. Reactive infiltration by Si: Infiltration versus wetting. Scripta Mater. 2010, 62, 966–971. [Google Scholar] [CrossRef]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Deryagin, B.V.; Melnikova,, N.K. Mechanism of moisture equilibrium and migration in soils. In Proceedings of the Highway Research Board, Special Report 40 of the Thirty-Seventh International Symposium on Water and Its Conduction in Soils, Washington, DC, USA, 6–10 January 1958; pp. 43–54. [Google Scholar]
- Assael, M.J.; Armyra, I.J.; Brillo, J.; Stankus, S.V.; Wu, J.; Wakeham, W.A. Reference Data for the Density and Viscosity of Liquid Cadmium, Cobalt, Gallium, Indium, Mercury, Silicon, Thallium, and Zinc. J. Phys. Chem. Ref. Data 2012, 41, 033101. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, T.; Paradis, P.-F.; Fujii, R.; Saita, Y.; Yoda, S. Thermophysical property measurements of liquid and supercooled iridium by containerless methods. Int. J. Thermophys. 2005, 26, 893–904. [Google Scholar] [CrossRef]
- Novakovic, R.; Tanaka, T. Bulk and surface properties of Al-Co and Co-Ni liquid alloys. Physica B 2006, 371, 223–231. [Google Scholar] [CrossRef]
- Schlesinger, M.E. Thermodynamics of solid transition-metal silicides. Chem. Rev. 1990, 90, 607–628. [Google Scholar] [CrossRef]
- Pasturel, A.; Hicter, P.; Cyrot-Lackmann, F. On the heats of formation of solid germanides and silicides of transition metals. Physica B 1984, 124, 247–250. [Google Scholar] [CrossRef]
- Shergin, L.M.; Popel, S.I.; Tsarevskii, B.V. Temperature dependence of the density and surface tension of Cobalt-Silicon and Nickel-Silicon melts. Pap. Inst. Metall. Acad. Sci. USSR Sverdl. 1971, 25, 52–61. (In Russian) [Google Scholar]
- Hibiya, T.; Morohoshi, K.; Ozawa, S. Oxygen partial pressure dependence on surface tension and its temperature coefficient for metallic melts: A discussion from the viewpoint of solubility and adsorption of oxygen. J. Mater. Sci. 2010, 45, 1986–1992. [Google Scholar] [CrossRef]
- Rhim, W.-K.; Ohsaka, K. Thermophysical properties measurement of molten silicon by high-temperature electrostatic levitator: Density, volume expansion, specific heat capacity, emissivity, surface tension and viscosity. J. Cryst. Growth 2000, 208, 313–321. [Google Scholar] [CrossRef]
- Terzieff, P. A pseudopotential approach to the viscosity of liquid Cu-based alloys. J. Alloys Compd. 2009, 473, 195–200. [Google Scholar] [CrossRef]
- Protopapas, P.; Andersent, H.C.; Parlee, N.A.D. Theory of transport in liquid metals. I. Calculation of self-diffusion coefficients. J. Chem. Phys. 1973, 59, 15–25. [Google Scholar] [CrossRef]
- Orton, B. A double hard sphere model for molten semiconductors and semimetals. J. Phys. Colloq. 1980, 41, C8-280–C8-283. [Google Scholar] [CrossRef]
- Zhang, L.; Du, Y.; Xu, H.; Pan, Z. Experimental investigation and thermodynamic description of the Co-Si system. Calphad 2006, 30, 470–481. [Google Scholar] [CrossRef]
- Paradis, P.-F.; Ishikawa, T.; Koike, N. Thermophysical property measurements of liquid and supercooled cobalt. High Temp.-High Press. 2008, 37, 5–11. [Google Scholar]
- Beltyukova, A.L.; Olyanina, N.V.; Ladyanov, V.I. Dependences of Co-Si melt viscosity on temperature and concentration. High Temp. 2019, 57, 41–48. [Google Scholar] [CrossRef]
- Rado, C.; Kalogeropoulou, S.; Eustathopoulos, N. Wetting and bonding of Ni-Si alloys on silicon carbide. Acta Mater. 1999, 47, 461–473. [Google Scholar] [CrossRef]
- Naidich, Y.V. Contact Phenomena in Metallic Alloys, 1st ed.; Naukova Dumka, Kiev, USSR: Kyiv, Ukraine, 1972; p. 172. (In Russian) [Google Scholar]
- Naidich, Y.V. Progress in Surface and Membrane Science; Cadenhead, D.A., Danielli, J.F., Eds.; Academic Press: Cambridge, MA, USA, 1981; Volume 14, p. 353. [Google Scholar]
- Calderon, N.R.; Voytovych, R.; Narciso, J.; Eustathopoulos, N. Pressureless infiltration versus wetting in AlSi/graphite system. J. Mater. Sci. 2010, 45, 4345–4350. [Google Scholar] [CrossRef]
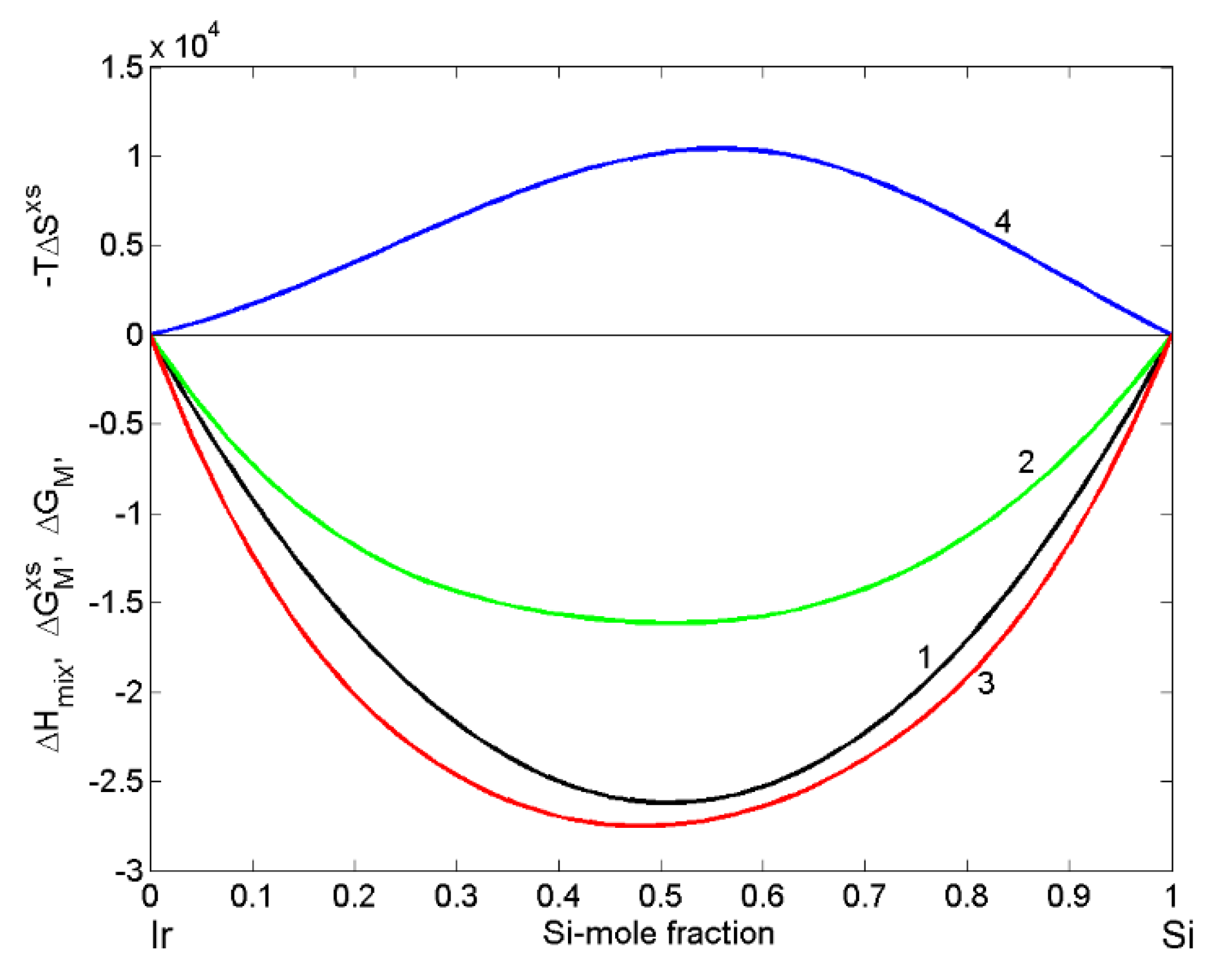
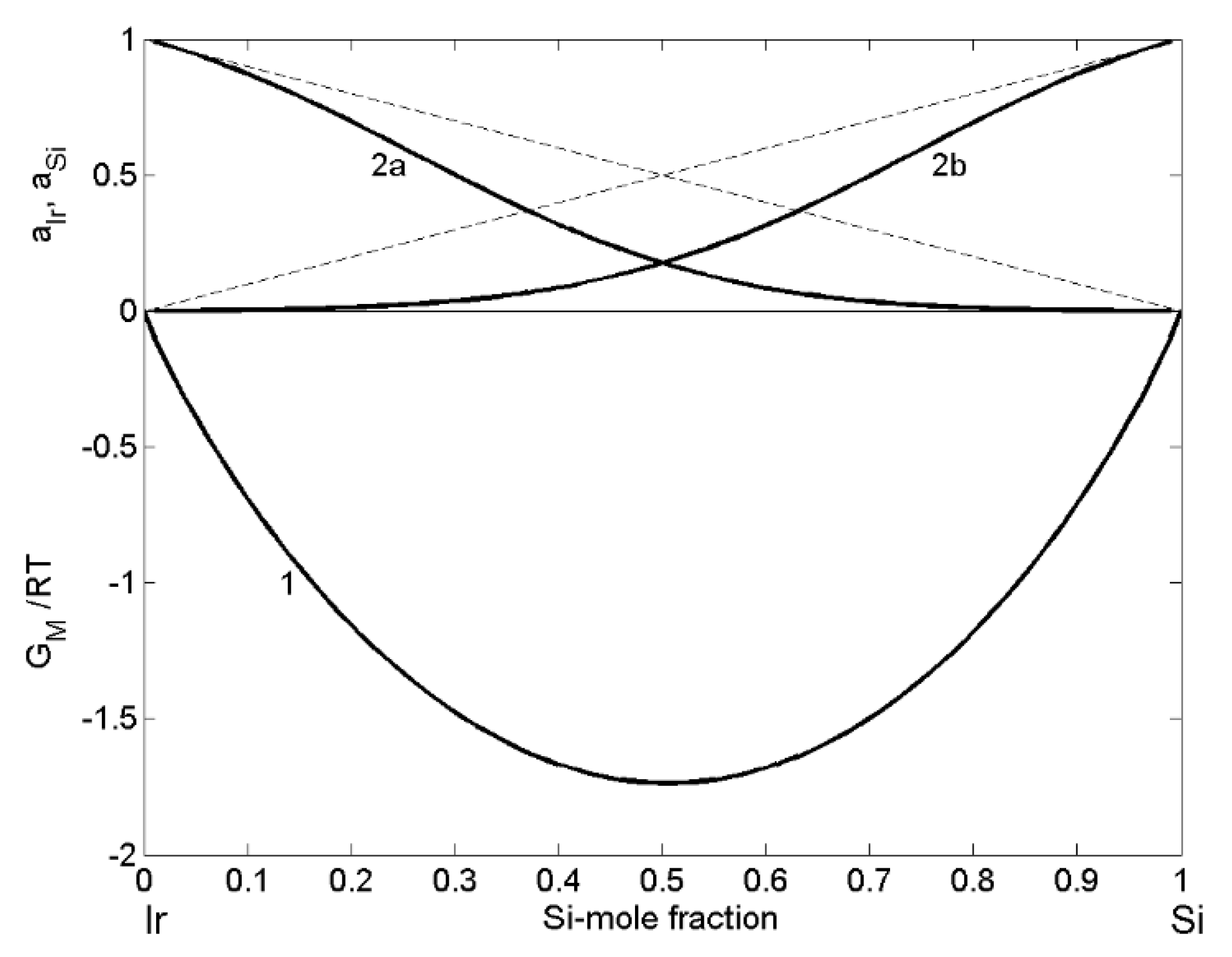

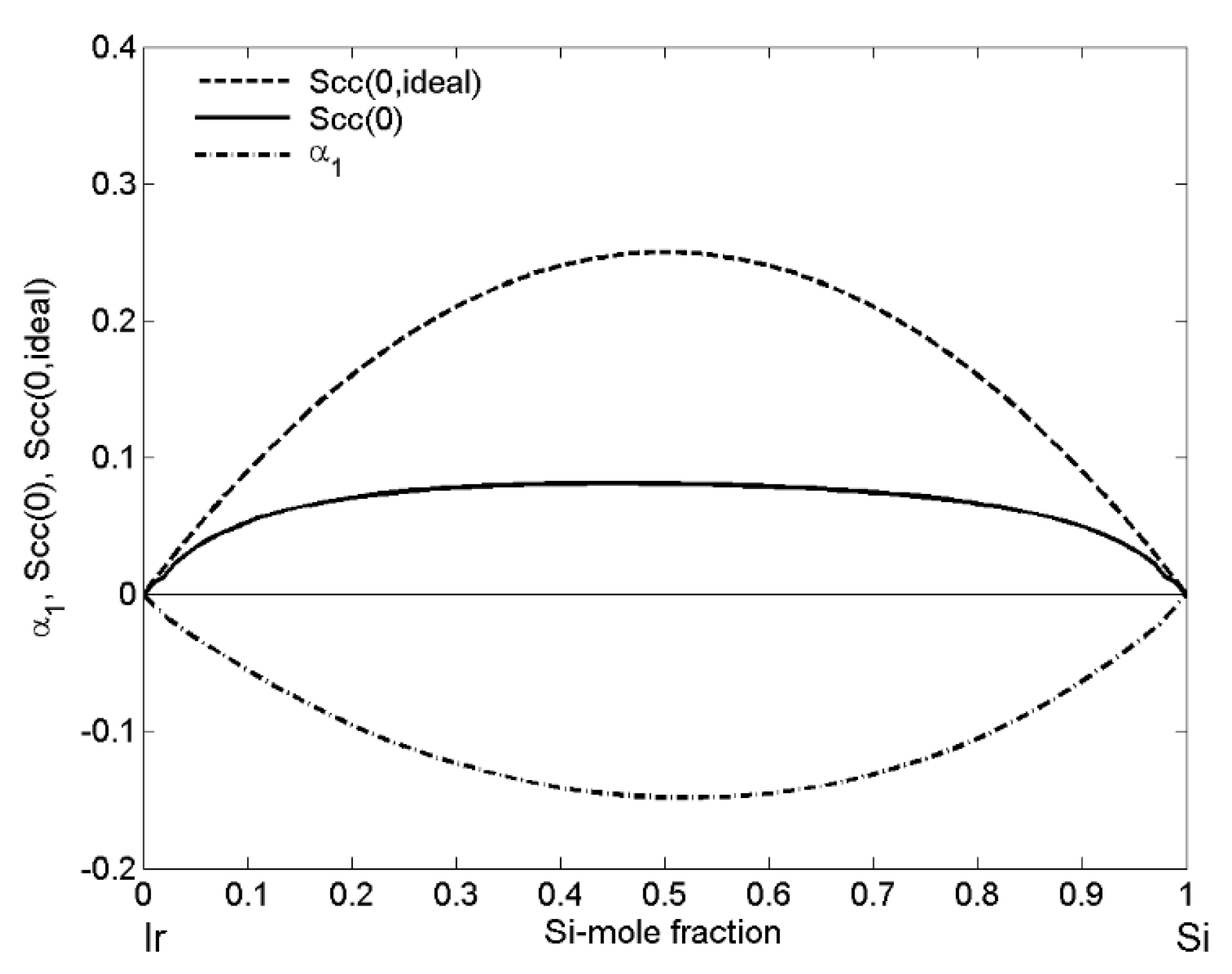
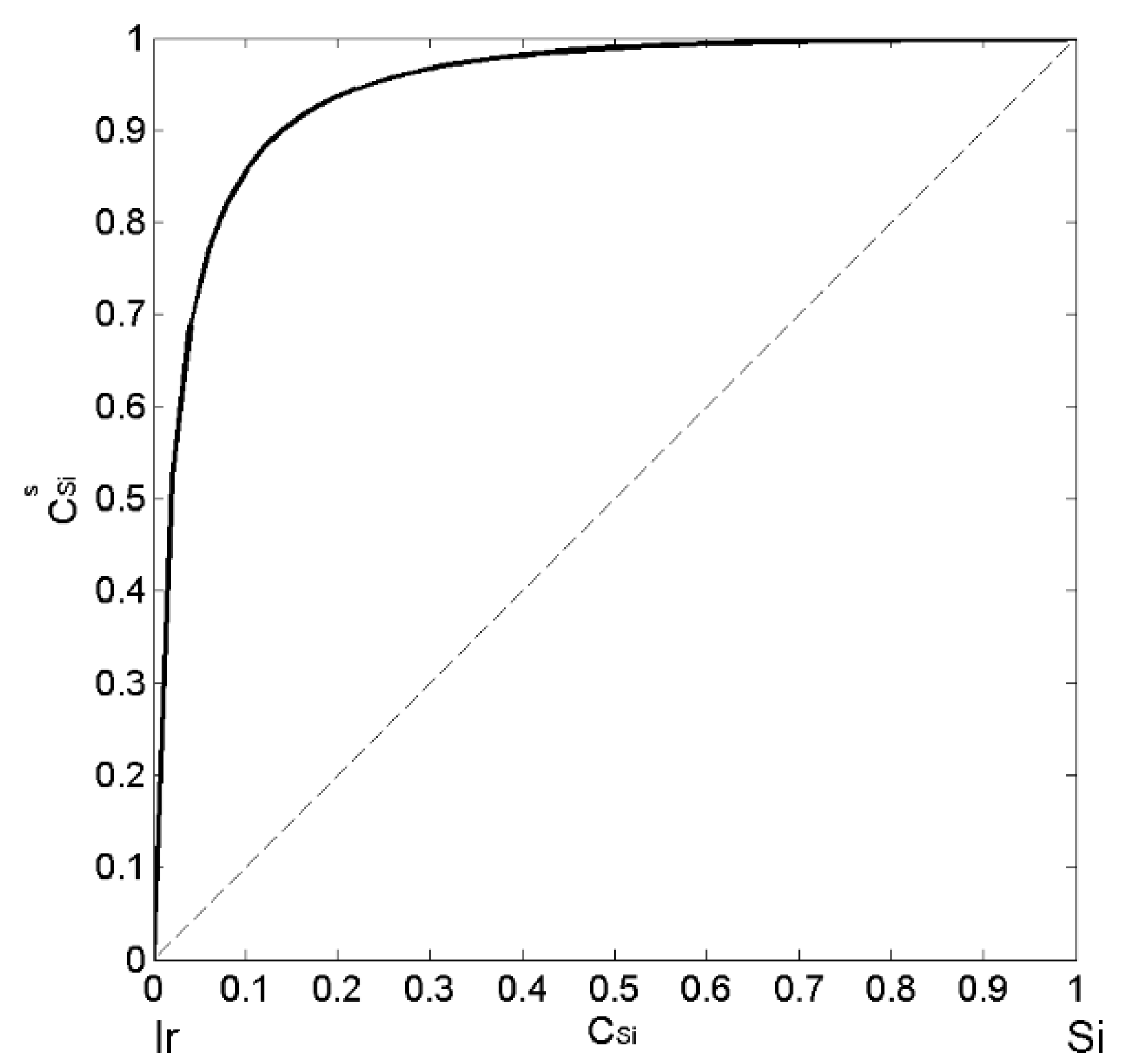

| xSi | ΔHM (kJ·mol−1) | (kJ·mol−1) | P | (kJ·mol−1) | (kJ·mol−1) | (cm3·mol−1) | (10−8 cm) | (10−8 cm) |
|---|---|---|---|---|---|---|---|---|
| 0.1 | −9.202 | −92.047 | 0.8006 | −457.83 | −407.02 | −0.1877 | 1.414 | 1.454 |
| 0.2 | −16.461 | −82.441 | 0.6027 | −447.52 | −397.11 | −0.3457 | 1.420 | 1.454 |
| 0.3 | −21.739 | −72.960 | 0.4096 | −431.75 | −386.51 | −0.4970 | 1.428 | 1.454 |
| 0.4 | −24.998 | −64.340 | 0.2354 | −409.27 | −373.28 | −0.6387 | 1.438 | 1.455 |
| 0.5 | −26.200 | −60.026 | 0.1455 | −386.40 | −348.51 | −0.7665 | 1.448 | 1.459 |
| 0.6 | −25.306 | −65.053 | 0.2339 | −382.42 | −304.80 | −0.8727 | 1.453 | 1.469 |
| 0.7 | −22.277 | −74.711 | 0.4086 | −390.22 | −261.29 | −0.9425 | 1.454 | 1.478 |
| 0.8 | −17.075 | −85.493 | 0.6022 | −400.64 | −224.52 | −0.9440 | 1.454 | 1.485 |
| 0.9 | −9.662 | −96.648 | 0.8.005 | −411.72 | −193.25 | −0.7921 | 1.454 | 1.491 |
(10−8 cm) | (J·K−1·mol−1) | (J·K−1·mol−1) | (J·K−1·mol−1) | (kJ·mol−1) | (kJ·mol−1) | (kJ·mol−1) | ||
| 0.1 | 1.4542 | −0.9548 | −0.0906 | −1.0454 | −7.2435 | −464.16 | −165.95 | |
| 0.2 | 1.4541 | −1.7936 | −0.4027 | −2.1963 | −12.3472 | |||
| 0.3 | 1.4540 | −2.5055 | −1.0079 | −3.5133 | −15.1588 | (10−8 cm) | (10−8 cm) | |
| 0.4 | 1.4538 | −3.0713 | −1.9258 | −4.9971 | −15.6388 | |||
| 0.5 | 1.4538 | −3.4509 | −2.5974 | −6.0484 | −14.8714 | 1.4091 | 1.4955 | |
| 0.6 | 1.4538 | −3.5526 | −1.9418 | −5.4945 | −15.0145 | |||
| 0.7 | 1.4540 | −3.2887 | −1.0163 | −4.3049 | −14.2137 | (cm3·mol−1) | (cm3·mol−1) | |
| 0.8 | 1.4541 | −2.6310 | −0.4054 | −3.0364 | −11.3881 | |||
| 0.9 | 1.4541 | −1.5506 | −0.0911 | −1.6417 | −6.5876 | 9.531 | 11.395 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novakovic, R.; Delsante, S.; Giuranno, D. Design of Composites by Infiltration Process: A Case Study of Liquid Ir-Si Alloy/SiC Systems. Materials 2021, 14, 6024. https://doi.org/10.3390/ma14206024
Novakovic R, Delsante S, Giuranno D. Design of Composites by Infiltration Process: A Case Study of Liquid Ir-Si Alloy/SiC Systems. Materials. 2021; 14(20):6024. https://doi.org/10.3390/ma14206024
Chicago/Turabian StyleNovakovic, Rada, Simona Delsante, and Donatella Giuranno. 2021. "Design of Composites by Infiltration Process: A Case Study of Liquid Ir-Si Alloy/SiC Systems" Materials 14, no. 20: 6024. https://doi.org/10.3390/ma14206024
APA StyleNovakovic, R., Delsante, S., & Giuranno, D. (2021). Design of Composites by Infiltration Process: A Case Study of Liquid Ir-Si Alloy/SiC Systems. Materials, 14(20), 6024. https://doi.org/10.3390/ma14206024








