A Multiphysics Peridynamic Model for Simulation of Fracture in Si Thin Films during Lithiation/Delithiation Cycles
Abstract
:1. Introduction
2. Method and Model
2.1. Bond-Based Peridynamic Mechanical Model
2.2. Peridynamic Diffusion Model
2.3. Coupled Peridynamic Chemo-Mechanical Model
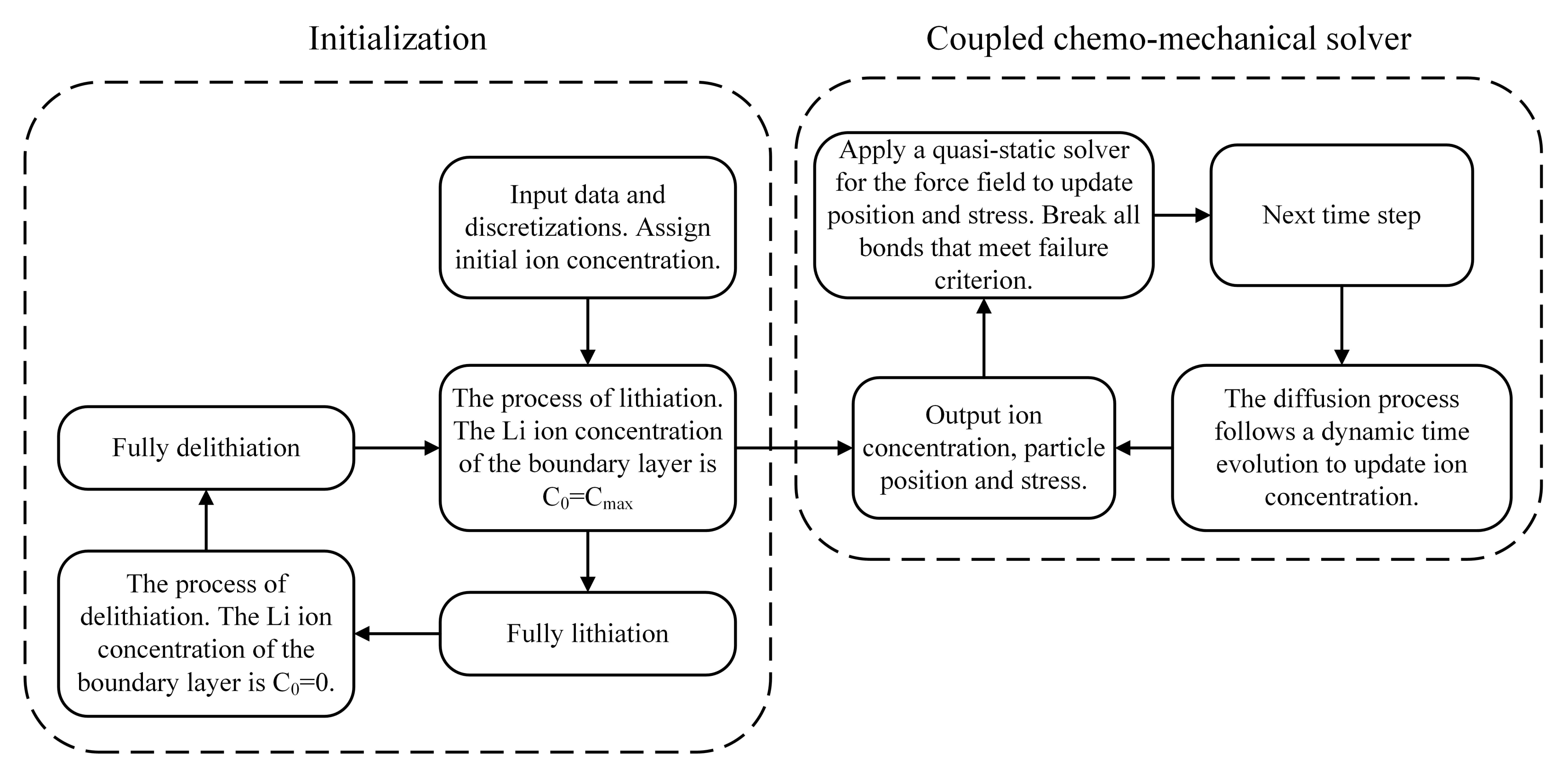
2.4. Flowchart of the Numerical Scheme
3. Numerical Examples
3.1. Numerical Model
3.2. Fracture of Continuous Membrane
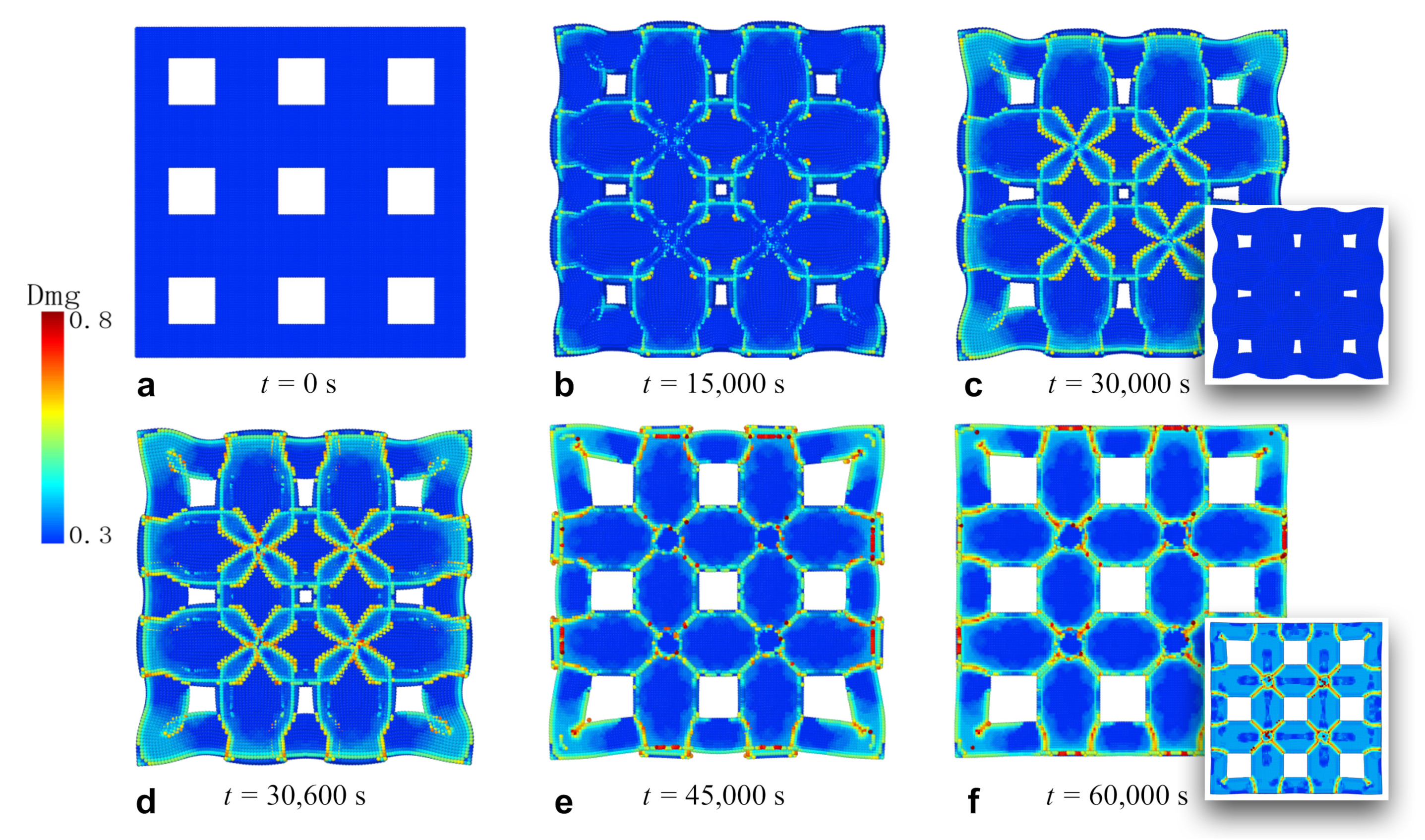
3.3. Fracture of Membrane with Square Holes
3.4. Fracture of Membrane with Circular Holes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boukamp, B.A.; Lesh, G.C.; Huggins, R.A. All-Solid Lithium Electrodes with Mixed-Conductor Matrix. J. Electrochem. Soc. 1981, 128, 725–729. [Google Scholar] [CrossRef]
- Chan, C.K.; Peng, H.; Liu, G.; McIlwrath, K.; Zhang, X.; Huggins, R.A.; Cui, Y. High-performance lithium battery anodes using silicon nanowires. Nat. Nanotech. 2008, 3, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.J. A review of the electrochemical performance of alloy anodes for lithium-ion batteries. J. Power Sources 2011, 196, 13–24. [Google Scholar] [CrossRef]
- Arora, P.; White, R.E.; Doyle, M. Capacity fade mechanisms and side reactions in lithium-ion batteries. J. Electrochem. Soc. 1998, 145, 3647. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wu, X.; Wang, Z.; Chen, L. Cracking causing cyclic instability of LiFePO4 cathode material. J. Power Sources 2005, 140, 125–128. [Google Scholar] [CrossRef]
- Son, D.; Kim, E.; Kim, T.G.; Kim, M.G.; Cho, J.; Park, B. Nanoparticle iron-phosphate anode material for Li-ion battery. Appl. Phys. Lett. 2004, 85, 5875. [Google Scholar] [CrossRef] [Green Version]
- Park, M.H.; Kim, K.; Kim, J.; Cho, J. Flexible dimensional control of high-capacity Li-ion-battery anodes: From 0D hollow to 3D porous germanium nanoparticle assemblies. Adv. Mater. 2010, 22, 415. [Google Scholar] [CrossRef]
- Cui, L.F.; Ruffo, R.; Chan, C.K.; Peng, H.L.; Cui, Y. Crystalline-amorphous core-shell silicon nanowires for high capacity and high current battery electrodes. Nano Lett. 2009, 9, 491–495. [Google Scholar] [CrossRef]
- Liu, N.; Wu, H.; McDowell, M.T.; Yao, Y.; Wang, C.; Cui, Y. A yolk–shell design for stabilized and scalable Li-ion battery alloy anodes. Nano Lett. 2012, 12, 3315–3321. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Lu, Z.; Zhao, J.; McDowell, M.T.; Lee, H.W.; Zhao, W.; Cui, Y. A pomegranate-inspired nanoscale design for large-volume- change lithium battery anodes. Nat. Nanotech. 2014, 9, 187–192. [Google Scholar] [CrossRef]
- Winter, M.; Besenhard, J.O. Electrochemical lithiation of tin and tin-based intermetallics and composites. Electrochim. Acta 1999, 45, 31–50. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, N.; Cui, Y. Promises and challenges of nanomaterials for lithium-based rechargeable batteries. Nat. Energy 2016, 1, 16071. [Google Scholar] [CrossRef]
- Liu, X.; Huang, J. In situ TEM electrochemistry of anode materials in lithium ion batteries. Energy Environ. Sci. 2011, 4, 3844–3860. [Google Scholar] [CrossRef]
- Xie, H.; Qiu, W.; Song, H.; Tian, J. InSitumeasurementofthedeformationandelas- tic modulus evolution in Si composite electrodes during electrochemical lithiation and delithiation. J. Electrochem. Soc. 2016, 163, A2685–A2690. [Google Scholar] [CrossRef]
- Sandu, G.; Brassart, L.; Ois Gohy, J.F.; Pardoen, T.; Melinte, S.; Vlad, A. Surface Coating Mediated Swelling and Fracture of Silicon Nanowires during Lithiation. ACS Nano 2014, 8, 9427–9436. [Google Scholar] [CrossRef]
- Shi, F.; Song, Z.; Gabor, A.; Somorjai, P.N.R.; Ritchie, R.O.; Komvopoulos, K. Failure mechanisms of single-crystal silicon electrodes in lithium-ion batteries. Nat. Commun. 2016, 7, 11886. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; McDowella, M.T.; Berlaa, L.A.; Nixa, W.D.; Cui, Y. Fracture of crystalline silicon nanopillars during electrochemical lithium insertion. Proc. Natl. Acad. Sci. USA 2012, 109, 4080–4085. [Google Scholar] [CrossRef] [Green Version]
- Christensen, J.; Newman, J. A mathematical model of stress generation and fracture in lithium manganese oxide. J. Electrochem. Soc. 2006, 153, A1019–A1030. [Google Scholar] [CrossRef]
- Zhao, K.; Pharr, M.; Vlassak, J.; Suo, Z. Inelastic hosts as electrodes for high-capacity lithium-ion batteries. J. Appl. Phys. 2011, 109, 016110. [Google Scholar] [CrossRef] [Green Version]
- Zhao, K.; Pharr, M.; Cai, S.; Vlassak, J.; Suo, Z. Large plastic deformation in high-capacity lithium-ion batteries caused by charge and discharge. J. Am. Ceram. Soc. 2011, 94, S226–S235. [Google Scholar] [CrossRef]
- Anand, L. A Cahn–Hilliard-type theory for species diffusion coupled with large elastic–plastic deformations. J. Mech. Phys. Solids 2012, 60, 1983–2002. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.; Liu, F.; Liu, Y. Analytical modeling of dislocation effect on diffusion induced stress in a cylindrical lithium ion battery electrode. J. Power Sources 2014, 272, 121–127. [Google Scholar] [CrossRef]
- Cui, Z.; Gao, F.; Qu, J. A finite deformation stress-dependent chemical potential and its applications to lithium ion batteries. J. Mech. Phys. Solids 2012, 60, 1280. [Google Scholar] [CrossRef]
- Hao, F.; Fang, D. Diffusion-Induced Stresses of Spherical Core-Shell Electrodes in Lithium-Ion Batteries: The Effects of the Shell and Surface/Interface Stress. J. Electrochem. Soc. 2013, 160, A595–A600. [Google Scholar] [CrossRef]
- Ma, Z.; Xie, Z.; Wang, Y.; Zhang, P.; Pan, Y.; Zhou, Y.; Lu, C. Failure modes of hollow coreeshell structural active materials during the lithiationedelithiation process. J. Power Sources 2015, 290, 114–122. [Google Scholar] [CrossRef]
- Zhao, K.; Pharr, M.; Hartle, L.; Vlassak, J.J.; Suo, Z. Fracture and debonding in lithium-ion batteries with electrodes of hollow coreeshell nanostructures. J. Power Sources 2012, 218, 6–14. [Google Scholar] [CrossRef]
- Xu, C.; Weng, L.; Chen, B.; Zhou, J.; Cai, R. An analytical model for the fracture behavior in hollow cylindrical anodes. Int. J. Mech. Sci. 2019, 157–158, 87–97. [Google Scholar] [CrossRef]
- Hao, F.; Fang, D. Tailoring diffusion-induced stresses of core- shell nanotube electrodes in lithium-ion batteries. J. Appl. Phys. 2013, 113, 013507. [Google Scholar] [CrossRef]
- Sun, G.; Sui, T.; Song, B.; Zheng, H.; Lu, L.; Korsunsky, A.M. On the fragmentation of active material secondary particles in lithium ion battery cathodes induced by charge cycling. Extrem. Mech. Lett. 2016, 9, 449–458. [Google Scholar] [CrossRef]
- Bucci, G.; Swamy, T.; Chiang, Y.M.; Carter, W.C. Modeling of internal mechanical failure of all-solid-state batteries during electrochemical cycling, and implications for battery design. J. Mater. Chem. A 2017, 5, 19422–19430. [Google Scholar] [CrossRef]
- Klinsmann, M.; Rosato, D.; Kamlah, M.; McMeeking, R.M. Modeling crack growth during Li insertion in storage particles using a fracture phase field approach. J. Mech. Phys. Solids 2016, 92, 313–344. [Google Scholar] [CrossRef]
- Réthoré, J.; Zheng, H.; Li, H.; Li, J.; Aifantis, K.E. A multiphysics model that can capture crack patterns in Si thin films based T on their microstructure. J. Power Sources 2018, 400, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Dozier, A.K.; Li, Y.; Yang, F.; Cheng, Y.T. Crack Pattern Formation in Thin Film Lithium-Ion Battery Electrodes. J. Electrochem. Soc. 2011, 158, A689–A694. [Google Scholar] [CrossRef]
- Li, T.; Gulzar, U.; Zaccaria, R.P.; Capiglia, C.; Hackney, S.A.; Aifantis, K.E. Damage Formation in Sn Film Anodes of Na-Ion Batteries. J. Phys. Chem. C 2019, 123, 15244–15250. [Google Scholar] [CrossRef]
- Silling, S. Reformulationofelasticitytheoryfordiscontinuitiesandlong-rangeforces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef] [Green Version]
- Silling, S.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic States and Constitutive Modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef] [Green Version]
- Silling, S.; Lehoucq, R. Peridynamic theory of solid mechanics. Adv. Appl. Mech. 2010, 44, 73–166. [Google Scholar]
- Chen, Z.; Bobaru, F. Peridynamic modeling of pitting corrosion damage. J. Mech. Phys. Solids 2015, 78, 352–381. [Google Scholar] [CrossRef]
- Chen, Z.; Jafarzadeh, S.; Zhao, J.; Bobaru, F. A coupled mechano-chemical peridynamic model for pit-to-crack transition in stress-corrosion cracking. J. Mech. Phys. Solids 2021, 146, 104203. [Google Scholar] [CrossRef]
- Shi, C.; Gong, Y.; Yang, Z.; Tong, Q. Peridynamic investigation of stress corrosion cracking in carbon steel pipes. Eng. Fract. Mech. 2019, 219, 1–11. [Google Scholar] [CrossRef]
- Tong, Q.; Li, S. Multiscale coupling of molecular dynamics and peridynamics. J. Mech. Phys. Solids 2016, 95, 169–187. [Google Scholar] [CrossRef]
- Tong, Q.; Li, S. A concurrent multiscale study of dynamic fracture. Comput. Methods Appl. Mech. Eng. 2020, 366, 113075. [Google Scholar] [CrossRef]
- Bohn, E.; Eckl, T.; Kamlah, M.; McMeeking, R. A Model for Lithium Diffusion and Stress Generation in an Intercalation Storage Particle with Phase Change. J. Electrochem. Soc. 2013, 160, A1638–A1652. [Google Scholar] [CrossRef]
- Wang, H.; Oterkus, E.; Oterkus, S. Peridynamic modelling of fracture in marine lithium-ion batteries. Ocean Eng. 2018, 151, 257–267. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Oterkus, E.; Oterkus, S. Predicting fracture evolution during lithiation process using peridynamics. Eng. Fract. Mech. 2018, 192, 176–191. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Oterkus, E.; Oterkus, S. Three-Dimensional Peridynamic Model for Predicting Fracture Evolution during the Lithiation Process. Energies 2018, 11, 1461. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Diffusion coefficient | m/s | ||
| Young’s modulus of lithiated Si | 12 | GPa | |
| Young’s modulus of TiC | GPa | ||
| Young’s modulus of Si-TiC | GPa | ||
| Poisson’s ratio | |||
| Fracture energy of Si in first lithiation | 2000 | J/m | |
| Fracture energy of Si in first delithiation | 400 | J/m | |
| Fracture energy of Si-TiC | 500 | J/m | |
| Partial molar volume of Si | m/mol | ||
| Gas constant | k | ||
| Temperature | T | 300 | K |
| Width of Si thin film | L | nm | |
| Thickness of Si thin film | H | 600 | nm |
| Width of TiC substrate | nm | ||
| Thickness of TiC substrate | 300 | nm | |
| Grid size | 100 | nm | |
| Horizon | 300 | nm | |
| Critical stretch of Si in first lithiation | |||
| Critical stretch of Si in first delithiation | |||
| Critical stretch of Si-TiC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Tong, Q. A Multiphysics Peridynamic Model for Simulation of Fracture in Si Thin Films during Lithiation/Delithiation Cycles. Materials 2021, 14, 6081. https://doi.org/10.3390/ma14206081
Wang X, Tong Q. A Multiphysics Peridynamic Model for Simulation of Fracture in Si Thin Films during Lithiation/Delithiation Cycles. Materials. 2021; 14(20):6081. https://doi.org/10.3390/ma14206081
Chicago/Turabian StyleWang, Xiaofei, and Qi Tong. 2021. "A Multiphysics Peridynamic Model for Simulation of Fracture in Si Thin Films during Lithiation/Delithiation Cycles" Materials 14, no. 20: 6081. https://doi.org/10.3390/ma14206081
APA StyleWang, X., & Tong, Q. (2021). A Multiphysics Peridynamic Model for Simulation of Fracture in Si Thin Films during Lithiation/Delithiation Cycles. Materials, 14(20), 6081. https://doi.org/10.3390/ma14206081






