Numerical and Experiment Studies of Different Path Planning Methods on Mechanical Properties of Composite Components
Abstract
:1. Introduction
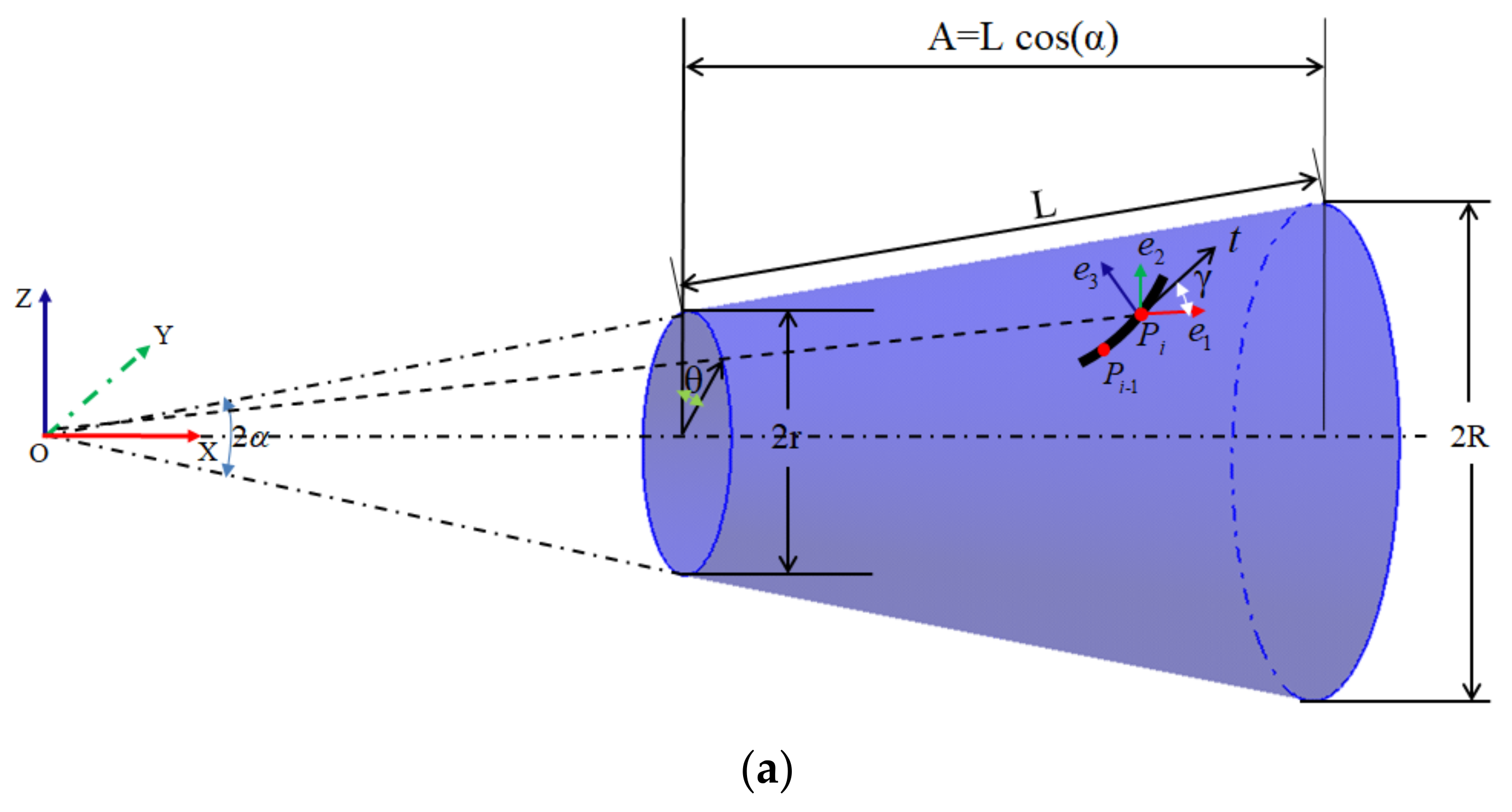
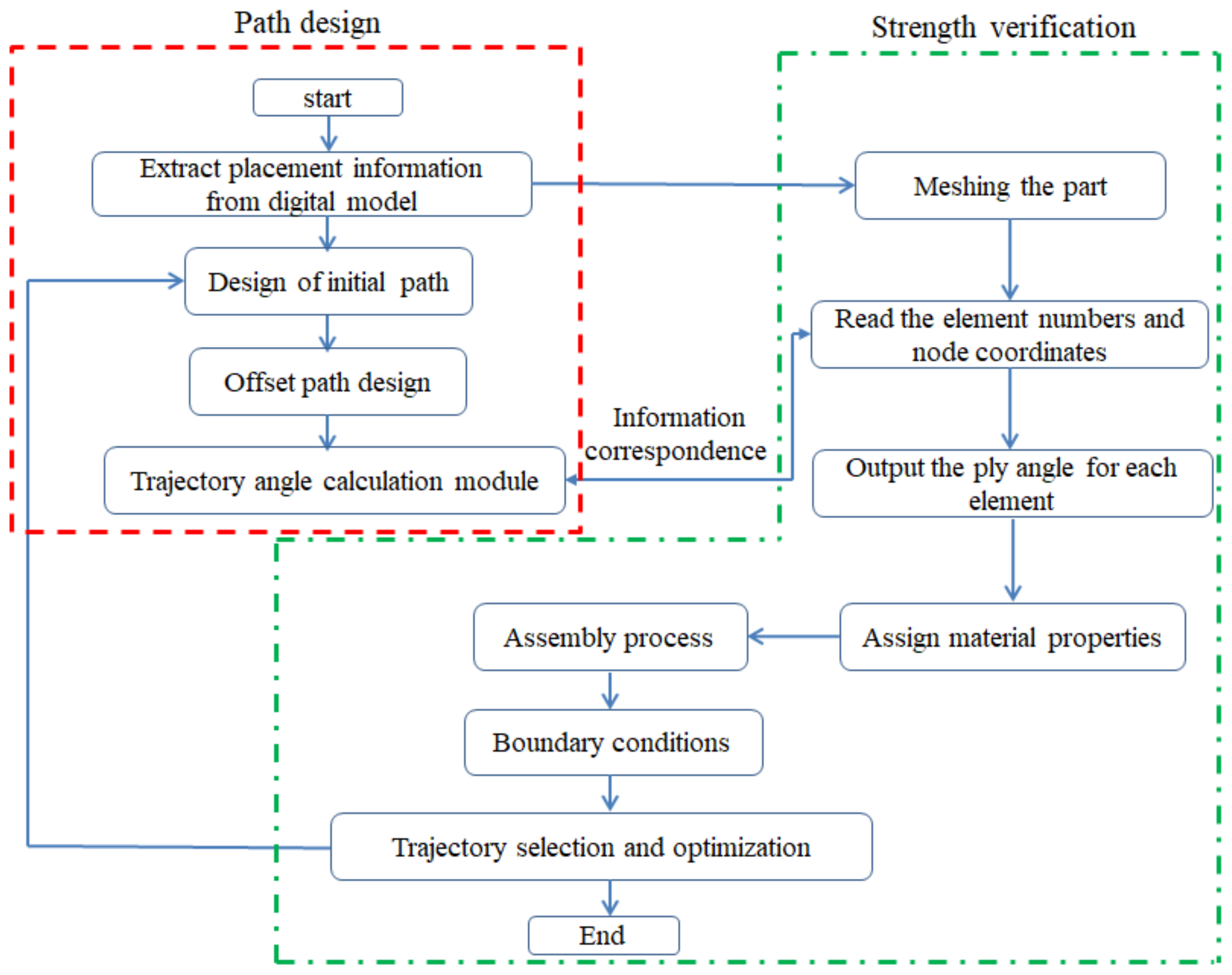
2. Path Planning for Composites Conical Shell
2.1. Numerical Model
2.2. Trajectory of Conical Shell and Its Manufacturability
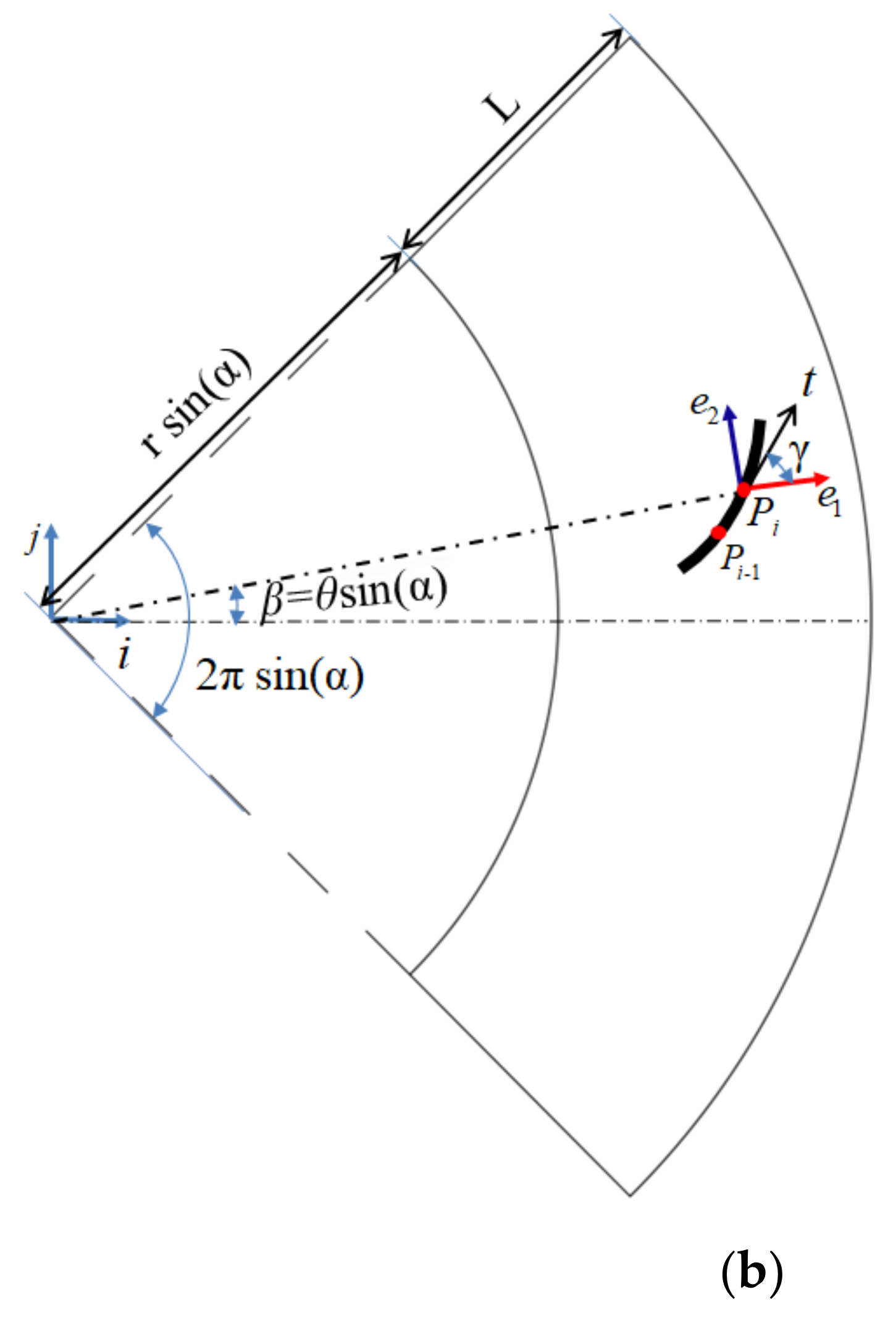
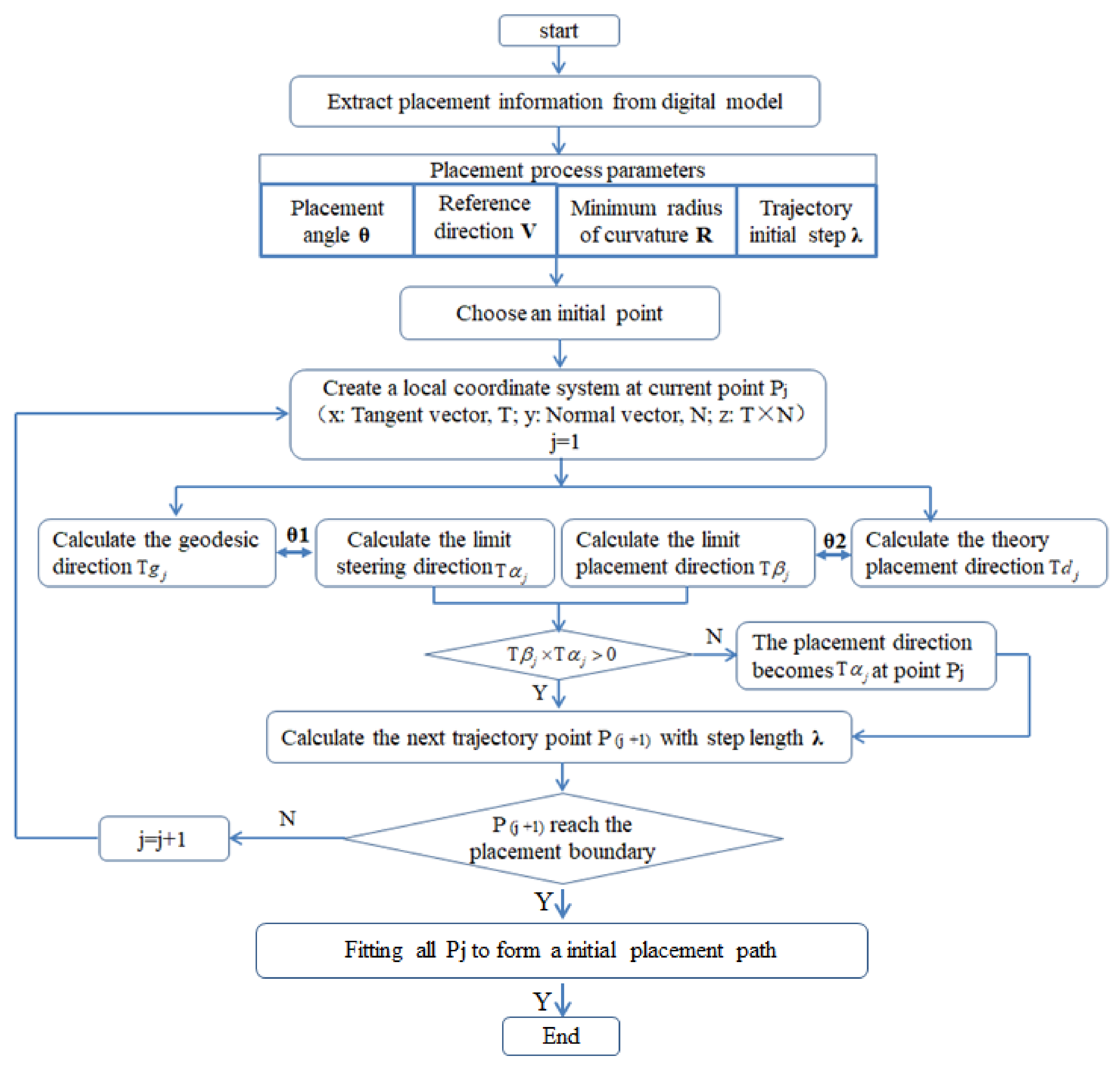
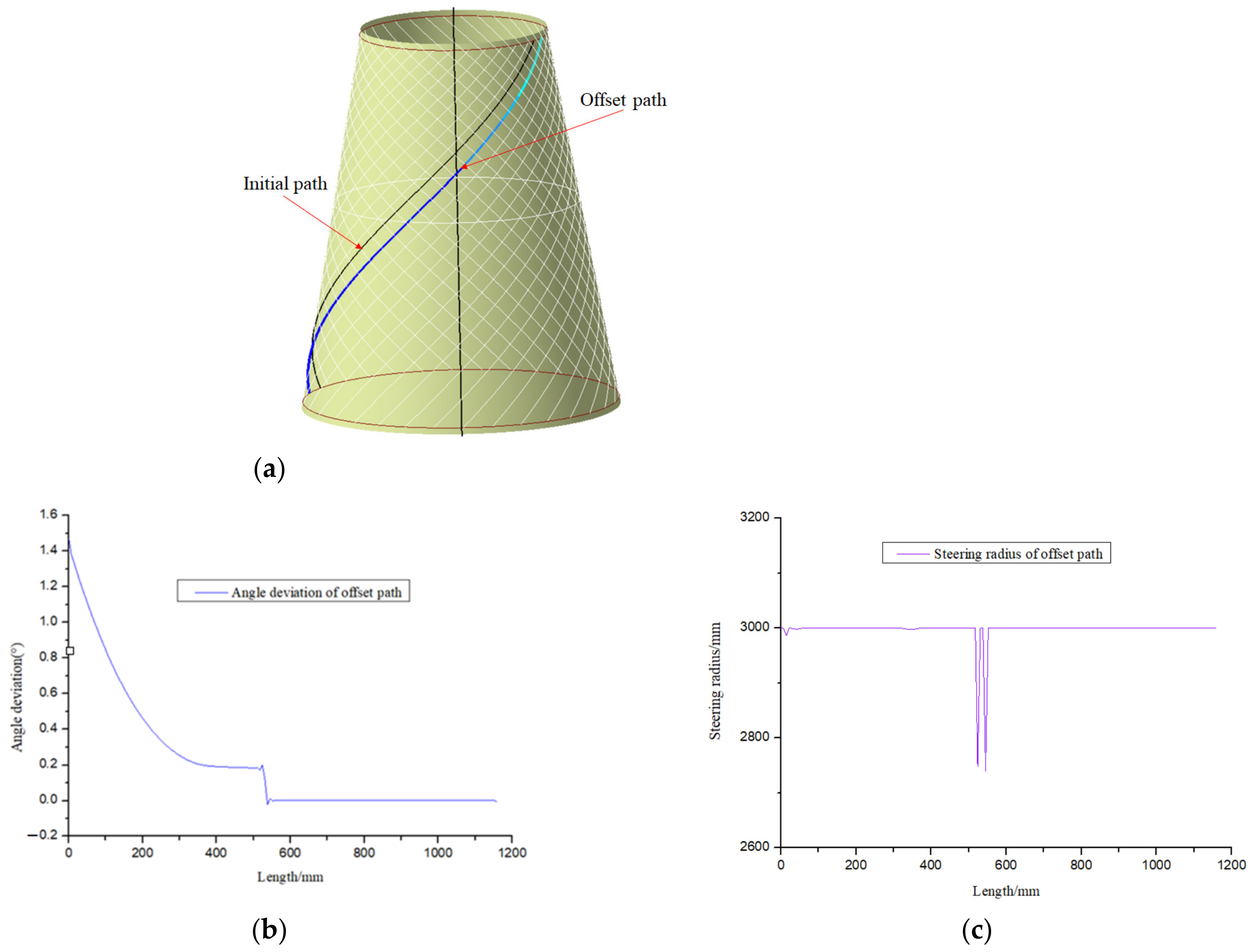
2.2.1. Initial Path Generation
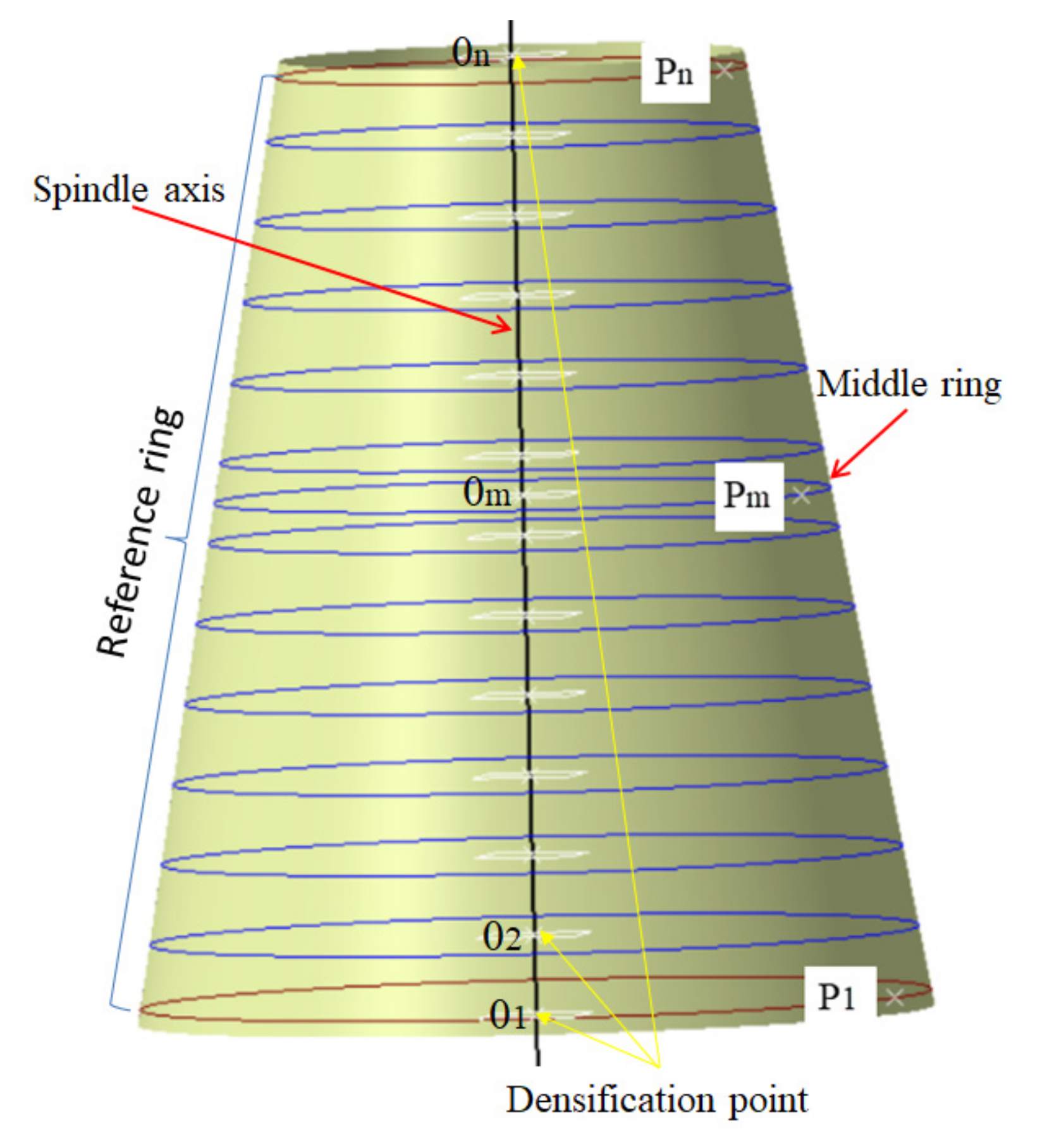
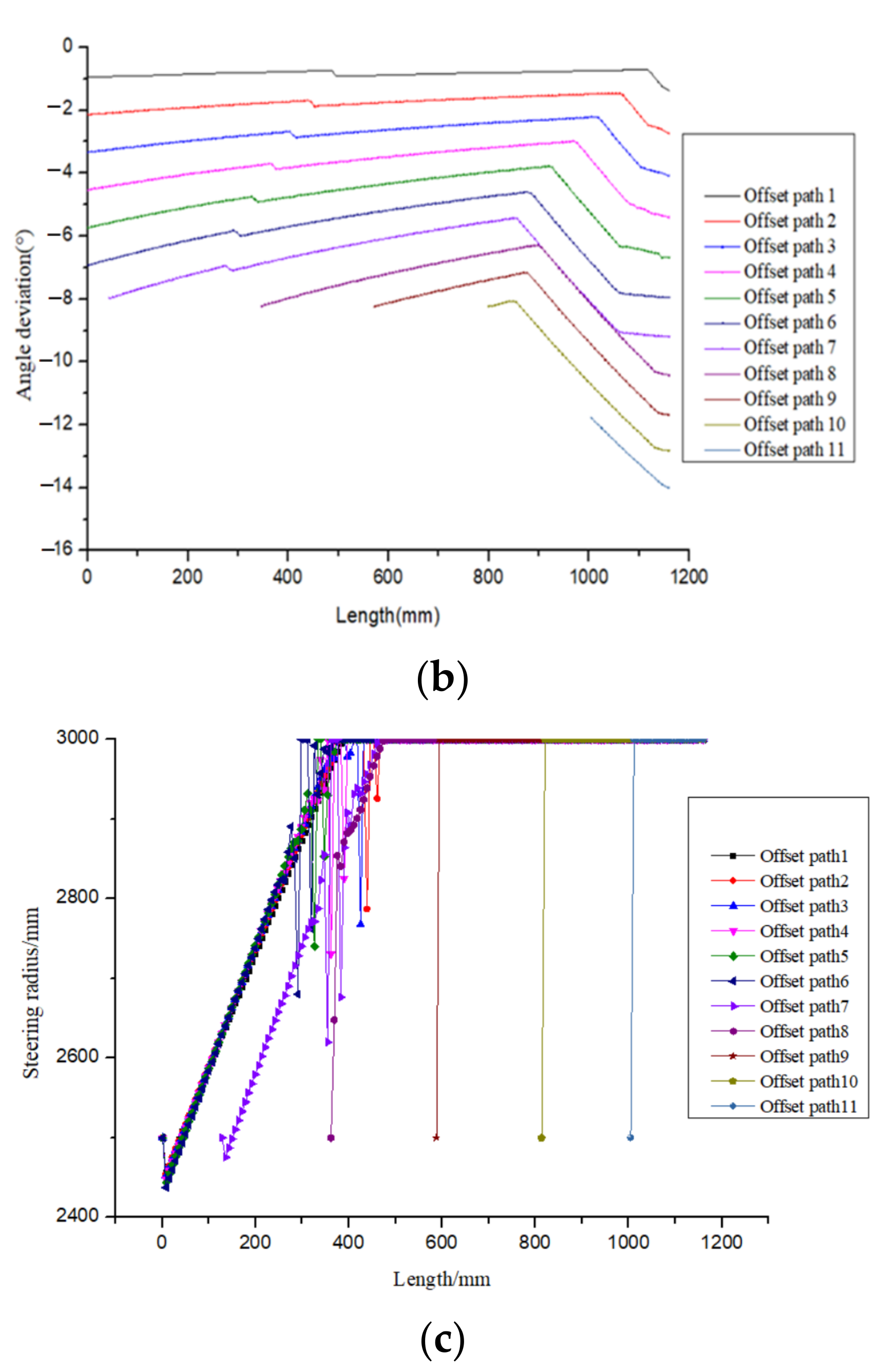
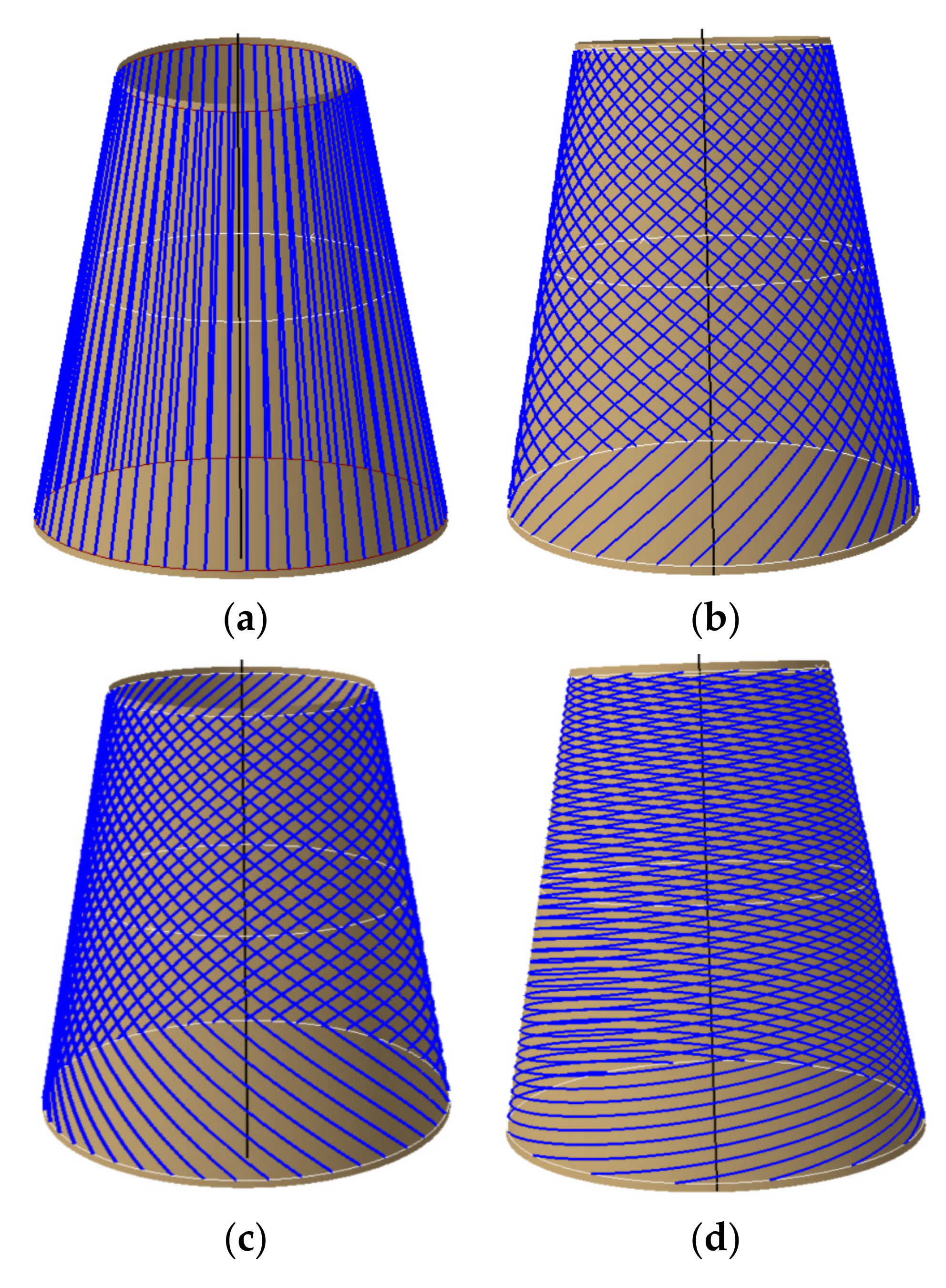
2.2.2. Densification and Coverage Algorithm of the Initial Path
3. Finite Element Analysis Based on Path Design
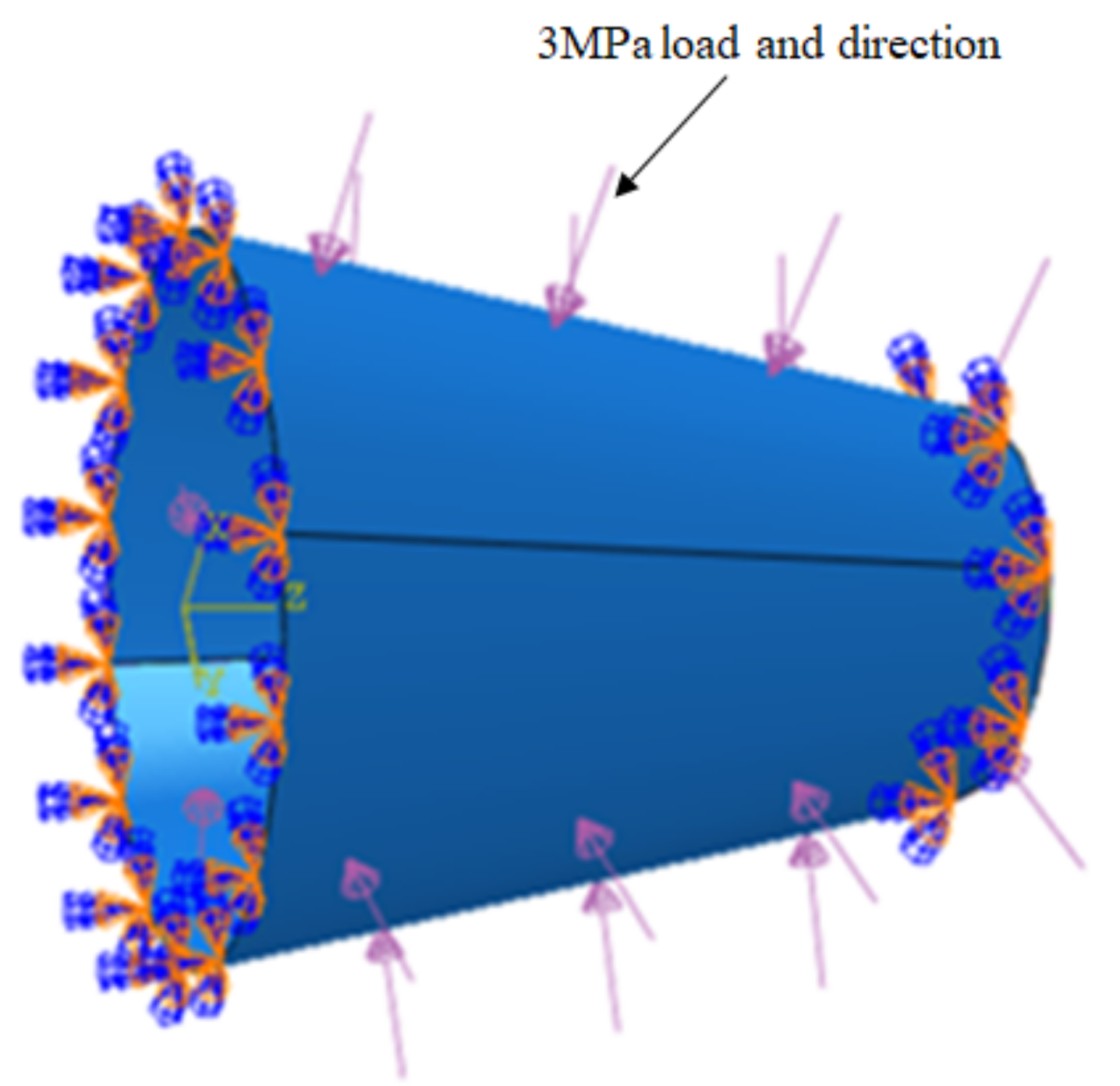
3.1. Material Parameters and Ply Settings
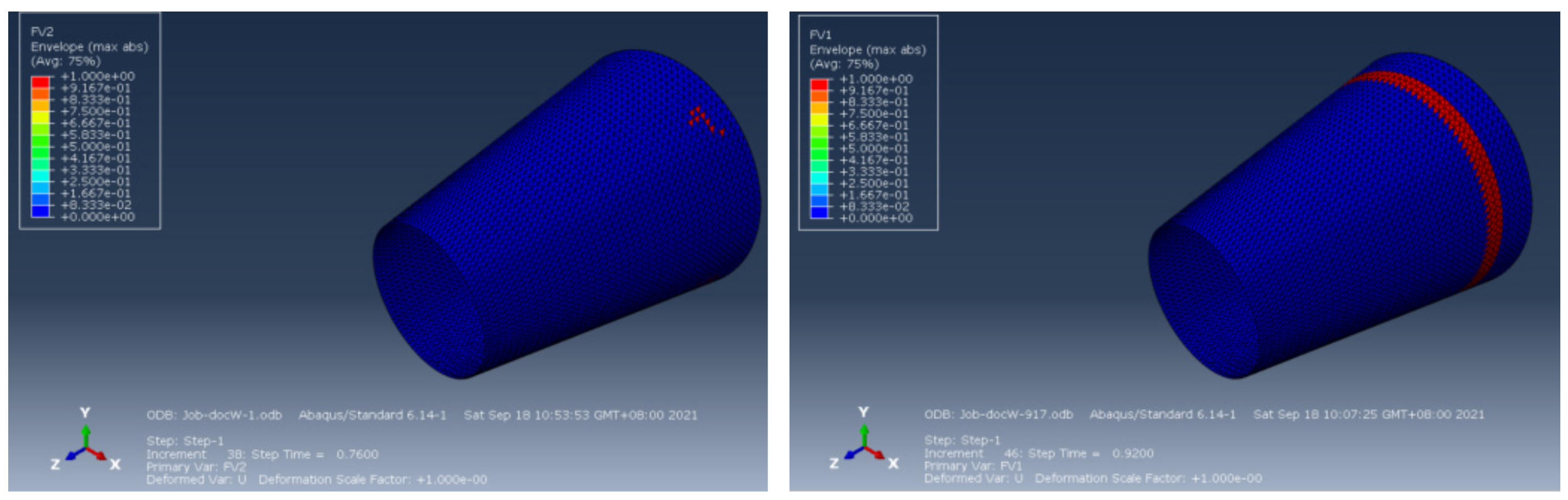
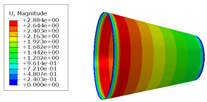
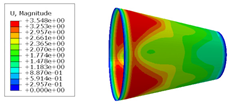
3.2. Simulation Results of Stress Distribution of Composite Conical Shell
4. Experimental and Analysis
5. Conclusions
- (1)
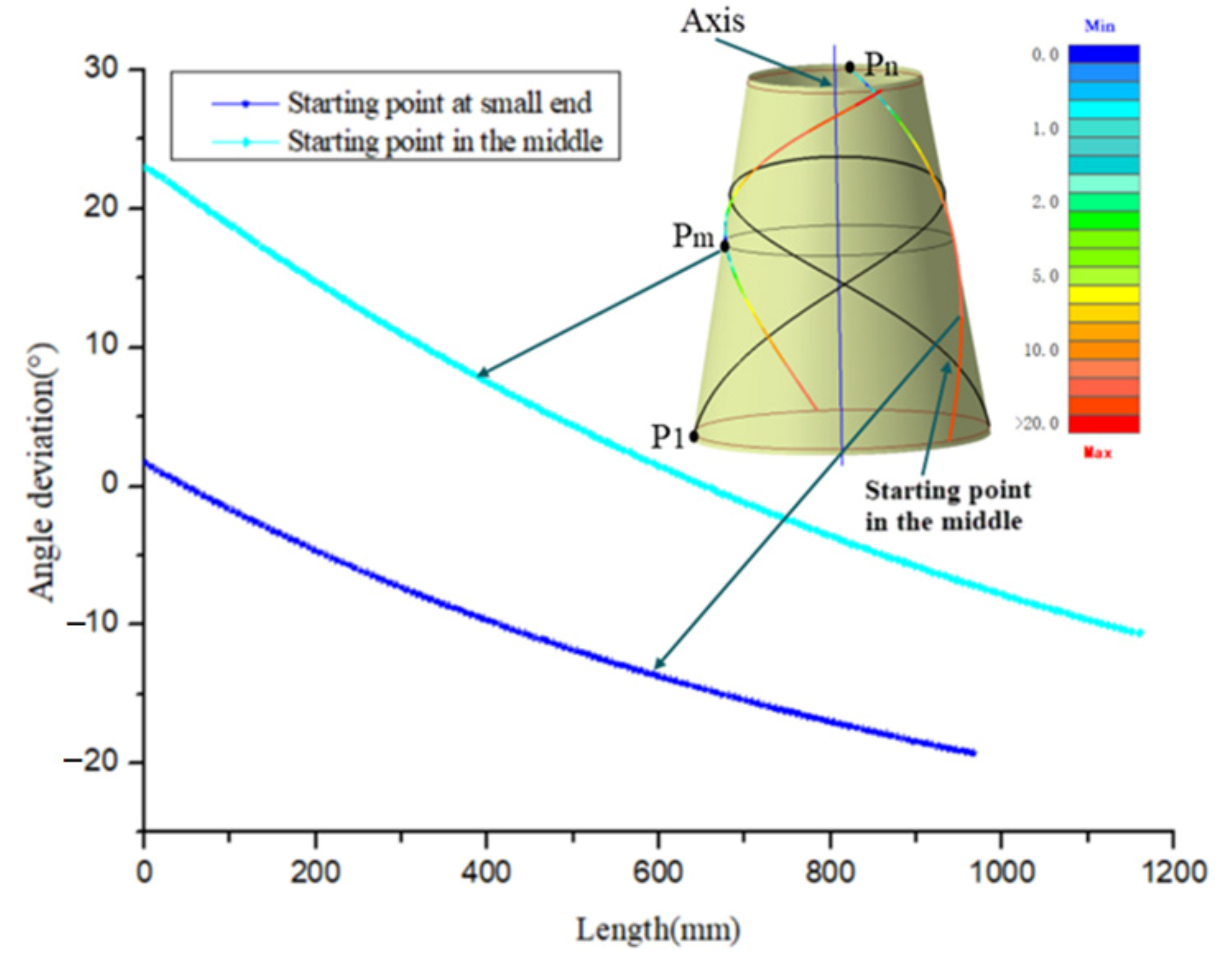
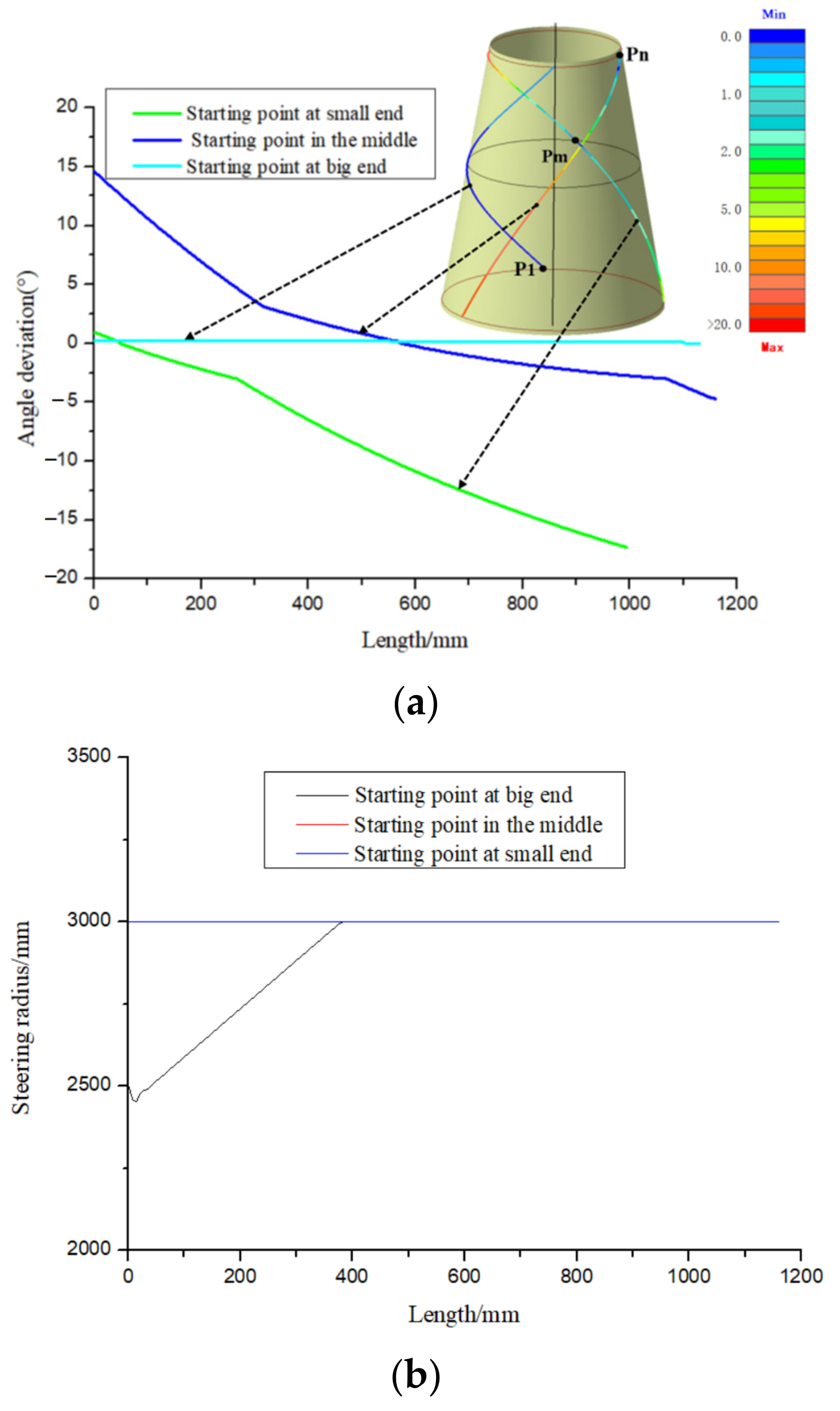
- The initial point is extremely important to the initial path and offset paths. If the initial point selection is unreasonable, on the one hand, which will lead to the failure of path generation because the occurrence of path turns back and cannot reach the boundary, on the other hand, when taking the initial point close to the boundary, the angle deviation can reach more than 20°, which cannot meet placement requirement. Therefore, it is necessary to iteratively optimize the initial point to design the initial path to make it have the best laying quality.
- (2)
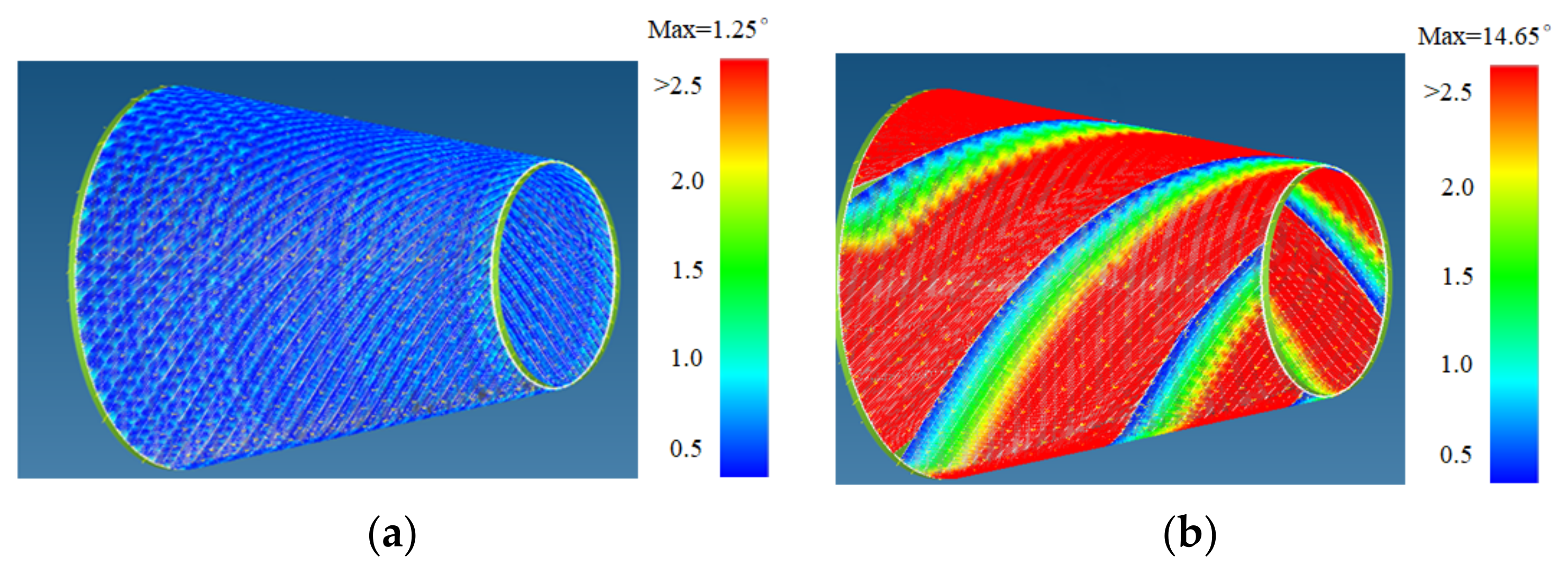
- The fixed angle algorithm meets the requirements of structural design, but it is easy to produce wrinkles. Compared with the fixed angle method, the geodesic method has an infinite curvature radius and no wrinkles will occur. However, it is very easy to cause the angle deviation to exceed its upper limit. The variable angle trajectory planning method is an ideal solution for the placement of composite conical shells at present because it comprehensively considers the angle deviation and steering radius of the path. For this cone shell, the angle deviation of the variable angle path designed by the path design software developed independently by our research group is less than 2 degrees, and the minimum steering radius of the path is greater than 2000 mm.
- (3)
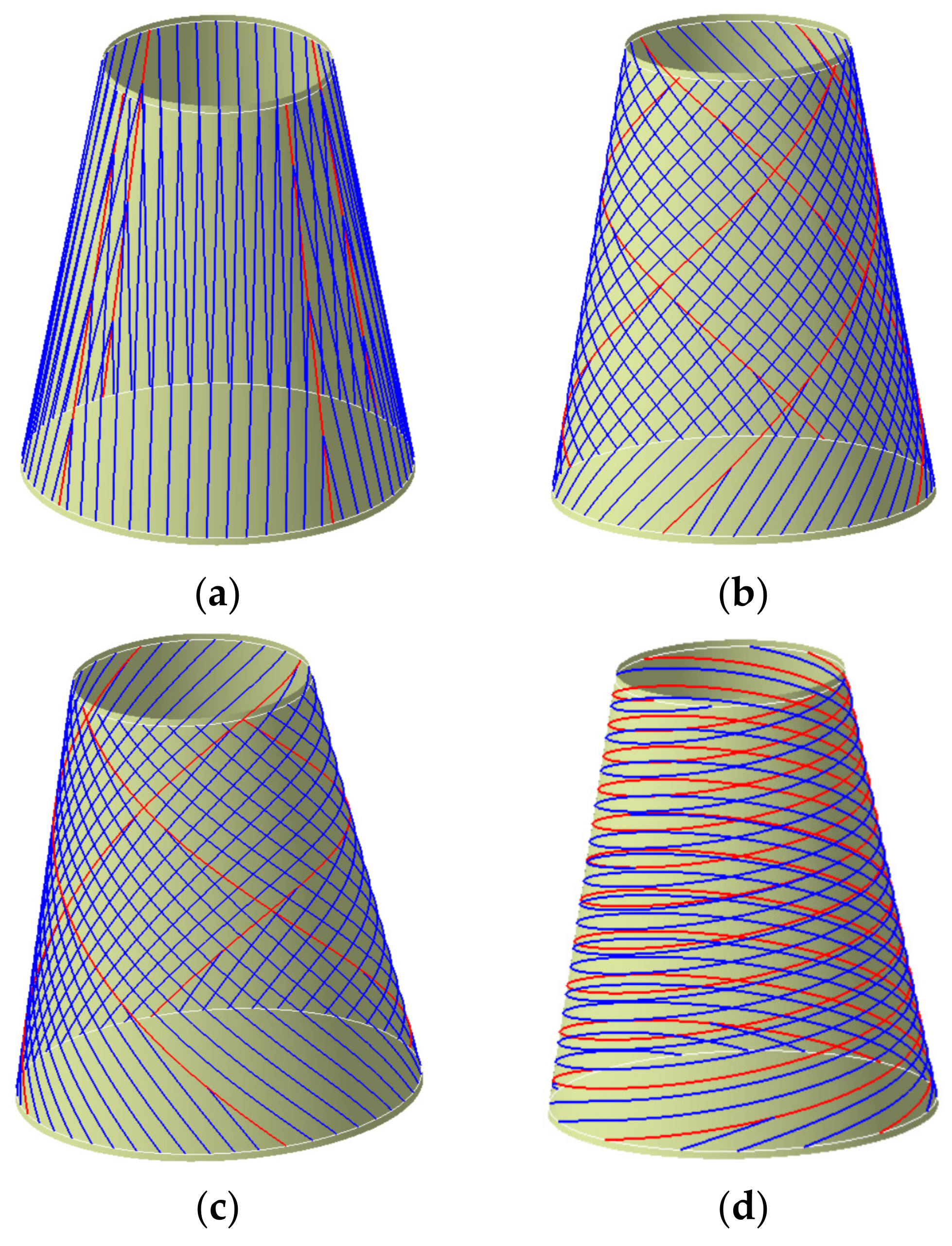
- By comparing the circumferential averaging variable angle path design method (Figure 13a), the partition variable angle path design method (Figure 14b) has smaller angle deviation, and the gaps/overlaps position are more evenly distributed on the surface of the conical shell. The possible explanation is that the size of path angle deviation and the position of the overlapping area formed by different path planning methods have a great impact on the mechanical performance. Therefore, the organic combination of defect suppression, path planning, and strength analysis greatly ensures the rationality of path design, which makes it possible to lay high-quality and efficient, especially for complex rotating bodies.
- (4)
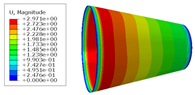
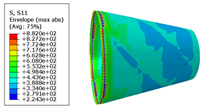
- According to the finite element analysis results of the cone shell with two trajectory planning methods of partition variable angle path and circumferential averaging variable angle path, it can be observed that the maximum deformation and maximum transverse and longitudinal stress of fiber of circumferential averaging variable angle path conical shell are reduced by 16.3%, 5.85%, and 19.76%, respectively, than that of the partition variable angle trajectory. Considering the manufacturability and strength of all laying paths, the design scheme based on circumferential averaging variable angle path is better than the partition variable angle path design scheme.
- (5)
- The actual placement experiment proves that the proposed path generation method can obtain a good placement effect. This fully shows that the path generation method has strong engineering practicability and can well ensure the quality of tow placement. In addition, both experiments and Finite element simulation results further verify the rationality of path design method proposed in this paper. The path planning algorithm that coordinates path planning and defect suppression plays an important role in optimizing placement trajectory and improving mechanical properties of parts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shirinzadeh, B.; Aized, T. Robotic fiber placement process analysis and optimization using response surface method. Int. J. Adv. Manuf. Technol. 2011, 55, 393–404. [Google Scholar]
- Wen, L.; Xiao, J.; Wang, X. Research progress of automatic composite placement technology in China. J. Nanjing Univ. Aeronaut. 2015, 47, 637–649. [Google Scholar]
- Asif, M.; Ahmed, I. Advanced composite material for aerospace application—A review. Int. J. Eng. Manuf. Sci. 2017, 7, 393–409. [Google Scholar]
- Marsh, G. Automating aerospace composites production with fiber placement. Reinf. Plast. 2011, 55, 32–37. [Google Scholar]
- Lemaire, E.; Zein, S.; Bruyneel, M. Optimization of composite structures with curved fiber trajectories. Compos. Struct. 2015, 131, 895–904. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Xiao, J.; Li, Y.; Chu, Q.; Xu, T.; Wang, B. An Experimental Study of the Influence of in-Plane Fiber Waviness on Unidirectional Laminates Tensile Properties. Appl. Compos. Mater. 2017, 24, 1321–1337. [Google Scholar] [CrossRef]
- Long, Y.; Chen, Z.; Shi, Y.; Mo, R. An accurate approach to roller path generation for robotic fiber placement of free-form surface composites. Robot. Comput. Integr. Manuf. 2014, 30, 277–286. [Google Scholar]
- Schueler, K.; Miller, J.; Hale, R. Approximate geometric methods in application to the modeling of fiber placed composite structures. J. Comput. Inf. Sci. Eng. 2004, 4, 251–256. [Google Scholar] [CrossRef]
- Duan, Y.; Ge, Y.; Xin, Z. Trajectory planning of fiber placement based on controlled angle and interval. J. Aeronaut. 2015, 25, 3475–3482. [Google Scholar]
- Qu, W.; Gao, J.; Yang, D.; He, R.; Yang, Q.; Cheng, L.; Ke, Y. Automated fiber placement path generation method based on prospective analysis of path performance under multiple constraints. Compos. Struct. 2021, 255, 112940. [Google Scholar] [CrossRef]
- Shirinzadeh, B.; Cassidy, G.; Oetomo, D.; Alici, G.; Ang, M. Trajectory generation for open-contoured structures in robotic fiber placement. Robot. Comput. Integr. Manuf. 2007, 23, 380–394. [Google Scholar] [CrossRef]
- Sonmez, F.; Akbulut, M. Process optimization of tape placement for thermoplastic composites. Compos. A 2007, 38, 2013–2023. [Google Scholar] [CrossRef]
- Brooks, T.; Martins, J. On manufacturing constraints for tow-steered composite design optimization. Compos. Struct. 2018, 204, 548–559. [Google Scholar] [CrossRef]
- Falcóa, O.; Mayugo, J.; Lopes, C.; Gascons, N.; Turon, A.; Costa, J. Variable-stiffness composite panels: As-manufactured modeling and its influence on the failure behavior. Compos. Part B Eng. 2014, 56, 660–669. [Google Scholar] [CrossRef]
- Gao, J.; Qu, W.; Yang, D.; Zhu, W.; Ke, Y. Two-Stage Sector Partition Path Planning Method for Automated Fiber Placement on Complex Surfaces. Comput. Aided Des. 2021, 132, 102983. [Google Scholar] [CrossRef]
- Zhao, C.; Xiao, J.; Huang, W.; Huang, X.; Gu, S. Layup quality evaluation of fiber trajectory based on prepreg tow deformability for automated fiber placement. J. Reinf. Plast Compos. 2016, 35, 1576–1585. [Google Scholar] [CrossRef]
- Zhang, P.; Sun, R.; Zhao, X.; Hu, L. Placement suitability criteria of composite tape for mould surface in automated tape placement. Chin. J. Aeronaut. 2015, 28, 1574–1581. [Google Scholar] [CrossRef] [Green Version]
- Qu, W.; He, R.; Cheng, L.; Yang, D.; Gao, J.; Wang, H.; Yang, Q.; Ke, Y. Placement suitability analysis of automated fiber placement on curved surfaces considering the influence of prepreg tow, roller and AFP machine. Compos. Struct. 2021, 262, 113608. [Google Scholar] [CrossRef]
- Blom, A.; Stickler, P.; Gürdal, Z. Optimization of a composite cylinder under bending by tailoring stiffness properties in circumferential direction. Compos. Part B 2010, 41, 157–165. [Google Scholar] [CrossRef]
- Xiong, W.; Xiao, J.; Wang, X.; Li, J.; Huang, Z. Algorithm of Adaptive Path Planning for automated Placement on Meshed Surface. Acta Aeronaut. Et Astronaut. Sin. 2013, 34, 434–441. [Google Scholar]
- Shirinzadeh, B.; Alici, G.; Foong, C.; Cassidy, G. Fabrication process of open surfaces by robotic fiber placement. Robot. Comput. Integr. Manuf. 2004, 20, 17–28. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, B.; Xiao, J. Macroscopic characterization of fibermicro-buckling and its influence on composites tensile performance. J. Reinf. Plast. Compos. 2016, 36, 196–205. [Google Scholar] [CrossRef]
- Debski, H.; Rozylo, P.; Teter, A. Buckling and limit states of thin-walled composite columns under eccentric load. Thin Walled Struct. 2021, 149, 106627. [Google Scholar] [CrossRef]
- Zimmermann, N.; Wang, P.H. A Review of Failure Modes and Fracture Analysis of Aircraft Composite Materials. Eng. Fail. Anal. 2020, 20, 104692. [Google Scholar] [CrossRef]
- Rozylo, P.; Debski, H.; Wysmulski, P.; Falkowicz, K. Numerical and experimental failure analysis of thin-walled composite columns with a top-hat cross section under axial compression. Compos. Struct. 2018, 204, 207–216. [Google Scholar] [CrossRef]
- Wu, K.; Turpin, J.; Stanford, B. Structural Performance of Advanced Composite tow-steered shells with cutouts. In Proceedings of the 55th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, National Harbor, MD, USA, 13–17 January 2014; p. 1056. [Google Scholar]
- Hu, H.; Ou, S. Maximization of the fundamental frequencies of laminated truncated conical shells with respect to fiber orientations. Compos. Struct. 2001, 52, 265–275. [Google Scholar] [CrossRef]
- Blom, A.; Tatting, B.; Hol, J.; Guerdal, Z. Fiber path definitions for elastically tailored conical shells. Compos. Part B 2009, 40, 77–84. [Google Scholar] [CrossRef]
- Beakou, A.; Cano, M.; Cam, J.; Verney, V. Modelling slit tape buckling during automated prepreg manufacturing: A local approach. Compos. Struct. 2011, 93, 2628–2635. [Google Scholar] [CrossRef] [Green Version]
- Duvaut, G.; Terrel, G.; Lene, F. Optimization of fiber reinforced composites. Compos. Struct. 2000, 48, 83–89. [Google Scholar] [CrossRef]
- Ghiasi, H.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Optimum stacking sequence design of composite materials Part II: Variable stiffness design. Compos. Struct. 2010, 93, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wehbe, R.; Tatting, B.; Rajan, S.; Harik, R.; Sutton, M.; Gürdal, Z. Geometrical modeling of tow wrinkles in automated fiber placement. Compos. Struct. 2020, 246, 112394. [Google Scholar] [CrossRef]
- Shinya, H.; Teruki, I.; Narita, Y. Multi-objective optimization of curvilinear fiber shapes for laminated composite plates by using NSGA-II. Compos. Part B Eng. 2013, 45, 1071–1078. [Google Scholar]






| Property | E1/GPa | E2/GPa | G12/GPa | G13/GPa | G23/GPa | |
|---|---|---|---|---|---|---|
| Values | 170 | 8.6 | 4.8 | 4.8 | 3.4 | 0.2823 |
| Fixed Angle Path | Partition Variable Angle Path | Circumferential Averaging Variable Angle Path |
|---|---|---|
 |  |  |
 |  |  |
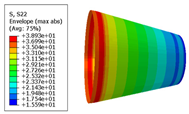 |  | 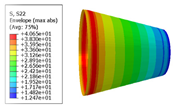 |
| Trajectory Design Scheme | U Max (mm) | S11 Max (MPa) | S22 Max (MPa) |
|---|---|---|---|
| Fixed angle trajectory | 2.884 | 776.3 | 38.93 |
| Partition variable angle trajectory | 3.548 | 882.0 | 50.66 |
| Circumferential averaging variable angle trajectory | 2.971 | 830.4 | 40.65 |
| Trajectory Design Scheme | Finite Element Simulation | Experimental Test |
|---|---|---|
| Partition variable angle trajectory | 4.56 MPa | 4.32 MPa |
| Circumferential averaging variable angle trajectory | 5.52 MPa | 5.38 MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Xiao, J.; Ju, X.; Dou, M.; Li, L.; Wang, X. Numerical and Experiment Studies of Different Path Planning Methods on Mechanical Properties of Composite Components. Materials 2021, 14, 6100. https://doi.org/10.3390/ma14206100
Wang D, Xiao J, Ju X, Dou M, Li L, Wang X. Numerical and Experiment Studies of Different Path Planning Methods on Mechanical Properties of Composite Components. Materials. 2021; 14(20):6100. https://doi.org/10.3390/ma14206100
Chicago/Turabian StyleWang, Dongli, Jun Xiao, Xiangwen Ju, Mingyue Dou, Liang Li, and Xianfeng Wang. 2021. "Numerical and Experiment Studies of Different Path Planning Methods on Mechanical Properties of Composite Components" Materials 14, no. 20: 6100. https://doi.org/10.3390/ma14206100
APA StyleWang, D., Xiao, J., Ju, X., Dou, M., Li, L., & Wang, X. (2021). Numerical and Experiment Studies of Different Path Planning Methods on Mechanical Properties of Composite Components. Materials, 14(20), 6100. https://doi.org/10.3390/ma14206100





