Grating Theory Approach to Optics of Nanocomposites
Abstract
:1. Introduction
2. Methodology
3. Numerical Experiments
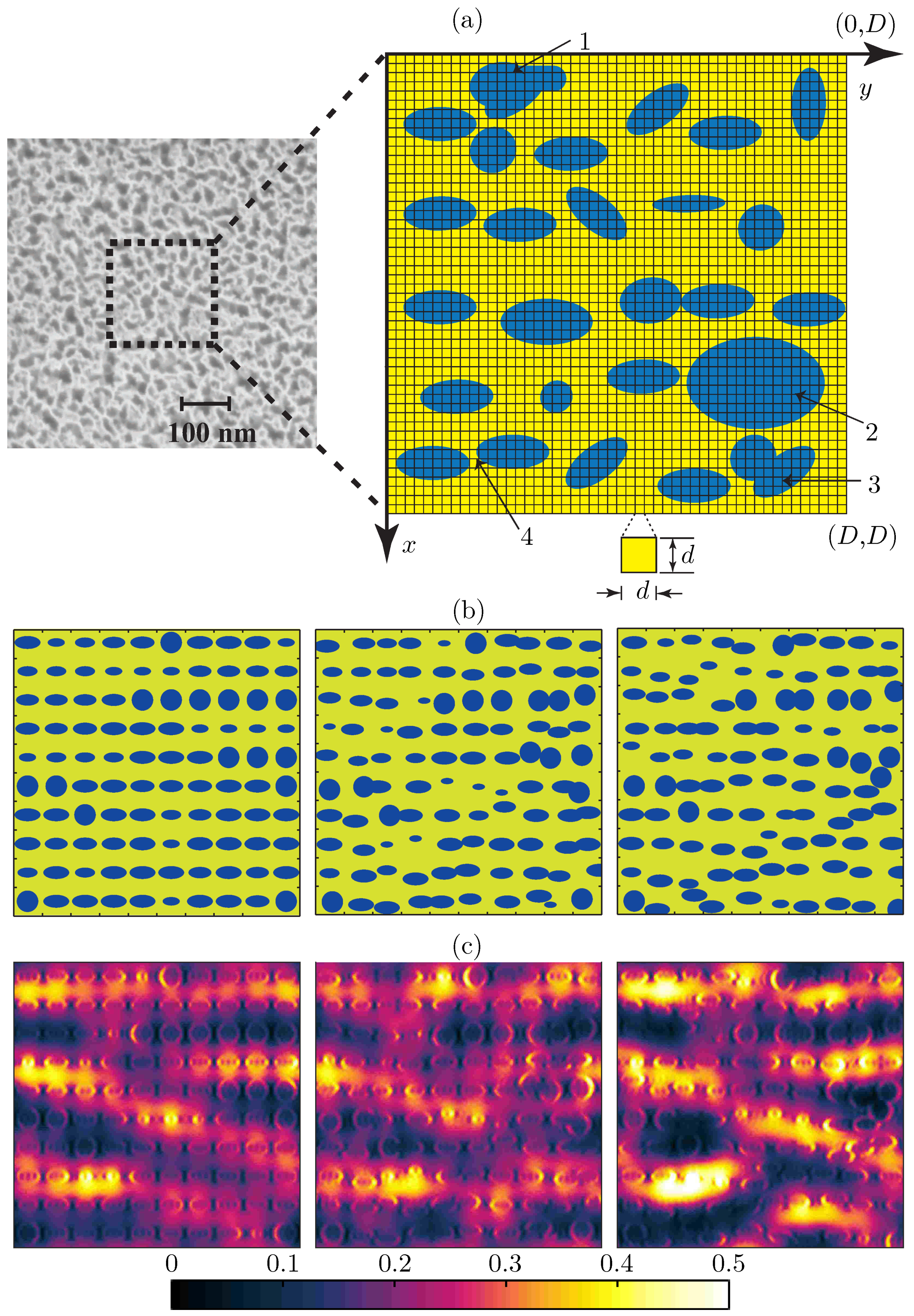
3.1. Porous Silicon
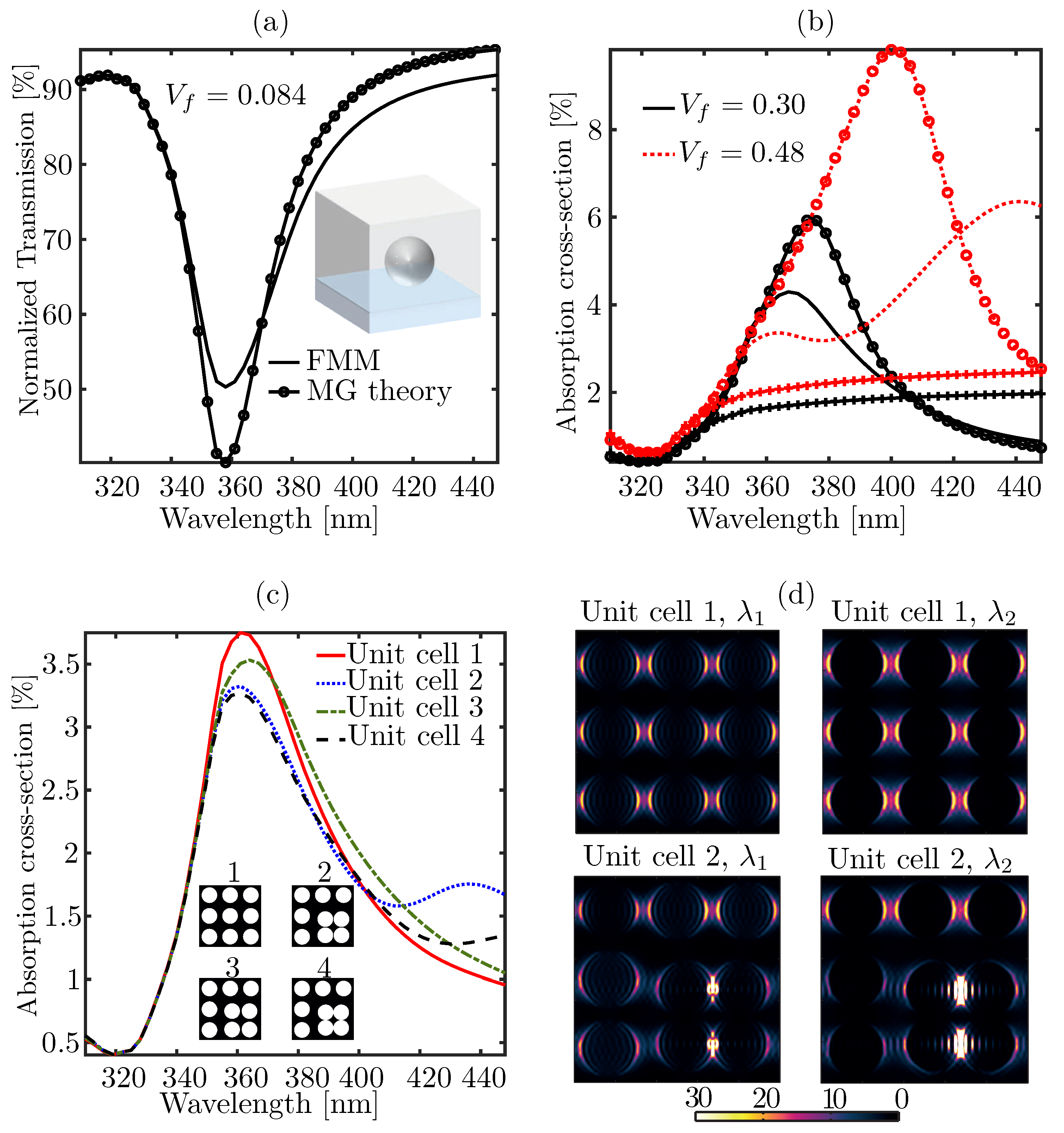
3.2. Silver (Ag) Nanospheres Arranged on a Glass Substrate
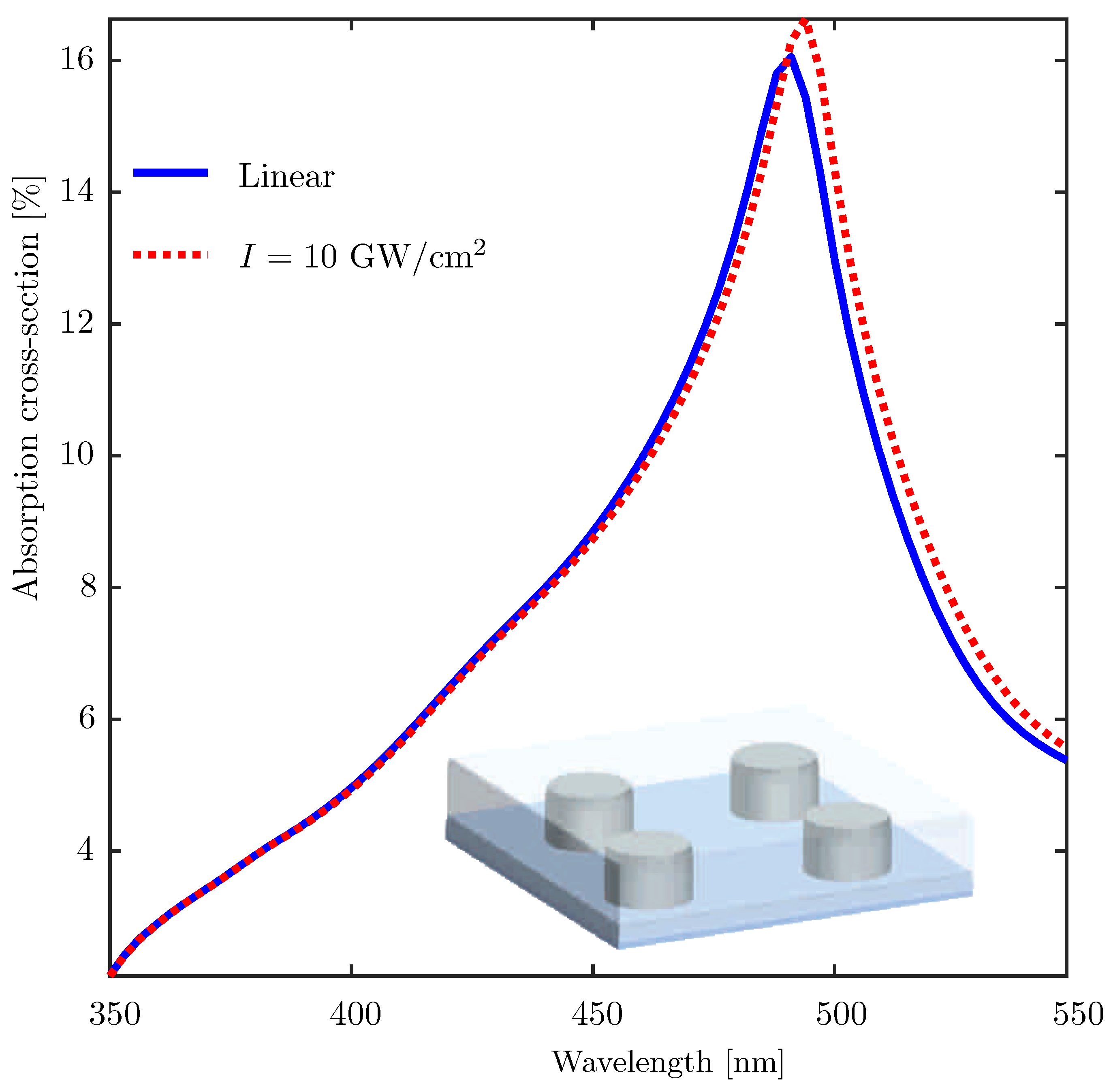
3.3. Ag Nanorods Embedded in a Kerr Nonlinear Host Matrix
4. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Convergence Tests
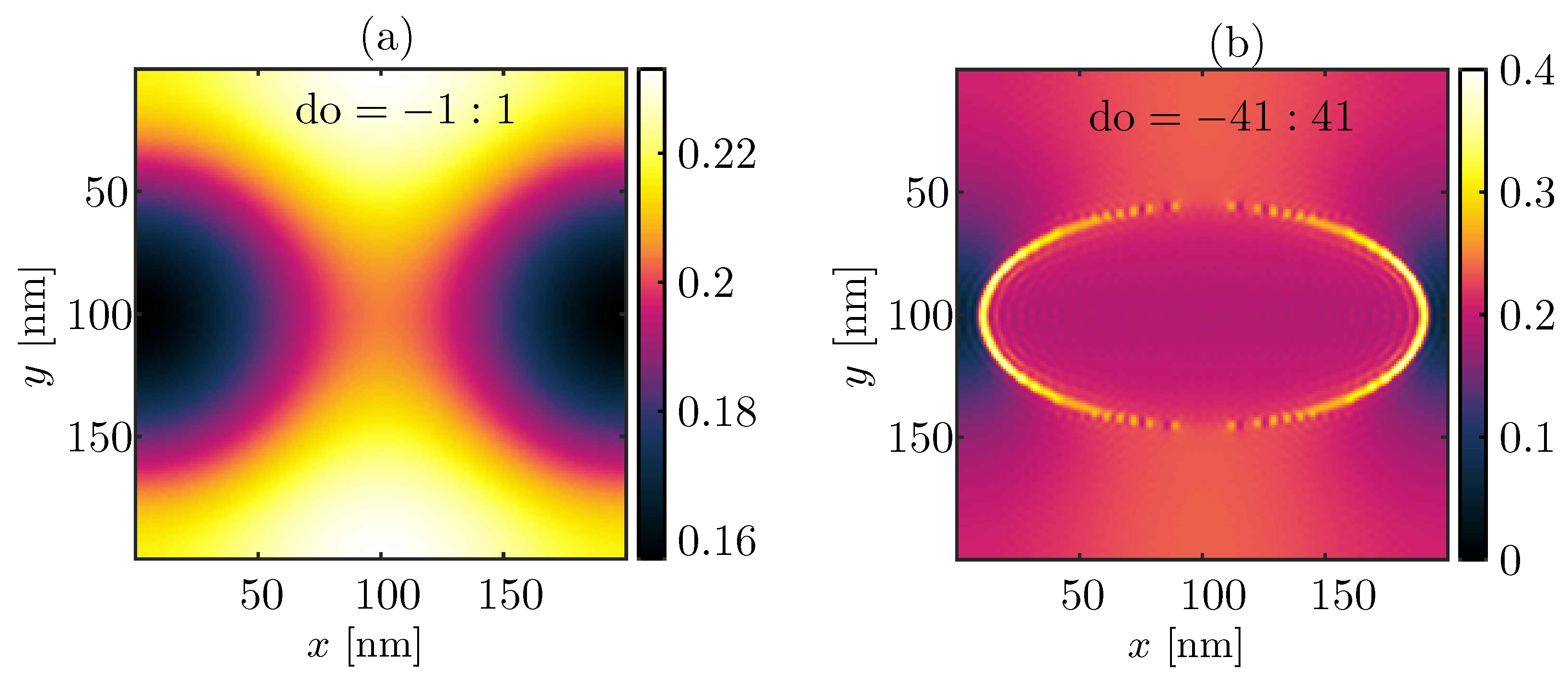
Appendix A.1. Near Field Intensity vs. Number of Fourier Coefficients: Por-Si
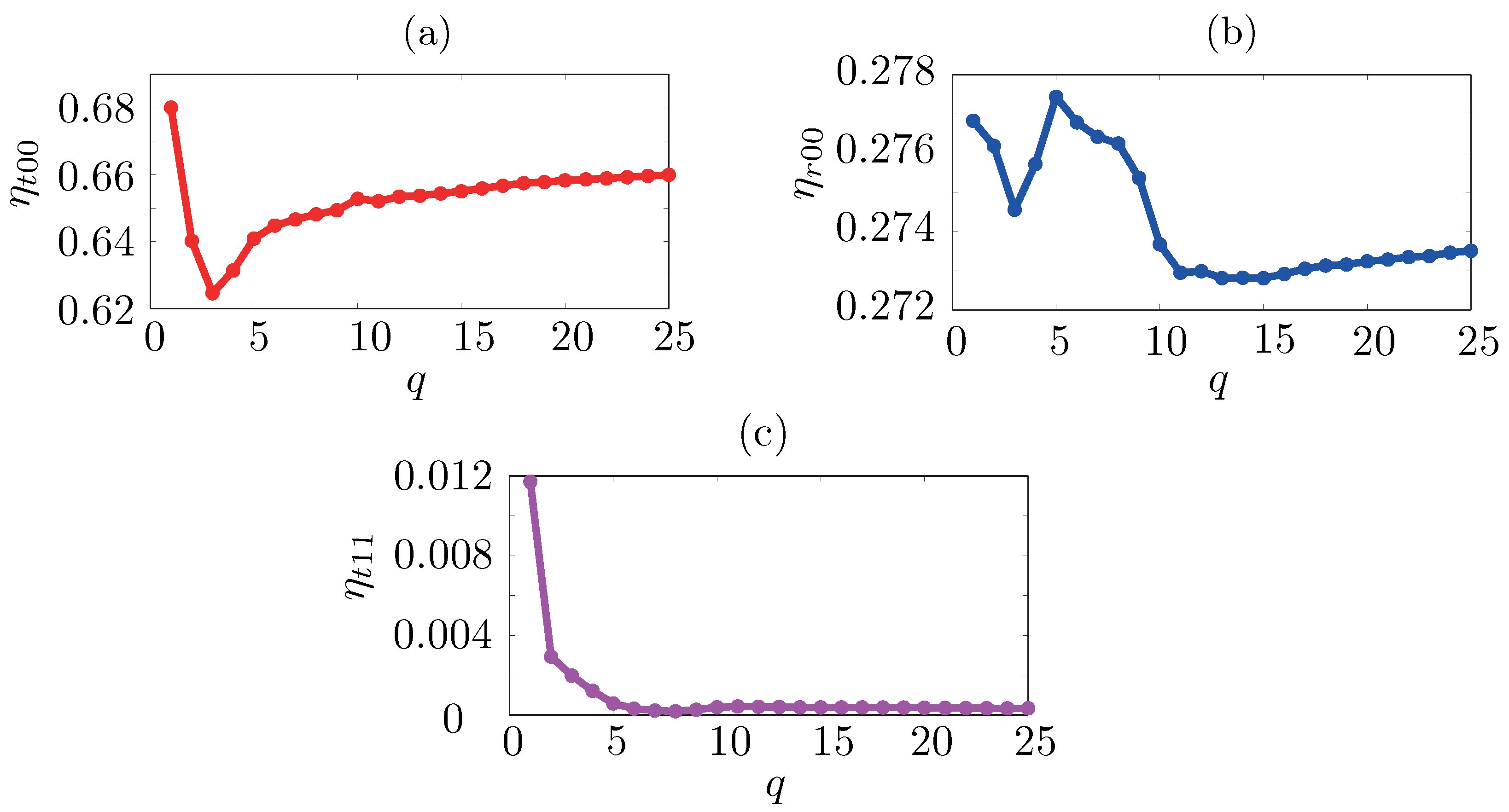
Appendix A.2. Diffraction Efficiencies vs. Number of Fourier Coefficients in FMM: Por-Si
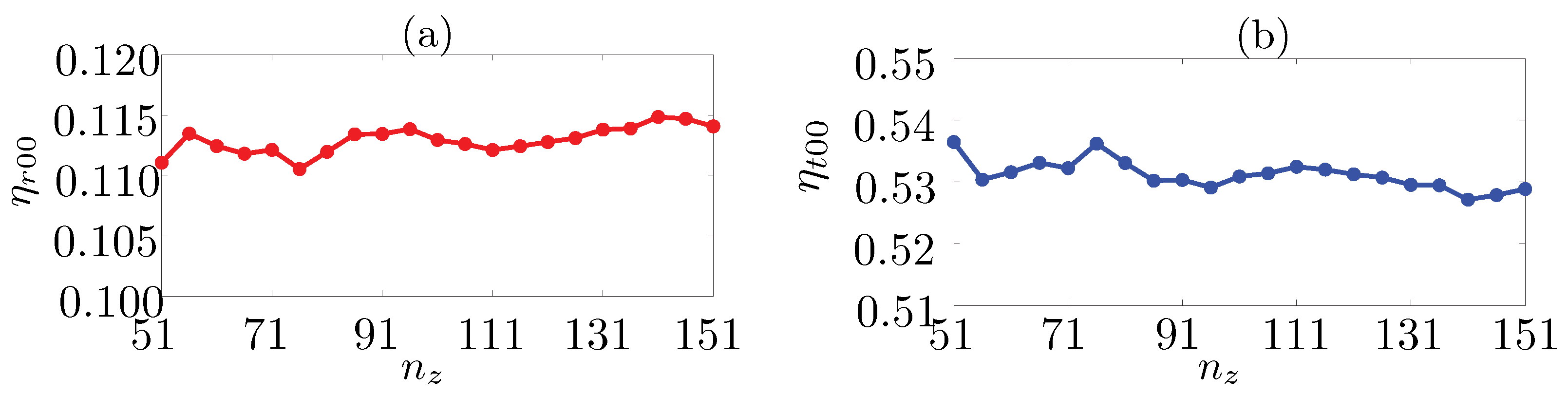
Appendix A.3. Diffraction Efficiencies vs. Number of Layers: Ag Spheres on Glass
Appendix B. Computing Time and Resources
- With along x and y, , and transverse sampling , the field calculation across the mid-plane of Ag nanospheres at each wavelength took about 792 s without implementing symmetry conditions and about 169.8 s if -type symmetry conditions are used as implemented in ref. [42].
- With and other parameters same as above, the calculation took about 24,787 s per wavelength without symmetry conditions and about 1195 s with the symmetry conditions.
References
- Beecroft, L.L.; Ober, C.K. Nanocomposite Materials for Optical Applications. Chem. Mater. 1997, 9, 1302–1317. [Google Scholar] [CrossRef]
- Guerreiro, P.T.; Ten, S.; Borrelli, N.F.; Butty, J.; Jabbour, G.E.; Peyghambarian, N. PbS quantum-dot doped glasses as saturable absorbers for mode locking of a Cr:forsterite laser. Appl. Phys. Lett. 1997, 71, 1595–1597. [Google Scholar] [CrossRef]
- Malyarevich, A.M.; Yumashev, K.V.; Lipovskii, A.A. Semiconductor-doped glass saturable absorbers for near-infrared solid-state lasers. J. Appl. Phys. 2008, 103, 081301. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chakravorty, D. Glass-metal nanocomposite synthesis by metal organic route. J. Phys. D Appl. Phys. 1989, 22, 1386–1392. [Google Scholar] [CrossRef]
- Chakravorty, D.; Basu, S.; Mukherjee, P.K.; Saha, S.K.; Pal, B.N.; Dan, A.; Bhattacharya, S. Novel properties of glass–metal nanocomposites. J. Non-Cryst. Solids 2006, 352, 601–609. [Google Scholar] [CrossRef]
- Tseng, Y.-C.; Darling, S.B. Block Copolymer Nanostructures for Technology. Polymers 2010, 2, 470–489. [Google Scholar] [CrossRef] [Green Version]
- Shao, H.-C.; Zhang, Y.-Y.; Hussain, S.; Liu, X.-C.; Zhao, L.-J.; Zhang, X.-Z.; Liu, G.-W.; Qiao, G.-J. Effects of Preform Structures on the Performance of Carbon and Carbon Composites. Sci. Adv. Mater. 2019, 11, 945–953. [Google Scholar] [CrossRef]
- Peigney, A.; Laurent, C.; Flahaut, E.; Rousset, A. Carbon nanotubes in novel ceramic matrix nanocomposites. Ceram. Int. 2000, 26, 677–683. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, M.G.; Kuo, S.W. Functional polyimide/polyhedral oligomeric silsesquioxane nanocomposites. Polymers 2018, 11, 26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohamed, M.G.; Kuo, S.W. Functional silica and carbon nanocomposites based on polybenzoxazines. Macromol. Chem. Phys. 2019, 220, 1800306. [Google Scholar] [CrossRef]
- Silvestre, J.; Silvestre, N.; de Brito, J. An overview on the improvement of mechanical properties of ceramics nanocomposites. J. Nanomater. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Menna, P.; Di Francia, G.; La Ferrara, V. Porous silicon in solar cells: A review and a description of its application as an AR coating. Sol. Energy Mater. Sol. Cells 1995, 37, 13–24. [Google Scholar] [CrossRef]
- Luan, F.; Gu, B.; Gomes, A.S.L.; Yong, K.-T.; Wen, S.; Prasad, P.N. Lasing in nanocomposite random media. Nano Today 2015, 10, 168–192. [Google Scholar] [CrossRef]
- Godovsky, D.Y. Device applications of polymer-nanocomposites. In Biopolymers · PVA Hydrogels, Anionic Polymerisation Nanocomposites; Springer: Berlin/Heidelberg, Germany, 2000; pp. 163–205. [Google Scholar]
- Kleemann, W. Multiferroic and magnetoelectric nanocomposites for data processing. J. Phys. D Appl. Phys. 2017, 50, 223001. [Google Scholar] [CrossRef]
- Barillaro, G.; Nannini, A.; Pieri, F. APSFET: A new, porous silicon-based gas sensing device. Sens. Actuators B Chem. 2003, 93, 263–270. [Google Scholar] [CrossRef]
- Dul, S.; Fambri, L.; Pegoretii, A. Development of new nanocomposites for 3D printing applications. In Structure and Properties of Additive Manufactured Polymer Components; Woodhead Publishing: Southston, UK, 2020; pp. 17–59. [Google Scholar]
- Hauert, R.; Patscheider, J. From alloying to nanocomposites—Improved performance of hard coatings. Adv. Eng. Mater. 2000, 2, 247–259. [Google Scholar] [CrossRef]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef]
- Hamanaka, Y.; Nakamura, A.; Omi, S.; del Fatti, N.; Vallée, F.; Flytzanis, C. Ultrafast response of nonlinear refractive index of silver nanocrystals embedded in glass. Appl. Phys. Lett. 1999, 75, 1712–1714. [Google Scholar] [CrossRef]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The Optical Properties of Metal Nanoparticles: The Influence of Size, Shape, and Dielectric Environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Mohan, S.; Lange, J.; Graener, H.; Seifert, G. Surface plasmon assisted optical nonlinearities of uniformly oriented metal nano-ellipsoids in glass. Opt. Express 2012, 20, 28655–28663. [Google Scholar] [CrossRef] [PubMed]
- Lama, P.; Suslov, A.; Walser, A.D.; Dorsinville, R. Plasmon assisted enhanced nonlinear refraction of monodispersed silver nanoparticles and their tunability. Opt. Express 2014, 22, 14014–14021. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, P. Metal nanoclusters in glasses as non-linear photonic materials. J. Mater. Sci. 1998, 33, 2235–2249. [Google Scholar] [CrossRef]
- Golovan, L.A.; Timoshenko, V.Y. Nonlinear-Optical Properties of Porous Silicon Nanostructures. J. Nanoelectron. Optoelectron. 2013, 8, 223–239. [Google Scholar] [CrossRef]
- Rane, A.V.; Kanny, K.; Abitha, V.K.; Thomas, S. Methods for synthesis of nanoparticles and fabrication of nanocomposites. In Synthesis of Inorganic Nanomaterials; Elsevier: Amsterdam, The Netherlands, 2018; pp. 121–139. [Google Scholar]
- Hulkkonen, H.H.; Salminen, T.; Niemi, T. Block Copolymer Patterning for Creating Porous Silicon Thin Films with Tunable Refractive Indices. ACS Appl. Mater. Interfaces 2017, 9, 31260–31265. [Google Scholar] [CrossRef] [PubMed]
- Maxwell Garnett, J.C.; Larmor, J., XII. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. Lond. A 1904, 203, 385–420. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Dolgaleva, K.; Boyd, R.W. Local-field effects in nanostructured photonic materials. Adv. Opt. Photonics 2012, 4, 1–77. [Google Scholar] [CrossRef] [Green Version]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizita¨tskonstanten und Leitfa¨higkeiten der Mischko ¨rper aus isotropen Substanzen. Ann. Physik 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Werdehausen, D.; Staude, I.; Burger, S.; Petschulat, J.; Scharf, T.; Pertsch, T.; Decker, M. Design rules for customizable optical materials based on nanocomposites. Opt. Mater. Express 2018, 8, 3456–3469. [Google Scholar] [CrossRef] [Green Version]
- Kozik, S.E.; Skoptsov, E.A.; Smirnov, A.G.; Binhussain, M.A. Effective Dielectric Constant of Composite Materials Based on Plasmon Nanoparticles of Arbitrary Shape. J. Appl. Spectrosc. 2015, 82, 409–414. [Google Scholar] [CrossRef]
- Stein, H.S.; Guevarra, D.; Newhouse, P.F.; Soedarmadji, E.; Gregoire, J.M. Machine learning of optical properties of materials–predicting spectra from images and images from spectra. Chem. Sci. 2019, 10, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Kushvaha, V.; Kumar, S.A.; Madhushri, P.; Sharma, A. Artificial neural network technique to predict dynamic fracture of particulate composite. J. Compos. Mater. 2020, 54, 3099–3108. [Google Scholar] [CrossRef]
- Sharma, A.; Kushvaha, V. Predictive modelling of fracture behaviour in silica-filled polymer composite subjected to impact with varying loading rates using artificial neural network. Eng. Fract. Mech. 2020, 239, 107328. [Google Scholar] [CrossRef]
- Li, L. New formulation of the Fourier modal method for crossed surface-relief gratings. J. Opt. Soc. Am. A 1997, 14, 2758–2767. [Google Scholar] [CrossRef]
- Li, L. Fourier modal method for crossed anisotropic gratings with arbitrary permittivity and permeability tensors. J. Opt. A Pure Appl. Opt. 2003, 5, 345–355. [Google Scholar] [CrossRef]
- Negro, L.D.; Boriskina, S.V. Deterministic aperiodic nanostructures for photonics and plasmonics applications. Laser Photonics Rev. 2012, 6, 178–218. [Google Scholar] [CrossRef]
- Li, L. Formulation and comparison of two recursive matrix algorithm for modeling layered diffraction gratings. J. Opt. Soc. Am. A 1996, 13, 1024–1035. [Google Scholar] [CrossRef] [Green Version]
- Li, L. Note on the S-matrix propagation algorithm. J. Opt. Soc. Am. A 2003, 20, 655–660. [Google Scholar] [CrossRef]
- Zhou, C.; Li, L. Formulation of the Fourier modal method for symmetric crossed gratings in symmetric mountings. J. Opt. A Pure Appl. Opt. 2004, 6, 43–50. [Google Scholar] [CrossRef]
- Bej, S.; Tervo, J.; Svirko, Y.P.; Turunen, J. Modeling the optical Kerr effect in periodic structures by the linear Fourier Modal Method. J. Opt. Soc. Am. B 2014, 31, 2371–2378. [Google Scholar] [CrossRef]
- Smith, R.L.; Collins, S.D. Porous silicon formation mechanisms. J. Appl. Phys. 1992, 71, R1–R22. [Google Scholar] [CrossRef]
- Beale, M.; Benjamin, J.; Uren, M.; Chew, N.; Cullis, A. An experimental and theoretical study of the formation and microstructure of porous silicon. J. Cryst. Growth 1985, 73, 622–636. [Google Scholar] [CrossRef]
- Korotcenkov, G. (Ed.) Porous Silicon: From Formation to Application: Formation and Properties, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016; Volume 1. [Google Scholar]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bej, S.; Saastamoinen, T.; Svirko, Y.P.; Turunen, J. Grating Theory Approach to Optics of Nanocomposites. Materials 2021, 14, 6359. https://doi.org/10.3390/ma14216359
Bej S, Saastamoinen T, Svirko YP, Turunen J. Grating Theory Approach to Optics of Nanocomposites. Materials. 2021; 14(21):6359. https://doi.org/10.3390/ma14216359
Chicago/Turabian StyleBej, Subhajit, Toni Saastamoinen, Yuri P. Svirko, and Jari Turunen. 2021. "Grating Theory Approach to Optics of Nanocomposites" Materials 14, no. 21: 6359. https://doi.org/10.3390/ma14216359
APA StyleBej, S., Saastamoinen, T., Svirko, Y. P., & Turunen, J. (2021). Grating Theory Approach to Optics of Nanocomposites. Materials, 14(21), 6359. https://doi.org/10.3390/ma14216359






