Time-History Analysis of Composite Materials with Rectangular Microstructure under Shear Actions
Abstract
:1. Introduction
2. Micropolar Continuum
3. Rectangular Microstructure
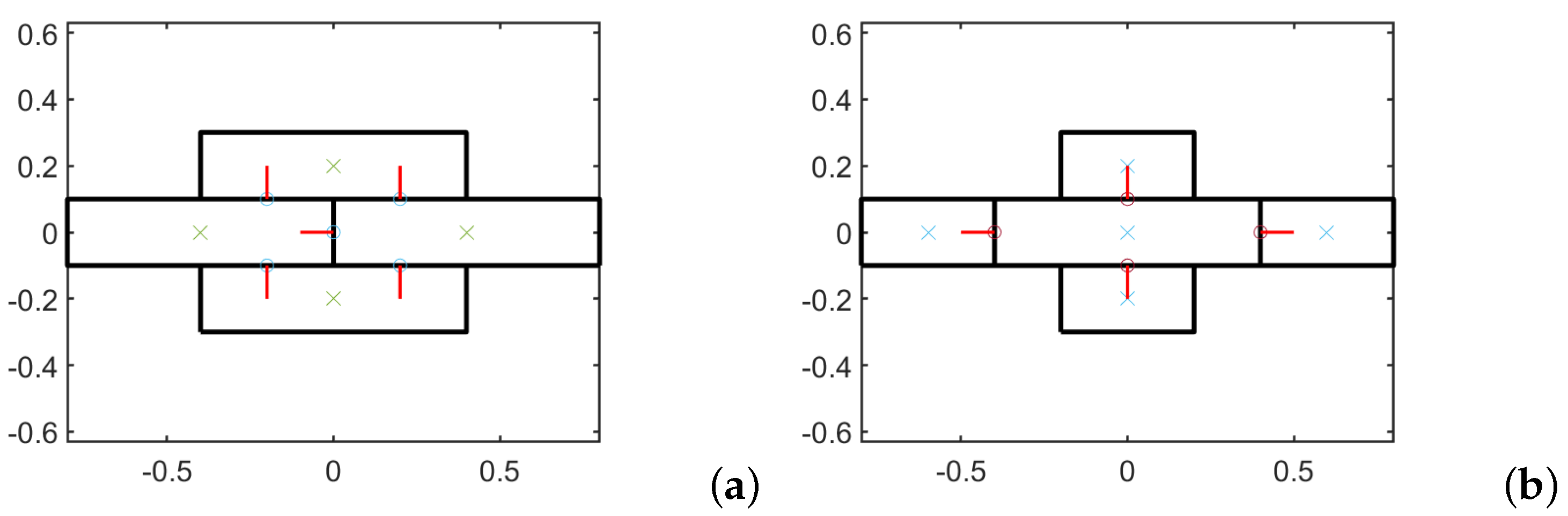
Reference Volume Element
4. Numerical Implementation
Continuum Model
5. Simulations
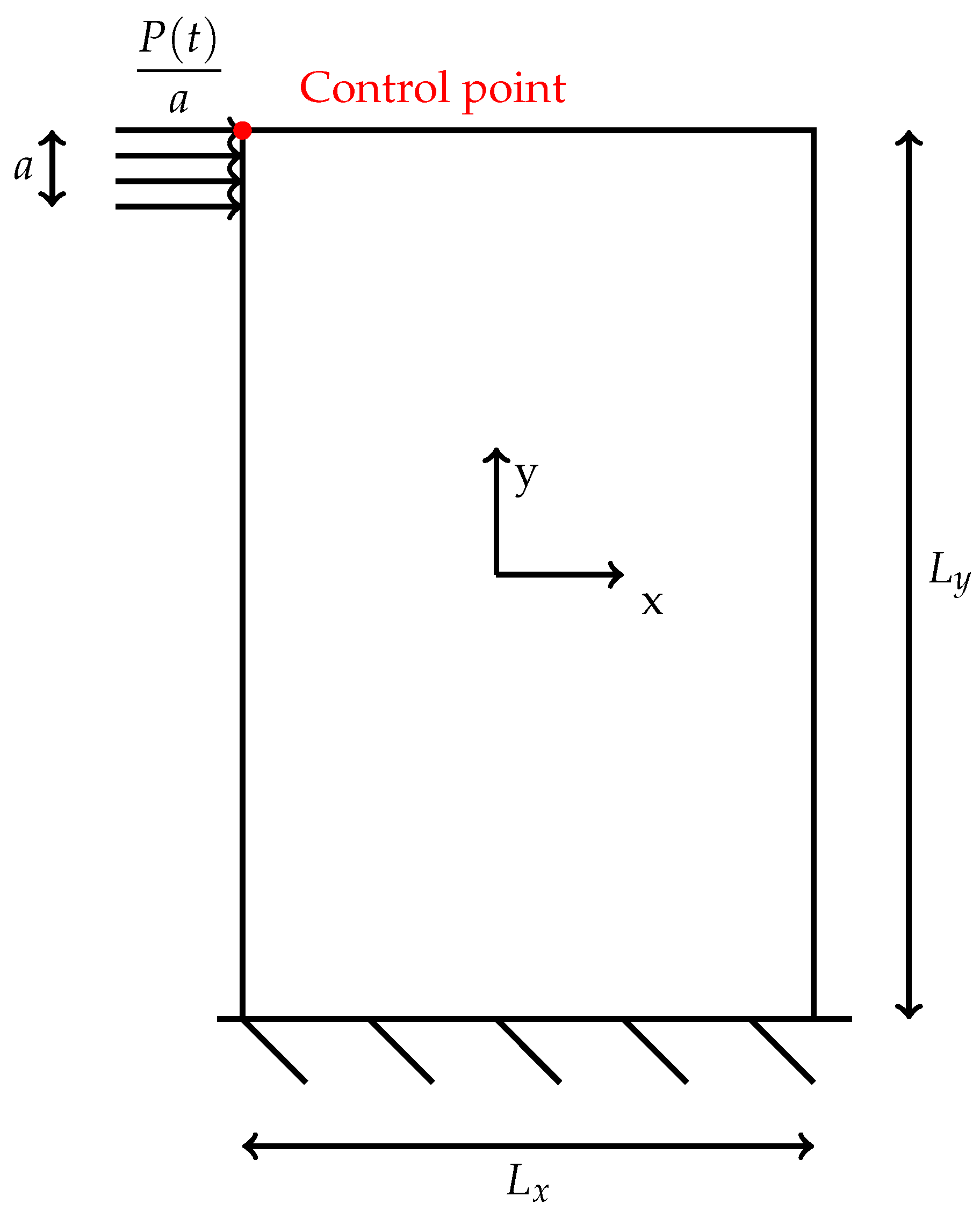
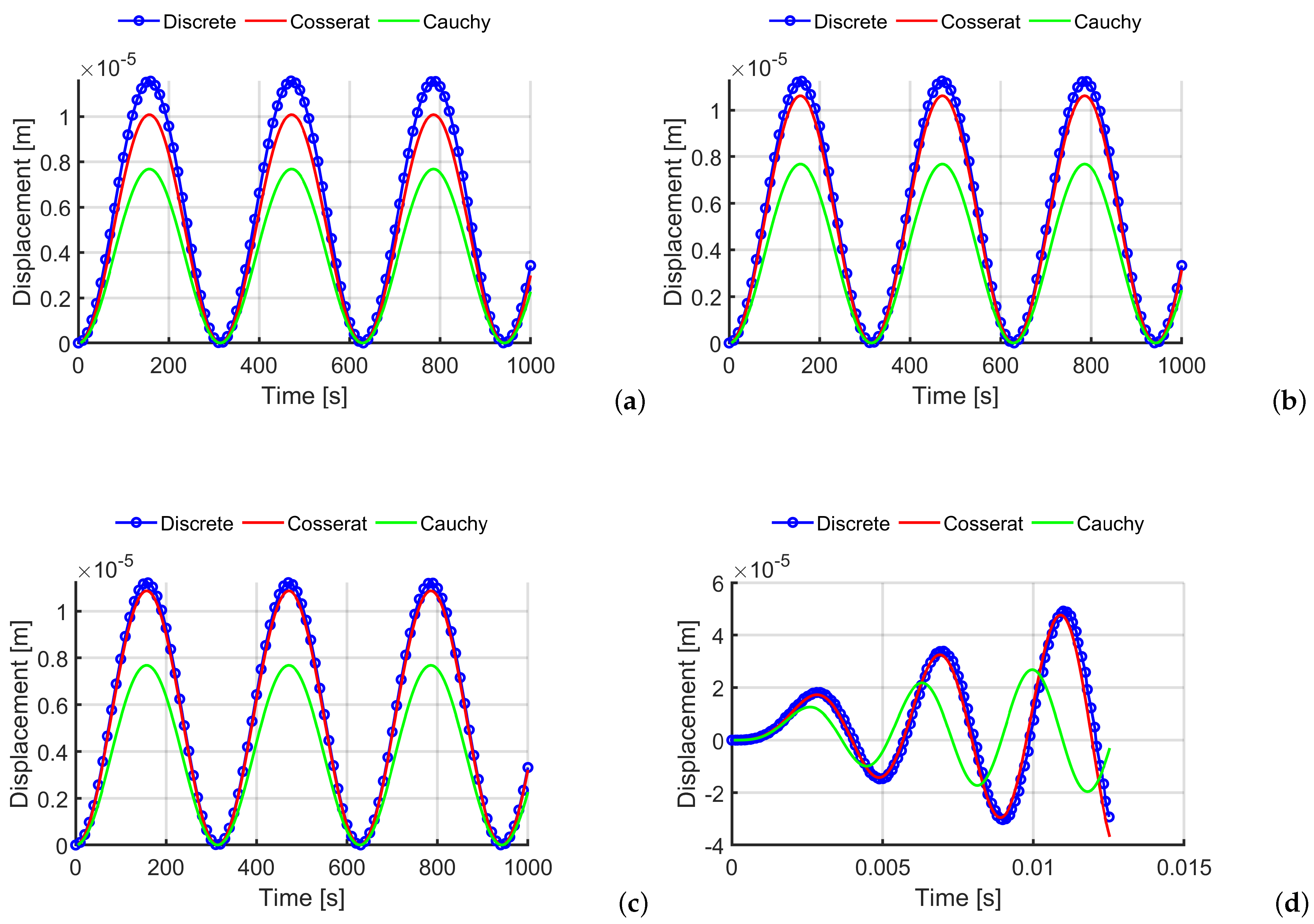
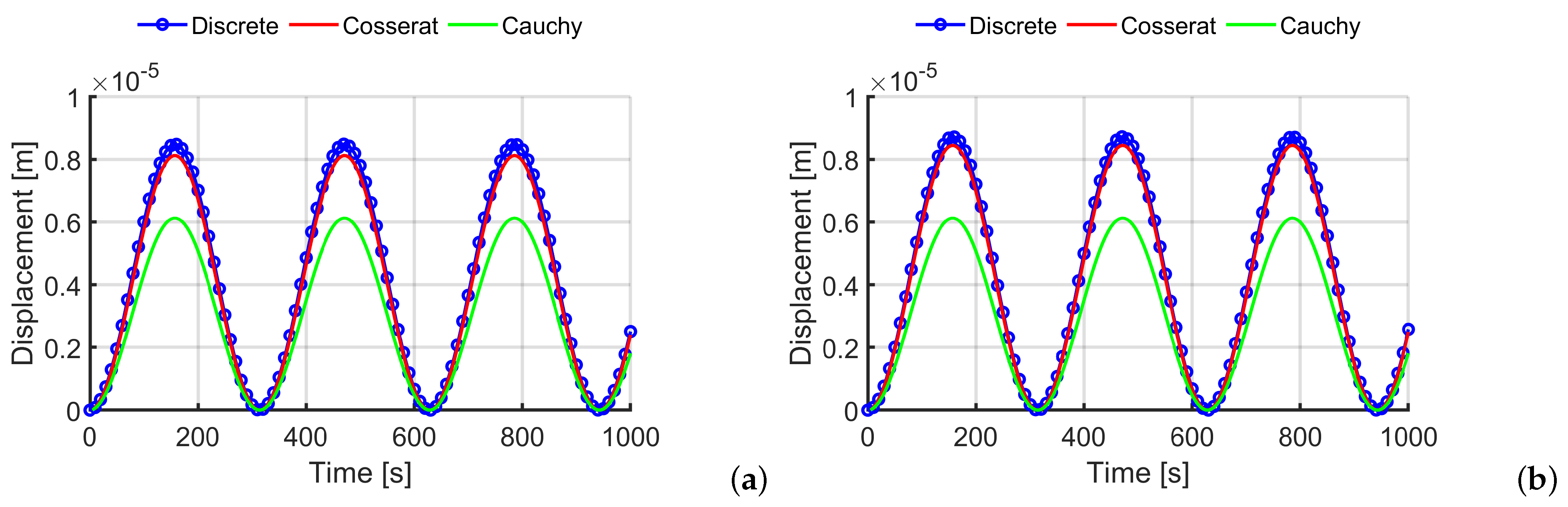
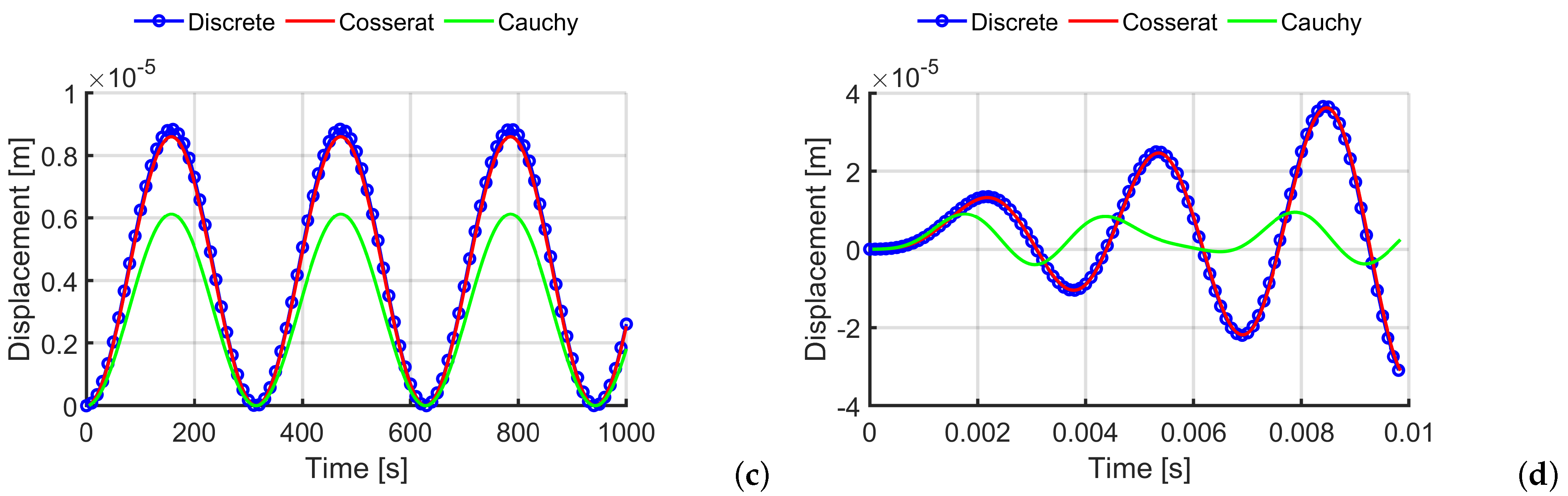
5.1. Time Transient Analysis
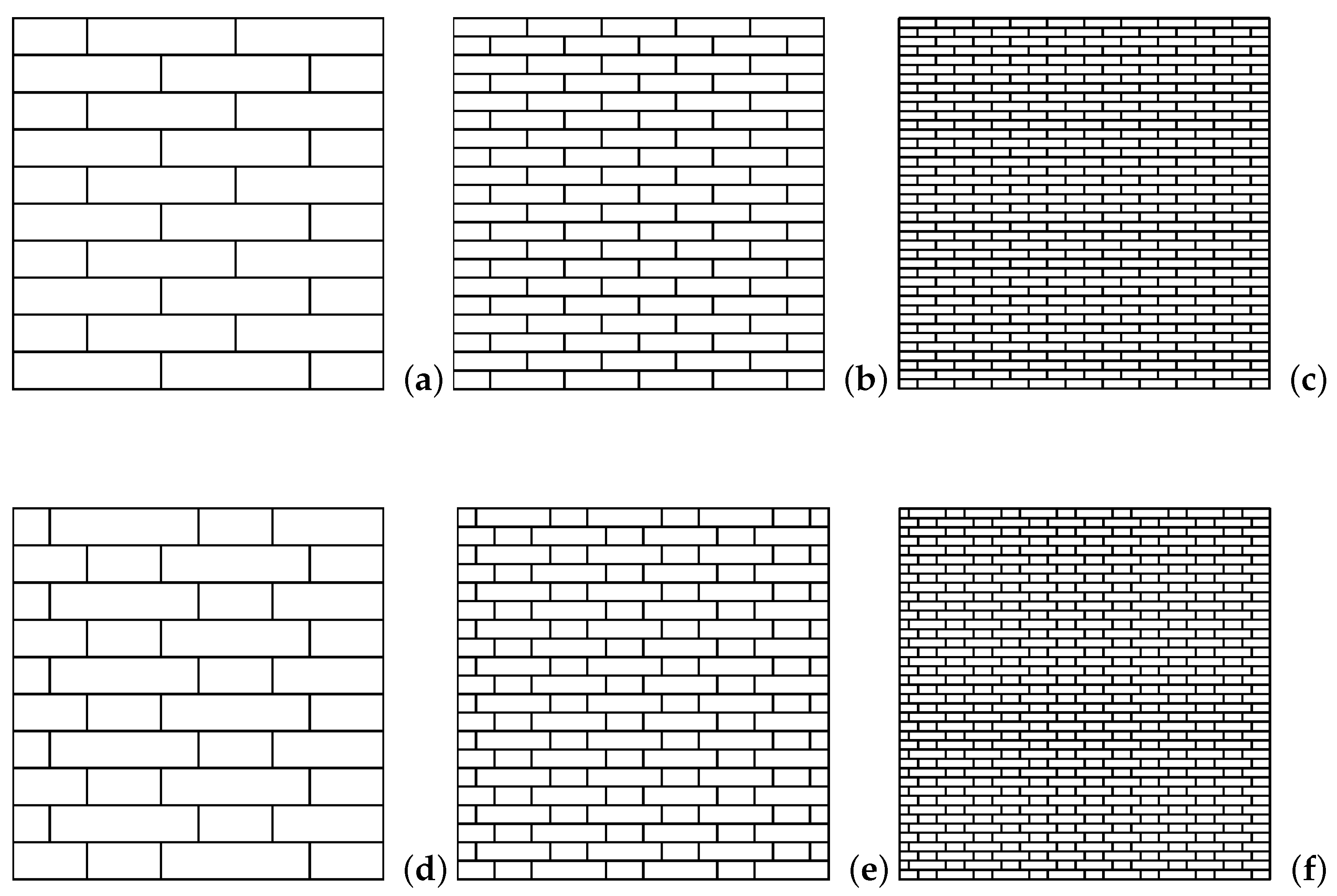
5.2. Texture 1
5.3. Texture 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sadowski, T.; Samborski, S. Prediction of the mechanical behaviour of porous ceramics using mesomechanical modelling. Comput. Mater. Sci. 2003, 28, 512–517. [Google Scholar] [CrossRef]
- Sadowski, T.; Samborski, S. Development of damage state in porous ceramics under compression. Comput. Mater. Sci. 2008, 43, 75–81. [Google Scholar] [CrossRef]
- Samborski, S.; Sadowski, T. Dynamic fracture toughness of porous ceramics. J. Am. Ceram. Soc. 2010, 93, 3607–3609. [Google Scholar] [CrossRef]
- Postek, E.; Sadowski, T. Assessing the influence of porosity in the deformation of metal–ceramic composites. Compos. Interfaces 2011, 18, 57–76. [Google Scholar] [CrossRef]
- Sadowski, T.; Postek, E.; Denis, C. Stress distribution due to discontinuities in polycrystalline ceramics containing metallic inter-granular layers. Comput. Mater. Sci. 2007, 39, 230–236. [Google Scholar] [CrossRef]
- Sadowski, T.; Marsavina, L. Multiscale modelling of two-phase ceramic matrix composites. Comput. Mater. Sci. 2011, 50, 1336–1346. [Google Scholar] [CrossRef]
- Boniecki, M.; Sadowski, T.; Gołębiewski, P.; Węglarz, H.; Piątkowska, A.; Romaniec, M.; Krzyżak, K.; Łosiewicz, K. Mechanical properties of alumina/zirconia composites. Ceram. Int. 2020, 46, 1033–1039. [Google Scholar] [CrossRef]
- Sadowski, T.; Łosiewicz, K.; Boniecki, M.; Szutkowska, M. Assessment of mechanical properties by nano-and microindentation of alumina/zirconia composites. Mater. Today Proc. 2021, 45, 4196–4201. [Google Scholar] [CrossRef]
- Gatta, C.; Addessi, D.; Vestroni, F. Static and dynamic nonlinear response of masonry walls. Int. J. Solids Struct. 2018, 155, 291–303. [Google Scholar] [CrossRef]
- Addessi, D.; Sacco, E. Enriched plane state formulation for nonlinear homogenization of in-plane masonry wall. Meccanica 2016, 51, 2891–2907. [Google Scholar] [CrossRef]
- Addessi, D.; Sacco, E. Homogenization of heterogeneous masonry beams. Meccanica 2018, 53, 1699–1717. [Google Scholar] [CrossRef]
- Baggio, C.; Trovalusci, P. Collapse behaviour of three-dimensional brick-block systems using non-linear programming. Struct. Eng. Mech. 2000, 10, 181. [Google Scholar] [CrossRef]
- Godio, M.; Stefanou, I.; Sab, K.; Sulem, J.; Sakji, S. A limit analysis approach based on Cosserat continuum for the evaluation of the in-plane strength of discrete media: Application to masonry. Eur. J. -Mech.-A/Solids 2017, 66, 168–192. [Google Scholar] [CrossRef] [Green Version]
- Baraldi, D.; Reccia, E.; Cecchi, A. In plane loaded masonry walls: DEM and FEM/DEM models. A critical review. Meccanica 2018, 53, 1613–1628. [Google Scholar] [CrossRef] [Green Version]
- Reccia, E.; Leonetti, L.; Trovalusci, P.; Cecchi, A. A multiscale/multidomain model for the failure analysis of masonry walls: A validation with a combined FEM/DEM approach. Int. J. Multiscale Comput. Eng. 2018, 16, 325–343. [Google Scholar] [CrossRef]
- Pepe, M.; Pingaro, M.; Trovalusci, P.; Reccia, E.; Leonetti, L. Micromodels for the in-plane failure analysis of masonry walls: Limit Analysis, FEM and FEM/DEM approaches. Frat. Integrità Strutt. 2020, 14, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Trovalusci, P.; Ostoja-Starzewski, M. Multiscale mechanical modelling of complex materials and engineering applications 2. Int. J. Multiscale Comput. Eng. 2011, 9, vii–ix. [Google Scholar] [CrossRef]
- Sadowski, T.; Trovalusci, P.; Schrefler, B.; de Borst, R. Multi-scale and multi-physics modelling for complex materials. Meccanica 2014, 49, 2549–2550. [Google Scholar] [CrossRef] [Green Version]
- Altenbach, H.; Sadowski, T. Failure and Damage Analysis of Advanced Materials; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Greco, F.; Leonetti, L.; Luciano, R.; Blasi, P.N. Effects of microfracture and contact induced instabilities on the macroscopic response of finitely deformed elastic composites. Compos. Part Eng. 2016, 107, 233–253. [Google Scholar] [CrossRef]
- De Borst, R. Simulation of Strain Localization: A Reappraisal of the Cosserat Continuum. Eng. Comp. 1991, 8, 317–332. [Google Scholar] [CrossRef]
- Sluys, L.; De Borst, R.; Mühlhaus, H.B. Wave propagation, localization and dispersion in a gradient-dependent medium. Int. J. Solids Struct. 1993, 30, 1153–1171. [Google Scholar] [CrossRef] [Green Version]
- Masiani, R.; Rizzi, N.; Trovalusci, P. Masonry as structured continuum. Meccanica 1995, 30, 673–683. [Google Scholar] [CrossRef]
- Masiani, R.; Trovalusci, P. Cosserat and Cauchy materials as continuum models of brick masonry. Meccanica 1996, 31, 421–432. [Google Scholar] [CrossRef]
- Trovalusci, P.; Masiani, R. Material symmetries of micropolar continua equivalent to lattices. Int. J. Solids Struct. 1999, 36, 2091–2108. [Google Scholar] [CrossRef]
- Trovalusci, P.; Masiani, R. A multifield model for blocky materials based on multiscale description. Int. J. Solids Struct. 2005, 42, 5778–5794. [Google Scholar] [CrossRef] [Green Version]
- Pau, A.; Trovalusci, P. Block masonry as equivalent micropolar continua: The role of relative rotations. Acta Mech. 2012, 223, 1455–1471. [Google Scholar] [CrossRef]
- Trovalusci, P.; Pau, A. Derivation of microstructured continua from lattice systems via principle of virtual works: The case of masonry-like materials as micropolar, second gradient and classical continua. Acta Mech. 2014, 225, 157–177. [Google Scholar] [CrossRef]
- Trovalusci, P. Molecular Approaches for Multifield Continua: Origins and current developments. In Multiscale Modeling of Complex Materials: Phenomenological, Theoretical and Computational Aspects; Sadowski, T., Trovalusci, P., Eds.; Springer: Vienna, Austria, 2014; pp. 211–278. [Google Scholar] [CrossRef]
- Tuna, M.; Trovalusci, P. Scale dependent continuum approaches for discontinuous assemblies: ‘Explicit’ and ‘implicit’ non-local models. Mech. Res. Commun. 2020, 103, 103461. [Google Scholar] [CrossRef]
- Tuna, M.; Leonetti, L.; Trovalusci, P.; Kirca, M. ‘Explicit’ and ‘implicit’ non-local continuous descriptions for a plate with circular inclusion in tension. Meccanica 2020, 55, 927–944. [Google Scholar] [CrossRef] [Green Version]
- Tuna, M.; Trovalusci, P. Stress distribution around an elliptic hole in a plate with ‘implicit’ and ‘explicit’ non-local models. Compos. Struct. 2021, 256, 113003. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar elasticity. In Microcontinuum Field Theories; Springer: Berlin/Heidelberg, Germany, 1999; pp. 101–248. [Google Scholar]
- Uzun, B.; Civalek, Ö. Nonlocal FEM formulation for vibration analysis of nanowires on elastic matrix with different materials. Math. Comput. Appl. 2019, 24, 38. [Google Scholar] [CrossRef] [Green Version]
- Barretta, R.; Luciano, R.; de Sciarra, F.M. A Fully Gradient Model for Euler-Bernoulli Nanobeams. Math. Probl. Eng. 2015, 2015, 495095. [Google Scholar] [CrossRef] [Green Version]
- Čanađija, M.; Barretta, R.; De Sciarra, F.M. A gradient elasticity model of Bernoulli–Euler nanobeams in non-isothermal environments. Eur. J.-Mech.-A/Solids 2016, 55, 243–255. [Google Scholar] [CrossRef]
- Barretta, R.; Faghidian, S.A.; Luciano, R. Longitudinal vibrations of nano-rods by stress-driven integral elasticity. Mech. Adv. Mater. Struct. 2019, 26, 1307–1315. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F. A Nonlocal Model for Carbon Nanotubes under Axial Loads. Adv. Mater. Sci. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Eshraghi, I.; Jalali, S.K.; Pugno, N.M. Imperfection sensitivity of nonlinear vibration of curved single-walled carbon nanotubes based on nonlocal timoshenko beam theory. Materials 2016, 9, 786. [Google Scholar] [CrossRef] [Green Version]
- Izadi, R.; Tuna, M.; Trovalusci, P.; Ghavanloo, E. Torsional characteristics of carbon nanotubes: Micropolar elasticity models and molecular dynamics simulation. Nanomaterials 2021, 11, 453. [Google Scholar] [CrossRef]
- Civalek, Ö.; Dastjerdi, S.; Akbaş, Ş.D.; Akgöz, B. Vibration analysis of carbon nanotube-reinforced composite microbeams. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Tocci Monaco, G.; Fantuzzi, N.; Fabbrocino, F.; Luciano, R. Trigonometric solution for the bending analysis of magneto-electro-elastic strain gradient nonlocal nanoplates in hygro-thermal environment. Mathematics 2021, 9, 567. [Google Scholar] [CrossRef]
- Akbaş, Ş.D.; Ersoy, H.; Akgöz, B.; Civalek, Ö. Dynamic Analysis of a Fiber-Reinforced Composite Beam under a Moving Load by the Ritz Method. Mathematics 2021, 9, 1048. [Google Scholar] [CrossRef]
- Addessi, D. A 2D Cosserat finite element based on a damage-plastic model for brittle materials. Comput. Struct. 2014, 135, 20–31. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A. Natural Frequency Analysis of Functionally Graded Orthotropic Cross-Ply Plates Based on the Finite Element Method. Math. Comput. Appl. 2019, 24, 52. [Google Scholar] [CrossRef] [Green Version]
- Capecchi, D.; Ruta, G.; Trovalusci, P. Voigt and Poincaré’s mechanistic–energetic approaches to linear elasticity and suggestions for multiscale modelling. Arch. Appl. Mech. 2011, 81, 1573–1584. [Google Scholar] [CrossRef]
- Colatosti, M.; Fantuzzi, N.; Trovalusci, P. Dynamic Characterization of Microstructured Materials Made of Hexagonal-Shape Particles with Elastic Interfaces. Nanomaterials 2021, 11, 1781. [Google Scholar] [CrossRef] [PubMed]
- Colatosti, M.; Fantuzzi, N.; Trovalusci, P.; Masiani, R. New insights on homogenization for hexagonal-shaped composites as Cosserat continua. Meccanica 2021. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Trovalusci, P.; Luciano, R. Material Symmetries in Homogenized Hexagonal-Shaped Composites as Cosserat Continua. Symmetry 2020, 12, 441. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, A.; Fantuzzi, N. MATLAB Codes for Finite Element Analysis 2nd Edition: Solids and Structures; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Trovalusci, P.; Luciano, R. Multiscale analysis of anisotropic materials with hexagonal microstructure as micropolar continua. Int. J. Multiscale Comput. Eng. 2020, 18, 265–284. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colatosti, M.; Fantuzzi, N.; Trovalusci, P. Time-History Analysis of Composite Materials with Rectangular Microstructure under Shear Actions. Materials 2021, 14, 6439. https://doi.org/10.3390/ma14216439
Colatosti M, Fantuzzi N, Trovalusci P. Time-History Analysis of Composite Materials with Rectangular Microstructure under Shear Actions. Materials. 2021; 14(21):6439. https://doi.org/10.3390/ma14216439
Chicago/Turabian StyleColatosti, Marco, Nicholas Fantuzzi, and Patrizia Trovalusci. 2021. "Time-History Analysis of Composite Materials with Rectangular Microstructure under Shear Actions" Materials 14, no. 21: 6439. https://doi.org/10.3390/ma14216439






