Mechanical Behavior Modelling and Filler Geometry Effect of Glass Filler Reinforced Starch-Epoxy Hybrid Matrix Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Manufacture of the Specimens
2.3. Quasi-Static Mechanical Tests
2.4. Microstructural Analysis of the Composites
3. Theoretical Background
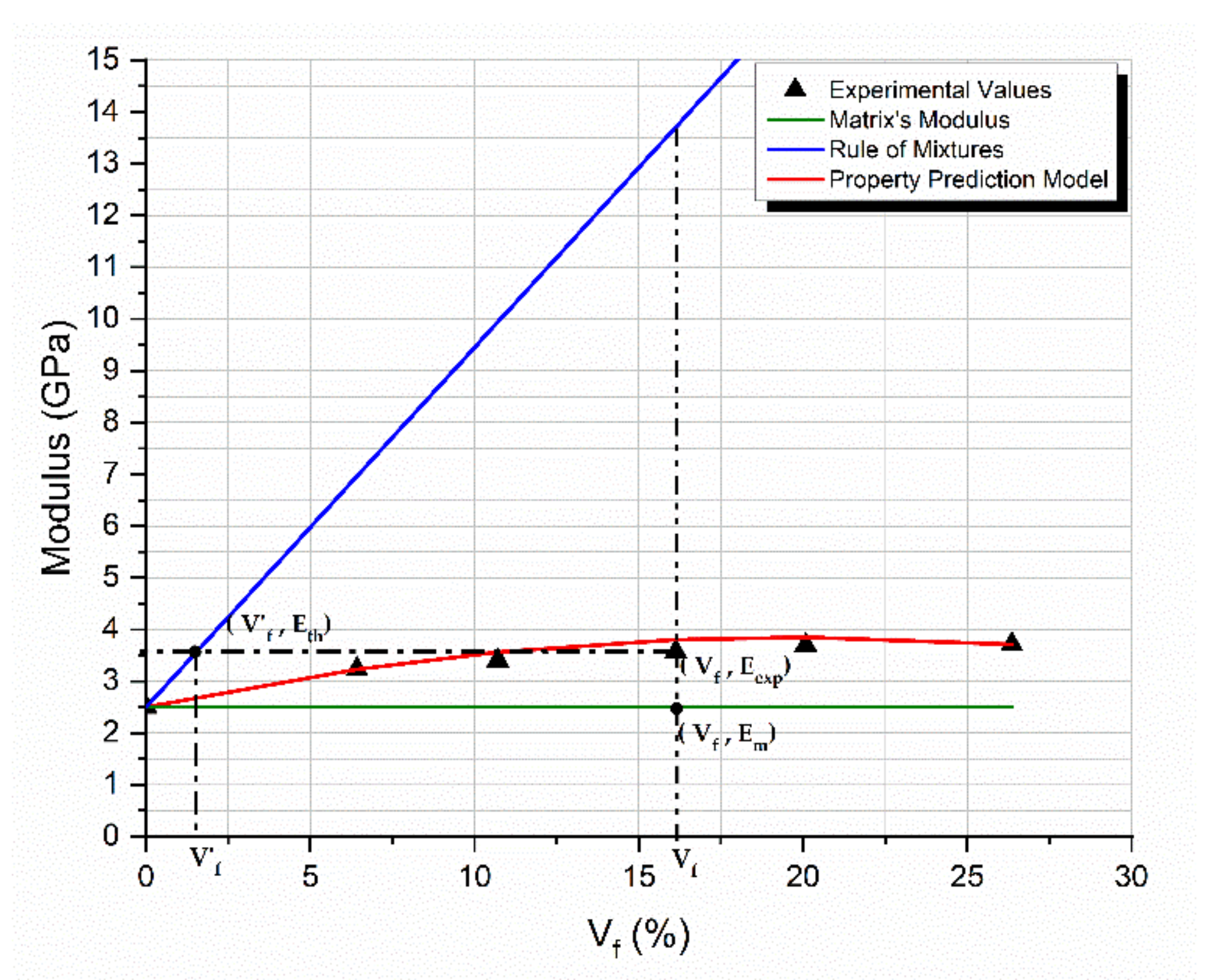
3.1. Property Prediction Model
- The model considers that, for any conditions given, the main parameters affecting the composite behavior are the filler-matrix adhesion and the filler dispersion within the matrix.
- The change of any property of the composite with the inclusion content can be described by a second-degree polynomial, which, depending on the value of its coefficients, can represent a straight line and/or a concave or convex parabolic curve:where, Pm is the property of the matrix.
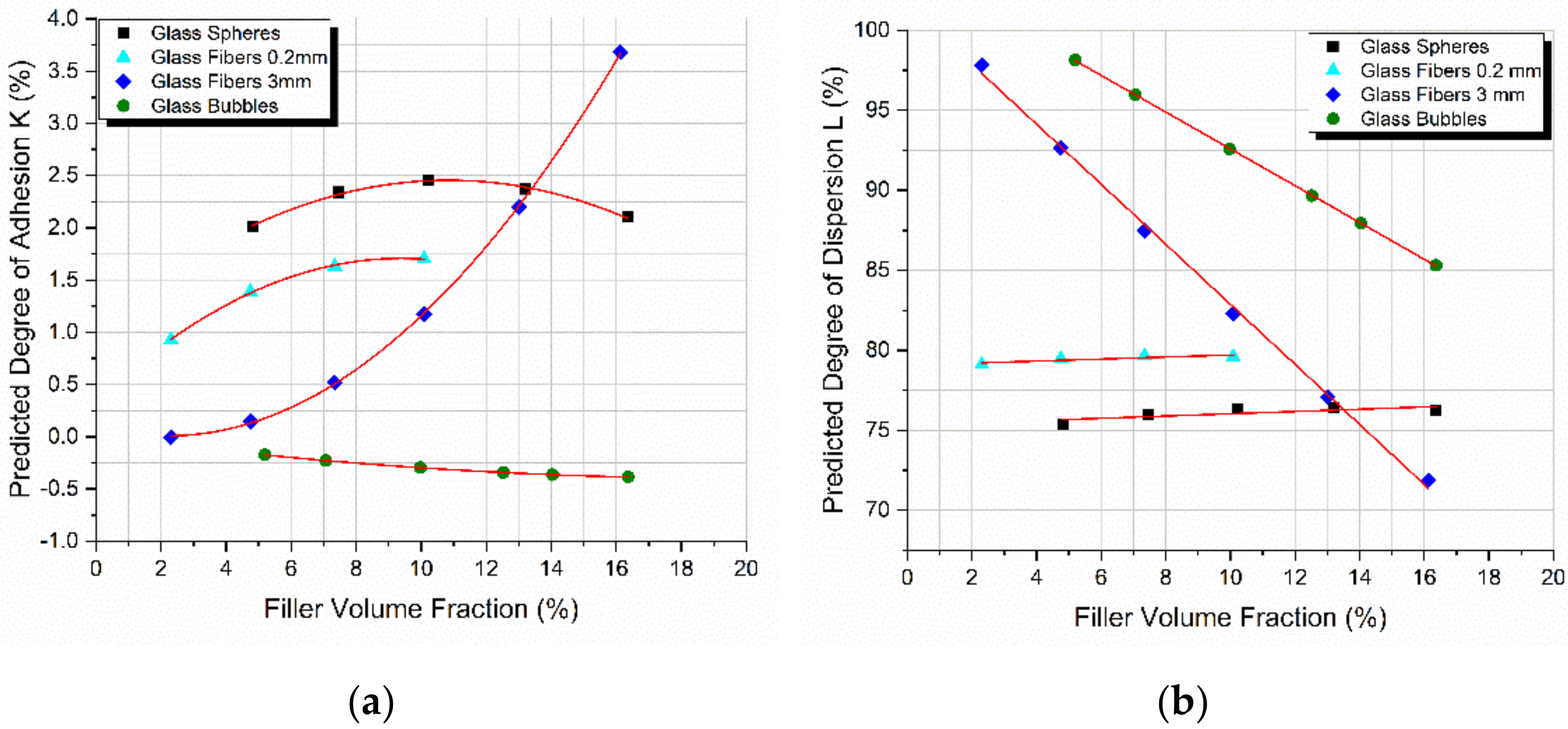
3.2. Degree of Adhesion and Degree of Dispersion
3.3. Model Application
- Step 1. Given two experimental points, (C1, P1) at low Cf and (C2, P2) at high Cf, the modulus prediction is obtained.
- Step 2. Using the modulus predicted values and applying Equations (7) and (9), the degree of adhesion K variation with the filler-volume fraction, Cf is obtained.
- Step 3. Using the modulus predicted values and applying Equations (7) and (10), the degree of dispersion L variation with the filler-volume fraction Cf is obtained.
4. Results and Discussion
4.1. Glass Spheres
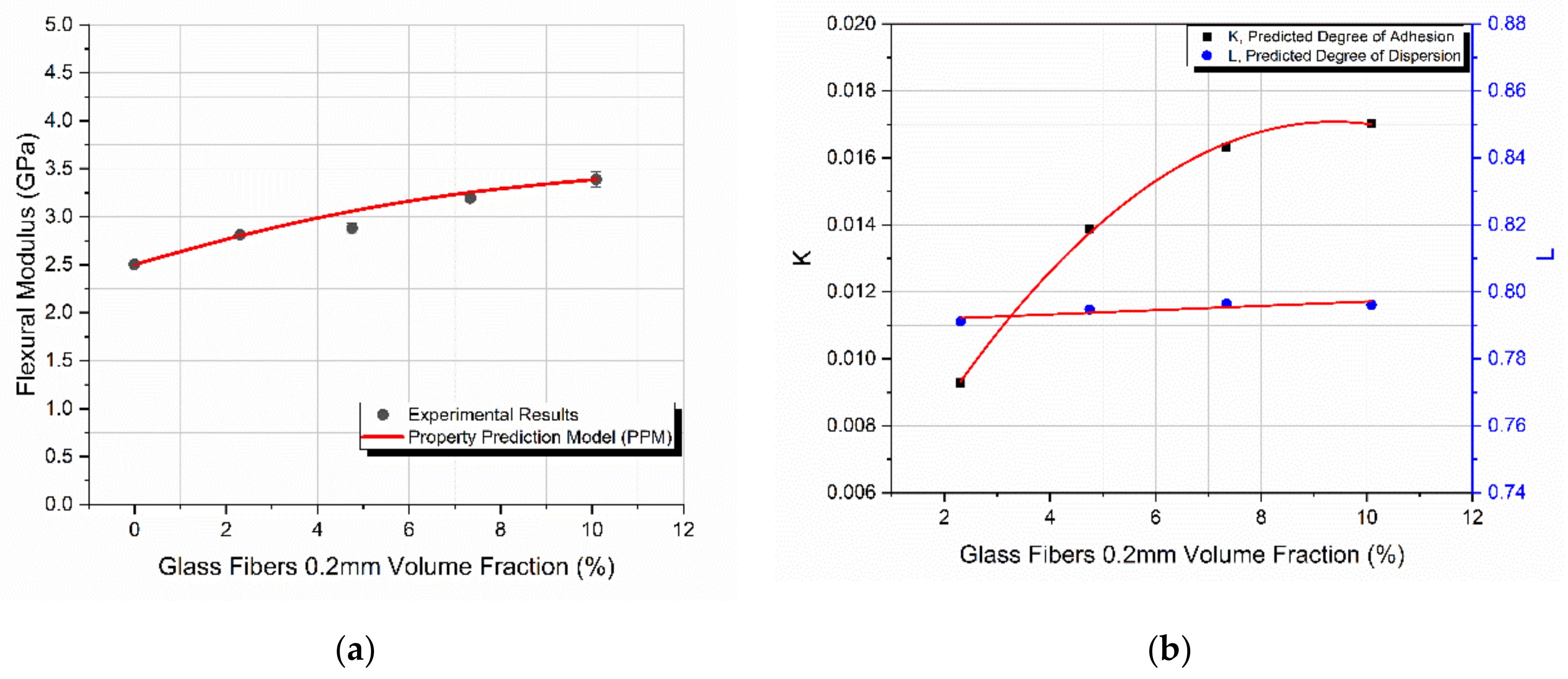
4.2. Glass Fibers of 0.2 mm in Length
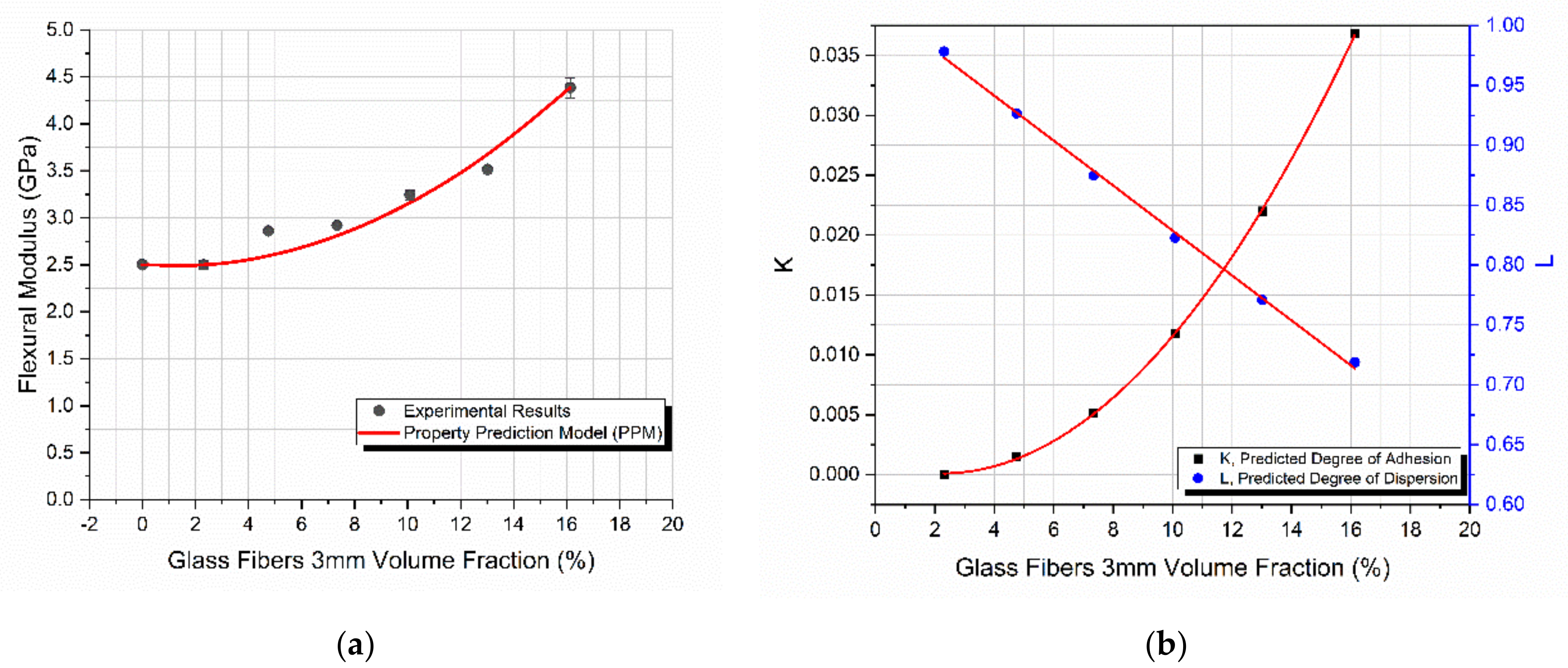
4.3. Glass Fibers of 3 mm in Length
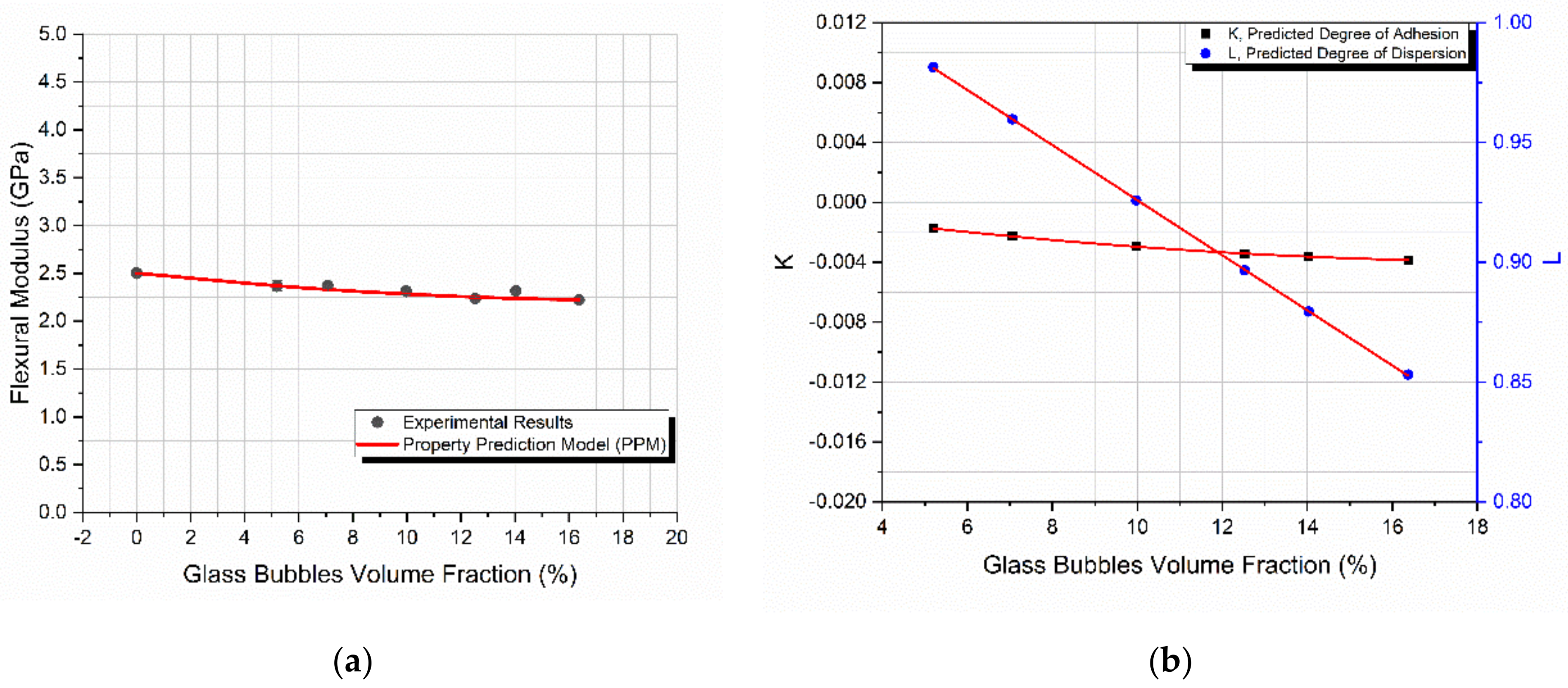
4.4. Glass Bubbles
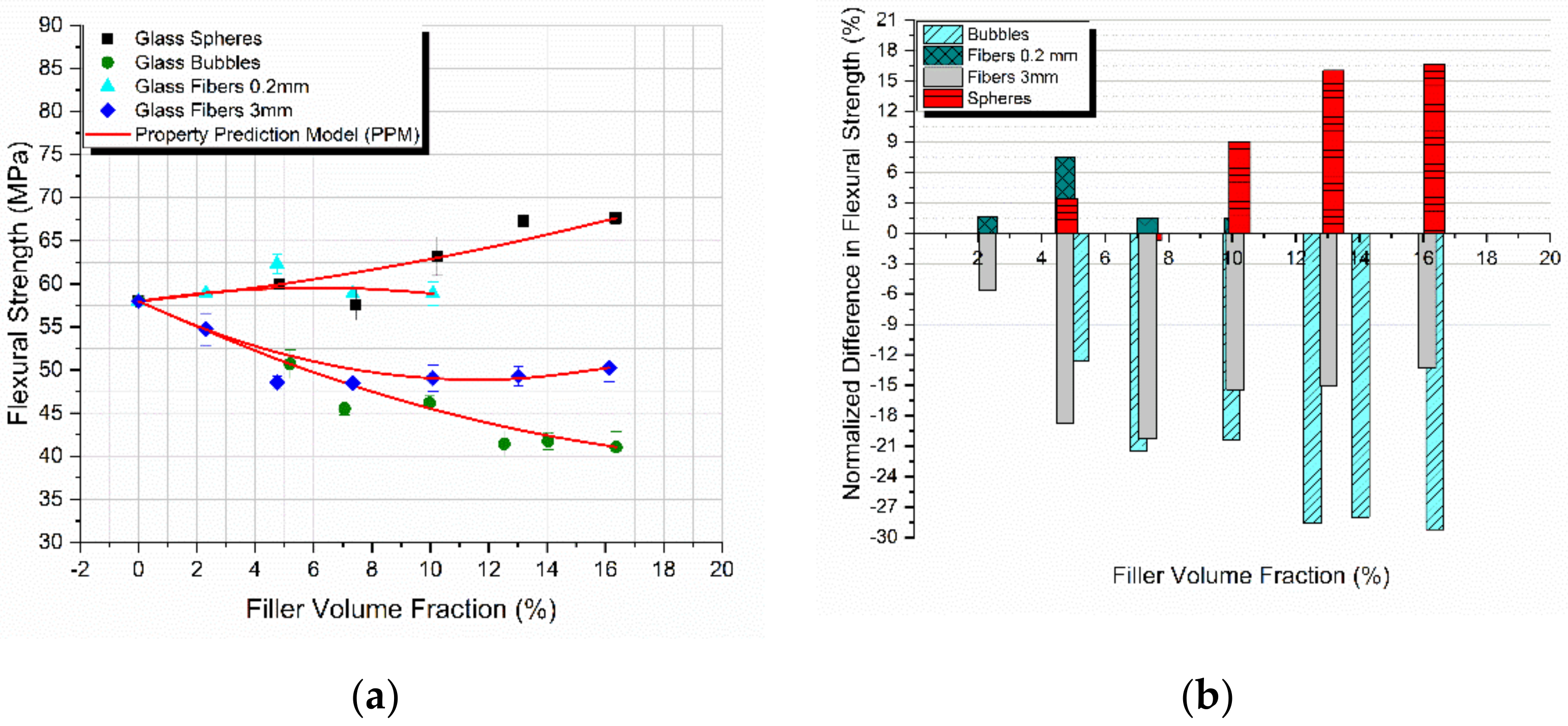
4.5. Comparison of the Predicted and Experimental Results
4.6. SEM Micrographs
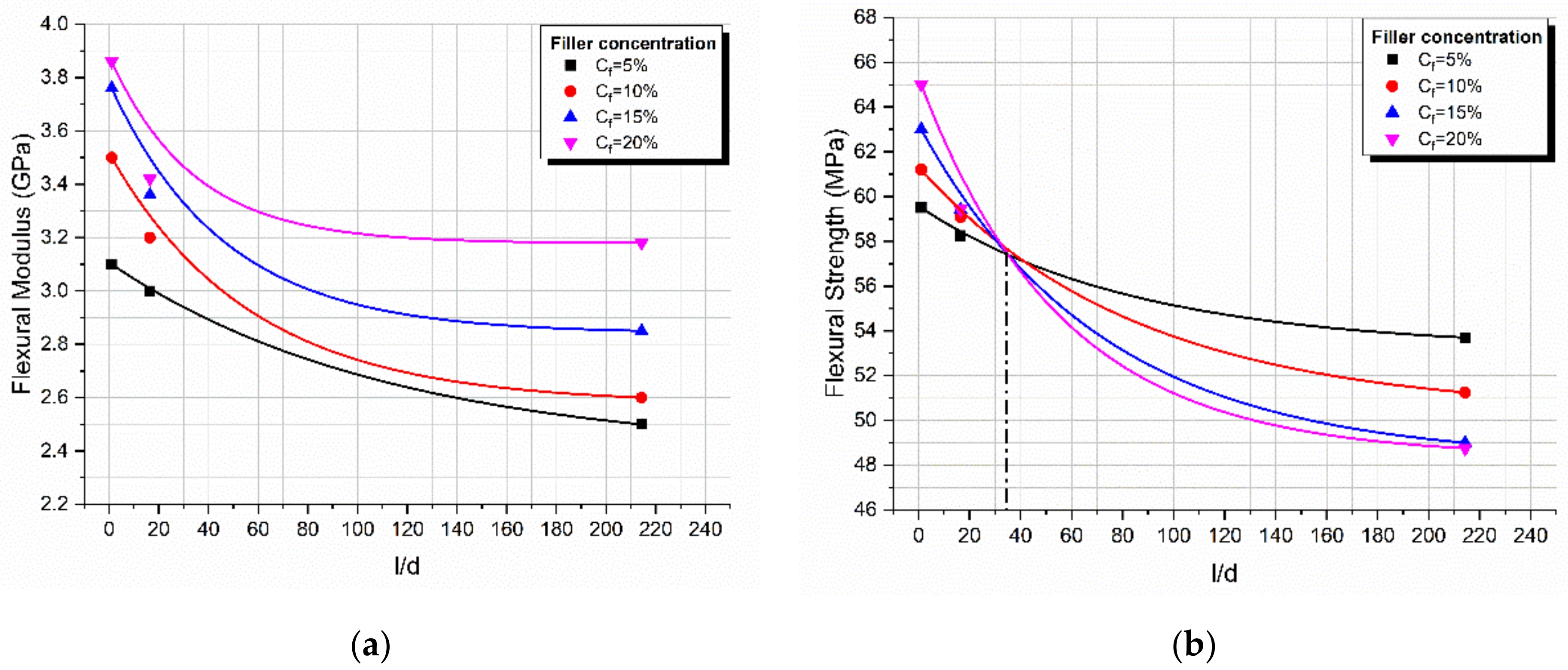
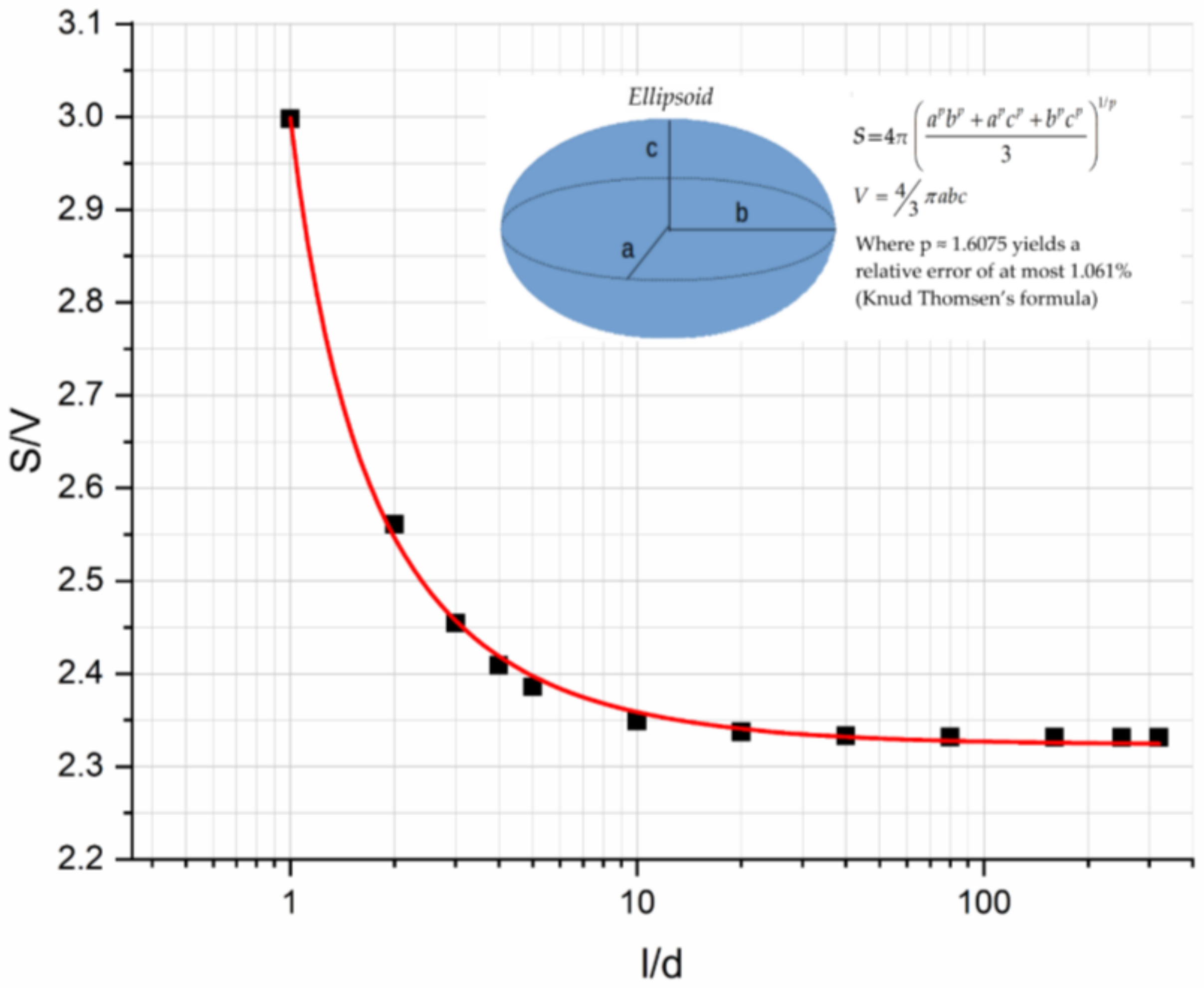
4.7. Geometrical Considerations
5. Conclusions
- A constant increase in the flexural modulus with the filler content for the composites reinforced with glass spheres and glass fibers was observed, while a small decrease in the glass bubble filled composites was found and this was in accordance with similar findings in the literature.
- A maximum increase in the modulus on the order of 75% was observed for the 3 mm glass fiber reinforced composites.
- In all cases, the PPM model perfectly predicted the flexural modulus variation with filler content.
- The degree of adhesion, K, as calculated from the PPM model followed the same trend of variation with filler loading as in the case of the flexural modulus.
- The degree of dispersion, L, as calculated from the PPM model, depending on the filler shape and dimensions and their tendency to agglomerate, in some cases decreased linearly while in other cases it remained practically constant.
- The maximum increase in the flexural strength observed was on the order of 16.5% for the glass sphere reinforced composites.
- In all cases, the PPM model perfectly predicted the flexural strength variation with the filler content.
- Materials characterized by high K-values (glass spheres, 0.2 mm glass fibers) showed an increase in flexural strength. On the contrary, materials with low K-values (3 mm glass fibers, glass bubbles) showed a decrease in strength with the filler-volume fraction.
- Concerning the effect of inclusion geometry on the flexural modulus, a decrease in the modulus with l/d was found and this was attributed to the decrease in the contact area per unit volume S/V of an ellipsoid inclusion as l/d increases.
- Finally, concerning the effect of inclusion geometry on the flexural strength, a decrease in strength with l/d was found, with a rate of strength decrease dependent upon the filler concentration.
- The flexural strength depends upon the inherent flaws that exist on the inclusion surface; therefore, the rate of strength decrease is proportional to the filler loading. At low values of l/d, the strength increases with filler loading while as l/d increases, this behavior is inverted.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patel, M.; Angerer, G.; Crank, M.; Schleich, J.; Marscheider-Weidemann, F.; Wolf, O.; Hüsing, B. Techno-Economic Feasibility of Large-Scale Production of Bio-Based Polymers in Europe; European Science and Technology Observatory: Seville, Spain, 2011. [Google Scholar]
- Lu, D.R.; Xiao, C.M.; Xu, S.J. Starch-based completely biodegradable polymer materials. Express Polym. Lett. 2009, 3, 366–375. [Google Scholar] [CrossRef]
- Jiang, T.; Duan, Q.; Zhu, J.; Liu, H.; Yu, L. Starch-based biodegradable materials: Challenges and opportunities. Adv. Ind. Eng. Polym. Res. 2020, 3, 8–18. [Google Scholar] [CrossRef]
- Zhang, X.; Teng, Z.; Huang, R. Biodegradable Starch/Chitosan Foam via Microwave Assisted Preparation: Morphology and Performance Properties. Polymers 2020, 12, 2612. [Google Scholar] [CrossRef]
- Ibrahim, K.A.; Naz, M.Y.; Shukrullah, S.; Sulaiman, S.A.; Ghaffar, A.; AbdEl-Salam, N.M. Nitrogen Pollution Impact and Remediation through Low Cost Starch Based Biodegradable polymers. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bulatović, V.O.; Mandić, V.; Grgić, D.K.; Ivančić, A. Biodegradable Polymer Blends Based on Thermoplastic Starch. J. Polym. Environ. 2020, 29, 492–508. [Google Scholar] [CrossRef]
- Bai, J.; Pei, H.; Zhou, X.; Xie, X. Reactive compatibilization and properties of low-cost and high-performance PBAT/thermoplastic starch blends. Eur. Polym. J. 2021, 143, 110198. [Google Scholar] [CrossRef]
- Willett, J.L.; Felker, F.C. Tensile yield properties of starch-filled poly(ester amide) materials. Polymer 2005, 46, 3035–3042. [Google Scholar] [CrossRef]
- Winkler, H.; Vorwerg, W.; Rihm, R. Thermal and mechanical properties of fatty acid starch esters. Carbohydr. Polym. 2014, 102, 941–949. [Google Scholar] [CrossRef] [PubMed]
- Ogunsona, E.; Ojogbo, E.; Mekonnen, T. Advanced material applications of starch and its derivatives. Eur. Polym. J. 2018, 108, 570–581. [Google Scholar] [CrossRef]
- Nawang, R.; Danjaji, I.D.; Ishiaku, U.S.; Ismail, H.; Mohd Ishak, Z.A. Mechanical properties of sago starch-filled linear low density polyethylene (LLDPE) composites. Polym. Test. 2001, 20, 167–172. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Kontaxis, L.C.; Koutsomitopoulou, A.F.; Zaoutsos, S.P. Stress relaxation behavior of starch powder epoxy resin composites. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Ji, M.; Li, F.; Li, J.; Li, J.; Zhang, C.; Sun, K.; Guo, Z. Enhanced mechanical properties, water resistance, thermal stability, and biodegradation of the starch-sisal fibre composites with various fillers. Mater. Des. 2021, 198, 109373. [Google Scholar] [CrossRef]
- Ramakrishna, G.; Kiran babu, P.; Purushothaman, K.; Sivakumar, E.R.; Sreenivasan, M. An analysis on natural fiber composite materials. Mater. Today Proc. 2021, 45, 6794–6799. [Google Scholar] [CrossRef]
- Sumarji, S.; Aqsho, M.G.D.; Basuki, H.A.; Asrofi, M. Tensile Properties and Fracture Morphology of Polyethylene Terephthalate Mixed Rice Starch Particle Based Blend Composites. Mater. Sci. Res. India 2020, 17, 47–53. [Google Scholar] [CrossRef]
- Berthelot, J.; Cole, M. The Constituents of a Composite Material. In Composite Materials: Mechanical Behavior and Structural Analysis; Materials Science; Springer: Berlin/Heidelberg, Germany, 1999; pp. 21–36. [Google Scholar]
- Yalcin, B.; Amos, S.E. Hollow Glass Microspheres in Thermoplastics. In Hollow Glass Microspheres for Plastics, Elastomers, and Adhesives Compounds; Elsevier: Amsterdam, The Netherlands, 2015; pp. 35–105. ISBN 9781455775507. [Google Scholar]
- Verweij, H.; De With, G.; Veeneman, D. Hollow glass microsphere composites: Preparation and properties. J. Mater. Sci. 1985, 20, 1069–1078. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.H.; Jen, M.H.R. Manufacturing and mechanical properties of glass bubbles/epoxy particulate composite. J. Compos. Mater. 1998, 32, 1356–1390. [Google Scholar] [CrossRef]
- Monfared, V. Problems in short-fiber composites and analysis of chopped fiber-reinforced materials. In New Materials in Civil Engineering; Elsevier: Amsterdam, The Netherlands, 2020; pp. 919–1043. [Google Scholar]
- Thomason, J.L. Glass fibre sizing: A review. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105619. [Google Scholar] [CrossRef]
- Yesgat, A.L.; Kitey, R. Effect of filler geometry on fracture mechanisms in glass particle filled epoxy composites. Eng. Fract. Mech. 2016, 160, 22–41. [Google Scholar] [CrossRef]
- Adachi, T.; Osaki, M.; Araki, W.; Kwon, S.C. Fracture toughness of nano- and micro-spherical silica-particle-filled epoxy composites. Acta Mater. 2008, 56, 2101–2109. [Google Scholar] [CrossRef]
- Nakamura, Y.; Yamaguchi, M.; Okubo, M.; Matsumoto, T. Effect of particle size on the fracture toughness of epoxy resin filled with spherical silica. Polymer 1992, 33, 3415–3426. [Google Scholar] [CrossRef]
- Kitey, R.; Tippur, H.V. Role of particle size and filler–matrix adhesion on dynamic fracture of glass-filled epoxy. I. Macromeasurements. Acta Mater. 2005, 53, 1153–1165. [Google Scholar] [CrossRef]
- Singh, S.S.; Parameswaran, V.; Kitey, R. Filler shape and volume fraction effect on dynamic compression behaviour of glass filler reinforced epoxy composites. Int. J. Mater. Struct. Integr. 2019, 13, 81–92. [Google Scholar] [CrossRef]
- Kushvaha, V.; Tippur, H. Effect of Filler Particle Shape on Dynamic Fracture Behavior of Glass-Filled Epoxy. Conf. Proc. Soc. Exp. Mech. Ser. 2013, 1, 513–522. [Google Scholar] [CrossRef]
- Pande, S.J.; Sharma, D.K. Fracture toughness of short glass fibre and glass particulate hybrid composites. Fibre Sci. Technol. 1984, 21, 307–317. [Google Scholar] [CrossRef]
- Malucelli, G.; Fioravanti, A.; Francioso, L.; De Pascali, C.; Signore, M.A.; Carotta, M.C.; Bonanno, A.; Duraccio, D. Preparation and characterization of UV-cured composite films containing ZnO nanostructures: Effect of filler geometric features on piezoelectric response. Prog. Org. Coat. 2017, 109, 45–54. [Google Scholar] [CrossRef]
- Leluk, K.; Frąckowiak, S.; Ludwiczak, J.; Rydzkowski, T.; Thakur, V.K. The Impact of Filler Geometry on Polylactic Acid-Based Sustainable Polymer Composites. Molecules 2020, 26, 149. [Google Scholar] [CrossRef] [PubMed]
- Bek, M.; Gonzalez-Gutierrez, J.; Kukla, C.; Črešnar, K.P.; Maroh, B.; Perše, L.S. Rheological Behaviour of Highly Filled Materials for Injection Moulding and Additive Manufacturing: Effect of Particle Material and Loading. Appl. Sci. 2020, 10, 7993. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhai, Z.; Drummer, D. Thermal Conductivity of Aluminosilicate- and Aluminum Oxide-Filled Thermosets for Injection Molding: Effect of Filler Content, Filler Size and Filler Geometry. Polymers 2018, 10, 457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, M.; Jang, J.; Suhr, J. Effect of filler geometry on coefficient of thermal expansion in carbon nanofiber reinforced epoxy composites. J. Nanosci. Nanotechnol. 2011, 11, 1098–1102. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Wang, X.; Lei, H.; Huo, J. Chemical modification of starch with epoxy resin to enhance the interfacial adhesion of epoxy-based glass fiber composites. RSC Adv. 2016, 6, 84187–84193. [Google Scholar] [CrossRef]
- Sandhu, K.S.; Singh, N. Some properties of corn starches II: Physicochemical, gelatinization, retrogradation, pasting and gel textural properties. Food Chem. 2007, 101, 1499–1507. [Google Scholar] [CrossRef]
- Glass Microspheres 2.5 g/cm3. Available online: https://shop1.r-g.de/en/art/210123 (accessed on 21 October 2021).
- Chopped Glass Fibre Strands 3 mm. Available online: https://shop1.r-g.de/en/art/210100 (accessed on 21 October 2021).
- Milled Glass Fibre 0.2 mm. Available online: https://shop1.r-g.de/en/art/210110 (accessed on 21 October 2021).
- 3MTM Glass Bubbles 0.12 g/cm3. Available online: https://multimedia.3m.com/mws/media/130063O/3mtm-glass-bubbles-selection-guide.pdf?fn=Microspheres%20Selection%20Guide%20Cel (accessed on 21 October 2021).
- Papanicolaou, G.C.; Koutsomitopoulou, A.F.; Sfakianakis, A. Effect of Thermal Fatigue on the Mechanical Properties of Epoxy Matrix Composites Reinforced with Olive Pits Powder. J. Appl. Polym. Sci. 2012, 124, 67–76. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Kontaxis, L.C.; Manara, A.E. Viscoelastic behaviour and modelling of nano and micro TiO2 powder-epoxy resin composites. Cienc. Tecnol. Mater. 2016, 28, 138–146. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Manara, A.E.; Kontaxis, L.C. Experimental and prediction study of displacement-rate effects on flexural behaviour in nano and micro TiO2 particles-epoxy resin composites. Polymers 2020, 12, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rabbi, F. Oxygen Flux and Dielectric Response Study of Mixed Ionic-Electronic Conducting (MIEC) Heterogeneous Functional Materials. Ph.D. Thesis, University of South Carolina-Columbia, Columbia, SC, USA, 8 September 2014. [Google Scholar]
- Roulin-Moloney, A.C.; Cantwell, W.J.; Kausch, H.H. Parameters determining the strength and toughness of particulate-filled epoxy resins. Polym. Compos. 1987, 8, 314–323. [Google Scholar] [CrossRef]
- D’Almeida, J.R.M.; De Carvalho, L.H. An investigation on the tensile strength of particulate filled polymeric composites. J. Mater. Sci. 1998, 33, 2215–2219. [Google Scholar] [CrossRef]
- Fu, S.Y.; Feng, X.Q.; Lauke, B.; Mai, Y.W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate-polymer composites. Compos. Part B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Tiedje, E.W.; Guo, P. Modeling the influence of particulate geometry on the thermal conductivity of composites. J. Mater. Sci. 2014, 49, 5586–5597. [Google Scholar] [CrossRef]



| Amylose Analogy (%) | 16.9–21.3 |
| Swelling power (g/g) | 13.7–20.7 |
| Solubility (%) | 9.7–15 |
| Water binding capacity (%) | 82.1–97.7 |
| Glass Transition Temperature (°C) | 70 |
| Physical and Geometrical Characteristics | Glass Spheres | Glass Fibers 0.2 mm | Glass Fibers 3 mm | Glass Bubbles |
|---|---|---|---|---|
| Glass type | Soda-lime glass | E-Glass | E-Glass | Borosilicate glass |
| Cross section | Circular | Circular | Circular | Circular |
| Dimensions | 1 diameter (av.): 120 μm | length (av.): 230 μm | length (av.): 3000 μm | diameter (av.): 65 μm |
| 2 l/d: 1 | l/d: 16.42 | l/d: 214.28 | l/d: 1 | |
| Density | 2.5 g/cm3 | 2.53–2.55 g/cm3 | 2.53–2.55 g/cm3 | 0.21 g/cm3 |
| Bulk density | 1.5 kg/dm3 | 0.45 kg/dm3 | 0.45 kg/dm3 | 0.125 kg/dm3 |
| Softening temperature | 470 °C | 840 °C | 840 °C | 795 °C |
| Volume Fraction (%) | |||
|---|---|---|---|
| Glass Spheres | Glass Fibers 0.2 mm | Glass Fibers 3 mm | Glass Bubbles |
| 4.82 | 2.31 | 2.31 | 5.20 |
| 7.45 | 4.75 | 4.75 | 7.00 |
| 10.23 | 7.34 | 7.34 | 9.97 |
| 13.19 | 10.09 | 10.09 | 12.53 |
| 16.35 | - | 13.01 | 14.04 |
| - | - | 16.13 | 16.37 |
| Glass Type | Filler-Volume Fraction (%) | Flexural Strength (MPa) | Standard Deviation (MPa) | Coeff. of Variation (%) |
|---|---|---|---|---|
| Hybrid Resin | 0.00 | 57.98 | 0.26 | 0.45 |
| Glass spheres | 4.82 | 59.94 | 0.50 | 0.83 |
| 7.45 | 57.57 | 1.77 | 3.08 | |
| 10.23 | 63.21 | 2.23 | 3.52 | |
| 13.19 | 67.28 | 0.70 | 1.03 | |
| 16.35 | 67.62 | 0.61 | 0.91 | |
| Glass fibers 0.2 mm | 2.31 | 58.95 | 0.54 | 0.92 |
| 4.75 | 62.35 | 1.13 | 1.81 | |
| 7.34 | 58.85 | 1.77 | 3.00 | |
| 10.09 | 58.87 | 1.35 | 2.30 | |
| Glass fibers 3 mm | 2.31 | 54.71 | 1.85 | 3.37 |
| 4.75 | 48.55 | 0.74 | 1.53 | |
| 7.34 | 48.47 | 2.79 | 5.76 | |
| 10.09 | 49.04 | 1.52 | 3.09 | |
| 13.01 | 49.29 | 1.13 | 2.30 | |
| 16.13 | 50.27 | 1.65 | 3.27 | |
| Glass Bubbles | 5.20 | 50.69 | 1.63 | 3.21 |
| 7.06 | 45.55 | 0.79 | 1.73 | |
| 9.97 | 46.17 | 0.83 | 1.81 | |
| 12.53 | 41.43 | 1.52 | 3.66 | |
| 14.04 | 41.75 | 0.98 | 2.36 | |
| 16.37 | 41.05 | 1.82 | 4.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontaxis, L.C.; Kozaniti, F.K.; Papanicolaou, G.C. Mechanical Behavior Modelling and Filler Geometry Effect of Glass Filler Reinforced Starch-Epoxy Hybrid Matrix Composites. Materials 2021, 14, 6587. https://doi.org/10.3390/ma14216587
Kontaxis LC, Kozaniti FK, Papanicolaou GC. Mechanical Behavior Modelling and Filler Geometry Effect of Glass Filler Reinforced Starch-Epoxy Hybrid Matrix Composites. Materials. 2021; 14(21):6587. https://doi.org/10.3390/ma14216587
Chicago/Turabian StyleKontaxis, Lykourgos C., Foteini K. Kozaniti, and George C. Papanicolaou. 2021. "Mechanical Behavior Modelling and Filler Geometry Effect of Glass Filler Reinforced Starch-Epoxy Hybrid Matrix Composites" Materials 14, no. 21: 6587. https://doi.org/10.3390/ma14216587
APA StyleKontaxis, L. C., Kozaniti, F. K., & Papanicolaou, G. C. (2021). Mechanical Behavior Modelling and Filler Geometry Effect of Glass Filler Reinforced Starch-Epoxy Hybrid Matrix Composites. Materials, 14(21), 6587. https://doi.org/10.3390/ma14216587








