Abstract
Asymmetric molecule strategy is considered an effective method to achieve high power conversion efficiency (PCE) of polymer solar cells (PSCs). In this paper, nine oligomers are designed by combining three new electron-deficient units (unitA)—n1, n2, and n3—and three electron-donating units (unitD)—D, E, and F—with their π-conjugation area extended. The relationships between symmetric/asymmetric molecule structure and the performance of the oligomers are investigated using the density functional theory (DFT) and time-dependent density functional theory (TD–DFT) calculations. The results indicate that asymmetry molecule PEn2 has the minimum dihedral angle in the angle between two planes of unitD and unitA among all the molecules, which exhibited the advantages of asymmetric structures in molecular stacking. The relationship of the values of ionization potentials (IP) and electron affinities (EA) along with the unitD/unitA π-extend are revealed. The calculated reorganization energy results also demonstrate that the asymmetric molecules PDn2 and PEn2 could better charge the extraction of the PSCs than other molecules for their lower reorganization energy of 0.180 eV and 0.181 eV, respectively.
1. Introduction
Polymer solar cells (PSCs) have attracted wide attention for their low-cost, lightweight, flexible, and roll-to-roll fabricating characters [1,2,3,4,5,6,7], and could be one promising candidate for next generation renewable energy techniques [8,9]. Generally, a classical bulk-heterojunction (BHJ) PSC device is based on the active layer blended with the electron donor and electron acceptor materials [10,11,12]. The power conversion efficiency (PCE) of the PSCs has been further improved by many new organic semiconductors that have been well-designed and synthesized during the past decades [13,14,15,16,17,18]. For electron donor materials, the representative donor–acceptor (D–A) polymers, such as PM6 [19], PBDT-C [15], and D18 [20], have shown excellent performance. To date, the PCE is over 18% [20]. The D–A structure played a key role to improve device properties since their suitable bandgaps and energy levels can be easily tuned [21,22,23]. In addition, a strong intramolecular charge transfer (ICT) can form between donor and acceptor units, which leads to the expansion of the absorption spectrum and an increase in the absorption coefficient [24]. To obtain more advanced PSCs, many strategies were applied to design promising polymer donor materials, such as the introduction of halogen atoms, side-chain engineering, symmetry-breaking strategies, ternary copolymerization strategy, etc. [25,26].
Among these strategies, the symmetry-breaking design concept is attractive due to its excellent molecular packing and the low nonradiative energy loss of the asymmetric structure [27,28,29,30,31]. Many asymmetric D–A polymers have been investigated to gain insight into their advantages. Supramolecular locks could form among the blend films by introducing asymmetric halogen atoms and alkyl chains, which is beneficial for high fill fact (FF) [32]. Yang’s research group systematically inspected asymmetric benzodithiophene (BDT) units [31,33] and asymmetric backbones [30], which could efficiently modulate molecular aggregation and crystallinity. Based on asymmetric indenothiophene polymers designed and synthesized by Zheng et al., the PCE improved from 5.40% to 9.14% [34]. He et al. developed chlorination-atom-based asymmetric thiophene polymers [35], which could be fabricated as a thick film and a PCE of up to 9.11% was obtained. The concept of asymmetric structure is also widely applied in designing non-fullerene acceptors (NAFs). Bo et al. introduced asymmetric side chains to fused-ring acceptors. When blending with PBDB-T, the molecular packing could be enhanced effectively and the phase separation could be optimized [36]. Chen et al. designed new small molecule acceptors with asymmetric 4-alkyl-8-alkoxybenzo[1,2-b:4,5-b′]dithiophene as the central unit, and a high FF of 75% was achieved [37]. Sun et al. synthesized asymmetric ADA type NAFs by extending the conjugation of the indacenodithiophene backbone, which could significantly improve device performance [38]. Recently, Yan et al. developed an asymmetric end group strategy to tune ANFs energy levels, resulting in high PCE of over 17% [28]. The design concept of asymmetric structures has been widely applied and has experienced rapid progress.
However, the intrinsic nature of the superior properties of asymmetric structures have rarely been studied in-depth, which is very important for designing high-performance donor/acceptor materials. In this work, as one of the most basic schemes, the asymmetric structures on the π-extend of the conjugate plane of the donor/acceptor units are mainly investigated. We start from a general structure unit (n1), as displayed in Figure 1, and extend the molecular conjugate plane, then we obtained the n2 and n3 units, and the donor units D, E, and F using the same method. Based on the D–A alternative principle, nine polymers are obtained, as shown in Figure 2. The units from n1 to n3 and D to F are monomers with a π-conjugation area expanded gradually. n2 and E are asymmetric structure units, so that the nature of the asymmetric structure can be deeply investigated. Quantum chemical methods are an economical and effective way to understand and predict molecular structure and properties, which could avoid cumbersome synthesis [39,40]. The properties of energy level and of the optical and excited states are crucial for polymer donors for the photo-electric conversion processes [41]. In this paper, density functional theory (DFT) is employed to optimize the geometries and calculate energy levels, ionization potentials (IP), electron affinities (EA), and reorganization energies (λ) [42]. In addition, the time-dependent density functional theory (TD–DFT) is employed to calculate the absorption spectrum and excited states [43]. As a result, we found that the asymmetric molecule PEn2 shows the minimum dihedral angles that could be beneficial to form better molecular stacking. This shows the advantage of asymmetric structures. The properties of energy level, energy gap (Eg), and the spectral absorption region could be regularly affected by changing the size of the conjugate region. The π-extend of the unitD/unitA has a close relation with the IP/EA of the molecules and further influences the charge extraction of the PSCs device. We hope that this study can offer an important guideline to the design of asymmetric donor polymers.
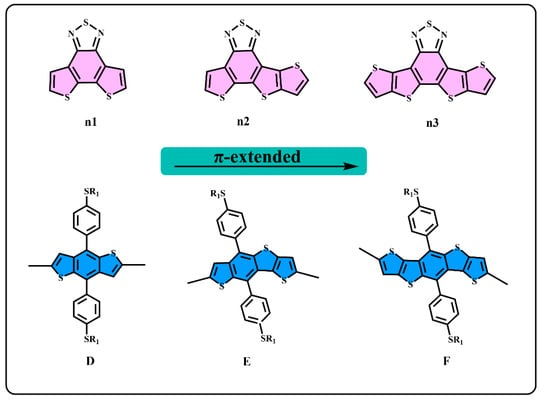
Figure 1.
The structure of n1, n2, n3, D, E, and F.
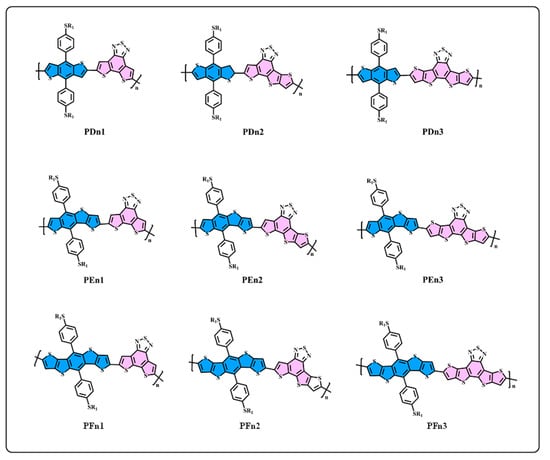
Figure 2.
The structure of D–A oligomers: PDn1, PDn2, PDn3, PEn1, PEn2, PEn3, PFn1, PFn2, and PFn3.
2. Computational Methods
The molecular structure at the ground state and the molecular electrostatic potential (ESP) of all the monomers, as shown in Figure 1, were optimized in the gas phase under the B3LYP-(D3)BJ/6-311G(d) level [44,45,46]. The nine oligomers, as shown in Figure 2, were optimized in chloroform using the conductor-like polarizable continuum model (CPCM) [47], under the B3LYP-(D3)BJ/6-311G(d) level. The electronic absorption spectra and other excited-state properties of the oligomers were calculated using the time-dependent density functional theory (TD-DFT) under the CAM-B3LYP/6-311G(d) [42,48] level, employing chloroform (CPCM) as a solvent. All the alkyl side chains were replaced by methyl groups. All the calculations were performed by Gaussian 09 package [49]. Furthermore, the absorption spectra and electron transitions were analyzed by Multiwfn 3.7 [50,51].
3. Results and Discussion
3.1. Molecule Design
We generally design molecules with large conjugated polycyclic aromatic units for D–A alternative oligomers, which could effectively increase the coplanarity and π-electron delocalization, and could thus benefit for the light absorption and charge transportation [52]. As revealed in previous research [52,53], the unitA blocks based on benzothiadiazole demonstrated excellent performance in organic electronics. In this work, we designed three benzothiadiazole-based moieties with the expansion of the conjugation area n1, n2, and n3, as shown in Figure 1. In addition, the phenyl substituted the benzo(1,2-b:4,5-b’)dithiophene (BDTP)-based two-dimensional (2D) electron-donating moieties have an advantage in the solubility, optical, and electrical properties [54]. Three electron-donating moieties based on BDTP (D, E, and F) were designed with gradual π-extend. n2 and E are asymmetric units. We further obtained PDn1, PDn2, PDn3, PEn1, PEn2, PEn3, PFn1, PFn2, and PFn3 by combining nine oligomers. As shown in Figure 2, the unitA conjugated area extended of the oligomers for each line from left to right, and the unitD conjugated area extended of the oligomers for each column from top to bottom. The nine molecules are evidently periodic variational in structure, and PDn2, PEn1, PEn2, PEn3, and PFn2 are asymmetric structures. In what follows, we will discuss the relationship between the structure and properties of these ideal molecules.
3.2. Geometric Optimization and Electronic Structure
The optimized geometry at the ground state of the unitD and unitA moieties exhibited good planarity, as shown in Supplementary Materials Figure S1. The calculated frontier molecular orbits (FMOs) of the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO) energy levels are shown in Supplementary Materials Figure S2. To deeply understand the charge distribution of the structures of the unitD and unitA moieties, the ESP was calculated and plotted, as shown in Figure 3. The blue and red color represent the high and low potential, respectively, which means the absence and abundance of electrons in this area, respectively. Intermediary transition colors depict the neutral electrostatic potentials. The results indicate that the conjugated thiophenes regions are highly electron-rich. Most of its positive regions are mainly localized at the hydrogen atoms in the non-conjugated methyl groups. The location of the electron-rich sulfur atoms is also evident, and they appear yellowish around these regions. For the moieties n1, n2, and n3, the N atoms connected directly to the S atoms, which attract considerable electron density. The electronegativity difference of atoms led to a redistribution of charge.
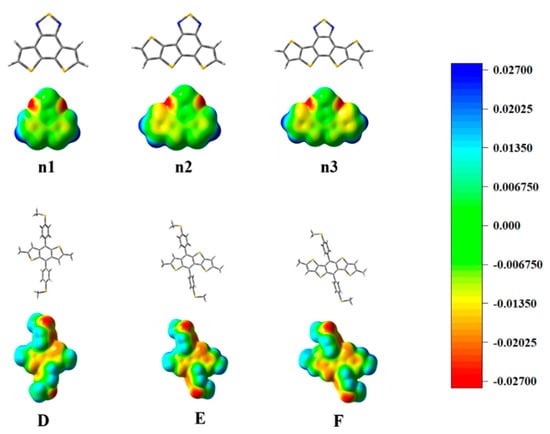
Figure 3.
The optimized geometry and ESP distributions (electron density isosurface, 0.001 au) on the n1, n2, n3, D, E, and F models.
As shown in Figure 4, the ground state geometry of oligomers was optimized. The dihedral angles (θ) between the two moieties of PDn1, PDn2, and PDn3 are 7.66°, 9.15°, and 24.25°, respectively. The θ of PFn1, PFn2, PFn3 are 18.45°, 19.93°, and 20.21°, respectively. The θ increased with the π-extended among the PDn and PFn series oligomers; it is very likely that the expansion of the conjugate area leads to the enhanced rigidity. This phenomenon also appeared among PEn1 and PEn3, as 10.11° and 20.31° respectively. The size of the conjugation region also significantly affected the molecular planarity. However, the θ (PEn2) was only 6.50°; it was compounded by two asymmetric units (E and n2). The PEn2 with the minimum dihedral angles will be beneficial for intermolecular π–π stacking, which may produce good molecular stacking morphology among the BHJ PSCs [55].
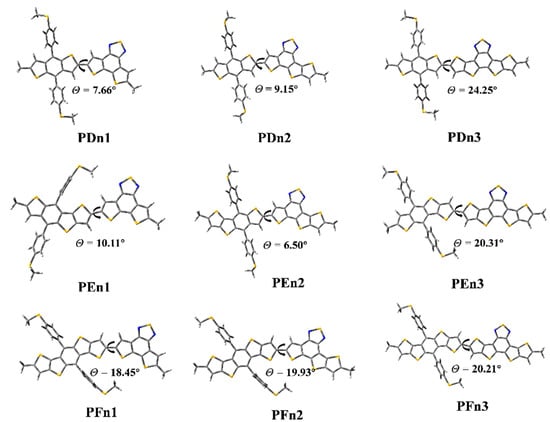
Figure 4.
The optimized geometry of the oligomers.
The values of HOMO and LUMO energy levels, and the energy difference (ΔH-L) between HOMO and LUMO values of the studied oligomers in solvent phases were also calculated and are presented in Table 1 and Figure 5. The HOMO increased, but LUMO declined with the moieties in the π–π conjugation region that extended gradually, which resulted in the decreased ΔH-L values. It means the π-extended strategy could effectively lower the LUMO and improve the HOMO simultaneously. The π-extended strategy could be applied to regulate the molecular energy level. Figure 5 distinctly shows the electron cloud density transition from HOMO to LUMO, which could be attributed to the ICT from donor unit to acceptor unit and the π–π* transition of the oligomers. It also indicates their good charge transfer capacity to a certain extent.

Table 1.
The optimized geometry of oligomers: dihedral angles (θ) of the D-A block, energies of HOMO, LUMO, Eg values, and VOC.
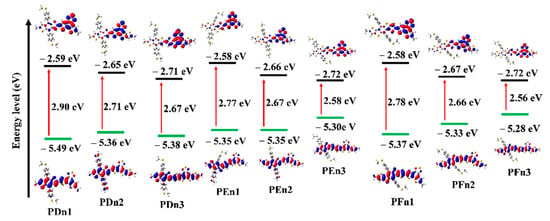
Figure 5.
Calculated frontier molecular orbital for all the molecules.
The PCE of the PSCs can be calculated by Equation (1) [56]:
where JSC, VOC, FF, and Pin are short-circuited current density, open-circuit voltage, fill factor, and incident light intensity, respectively. The illustration of the working mechanism of the D/A blend and the device structure are displayed in Figure 6. The voltage is proportional to PCE and a higher VOC would be of benefit to achieve a high PCE, which could be estimated by Equation (2) [56]:
where and represent the energy level of HOMO (donor) and LUMO (acceptor), respectively. The value of 0.5 V is the non-fullerene PSCs empirical factor of efficient charge separation [57]. In this paper, a well-known NAFs ITIC was selected [57] and calculated under the B3LYP-D3(BJ)/6-311G(d) level. The calculated energy levels of ITIC are −5.64 eV (HOMO) and −3.56 eV (LUMO). The ITIC optimized geometry, energy level, and orbital electron cloud density distribution are shown in Supplementary Materials Figure S3. The calculated VOC are summarized in Table 1.
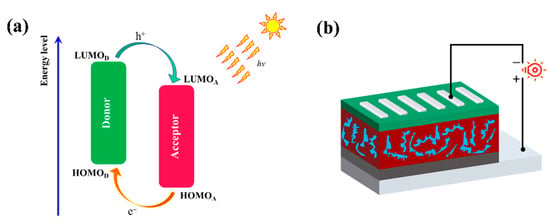
Figure 6.
(a) Schematic illustration of the energy levels at the interface of polymer/ITIC pair in PSCs. (b) Device structure.
3.3. Spectral Properties
For organic semiconductor materials in PSCs, the sunlight absorbance and absorption spectrum of molecules play a vital role in the photoelectric conversion process. To deeply investigate the optical properties of these molecules, the light absorption spectra were simulated, as shown in Figure 7. All the nine spectra also expend two main absorption areas located at ~300 nm (peak 1) and 400~460 nm (peak 2). As an instance of PDn1, PDn2, and PDn3, peak 2 redshifts move from 410.4 nm to 439 nm, but peak 1 shifts slightly. Compared with PDn1, PDn2, and PDn3, the peak 2 redshift is mainly attributed to the π-extended unitA. According to molecular orbital theory, the π–π conjugation extended region could increase the energy of π orbital, but lower the π* and lower the energy gap (Eg), which correspond well to Table 1. The higher light-harvesting efficiency (LHE) value of the molecules would be of benefit for the high JSC of the PSCs devices. The corresponding LHE can be calculated by Equation (3) [58]:
where f is the oscillator strength of the donor molecule. The higher f of the transition suggests a larger absorption coefficient [59]. The results of the calculations indicate that, with the increase in the conjugation region, the LHE increased, and PFn3 has the maximum LHE 0.975. Other crucial spectroscopic parameters, such as the vertical excitation energies and compositions of vertical transitions in terms of molecular orbital, were carried out through TD–DFT calculations. The corresponding results were extracted and are summarized in Table 2.
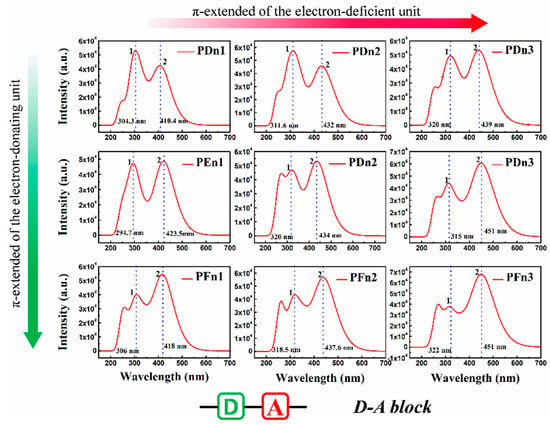
Figure 7.
The simulated absorption spectrum for PDn1, PDn2, PDn3, PEn1, PEn2, PEn3, PFn1, PFn2, and PFn3. The value of the FWHM is 0.333 eV.

Table 2.
The table shows the absorption wavelength (λmax), vertical transition energies (eV), main transition contribution, the oscillator strengths (f) of all the molecules, the lifetime of spontaneous radiation τ(ns), and light-harvesting efficiencies (LHE).
According to the PSCs photoelectric conversion mechanism, the excitons were generated by donor materials after absorbing light, then diffused to the D/A interface and, lastly, split into electrons and holes. Nevertheless, the excitons were bounded by the Coulomb attraction and would not directly split into free charges. Generally, the Coulomb attraction is defined as exciton binding energy (Eb). The Eb could be estimated by Equation (4) [60]:
In addition, the amount of excitons that arrive at the D/A interface is determined by the exciton diffusion length (LD). Generally, a long exciton lifetime τ (ns) corresponds to a long LD of the material in a solid film. In this paper, τ could be evaluated by the Einstein spontaneous emission relationship [61]:
where in Eif is the excitation energy in cm−1. Based on Equation (5), a lower f and Eif will lead to a larger τ. The calculated τ results are summarized in Table 2; PDn2 had the longest τ = 2.56 ns. This means that the excitons produced by PDn2 have a higher probability of arriving at the D/A interface under the circumstance of neglecting other factors, which would be of benefit to achieve a high PCE.
3.4. Ionization Potential (IP) and Electron Affinity (EA)
The holes/electrons transport barriers of the active layer in the PSCs can be determined by the vertical ionization potentials (IP) and electron affinities (EA) of the molecule, which is an important reference for molecular design. Ordinarily, a small IP could lower the hole injection barrier, and a larger EA makes the electron injection easier [62]. The IP and EA of the molecules could be calculated by Equations (6) and (7):
The calculated IP/EA valances result of the nine molecules indicated close relations with their unitD/unitA conjugate area sizes. For instance, the IP valances of PDn1, PEn1, and PFn1 are 5.56 eV, 5.42 eV, and 5.44 eV, respectively, while the EA valances are almost unchanged with the π-extended of the unitD. This indicates that the IP valances are in intimate connection with the unitD. PEn1 is an asymmetric molecule for their block with asymmetry unitD. Meanwhile, compared with PDn1, PDn2, and PDn3, the EA valances increased with the π-extended of the unitA. The results suggested the IP and EA values could be regulated by changing the magnitude of the conjugate region. It could be a useful way to design PSCs donor materials.
3.5. Reorganization Energy
The excitons generated by the donor materials diffused and arrived at D/A interface, which split into electrons and holes under the energy difference of the donor and acceptor. Then, the electron/hole was transmitted in the double continuous interpenetrating network active layer and collected by the corresponding electrode in the terminal. The charge transfer mechanism of the active layer is an incoherent hopping model, which could be described as electron/hole transport only between adjacent molecules. The charge transfer rate constants (k) can be calculated by Equation (8) [62], based on the semiclassical Marcus theory:
The reorganization energy (λ) is closely connected with the mobilities of organic materials [63] so that the λ is significant to predict the charge extract property within PSC device. It is the sum of two energy terms, as shown in Figure 8, and λ1 and λ2 could be described as [62]:
where E(M+) and E(M) are the energy of neutral molecules at the cationic structure and neutral ground state, respectively. The E+(M) and E+(M+) are the energy of the cation at the optimized structure of the neutral molecule and cation structure, respectively. The calculated λ results are summarized in Table 3; PFn1 has the maximum λ 0.531 eV, and PDn2 and PEn2 have the near minimum λ, 0.180 eV and 0.181 eV, respectively. According to Equation (8), the lower λ is, the higher k will be. It can be seen that, except PFn2, all the asymmetric molecules have a comparatively low λ [64,65,66,67]. This means that these asymmetric molecular skeletons in charge carrier transport have advantages in comparison with symmetry skeletons.
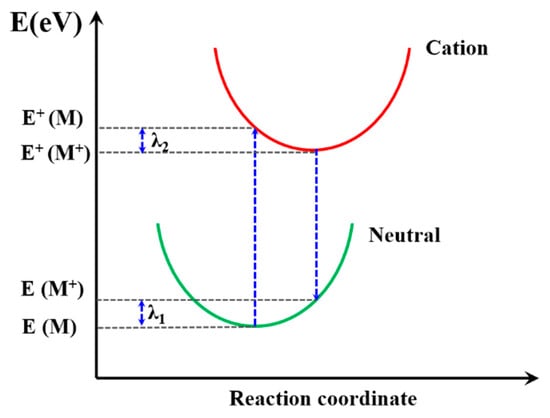
Figure 8.
Schematic plot of reorganization energy.

Table 3.
Calculations of vertical ionization potentials (IP), electron affinities (EA), and reorganization energy (λ).
4. Conclusions
In this work, three new electron-deficient units (n1, n2, and n3) and three electron-donating units (D, E, and F) were elaborately designed, and nine oligomers were obtained by combining different π-conjugation area unitA and unitD. The structure–performance relationships of the nine oligomers were systematically investigated by the quantum mechanical calculations. The nine symmetry or asymmetry molecule structures have been calculated at the B3LYP-D3(BJ)/6-311G(d) level and using chloroform as the solvent. The results of the DFT calculations indicate that asymmetry molecule PEn2 has the minimum dihedral angle among all the molecules, which points to the advantages in the molecular stacking of asymmetric structures. The energy level and Eg also periodically changed along with the molecule structure periodic variation. The results of the TD–DFT calculations indicate that the spectral absorption region/peak could be regularly affected by changing the π-extended size. The size of the conjugate region of the unitD/unitA has close relation with IP/EA values. The calculated reorganization energy also demonstrated that asymmetric molecules PDn2 and PEn2 are more conducive to realize a higher PCE, because of their lower λ. The results certified that the asymmetric structure could be of benefit to the charge extraction within the PSCs device. There are still some limitations to accurately predict the real material properties in the application of the complex in real bulk-heterojunction solar cells, but our work has illustrated the advantages of asymmetric molecules, which also can be applied to molecule design.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/ma14216723/s1: Figure S1: The side view of the optimized geometry of the monomers at ground state; Figure S2: The HOMO and LUMO orbital electron cloud distribution of the monomers; Figure S3: The optimized geometry at ground state and HOMO and LUMO orbital electron cloud distribution of the ITIC.
Author Contributions
Formal analysis, Z.L., L.Y., X.L. and D.L.; funding acquisition, L.Y., J.S., X.H.; investigation, X.L., P.G., J.S.; methodology, J.S., J.L. and X.H.; software, Z.L., P.G.; writing—original draft, Z.L., P.G., J.L., D.L.; writing—review & editing, Z.L. and L.Y., J.L. All authors have read and agreed to the published version of the manuscript.
Funding
We are deeply grateful to the National key R&D Program of China (2019YFA0706402), and the National Natural Science Foundation of China (62027822, 61690221), Dean Foundation of China Academy of Engineering Physics (No. YZJJLX2017001) for financial support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All datasets generated for this study are included in the article.
Acknowledgments
The authors thank the computational resources provided by the HPCC platform of Xi’an Jiaotong University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, G.; Shrotriya, V.; Huang, J.; Yao, Y.; Moriarty, T.; Emery, K.; Yang, Y. High-efficiency solution processable polymer pho-tovoltaic cells by self-organization of polymer blends. Nat. Mater. 2005, 4, 864–868. [Google Scholar] [CrossRef]
- Zhang, Y.; Hau, S.K.; Yip, H.-L.; Sun, Y.; Acton, O.; Jen, A. Efficient Polymer Solar Cells Based on the Copolymers of Benzodithiophene and Thienopyrroledione. Chem. Mater. 2010, 22, 2696–2698. [Google Scholar] [CrossRef]
- Peet, J.; Kim, J.Y.; Coates, N.E.; Ma, W.L.; Moses, D.; Heeger, A.J.; Bazan, G.C. Efficiency enhancement in low-bandgap polymer solar cells by processing with alkane dithiols. Mater. Sustain. Energy 2010, 6, 47–50. [Google Scholar] [CrossRef]
- Zhang, F.; Mammo, W.; Andersson, L.M.; Admassie, S.; Andersson, M.R.; Inganäs, O. Low-Bandgap Alternating Fluorene Copolymer/Methanofullerene Heterojunctions in Efficient Near-Infrared Polymer Solar Cells. Adv. Mater. 2006, 18, 2169–2173. [Google Scholar] [CrossRef]
- Tamayo, A.B.; Walker, B.; Nguyen, T.-Q. A Low Band Gap, Solution Processable Oligothiophene with a Diketopyrrolopyrrole Core for Use in Organic Solar Cells. J. Phys. Chem. C 2008, 112, 11545–11551. [Google Scholar] [CrossRef] [Green Version]
- Wang, E.; Wang, L.; Lan, L.; Luo, C.; Zhuang, W.; Peng, J.; Cao, Y. High-performance polymer heterojunction solar cells of a polysilafluorene derivative. Appl. Phys. Lett. 2008, 92, 33307. [Google Scholar] [CrossRef]
- Liu, X.; Ma, R.; Wang, Y.; Du, S.; Tong, J.; Shi, X.; Li, J.; Bao, X.; Xia, Y.; Liu, T.; et al. Significantly Boosting Efficiency of Polymer Solar Cells by Employing a Nontoxic Halogen-Free Additive. ACS Appl. Mater. Interfaces 2021, 13, 11117–11124. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Cao, Y.; Gao, J.; Wang, D.; Yu, G.; Heeger, A.J. Electrochemical properties of luminescent polymers and polymer light-emitting electrochemical cells. Synth. Met. 1999, 99, 243–248. [Google Scholar] [CrossRef]
- Liang, Z.; Tong, J.; Li, H.; Wang, Y.; Wang, N.; Li, J.; Yang, C.; Xia, Y. The comprehensive utilization of the synergistic effect of fullerene and non-fullerene acceptors to achieve highly efficient polymer solar cells. J. Mater. Chem. A 2019, 7, 15841–15850. [Google Scholar] [CrossRef]
- Li, J.; Liang, Z.; Li, X.; Li, H.; Wang, Y.; Qin, J.; Tong, J.; Yan, L.; Bao, X.; Xia, Y. Insights into Excitonic Dynamics of Terpol-ymer-Based High-Efficiency Nonfullerene Polymer Solar Cells: Enhancing the Yield of Charge Separation States. ACS Appl. Mater. Interfaces 2020, 12, 8475–8484. [Google Scholar] [CrossRef]
- Li, X.M.; Liang, Z.Z.; Wang, H.; Qiao, S.L.; Liu, Z.L.; Jiang, H.X.; Chen, W.C.; Yang, R.Q. Fluorinated D1((0.5))-A-D2((0.5))-A model terpolymer: Ultrafast charge separation kinetics and electron transfer at the fluorinated D/A interface for power con-version. J. Mater. Chem. A 2020, 8, 1360–1367. [Google Scholar] [CrossRef]
- Liu, X.; Liang, Z.; Du, S.; Tong, J.; Li, J.; Zhang, R.; Shi, X.; Yan, L.; Bao, X.; Xia, Y. Non-Halogenated Polymer Donor-Based Organic Solar Cells with a Nearly 15% Efficiency Enabled by a Classic Ternary Strategy. ACS Appl. Energy Mater. 2021, 4, 1774–1783. [Google Scholar] [CrossRef]
- Liu, X.; Du, S.; Fu, Z.; Chen, C.; Tong, J.; Li, J.; Zheng, N.; Zhang, R.; Xia, Y. Ternary solar cells via ternary polymer donors and third component PC71BM to optimize morphology with 13.15% efficiency. Sol. Energy 2021, 222, 18–26. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, X.; Wang, Y.; Du, S.; Tong, J.; Li, J.; Zhang, R.; Yang, C.; Xia, Y. Enhance the efficiency of polymer solar cells through regulating phase segregation and improving charge transport via non-toxic halogen-free additive. Sol. Energy 2021, 218, 375–382. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, C.; Peng, Y.; Wang, N.; Liu, X.; Du, S.; Tong, J.; Li, J.; Xia, Y. An alcohol-soluble small molecule as efficient cathode interfacial layer materials for polymer solar cells. Opt. Mater. 2021, 113, 110909. [Google Scholar] [CrossRef]
- Wang, E.; Ma, Z.; Zhang, Z.; Vandewal, K.; Henriksson, P.; Inganäs, O.; Zhang, F.; Andersson, M.R. An Easily Accessible Isoindigo-Based Polymer for High-Performance Polymer Solar Cells. J. Am. Chem. Soc. 2011, 133, 14244–14247. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Zhang, S.; He, C.; Zhang, J.; Yao, H.; Yang, Y.; Zhang, Y.; Zhao, W.; Hou, J. New Wide Band Gap Donor for Efficient Fullerene-Free All-Small-Molecule Organic Solar Cells. J. Am. Chem. Soc. 2017, 139, 1958–1966. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Huo, L.; Chandrabose, S.; Chen, K.; Han, G.; Qi, F.; Meng, X.; Xie, D.; Ma, W.; Yi, Y.; et al. Optimized Fibril Network Morphology by Precise Side-Chain Engineering to Achieve High-Performance Bulk-Heterojunction Organic Solar Cells. Adv. Mater. 2018, 30, e1707353. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; Cui, Y.; Qian, D.; Ponseca, C.S.; Honarfar, A.; Xu, Y.; Xin, J.; Chen, Z.; Hong, L.; Gao, B.; et al. 14.7% Efficiency Organic Photovoltaic Cells Enabled by Active Materials with a Large Electrostatic Potential Difference. J. Am. Chem. Soc. 2019, 141, 7743–7750. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, Z.; Zhang, G.; McDowell, C.; Luo, P.; Jia, X.; Ford, M.J.; Wang, M.; Bazan, G.C.; Huang, F.; et al. Toward High Efficiency Polymer Solar Cells: Rearranging the Backbone Units into a Readily Accessible Random Tetrapolymer. Adv. Energy Mater. 2018, 8, 1701668–1701676. [Google Scholar] [CrossRef]
- Fan, B.; Zhang, D.; Li, M.; Zhong, W.; Zeng, Z.; Ying, L.; Huang, F.; Cao, Y. Achieving over 16% efficiency for single-junction organic solar cells. Sci. China Ser. B Chem. 2019, 62, 746–752. [Google Scholar] [CrossRef]
- Zhang, M.; Guo, X.; Ma, W.; Ade, H.; Hou, J. A Large-Bandgap Conjugated Polymer for Versatile Photovoltaic Applications with High Performance. Adv. Mater. 2015, 27, 4655–4660. [Google Scholar] [CrossRef]
- Liu, Q.S.; Jiang, Y.F.; Jin, K.; Qin, J.Q.; Xu, J.G.; Li, W.T.; Xiong, J.; Liu, J.F.; Xiao, Z.; Sun, K.; et al. 18% Efficiency organic solar cells. Sci. Bull. 2020, 65, 272–275. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Champion, R.D.; Jenekhe, S.A. Conjugated donor-acceptor copolymer semiconductors with large intramolecular charge transfer: Synthesis, optical properties, electrochemistry, and field effect carrier mobility of thienopyrazine-based co-polymers. Macromolecules 2006, 39, 8712–8719. [Google Scholar] [CrossRef]
- Darling, S.B. Block copolymers for photovoltaics. Energy Environ. Sci. 2009, 2, 1266–1273. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, J.; Yip, H.-L.; Chen, K.-S.; Zeigler, D.F.; Sun, Y.; Jen, A.K.-Y. Indacenodithiophene and Quinoxaline-Based Conjugated Polymers for Highly Efficient Polymer Solar Cells. Chem. Mater. 2011, 23, 2289–2291. [Google Scholar] [CrossRef]
- Li, Y.W.; Xue, L.L.; Li, H.; Li, Z.F.; Xu, B.; Wen, S.P.; Tian, W.J. Energy Level and Molecular Structure Engineering of Conju-gated Donor-Acceptor Copolymers for Photovoltaic Applications. Macromolecules 2009, 42, 4491–4499. [Google Scholar] [CrossRef]
- Kang, T.E.; Kim, K.-H.; Kim, B.J. Design of terpolymers as electron donors for highly efficient polymer solar cells. J. Mater. Chem. A 2014, 2, 15252–15267. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.M.; Chen, S.; Kumari, T.; Kang, S.; Cho, Y.; Yang, C. Organic Photovoltaics with Multiple Donor–Acceptor Pairs. Adv. Mater. 2019, 31, e1804762. [Google Scholar] [CrossRef]
- Wang, X.; Han, J.; Huang, D.; Wang, J.; Xie, Y.; Liu, Z.; Li, Y.; Yang, C.; Zhang, Y.; He, Z.; et al. Optimized Mo-lecular Packing and Nonradiative Energy Loss Based on Terpolymer Methodology Combining Two Asymmetric Segments for High-Performance Polymer Solar Cells. ACS Appl. Mater. Interfaces 2020, 12, 20393–20403. [Google Scholar] [CrossRef]
- Luo, Z.; Ma, R.; Liu, T.; Yu, J.; Xiao, Y.; Sun, R.; Xie, G.; Yuan, J.; Chen, Y.; Chen, K.; et al. Fine-Tuning Energy Levels via Asymmetric End Groups Enables Polymer Solar Cells with Efficiencies over 17%. Joule 2020, 4, 1236–1247. [Google Scholar] [CrossRef]
- Li, S.X.; Zhan, L.L.; Jin, Y.Z.; Zhou, G.Q.; Lau, T.K.; Qin, R.; Shi, M.M.; Li, C.Z.; Zhu, H.M.; Lu, X.H.; et al. Asymmetric Electron Acceptors for High-Efficiency and Low-Energy-Loss Organic Photovoltaics. Adv. Mater. 2020, 32, 2001160–2001169. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Du, Z.; Dou, K.; Jiang, H.; Gao, C.; Han, L.; Yang, R. A Maverick Asymmetrical Backbone with Distinct Flanked Twist Angles Modulating the Molecular Aggregation and Crystallinity for High Performance Nonfullerene Solar Cells. Adv. Energy Mater. 2018, 9, 1802530–1802540. [Google Scholar] [CrossRef]
- Liu, D.Y.; Wang, J.Y.; Gu, C.Y.; Li, Y.H.; Bao, X.C.; Yang, R.Q. Stirring Up Acceptor Phase and Controlling Morphology via Choosing Appropriate Rigid Aryl Rings as Lever Arms in Symmetry-Breaking Benzodithiophene for High-Performance Full-erene and Fullerene-Free Polymer Solar Cells. Adv. Mater. 2018, 30, 1705870–1705878. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Li, M.; Guo, Y.; Lu, H.; Song, J.; Bo, Z.; Wang, H. Dibenzopyran-Based Wide Band Gap Conjugated Copolymers: Structural Design and Application for Polymer Solar Cells. ACS Appl. Mater. Interfaces 2016, 8, 31348–31358. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.Y.; Zhu, Q.Q.; Gu, C.Y.; Wang, J.Y.; Qiu, M.; Chen, W.C.; Bao, X.C.; Sun, M.L.; Yang, R.Q. High-Performance Photo-voltaic Polymers Employing Symmetry-Breaking Building Blocks. Adv. Mater. 2016, 28, 8490–8498. [Google Scholar] [CrossRef]
- Wang, M.; Cai, D.; Yin, Z.; Chen, S.-C.; Du, C.-F.; Zheng, Q. Asymmetric-Indenothiophene-Based Copolymers for Bulk Heterojunction Solar Cells with 9.14% Efficiency. Adv. Mater. 2016, 28, 3359–3365. [Google Scholar] [CrossRef]
- Mo, D.Z.; Wang, H.; Chen, H.; Qu, S.W.; Chao, P.J.; Yang, Z.; Tian, L.L.; Su, Y.A.; Gao, Y.; Yang, B.; et al. Chlorination of Low-Band-Gap Polymers: Toward High-Performance Polymer Solar Cells. Chem. Mater. 2017, 29, 2819–2830. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, C.; Liu, Y.; Bi, Z.; Zhang, Z.; Xu, X.; Ma, W.; Bo, Z. Fused-Ring Acceptors with Asymmetric Side Chains for High-Performance Thick-Film Organic Solar Cells. Adv. Mater. 2017, 29, 1703527–1703533. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Wang, Y.; Song, L.-C.; Liu, F.; Wan, X.; Zhang, H.; Chen, Y. Small Molecules with Asymmetric 4-Alkyl-8-alkoxybenzo[1,2-b:4,5-b′]dithiophene as the Central Unit for High-Performance Solar Cells with High Fill Factors. Chem. Mater. 2017, 29, 3694–3703. [Google Scholar] [CrossRef]
- Song, J.; Li, C.; Ye, L.; Koh, C.; Cai, Y.; Wei, D.; Woo, H.Y.; Sun, Y. Extension of indacenodithiophene backbone conjugation enables efficient asymmetric A–D–A type non-fullerene acceptors. J. Mater. Chem. A 2018, 6, 18847–18852. [Google Scholar] [CrossRef]
- Chochos, C.L.; Avgeropoulos, A.; Lidorikis, E. Theoretical study of phenyl-substituted indacenodithiophene copolymers for high performance organic photovoltaics. J. Chem. Phys. 2013, 138, 064901. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, H.B.; Sun, S.L.; Geng, Y.; Wu, Y.; Su, Z.M. Density functional theory characterization and design of high-performance diarylamine-fluorene dyes with different pi spacers for dye-sensitized solar cells. J. Mater. Chem. 2012, 22, 568–576. [Google Scholar] [CrossRef]
- Bredas, J.L.; Norton, J.E.; Cornil, J.; Coropceanu, V. Molecular understanding of organic solar cells: The challenges. ACC Chem. Res. 2009, 42, 1691–1699. [Google Scholar] [CrossRef]
- Ahmed, S.; Dutta, R.; Kalita, D.J. Strategical designing of diketopyrrolopyrrole-thiophene based donor-acceptor type organic oligomers and study their transport properties: A DFT/TD-DFT perspective. Chem. Phys. Lett. 2019, 730, 14–25. [Google Scholar] [CrossRef]
- Liang, Y.J.; Zhao, Z.W.; Geng, Y.; Pan, Q.Q.; Gu, H.Y.; Zhao, L.; Zhang, M.; Wu, S.X.; Su, Z.M. Can we utilize the higher Frenkel exciton state in biazulene diimides-based non-fullerene acceptors to promote charge separation at the donor/acceptor interface? New J. Chem. 2020, 44, 9767–9774. [Google Scholar] [CrossRef]
- Mabrouk, A.; Alimi, K.; Molinie, P.; Nguyen, T.P. A combined experimental and theoretical study on the effect of doping and interface form;ation on Ppv-ether copolymer. J. Phys. Chem. B 2006, 110, 1141–1150. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Khalid, M.; Khera, R.A.; Jabeen, S.; Langer, P.; Iqbal, J. Designing 2D fused ring materials for small molecules organic solar cells. Comput. Theor. Chem. 2020, 1183, 112848. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01.; Gaussian, Inc: Wallingford, CT, USA, 2013. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Chen, Q. An sp-hybridized all-carboatomic ring, cyclo[18]carbon: Electronic structure, electronic spectrum, and optical nonlinearity. Carbon 2020, 165, 461–467. [Google Scholar] [CrossRef]
- Wang, Y.; Michinobu, T. Benzothiadiazole and its pi-extended, heteroannulated derivatives: Useful acceptor building blocks for high-performance donor-acceptor polymers in organic electronics. J. Mater. Chem. C 2016, 4, 6200–6214. [Google Scholar] [CrossRef] [Green Version]
- Mei, C.-Y.; Liang, L.; Zhao, F.-G.; Wang, J.-T.; Yu, L.-F.; Li, Y.-X.; Li, W.-S. A Family of Donor–Acceptor Photovoltaic Polymers with Fused 4,7-Dithienyl-2,1,3-benzothiadiazole Units: Effect of Structural Fusion and Side Chains. Macromolecules 2013, 46, 7920–7931. [Google Scholar] [CrossRef]
- Li, X.; Huang, G.; Zheng, N.; Li, Y.; Kang, X.; Qiao, S.; Jiang, H.; Chen, W.; Yang, R. High-Efficiency Polymer Solar Cells Over 13.9% With a High V OC Beyond 1.0 V by Synergistic Effect of Fluorine and Sulfur. Sol. RRL 2019, 3, 1900005–1900011. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, J.; Yin, X.; Hu, Z.; Jiang, Y.; Sun, J.; Zhou, J.; Zhang, F.; Russell, T.P.; Liu, F.; et al. Conformation Locking on Fused-Ring Electron Acceptor for High-Performance Nonfullerene Organic Solar Cells. Adv. Funct. Mater. 2018, 28, 1705095–1705102. [Google Scholar] [CrossRef]
- Wu, L.-N.; Yin, H.; Li, M.-Y.; Sun, G.-Y.; Jin, G.-D. Density functional theory analysis for the limitations of fluoranthene-fused imide based small molecule acceptor materials in photovoltaic performance. Comput. Theor. Chem. 2019, 1156, 37–42. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, J.; Zhang, Z.-G.; Bai, H.; Li, Y.; Zhu, D.; Zhan, X. An Electron Acceptor Challenging Fullerenes for Efficient Polymer Solar Cells. Adv. Mater. 2015, 27, 1170–1174. [Google Scholar] [CrossRef]
- Wang, Z.; Ivanov, M.; Gao, Y.; Bussotti, L.; Foggi, P.; Zhang, H.; Russo, N.; Dick, B.; Zhao, J.; DI Donato, M.; et al. Spin–Orbit Charge-Transfer Intersystem Crossing (ISC) in Compact Electron Donor–Acceptor Dyads: ISC Mechanism and Application as Novel and Potent Photodynamic Therapy Reagents. Chem. A Eur. J. 2019, 26, 1091–1102. [Google Scholar] [CrossRef] [PubMed]
- Vandewal, K.; Tvingstedt, K.; Gadisa, A.; Inganas, O.; Manca, J.V. On the origin of the open-circuit voltage of polymer-fullerene solar cells. Nat. Mater. 2009, 8, 904–909. [Google Scholar] [CrossRef] [PubMed]
- Köse, M.E. Evaluation of Acceptor Strength in Thiophene Coupled Donor–Acceptor Chromophores for Optimal Design of Organic Photovoltaic Materials. J. Phys. Chem. A 2012, 116, 12503–12509. [Google Scholar] [CrossRef]
- Zaier, R.; Hajaji, S.; Kozaki, M.; Ayachi, S. DFT and TD-DFT studies on the electronic and optical properties of linear pi-conjugated cyclopentadithiophene (CPDT) dimer for efficient blue OLED. Optic. Mater. 2019, 91, 108–114. [Google Scholar] [CrossRef]
- Tripathi, A.; Prabhakar, C. Impact of replacement of the central benzene ring in anthracene by a heterocyclic ring on electronic excitations and reorganization energies in anthratetrathiophene molecules. J. Chin. Chem. Soc. 2018, 65, 918–924. [Google Scholar] [CrossRef]
- Luo, D.M.; Jin, R.F. Theoretical characterisation and design of D-pi-A star-shaped molecules with triphenylamine as core and diketopyrrolopyrroles as arms for organic solar cells. Mol. Phys. 2019, 117, 1825–1832. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).