Three-Dimensional Bending Analysis of Multi-Layered Orthotropic Plates by Two-Dimensional Numerical Model
Abstract
:1. Introduction
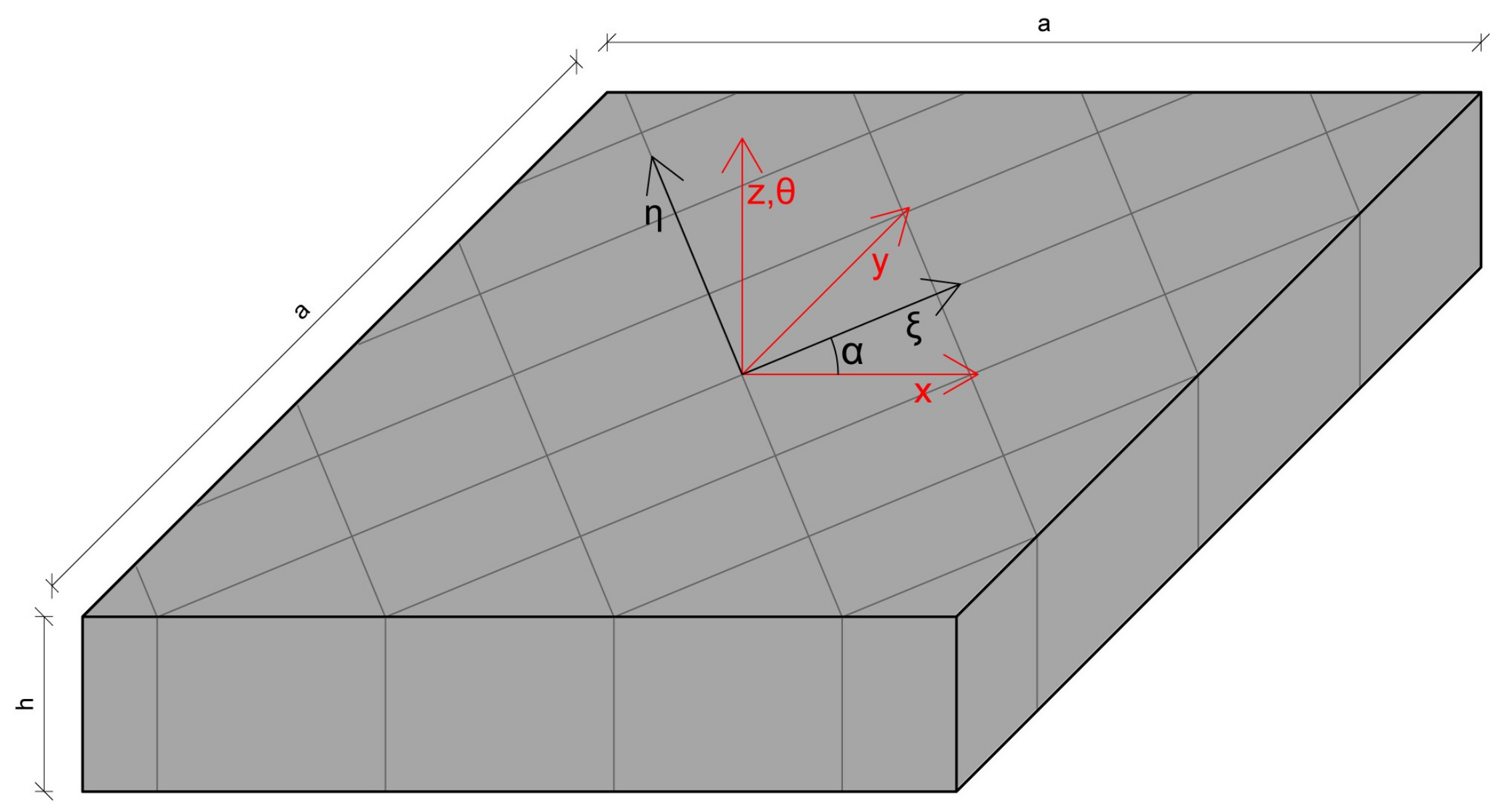
2. Variational Formulation of the Problem
3. Approximations
4. Examples
4.1. Example 1
4.2. Example 2
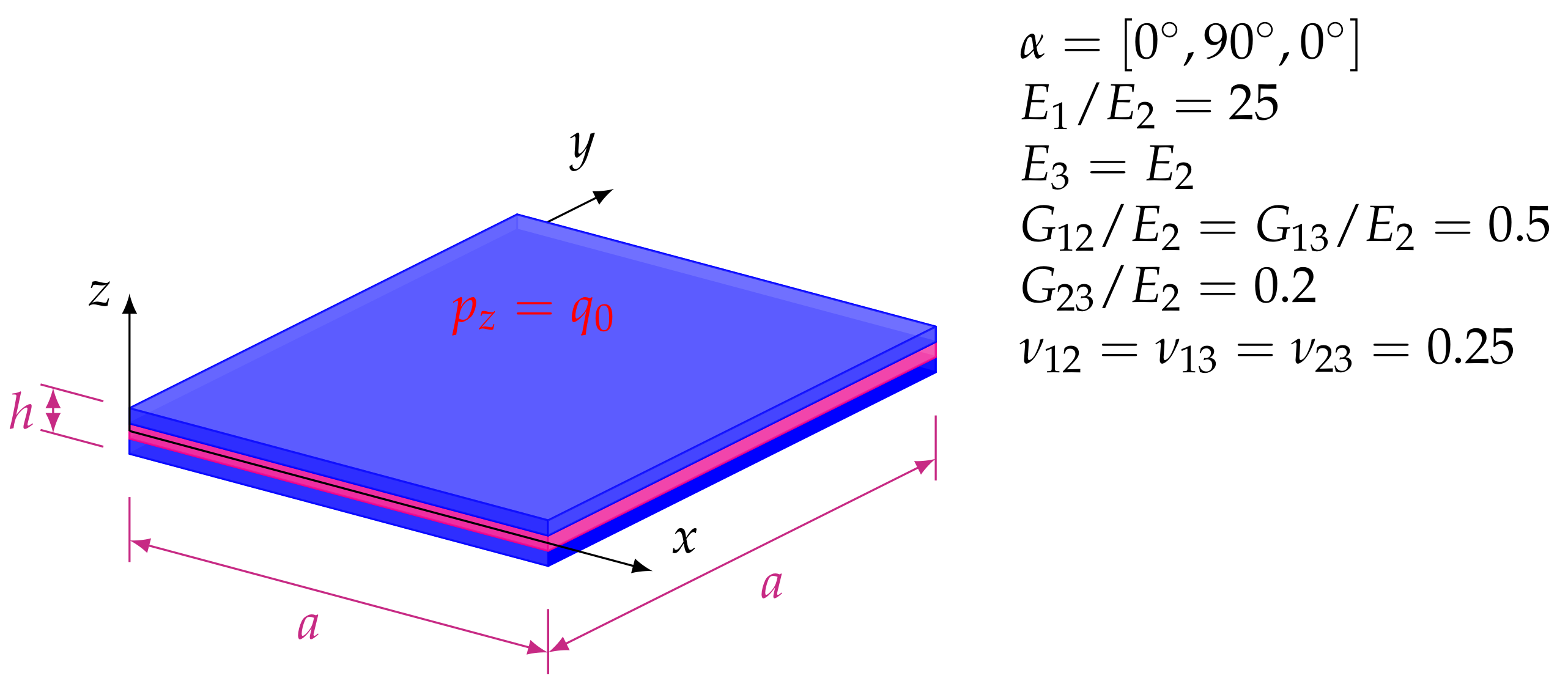
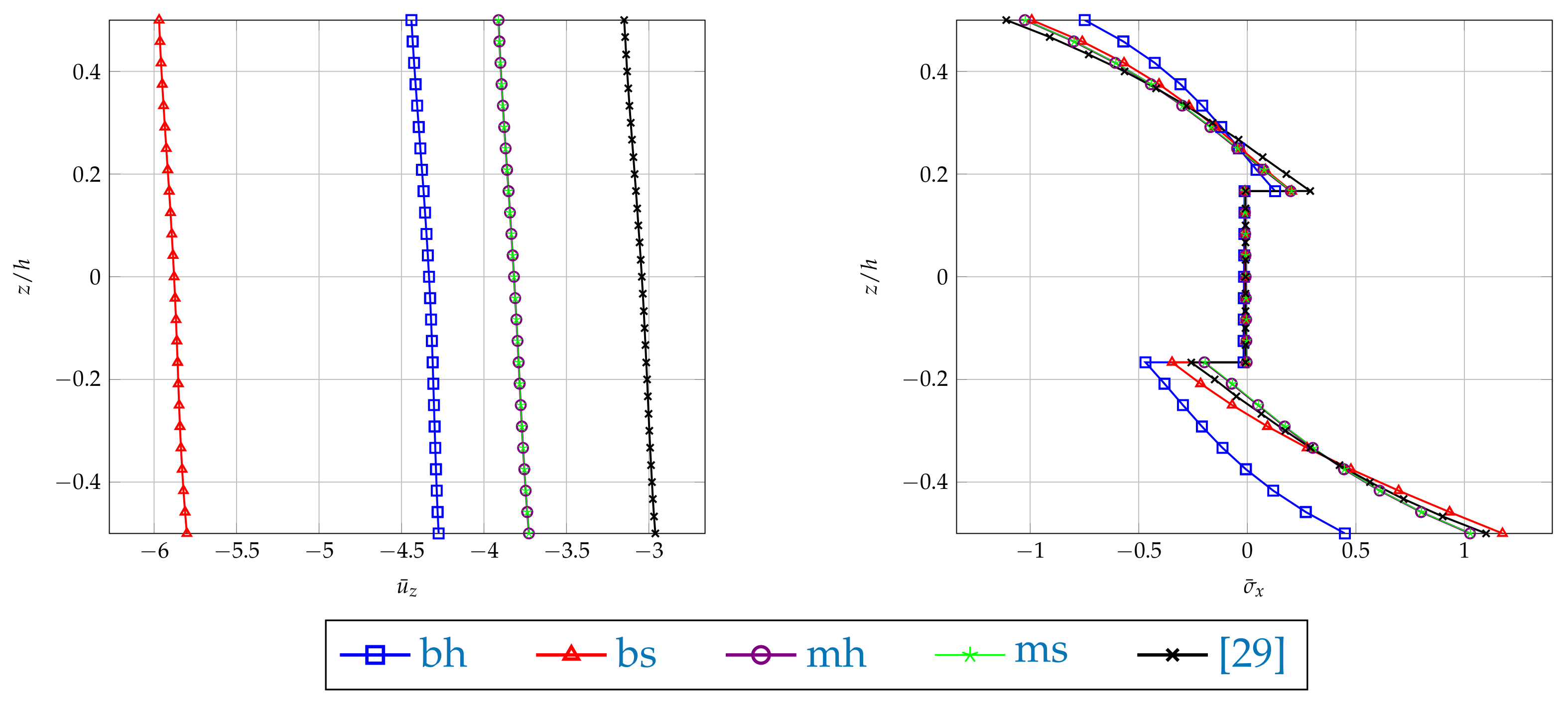
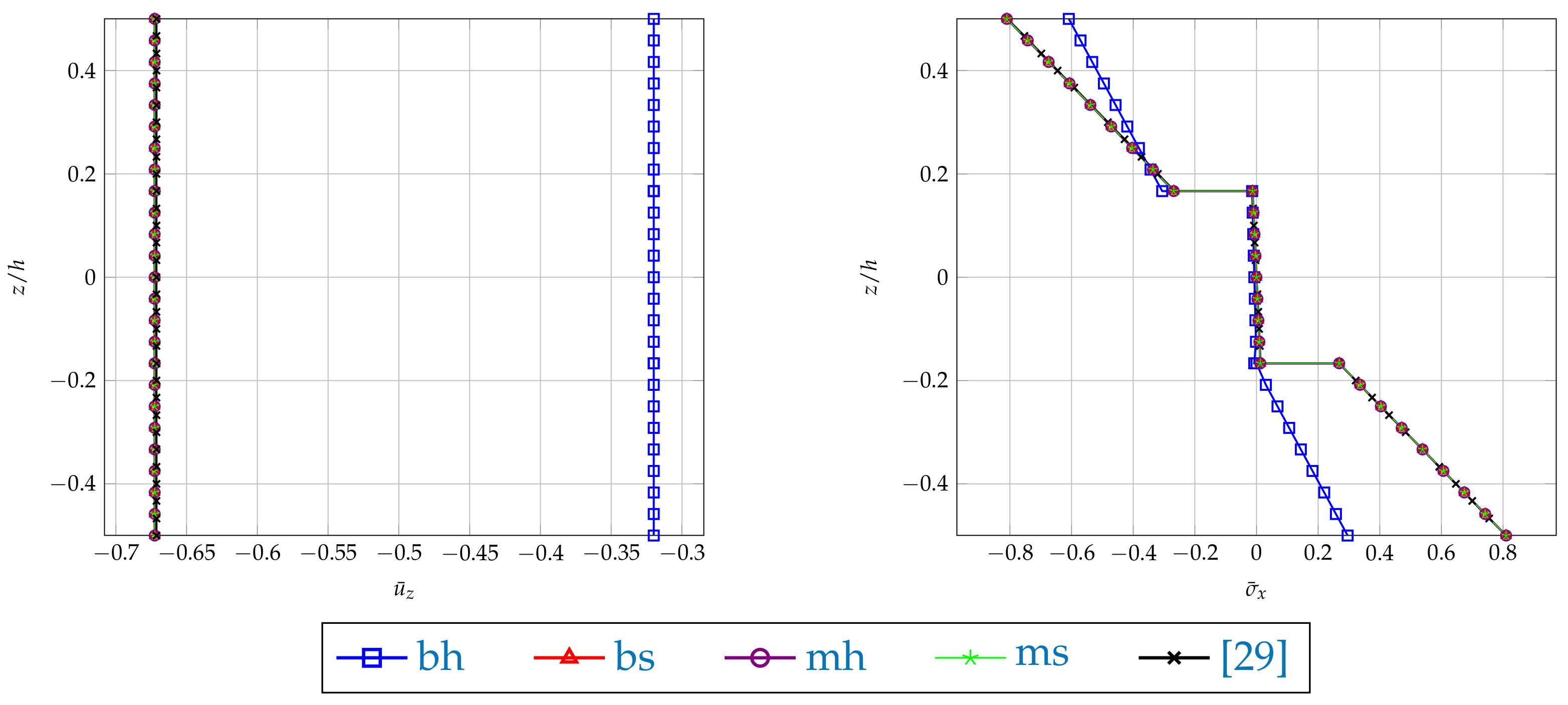
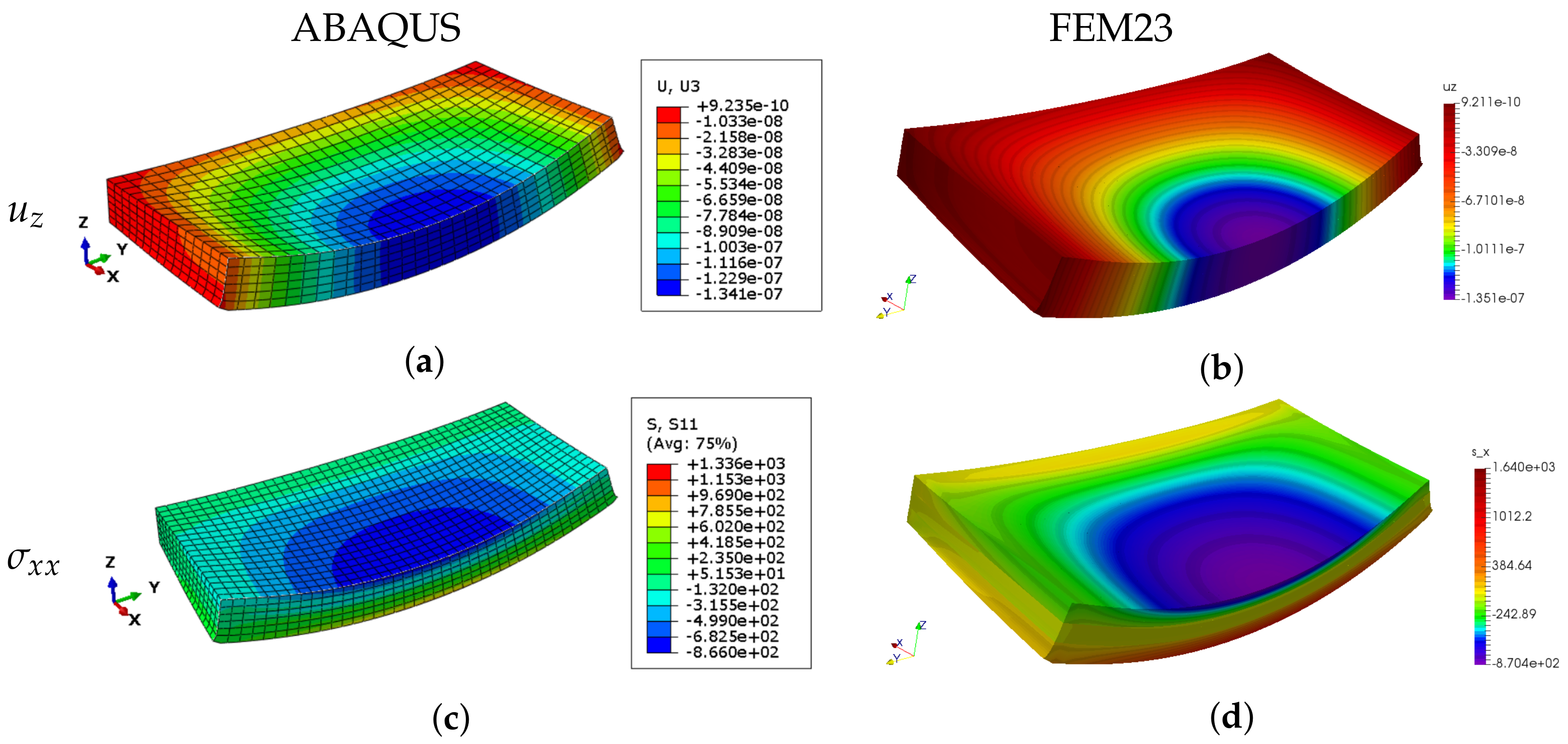
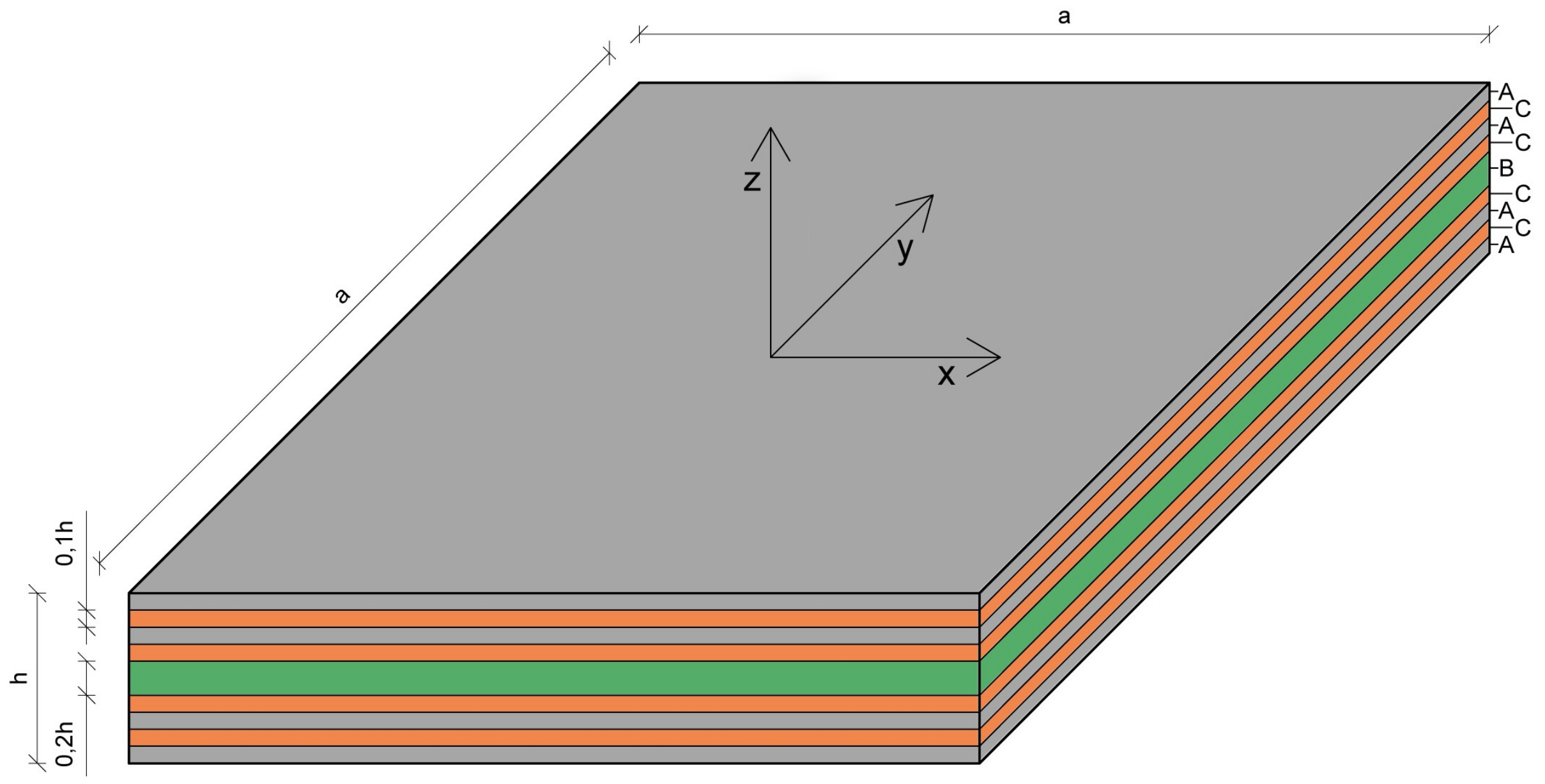
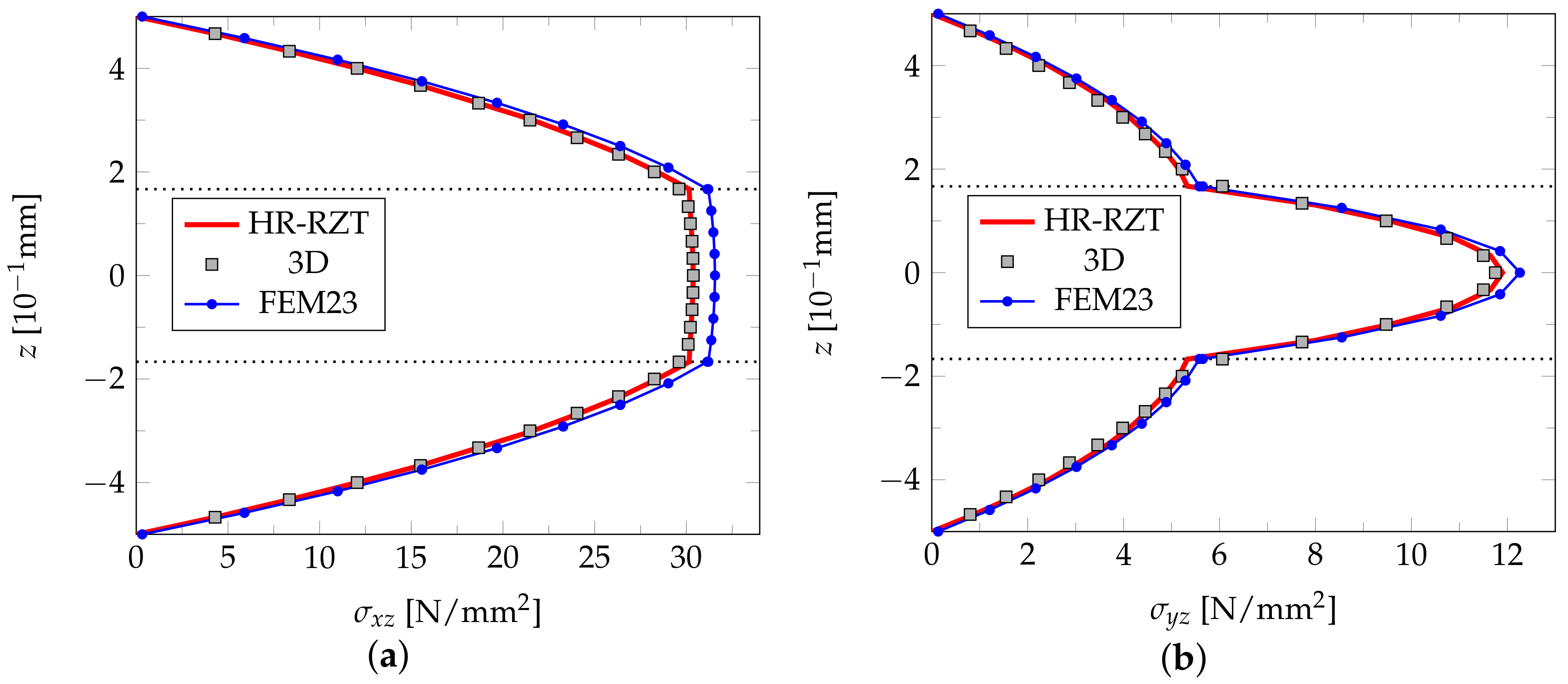
4.3. Example 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaśkowiec, J.; Pluciński, P.; Stankiewicz, A.; Cichoń, C. Three–dimensional modelling of laminated glass bending on two-dimensional in–plane mesh. Compos. Part B Eng. 2017, 120, 63–82. [Google Scholar] [CrossRef]
- Pluciński, P.; Jaśkowiec, J. Three-dimensional analysis of laminated plates with functionally graded layers by two-dimensional numerical model. Eng. Trans. 2020, 68, 21–45. [Google Scholar]
- Bognet, B.; Bordeu, F.; Chinesta, F.; Leygue, A.; Poitou, A. Advanced simulation of models defined in plate geometries: 3D solutions with 2D computational complexity. Comput. Methods Appl. Mech. Eng. 2012, 201–204, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Bognet, B.; Leygue, A.; Chinesta, F. Separated representations of 3D elastic solutions in shell geometries. Adv. Model. Simul. Eng. Sci. 2014, 1, 34. [Google Scholar] [CrossRef] [Green Version]
- Vidal, P.; Gallimard, L.; Polit, O. Proper Generalized Decomposition and layer-wise approach for the modeling of composite plate structures. Int. J. Solids Struct. 2013, 50, 2239–2250. [Google Scholar] [CrossRef]
- Pluciński, P.; Jaśkowiec, J. Thermo-mechanical modelling of laminated glass with the use of two-dimensional in-plane mesh. Compos. Struct. 2019, 207, 935–948. [Google Scholar] [CrossRef]
- Jaśkowiec, J.; Stankiewicz, A.; Pluciński, P. Three-dimensional numerical modelling of multi-layered shell structures using two-dimensional plane mesh. Adv. Eng. Softw. 2020, 149, 102840. [Google Scholar] [CrossRef]
- Mohagheghian, I.; Wang, Y.; Zhou, J.; Yu, L.; Guo, X.; Yan, Y.; Charalambides, M.N.; Dear, J.P. Deformation and damage mechanisms of laminated glass windows subjected to high velocity soft impact. Int. J. Solids Struct. 2017, 109, 46–62. [Google Scholar] [CrossRef]
- Santarsiero, M.; Bedon, C.; Louter, C. Experimental and numerical analysis of thick embedded laminated glass connections. Compos. Struct. 2018, 188, 242–256. [Google Scholar] [CrossRef] [Green Version]
- Vedrtnam, A.; Pawar, S. Experimental and simulation studies on flexural strength of laminated glass using ring-on-ring and three-point bending test. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 3930–3941. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Pawar, S. Experimental and simulation studies on fracture and adhesion test of laminated glass. Eng. Fract. Mech. 2018, 190, 461–470. [Google Scholar] [CrossRef]
- Rajaneesh, A.; Patel, H.G.; Shimpi, R.P. Finite element bending and free vibration analysis of layered plates using new first order shear deformation theory. Compos. Struct. 2021, 257, 113143. [Google Scholar] [CrossRef]
- Liu, C.; Yu, J.; Zhang, B.; Zhang, X. Reflection and transmission of elastic waves in the multilayered orthotropic couple-stressed plates sandwiched between two elastic half-spaces. Appl. Math. Model. 2019, 75, 52–72. [Google Scholar] [CrossRef]
- Ugrimov, S.V.; Shupikov, A.N. Layered orthotropic plates. Generalized theory. Compos. Struct. 2015, 129, 224–235. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, Z.; Ullah, S.; Zhang, J.; Gao, Y. Analytical bending solutions of orthotropic rectangular thin plates with two adjacent edges free and the others clamped or simply supported using finite integral transform method. Adv. Civ. Eng. 2020, 2020, 8848879. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Q.; Ullah, S.; Geng, L.; Civalek, Ö. A new analytical solution of vibration response of orthotropic composite plates with two adjacent edges rotationally-restrained and the others free. Compos. Struct. 2021, 266, 113882. [Google Scholar] [CrossRef]
- Cui, J.; Li, Z.; Ye, R.; Jiang, W.; Tao, S. A semianalytical three-dimensional elasticity solution for vibrations of orthotropic plates with arbitrary boundary conditions. Shock Vib. 2019, 2019, 1237674. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Morozov, N.F.; Tovstik, P.E.; Tovstik, T.P. Two-dimensional linear models of multilayered anisotropic plates. Acta Mech. 2019, 230, 2891–2904. [Google Scholar] [CrossRef]
- Schreiber, P.; Mittelstedt, C.; Beerhorst, M. Buckling of shear-deformable orthotropic laminated plates with elastic restraints. Thin-Walled Struct. 2020, 157, 107071. [Google Scholar] [CrossRef]
- Wang, X.E.; Huang, X.H.; Yang, J.; Hou, X.; Zhu, Y.; Xie, D. Experimental and analytical study on the pre-crack impact response of thick multi-layered laminated glass under hard body impact. Int. J. Mech. Sci. 2021, 206, 106613. [Google Scholar] [CrossRef]
- Marchetti, F.; Roozen, N.B.; Segers, J.; Ege, K.; Kersemans, M.; Leclere, Q. Experimental methodology to assess the dynamic equivalent stiffness properties of elliptical orthotropic plates. J. Sound Vib. 2021, 495, 115897. [Google Scholar] [CrossRef]
- Rühl, A.; Kolling, S.; Schneider, J. A transparent three-layered laminate composed of poly(methyl methacrylate) and thermoplastic polyurethane subjected to low-velocity impact. Int. J. Impact Eng. 2020, 136, 103419. [Google Scholar] [CrossRef]
- Ziya-Shamami, M.; Babaei, H.; Mostofi, T.M.; Khodarahmi, H. Structural response of monolithic and multi-layered circular metallic plates under repeated uniformly distributed impulsive loading: An experimental study. Thin-Walled Struct. 2020, 157, 107024. [Google Scholar] [CrossRef]
- Hwu, C. Anisotropic Elastic Plates; Springer: New York, NY, USA, 2014. [Google Scholar]
- Szabó, B.A.; Sahrmann, G.J. Hierarchic plate and shell models based on p-extension. Int. J. Numer. Methods Eng. 1988, 26, 1855–1881. [Google Scholar] [CrossRef]
- Zboiński, G. Hierarchical Modeling and Finite Element Approximation for Adaptive Analysis of Complex Structures. Ph.D. Thesis, Gdańsk University of Technology, Gdańsk, Poland, 2001. [Google Scholar]
- Zboiński, G. Adaptive hpq finite element methods for the analysis of 3d-based models of complex structures. Part 1. Hierarchical modeling and approximationsr estimation. Comput. Methods Appl. Mech. Eng. 2010, 1999, 2913–2940. [Google Scholar] [CrossRef]
- Zboiński, G. Adaptive hpq finite element methods for the analysis of 3d-based models of complex structures. Part 2. A posteriori error estimation. Comput. Methods Appl. Mech. Eng. 2013, 267, 531–565. [Google Scholar] [CrossRef]
- Carrera, E.; Ciuffreda, A. A unified formulation to assess theories of multilayered plates for various bending problems. Compos. Struct. 2005, 69, 271–293. [Google Scholar] [CrossRef]
- Vuksanović, Đ.M.; Ćetković, M. Analytical solution for multilayer plates using general layerwise plate theory. Facta Univer.-Ser. Archit. Civ. Eng. 2005, 3, 121–136. [Google Scholar] [CrossRef]
- Köpple, M.; Wagner, W. A mixed finite element model with enhanced zigzag kinematics for the non-linear analysis of multilayer plates. Comput. Mech. 2020, 65, 23–40. [Google Scholar] [CrossRef]
- Gruttmann, F.; Wagner, W.; Knust, G. A coupled global-local shell model with continuous interlaminar shear stresses. Comput. Mech. 2016, 57, 237–255. [Google Scholar] [CrossRef]



| Theory | 3D Analysis | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [30] | [29] | FEM23 | FEM (Abaqus) | |||||||
| mh | ms | bh | bs | mh | ms | bh | bs | |||
| 4 | 3.079 | 3.044 | 3.818 | 3.818 | 4.333 | 5.878 | 3.98 | 3.98 | 4.04 | 5.55 |
| 10 | 1.156 | 1.154 | 1.214 | 1.213 | 0.937 | 1.351 | 1.22 | 1.22 | 0.906 | 1.34 |
| 100 | 0.671 | 0.671 | 0.678 | 0.672 | 0.316 | 0.672 | 0.672 | 0.672 | 0.314 | 0.672 |
| 4 | 1.116 | 1.117 | 1.026 | 1.028 | 0.450 | 1.175 | 1.015 | 1.016 | 0.441 | 1.192 |
| 10 | 0.872 | 0.871 | 0.881 | 0.882 | 0.442 | 0.874 | 0.880 | 0.880 | 0.417 | 0.875 |
| 100 | 0.808 | 0.808 | 0.810 | 0.810 | 0.215 | 0.810 | 0.810 | 0.810 | 0.288 | 0.810 |
| A | B | C | |
|---|---|---|---|
| [N/mm] | 157,900 | 191.5 | 104 |
| [N/mm] | 9584 | 191.5 | |
| [N/mm] | 9584 | 1915 | |
| [-] | 0.32 | 6.58 | 0.3 |
| [-] | 0.32 | 6.43 | |
| [-] | 0.49 | 6.43 | |
| [N/mm] | 5930 | 4.23 | 40 |
| [N/mm] | 5930 | 365.1 | |
| [N/mm] | 3227 | 1248 |
| Laminate | Layer Sequence | |
|---|---|---|
| L1 | A/C/A | 0.1/0.8/0.1 |
| L2 | A/C/A/C/B/C/A/C/A | 0.1/0.1/0.1/0.1/0.2/0.1/0.1/0.1/0.1 |
| [N/mm] | 125,000 |
| [N/mm] | 7400 |
| [N/mm] | 7400 |
| [-] | 0.34 |
| [-] | 0.34 |
| [-] | 0.37 |
| [N/mm] | 4800 |
| [N/mm] | 4800 |
| [N/mm] | 2700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pluciński, P.; Jaśkowiec, J.; Wójtowicz, M. Three-Dimensional Bending Analysis of Multi-Layered Orthotropic Plates by Two-Dimensional Numerical Model. Materials 2021, 14, 6959. https://doi.org/10.3390/ma14226959
Pluciński P, Jaśkowiec J, Wójtowicz M. Three-Dimensional Bending Analysis of Multi-Layered Orthotropic Plates by Two-Dimensional Numerical Model. Materials. 2021; 14(22):6959. https://doi.org/10.3390/ma14226959
Chicago/Turabian StylePluciński, Piotr, Jan Jaśkowiec, and Maciej Wójtowicz. 2021. "Three-Dimensional Bending Analysis of Multi-Layered Orthotropic Plates by Two-Dimensional Numerical Model" Materials 14, no. 22: 6959. https://doi.org/10.3390/ma14226959
APA StylePluciński, P., Jaśkowiec, J., & Wójtowicz, M. (2021). Three-Dimensional Bending Analysis of Multi-Layered Orthotropic Plates by Two-Dimensional Numerical Model. Materials, 14(22), 6959. https://doi.org/10.3390/ma14226959






